Introduction

The brain is a complex network on multiple spatial and time scales. Neural assemblies such as local networks of neurons transiently linked by selective interactions are considered to be largely distributed and linked to form a network (Varela et al. 2001). For example, a single neuron in the vertebrate cortex may connect to more than ten thousands postsynaptic neurons via synapses in the forming of complex neural networks (Gerstner and Kistler 2002). Some experiments have shown that the brain can exhibit a small-world network (Bassett and Bullmore 2006). It supports both segregated and distributed information processing. Analysis of the different networks shows that the distribution of functional connections and the probability of finding a link versus distance are both scale-free. Moreover, it displays the small characteristic path length and the large clustering coefficient, which are the typical properties of small-world networks. Therefore, it is feasible to employ networks to investigate the complex phenomena of neural systems observed in the brain cortex.

Recently, much attention has been paid to the networks with variable random connectivity. Increasing the randomness of the network topology leads to an enhancement of temporal coherence and spatial synchronization of the neuronal networks (Zheng and Lu 2008; Sun et al. 2008; Gong et al. 2006; Kwon and Moon 2002). Effects of small-world connectivity on noise-induced spatial patterns in two-dimensional continuous neuronal networks have also been investigated in (Perc 2005a, 2007a). Spatiotemporal evolution and resonance dynamics of small-world networks have further been extended to other excitable systems (Perc 2007b, c, 2008; Perc et al. 2009). It was shown that the introduction of long range couplings can induce decoherence of otherwise coherent noise-induced spatial patterns in the network with regular connectivity. Effects of randomness on chaos and order of coupled logistic maps was considered in (Savi 2007). Stochastic and coherence resonance phenomena were already studied in one-dimensional networks with small-world connectivity (Gao et al. 2001). In both cases, it was reported that the introduction of shortcut links between randomly chosen sites can increase the global synchrony of the network. However, little attention has been paid to the explicit analysis of effects of the small-world connectivity on the noise-induced pattern formation and order in two-dimensional discrete neuronal networks.

Two-dimensional Rulkov map neuronal networks have been regarded as alternative models for investigating the complex dynamics of neuronal systems. It seems that the analysis of complex neurobiological networks is computationally efficient by means of a map neuron model. Dynamical behaviors of map neuron networks that interconnected by synaptic currents are very similar to those found with Hodgkin–Huxley models and in experiments (Rulkov et al. 2004). Spatial order out of noise has been extensively investigated and profound phenomena have been explored (Perc 2005b, c; Perc and Marhl 2005). Patterns and collective phenomena are studied in networks of nonhomogeneous oscillatory neurons and mixtures of oscillatory and excitable neurons, with dynamics of each neuron described by a two-dimensional (2D) Rulkov map neuron (Wang et al. 2007). It is shown that as the coupling strength is increased, typical patterns emerge spatially, which propagate through the networks in the form of beautiful target waves or parallel ones depending on the size of networks. The influence of diversity on the dynamics of spiking in spatially extended systems with global or diffusive couplings, which is locally modeled by a Rulkov map neuron, has been investigated and the enhancement of neuronal coherence by diversity can be shown in the coupled models (Chen et al. 2008). In the present paper, we will investigate the effects of the noise and small-world connectivity on pattern formation and order in two-dimensional discrete networks.

The rest is organized as follows. In section “Network of map neurons”, we introduce the network of map neurons. The spatiotemporal coherence resonance and firing synchronization of the given network are studied in section “Spatiotemporal coherence resonance and firing synchronization”. Finally, the conclusion is made in section “Conclusion”.

Network of map neurons

The dynamics of the Rulkov neuronal network with small-world connectivity and noises can be described by the following equations,

$$ \left\{ \begin{gathered} x^{(i,j)} (n + 1) = f(x^{(i,j)} (n),y^{(i,j)} (n)) + g\sum\limits_{kl} {\varepsilon_{ijkl} } (x^{(k,l)} (n) - x^{(i,j)} (n)) + \xi^{(i,j)} (n), \hfill \\ y^{(i,j)} (n + 1) = g(x^{(i,j)} (n),y^{(i,j)} (n)),\quad i,j = 1,2, \ldots ,N \hfill \\ \end{gathered} \right. $$
(1)

where

$$ f(x,y) = \frac{\alpha }{{1 + x^{2} }} + y, $$
$$ g\left( {x, y} \right) = y - \beta x - \delta , $$

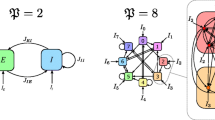
x (i,j)(n) is the membrane potential of the neuron labeled (i, j), and y (i,j)(n) is the variation of ion concentration. These represent the fast and slow dynamics, respectively. The slow evolution of y (i,j)(n) is due to the small values of the positive parameters β and δ. By choosing β = δ = 0.001 ≪ 1, we thus know that y (i,j)(n) changes slowly in comparison with x (i,j)(n). n is the discrete time series, while α are control parameters of the networks. Moreover, ξ (i,j) is additive spatiotemporal Gaussian noise with zero mean, white in space and time, and variance D 2 (García-Ojalvo and Sancho 1999), and D is noise level. The sum in Eq. (1) runs over all lattice sites, whereby ɛ ijkl  = 1 if the site (k, l) is coupled to (i, j), whilst otherwise ɛ ijkl  = 0. If the fraction of randomly introduced shortcuts, i.e. rewired links, p equals zero, ɛ ijkl  = 1 only if (k, l) indexes one of the four nearest neighbours of site (i, j). Thereby, we obtain a diffusively coupled regular spatial network of excitable units, whereby the coupling coefficient g equals the diffusion constant and periodic boundary conditions of the coupling are used such that the networks studied are spatially extended square lattices. In addition, the long-rang connections are introduced to investigate spatiotemporal dynamics of the neuronal networks. To do this, the existing links that form the basic square lattice will be cut and then rewired to some other neurons on top of the basic nearest-neighbor interactions. Namely, if p > 0, the corresponding fraction of links is randomly rewired, i.e. indexes k and l are shuffled for a given fraction p of randomly chosen sites (i, j), keeping ɛ ijkl  = 1 to form a spatial network with small-world connectivity, as described in (Perc 2007a, b, c; Watts and Strogatz 1998).

Nonlinear dynamics of an individual Rulkov map neuron, which depends on the control parameter α has been extensively investigated (Rulkov 2001). Results showed that when the parameter α is changed, the neuron exhibits rich firing behaviors, such as silent, periodic and/or chaotic spiking, spiking-bursting behaviors. For α < 2.0, the map exhibits a single excitable steady state. For α > 2.0, the excitable steady state loses its stability via a Hopf bifurcation, and then the neuron begins to oscillate. By setting α = 1.99, the system thus occupies the excitable steady state (x*, y*) = (−1, −1.995), which are also the initial conditions we will use in all subsequent calculations. In what follows, we investigate the firing synchronization and order behaviors in the network with small-world connection.

Spatiotemporal coherence resonance and firing synchronization

In this section, we study noise-induced temporal and spatial dynamics of the system. Initially, without randomly rewired links, that is, p = 0, characteristic snapshots of the spatial profile of x for three different noise levels D, are presented in the upper row of Fig. 1 to envision the spatial dynamics of the Rulkov map neuronal networks. By inspecting the spatial profiles in the upper row of Fig. 1, it is obvious that there indeed exist an intermediate value of D, at which the coherent pattern formation in the media is resonantly pronounced; yielding well-ordered circular waves in the spatial profile of x (see Fig. 1b1). On the other hand, smaller D is unable to excite the system strong enough to evoke any particular spatial dynamics in the media, whilst for larger D the pattern formation becomes disordered so that the spatial profile again lacks any visible structure or order. Furthermore, in order to capture the essence of spatiotemporal dynamics by presenting time traces of a firing rate function γ, which simply measures the fraction of spatial units that have values of variable x above a certain threshold x th = −0.1 at any given time t. It can be described as follows: suppose that m neurons fire at the given discrete time n, then we define a function \( \gamma = \frac{m}{{N^{2} }} \). Clearly, γ = 0 means that none of the spatial elements is perturbed strongly enough for x to exceed x th, whilst γ = 1 indicates that all spatial units are simultaneously in the excitable state, which constitutes global synchrony and thus corresponds to the most ordered temporal dynamics of the studied neuronal networks. Firing rate functions corresponding to the presented spatial profiles are shown in the bottom row of Fig. 1. It is shown that for D = 0.0018 the firing-rate function γ varies nearly period in time, indicating some extended of noise-induced spatial order in the system. In addition, its maximum value γ = 0.1093 indicates the fact that at most only 10.93 % of all spatial units can be simultaneously driven to the excitable state. When the noise intensity is increased to 0.0024, the number of firing neurons is increased and there are at most 20.06 % of all neurons driven to spike at some certain time.

Fig. 1
figure 1

Noise-induced spatiotemporal (bottom row) and spatial (upper row) dynamics in the exclusively diffusive coupled neuronal network (p = 0) for various noise levels: a 1 and a 2 D = 0.0013, b 1 and b 2 D = 0.0018, c 1 and c 2 D = 0.0024. Spatial profiles are depicted on a 128 × 128 square grid. Here g = 0.003

Full size image

To enable a quantitative analysis of the observed phenomenon outlined in Fig. 1, we calculate the structure function of the system according to the equation

$$ Q\left( {k_{x} ,k_{y} } \right) = < H^{2} \left( {k_{x} ,k_{y} } \right) > , $$
(2)

where H(k x , k y ) is the spatial Fourier transform of the x-field at a particular t and \( < \cdot > \) is the ensemble average over noise realizations. It is evident that space structure function Q can be interpreted as the space power spectrum of the system. The results from numerical simulations for different noise levels are presented in Fig. 2. The three depicted panels correspond to the same values of couple strength as used already in Fig. 1. From Fig. 2a, c, it can be observed nicely that for small and large noise levels the presented spectra show no particularly expressed spatial frequency. Only for intermediate levels of noise the spatial structure function develops several well-expressed circularly symmetric rings, indicating the existence of a preferred spatial frequency induced by additive Gaussian noise. As the noise level is increased, random fluctuations start to dominate the spatial dynamics and thus, similar as by small noise levels, the characteristic waterfall-like outlay of Q(k x , k y ) vanishes and no preferred spatial frequency can be inferred.

Fig. 2
figure 2

The spatial structure function of x (i,j) obtained for a D = 0.0013, b D = 0.0018, c D = 0.0024. Here g = 0.003, p = 0

Full size image

Moreover, we exploit the circular symmetry of the structure function by calculating the circular average of Q(k x , k y ) according to the equation

$$ q(k) = \int\limits_{{\Upomega_{k} }} {Q(\mathop k\limits^{ \to } )d\Upomega_{k} } , $$
(3)

where \( \overrightarrow {k} = (k_{x} ,k_{y} ) \) and Ω k is a circular shell of radius \( k = |\overrightarrow {k} | \). Figure 3 shows three q(k) obtained for the same values of p and D as used in Fig. 2. In accordance with results published recently [4], it can be observed that for p = 0 and D = 0.0018 there exists a particular spatial frequency, marked with the thin dashed line at k = k max, that is greatly enhanced for intermediate D. On the other hand, the fingerprint of spatial coherence reduces substantially for D = 0.0024 (note that the peak at k = k max it disappears completely). To quantify the ability of each D to extract the characteristic spatial frequency of the medium more precisely, we calculate the signal-to-noise ratio (SNR) as the peak height at k max normalized with the background fluctuations in the system; namely \( SNR = q(k_{\hbox{max} } )/\widetilde{q}, \) where \( \widetilde{q} = \frac{1}{2}\left[ {q\left( {k_{\hbox{max} } - \Updelta k_{a} } \right) + q\left( {k_{\hbox{max} } + \Updelta k_{b} } \right)} \right] \) is an approximation for the level of background fluctuations in the system, whereby Δk a and Δk b mark the estimated width of the peak around k max at the optimal D. This is the spatial counterpart of the measure frequently used for quantifying constructive effects of noise in the temporal domain of dynamical systems, whereas a similar measure for quantifying effects of noise on the spatial dynamics of spatially extended systems was also used in. Figure 4 shows how the SNR varies with D. It is evident that there exists an optimal level of additive Gaussian noise for which the peak of the circularly averaged structure function is best resolved, thus clearly indicating the existence of spatial coherence resonance in the square-lattice map neuronal network.

Fig. 3
figure 3

The circular averages of structure functions presented in Fig. 2. Here g = 0.003, p = 0

Full size image
Fig. 4
figure 4

The dependence of SNR on D. Here g = 0.003, p = 0

Full size image

Next, we analyze the noise-induced temporal and spatial dynamics of the system also for p > 0, that is, small-world coupled networks. We start the study by visually inspecting four characteristic spatial profiles of x obtained by various p at a near optimal D for noise-induced pattern formation in the studied excitable media. Results presented in Fig. 5 clearly show that increasing values of p hinder coherent pattern formation. Importantly, whilst spatial profiles obtained by p = 0 and p = 0.001 present compelling evidences of noise-induced self-organization in excitable neuronal networks and qualitatively differ only minutely, substantial spatial decoherence can be visually assessed already at p = 0.005. Thus if only 0.5 % of all links constituting the planar network are randomly rewired, spatiotemporal noisy perturbations are unable to induce coherent patterns in the neuronal networks. At p = 0.01, the spatial decoherence is pronounced even more profoundly, thus indicating the destructive nature of increasing values of p on the noise-induced spatial dynamics. Although the intermediate values of D are no longer able to induce coherent pattern formation in the spatial domain, there appears nearly perfect synchrony, i.e., temporal order, in the system, as shown in bottom row of Fig. 5. Similarly as by p = 0, γ varies periodically in time.

Fig. 5
figure 5

Noise-induced temporal (bottom row) and spatial (upper row) dynamics in a small-world diffusive coupled (D = 0.0018) media for various fractions p of randomly rewired links: a 1 and a 2 p = 0.0001, b 1 and b 2 p = 0.005, c 1 and c 2 p = 0.01. Spatial profiles are depicted on a 128 × 128 square grid. Here g = 0.003

Full size image

In what follows, we will quantify the temporal order in the media more precisely. We calculate the autocorrelation of the firing-rate function γ according to the equation \( C(\tau ) = \frac{{ < \widetilde{\gamma }(t)\widetilde{\gamma }(t + \tau ) > }}{{ < \widetilde{\gamma }^{2} > }},\quad \widetilde{\gamma } = \gamma - < \gamma > \). One can see from Fig. 5 that the correlations are indeed much more pronounced for the moderate fractions p of randomly rewired links. To describe this effect with a single quantity, the characteristic correlation time τ c can be evaluated by the formal equation \( \tau_{c} = \int_{0}^{\infty } {C^{2} (t){\text{d}}t} \) (Pikovsky and Kurths 1997). The curve of τ c versus p is displayed in Fig. 6 for g = 0.003, D = 0.0018. There is a clear peak in the curve, indicating the occurrence of clearly ordered temporal behavior. This shows that the system dynamics can exhibit somewhat resonant behavior with an optimal level of p.

Fig. 6
figure 6

Correlation time τ c versus fractions p of randomly rewired links for the Rulkov neuronal network with g = 0.003, D = 0.0018

Full size image

Conclusion

In summary, the effects of noise and the small-world connectivity on spatial unit are studied in Rulkov map neuronal networks. It is shown that collective behavior, such as various spatiotemporal patterns and firing synchronization can be observed in noisy environment. It is also found that noise can induce spatial coherence resonance in the diffusive neuronal network.

However, the small-world connectivity of spatial units facilitates global synchronization of excitatory events and thus temporal order in the system, whereas, on the other hand hinders coherent patter formation. The constructive effect of small-world connectivity on the temporal order is argued to originate from the effective shortening of typical path lengths between arbitrary spatial units, which facilitates information transduction among distant parts of the network, while the disordering effect on the spatial scale is attributed to the small-world networks that can effectively disrupts the internal spatial scale of the media already at small p.

For neural systems, it has been argued that excitable media guarantee robust signal propagation through the tissue in a substantially noisy environment (Izhikevich 2000). Results presented in this paper can be important guidance for understanding and controlling pathological types and evolution of waves in human brain.