Introduction

The rapid development of modern neuroscience have brought us enormously unprecedented knowledge about the brain and neural system, but the understanding of higher brain functions such as cognition, memory and communication, remains shallow partly due to the extremely structural and functional complexity of the brain. Faced with the observation of a large number of complex spatiotemporal dynamics in the brain, ranging from the microscopic to the macroscopic level, the conventional approach tends to find the direct correspondence between some specified areas and their functions. This approach could immediately facilitate the clinical application, but it is evidently restricted or incomplete, as spatiotemporal dynamics in neural systems could emerge over multiple scales of space and time. In contrast, another approach favors the investigation of the relationship between spatiotemporal dynamics and brain functions systematically using heuristic dynamical models. In the last few decades, the latter method has attracted attention and many dynamical models have been proposed and studied extensively, such as various network models of neurons (Hopfield 1982; Wilson and Cowan 1972; Tsuda et al. 1987; Skarda and Freeman 1987; Arbib 2003).

However, the object treated in the models proposed to date was a single brain, or a single neural network module. As well known, each brain is not merely an isolated existence in the world, but an open one that keeps communicating with ever-changing environment. Therefore, it is crucial to understand the neural mechanism of the interaction between multiple brains from experimental and theoretical aspects. Remarkably, the experimental discovery of mirror neurons in nonhuman primates (Rizzolatti and Craighero 2004; Arbib 2006), humans (Keysers and Gazzola 2010), and other species, including birds (Prather et al. 2008), suggests that mirror neurons are involved in mutual understanding (Keysers and Gazzola 2010). In particular, recent experiments using fMRI have shown synchronized firing phenomena in communicating subjects when a guesser observed the gesture of a gesture who is another individual (Schippers et al. 2010) and when a listener understood a story told by a speaker (Stephens et al. 2010). These findings provided the important implication that similar spatiotemporal dynamics could emerge in heterogeneous brains when two people understand each other. Thus, it is reasonable to assume that mutual understanding could be realized by a learning process that involves memory transmission between different brains. In order to verify the assumption theoretically, we try to construct a heuristic model by which a communicating process between two brains can be emulated. Before illustrating the model in detail, we first consider the following typical communication scenario.

Two individuals, here named agent A and agent B, are communicating. A is introducing new things to B, who has no prior knowledge about these things. Finally, agent B understands A.

In this case, the dynamics emerging in the brain of agent B would show a transitory character, such as a state transition from an “I do not know” state to an “I know” state, via learning. The problem resides in how to describe these dynamics, which are associated with the proceeding of adaptive learning. Remarkably, various experiments and theories have suggested that chaos is crucial for learning (Tsuda et al. 1987; Skarda and Freeman 1987; Tsuda 1991, 1992; Nara and Davis 1992; Sano 2000; Tsuda 2001; Kay 2003; Kozma and Freeman 2001; Raffone and van Leeuwen 2003), and recent studies on autonomous robots have shown that chaotic neural dynamics could be potentially useful to solve complex ill-posed problems via simple rule(s) (Li et al. 2007; Li and Nara 2008a, b; Yoshida et al. 2010; Li and Nara 2012). These studies implied that chaotic neural dynamics could play an important role in adaptively coping with the onset of uncertainty from the ever-changing environment. Thus, we have been interested in understanding the relation between chaotic neural dynamics and communication. In particular, Freeman’s experimental works showed that chaotic activity works as a novelty filter, namely an “I do not know” state. Interestingly, Sano showed that the interaction of two chaotic neural network modules can produce not only embedded memory representations, but also novel memories, and argued that those memory representations correspond to an “I know” state (Sano 2000). Therefore, we elaborated the following working hypotheses for the dynamics that emerge in the course of communication. First, valid information about introduced things is transmitted to B when A is retrieving a relevant memory, i.e., when attractor dynamics is emerging in the brain of A. Second, when B is in the “I do not know” state, chaotic dynamics is emerging in the brain of agent B because B has no prior knowledge about the thing. In particular, chaotic itinerancy can appear as the chaotic transitions among memories (Tsuda et al. 1987; Tsuda 1991, 1992, 2001). Third, when agent B understands such things, attractor dynamics similar to those of agent A should emerge in the brain of agent B because the memories in A about those things have been transmitted into the brain of agent B, which implicitly suggests that these dynamical processes include an additional learning in which the storing of new memories is required without the destruction of any old memories.

Based on these working hypotheses, we propose a preliminary idea to emulate the process of memory transmission via which two neural networks with different memories learn from each other through a communicating process between them. One important problem is how to choose a neural network model to implement this process. Obviously, the memory transmission in communicating actions is a dynamical process, thus, intermittent memory retrieval is required for the emulation of the process of memory transmission. In this respect, the nonequilibrium neural network model proposed by Tsuda et al. (1987) could be a good candidate because it is easy to produce a dynamical process of intermittent memory retrieval expressed by chaotic itinerancy (Tsuda 1991; Kaneko and Tsuda 2003). Previous studies of chaos in the nonequilibrium neural network suggest that cortical chaos may serve for dynamically linking true memories, as well as for memory search (Tsuda et al. 1987; Nara and Davis 1992). Furthermore, there exists an area of additional learning in parameter space (Tsuda 1992). Thus, to investigate the communicating process, we construct a model consisting of two nonequilibrium neural networks. Regarding learning, here we propose a learning algorithm called novelty-induced learning. The term “novelty-induced learning” implies that communicating individuals do not learn all incoming information but may prefer to learn new or novel information that concerns them. Many experimental findings related to this type of learning have been reported; for instance, novelty information enhances learning and the hippocampus is regarded as a novelty detector (Meeter et al. 2004; Jenkins et al. 2004; Yamaguchi et al. 2004; Bunzeck and Duzel 2006; Axmacher et al. 2010). In the present paper, we showed that computer experiments with novelty-induced learning assure the simultaneous processing of the maintenance of own memories and of the learning of new memories.

The organization of the paper is as follows. In the next section , a brief introduction to the nonequilibrium neural network model is provided. After that section, we describe the construction of a communicating model and of a novelty-induced learning process to implement memory transmission. In the subsequent section, the simulation results are presented. The final section is devoted to the summary of results and discussion.

Nonequilibrium neural networks

Network construction

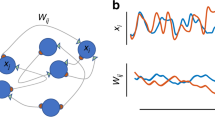
The nonequilibrium neural network model adopted here, which was based on the model proposed by Tsuda (1987, 1992), is shown in Fig. 1. The network consists of two kinds of probabilistic neurons: N pyramidal neurons (denoted by S) and N stellate neurons (denoted by R), which are the most important types of neurons in neocortical columns. All pyramidal neurons are supposed to form a fully interconnected recurrent neural network, whereas each stellate neuron is supposed to receive input from all pyramidal neurons and send output to only one corresponding pyramidal neuron. We assumed that memories are embedded in synaptic connections between pyramidal neurons. Each memory is an N-dimensional vector consisting of firing states of pyramidal neurons, each of which is encoded into two values: +1 (when firing) or −1 (when not firing). The state of each neuron has analog values, from −1.0 to +1.0. The neural dynamics of each neuron is defined as follows.

$$ S_{i}(t+1)=f^{p}\left(\sum_{j=1}^{N}W_{ij}S_{j}(t)+d_{i}R_{i}(t)-\delta_{i} \Upphi_{i} (t)\right), $$
(1)
$$ R_{i}(t+1)=f^{p}\left(\sum_{j=1}^{N}e_{j}S_{j}(t)\right), $$
(2)

where \(\Upphi (t)=x(t_1), t_1=max_{t>s}\{s|x(s)=x(s-1)\}\), where x(t) is given by

$$ x(t)=\sum_{j=1}^{N}W_{ij}S_{j}(t), $$

and δ i  = 1.0. The activation functions of pyramidal neurons S i and those of stellate neurons R i are independently determined by the following probabilistic law.

$$ y(t + 1) = f^{p} (z) = \left\{ {\begin{array}{*{20}c} {\tanh (\gamma z)} \hfill & {{\text{with}}\;{\text{probability }}p,} \hfill \\ {y(t)} \hfill & {{\text{with}}\;{\text{probability }}1 - p,} \hfill \\ \end{array} } \right. $$

where y denotes the activity of S or R, z represents each membrane potential, and the parameter γ describes the steepness of the function. The results of our simulation showed that larger γ values favor the production of dynamical associative process in the network. We have used γ = 10.

Fig. 1
figure 1

A nonequilibrium neural network model

Full size image

M memories are initially embedded in the network by the following well-known Hebbian algorithm,

$$ W_{ij}(0)=\sum_{\mu=1}^{M}\xi_{i}^{(\mu)}\xi_{j}^{(\mu)}, $$
(3)

where 1 ≤ i, j ≤ N and N-dimensional vector \({\varvec{\xi}}^{\mu}\) (1 ≤  μ ≤ M) denotes the μ-th memory of M embedded memories.

The synaptic connections from S i to R i are denoted by e i , which is supposed to stem from axon collaterals of pyramidal neurons. As the distribution of axon collaterals is random (Szentágothai 1975) and there are intervenient inhibitory neurons, such as basket cells, we assumed that the values of e i take a quasi-random numbers distributed uniformly over [ −α, α]. The synaptic connections d i from the R units to the S units are more specific, but are similarly assumed to take a quasi-random numbers distributed uniformly over [ −β, β], as a stellate cell establishes a synaptic contact with a basal dendrite of the pyramidal cell via spines, which exhibit variable distribution in their location on the pyramidal dendrite (Crick and Asanuma 1987), and via the intervenient inhibitory small basket cells (Szentágothai 1975).

In contrast with the typical Hopfield neural network, the nonequilibrium neural network includes two subsystems that can lead the system either to convergent dynamics or to divergent dynamics. First, recurrent connections W ij of pyramidal neurons S(t) enable the network to perform attractor dynamics, like a Hopfield network, whereas the presence of the feedback ϕ i (t) leads to the instability of the network. The feedback ϕ i (t) originates from the temporal states of pyramidal neurons and works only when pyramidal neurons reach a steady state, namely S(t) = S(t − 1), the two-step steady state form of which is not essential, and a k-step steady state may be applicable. Thus, the network shows a successive retrieval of embedded memories instead of a gradually converging dynamics. In previous work, Tsuda and his colleagues found a quasi-deterministic law at the level of a macro variable that suggests that the successive retrievals of embedded memories are not random dynamics but deterministic chaos, which can be called chaotic itinerancy (Tsuda et al. 1987, 1991, 1992, 2001; Kaneko and Tsuda 2003). Referring to the working hypotheses mentioned in Section “Introduction”, the nonequilibrium neural network is undoubtedly a model that is suitable for emulating communicating processes.

Dynamics measure: direction cosine

As evolutionary dynamics of the nonequilibrium neural network show a successive retrieval of embedded memories, a direction cosine is required as an appropriate dynamics measure and is defined as follows.

$$ D^{\mu}(t)=\frac{\user2{S}(t) \cdot \user2{\xi}^{\mu}} {\parallel \user2{S}(t)\parallel \times \parallel \user2{\xi}^{\mu}\parallel}, $$
(4)

where memories \(\{\user2{\xi}^{\mu}\} (1 \leq \mu \leq M)\) are equivalent to the coordinates of the state pattern \(\user2{S}(t)\) in the state space and D μ(t) is a temporal variable with values ranging from −1.0 to +1.0. When D μ(t) of \(\user2{S}(t)\) is −1.0 or +1.0, a memory or its negative pattern is retrieved. We identified these two patterns. By virtue of this measure, we were able to trace clearly the dynamical processes of the nonequilibrium neural network. An example is provided in Fig. 4a, where the number of embedded memories is M = 2 and each memory is represented by a specific color. Evolutionary dynamics exhibits a successive retrieval of embedded memories. These intermittent behaviors can provide the basis for a communication model, which is described in the next section.

Communication model

Construction and embedded memories

Communication has become one of the central topics in scientific research because of the rapid development of techniques that allow simultaneous measurements in different brains. Although many models have been proposed to interpret various communication behaviors, no neural-based model has been proposed to date. Here, a communication model consisting of two nonequilibrium neural networks was constructed and is shown in Fig. 2.

Fig. 2
figure 2

Communication model consisting of two nonequilibrium neural networks

Full size image

In this model, dynamical behaviors produced by two coupled nonequilibrium neural networks were adopted to emulate the complex dynamics emerging in communicating brains. The state patterns of the two networks at time t are denoted by \(\user2{S}_A(t)\) and \(\user2{S}_B(t)\), respectively.

According to Eq. 1, the neural dynamics of the state pattern \(\user2{S}_A(t)\) is defined by

$$ S_{A,i}(t+1)=f^{p}\left(\sum_{j=1}^{N}W_{A,ij}S_{A,j}(t)+d_{i}R_{A,i}(t)-\delta_{i} \Upphi_{A,i} (t)+\sigma_{A,i}(t)I_{A,i}(t)\right), $$
(5)
$$ R_{A,i}(t+1)=f^{p}\left(\sum_{j=1}^{N}e_{j}S_{A,j}(t)\right), $$
(6)
$$ I_{A,i}(t)=\sum_{j=1}^{N}C_{A,ij}S_{B,j}(t), $$
(7)

where \(\user2{C}_{A,ij}\) is the coupling strength from the j-th neuron in B to the i-th neuron in A. In terms of the coupling item in Eq. 5, σ A,i(t) is a temporal variable to enable the coupling from B to A to switch on/off intermittently. According to the above hypothesis that an effective message forms when a certain memory is retrieved, we assumed that the state of σ A,i (t) depends on whether or not the state pattern \(\user2{S}_B(t)\) reaches a steady state, so that σ A,i is defined by

$$ \sigma_{A,i}(t)= \left\{ \begin{array}{ll} 1& \hbox{if } \user2{S}_B(t)=\user2{S}_B(t-1),\\ 0 & \hbox{otherwise.} \end{array} \right. $$

Under this condition, our model can realize a dynamic, intermittent communication between agent A and B instead of conventional continued couplings. This enables us to emulate the communication scenario proposed above more objectively. Similar to Eq.5, we can define the neural dynamics of the state pattern \(\user2{S}_B(t)\)

$$ S_{B,i}(t+1)=f^{p}\left(\sum_{j=1}^{N}W_{B,ij}S_{B,j}(t)+d_{i}R_{B,i}(t)-\delta_{i} \Upphi_{B,i} (t)+\sigma_{B,i}(t)I_{B,i}(t)\right), $$
(8)
$$ R_{B,i}(t+1)=f^{p}\left(\sum_{j=1}^{N}e_{j}S_{B,j}(t)\right), $$
(9)
$$ I_{B,i}(t)=\sum_{j=1}^{N}C_{B,ij}S_{A,j}(t). \\ $$
(10)

Generally, communicating individuals always have different experiences and learning tends to occur only when messages from a sender are new for a receiver. Thus, it is reasonable to consider that they have different old memories at the beginning of communication and try to learn new information. In Eq. 3, different memories are embedded into the two networks. If we take \(\user2{\xi}_A^{(\mu)}\) as a column vector and \((\user2{\xi}_A^{(\mu)})^T\) as its transpose, the initial synaptic connections of the two networks are defined by:

$$ \user2{W}_{A}(0)=\sum_{\mu=1}^{M_A}\user2{\xi}_A^{(\mu)} \cdot (\user2{\xi}_{A}^{(\mu)})^T,\\ $$
(11)
$$ \user2{W}_{B}(0)=\sum_{\nu=1}^{M_B}\user2{\xi}_B^{(\nu)} \cdot (\user2{\xi}_{B}^{(\nu)})^T, $$
(12)

where M A and M B are the number of embedded memories in the two networks, respectively. As memories can be represented by vectors, their relations are naturally classified by uncorrelated or correlated vectors. First, we considered the special case in which they are uncorrelated, namely they are pairwise orthogonal.

For the sake of tracing the evolutionary dynamics of the two networks, we can calculate direction cosines of \(\user2{S}_A(t)\) and \(\user2{S}_B(t)\) using Eq. 4. In the communication model, we are concerned with not only old memories, but also new memories learned from the information sent by the counterpart through communication behaviors; thus, all memories embedded in the two networks are regarded as “coordinates”, which can be defined as follows.

$$ D_{A\leftarrow A}^{\mu}(t)=\frac{\user2{S}_A(t) \cdot \user2{\xi}_A^{\mu}}{\parallel \user2{S}_A(t)\parallel \times \parallel \user2{\xi}_A^{\xi}\parallel},\\ $$
(13)
$$ D_{A\leftarrow B}^{\nu}(t)=\frac{\user2{S}_A(t) \cdot \user2{\xi}_B^{\nu}}{\parallel \user2{S}_A(t)\parallel \times \parallel \user2{\xi}_B^{\nu}\parallel},\\ $$
(14)
$$ D_{B\leftarrow A}^{\mu}(t)=\frac{\user2{S}_B(t) \cdot \user2{\xi}_A^{\mu}}{\parallel \user2{S}_B(t)\parallel \times \parallel \user2{\xi}_A^{\xi}\parallel},\\ $$
(15)
$$ D_{B\leftarrow B}^{\nu}(t)=\frac{\user2{S}_B(t) \cdot \user2{\xi}_B^{\nu}}{\parallel \user2{S}_B(t)\parallel \times \parallel \user2{\xi}_B^{\nu}\parallel},\\ $$
(16)

where \(D_{A\leftarrow B}^{\nu}(t)\) means the direction cosine of \(\user2{S}_A\) with memory \(\user2{\xi}_B^{\nu}\) embedded in the network B. Similarly, \(D_{A\leftarrow A}^{\mu}(t), D_{B\leftarrow A}^{\mu}(t)\), and \(D_{B\leftarrow B}^{\nu}(t)\) are defined. To observe the dynamical process clearly, we represented these four types of dynamics measures in four different figures, where the evolution of the dynamics in one network is the combination of two figures. For example, the evolution of the dynamics of \(\user2{S}_A(t)\) consists of \(D_{A\leftarrow A}^{\mu}(t)\) and \(D_{A\leftarrow B}^{\nu}(t)\). For the memories shown in Fig. 3, in which these two networks do not communicate with each other, their evolution of the dynamics are represented in Fig. 4. Both the top two panels represent the evolution of the dynamics of \(\user2{S}_A(t)\). Due to no learning effect in this case, agent A and B are independent each other. Thus itinerant dynamics of memory retrieval only emerges in their own memories, as is shown in the top and bottom panels which represent \(D_{A\leftarrow A}^{\mu}(t)\) and \(D_{B\leftarrow B}^{\nu}(t)\), respectively. However, the middle two panels, which represent \(D_{A\leftarrow B}^{\nu}(t)\) and \(D_{B\leftarrow A}^{\mu}(t)\), show the learning effect from the communicating counterpart. In this case, neither A nor B retrieved any new memory because they do not learn each other.

Fig. 3
figure 3

Four pairwise orthogonal memories

Full size image
Fig. 4
figure 4

Dynamics measure of two nonequilibrium networks in the case in which they do not learn from each other, namely they are independent: (a) and (b) represent evolutionary dynamics of \(\user2{S}_A(t)\). \(D_{A\leftarrow A}^{\mu}(t)\) exhibits a successive memory retrieval, but \(D_{A\leftarrow B}^{\nu}(t)\) does not show any memory retrieval because A does not learn B. Different colors of lines correspond to different embedded memories: \(\user2{\xi}_A^{1}\)(red), \(\user2{\xi}_A^{2}\)(green), \(\user2{\xi}_B^{1}\)(blue), \(\user2{\xi}_B^{2}\)(violet). c and d Represent the evolutionary dynamics of \(\user2{S}_B(t)\). Similar results can be observed clearly. (Color figure online)

Full size image

Novelty-induced learning

Communication is not simply a process of retrieval of old memories; rather, it is a creative process that involves the coexistence of old and new memories. Many studies in the fields of sociology, psychology, and linguistics have suggested that communication behaviors are realized by a selective learning process. In psychology, selective learning is defined by the ability to select and learn particular items of higher value from a broader array of available information (Adler and Rodman 2009). This definition implies that one does not learn all available information, but only a particular part with higher value. Thus, one question arises: “What is this particular part with higher value in communication behaviors?” As is well known, novel information can often attract more attention and can be more easily remembered. Interestingly, several recent experiments from behavioral to molecular levels have shown that novel stimuli facilitate synaptic plasticity and learning (Gu 2002; Li et al. 2003; Otani et al. 2003). These results provide the important biological implication that a novelty detector must be activated in the neural system when a novel stimulus is presented. Thus, in the communication model, it is desirable that novelty be regarded as a signal that facilitates synaptic plasticity and learning.

In our communication model, novelty was introduced to implement the process of selective learning. Generally, the extent of the novelty of an incoming pattern can be estimated using a measure of the extent to which the pattern mismatches the memories, which can be calculated based on the Hamming distances between the incoming pattern and the memories. For a message sent by a sender at time τ, the message is denoted as one incoming pattern by \(\user2{S}^I(\tau)\). If we assume that the receiver has M memories \({\varvec{\eta}}^{\alpha} (1 \leq \alpha \leq M)\) at that time, the novelty measure H(τ) for the incoming pattern is defined by

$$H(\tau )\left\{ {\begin{array}{*{20}c} {0.0} \hfill & {{\text{if}}\;{\text{exists}}\;1.0 \in \{ F_{\alpha } (\tau )|1 \le \alpha \le M\} ,} \hfill \\ {1.0 - \min \left\{ {F_{\alpha } (\tau )|1 \le \alpha \le M} \right\}} \hfill & {{\text{otherwise,}}} \hfill \\ \end{array} } \right.$$
(17)

where

$$ F_{\alpha}(\tau)=\left|\frac{\user2{S}^I(\tau) \cdot {\varvec{\eta}}_{\alpha}}{\parallel \user2{S}^I(\tau)\parallel \times \parallel {\varvec{\eta}}_{\alpha}\parallel}\right|.\\ $$
(18)

Note that 0.0 ≤ H(τ) ≤ 1.0. Using the novelty measure H(τ), we replaced the Hebbian learning rule by the following modified one, which we termed novelty-induced learning.

$$ W_{ij}(t+1)=W_{ij}(t)+\Updelta W_{ij}(t),\\ $$
(19)
$$ \Updelta W_{ij}(t)=\epsilon S_{i}(t)S_{j}(t)H(t).\\ $$
(20)

When the incoming pattern is quite novel, the novelty measure H(t) gives a value approximating 1.0, so that the learning rate is nearly kept. Conversely, when the incoming pattern is not too novel, the novelty measure gives a value approximating 0.0, which can weaken the learning rate. In particular, when the incoming pattern \(\user2{S}^I(\tau)\) is the same as one of the receiver’s memories, there exists 1.0 in the set {F α(τ)|1 ≤ α ≤ M}. According to the definition of novelty, H(t) = 0.0 which means that the only thing the receiver needs to do is to retrieve the relevant memory and thus learning of the incoming pattern becomes unnecessary, then the learning process is terminated. Using this novelty-induced learning rule, a selective learning process can be implemented in our model.

Simulation and results

Using novelty-induced learning, an additional learning can be accomplished successfully without destroying all own memories. In the following subsections, we will present the simulation results.

Unidirectional and bidirectional memory transmission

Unidirectional memory transmission is a particular case of communication in which the learning process is implemented only in the receiver. Here, we take agent B as a receiver and agent A as a sender. The information only flows from agent A to agent B. In other words, the memories of agent B should be expanded, but his own memories should be kept unchanged. Specifically, when a steady state occurs in agent A, agent A sends the message to agent B. Then, the novelty of the message is measured using Eq. 17 so as to determine how much of the system B should learn from agent A. With the passing of time, once agent A has sent sufficient message to agent B, agent B can also retrieve memories that formerly belonged to agent A, which can be thought of as “understanding”. Figure 5 shows an example of this kind of unidirectional learning. A comparison of these results with those obtained without learning, shown in Fig. 4, indicates that new learned memories from agent A are itinerantly retrieved by agent B, as shown in Fig. 5c. Concomitantly, old memories in agent B are not destroyed and their retrieval is maintained, which is shown in Fig. 5d. Obviously, the new and old memories of agent B coexist to form successive retrievals after agent B has accomplished an additional learning successfully.

Fig. 5
figure 5

Dynamics measure of unidirectional learning when A is a sender and B is a receiver: (a) and (b) represent the evolutionary dynamics of \(\user2{S}_A(t)\). As A does not learn, only \(D_{A\leftarrow A}^{\mu}(t)\) shows successive memory retrieval. c and d Represent the evolutionary dynamics of \(\user2{S}_B(t)\). At the initial stage, only \(D_{B\leftarrow B}^{\nu}(t)\) exhibits successive memory retrieval but, finally, \(D_{B\leftarrow A}^{\mu}(t)\) also shows retrieval of new memories, which implies that B has learned from A. Different colors of lines correspond to different embedded memories: \(\user2{\xi}_A^{1}\)(red), \(\user2{\xi}_A^{2}\)(green), \(\user2{\xi}_B^{1}\)(blue), \(\user2{\xi}_B^{2}\)(violet). (Color figure online)

Full size image

Bidirectional memory transmission is essential for interpersonal communication because of the requirement of the exchange of information. Here, agent A or agent B may become either a sender or a receiver, depending on their states. Once a steady state occurs in one of the two agents, the agent is a sender and the other is a receiver. When agent A and B communicate with each other, novelty-induced learning is implemented in these two agents. Although they have different memories before communication, both agent A and agent B show successive retrieval of memories, including new ones, after learning. A bidirectional learning example is shown in Fig. 6, in which b and c show itinerant retrieval of new learned memories of agent A and agent B, respectively. In Fig. 6a and d, itinerant retrievals of their old memories are still going, which means that old memories are not yet destroyed by the formation of new memories.

Fig. 6
figure 6

Dynamics measure of bidirectional learning when A and B learn from each other: (a) and (b) represent the evolutionary dynamics of \(\user2{S}_A(t)\). c and d Represent the evolutionary dynamics of \(\user2{S}_B(t)\). At the initial stage, only \(D_{A\leftarrow A}^{\mu}(t)\) and \(D_{B\leftarrow B}^{\nu}(t)\) exhibits successive memory retrieval, but, finally, \(D_{A\leftarrow B}^{\nu}(t)\) and \(D_{B\leftarrow A}^{\mu}(t)\) also shows retrieval of new memories, which implies that and B have learned from each other. Different colors of lines correspond to different embedded memories: \(\user2{\xi}_A^{1}\)(red), \(\user2{\xi}_A^{2}\)(green), \(\user2{\xi}_B^{1}\)(blue), \(\user2{\xi}_B^{2}\)(violet). (Color figure online)

Full size image

Basin visiting measure

The above results show that novelty-induced learning enables the two networks not only to learn from each other, but also to maintain old memories. If we conceive the phase space as a memory landscape, memory transmissions result in the formation of a new landscape in which new and old memories can coexist. In the landscape, each memory can often be regarded as an attractor or, more precisely, as an attractor in a geometric sense with a basin in which any initial state will asymptotically converge to the attractor. The previous works of Tsuda and his colleagues indicate that chaotic itinerancy in nonequilibrium neural networks cannot be represented by such an attractor because dynamical behaviors in the network do not show a convergent process; rather, they exhibit an itinerant process among attractor ruins or quasi attractors (Tsuda 1991, 1992, 2001). Attractor ruins are defined in the theory of chaotic itinerancy proposed by Ikeda (1989), Kaneko (1990), Tsuda (1991). An attractor ruin is a weakly destabilized Milnor attractor (Milnor 1985), which can be a fixed point, a limit cycle, a torus or a strange attractor that possesses unstable directions. Dynamical orbits are attracted to a certain attractor ruin, but they leave via an unstable manifold after a short or long stay around it and move toward another attractor ruin. This successive chaotic transition continues unless a strong input is received. More detailed illustrations and examples can be found in (Kaneko and Tsuda 2003) and recent reports also suggested that chaotic transient dynamics can be generated in a chain of neurons with gap junction, and clear attractor ruins were shown via pioncáre map (Tsuda et al. 2004; Tadokoro et al. 2011). In this model, memory patterns perform as attractor ruins. As we observed a similar itinerant behavior among attractor ruins, we cannot simply evaluate the memory landscape. However, the dynamical trajectory in the phase space can be tracked when the network is evolving. Thus, we can calculate the visiting distributions of the trajectory to compare the changing memory landscape among different learning types.

For a long time T, we can obtain a trajectory that is a series of state patterns \(\{\user2{S}(t)\} (0 \leq t \leq T)\). Regarding the state pattern \(\user2{S}(t)\), we have to determine which basin it belongs to. Here, we propose a simple way to achieve this based on the definition of a geometric attractor. First, we assumed that each embedded memory is an attractor in N-dimensional phase space, which has a corresponding basin. At time t, the landscape of the phase space is determined by a weight matrix {W ij (t)}, i.e., attractor basins are arranged by {W ij (t)}. Second, the definition of a geometric attractor requires that all points that are sufficiently close to an attractor in the phase space are absorbed to the attractor; thus, if {W ij (t)} is extracted to reconstruct a typical Hopfield network with the same dimension, the landscape of the phase space at time t is kept in this new network. Third, in this situation, if \(\user2{S}(t)\) is taken as the initial state pattern of this new network, the development of the new network should asymptotically converge to the corresponding attractor. In this way, the basin to which each \(\user2{S}(t)\) belongs can be determined. Specifically, an attractor is denoted by \({\varvec{\psi}}_{\beta}\) and the corresponding basin, B β . If \(\user2{S}(t)\) asymptotically converges to \({\varvec{\psi}}_{\beta}\) as the new network evolves, it is recorded as:

$$ \rho_{\beta} (t)= \left\{ \begin{array}{ll} 1 &\hbox{if }\user2{S}(t) \in B_{\beta} ,\\ 0 & \hbox{otherwise}. \end{array} \right . $$

where \(\beta \in [1, M_{\hbox{A}}+M_{\hbox{B}}+2]\). Here, those basins corresponding to embedded memories of agents A and B are denoted by \(1 \leq \beta \leq M_{\hbox{A}}+M_{\hbox{B}}\), respectively. Two special cases are β = M A  + M B  + 1 and M A  + M B  + 2, where β = M A  + M B  + 1 corresponds to the case of formation of new attractor ruins defined by the state pattern that has reached convergence but did not converge into one of embedded memories within L max  = 500 steps, whereas β  = M A  + M B  + 2 is for the exceptional case of inability to reach convergence within L max  = 500 steps. When the network evolves for a long time T, we can measure the statistics of the distribution of the frequency of the visit in the basin of each attractor, which is called a basin visiting measure. If π β (t) is denoted as a basin visiting measure in the basin of memory \({\varvec{\psi}}_{\beta}\), it can be defined as follows.

$$ \pi_{\beta} =\frac{1}{T}\sum_{t}^T\rho_{\beta}(t). $$
(21)

Several examples of the basin visiting measure are shown in Fig. 7, where a and b illustrate the following case. When the systems A and B are independent, i.e., they do not learn from each other, the dynamical trajectory of \(\user2{S}_A(t)\) only passes through the basins of two embedded memories and visits those basins almost evenly. In a similar way, the dynamical trajectory of \(\user2{S}_B(t)\) also only passes through those basins. In contrast to these results, when novelty-induced learning is adopted, some interesting phenomena occur. Figure 7c and d depicts a case in which the dynamical trajectory of \(\user2{S}_B(t)\) has passed through not only their basins, but also the basins corresponding to embedded memories in system A when B learns system A. Furthermore, Fig. 7e and f shows that the dynamical trajectories of both \(\user2{S}_A(t)\) and \(\user2{S}_B(t)\) have passed through all the basins corresponding to all memories embedded in the two systems when A and B learn from each other. Interestingly, in novelty-induced learning, the number of new attractor ruins increases, despite that fact that attractors corresponding to embedded memories dominate. Intuitively, this suggests that the landscape of phase space has been changed extensively, so that new and old attractors can coexist. More implicitly, these new attractor ruins could be quite important to human communication because communicating behaviors is a creative process. As mentioned above, mutual understanding is the key purpose of communication, however, mutual understanding is not a merely copy between two agent’s memories but rather a creative reorganization among new and old information. These new attractor ruins are different from any of two agent’s embedded memories, thus it is reasonable that they are considered as creative memories.

Fig. 7
figure 7

Basin visiting measure of the dynamical trajectories of \(\user2{S}_A(t)\)(left) and \(\user2{S}_B(t)\) (right): the horizontal axis represents the basin number β (1 ≤ β ≤ 6), where number 5 is for the case of formation of new attractor ruins and number 6 is for the exceptional case of inability to reach convergence during \(L_{\hbox{max}}=500\) steps. The length of the steps used for evaluation is T = 10,000. (a) and (b) show a case without interactive learning. (c) and (d) show a case with unidirectional learning in which B learned from A. (e) and (f) show a case with bidirectional learning in which A and B learned from each other

Full size image

Nonorthogonal memories and critical overlap

In the biological sense, it is unrealistic to completely distinguish memory patterns because they are not strictly orthogonal in most situations. For example, information exchanged between two agents is usually correlated but is neither isolated nor independent. Thus, one question about the model arises: can the communication model work well in the case of two systems that have correlated memories? One can introduce a correlation of memory using the following simple method. The idea is to change the degree of overlap between memories, which is denoted by σ(0 ≤ σ ≤ N), where we assume σ = 0 when the embedded memories are mutually orthogonal. If σ is larger than 0, the embedded memories could become mutually nonorthogonal. With the increase of σ, the overlapped parts of embedded memories increase; thus, the value of σ can be used to measure memory correlation. In our simulation, we found that there is a critical overlapping σ = N C beyond which memory transmission cannot occur. We investigated the relation among the system size N, the number of memories M, and the critical overlapping N C . For each N and M, we used U randomly generated initial patterns for the determination of the critical overlapping N C . In our simulation, the system size was \(N \in\{32,64,128,256,512,1024,2048\}\) and the number of embedded memories was \(M \in\{1,2,3,4,5\}\). The mean and the standard deviation of critical overlapping N C over U = 100 trials were calculated and the results are shown in Fig. 8a. For a certain number of memories M, N C was almost directly proportional to the system size N. Furthermore, we used the ratio η C  = N C /N, which represents the proportion of the critical overlapping in relation to the system size. With the increase of the system size N, η C became saturated around 500 neurons, which is shown in Fig. 8b.

Fig. 8
figure 8

Critical overlapping distribution in the case of nonorthogonal memories: the abscissa of (a) and (b) represents the system size of the networks. The ordinate of (a) represents the critical overlapping N C of the number of neurons. The ordinate of (b) represents the critical ratio η C  = N C /N of the number of neurons

Full size image

However, Fig. 8 also shows that increasing the number of embedded memories causes a decline of the critical point of overlapping. This prompts the question of whether it will go to zero when the number of embedded memories goes to infinity. We successfully estimated the final critical ratio \(\eta_C^{\ast}\) by assuming that the critical ratio η C obeys an exponential distribution on the number of embedded memories M, which is derived by:

$$ \eta_C(M)=ae^{-bM}+c. $$
(22)

We used Eq. 22 to fit the critical ratios using a nonlinear optimization method (the Levenberg–Marquardt Method). The simulated and fitted data are shown in Fig. 9; we obtained the following parameter values: \(a= 1.030691910275422\ldots, b=0.919253449357962\ldots, c=0.070884349478589\ldots\). If c is zero, the critical number of neuron will tend to zero when the number of embedded memories is sufficiently large. However, the results did not show that case. Since we have taken statistical measure on many trials and obtained this deviation based on a quantitative approach, we can confirm that the deviation from zero is not random deviation due to noise. Thus, it is interesting to see a fact that c was not zero because it means that there is always a region in which overlapped memories can be utilized to implement this type of communication model successfully.

Fig. 9
figure 9

Critical point with respect to the number of embedded memories: with the increase of the number \(M (M=1,2,\cdots)\), the critical point ratio η C (M) decreases exponentially. The red circles with error bars indicate the mean <η C (M) > and standard deviation of simulated data. The curve with blue points was fitted using the Levenberg–Marquardt method. (Color figure online)

Full size image

Discussion and summary

This paper describes a communication model consisting of two heterogeneous nonequilibrium neural networks that communicate dynamically with each other. Using novelty-induced learning, mutual understanding was interpreted as a learning process involving memory transmission between communicating individuals. As mentioned above, the transition of cortical dynamics from “I do not know” to “I know” states must involve a process of reorganization or reconfiguration of the memory landscape, which could be illustrated by the distribution of the frequency of visit in different memory basins.

The present results include four important implications. First, mutual understanding could be accomplished by memory transmission between heterogeneous brains via transitory neural dynamics in the form of chaotic itinerancy. This is consistent with the results of several recent experimental reports on mirror neurons, which suggest that our brains are not only responsible for individual behaviors, but also replicate the behaviors of others (Rizzolatti and Craighero 2004; Arbib 2006). In particular, recent fMRI experiments have demonstrated the presence of synchronized firing phenomena in communicating subjects (Schippers et al. 2010; Stephens et al. 2010). This synchronous firing in communicating brains implies that mutual understanding involves memory transmission to produce similar dynamics in heterogeneous brains.

Second, the introduction of novelty-induced learning enables the successful implementation of memory transmission, which implies that the extent of the novelty of incoming signal/information strongly affects the efficiency of learning, such as motivation and intention. Remarkably, a large number of experimental reports in the field of neurophysiology have suggested that novel stimuli can effectively enhance learning and memory (Bunzeck and Duzel 2006; Jenkins et al. 2004; Nyberg 2005; Tulving et al. 1996; Ranganath and Rainer 2003). The novelty of external stimuli is an important factor that could determine what we should learn and how much we should learn. Many other experimental findings have indicated that the hippocampus is the detector of novelty and that many neurotransmitters play important roles in signaling the novelty of stimuli(Nyberg 2005).

Third, novelty-induced learning facilitates selective learning because the change of novelty brings about the intermittency of the learning process. The memory landscape changes gradually in the course of intermittent learning. Understanding may be achieved when the effect of learning is sufficient to form a new memory. This could provide a partial explanation for the fact that we often cannot repeat the words of others accurately after a conversation, although we can reproduce their meaning well.

Fourth, when novelty-induced learning is introduced into the model, several new attractor ruins are generated, which is shown in Fig. 7. In a certain sense, these new attractor ruins may have a crucial meaning because they suggest that novel memories, which are different from embedded memories, are generated during the process of communication. The purpose of communication is to obtain mutual understanding on the one hand and to inspire creative works on the other. On many occasions, the latter could be more important because of the requirement of cooperation. Undoubtedly, novel memories generated during communication may facilitate the generation of creative ideas. From this viewpoint, the present simple model provides additional possibilities regarding communication.

The present study provided only a basic concept to investigate the neural mechanism of communication in terms of complex and dynamical systems based on a dynamical viewpoint. Additional investigations using more realistic models will be performed in the near future.