Fast computation of polar harmonic transforms

Abstract

Polar harmonic transforms (PHTs) are orthogonal rotation invariant transforms that provide many numerically stable features. The kernel functions of PHTs consist of sinusoidal functions that are inherently computation intensive. We develop a fast approach for their computation using recursion and 8-way symmetry/anti-symmetry property of the kernel functions. The clustering of pixels at eight radially symmetrical locations enhances the speed of computation. Experimental results show that the proposed method is faster by a factor lying between three and four compared to the existing fast method.

1 Introduction

Region-based image descriptors capture the global properties of the pixel distribution in the entire image, and hence they are extensively used in many pattern recognition and computer vision applications. Rotation invariant pattern representation is an essential requirement because images that are rotated versions of each other perceived to be the same by human beings. Therefore, the pattern recognition systems should mimic the human perception by presenting methods that handle rotation, change in size and location. Rotation invariant moments and transforms are such processes, which successfully deal with these situations. There are two types of rotation invariant moments and transforms: orthogonal and non orthogonal. The orthogonal rotation invariant moments (ORIMs) and orthogonal rotation invariant transforms (ORITs) are more effective in performance because they have minimum information redundancy and hence better information compactness. A few low order moments and transforms are sufficient to capture the essential features of an image. Among the ORIMs Zernike moments (ZMs), pseudo Zernike moments (PZMs) and orthogonal Fourier Mellin moments (OFMMs) [1, 2] are the most popular. The ORITs that were introduced recently by Yap et al. [3] include the polar complex exponential transforms (PCET), polar cosine transforms (PCT) and polar sine transforms (PST). These transforms are collectively known as PHTs. The difference between ORIMs and ORITs is that the radial parts of the kernel functions in ORIMs are polynomials and in ORITs these are sinusoidal functions. The PHTs are preferred to ORIMs because PHTs are computationally very fast [4] and the high order transforms are numerically stable, where as the ORIMs are less efficient and high order moments are numerically unstable. Because of their attractive features, PHTs have recently been used in many image processing applications. Liu et al. [5] observed that PHTs-based features yield results comparable to state-of-the-art methods for fingerprint classification. An extensive evaluation of invariance property of PHTs for image representation in terms of rotation, scale and noise has been conducted by Li et al. [6]. The authors observed that the ORITs are more suitable than ORIMs for applications, which require many features. The results are compared with ZMs and PZMs, and it is observed that the performance of PHTs is better than that of ZMs and PZMs. Recently, Miao, et al. [7] have applied PHTs on Radon images for object recognition. They have also compared their results with that obtained by ZMs, OFFMs and Radial Fourier Mellin moments. Through the theoretical analysis and experimental results, it is observed that the performance of PHTs for image description is much better than the three moments especially under noisy conditions. Hoang and Tabbone [8] introduce a class of harmonic radial kernels that satisfy orthogonality conditions and derive PCET as a special case. Experimental results prove the effectiveness of this class of transforms for the description performance and pattern recognition ability. Singh et al. [9] perform the image reconstruction analysis of PHTs and show that PCET provide much better reconstructed images than ORIMs and other types of PHTs.

In this paper, we propose a method for the fast computation of the PHTs by developing recursive relations for the radial and angular parts of the kernel functions of the transform. An 8-way symmetry/anti-symmetry property is used to enhance the speed of the algorithm. The clustering of pixels at eight radially symmetric location’s results in a fast algorithm. These algorithms can be used for invariant pattern and shape recognition problems in real-time environment or on devices with low computation power.

The rest of the paper is organized as follows. An overview of PHTs with their discrete computational framework is presented in Sect. 2. The fast recursive relations, 8-way symmetry/anti-symmetry, and clustering of image pixels are discussed in Sect. 3. The speed performance experimental results are given in Sect. 4. Conclusion is discussed in Sect. 5.

2 Polar harmonic transforms

Polar harmonic transforms consist of the polar complex exponential transform (PCET), PCT and PST [3]. They have identical mathematical representation with a difference in the radial part of the kernel function. Let $f(r,\theta )$ be a continuous image function defined on a unit disk $D = \{ (r,\theta )\,0 \le r \le 1,\,\,0 \le \theta \le 2\pi \}$. The PHTs of order n and repetition m are defined by

$$ A_{nm} = \lambda \int\limits_{0}^{2\pi } { \, \int\limits_{0}^{1} {f(r,\theta ) \, } V_{nm}^{*} (r,\theta ) \, r{\text{d}}r{\text{d}}\theta } $$

(1)

where n, m = 0, ±1, ±2,.... The kernel function $V_{nm}^{*} (r,\theta )$ is the complex conjugate of the function $V_{nm} (r,\theta )$ determined by

$$ V_{nm} (r,\theta ) = R_{n} (r)e^{jm\theta } $$

(2)

with $j = \sqrt { - 1}$. The radial part of the kernel function and the parameter $\lambda$ are expressed as

$$ {\text{PCET}}:R_{n} (r) = e^{{j2\pi nr^{2} }} , \, \,\lambda = \frac{1}{\pi } $$

(3)

$$ {\text{PCT}}\,{\text{and PST}}:R_{n} (r) = \left\{ \begin{gathered} \cos (\pi nr^{2} ),\quad {\text{for}}\,{\text{PCT}} \hfill \\ \sin (\pi nr^{2} ),\quad {\text{for}}\,{\text{PST}} \hfill \\ \end{gathered} \right. $$

(4)

$$ \lambda = \left\{ \begin{gathered} \frac{1}{\pi },\quad n = 0 \hfill \\ \frac{2}{\pi },\quad n \ne 0 \hfill \\ \end{gathered} \right. $$

(5)

The radial part of the kernel function satisfies the orthogonality condition

$$ \int\limits_{0}^{1} {R_{n} (r)\left[ {R_{n'} (r)} \right]^{*} rdr = \frac{1}{2}\delta_{nn'} } $$

(6)

where $\delta_{nn'} = 1$ if $n = n'$, and 0 otherwise.

Also, the complete kernel function $V_{nm} (r,\theta )$ satisfies the orthogonality condition

$$ \int\limits_{0}^{2\pi } { \, \int\limits_{0}^{1} {V_{nm} (r,\theta )\left[ {V_{n'm'} (r,\theta )} \right]^{*} r{\text{d}}r{\text{d}}\theta } = } \pi \delta_{nn'} \delta_{mm'} $$

(7)

The orthogonality property of the kernel function enables the image function $f(r,\theta )$ to be reconstructed

$$ \hat{f}(r,\theta ) = \sum\limits_{{n = - n_{\max } }}^{{n_{\max } }} {\sum\limits_{{m = - m_{\max } }}^{{m_{\max } }} {A_{nm} V_{nm} (r,\theta )} } $$

(8)

where $n_{\max }$ and $m_{\max }$ are the highest allowed values of n and m, respectively. Greater number of transform coefficients used in the reconstruction helps $\hat{f}(r,\theta )$ to be closer to $f(r,\theta )$.

The magnitude of transform coefficients is rotation invariant. Let $A_{nm}^{\alpha }$ be the transform coefficients of the image function $f(r,\,\theta + \alpha )$ obtained by rotating an image by an angle $\alpha$ about its center, then it can be shown that

$$ A_{nm}^{\alpha } = A_{nm} e^{ - jm\alpha } $$

(9)

Thus, yielding a very important property of rotation invariance of its magnitude, namely, $\left| {A_{nm}^{\alpha } } \right| = \left| {A_{nm} } \right|.$

Deriving PHTs using Eq. (1) is difficult because in digital image processing, the image function $f(r,\theta )$ is discrete, and defined in rectangular coordinates system. Let N × N be an image with (i, k) representing a pixel at the ith row and jth column. We perform a mapping of pixel’s grid from N × N square domain to [−1,1] × [−1,1] with the help of the following transformations

$$ x_{i} = \frac{2i + 1 - N}{N},y_{k} = \frac{2k + 1 - N}{N},i,k = 0,1, \ldots ,N - 1 $$

(10)

with $\Updelta x = \Updelta y = \frac{2}{N}$

The unit continuous disk $D = \{ f(r,\theta )\,0 \le r \le 1,\,0 \le \theta \le 2\pi \}$ is now approximated by a unit digital disk $D' = \{ f(i,k),\,x_{i}^{2} + y_{k}^{2} \le 1\} .$ The mapping process allows only those pixels to belong to D′ whose centers $(x_{i} ,\,y_{k} )$ lie within the unit disk D′. This approximation is depicted in Fig. 1a and b, where Fig. 1a is an 8 × 8 pixels grid and the continuous unit disk D and Fig. 1b represents the approximated unit disk D′ and the pixels whose centers lie within the unit disk D′ are shaded with gray color. Thus, Eq. (1) for the computation of PHTs assume the form

Fig. 1

a An 8 × 8 pixel grid and the continuous inscribed circle D, and b the approximation of the circle D′

$$ \begin{aligned} A_{nm} =\, & \lambda \int\limits_{x = - 1}^{1} {\int\limits_{y = - 1}^{1} {f(x,y)V_{nm}^{*} (x,y){\text{d}}x{\text{d}}y} } \\ & x_{i}^{2} + y_{k}^{2} \le 1 \\ \end{aligned} $$

(11)

where $r = \sqrt {x^{2} + y^{2} }$ and $\theta = \tan^{ - 1} (y/x),$ and $V_{nm}^{*} (x,y)$ derives from Eq. (2) with the change of coordinates from polar system to Cartesian system.

The image function $f(x,y)$ is discrete. Assuming that the function value $f(x,y) = f(i,k)$ is constant over a pixel grid $\left[ {x_{i} - \frac{\Updelta x}{2},\,y_{k} - \frac{\Updelta y}{2}} \right] \times \left[ {x_{i} + \frac{\Updelta x}{2},y_{k} + \frac{\Updelta y}{2}} \right]$, then Eq. (11) can be approximated by

$$ A_{nm} = \lambda \sum\limits_{i = 0}^{N - 1} {\sum\limits_{{\mathop {k = 0}\limits_{{x_{i}^{2} + y_{k}^{2} \le 1}} }}^{N - 1} {f(i,k)} \int\limits_{{x_{i} - \frac{\Updelta x}{2}}}^{{x_{i} + \frac{\Updelta x}{2}}} { \, \int\limits_{{y_{k} - \frac{\Updelta y}{2}}}^{{y_{k} + \frac{\Updelta y}{2}}} {V_{nm}^{*} (x,y){\text{d}}x{\text{d}}y} } } $$

(12)

No analytical solution exists for double integration involved in the right hand side of Eq. (12), therefore, normally a zeroth order approximation is used [3].

$$ A_{nm} = \frac{4\lambda }{{N^{2} }}\sum\limits_{i = 0}^{N - 1} {\sum\limits_{\mathop{k = 0}\limits_{x_{i}^{2} + y_{k}^{2} \le 1 } }^{N - 1} {f(i,k)V_{nm}^{*} (x_{i} ,y_{k} )} } $$

(13)

Alternatively, PHTs can be computed in polar coordinates as suggested by [10, 11] for ORIMs such as the ZMs, PZMs and OFMMs. However, like ORIMs, computation of PHTs in polar coordinates requires reconfiguration of image pixels in polar coordinates. This process involves interpolation error because the pixel intensities are required to be determined at new locations [10, 11]. Therefore, normally PHTs are computed using Eq. (13) as explained in [3].

3 Fast computations of kernel functions

An attractive characteristic of PHTs is their low computation requirement of kernel functions as compared to ORIMs whose kernel functions are computation intensive because of the presence of high order of polynomials and factorial terms. Nevertheless, the kernel functions of PHTs comprise the sinusoidal functions. The computation cost of these functions is still high. In a recent paper by Yang et al. [4], 8-way symmetry/anti-symmetry is used for the calculation of the radial and angular sinusoidal functions, which increases the computation speed by a factor of six to eight. The time taken for the evaluation of trigonometric functions is very high. Thus, the computation of sinusoidal functions even in an octant of an image is time consuming. The high time requirement is gauged from the fact that the evaluation of cosine and sine functions of an image of size $N\, \times \,N$ pixels (with $N\, = {\text{ even}}$) is required to be computed at $N(N + 2)/8$ locations over an octant and if the maximum order and repetition are n _max and m _max, respectively, then the time complexity is O(N ² n _max m _max) which is very high. This time complexity cannot be reduced even after saving these values in tables. We propose recursive algorithms for the calculation of trigonometric functions for the radial and angular parts of the kernel functions. It is shown that while the angular part does not involve the computation of trigonometric functions through inbuilt library functions even for once, the radial part requires their evaluation only once at a pixel location and the higher order trigonometric functions are computed recursively. The proposed method is similar to the recursive approach adopted for angular functions for the calculation of ZMs by Singh and Walia [12].

3.1 Computation of angular functions

The angular functions $e^{jm\theta } = \cos (m\theta ) + j\sin (m\theta )$ can be computed efficiently for $m = 0,1,2, \ldots ,m_{\max }$ at a pixel location (i, k). For this purpose, we use the following recurrence relations to evaluate $\cos (m\theta )\;{\text{and}}\;\sin (m\theta ) .$

$$ \cos ((m + 1)\theta ) = \cos (\theta )\,\cos (m\theta ) - \sin (\theta )\,\sin (m\theta ) $$

(14)

$$ \sin ((m + 1)\theta ) = \sin (\theta )\,\cos (m\theta ) + \cos (\theta )\,\sin (m\theta ) $$

(15)

where $m = 0,1,2, \ldots ,m_{\max } ,\,r = \sqrt {x_{i}^{2} + y_{k}^{2} } ,\,\cos (\theta ) = x_{i} /r,\,\sin (\theta ) = y_{k} /r,\,\,x_{i} {\text{ and }}y_{k}$ are given in Eq. (10), and $\cos (0) = 1.0\,{\text{ and}}\, \, \sin (0) = 0.0.$ We use two tables, say, cos_theta[m _max + 1] and sin_theta[m _max + 1] , to save the values in memory. The extra space required for saving the tables is $2(m_{\max } + 1)$ words. We compute $\cos (m\theta )$ directly using library function and through recursion for $m = 15{\text{ and }}40$, and $\theta = \pi /8,\,\pi /7,\pi /6,\pi /3,{\text{ and }}\pi /2.$ The computation is performed in Microsoft’s Visual C ++6.0 under Windows environment with double precision arithmetic, which provides accuracy up to 15 decimal places. The results are quoted in Table 1 and show that the error accumulated during recursion is negligible. The differences in results are very small, which are of the order between $10^{ - 15} {\text{ and }}10^{ - 16}$ and consistent with the finite precision arithmetic being used.

Table 1 Comparison of values of $\cos (m\theta )$ computed directly using library function and using recursion, Eqs. (14) and (15)

3.2 Computation of radial functions

We now focus toward the computation of radial function of PCET. The calculation for PCT and PST follows the similar steps. The radial functions $e^{{j\,2\pi nr^{2} }} = \,\cos (2\pi nr^{2} ) + j\,\,\sin (2\pi nr^{2} )$ can be computed recursively for different orders n. For the order $n = 1$, the computation of $\cos (2\pi r^{2} )$ and $\sin (2\pi r^{2} )$ is performed directly using the library functions. For orders $n > 1$, Eqs. (16) and (17) are used to compute $\cos (2\pi nr^{2} )$ and $\sin (2\pi nr^{2} )$ recursively.

$$ \cos (2\pi r^{2} (n + 1)) = \cos (2\pi r^{2} )\,\cos (2\pi r^{2} n) - \sin (2\pi r^{2} )\,\sin (2\pi r^{2} n) $$

(16)

$$ \sin (2\pi r^{2} (n + 1)) = \sin (2\pi r^{2} )\,\cos (2\pi r^{2} n) + \cos (2\pi r^{2} )\,\sin (2\pi r^{2} n) $$

(17)

where $n = 1,2,3, \ldots ,n_{\max }$

3.3 Eight way symmetry/anti-symmetry of radial and angular functions

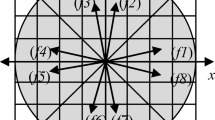
The radial functions $e^{{j2\pi nr^{2} }}$ of PCET assume the same values at 8-radially symmetric locations denoted by $P_{1}$ through $P_{8}$ within a circle as shown in Fig. 2. Let the center of the circle be at origin (0,0) with the digital radius R = N/2. Let a pixel $P_{1} (i,k),\;i = 0,1,2, \ldots ,R - 1;\;k = 0,1,2, \ldots ,i$ be given in the first octant of the circle with the coordinates of its center (the center of (i,=k) pixel grid) $x_{i} = (2i + 1)/N,\;\,y_{k} = (2k + 1)/N$, mapped within the unit disk, then $r = \sqrt {x_{i}^{2} + y_{k}^{2} }.$ The seven other pixels located at radially symmetric locations P ₂ through $P_{8}$ are given by$P_{2} (k,i),\,\;P_{3} ( - k - 1,\,i),\,\;P_{4} ( - i - 1,k),\,\;P_{5} ( - i - 1,\, - k - 1),\,\;P_{6} ( - k - 1, - i - 1),\,\;P_{7} (k, - i - 1),\;{\text{and}}\;P_{8} (i, - k - 1) .$ It can be easily verified that the centers of these pixel grids have the same values of r. Since we are referring the pixels w.r.t. the center of the digital image assumed to be at (0,0), we have negative indices while referring them. In actual implementation, we add R with each pixel location. For example, the pixel $P_{1} (i,k)$ will be referred to as $P_{1} (R + i,R + k),$ $i = 0,1,2, \ldots ,R - 1,\,k = 0,1,2, \ldots ,i,$ meaning thereby that the origin of the image is at the top left corner of the square domain. When $k = i$, 4-way symmetry is considered instead of 8-way symmetry because of the digital nature of the circle. Moreover, in the above discussion, we have assumed N to be even. However, the treatment is the same for odd N except for a pixel at the center of the image for which the computation is performed separately. Also for odd N, 4-way symmetry exists for $k = 0$ (along axes) and $k = i$ (along diagonals).

Fig. 2

8-way symmetry of a pixel $P_{1} (i,k)$ with $x_{i} = (2i + 1)/N, \, y_{k} = (2k + 1)/N.$ The origin of the coordinate system is at the center of the image

Further, if the pixel (i, k) makes an angle $\theta$ with x-axis with $\theta = \tan^{ - 1} (y_{k} /x_{i} )$, than the seven radially symmetric pixels P ₂ through P ₈ will make angles $\frac{\pi }{2} - \theta ,\,\,\frac{\pi }{2} + \theta ,\,\,\pi - \theta ,\,\,\pi + \theta ,\,\,\frac{3\pi }{2} - \theta ,\,\,\frac{3\pi }{2} + \theta ,\,\,{\text{and}}\,\,2\pi - \theta ,$ respectively. Therefore, if $\cos (m\theta )$ and $\sin (m\theta )$ are evaluated at P ₁, then their values can be used for locations P ₂ through P ₈ as shown in Tables 2 and 3. This situation is further explained in Sect. 3.4. The symmetry/anti-symmetry property reduces the requirement of performing the calculations from $N^{2}$ locations to $N(N + 2)/8$ locations.

Table 2 Values of $\cos (m\theta )$ at eight symmetric/anti-symmetric locations $P_{1}$ through $P_{8} .$

Table 3 Values of $\sin (m\theta )$ at eight symmetric/anti-symmetric locations $P_{1}$ through $P_{8}$

3.4 Clustering of image pixels

Significant enhancement in speed can be achieved by clustering the eight symmetrically located pixels. The clustering of pixels is achieved using 8-way symmetry/anti-symmetry property of radial and angular parts of kernel functions, explained by rewriting Eq. (13) in the form

$$ A_{{nm}} = \frac{{4\lambda }}{{N^{2} }}\sum\limits_{{i = 0}}^{{N - 1}} {\sum\limits_{\begin{subarray}{l} k = 0 \\ x_{i}^{2} + y_{k}^{2} \le 1 \end{subarray} }^{{N - 1}} {f(i,k)\left[ \begin{gathered} \{ \cos (2\pi nr_{{ik}}^{2} )\cos (m\theta _{{ik}} ) - \sin (2\pi nr_{{ik}}^{2} )\sin (m\theta _{{ik}} )\} - \hfill \\ j\{ \sin (2\pi nr_{{ik}}^{2} )\cos (m\theta _{{ik}} ) + \cos (2\pi nr_{{ik}}^{2} )\sin (m\theta _{{ik}} )\} \hfill \\ \end{gathered} \right]} } $$

(18)

where $r_{ik}^{2} = \sqrt {x_{i}^{2} + y_{k}^{2} } ,\,\,\theta_{ik} = \tan^{ - 1} (y_{k} /x_{i} ).$ The 8-way symmetry/anti-symmetry property leads Eq. (18) to

$$ A_{nm} = \frac{4\lambda }{{N^{2} }}\sum\limits_{i = 0}^{R - 1} {\sum\limits_{k = 0}^{i} {\left[ \begin{gathered} \left\{ \left(\sum\limits_{u = 1}^{8} {f_{u} } \cos (\theta_{u} )\right)\cos (2\pi nr_{ik}^{2}) - \left(\sum\limits_{u = 1}^{8} {f_{u} } \sin (\theta_{u} )\right)\sin (2\pi nr_{ik}^{2} )\right\} - \hfill \\ j\left\{ \left(\sum\limits_{u = 1}^{8} {f_{u} } \cos (\theta_{u} )\right)\sin (2\pi nr_{ik}^{2} ) + \left(\sum\limits_{u = 1}^{8} {f_{u} \sin (\theta )_{u} } \right)\cos (2\pi nr_{ik}^{2} )\right\} \hfill \\ \end{gathered} \right]} } $$

(19)

where $\begin{gathered} f_{1} = f(R + i,\,R + k),\,f_{2} = f(R + k,\,R + i),\, \ldots ,\,f_{8} = f(R + i,R - k - 1),\theta_{1} = m\theta_{ik} ,\,\theta_{2} = m(\frac{\pi }{2} - \theta_{ik} ), \ldots , \hfill \\ \theta_{8} = m(2\pi - \theta_{ik} ),x_{i} = (2i + 1)/N,\,y_{k} = (2k + 1)/N. \hfill \\ \end{gathered}$ After simplification, Eq. (19) becomes

$$ A_{nm} = \frac{4\lambda }{{N^{2} }}\sum\limits_{i = 0}^{R - 1} {\sum\limits_{k = 0}^{i} {\left[ \begin{gathered} [\{ F_{1} \cos (m\theta_{ik} ) + F_{2} \sin (m\theta_{ik} )\} \cos (2\pi nr_{ik}^{2} ) - \{ F_{3} \cos (m\theta_{ik} ) + F_{4} \sin (m\theta_{ik} )\} \sin (2\pi nr_{ik}^{2} )] - \hfill j[\{ F_{1} \cos (m\theta_{ik} ) + F_{2} \sin (m\theta_{ik} )\} \sin (2\pi r_{ik}^{2} ) + \{ F_{3} \cos (m\theta_{ik} ) + F_{4} \sin (m\theta_{ik} )\} \cos (2\pi nr_{ik}^{2} )] \hfill \\ \end{gathered} \right]} } $$

(20)

The trigonometric functions $\cos (\theta_{u} )$ and $\sin (\theta_{u} ),\quad u = 1,\,2,\, \ldots ,\,8$ are converted to $\cos (m\theta_{ik} )$ and $\sin (m\theta_{ik} )$ for various values of m according to Tables 2 and 3, respectively. The pixels are clustered in blocks represented by $F_{1} ,\,\,F_{2} ,\,\,F_{3} \quad {\text{and}}\quad F_{4}$ expressed in pixel values $f_{1}$ through $f_{8}$ as given in Table 4. Corresponding to each pixel location in an octant there are N(N + 2)/8 blocks. When k = i there is a 4-way symmetry (along diagonals of the square image), which can be treated separately or this case can be solved using Eq. (20) itself by letting $f_{2} = f_{4} = f_{6} = f_{8} = 0.$

Table 4 Clustering of image pixels of 8-radially symmetrical locations

4 Experimental results

We analyze the results by implementing three algorithms. The first algorithm implements the traditional algorithm of PHTs. The second algorithm uses the 8-way symmetry/anti-symmetry properties of the radial and angular functions [4]. The third algorithm, proposed in this paper, uses recursion for the kernel functions and clusters the image pixels and uses the symmetry/anti-symmetry properties. These algorithms are called algorithm A, B, and C, respectively. Clearly algorithm C will provide the improvement in speed performance over the existing fast method, represented by the algorithm B. These algorithms are implemented in Visual C ++ 6.0 under Microsoft Windows environment on a PC with 3.0 GHz CPU and 2 GB RAM. Since the CPU elapse time depends on the size of the image N, not on image contents, we do not mention any particular image in our experimental results. Further, the kernel functions of PCET, PCT and PST have similar forms; the results are presented for PCET only. The qualitative trend of CPU elapse time will be the same for PCTs and PSTs.

The growth of the CPU elapse time for the transform order $n$ and repetition $m$ is shown in Fig. 3a and b for N = 256. Figure 3a depicts CPU elapse time for the three algorithms. To highlight differences in CPU elapse time between Algorithm B and Algorithm C, Fig. 3b is used. The results show that the proposed algorithm reduces the CPU elapse time for all orders. The quantitative values of the CPU time are given in Table 5. The proposed algorithm is faster by a factor of three to four which is evident from the table. This is a significant improvement over the 8-way symmetry/anti-symmetry property represented by Algorithm B. To show the variation of the CPU elapse time w.r.t the size of the image, we consider various values of N ranging from 64 through 512. The results are shown in Fig. 4a and b, where Fig. 4a depicts the CPU elapse time for all three algorithms and Fig. 4b highlights the difference between Algorithm B and Algorithm C. The proposed method is much faster than the existing fast method.

Fig. 3

CPU elapse time (s) for the computation of PCETs for image resolution 256 × 256 pixels and various orders and repetitions of transforms from n _max = m _max = 2 through n _max = m _max = 24, a comparison among Algorithms A, B, and C, and b comparison between Algorithms B, and C

Table 5 CPU elapse time (s) for the computation of PCET for Algorithms A, B, and C for image resolution 256 × 256 pixels and for various order and repetition of transforms from n _max = m _max = 2 through n _max = m _max = 24

Fig. 4

CPU elapse time (s) for the computation of PCETs for fixed order and repetition n _max = m _max = 24 and various resolutions from 64 × 64 pixels through 512 × 512 pixels, a comparison among Algorithms A, B, and C, and b comparison between Algorithms B, and C

5 Conclusion

A fast method is developed in this paper for the calculation of PHTs, which uses recursion for the evaluation of the sinusoidal functions that comprise the kernel of the transforms. Additional enhancement in speed is achieved by clustering the image pixels that lie at eight radially symmetric locations of an octant of an image. The results of the algorithm are compared with an existing fast method, which uses 8-way symmetry/anti-symmetry property of the radial and angular parts of the kernel function. The proposed method provides a speed enhancement by a factor of three to four, a significant improvement over the existing fast method. This shows that the proposed method is suitable for applications where PHT coefficients are used as features in real-time environment involving large databases or on devices with low computation power.