Introduction

Autopsy imaging (Ai) is a new concept of postmortem imaging that has been developed in Japan. It enhances the classic autopsy by enabling more reliable results to be obtained [1]. According to [2], it is estimated that more than 20,000 postmortem computed tomography (PMCT) procedures are performed in Japan each year. However, a state-of-the-art CT scanner outputs over a thousand slice images per cadaver, which places a heavy burden on radiologists. In addition, it is difficult to interpret a PMCT scan correctly owing to postmortem changes. Therefore, a computer-aided diagnosis (CAD) system is required to assist radiologists. The automatic segmentation of abdominal organs from CT or PMCT scans has been a challenging task in CAD owing to the lower signal-to-noise ratio as well as their higher variability in terms of shape and location. Though many researchers have developed abdominal organ segmentation algorithms using various approaches during the last two decades, no study has focused on the automated segmentation of PMCT scans except for our preliminary study [3]. In general, the automated segmentation of PMCT scans is much harder than that of in vivo ones; however, it is useful to review studies related to automated liver segmentation from in vivo CT scans. We introduce several segmentation algorithms based on the techniques used in, for example, machine learning, atlas, and statistical shape model (SSM), following which we discuss the difficulties faced in the segmentation of PMCT volumes.

Fig. 1
figure 1

Example of in vivo and postmortem CT images: a an example of in vivo CT, b an example of PMCT with severe pathology, postmortem changes, and artifacts and c an example of PMCT with postmortem changes. The red line shows the contour of the true liver

Full size image

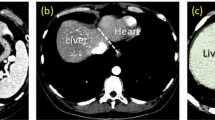
Machine learning is a general approach for image segmentation. Liver segmentation methods using different machine learning techniques such as support vector machine, neural network, and fuzzy rules are reviewed in [4]. However, these approaches depend on local intensity features and suffer from the lack of prior knowledge of the shape, which is useful to prevent unnatural segmentation results. Thus, it is difficult to segment a postmortem liver because of low contrast between the lung and the liver (cf. Fig. 1b).

An atlas-based method is another general segmentation framework. Park et al. [5] and Shimizu et al. [6] proposed abdominal organ segmentation algorithms using a combination of a probabilistic atlas (PA) and a maximum a posteriori (MAP) approach for multi-organ segmentation, including the liver. In recent years, multi-atlas methods have become a popular approach. These methods propagate segmentation labels by warping manually segmented labels using a transformation by a nonlinear registration technique. Chu et al. [7] and Wolz et al. [8] adopted a hierarchical approach for robust registration and applied their algorithms to abdominal organ segmentation, including the liver, kidneys, pancreas, and spleen. Umetsu et al. [9] and Tong et al. [10] respectively proposed slab- and patch-based segmentation algorithms to cope with large inter-subject variability.

Fig. 2
figure 2

An example of the coronal slice of the PMCT shown in Fig. 1c with a PA generated from an SSM trained from in vivo datasets and b MAP-based segmentation result using the resulting posterior probability obtained using a PA-guided EM algorithm. The red contour shows the true boundary of the liver. Owing to postmortem changes (e.g., respiratory arrest), the shape and location of the postmortem liver cannot be explained by conventional SSM

Full size image

SSM is a commonly used tool for abdominal organ segmentation. An SSM-based liver segmentation algorithm proposed by Kainmüller et al. [11] achieved the best performance in the Grand Challenge workshop [12]. Many SSM construction methods have been developed, as shown in a comprehensive review by Heimann and Meinzer [13], among which the point distribution model (PDM) [14] is the most popular approach. The level set distribution model (LSMD) is also a popular SSM, as reviewed by Cremers et al. [15] with applications to segmentation. In the segmentation process, most algorithms require searching for the optimal shape from the SSM that best describes the target liver shape, which is used as a shape prior for subsequent refinement processes such as free form deformation [11] and graph cuts [16]. To obtain better shape priors, several authors employed a conditional model. Tomoshige et al. [17] developed a liver segmentation algorithm based on relaxed conditional SSM by considering the uncertainties of the conditions. Okada et al. [18] improved the multi-organ segmentation performance using an SSM conditioned by other previously segmented structures. Instead of using a single shape prior, Linguraru et al. [19] introduced shape constraints using Parzen shape windows and performed graph cuts to segment the liver, spleen, and kidneys.

When we apply the conventional segmentation algorithms of an in vivo liver to PMCT, the segmentation fails owing to the large variation in the location of liver (see Fig. 2). Thus, the location of the liver must be standardized to the same extent as that of the in vivo liver. However, it is difficult to achieve good performance in spatial standardization [6, 18] because of the much smaller contrast between the lung and the liver as well as the larger variation in the location of the postmortem liver (see Fig. 1b, c). When a standardization process fails, the parameter estimation process, such as a PA-guided expectation–maximization (EM) algorithm [6], will provide inaccurate parameters, resulting in poor performance.

To overcome the difficulties faced in the spatial standardization of the postmortem liver, a dynamic PA was proposed in [3], where the location of the PA of the liver generated from SSM is updated dynamically using the previous segmentation result. This method consists of three steps: (i) rough segmentation based on MAP principle [6] and (ii) SSM-based patient-specific shape estimation followed by (iii) fine segmentation based on graph cuts using the patient-specific shape as a shape constraint. However, the previous segmentation method has some limitations. First, it always used a PA generated from SSM with a Gaussian distribution centered at the mean. Such a PA might not be able to well describe an irregular shape. Second, the location of the PA was updated based on a heuristic rule, and it was not clear what objective function was optimized during the MAP segmentation. Moreover, the convergence of the algorithm is not guaranteed theoretically.

In this study, we developed a novel segmentation algorithm that is superior to that reported previously [3] with respect to the following viewpoints.

  1. 1.

    To cope with the higher variability of the organ in terms of location and shape, the proposed algorithm searches for not only the shape but also the location parameters of a given liver from which patient-specific PA is generated.

  2. 2.

    The location and shape parameters are optimized based on the proposed SSM-guided EM algorithm instead of the conventional heuristic manner. This optimization process is theoretically guaranteed to converge.

  3. 3.

    The proposed algorithm achieved an average Jaccard index (JI) of 0.8501 in the experiment using 32 PMCT volumes, which was superior to that of the previous PMCT liver segmentation method [3].

The remainder of this paper is organized as follows. In “SSM for postmortem liver” section, we briefly introduce the method to construct SSMs for a postmortem liver, as described in [20]. “Liver segmentation with an SSM” section describes the proposed segmentation algorithm based on SSMs. “Experiments” Section  4 presents the experimental setup and results. Finally, “Discussions” section presents the discussions.

SSM for postmortem liver

Level set distribution model (LSDM)

In this study, we employ an LSDM [21] that does not require correspondence between shapes. Before constructing an SSM, the spatial standardization of the training liver label volume was carried out so that they have the same image size, resolution, as well as gravity points among the training cases. Thus, our model explains only the variation in shapes. Sub-section “Extension of LSDM and generation of patient-specific PA” introduces the extension of our LSDM to explain the location.

Let us denote \( \varOmega =\left\{ \varvec{r}^1,\ldots ,\varvec{r}^N\right\} \subset \mathbb {R}^3 \) as a set of position vectors of the center of voxels on a 3D rectangular lattice in an image, where \(N = N_x \times N_y \times N_z\) is the number of voxels. We define each training shape as a set of voxels inside the boundary in an image space \(2^\varOmega \). A training shape \(X\in 2^\varOmega \) is represented as a zero-sublevel set of a function \(\phi :\varOmega \rightarrow \mathbb {R}\), which is referred to as a level set function, as follows:

$$\begin{aligned} X = \{ \varvec{r}\in \varOmega | \phi (\varvec{r}) < 0 \} \end{aligned}$$
(1)

The level set function is defined by a signed Euclidean distance function:

$$\begin{aligned} \phi (\varvec{r}) = \left\{ \begin{array}{l@{\quad }l} - \hbox {dist}(\varvec{r},X^\complement ) &{}\text {if }\;\varvec{r}\in X\\ \hbox {dist}(\varvec{r},X) &{}\text {if }\;\varvec{r}\in X^\complement \end{array}\right. . \end{aligned}$$
(2)

where \(\hbox {dist}(\varvec{r},R) = \min _{\varvec{\varvec{s}}\in R}{\left\| {\varvec{r}-\varvec{s}}\right\| _2}\) is the distance from an end point of a vector \(\varvec{r}\) to the region R.

The input to the training algorithm of LSDM is a set of \(N\)-dimensional vectors of the level-set function \(\varvec{\varphi }= [\phi (\varvec{r}^1), \ldots , \phi (\varvec{r}^N)]^\top \in \mathbb {R}^N\). We introduce a function \(\mathcal {F}: X \mapsto \varvec{\varphi }\). Given a set of \(M\) training shapes \(\{X^j\}_{j=1}^M\subset 2^\varOmega \), vector \(\varvec{\varphi }^j= \mathcal {F}(X^j)\) is computed for each shape, and the data matrix \(\varvec{\varPhi }=[\varvec{\varphi }^1,\ldots ,\varvec{\varphi }^M]\) is generated. We employed weighted PCA for statistical analysis, in which PCA is applied on the weighted data matrix \(\varvec{\varPhi }' = W\varvec{\varPhi }\) [22]. The weight matrix \(W=\hbox {diag}(w(\varvec{r}^1),\ldots ,w(\varvec{r}^N))\) is computed by

$$\begin{aligned} w(\varvec{r})=\frac{1}{M} \sum _{j=1}^M{ \frac{1}{1+\exp {(\gamma \big |\phi ^j(\varvec{r})\big |)}} } \end{aligned}$$
(3)

with \(\gamma \) determined empirically. Finally, PCA yields the following parametrization of the level set function:

$$\begin{aligned} \phi _{\varvec{\alpha }}(\varvec{r}) = {\mu }(\varvec{r}) + \sum _{j=1}^d{u_j(\varvec{r}) {\alpha }_j} \end{aligned}$$
(4)

where \({\mu }(\varvec{r})\) is an average and \(u_j(\varvec{r})\) is the \(j\)th principal component of the level set functions. \({\varvec{\alpha }}= \left[ {\alpha }_1,\ldots ,{\alpha }_d\right] ^\top \) is a coefficient vector, where \(d~({<}M)\) is the number of principal components.

SSM based on synthesis-based learning

In our previous study [20], we trained three conventional SSMs from a postmortem (dead) liver label dataset \(\mathcal {D}\subset 2^\varOmega \), an in vivo (living) liver label dataset \(\mathcal {L}\subset 2^\varOmega \), and a combination of the two datasets \(\mathcal {D}\cup \mathcal {L}\), which are referred to as SSM\(^D\), SSM\(^L\), and SSM\(^{D+L}\), respectively, in this paper. In addition, five SSMs were proposed by combining \(\mathcal {D}\) with an artificial liver label dataset \(\widetilde{\mathcal {D}}\) synthesized via geometrical and/or statistical transformations of the living liver label dataset \(\mathcal {L}\).

Statistical transformation

The statistical transformations were carried out in the eigenshape space constructed using the PCA of the level set functions of liver labels such that the distribution of the living liver labels was identical to that of the dead liver labels by translating and/or rotating the coordinate system of the eigenshape space. We denote \(\widetilde{\mathcal {D}}_T = \mathcal {T}_T(\mathcal {L})\) as the translation transformation of the dataset \(\mathcal {L}\), and it is defined as follows:

$$\begin{aligned} \mathcal {T}_T(\mathcal {L})=\{\mathcal {F}^{-1}(\mathcal {F}(X) - {\varvec{{\mu }}}_\mathcal {L}+ {\varvec{{\mu }}}_\mathcal {D})|X\in \mathcal {L}\}. \end{aligned}$$
(5)

where \({\varvec{{\mu }}}_\mathcal {X}= \frac{1}{|\mathcal {X}|} \sum _{X\in \mathcal {X}}\mathcal {F}(X)\) denotes the average vector over \(\mathcal {X}\in \{\mathcal {L},\mathcal {D}\}\).

The translation with rotation transformation from \(\mathcal {L}\) to \(\mathcal {D}\) is formulated as follows:

$$\begin{aligned} \mathcal {T}_{TR}(\mathcal {L})=\{\mathcal {F}^{-1}({\varvec{U}}_\mathcal {D}{\varvec{U}}_\mathcal {L}^\dagger (\mathcal {F}(X) - {\varvec{{\mu }}}_\mathcal {L}) + {\varvec{{\mu }}}_\mathcal {D})|X\in \mathcal {L}\} \end{aligned}$$
(6)

where \((\cdot )^\dagger \) is the pseudo-inverse operator. \({\varvec{U}}_\mathcal {X}\) (\(\mathcal {X}\in \{\mathcal {L},\mathcal {D}\}\)) is a matrix that consists of the first t principal components of the feature vectors of \(\{\mathcal {F}(X)\}_{X\in \mathcal {X}}\), where t is set as \(\min (\left| {\mathcal {L}}\right| ,\left| {\mathcal {D}}\right| ) - 1\).

Geometrical transformation

The geometrical transformation aligns liver labels using an affine transformation that represents the changes from a living liver to a dead one:

$$\begin{aligned} \mathcal {T}_A(\mathcal {L})=\{\mathcal {A}_\mathcal {L}(X)|X\in \mathcal {L}\} \end{aligned}$$
(7)

where \(\mathcal {A}_\mathcal {L}(X)\) is an affine transformation of the shape \(X\in \mathcal {L}\):

$$\begin{aligned} \mathcal {A}_\mathcal {L}(X)=\{\varvec{M}_\mathcal {L}(\varvec{r}-\varvec{g})+\varvec{g}| \varvec{r}\in X \}. \end{aligned}$$
(8)

Because all training shapes are aligned such that they have the same centroid \(\varvec{g}\), we ensure that the transformation is constant for \(\varvec{g}\). The optimal affine matrix \(\varvec{M}_\mathcal {L}\) is obtained by minimizing the average symmetric surface distance between the mean shapes \(\mathcal {F}^{-1}({\varvec{{\mu }}}_\mathcal {D})\) and \(\mathcal {F}^{-1}({\varvec{{\mu }}}_\mathcal {L})\).

SSMs to be compared

In this study, we compared the segmentation performance among algorithms with eight different SSMs in terms of which SSM is the most suitable for PMCT volume segmentation. Three of them are the conventional SSMs learnt only from the original dataset—\(\mathcal {D}\), \(\mathcal {L}\), and \(\{\mathcal {D}\cup \mathcal {L}\}\); we refer to these as SSM\(^D\), SSM\(^L\), and SSM\(^{D+L}\), respectively. The remaining five SSMs are learnt from the synthesized label dataset combined with the original dataset \(\mathcal {D}\). By using the three types of transformations \(\mathcal {T}_T(\cdot )\), \(\mathcal {T}_{TR}(\cdot )\), and \(\mathcal {T}_A(\cdot )\), we synthesized five artificial postmortem datasets: \(\widetilde{\mathcal {D}}_T = \mathcal {T}_T(\mathcal {L})\), \(\widetilde{\mathcal {D}}_{TR} = \mathcal {T}_{TR}(\mathcal {L})\), \(\widetilde{\mathcal {D}}_A = \mathcal {T}_A(\mathcal {L})\), \(\widetilde{\mathcal {D}}_{AT} = \mathcal {T}_T\circ \mathcal {T}_A(\mathcal {L})\), and \(\widetilde{\mathcal {D}}_{ATR} = \mathcal {T}_{TR}\circ \mathcal {T}_A(\mathcal {L})\). The SSMs constructed from \(\{\mathcal {D}\cup \widetilde{\mathcal {D}}_T\}\), \(\{\mathcal {D}\cup \widetilde{\mathcal {D}}_{TR}\}\), \(\{\mathcal {D}\cup \widetilde{\mathcal {D}}_A\}\), \(\{\mathcal {D}\cup \widetilde{\mathcal {D}}_{AT}\}\), and \(\{\mathcal {D}\cup \widetilde{\mathcal {D}}_{ATR}\}\) are called SSM\(^{D+T}\), SSM\(^{D+TR}\), SSM\(^{D+A}\), SSM\(^{D+AT}\), and SSM\(^{D+ATR}\), respectively.

Liver segmentation with an SSM

Figure 3a shows the flow of the conventional liver segmentation algorithm for PMCT [3]. After the preprocessing, including the rescaling and cropping of an input image as well as body cavity segmentation, liver segmentation is carried out by three steps. The first step is a rough segmentation based on the MAP principle, where the posterior probability is calculated with a PA whose center is \({\varvec{t}}\) and the likelihood whose intensity distribution parameter (\(\varTheta \)) of a given CT volume is estimated by the PA-guided EM algorithm [6]. Parameter \(\varTheta \) is initialized using training data, and \({\varvec{t}}\) is initialized as \({\varvec{t}}^{(0)}\), which is calculated from the body cavity segmentation (see “Experimental setup” section). After the estimation of \(\varTheta \), MAP segmentation is carried out and the gravity point of the segmented liver \(\varvec{g}\) is calculated. If the distance between the gravity point \(\varvec{g}\) and the current estimation \({\varvec{t}}\) is larger than the threshold T, \({\varvec{t}}\) is replaced by \(\varvec{g}\) and the algorithm returns to the EM algorithm. If not, a patient-specific shape estimation is performed using MAP segmentation. This process finds the shape closest to the MAP segmentation from the SSM, in which the shape parameter \({\varvec{\alpha }}\) is optimized in terms of the surface distance between the segmentation result and a shape from the SSM. The final step is fine segmentation based on graph cuts using the obtained patient-specific shape as a shape constraint.

Fig. 3
figure 3

Difference between the flow of a conventional [3] and b proposed segmentation methods. The differences are indicated in red

Full size image

Unlike the previous algorithm, our EM algorithm optimizes the location and shape parameter of the SSM simultaneously; we call this algorithm the SSM-guided EM algorithm in this study. Because the SSM-guided EM algorithm yields parameters that well estimate the location and shape of a target liver, a further patient-specific shape estimation step is not required. Figure 3b shows the proposed algorithm, with enhancements that differ from those of the conventional method [3] being indicated by the red dotted box. After the preprocessing, the proposed method performed parameter estimation of the location and shape of a given liver in an input volume by the proposed SSM-guided EM algorithm. The parameters are used to generate a patient-specific PA as well as patient-specific shape used in the subsequent process, namely, the refinement process based on graph cuts [16] with the location and shape priors. The posterior probability calculated using the patient-specific PA as well as the estimated shape are used in the objective function to be minimized.

SSM-guided EM algorithm

Extension of LSDM and generation of patient-specific PA

To estimate the location of a liver using the proposed algorithm, we extend the formulation of LSDM in Eq. (4) as follows so that it can translate its position with vector \({\varvec{t}}= [t_x,t_y,t_z] \in \mathbb {Z}^3\).

$$\begin{aligned} \phi _{\varvec{\alpha }}(\varvec{r}-{\varvec{t}}) = {\mu }(\varvec{r}-{\varvec{t}}) + \sum _{j=1}^{d}{u_j(\varvec{r}-{\varvec{t}}) \alpha _j} \end{aligned}$$
(9)

We use LSDM for generating the shape label volume as well as the PA. The shape label volume is defined as \(\varvec{S}({\varvec{\alpha }},{\varvec{t}})\in \{0,1\}^N\), whose value at \(i\)th voxel is

$$\begin{aligned} S_i({\varvec{\alpha }},{\varvec{t}}) = \mathcal {H} \left( \phi _{\varvec{\alpha }}(\varvec{r}^i-{\varvec{t}}) \right) \end{aligned}$$
(10)

where \(\mathcal {H}(\cdot )\) is a Heaviside function. Because the level set function that we modeled can be interpreted as a LogOdds maps [23], the PA \(\varvec{A}({\varvec{\alpha }},{\varvec{t}})\in [0,1]^N\) is naturally defined using a sigmoid function:

$$\begin{aligned} A_i({\varvec{\alpha }},{\varvec{t}}) = \varsigma _a(\phi _{\varvec{\alpha }}(\varvec{r}^i-{\varvec{t}})) = \frac{1}{1+\exp { \left( a \cdot \phi _{\varvec{\alpha }}(\varvec{r}^i-{\varvec{t}}) \right) }} \end{aligned}$$
(11)

where \(\varsigma _a(v) = \frac{1}{1+\exp { (av) }}\) is a sigmoid function with constant parameter \(a>0\).

Probabilistic model for SSM-guided EM algorithm

First, we introduce a general notation of the probabilistic model for the image segmentation considered in this study. Let \(\mathbf {y}=(y_1,\ldots ,y_N)\) be a set of \(N\) observations, where \(y_i\in \mathbb {R}\) denotes a CT value at the \(i\)th voxel. We assume that the value \(y_i\) is generated from one of the \(K\) probability distributions indexed by class label \(x_i\in \{1,\ldots , K\}\). Assuming that each observation \(y_i\) is modeled as iid based on a spatially varying finite mixture model (SVMM) [24], the joint density function of \(\mathbf {y}\) can be formulated as

$$\begin{aligned} p(\mathbf {y}|\varTheta ,\varPsi ) = \prod _{i=1}^N{ \sum _{k=1}^{K}{ p(y_i| x_i= k, \varTheta ) p(x_i= k| \varPsi ) }} \end{aligned}$$
(12)

where \(\varTheta \) and \(\varPsi \), explained in detail later, are the model parameters to be estimated from the given observation \(\mathbf {y}\) by maximizing the following log-likelihood function:

$$\begin{aligned}&\ell (\varTheta , \varPsi | \mathbf {y}) = \ln {p(\mathbf {y}|\varTheta ,\varPsi )}\nonumber \\&\quad = \sum _{i=1}^N{ \ln {\sum _{k=1}^K{ p(y_i| x_i= k, \varTheta ) p(x_i= k| \varPsi ) }}}. \end{aligned}$$
(13)

Once the maximum likelihood estimator \((\hat{\varTheta }, \hat{\varPsi })\) is obtained, class labeling \(\hat{\mathbf {x}}=(\hat{x}_1,\ldots ,\hat{x}_N)\) can be calculated by following the MAP rule:

$$\begin{aligned} \hat{x}_i= & {} \mathop {\hbox {arg max}}\limits _{x_i}{p(x_i| y_i, \hat{\varTheta }, \hat{\varPsi })} \nonumber \\= & {} \mathop {\hbox {arg max}}\limits _{x_i}{p(y_i| x_i, \hat{\varTheta }) p(x_i| \hat{\varPsi })} . \end{aligned}$$
(14)

Equation (14) is derived by assuming that \(\varTheta \) and \(\varPsi \) are independent of each other. We assume that \(x_i=1\) is the class of the liver and that \(x_i\ne 1\) shows those of the other organs or tissues.

The observation model of \(y_i\) is assumed to be

$$\begin{aligned} p(y_i= y| x_i= k, \varTheta )= & {} \mathcal {N}({y_i;\theta _k})\nonumber \\= & {} \frac{1}{\sigma _k\sqrt{2\pi }} \exp {\left\{ -\frac{(y-\mu _k)^2}{2\sigma _k^2}\right\} }.\nonumber \\ \end{aligned}$$
(15)

which is the Gaussian distribution of the \(k\)th class with mean and standard deviation of \((\mu _k,\sigma _k) \in \varTheta \).

\(p(x_i= k | \varPsi ) = \pi _k(\varvec{r}^i;\varPsi )\) shows the mixture ratio, that is, the probability that the \(i\)th voxel belongs to the \(k\)th class. Unlike the original SVMM [24], in which the mixture ratio is assigned to each voxel independently, our mixture ratio is defined by a patient-specific PA generated from the SSM with parameter \(\varPsi = \{{\varvec{\alpha }},{\varvec{t}}\}\) as follows:

$$\begin{aligned} p(x_i= k | \varPsi )= & {} \pi _k(\varvec{r}^i;\varPsi ) \nonumber \\= & {} \left\{ \begin{array}{l@{\quad }l} A_i({\varvec{\alpha }},{\varvec{t}}) &{}\text {if }\;k=1\\ \frac{1}{K-1}(1 - A_i({\varvec{\alpha }},{\varvec{t}})) &{}\text {if }\;k\in \{2,\ldots ,K\} \end{array}\right. \nonumber \\ \end{aligned}$$
(16)

Here, we assume that \(k=1\) indicates the class of the liver. Eq. (16) satisfies the necessary condition for the mixture ratio: \(\sum _{k=1}^{K}{\pi _k(\varvec{r}^i;\varPsi )} = 1\) and \(0\le \pi _k(\varvec{r}^i;\varPsi )\le 1\).

Finally, our mixture model is formulated as follows:

$$\begin{aligned} p(\mathbf {y}|\varTheta ,\varPsi ) = \prod _{i=1}^N{ \sum _{k=1}^{K}{ \pi _k(\varvec{r}^i;\varPsi ) \mathcal {N}({y_i;\theta _k}) }}. \end{aligned}$$
(17)

Parameter estimation using SSM-guided EM algorithm

Because the log likelihood of Eq. (13) cannot be maximized directly, we employ an EM algorithm. The parameters of the Gaussians \(\varTheta = \left\{ (\mu _k,\sigma _k); k=1,\ldots ,K\right\} \) and \(\varPsi = \{{\varvec{\alpha }},{\varvec{t}}\}\) are given by maximizing the expected value of the log likelihood function of the complete data:

$$\begin{aligned}&Q\left( {\varTheta ,\varPsi }\big |{{\varTheta }',{\varPsi }'}\right) \nonumber \\&\quad = E_{\mathbf {x}|\mathbf {y},\varTheta ',\varPsi '} [ \ln {p(\mathbf {x}, \mathbf {y}; \varTheta , \varPsi )} ] \end{aligned}$$
(18)
$$\begin{aligned}&\quad = \sum _{i=1}^N{\sum _{k=1}^K{p(x_i= k| y_i, \varTheta ', \varPsi ') \ln {p(x_i= k, y_i| \varTheta , \varPsi )}}}. \end{aligned}$$
(19)

The EM algorithm needs the conditional distribution to be calculated based on current parameters \(\{\varTheta ',\varPsi '\}\) (E-step):

$$\begin{aligned} z_k^i\leftarrow p(x_i= k| y_i, \varTheta ', \varPsi ') = \frac{\mathcal {N}({y_i;\theta '_k}) \pi _k(\varvec{r}^i;\varPsi ')}{\sum _{k=1}^K{\mathcal {N}({y_i;\theta '_k}) \pi _k(\varvec{r}^i;\varPsi ')}}. \end{aligned}$$
(20)

Furthermore, the following log-likelihood corresponding to the complete data (M-step) needs to be maximized:

$$\begin{aligned}&Q\left( {\varTheta ,\varPsi }\big |{\varTheta ',\varPsi '}\right) \nonumber \\&\quad = \sum _{i=1}^N{\sum _{k=1}^K{ z_k^i\left\{ \ln {\mathcal {N}({y_i;\theta _k})} + \ln {\pi _k(\varvec{r}^i;\varPsi )} \right\} }}. \end{aligned}$$
(21)
Fig. 4
figure 4

Pseudocode of the SSM-guided EM algorithm

Full size image

At the E-step, instead of updating all the parameters \(\varTheta \), \(\varPsi \)=(\({\varvec{\alpha }}\), \({\varvec{t}}\)), we update one of them and fix other parameters to the previous ones. When \(\varPsi \) is fixed to \(\varPsi '\), the maximization of Eq. (21) in terms of \(\varTheta \) is known to have an explicit solution, and thus, \(\theta '_k= (\mu '_k, \sigma '_k)\) can be updated as follows:

$$\begin{aligned}&\mu '_k\leftarrow \frac{\sum _{i=1}^N{z_k^iy_i}}{\sum _{i=1}^N{z_k^i}} \end{aligned}$$
(22)
$$\begin{aligned}&{\sigma '_k}^2 \leftarrow \frac{\sum _{i=1}^N{z_k^i(y_i- \mu '_k)^2 }}{\sum _{i=1}^N{z_k^i}} \end{aligned}$$
(23)

The maximization of Eq. (21) with respect to \({\varvec{\alpha }}\) or \({\varvec{t}}\) under fixed \(\varTheta \), however, is difficult because of the non-convexity of the function. Therefore, we increase Eq. (21) based on a gradient descent algorithm with adaptive step size instead of maximizing it, which is generally referred to as the generalized EM algorithm and is also guaranteed to converge as with the original EM algorithm [25]:

$$\begin{aligned}&{{\varvec{t}}}' \leftarrow {{\varvec{t}}}'+\eta _{\varvec{t}}\nabla f({\varvec{t}}') \quad \text {where} \quad f({\varvec{t}}) = Q\left( {{\varTheta }',{{\varvec{\alpha }}}',{\varvec{t}}}\big |{{\varTheta }',{{\varvec{\alpha }}}',{{\varvec{t}}}'}\right) \nonumber \\\end{aligned}$$
(24)
$$\begin{aligned}&{{\varvec{\alpha }}}' \leftarrow {{\varvec{\alpha }}}'+\eta _{\varvec{\alpha }}\nabla g({{\varvec{\alpha }}}') \quad \text {where} \quad g({\varvec{\alpha }}) = Q\left( {{\varTheta }',{\varvec{\alpha }},{{\varvec{t}}}'}\big |{{\varTheta }',{{\varvec{\alpha }}}',{{\varvec{t}}}'}\right) \nonumber \\ \end{aligned}$$
(25)

Here, \(\eta _{\varvec{t}}\) and \(\eta _{{\varvec{\alpha }}}\) are the step size selected adaptively from predefined sets \(H_{{\varvec{t}}}\) and \(H_{{\varvec{\alpha }}}\) so that \(f({\varvec{t}})\) and \(f({\varvec{\alpha }})\) attain the maximum value, respectively. The computation of the gradients \(\nabla f({{\varvec{t}}}')\) and \(\nabla g({\varvec{\alpha }}')\) are given in “Appendix”. Figure 4 shows the pseudocode of the SSM-guided EM algorithm. Each iteration consists of three EM procedures. At the first M-step, \(\varTheta '\) is updated by Eqs. (22) and (23). The second and third M-steps are used for updating \({\varvec{t}}'\) and \({\varvec{\alpha }}'\) based on Eqs. (24) and (25), respectively. The algorithm is terminated when the improvement of the likelihood is smaller than a relative bound \(\varepsilon \cdot |\ell (\varTheta ^{(n)}, \varPsi ^{(n)} | \mathbf {y})|\) or the number of iterations reaches \(n=N^\text {max}\). We used \(\varepsilon =10^{-6}\) and \(N^\text {max}=30\) in this study.

Fine segmentation with graph cuts

By using the estimated parameters \(\{\hat{\varTheta },\hat{{\varvec{\alpha }}},\hat{{\varvec{t}}}\}\), fine segmentation is performed based on graph cuts [16], which is an efficient optimization method for the binary labeling problem using the s-t min-cut algorithm. Let \(\mathcal {B}= \left\{ 0,\,1\right\} \) denote a set of binary labels, where 0 and 1 correspond to the background and foreground, respectively. Given a CT image \(\varvec{I}= (I_1,\ldots ,I_N)\), the graph cut algorithm optimizes the binary labeling \(\varvec{L}=(L_1,\ldots ,L_N)\in \mathcal {B}^N\) so that the following function is minimized.

$$\begin{aligned} E(\varvec{L})= & {} \lambda \sum _{i\in \mathcal {V}}{E^{\text {region}}_{i}(L_i)} \nonumber \\&+ \sum _{(i,j) \in \mathcal {E}} {\left\{ c E^{\text {boundary}}_{ij} + (1-c) E^{\text {shape}}_{ij} \right\} \cdot \delta _{L_i\ne L_j}}\nonumber \\ \end{aligned}$$
(26)

where \(\mathcal {V}\) and \(\mathcal {E}\) are a set of all voxels and all neighboring voxel pairs, respectively. \(c\in [0,1]\) and \(\lambda >0\) are constant parameters. Function \(\delta _{L_i\ne L_j}\) is defined as

$$\begin{aligned} \delta _{L_i\ne L_j} = \left\{ \begin{array}{l@{\quad }l} 1 &{} \,\text {if}\; L_i\ne L_j\\ 0 &{} \,\text {if}\; L_i= L_j\end{array} \right. . \end{aligned}$$
(27)

The first term \(E^{\text {region}}_{i}(L_i)\) is a regional term derived from the posterior probability with parameters estimated by the proposed EM algorithm described in the previous section:

$$\begin{aligned}&E^{\text {region}}_{i}(L_i) \nonumber \\&\quad = \left\{ \begin{array}{l@{\quad }l} \sum _{k\in \{2,3,4\}} p(x_i=k| y_i= I_i; \hat{\varTheta },\hat{\varPsi }) &{} \,\text {if}\; L_i= 1 \\ p(x_i= 1 | y_i= I_i; \hat{\varTheta },\hat{\varPsi }) &{} \,\text {if}\; L_i= 0 \end{array} \right. \nonumber \\ \end{aligned}$$
(28)

The second term \(E^{\text {boundary}}_{ij}\) is the boundary term

$$\begin{aligned} E^{\text {boundary}}_{ij} = \exp {\left\{ -\frac{(I_j-I_i)^2}{2 \sigma ^2} \right\} } \cdot \frac{1}{\left\| {\varvec{r}^j- \varvec{r}^i}\right\| } \end{aligned}$$
(29)

where \(\sigma >0\) is a constant parameter. The third therm \(E^{\text {shape}}_{ij}\) is the shape term that plays similar role in [26]:

$$\begin{aligned} E^{\text {shape}}_{ij} = \sqrt{\frac{1}{2} \left( 1 - \frac{\phi ^{\text {PSS}}(\varvec{r}^j) - \phi ^{\text {PSS}}(\varvec{r}^i) }{\left\| {\varvec{r}^j- \varvec{r}^i}\right\| } \right) } \end{aligned}$$
(30)

where \(\phi ^{\text {PSS}}(\varvec{r})\) denotes the signed distance function of the estimated patient-specific shape \(\varvec{S}(\hat{{\varvec{\alpha }}},\hat{{\varvec{t}}})\). An example of the gradient of the signed distance function \( \nabla \phi ^{\text {PSS}}(\varvec{r}) \) is shown in Fig. 5.

Fig. 5
figure 5

An example of the a input CT image, b posterior probability of liver, and c gradient of the signed distance function of the estimated shape prior

Full size image

Experiments

Dataset

We collected 144 in vivo and 32 postmortem CT volumes acquired from different patients or cadavers. The image size was 512 \(\times \) 512 \(\times \) (154–3201), with voxel sizes of (0.546–1.091) \(\times \) (0.546–1.091) \(\times \) (0.5–1.25) mm. The z-slice of the postmortem CT volume ranges from above the shoulder level to below the upper thigh.

For every CT volume, the true liver label volume was manually delineated by experts. Similar to the previous study [3], we evaluated the performance of the proposed segmentation algorithm between the eight SSMs in a twofold cross validation manner. We randomly split the 144 in vivo and the 32 postmortem dataset in half, that is, 72/72 and 16/16 cases, respectively. 72 in vivo and 16 postmortem cases were used to train the SSM. The SSM construction was performed in a reduced domain, (\(170\times 170\times 170\) [voxels]; 2.0 [mm/voxel] isotropic). The performance of the segmentation was tested using the remaining 16 postmortem cases. The process of training and testing was repeated after changing the role of the two datasets.

Preprocessings

Before executing the algorithm, the slice size of the input CT volume was standardized to be \(256\times 256\), and the size of the voxel was converted to obtain an isotropic voxel using trilinear interpolations. In the following process, a volume is assumed to have isotropic voxels.

Bounding slice estimation

The input volume is automatically cropped between the shoulder level (\(z=z_0\)) and upper thigh (\(z=z_1\)). Figure 6 illustrates how to estimate \(z_0\) and \(z_1\). First, the bone region is roughly segmented with threshold 100 [H.U.], and then, the number of voxels segmented as bone is accumulated along the y-axis (anterior-to-posterior direction). By automatically thresholding the accumulated value, the x-z image of the bone is generated as shown in the top row of Fig. 6, where thresholding value is fixed to 5 in a whole experiment.

Fig. 6
figure 6

Example of the estimation of the bounding slices \(z_0\) and \(z_1\) based on the bone segmentation projected onto the coronal plane

Full size image

Then, for each z-coordinate on the 2D bone image, \(d^{\mathrm{outside}}(z)\) and \(d^{\mathrm{inside}}(z)\) are calculated. \(d^{\mathrm{outside}}(z')\) is the maximum distance between two bone pixels along the line \(z=z'\). \(d^{\mathrm{inside}}(z')\) is the distance between the first bone pixels found by searching toward opposite directions from the middle x-coordinate along the line \(z=z'\). Finally, \(z_0\) is found as the first slice for which \(d^{\mathrm{outside}}(z)\) is greater than \(d_0=270\) mm (middle row of Fig. 6), and \(z_1\) is found as the last slice for which \(d^{\mathrm{inside}}(z)\) is smaller than \(d_1=460\) mm (bottom row of Fig. 6).

Extraction of body cavity

We then extract the body cavity region that is used as a region of interest (ROI) in the segmentation process as well as for estimating the initial location parameter \({\varvec{t}}^{(0)}\). Figure 7 shows an example of the body cavity segmentation process. Let us denote \(\varOmega ^\text {body}\) and \(\varOmega ^\text {bone}\) (\(\varOmega ^\text {body} \subset \varOmega \), \(\varOmega ^\text {bone} \subset \varOmega \), and \(\varOmega ^\text {body} \ne \varOmega ^\text {bone}\)) as sets of voxels of the body trunk and bone extracted by the thresholding-based algorithm, respectively; furthermore, we denote \(\varGamma ^\text {body}\) as an external surface of the body trunk \(\varOmega ^\text {body}\). The body cavity region is calculated from \(\varOmega ^\text {body}\), \(\varOmega ^\text {bone}\), and \(\varGamma ^\text {body}\) shown in Fig. 7b as described below. First, for each surface voxel \(\varvec{s} \in \varGamma ^\text {body}\), we estimate the distance from \(\varvec{s}\) to the body cavity based on the distance between the rib and the body surface as follows:

$$\begin{aligned} r(\varvec{s}) = \left\| {\varvec{n}_{\varOmega ^\text {bone}}(\varvec{s}) - \varvec{n}_{\varGamma ^\text {body}}(\varvec{n}_{\varOmega ^\text {bone}}(\varvec{s}))}\right\| + C \end{aligned}$$
(31)

where \(\varvec{n}_R(\varvec{s}) = {\mathop {\hbox {arg min}}\limits }_{\varvec{t} \in R}{\left\| {\varvec{s}-\varvec{t}}\right\| }\) is the nearest voxel from \(\varvec{s}\) in a set R, and C is a constant value introduced to reduce the estimation error. We employed \(C = 2\) voxels decided experimentally. Figure 8 illustrates the calculation of Eq. (31), and Fig. 7c shows an example of \(r(\varvec{s})\). Subsequently, we extract the body cavity based on the following equation:

$$\begin{aligned}&\varOmega ^\text {BodyCavity} \nonumber \\&\quad = \left\{ \varvec{s} \in \varOmega ^\text {body} \big | \Vert \varvec{s}-\varvec{n}_{\varGamma ^\text {body}}(\varvec{s}) \Vert - r(\varvec{n}_{\varGamma ^\text {body}}(\varvec{s})) > 0 \right\} .\nonumber \\ \end{aligned}$$
(32)

An example that satisfies the equation is shown in Fig. 7d. Equations (31) and (32) can be calculated efficiently using Euclidean distance transformation [27] and Voronoi diagram construction [28]. Finally, we refine the body cavity segmentation result by applying erosion with a ball structuring element of a radius of 10 voxels, extraction of the largest connected component with 26-connectivity, followed by dilation with a radius of 10 voxels (cf. Fig. 7f).

Fig. 7
figure 7

Example of the body cavity segmentation: a an input image, b \(\varOmega ^\text {body}\), \(\varOmega ^\text {bone}\), and \(\varGamma ^\text {body}\), c \(r(\varvec{s})\) for \(\varvec{s}\in \varGamma ^\text {body}\), d \(\Vert \varvec{s}-\varvec{n}_{\varGamma ^\text {body}}(\varvec{s})\Vert -r(\varvec{n}_{\varGamma ^\text {body}}(\varvec{s}))\) for \(\varvec{s}\in \varOmega ^\text {body}\), e \(\varOmega ^\text {BodyCavity}\) calculated using Eq. (32), and f refined body cavity

Full size image
Fig. 8
figure 8

Illustration of the calculation of Eq. (31). For each voxel \(\varvec{s}\) in \(\varGamma ^\text {body}\), its nearest bone voxel \(\varvec{n}_{\varOmega ^\text {bone}}(\varvec{s})\) and its nearest body surface voxel \(\varvec{n}_{\varGamma ^\text {body}}(\varvec{n}_{\varOmega ^\text {bone}}(\varvec{s}))\) are calculated

Full size image

Experimental setup

The number of principal components \(d\) was chosen for each SSM independently so that the cumulative contribution ratio was equal to 0.95, which is the same setting as that in [20]. We used the parameter for weighted PCA, \(\gamma =0.25\), which is also the same value as that employed in [20]. The parameter of the sigmoid function a used to generate PA (Eq. (11)) was optimized so that the conventional model SSM\(^D\) shows the highest performance (JI) in the MAP segmentation. We compared the segmentation performance between three conventional SSMs {SSM\(^D\), SSM\(^L\), SSM\(^{D+L}\)} and five proposed SSMs {SSM\(^{D+T}\), SSM\(^{D+TR}\), SSM\(^{D+A}\), SSM\(^{D+AT}\), SSM\(^{D+ATR}\)}.

The number of classes of the mixture model was \(K = 4\), which represents the liver, heart, kidneys, and other organs or tissues. The initial parameter \(\varTheta ^{(0)}\) was learnt from in vivo CT volumes instead of using a postmortem dataset because no true label of the heart and kidneys in PMCT is available at present. The initial estimate of the shape parameter is set as \({\varvec{\alpha }}^{(0)}=\left[ 0,\ldots ,0\right] ^\top \). The initial translation parameter \({\varvec{t}}^{(0)}=[t_x^{(0)},t_y^{(0)},t_z^{(0)}]^\top \) is defined based on the surrounding anatomical structures, as shown in Fig. 9.

Fig. 9
figure 9

Estimation of the gravity center of the liver, that is, initial estimate of the translation parameter \({\varvec{t}}^{(0)}=[t_x^{(0)},t_y^{(0)},t_z^{(0)}]^\top \) (left z-coordinate, right x- and y-coordinates). \(t_z^{(0)}\) is calculated by the interior division of the z-level between shoulder \(z=z_0\) and upper thigh \(z=z_1\) with the division ratio \(s_z:(1-s_z)\). \((t_x^{(0)},t_y^{(0)})\) is calculated by dividing the x and y range of the bounding box of the body cavity at slice \(t_z^{(0)}\) with the division ratio \(s_x:(1-s_x)\) and \(s_y:(1-s_y)\). The parameters \(s_x, s_y\) and \(s_z\) are learnt from the training PMCT dataset

Full size image

We performed graph cut segmentation for the test cases with all the possible combinations of parameters under \(\lambda \in [0.06,0.10,\ldots ,0.18]\), \(\sigma \in [4,5,\ldots ,12]\), and \(c\in [0.5,0.6,\ldots ,0.9]\). Finally, we chose the best parameter combination for each SSM independently based on the average JI.

Results

We evaluated the performance of MAP segmentation and the graph-cut-based refinement based on JI. Note that MAP segmentation was not actually performed in the proposed segmentation. However, to evaluate the accuracy of posterior probability estimation, we temporarily evaluated the performance of MAP segmentation. We executed the proposed algorithm with unoptimized MATLAB code on the Intel® Xeon® CPU E5-2687W. The algorithm took about 30 s for preprocessing, 14 min for the SSM-guided EM algorithm and 1 min for graph-cut-based refinement per a case on average.

Fig. 10
figure 10

JI between true liver and the MAP segmentation. The numerals above the box plots show average JIs, where the highest value is indicated in red. Statistical difference between the best SSM\(^{D+A}\) and all other SSMs are displayed (\(*p < 0.05\))

Full size image
Fig. 11
figure 11

JI between true liver and the graph cut refinement result. The numerals above the box plots show average JIs, where the highest value is indicated in red. Statistical differences between the best SSM\(^{D+A}\) and all other SSMs are displayed (\(*p < 0.05\))

Full size image
Fig. 12
figure 12

Graph cut segmentation results for the PMCT cases shown in Fig. 1: a result for the PMCT case shown in Fig. 1b and b result for the PMCT case shown in Fig. 1c. The yellow contour shows the segmented liver region and the red line shows the contour of the true liver

Full size image
Fig. 13
figure 13

Typical example of the MAP segmentation (top row), location and shape estimation (middle row), and graph cut result (bottom row) compared between conventional models {SSM\(^D\), SSM\(^L\), SSM\(^{D+L}\)} and the best SSM\(^{D+A}\)

Full size image

Figure 10 compares the JIs of the proposed MAP segmentation result between eight SSMs. We found that SSM\(^{D+A}\) showed the highest performance on average. To see the difference of JIs between SSMs, Friedman test, a non-parametric equivalent to the one-way ANOVA, was performed with the Nemenyi test [29] as post hoc test. The null hypothesis is that there are no difference between methods in terms of mean rank of JI. The Friedman test rejected the null hypothesis with \(p<0.05\). The result of post hoc test is displayed above the box plots in Fig. 10 between SSM\(^{D+A}\) and all other SSMs. The MAP segmentation performance of SSM\(^{D+A}\) was found to be statistically different from that of all conventional SSMs {SSM\(^D\),SSM\(^L\),SSM\(^{D+L}\)} and two synthesis-based SSMs {SSM\(^{D+TR}\), SSM\(^{D+ATR}\)}. On the other hand, statistically significant difference was not observed between SSM\(^{D+A}\) and {SSM\(^{D+T}\), SSM\(^{D+AT}\)}.

Figure 11 shows the performance of the graph-cut-based refinement result. Statistical test was applied with the same way in Fig. 10. The SSM\(^{D+A}\) showed the highest performance (JI: 0.8516) and was statistically different from other SSMs except for {SSM\(^{D+T}\), SSM\(^{D+AT}\)}, which was consistent with the performance of MAP segmentation. To enable comparison with other studies, we evaluated Dice similarity index (DSI) and average symmetric surface distance (ASSD) [12] of the method with SSM\(^{D+A}\), which were 0.9145 and 2.928 mm, respectively.

Figure 12 shows the graph cut segmentation result for the two PMCT cases shown in Fig. 1 using the proposed algorithm with SSM\(^{D+A}\). Although they have a considerable amount of postmortem change, the JIs of 0.856 and 0.879 are higher than the average of 0.8516.

Figure 13 shows typical results of the MAP segmentation, location and shape estimation, and graph cut segmentation using conventional SSMs (i.e., {SSM\(^D\), SSM\(^L\), SSM\(^{D+L}\)}) and the best SSM\(^{D+A}\). Compared to the conventional SSMs, SSM\(^{D+A}\) showed better results in the MAP segmentation and shape estimation. As a result, SSM\(^{D+A}\) achieved the best performance in the graph cut segmentation result.

Fig. 14
figure 14

Comparison of eight SSMs using JI between the true label and the estimated shape label \(\varvec{S}(\hat{{\varvec{\alpha }}},\hat{{\varvec{t}}})\) optimized by the proposed EM algorithm, which was used to define the shape term (Eq. (30)) in the subsequent graph cut segmentation. The numerals above the box plots show the average JIs, where the highest value was indicated in red. Friedman test was applied with a post hoc test, i.e., Nemenyi test, and the statistical differences between the best SSM\(^{D+A}\) and all the other SSMs are displayed (\(*p < 0.05\))

Full size image
Fig. 15
figure 15

Relationship between “performance of location and shape estimation” versus those of a “MAP segmentation” and b “graph cut segmentation”

Full size image

Discussions

In the following sections, we discuss the segmentation performance from different aspects, namely, comparison of results with eight SSMs, effectiveness of location and shape estimation, and comparison with the previous segmentation algorithm [3].

Comparison of results with eight SSMs

First, we would like to discuss the difference in the segmentation performance among eight SSMs. The experimental results for the test cases indicate that SSM\(^{D+A}\) showed the best MAP segmentation as well as graph cut refinement with no significant difference with {SSM\(^{D+T}\), SSM\(^{D+AT}\)}. The success of the MAP and graph cut segmentation depends on the accuracy in location and shape parameter estimation, which can be quantified by the JI between the true label and the estimated shape label \(S(\hat{{\varvec{\alpha }}},\hat{{\varvec{t}}})\) by the proposed EM algorithm, as shown in Fig. 14. The results in this figure are consistent with those shown in Fig. 10, namely, that SSM\(^{D+A}\) showed the highest performance among the eight SSMs and that {SSM\(^{D+T}\), SSM\(^{D+A}\), SSM\(^{D+AT}\)} are the best SSMs with no significant differences. We also evaluated the correlation between the JIs of the estimated shape label \(S(\hat{{\varvec{\alpha }}},\hat{{\varvec{t}}})\) by the best model SSM\(^{D+A}\) and those of MAP segmentation. Figure 15 shows the correlation as well as the correlation with graph cut segmentation, in which positive correlations were observed for both MAP and graph cut segmentation. Pearson’s linear correlation coefficients were \(R^2 = 0.9560\) and \(R^2 = 0.9263\) (\(p < 0.01\); H\(_0\), no correlation). From the above facts, we concluded that {SSM\(^{D+T}\), SSM\(^{D+A}\), SSM\(^{D+AT}\)} provided better shape and location priors, and these priors boosted the performance of MAP and graph cut segmentation.

We supposed that high performance in shape estimation could be derived from the high performance of SSM that was evaluated in our previous study [20]. In that paper, we reported that the best SSM with respect to the performance of SSM (i.e., generalization and specificity) was SSM\(^{D+T}\), and there was no significant difference between SSM\(^{D+T}\) and SSM\(^{D+AT}\). In general, an SSM with higher generalization/specificity is expected to lead to higher performance in segmentation. For example, because SSM\(^L\) with lower generalization and specificity cannot describe the postmortem liver shape properly, it failed in segmentation, as shown in Fig. 13. In contrast, SSM\(^{D+A}\) that has higher performance in describing a postmortem liver shape achieved the best segmentation result. Therefore, we concluded that the success of the segmentation with {SSM\(^{D+T}\), SSM\(^{D+AT}\)} can be accounted for by the high performance of the SSMs. Although SSM\(^{D+A}\) was inferior to these SSMs in terms of both model performance indices, the segmentation performance was statistically comparable to those with the SSMs. One possible reason for the high segmentation performance of SSM\(^{D+A}\) may be its highest generalization [20].

Fig. 16
figure 16

Comparison between the proposed segmentation result using SSM\(^{D+A}\) and that without estimated parameters \({\varvec{\alpha }}\) and \({\varvec{t}}\). The numerals shown above the box plots are the average JIs

Full size image
Fig. 17
figure 17

Typical result of the proposed method using SSM\(^{D+A}\) with (left column) and without estimated parameters \({\varvec{\alpha }}\) and \({\varvec{t}}\) (right column). The upper row shows the isocontours of the prior probability, or PA, generated from SSM\(^{D+A}\), and the bottom row represents the MAP segmentation using the prior probability

Full size image

Effectiveness of location and shape estimation

In this subsection, we discuss the effectiveness of the location and shape parameters (\({\varvec{\alpha }},~{\varvec{t}}\)) estimated via the proposed EM algorithm. To prove the impact, we compared the proposed segmentation results to those without estimated location and shape parameters. In the method without the estimated parameters, we fixed the parameters to initial values, that is, \({\varvec{\alpha }}^{(0)}=\left[ 0,\ldots ,0\right] ^\top \) and \({\varvec{t}}^{(0)}=[t_x^{(0)},t_y^{(0)},t_z^{(0)}]^\top \), except for the GMM parameter of the intensity distribution \(\varTheta \), which is theoretically equal to a conventional EM algorithm for GMM. For this comparison, the parameters for graph cuts were optimized on the training dataset for each method independently over the search range we mentioned in “Experimental setup” section. Figure 16 shows the result for the SSM\(^{D+A}\), in which the proposed method outperformed the method without location and shape parameter estimation of \({\varvec{\alpha }}\) and \({\varvec{t}}\) in terms of the performance of the estimated shape label, MAP segmentation, as well as graph cut segmentation. According to the typical result shown in Fig. 17, the proposed method successfully estimated the location as well as the shape of the liver, resulting in more patient-specific prior probability and higher performance in MAP and graph cut segmentation. In contrast, the conventional algorithm without parameter estimation failed in segmentation because of large displacement of the liver from the average location. From the above results, we concluded that the estimation of \({\varvec{\alpha }}\) and \({\varvec{t}}\) using the proposed EM algorithm improved the segmentation performance.

Fig. 18
figure 18

Number of iterations versus a log likelihood (Eq. (13)) divided by number of voxels in a given test volume, b JIs of estimated shape labels, and c JIs of MAP segmentation, where the thin lines shows the plot for 32 test cases and the bold line with the marker indicates the average at each iteration

Full size image

It is also useful to evaluate the log-likelihood function of Eq. (13) for all test cases and the relationship with estimated shape label \(\varvec{S}(\hat{{\varvec{\alpha }}},\hat{{\varvec{t}}})\) as well as MAP segmentation so as to determine whether the algorithm works well. Figure 18 shows the number of iterations in the proposed EM algorithm versus the log likelihood (Eq. (13)), transitions of JIs of the shape label \(\varvec{S}(\hat{{\varvec{\alpha }}},\hat{{\varvec{t}}})\), and MAP segmentation. We confirmed from Fig. 18a that the log likelihood monotonically increased with the number of iterations, which was expected as mentioned in “Liver segmentation with an SSM” section. In addition, it was found from Figs. 18b, c that the performance of the patient-specific shape and MAP segmentation for most cases increased as the likelihood increased. Figure 19 shows the extent of improvement, in which a smaller initial shape was enlarged to be closer to the true boundary with increasing number of iterations. The JI for this case changed from 0.4964 to 0.8549. Because the JIs of most cases converged at around the iteration step \(n=15\), we set the maximum number of iterations as \(N^{\text {max}} = 30\) in our study.

Fig. 19
figure 19

Isocontour of PA and MAP segmentation (yellow) for different number of iterations \(n=1,3,5,10,30\)

Full size image

Comparison with the previous segmentation algorithm [3]

In this subsection, we compared the proposed segmentation results with the previous results. Figure 20 shows the relationship of performance between the proposed algorithm with SSM\(^{D+A}\) and the previous one based on the atlas-guided EM algorithm with dynamic PA [3]. The comparison was conducted with the same test dataset (32 PMCT volumes) and the same SSM (SSM\(^{D+A}\)). Red crosses above the diagonal dotted lines are the cases whose JIs are higher than those of the conventional algorithm. For example, we found that the proposed algorithm showed higher performance in the graph cut segmentation for 26 out of 32 cases. The Wilcoxon signed rank test between the proposed and conventional algorithms was carried out for all cases, and we confirmed the statistical differences from the previous method.

Fig. 20
figure 20

Conventional method [3] versus proposed method using SSM\(^{D+A}\) in terms of the performance of a MAP segmentation, b location and shape estimation and c graph cut segmentation

Full size image
Fig. 21
figure 21

Failure case by the proposed algorithm using SSM\(^{D+A}\): a input image, b MAP segmentation and c graph cut segmentation results. The red line shows the true contour of the liver

Full size image

Limitations

Finally, we would like to discuss the limitations of the proposed algorithm. Figure 21 shows the worst-case performance both in MAP and graph cut segmentation using the proposed method with SSM\(^{D+A}\). The lower performance in MAP segmentation was caused by failure in shape and location as well as GMM parameter estimation, which resulted in an inaccurate graph cut segmentation result. The major reasons behind the failure are listed below.

  • The SSM could not describe the atypical shape shown in Fig. 21. We measured the generalization of the case by the projection of the true shape label shown in Fig. 21 to the eigenshape space of SSM\(^{D+A}\) and back-projection. The JI between the true label and the label after back-projection was 0.414, which is much smaller compared with the generalization or the average JI over all cases (0.837) reported in [20]. Consequently, we concluded that the difficulties faced in describing the shape of the case resulted in the failure of parameter estimation.

  • The solution by the proposed EM algorithm may be stuck in a local minimum. We measured the Mahalanobis distance between the shape shown in Fig. 21 and the average shape of SSM\(^{D+A}\) (\(=\)initial values \({\varvec{\alpha }}^{(0)}=\left[ 0,\ldots ,0\right] ^\top \) of the proposed EM algorithm) in the level set space and found that the distance 12.70 was the largest among the 32 test cases. Generally speaking, larger Mahalanobis distance from the initial values can increase the risk of being trapped in local minima.

  • The intensity model, or a mixture of Gaussian distributions, were trained from in vivo CT volumes because of the lack of labels of surrounding organs in a postmortem body. The trained parameters of the distribution might not explain the intensity changes caused by artifacts from arms, severe pathologies, as well as postmortem changes.

Conclusions

We presented an SSM-guided EM algorithm for automated liver segmentation from a PMCT volume. The proposed EM algorithm estimates not only the parameters of the intensity distribution model but also the location and shape parameters of a liver from a given PMCT volume simultaneously. This type of algorithm is particularly useful in PMCT volume segmentation without spatial standardization because of the large variation in location and shape owing to severe pathology and/or postmortem changes. In addition, from a theoretical viewpoint, the advantage relative to the conventional segmentation algorithm for PMCT [3] is that the proposed EM algorithm maximizes an objective function that is guaranteed to converge. We validated the performance of the proposed segmentation algorithm using 144 in vivo and 32 postmortem CT images. The algorithm with SSM\(^{D+A}\) found to be statistically comparable to that with {SSM\(^{D+T}\), SSM\(^{D+AT}\)} and was significantly better compared to the conventional SSMs {SSM\(^D\), SSM\(^L\), SSM\(^{D+L}\)} in terms of segmentation accuracy. The proposed EM algorithm provided better priors in location and shape than the conventional EM algorithm for GMM that estimates the intensity distribution parameters only.

In order to cope with intensity changes caused by artifacts, diseases, as well as postmortem changes, we plan to develop a statistical model of the intensity changes of the postmortem CT images, such as in [30]. Furthermore, we will improve the performance of the SSM by using the relaxed conditional SSM [17] that was reported to be beneficial, especially for atypical liver shapes. To solve the local minimum problem, we also plan to develop global and simultaneous optimization of the shape and location priors as well as segmentation labels, inspired by [31].