Extending the Mathematical Palette for Developmental Pattern Formation: Piebaldism

Abstract

Here, we present a theoretical investigation with potential insights on developmental mechanisms. Three biological factors, consisting of two diffusing factors and a cell-autonomous immobile transcription factor are combined with different feedback mechanisms. This results in four different situations or fur patterns. Two of them reproduce classical Turing patterns: (1) regularly spaced spots, (2) labyrinth patterns or straight lines with an initial slope in the activation of the transcription factor. The third situation does not lead to patterns, but results in different homogeneous color tones. Finally, the fourth one sheds new light on the possible mechanisms leading to the formation of piebald patterns exemplified by the random patterns on the fur of some cows’ strains and Dalmatian dogs. Piebaldism is usually manifested as white areas of fur, hair, or skin due to the absence of pigment-producing cells in those regions. The distribution of the white and colored zones does not reflect the classical Turing patterns. We demonstrate that these piebald patterns are of transient nature, developing from random initial conditions and relying on a system’s bistability. We show numerically that the presence of a cell-autonomous factor not only expands the range of reaction diffusion parameters in which a pattern may arise, but also extends the pattern-forming abilities of the reaction–diffusion equations.

1 Introduction

The various patterns on the surface of animals (fur, skin, feathers) have always been intriguing because of their diversity and presumed functions. The coloration of mammals is due to melanin pigments that are produced by melanocytes. Melanocytes are located in the stratum basale layer of the skin’s epidermis and in hair follicles; melanocytes secrete mature melanosomes to surrounding keratinocytes (Lin and Fisher 2007). They differentiate from undifferentiated precursor cells, called melanoblasts (Hirobe 2011). The localized changes in the homogeneous distribution of melanocytes (or in the pigment synthesis pathway) result in different patterns (Mills and Patterson 2009). The various presumed biological functions of these patterns include a role in camouflage or mimicry, rather than for communication or other physiological functions (Allen et al. 2011). Zebra stripes most probably serve as a dazzle pattern. Unlike other forms of camouflage, the intention of a dazzle pattern is not to conceal, but to make it difficult to estimate a target’s range, speed, and the direction of motion (How and Zanker 2014). Zebra stripes not only confuse big predators like lions, but also make zebra fur less attractive for flies (Egri et al. 2012).

The pattern formation mechanisms have been largely debated since the pioneering work of Alan Turing, who proposed a reaction–diffusion model to explain how very distinctive patterns may arise autonomously (Turing 1952). Almost all natural occurring patterns can be recapitulated by this model; the seminal idea has served many different purposes (Murray 1989; Salsa et al. 2013). However, reaction–diffusion equations have not been used to explain piebald patterns, one example being the fur pattern of Dalmatian dogs. These so-called piebald patterns show randomly distributed dots of different sizes. The pigmented spots are the result of the stochastic migration of primordial pigment cells (melanoblasts) from the neural crest to their final locations in the skin of the early embryo (Li et al. 2011; Mort et al. 2016). However, the mathematical model considering only the random movement of melanoblasts does not produce sharp edges between the colored and the melanocyte-free regions (Mort et al. 2016). The spots on Dalmatian dogs appear after their birth with increasing sizes and contrasts, indicating that other additional mechanisms are involved in their formation. For example, melanoblasts are unable to differentiate into melanocytes or to survive in white patches, most probably due to a lack of diffusion factors originating from neighboring cells present in the skin. Melanocyte proliferation, distribution, differentiation, and melanogenesis are under the control of factors secreted by surrounding keratinocytes (Cichorek et al. 2013). Moreover, dermal fibroblasts act on melanocytes directly and indirectly by secreting a large number of cytokines and factors. These factors bind to the corresponding receptors present in melanocytes and modulate intracellular signaling cascades related to melanocyte functions (Wang et al. 2017). Consequently, the observed patterns in melanocyte activity and distribution should be already visible in the spatial differences of diffusion factor concentrations released by keratinocytes and dermal fibroblasts. Previous studies have revealed that white parts of the piebald patterns resulted from the absence of melanocytes in this area (Spritz 1994). On the other hand, the white stripes of the African striped mice (Rhabdomys pumilio) and the Eastern chipmunks (Tamias striatus) are actually the result of impaired melanocyte differentiation processes (Mallarino et al. 2016).

Although patterning in a variety of biological contexts can be described in mathematical terms to be operating via Local Activation coupled with Long-range Inhibition (LALI), it has always been recognized that cells must translate the diffusion factor-encoded information into a biological signal. The importance of transcription factors (TFs)—as cell-autonomous factors—in the pattern formation is highlighted by microbiological experiments with synthetic gene circuits. The experiments revealed very versatile pattern-forming abilities of the genetically engineered organisms including the programmed bull’s eye pattern (Basu et al. 2005), synchronized oscillations and traveling waves among cells (Danino et al. 2010), sequentially developing stripes (Liu et al. 2011) or rings (Cao et al. 2016). Cell-autonomous/transcription factor(s) have been considered in some mathematical studies (Marcon et al. 2016; Raspopovic et al. 2014). These models produce the classical Turing patterns with an expanding range of reaction–diffusion parameters.

In this study, we present a theoretical investigation with potential insights on developmental mechanisms by considering explicitly a non-diffusing transcription factor (TF) together with two diffusion factors. This allows the generation of regular (stripes, dots) and irregular (piebald) patterns. This model aims at expanding the range of pattern-forming abilities of the reaction–diffusion equations and provides a useful tool for understanding the formation of piebald patterns. Additionally, we highlight that these piebald patterns are of transient nature. However, scaling the activation levels of TFs permits regulating the speed of the pattern formation; if this value is close to zero, we show numerically that the pattern formation dynamics is halted and the pattern does not change significantly over time.

2 Methods

2.1 Concept

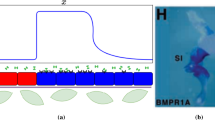
Diffusion factors are mobile compounds; they move rather freely in the extracellular space or between cells via gap junctions (e.g., microRNAs). Many modeling frameworks consider two diffusing agents and the relationships between them: a (self) activator (A) and a (self) inhibitor (I). Aligning with this, we call one diffusion factor A (activator) and the other one I (inhibitor), whose denomination corresponds to the classical situation of interest. However, the purpose of this study is to go beyond these relationships. Thus, we prefer to consider A and I as being simply two diffusion factors and define their precise roles via particular feedback functions. Activation and inhibition are thus encoded within particular feedback functions. The diffusion factors bind to their corresponding receptors usually localized on the surface of a cell. This induces a signaling cascade that leads to the shuttling of the TF between the cytosol and the nucleus (Cai et al. 2008; Nakayama et al. 2008; Nelson et al. 2004). TFs are proteins that bind to DNA regulatory sequences (enhancers and silencers) to modulate the rate of gene transcription. This may result in increased or decreased gene transcription and protein synthesis (Adcock and Caramori 2009). We suppose that if a given TF is retained in the nucleus for a sufficiently long period of time, then it stimulates the translation of the “color gene,” whose product acts as an attractant or activator for melanoblasts/melanocytes (MA), and TFs either inhibit or induce the synthesis of diffusion factors. This results in the following four situations: (I) Activating: The activated TF stimulates the production of the activator (A) and the inhibitor (I); (II) Inhibiting: The activated TF inhibits the production of the activator and the inhibitor; (III) Mixed I: The activated TF promotes the production of the activator, but blocks the production of the inhibitor; (IV) Mixed II: The activated TF hinders the production of the activator, but triggers the production of the inhibitor. Activation and inhibition are thus encoded within particular feedback functions of the TFs leading to four specific situations. A schematic representation is depicted in Fig. 1.

Fig. 1

Schematic representation of the model: a The two-component model uses a mathematical concept operating via local activation coupled with long-range inhibition with a diffusible activator (A) and inhibitor (I). b–e The model of the current study, a three-component model assumes that cells must translate the diffusion factor-encoded information into a biological signal. Diffusion factors A and I bind to the corresponding receptors (blue and red rectangles) activating or inhibiting the transcription factor (TF). The activated TF translocates to the nucleus and (I) stimulates the translation of the “color gene” acting as an attractant and (II) moreover leads to the synthesis or the inhibition of the activator A and the inhibitor I. This defines four different feedback loops (Color figure online)

We assume that S, the activity levels of TFs present in the nucleus, can be considered as a proxy measure for the expression level of the melanocyte activator/attractant (MA) within the system. To coordinate these activities, often with great spatiotemporal and tissue-specific precision as required for developmental programs, several types of cellular posttranslational modifications of TFs may occur. These include phosphorylation, sumoylation, ubiquitination, acetylation, glycosylation, and methylation among others (Filtz et al. 2014). These long-term modifications influence the sensitivity of TFs to external signals, slowing down the velocity of developing patterns. This effect is taken into consideration in our model using a novel parameter, called “reaction velocity.”

We consider that the pre-pattern develops in the layer of embryonic keratinocytes or in dermal fibroblasts and that the melanocyte differentiation/distribution follows this pre-pattern. Similar mechanisms have been described for the spacing of skin appendages (hairs, glands). In this case, WNT acting as a short-range activator and its inhibitor DKK acting as a long-range inhibitor have been identified as primary determinants of murine hair follicles spacing. Both factors are derived from the mesenchymal/dermal fibroblast cell layer (Sick et al. 2006).

2.2 Mathematical Model

Let $A\left( {t, x} \right)$ denote the concentration of the activator at time $t$ and position $x$, $I$ the inhibitor concentration, and $S$ the activity level of TFs present in the nucleus. TFs can also be viewed as a proxy for the expression level of the melanocyte activator/attractant (MA) within the system. We use the following reaction–diffusion equations for the activators and inhibitors:

$$ \frac{{\partial A\left( {t, x} \right)}}{\partial t} = b_{a} f\left( {S\left( {t, x} \right)} \right) - d_{a} A\left( {t, x} \right) + D_{a} \nabla^{2} A\left( {t, x} \right) + A\left( {t,x} \right)*\xi_{a} $$

(1)

$$ \frac{{\partial I\left( {t, x} \right)}}{\partial t} = b_{i} g\left( {S\left( {t, x} \right)} \right) - d_{i} I\left( {t, x} \right) + D_{i} \nabla^{2} I\left( {t, x} \right) + I\left( {t,x} \right)*\xi_{i} $$

(2)

where $b_{a}$ is the production rate, $d_{a}$ is the degradation rate, and $D_{a}$ is the diffusion coefficient of the activator, while $b_{i}$, $d_{i}$, and $D_{i}$ are the production rate, degradation rate, and diffusion coefficient of the inhibitor, respectively. The random variables $\xi_{a}$ and $\xi_{i}$ are distributed normally $\xi_{a} \sim {\mathbf{\mathcal{N}}}\left( {0, \sigma_{a}^{2} } \right)$ and $\xi_{i} \sim {\mathbf{\mathcal{N}}} \left( {0, \sigma_{i}^{2} } \right)$, in line with the study of Zheng et al. (2017). We use a multiplicative white noise in the stochastic differential equation; the absolute value of such a noise is larger at higher concentrations of $A$ and $I$. This is in agreement with the experimental finding that the noise, defined as the ratio between variance and mean, increases significantly when the translation efficiency, i.e., the production rate, increases (Thattai and van Oudenaarden 2001). If not mentioned explicitly, $\sigma_{a}^{2} = \sigma_{i}^{2} = 0$, i.e., there is no stochasticity in the dynamics of the system. The functions $f$ and $g$ permit distinguishing between the different situations of interest, i.e., (1) in the Activating situation, $f\left( s \right) = s$ and $g\left( s \right) = s$, (2) in the Inhibiting situation $f\left( s \right) = 1/s$ and $g\left( s \right) = 1/s$, (3) in the Mixed I situation, $f\left( s \right) = s$ and $g\left( s \right) = 1/s$, and (4) in the Mixed II situation, $f\left( s \right) = 1/s$ and $g\left( s \right) = s$. The dynamics of the TFs is implemented by the following differential equation:

$$ \frac{{dS\left( {t,x} \right)}}{dt} = r_{v} \left( t \right) \cdot \left( {b_{s} \frac{{\left( {A/I} \right)^{2} }}{{K + \left( {A/I} \right)^{2} }} - d_{s} S\left( {t, x} \right) + r_{p } } \right), $$

(3)

where $b_{s}$ is the transport rate of activated TFs to the nucleus, $d_{s}$ is the removal rate of TFs from nucleus; $r_{p}$ is a small constant transport rate of the activated TFs into the nucleus. Thus, the quantity $S$ can be regarded as the degree of activation of TFs, if $A \gg I$, $S \approx (b_{s} + r_{p } )/d_{s}$ and if $I \gg A$, $S \approx r_{p } /d_{s}$. The function $r_{v} \left( t \right)$ is the reaction velocity. It represents the effectiveness of the system to translate local differences in the diffusion factors into the degree of activation of TFs. If not specified, we will consider $r_{v} \left( t \right) \equiv 1$. Otherwise, we will assume that the reaction velocity decreases with time with the maximal value of $1$ at time $t = 0$. In our simulations, we take a Hill-type function,

$$ r_{v} \left( t \right) = \left\{ {\begin{array}{*{20}l} {1,\quad t < t_{0} } \hfill \\ {\frac{{k_{v}^{\eta } }}{{k_{v}^{\eta } + \left( {t - t_{0} } \right)^{\eta } }}, \quad t \ge t_{0} } \hfill \\ \end{array} } \right., $$

(4)

where $t_{0}$ is the time at which the reaction velocity begins to decrease, $\eta \ge 1$ the Hill coefficient and $k_{v} > 0$ the half-saturation constant.

We take the initial conditions ($t = 0$) for $A$, $I$, and $S$ to be random and uniformly distributed in the interval $J_{ini} = \left[ {0.5, 1.5} \right]$. We also test an initial tendency slope in the TFs’ number (linear vertical gradient, from $S_{\hbox{max} }$ to $S_{\hbox{min} }$). These choices are intended to enable the apparition of all patterns of interest without investigating particular initial condition as will be shown in the following section and specified in the Supplementary Material.

The domain of integration is a square in ${\mathbb{R}}^{2}$, and Eqs. (1) and (2) are treated with no-flux boundary conditions. All simulations were performed in Matlab R2012b. (Mathworks Inc., MA) using finite differences. Parameters used in our simulations are shown in Table 1, otherwise they are specified in the figure legends. We set the time-step $\Delta t = 0.01$. The reference spatial domain $\left[ {a,b} \right] \times \left[ {a,b} \right]$ was discretized, such that $\Delta x = \Delta y = \frac{b - a}{M}$, where the parameters are $a = - 1$, $b = 1$, and $M = 100$. We used the forward Euler method to compute the solution in time, and a second-order central finite differences approximation was used to evaluate the diffusion term. In all cases, the number of time steps chosen was small enough to observe no discernible change in the solution; in particular, when we used smaller discretization time steps ($\Delta t = 0.001$), the solution did not change significantly. The differential equations were simulated with no-flux boundary conditions. All our simulations were stopped at the indicated runtime $T_{e}$, The Matlab code for Turing pattern generation presented by Schneider (2012) has been used as an initial framework for our program. The units are as follows: $b_{a}$, $b_{i}$, $b_{s}$,$d_{a}$, $d_{i}$, $d_{s}$: time⁻¹; $D_{a}$, $D_{i}$: length²/time; $\nabla^{2}$ length⁻²; $A$, $I$, and $S$: molecules/length³; $\Delta t$, $T_{e}$: time; $r_{p }$: molecules∙length⁻³ time⁻¹; $k_{v}$: time,$r_{v}$, $\eta$, $M$: without units; $a$, $b$, $\Delta x$, $\Delta y$: length. We used arbitrary parameter values for our simulations, since juvenile or adult mammals have already developed patterns (e.g., zebras) and there are no exact data of stripes development during embryonic lifetimes. Nevertheless, adjustment of our model to potential future real data is possible. This has been demonstrated by fitting the parameters of Turing equations to the stripes development on the skin of the marine angelfish Pomacanthus (Kondo and Asai 1995).

Table 1 Parameters used in our simulations, otherwise they are specified in the figure legends

3 Results

3.1 The Four Situations

The situation defined as “Activating” leads to the generation of prototypical Turing patterns. As shown in previous systems, changing one parameter produces regularly spaced black or white dots in a background of the opposite color (Fig. 2a, c, respectively) and labyrinth patterns in between (Miyazawa et al. 2010). To achieve such labyrinth patterns, the inhibitor needs to diffuse faster than the activator (Fig. 2b). The usage of concentration gradients has already been proposed and was shown to play a role in stripes formation (Hiscock and Megason 2015; Quininao et al. 2015). If one uses a linear gradient for the activation level of TF, the system forms regular stripes and the slope of this gradient determines the two poles (Fig. 2d). The positive pole is at the top of the slope (highest initial activity), while the negative pole is at its bottom (lowest initial activity). When starting the simulation, the first stripe appears extremely fast and close to the negative pole and the stripe generation starts from both poles. After some time, it ends in the middle of the domain, even if the negative pole is more effective, i.e., faster, in the stripe generation.

Fig. 2

Simulations. Initial conditions are set uniformly and randomly on $J_{\text{ini}} = \left[ {0.5, 1.5} \right]$, for $A$, $I$, and $S$ for all $x$. In all figures, $S$ was plotted. Activating situation: “Turing patterns,” i.e., regular dots and labyrinth patterns, can be generated with $d_{s} = d_{a} = d_{i} = 0.1$, $b_{s} = 1$, $b_{i} = 0.3$, $D_{a} = 0.00008$, $D_{i} = 0.005$, $K = 50$, $r_{p } = 0.001$, $T_{e} = 8000$, and a$b_{a} = 0.5$, b$b_{a} = 1.1$, and c$b_{a} = 1.5$. In d, a linear slope for the initial conditions of $S$ is used. Regular stripes begin to form at the negative pole (where there is less initially activated TF). They remain regular only when close to the poles. The previous parameters are used with $b_{a} = 1.1$ and initial conditions for $S$ set linearly along the $y$ axis between $\left[ {0.5,8} \right]$. Inhibiting situation: Regular dots and labyrinths are obtained. Parameters are similar to the previous situation (b), but $b_{a} = 0.9$ is fixed, $D_{a} = 0.005$, $D_{i} = 0.00008$, and $b_{i}$ varies such that e$b_{i} = 0.5$, f$b_{i} = 2$, and g$b_{i} = 2.85$. Mixed I situation: Transient piebald patterns are generated. They strongly depend on the initial conditions. Here, we use a large dispersal for the initial values of $A$ and $I$ ($J_{\text{ini}} = \left[ {0.5, 100.5} \right])$ that enables both stable equilibria to be transiently attained with low diffusion. The parameters are similar to the previous situation, but $b_{a} = 1$, $D_{a} = 0.00006$, $D_{i} = 0.00001$, and $b_{i}$ varies such that h$b_{i} = 0.11$, i$b_{i} = 0.125$, and j$b_{i} = 0.15$. In k, we used a linear initial gradient along the $y$-axis for $S$ with values between $\left[ {0.4, 1.6} \right]$ and $b_{i} = 0.125$. The simulation was stopped at $T_{e} = 100$. Mixed II situation: Gray tones are obtained. Parameters are $d_{s} = d_{a} = d_{i} = 0.1$, $b_{s} = 1$, $b_{i} = 0.01$, $D_{a} = 0.0001$, $D_{i} = 0.003$, and l$b_{a} = 0.01$, m$b_{a} = 1$, and n$b_{a} = 10$. The simulation was stopped at $T_{e} = 100$

In the Supplementary Material S1 Text, all mathematical details are provided to show that this case leads to similar conditions as the ones Turing found for diffusion-driven instability: The system’s steady-state is always stable in the absence of diffusion, and the condition for diffusion-driven instability is illustrated in Fig. S1A.

The Inhibiting situation also generates regularly distributed dots as well as labyrinths. However, the diffusion coefficient of the activator needs to be higher than the one for the inhibitor, as illustrated in Fig. 2e–g. The structure of this model is similar to the model proposed by Raspopovic (Raspopovic et al. 2014).

A mathematical analysis shows similar results as the ones provided in the activating situation (see Supplementary Material and Fig. S1). In both situations, the steady states are of the same nature (linearly stable without diffusion). The roles of the substances $A$ and $I$ are reversed and similarly are the conditions leading to diffusion-driven instability.

The Mixed I situation generates the “classical” piebald patterns as observed in Dalmatian dogs (Canis lupus familiaris) (Fig. 3a–c). As in the activating case, modifying one parameter in the model (e.g., the production rate of the so-called inhibitor $b_{i}$) results in variations of the patterns. It varies from randomly distributed and inhomogeneous white spots (Fig. 2h) to inhomogeneous black spots (Fig. 2j). In the intermediate situation, black and white spots are relatively well dispersed (Fig. 2i). A gradient of the initial activity of the immobile TF leads to a concentration of the white spots at the bottom of the rectangular domain (negative pole), while the remaining surface (upper part) is uniformly black (Fig. 2k). Such particular patterns are commonly observed on the coat of Landseer Newfoundland dogs (Canis lupus familiaris) and Holstein–Friesian cattle (Bos taurus) (Pape 1990). One of the differences between the Mixed I case and the two previous ones is the system’s steady state, when considering $D_{a} = D_{i} = 0$. Here, the mechanism leading to the pattern formation is slightly different from the original analysis of Turing; the system with $D_{a} = D_{i} = 0$ is bistable, see Supplementary Material. As such, in this case, the initial conditions determine the long-term behavior of $S\left( {t,x} \right)$, which may attain two different states (e.g., black and white) as time increases. The random arrangement of the obtained patches results thus directly from the noisy initial conditions; Fig. S2B in the Supplementary Material illustrates the two basins of attraction for such a system. The choice of our initial conditions $J_{\text{ini}}$ was selected to make model frameworks comparisons easier. In this case, the spread of this interval is sufficiently large to attain both steady states for certain parameter ranges of other kinds, as $b_{i}$ or $b_{a}$ (see Fig. S2 in the S1 Text). This spread is thus a requirement for piebald patterns to be expressed within our model. The pigmented spots are the result of the stochastic migration of primordial pigment cells (melanoblasts) from the neural crest to their final locations in the skin of the early embryo (Li et al. 2011; Mort et al. 2016). Although the mathematical model considering only the random movement of melanoblasts does not produce sharp edges between the colored and the melanocyte-free regions (Mort et al. 2016), the initial noisy random condition, the pre-requirement of our model, can be explained by a model incorporating random melanoblast migration with proliferation in the skin of the developing embryo (Mort et al. 2016). Adding diffusion to the modeling smoothens and destabilizes the long-term behavior of $S\left( {t,x} \right)$, with visible transient patterns appearing, if parameters $D_{a}$ and $D_{i}$ are sufficiently small. The numerical analysis performed in the Supplementary Material led to the bifurcation diagram of Fig. S2A. This illustrates the system’s bistability and diffusion-driven instability. The spots on Dalmatian dogs appear after their birth with increasing sizes and contrasts, indicating that a reaction–diffusion mechanism may also be involved in their formation (Fig. 3a–c).

Fig. 3

Developing patterns on the fur of Dalmatian dogs. Newborn Dalmatian dogs have no or very small black dots (a). The same dog at the age of 10 weeks (b) and 6 years (c). Newly developed dots are marked with yellow arrows. Some dots show an increase in their relative size (red arrowheads). Dalmatians were photographed by Nina Hedvig Eriksen (Color figure online)

In the Mixed II situation, differences in diffusion rates do not play a role. This mechanism generates different levels of $S$, but does not produce patterns in the long-term behavior of $S\left( {t,x} \right)$ (Fig. 2l–n). A numerical analysis of the situation shows mono-stability in the absence of diffusion and no diffusion-driven instability, which leads to simple color tones, see S1 Text.

3.2 The Effect of Initial and Dynamical Noise on the Pattern

We distinguish initial noise (uniform distribution on a support denoted by $J_{\text{ini}}$ in the concentrations of diffusion factors and TFs, which essentially leads to different initial conditions and dynamical noise involved in the process.

We found that the initial noisy conditions have a particularly strong effect determining the final pattern, as explained in the Mixed I situation. Similarly, the initial noisy conditions almost entirely determine the precise expression of the Turing patterns in Activating and Inhibiting situations as shown in Fig. 4 (upper row) versus Fig. 4 (middle row), if there is only moderate noise during the process.

Fig. 4

Robustness to noise. a The four situations are represented in each case with identical (fixed) initial conditions. In the top row, $\sigma_{a} = \sigma_{i} = 0$, and there is no extrinsic noise in the system. In the middle row, $\sigma_{a} = \sigma_{i} = 0.01$; thus, $\xi_{a}$ and $\xi_{b}$ are uniformly distributed random variables. In the lower row, $\sigma_{a} = \sigma_{i} = 0.1$. First column Activating situation, with parameters as in Fig. 2b. Second column Inhibiting situation, with parameters as in Fig. 2F. Third column Mixed I situation, with the parameters as in Fig. 2I. Fourth column Mixed II situation, with parameters as in Fig. 2M. b, c Development of $S$ activation at a given position (blue spot) $x$ in the case of an Activating situation. Red line: $\sigma_{a} = \sigma_{i} = 0$; green line: $\sigma_{a} = \sigma_{i} = 0.01$; blue line: $\sigma_{a} = \sigma_{i} = 0.1$. d Periodogram of the blue line using fast Fourier transformation (dB = decibel, rad = radian) (Color figure online)

However, strong noise influences the resulting pattern outcomes (see Fig. 4 (upper row) versus Fig. 4 (lower row)). Overall, the model proposed here is thus particularly robust to small stochastic variations that may occur during chemical reactions and relies mostly on the interacting structures between the diffusing agents and the TFs, encoded in our functions $f$ and $g$ as well as in the initial conditions.

Time series of changes in $S$ at the position of $x$ are presented in the Activating situation (Fig. 4b, c). A periodogram of the time series of Activating situation at the highest dynamical noise $\sigma_{a} = \sigma_{i} = 0.1$ is presented in Fig. 4d using fast Fourier transformation. The periodogram shows a steep increase at the lower frequencies.

3.3 Pattern “Freezing”

We can regulate the speed of the pattern formation using the parameter $r_{v}$ seen as a scaling for the activation levels of TFs, due to posttranslational modifications (Filtz et al. 2014). If this value is close to zero, the pattern formation dynamics is halted (“frozen”) and the pattern will not change significantly over time (Fig. 5). Thus, assuming such a mechanism, a transient pattern such as the piebald pattern may last in a given form on the animal coat for a very long period. A detailed analysis of the pattern-freezing phenomenon in the Activating situation has been performed in another study (Dougoud et al., under review).

Fig. 5

Freezing of the piebald pattern. Top row: The simulation is based on Mixed I situations with the parameters as in Fig. 2I, middle row) The pattern develops as in the top row and is frozen with $k_{v} = 100$patches, we consider, $\eta = 3$, and $t_{v} = 300$. Bottom row: The pattern develops as in the top row and is frozen with $k_{v} = 100$, $\eta = 3$, and $t_{v} = 0$

3.4 A Model Extension for Describing Overlapping Patterns

Interesting situations can also occur when multiple diffusion factors are involved in the system, e.g., two activators and two inhibitors. Two mechanisms need thus to be considered at the same time. For this purpose, let $A_{1} \left( {t,x} \right)$ be the concentration of the first activator at place $x$ and time $t$$A_{2} \left( {t,x} \right)$ the concentration of the second activator at place $x$ and time $t$ and similarly for $I_{1}$$I_{2}$$S_{1}$, and $S_{2}$. All these quantities follow these differential equations:

$$ \frac{{\partial A_{k} \left( {t, x} \right)}}{\partial t} = b_{a,k} f_{k} \left( {S_{k} \left( {t, x} \right)} \right) - d_{a,k} A_{k} \left( {t, x} \right) + D_{a,k} \nabla^{2} A_{k} \left( {t, x} \right) $$

(5)

$$ \frac{{\partial I_{k} \left( {t, x} \right)}}{\partial t} = b_{i,k} g_{k} \left( {S_{k} \left( {t, x} \right)} \right) - d_{i,k} I_{k} \left( {t, x} \right) + D_{i,k} \nabla^{2} I_{k} \left( {t, x} \right) $$

(6)

$$ \frac{{dS_{k} \left( {t,x} \right)}}{dt} = r_{v} \left( t \right) \cdot \left( {b_{s,k} \frac{{\left( {\frac{{A_{k} }}{{I_{k} }}} \right)^{2} }}{{K + \left( {\frac{{A_{k} }}{{I_{k} }}} \right)^{2} }} - d_{s,k} S_{k} \left( {t, x} \right) + r_{p.k } } \right) $$

(7)

With $k = 1,2$ and where $f_{k}$ and $g_{k}$ are functions similar to the functions $f$ and $g$ defined according to the situations of interest. All other parameters are defined similarly as before. The substances $S_{k}$ are constructed in an analogous way as before. Then, the substance of interest $S$, i.e., the concentration of the melanocyte attractant/activator, is a combination of $S_{1}$ and $S_{2}$, i.e., within this framework, we track

$$ S \left( {t, x} \right) = \alpha_{1} S_{1} \left( {t, x} \right) + \alpha_{2} S_{2} \left( {t,x} \right), $$

(8)

where $\alpha_{1} ,\alpha_{2}$ are positive constants that we choose such that $\alpha_{1} + \alpha_{2} = 1$. For example, to produce the patterns shown in Fig. 6a, with regular stripes and irregular patches, we consider the Mixed I situation with

$$ f_{1} \left( s \right) = s,\quad g_{1} \left( s \right) = \frac{1}{s} $$

and the Activating situation

$$ f_{2} \left( s \right) = s,\quad g_{2} \left( s \right) = s, $$

while the substances $S$ are such that

$$ S\left( {t,x} \right) = \left\{ {\begin{array}{*{20}l} {S_{1} \left( {t, x} \right), \quad S_{1} \left( {t, x} \right) = r_{p} /d_{s} } \hfill \\ {\alpha_{1} S_{1} \left( {t,x} \right) + \alpha_{2} S_{2} \left( {{\text{t}},{\text{x}}} \right), \quad S_{1} \left( {t, x} \right) > r_{p} /d_{s} } \hfill \\ \end{array} } \right. $$

Fig. 6

Overlapping patterns. a Cats contain both set of genes required for piebald patterns and Turing-based stripe formation. (photographed by Viktoria Szabolcsi). b In a zebra–horse hybrid animal, the stripes generated by a Turing mechanism appear only on the dark part of the piebald pattern (photographed by Yannik Willing). c, d In the overlapping model, there are two sets of components: activating diffusion factors (A1, A2) and inhibiting diffusion factors (I1, I2) and transcription factors (S1, S2) for the piebald pattern and Turing pattern generation, respectively. The S1 (melanocyte attractant) and (S2) (melanocyte stimulant) interacting with each other, as described in Sect. 2. c Parameters are the same as in Fig. 5 (middle row) for piebald patterns and as in Fig. 2a for Turing patterns, except that $b_{a} = 0.7$. d Parameters are the same as shown in Fig. 5 (middle row) for piebald patterns and as in Fig. 2d for Turing patterns (color figure online)

This denotes that since in the region of white patches, regular stripes cannot develop (there is no melanocyte in this region $S_{1} \left( {t, x} \right) \approx 0$), melanocyte differentiation can only occur in the areas with black patches. We assume that although the $S_{2}$-related diffusion factor produced by keratinocytes and dermal fibroblasts (acting as an activator for melanocyte differentiation) is produced in the white patches as well, it cannot exert its effect. Indeed, in such regions, there are no melanocytes, on which an effect could be exerted.

3.5 Overlap of Regular and Irregular Piebald Patterns

Performing a “genetic cross” of animals using Turing pattern and piebald pattern generating processes for their fur coat patterns reveals a spatial overlap of the two patterns, as exemplified by the fur patterns of a zebra–horse hybrid (Equus zebra ♀ X Equus caballus ♂) (Fig. 6a) or a cat (Felis catus) (Fig. 6b). In both of these examples, the pattern does not appear on the white region of the piebald patches. It is also worth noting that the background of the stripes on the hybrid animal is darker compared to the regular white–black stripes present on a zebra fur. This indicates that the two pattern-forming situations tend to overlap. The presented simulations (Fig. 6c, d) reveal a very similar pattern formation highly reminiscent of the pattern seen on the photographs of the cat and horse hybrid.

4 Discussion

A third non-diffusing factor has already been considered in some previous mathematical works (Klika et al. 2012; Marcon et al. 2016; Raspopovic et al. 2014), investigating the effect of cell-autonomous factor(s) on the parameter range of reaction–diffusion equations producing Turing-type patterns. The third non-moving component is considered to be a cell membrane receptor (Marciniak-Czochra 2003), an extracellular matrix molecule reversibly binding to diffusion factors (Korvasova et al. 2015) or a transcription factor (Raspopovic et al. 2014). Mathematical analysis of three- and multi-component systems revealed that in the presence of a non-moving component the pattern may be formed within a wider range of the diffusion parameters; patterns may be formed with equal diffusivities of activator and inhibitor (Marcon et al. 2016), with two activators (Korvasova et al. 2015) or even with only one diffusive component (Anma et al. 2012; Marcon et al. 2016). Here, we showed that the presence of a cell-autonomous factor not only expands the range of reaction–diffusion parameters in which the pattern may be formed, but also extends pattern-forming abilities of the reaction–diffusion equations. The Supplementary Material S1 Text provides a detailed mathematical and numerical analysis of the former. It also sheds light on its importance compared to a two-factor reduction of the model in producing piebald patterns (Fig. S5).

Searching for the precise molecular identity of the model’s components ($A$, $I$, ${\text{TF}}$, and ${\text{MA}}$) is a challenging task for experimental work, but analyzing the existing literature allows to select some candidates. In the Activating and Inhibiting situations, our model produces Turing-type patterns. This type of pattern has been experimentally investigated in felids. In these, pigment-type switching controlled by Asip and Edn3, both factors acting in a paracrine way, is the major determinant of color patterns (Kaelin et al. 2012). These factors originate from the dermal papilla of hair follicles and influence the pigment synthesis pathway leading to the production of either eumelanin (brown–black) or pheomelanin (yellow–red) (Mills and Patterson 2009). The production of Asip is promoted by the morphogen BMP4 (Abdel-Malek and Swope 2011). The latter is assumed to work as an inhibitory molecule in several Turing-type developmental processes (Miura 2007). The activatory molecule is assumed to be the bFGF diffusion factor produced by fibroblasts in the dermis. The factor bFGF and other Ras/MAPK pathway activators inhibit BMP signaling through MAPK-mediated phosphorylation of SMAD transcription factors (Sapkota et al. 2007). Besides that, the secreted protein Wnt acting via the Wnt/β-catenin signaling pathway also inhibits BMP4 production (Baker et al. 1999). Wnt and BMP4 have been already proposed serving as a Turing pair in digit development (Raspopovic et al. 2014). Theoretically, noggin, another secreted protein, also operates together with BMP4 as a Turing pair, because noggin (i) extracellularly binds BMP4, (ii) inhibits the effect of BMP4, and (iii) modulates its diffusion parameters forming a noggin/BMP4 pair (McMahon et al. 1998). Molecular analysis also revealed that a transmembrane aminopeptidase, tabulin, is playing a role in the blotched tabby cat and king cheetah pattern formation (Kaelin et al. 2012). Most probably, this protein interferes with the movement of diffusion factors. A recent finding shows that in African striped mice (Rhabdomys pumilio) and in Eastern chipmunks (Tamias striatus), the periodic dorsal stripes are the result of differences in melanocyte differentiation and that the transcription factor ALX3 is a regulator of this process (Mallarino et al. 2016).

The localized absence of the pigment-producing melanocytes results in irregular patches of white (piebald pattern) coloration on an animal skin. Although children born with piebaldism had been displayed in circuses as “The Zebra People” (Huang and Glick 2016), one needs to reconcile that the piebald patterns and zebra stripes are the result of different processes. Piebald patterns are not restricted to animals such as horses, dogs, birds, cats, pigs, and cattle, but are also observable on human skin. Usually piebaldism does not change with time; however, the “colorless” areas occasionally shrink or in some cases may spontaneously disappear (“heal”) (Frances et al. 2015). In line with our model, this indicates that generally a piebald pattern is a transient pattern. One can also observe that the relative sizes of irregular patches of piebald patterns are increasing with time. If we suppose that the pattern-freezing phenomenon occurs at different developmental stages of piebald pattern formation, this will lead to smaller or bigger patches on animals coat. To give an example from the animal kingdom, one can compare the patterns of Appaloosa (small irregular patches) and Tobiano (big irregular patches) horses (Equus caballus) or the patterns of Dalmatian and Landseer Newfoundland dogs (Canis lupus familiaris).

The molecular background of the piebald pattern is the altered melanocyte distribution. The diffusion factor SCF and its receptor KIT on melanocytes were identified as factors for melanocyte survival and distribution. The clinical features and phenotypic severity of piebaldism clearly correlate with the site and the type of mutations in the KIT gene encoding the KIT receptor (Oiso et al. 2013; Spritz 1994). Its ligand, the diffusion factor SCF, produced by keratinocytes and dermal fibroblasts, also serves as a chemoattractant for melanocytes. Besides that, mutations in the diffusion factor endothelin 3 (ET3) and its receptor, EDNRB, have been implicated in the Waardenburg syndrome type 4, a disease characterized by piebaldism (Attie et al. 1995). Interestingly, although in the normal skin, the uniform melanocyte distribution is maintained and is restored after temporal destruction of melanocytes due to UV-light overexposure or moderate wound infliction (Griffiths et al. 2016), the zone with the piebald pattern does not heal as well. According to our model, this may be due to the presence of a yet unidentified inhibitor present in the non-pigmented region (Fig. 1d).

In conclusion, we demonstrated in our modeling framework that noisy initial conditions coupled with well-defined feedback loops of the interacting factors determine which patterns are generated. As such, piebald patterns are produced when TFs trigger the production of activators, while at the same time block the production of inhibitor. Although the model parameters have not been adjusted to a specific pattern in this study, our model allows to easily reproduce current Turing patterns. At the same time, our framework sheds new light on phenomena such as piebaldism.