Mathematical Model of Contractile Ring-Driven Cytokinesis in a Three-Dimensional Domain

Abstract

In this paper, a mathematical model of contractile ring-driven cytokinesis is presented by using both phase-field and immersed-boundary methods in a three-dimensional domain. It is one of the powerful hypotheses that cytokinesis happens driven by the contractile ring; however, there are only few mathematical models following the hypothesis, to the author’s knowledge. I consider a hybrid method to model the phenomenon. First, a cell membrane is represented by a zero-contour of a phase-field implicitly because of its topological change. Otherwise, immersed-boundary particles represent a contractile ring explicitly based on the author’s previous work. Here, the multi-component (or vector-valued) phase-field equation is considered to avoid the emerging of each cell membrane right after their divisions. Using a convex splitting scheme, the governing equation of the phase-field method has unique solvability. The numerical convergence of contractile ring to cell membrane is proved. Several numerical simulations are performed to validate the proposed model.

1 Introduction

Although cell division is one of the most fundamental and important phenomena of living cells, its general principles are still not clear because of its complicated process (Pollard and Cooper 2008). A plausible hypothesis of the division is that the formation of a contractile ring (CR) drives the physical division process by dragging the cell membrane (Shlomovitz and Gov 2008) and there are many studies on the function of a CR during the final step of cell division (called cytokinesis) (Bathe and Chang 2010; Bi et al. 1998; Calvert et al. 2011; Carvalgo and Oegema 2009; Celton-Morizur et al. 2004; Chang et al. 1997; Jochova et al. 1991; Kamasaki et al. 2007; Mandato and Berment 2001; Pelham and Chang 2002). However, assembly or dynamics of a CR in a cytokinesis is still poorly understood (Wang 2008). It is important to come up with testable models to decipher detailed assembly and dynamics from the amount of experimental observation or data. For example, biologists have addressed the experimental results of the relationship between cytokinesis and cancer cells (Daniels et al. 2004; Gisselsson et al. 2010; Kang et al. 2010) and it could be extremely expensive in a temporal or financial aspect to test each undesirable case in a laboratory, whereas its difficulty can be resolved by establishing a reliable computational model. Vavylonis et al. (2008) considered a simple numerical model for assembly mechanism of the CR for cytokinesis by fission yeast using the Monte Carlo method. Zhou et al. (2015) studied spatially coordinate curvature-dependent septum assembly of a CR during fission yeast cytokineses. Recently, Koudehi et al. (2016) performed numerical simulations to show the effect of actin spherical confinement and cross-linking in CR formation, and Lee et al. (2016) proposed a numerical model for a CR in a three-dimensional domain using an immersed-boundary (IB) method comparing its numerical result with an experimental data.

The phase-field (PF) method, whose governing equation is the Cahn–Hilliard (CH) equation (Cahn and Hilliard 1958), is a useful mathematical tool to resolve an interfacial problem when topological changes occur, such as solidification dynamics (Wheeler et al. 1992), image inpainting (Bertozzi et al. 2007; Li et al. 2015), tumor growth (Chen et al. 2014), multi-phase fluid flows (Lee et al. 2016). A multi-component system of the CH equation was first generalized in the de Fontaini’s literature (1967). Lee and Kim considered a second-order accurate nonlinear difference scheme for generalized multi-component CH system (Lee and Kim 2008). Zhao and Wang Zhao and Wang (2016b, 2016a) proposed cytokinesis models using the phase-field method with a contractile forcing term.

The IB method was originally developed by Peskin (Peskin 1972), and it has an advantage presenting flexible boundaries to move or change shapes in a complicated fashion. An elastic boundary problem has been simulated using the IB method, such as the dynamics of a bent and twisted rod (Lim et al. 2008; Lim 2010), a deformable fiber (Vahidkhah and Abdollahi 2012), a wall modeling (Chen et al. 2014; Posa and Balaras 2014), and fluid flows between eccentric rotating cylinders (Botella et al. 2015).

In this paper, a process of contractile ring-driven cytokinesis is modeled by using PF and IB methods in a three-dimensional domain. The CR is represented by the Lagrangian particles using the IB method based on Lee et al. (2016) without a point-deleting algorithm. However, the IB method has a numerical difficulty when the boundaries suffer the topological changes like emerging or division; therefore, the PF method is used to describe the dynamics of the cell membrane because the topological change, cell division, is more easily described than using the IB method fully. To avoid merging the divided cell membranes again, the vector-valued CH systems are considered rather than the original CH equation.

The rest of the paper is organized as follows: The governing equations and their properties are introduced in Sect. 2. The discretization of the equations and numerical solutions are given in Sect. 3. The simulation results are shown in Sect. 4. The conclusion is drawn in Sect. 5.

2 Mathematical Model

A contractile ring and a cell membrane are considered by using the IB and PF methods, respectively, in a three-dimensional incompressible fluid. Here, the incompressible fluid can be modeled by the Navier–Stokes equation as explained in the later section.

2.1 Fluid Motion

The cytokinesis is accomplished by a CR assembling just beneath the plasma membrane and contracting to divide one mother cell into two daughter cells. Concurrently, a new membrane is inserted into the plasma membrane by the fusion of intracellular vesicles (Alberts et al. 2002). Since describing the above processes exactly is too complicated in a modeling, the cell surface is modeled by the fluid interface for simplicity (Li and Kim 2016). The equations of fluid motion are given as

$$\begin{aligned}&\frac{\partial \mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u} = -\nabla p + \frac{1}{Re} \Delta \mathbf{u} + \frac{1}{We} \mathbf{f}, \quad \hbox {in}\quad \Omega \times (0, \infty ), \end{aligned}$$

(1)

$$\begin{aligned}&\nabla \cdot \mathbf{u} = 0, \end{aligned}$$

(2)

where $\mathbf{u}(\mathbf{x}, t) = (u(\mathbf{x}, t), v(\mathbf{x}, t), w(\mathbf{x}, t))$ is the fluid velocity, $\mathbf{x} = (x,y,z)$ is the Cartesian coordinate in $\Omega = (a_x,b_x) \times (a_y,b_y) \times (a_z,b_z) \subset \mathbb {R}^3$, t is the time variable, $p(\mathbf{x},t)$ is the pressure, $Re = \rho U^* L^* / \eta$ is the Reynolds number, and $We = \rho \left( U^* \right) ^2 L^* / \sigma$ is the Weber number with the density $\rho$, the viscosity $\eta$, the force density coefficient $\sigma$, the characteristic velocity $U^*$, and the characteristic length $L^*$. Here, the periodic boundary condition is implemented. $\mathbf{f} = \left( f^x(\mathbf{x},t), f^y(\mathbf{x},t), f^z(\mathbf{x},t)\right)$ is the fluid force density defined by $\mathbf{f}_m + \mathbf{f}_r$ with the force densities $\mathbf{f}_m$ and $\mathbf{f}_r$ generated by the cell membrane and the contractile ring, respectively.

2.2 Cell Membrane

For a lipid membrane, its elasticity is governed by the Helfrich free energy functional expressed by curvatures of the membrane (Helfrich 1973) and it is known that the bending energy given by the Helfrich Hamiltonian can be derived from the Landau–Ginzburg model (Gompper and Zschoke 1991). Note that the Landau–Ginzburg free energy functional leads to the CH equation on a solution conserved space. Therefore, the shape of the cell membranes is described by a zero-contour of a diffused-interface PF function ${\varvec{\phi }}(\mathbf{x},t) = (\phi _1(\mathbf{x},t), \phi _2(\mathbf{x},t), \ldots , \phi _N(\mathbf{x},t))$, governed by the advective N-component CH equation (Lee et al. 2016):

$$\begin{aligned} \frac{\partial \phi _i}{\partial t} + \mathbf{u} \cdot \nabla \phi _i = \frac{1}{Pe} \Delta \left( f(\phi _i) - \epsilon ^2 \Delta \phi _i + \beta ({\varvec{\phi }}) \right) , \quad \hbox {for}\quad i = 1, 2, \ldots , N, \end{aligned}$$

(3)

where $\phi _i$ is the volume fraction (here $\phi _i = 1$ in ith component and $\phi _i = -1$ in other components. See Fig. 1), $Pe = L^* U^* / M$ is the Peclet number with the mobility M, $f(\phi _i) = \phi _i^3 - \phi _i$, $\epsilon$ is the constant related to the interface thickness, and $\beta ({\varvec{\phi }}) = - \sum _{i=1}^N f(\phi _i) / N$ is the Lagrangian multiplier. Here, $\beta ({\varvec{\phi }})$ makes $\sum _{i=1}^N \phi _i = 2 - N$ and it implies that $\phi _{N}$ can be decided without solving (3). The periodic boundary condition is also implemented as the fluid velocity field. The force density $\mathbf{f}_m$ is defined as the surface tension force of $\phi _i$ written in the form (Kim 2005)

$$\begin{aligned} \mathbf{f}_m (\mathbf{x},t) = - \sum _{i=1}^{N-1} \frac{\alpha \epsilon }{We} \nabla \cdot \left( \frac{\nabla \phi _i}{\left| \nabla \phi _i \right| } \right) \left| \nabla \phi _i \right| \nabla \phi _i, \end{aligned}$$

(4)

where $\alpha$ is the correction coefficient for a diffused-interface model.

Fig. 1

Schematic illustration for the distribution of $\phi (\mathbf{x},t)$ when $N=4$

2.3 CR

The CR generates the constricting force to divide a cell into two cells during cytokinesis by creating a cleavage furrow (Miller 2011). For simplicity, I consider a CR as a certainly elastic shrinking loop as in my previous result (Lee et al. 2016). The evolution equation of the CR positions, defined as Lagrangian variables $\mathbf{X}_i(s_i,t) = ( X_i(s_i,t), Y_i(s_i,t), Z_i(s_i,t) )$ for $i=1, \ldots , N-1$ with parameters $s_i$ in $[0, L_{i,t}]$, where $L_{i,t}$ is the unstressed length of the ith ring, is given by

$$\begin{aligned} \frac{\partial \mathbf{X}_i(s_i,t)}{\partial t} = \mathbf{U}_i(s_i,t) = \int _\Omega \left( -\phi _i (\mathbf{x},t) \right) \mathbf{u}(\mathbf{x},t) \delta \left( \mathbf{x} - \mathbf{X}_i(s_i,t) \right) \mathrm{d}{} \mathbf{x}, \end{aligned}$$

(5)

where $\mathbf{U}_i(s,t)$ is the ith CR velocity on $\mathbf{X}_i(s_i,t)$ and $\delta (\mathbf{x})$ is the three-dimensional Dirac delta function. Here, the term $\left( -\phi _i(\mathbf{x},t) \right)$ makes the CR position on the cell membrane. In the model, the elastic force for the CR is generated by reducing $L_{t,i}$ as time evolves end the force density $\mathbf{f}_r$ is defined as the following integration

$$\begin{aligned} \mathbf{f}_r (\mathbf{x},t) = \sum _{i=1}^{N-1} \int _0^{L_{i,t}} \mathbf{F}_{r,i} (s_i,t) \delta (\mathbf{x} - \mathbf{X}_i(s_i,t))\mathrm{d}s, \end{aligned}$$

(6)

where $\mathbf{F}_{r,i}(s_i,t) = \partial \left[ T_i(s_i,t) {\varvec{\tau }}_i(s_i,t) \right] / \partial s$ is the elastic force density of the ith CR, $T_i(s_i,t) = \sigma \left( \left| {\partial \mathbf{X}_i}/{\partial s_i} \right| -1 \right)$ is the tension of the ith CR, and ${\varvec{\tau }}_i(s_i,t) = ({\partial \mathbf{X}_i/\partial s_i})/{\left| \partial \mathbf{X}_i / \partial s_i \right| }$ is the unit tangent vector to the ith CR. The detailed descriptions can be referred in Lee et al. (2016).

2.4 Cell Growth

To model a series of cell divisions, a growth term of the cell should be added in (3) between each cytokinesis. In a tumor growth model (Britton 2003), a growth term is considered as

$$\begin{aligned} \rho _t (\mathbf{x},t) + \nabla \cdot \left[ \rho (\mathbf{x},t) \mathbf{u}(\mathbf{x},t) \right] = \lambda _p \rho (\mathbf{x},t), \quad \hbox {in}\quad \Omega _t, \end{aligned}$$

(7)

where $\rho (\mathbf{x},t)$ is the tumor density, $\lambda _p$ is the proliferation rate, and $\Omega _t$ is the tumor domain. Furthermore, Eq. (7) can be written as

$$\begin{aligned} \nabla \cdot \mathbf{u}(\mathbf{x},t) = \lambda _p, \quad \hbox {in}\quad \Omega _t, \end{aligned}$$

(8)

with the constant density of the tumor, i.e., $\rho (\mathbf{x},t) \equiv \rho _0$. Applying (8) to a PF model (3), the result is

$$\begin{aligned} {\begin{matrix} &{} \frac{\partial \phi _i}{\partial t} + \mathbf{u} \cdot \nabla \phi _i = \frac{1}{Pe} \Delta \left( f(\phi _i) - \epsilon ^2 \Delta \phi _i + \beta ({\varvec{\phi }}) \right) + \frac{\lambda }{2} \left( 1 + \phi _i \right) , \\ &{} \quad \hbox {for}\quad i = 1, 2, \ldots , N-1, \end{matrix}} \end{aligned}$$

(9)

where

$$\begin{aligned} \lambda = \left\{ \begin{array}{ll} \lambda _p, &{}\quad \hbox {in a cell growth level} \\ 0, &{}\quad \hbox {otherwise.} \end{array} \right. \end{aligned}$$

3 Numerical Method

First, the discretization of each variable is introduced before considering numerical solvers for governing equations. Let the set of cell-centered grid points $\Omega _h = \left\{ (x_j, y_k, z_l): x_j = (j-0.5)h, y_k = (k-0.5)h, z_l = (l-0.5)h \right\}$ be the phase-field computational domain for $j=1, \ldots , N_x$, $k=1, \ldots , N_y$, and $l=1, \ldots , N_z$, where $h = (b_x - a_x)/N_x = (b_y - a_y)/N_y = (b_z - a_z)/N_z$ is the uniform spatial step size with the numbers of points $N_x$, $N_y$, and $N_z$ in x-, y-, and z-directions, respectively. Let $\phi _i(\mathbf{x},t)$ and $p(\mathbf{x},t)$ approximate on $\Omega _h$ by denoting $\phi _i(x_j, y_k, z_l, n\Delta t)$ and $p(x_j, y_k, z_l, n\Delta t)$ as $\phi ^n_{i,jkl}$ and $p^n_{jkl}$, respectively, where n is the integer and $\Delta t$ is the spatial step size. Similarly, let $\mathbf{u}$ approximate as $(u_{j+\frac{1}{2},kl}, v_{j,k+\frac{1}{2},l}, w_{jk,l+\frac{1}{2}})$ on cell-edged points (called a marker-and-cell (MAC) mesh; Harlow and Welch 1965) (See Fig. 2). The notations ${\varvec{\phi }}^n$, $\mathbf{u}^n$ are used when approximating only along the temporal axis.

Fig. 2

Schematic of a grid and variables

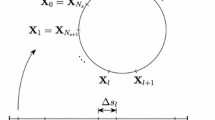
Moreover, let $\Delta s_{i,m}^n$ be the time-dependent step size satisfying $L_{i,t} = \sum _{m=0}^{N_{i,s}-1} \Delta s^n_{i,m} = \alpha _i(t^n) L{i,0}$, where $N_{i,s}$ is the number of ith variable intervals, $\alpha _i(t^n)$ is a scaling factor function at time $t = t^n$, and $L_{i,0}$ is the initial length of the ith CR. Then, $s^n_{i,m} = 0$ and $s^n_{i,m+1} = s^n_{i,m} + \Delta s^n_{i,m}$ for $m = 0, \ldots , N_{i,s}-1$. The discrete ith CR position is defined as $\mathbf{X}^n_{i,m} = \mathbf{X}(s^n_{i,m}, n\Delta t) = (X^n_i, Y^n_i, Z^n_i)$ for $m = 1, \ldots , N_{i,s}$. Note that $\mathbf{X}^n_{i,0} = \mathbf{X}^n_{i,N_{i,s}}$ and $\mathbf{X}^n_{N_{i,s}+1} = \mathbf{X}^n_1$ because of the periodicity. This parametrization of $\mathbf{X}_i (s_i, t)$ is schematically illustrated in Fig. 3.

Fig. 3

Schematic of parametrization of $\mathbf{X}(s,t)$. To simplify, the phase index i is omitted in this figure

Next, the discrete operators are defined. The discrete gradient operator $\nabla _d$ is defined as

$$\begin{aligned} \nabla _d \phi ^n_{jkl} = \left( \frac{\phi ^n_{j+\frac{1}{2},kl} - \phi ^n_{j-\frac{1}{2},kl}}{h}, \frac{\phi ^n_{j,k+\frac{1}{2},l} - \phi ^n_{j,k-\frac{1}{2},l}}{h}, \frac{\phi ^n_{jk,l+\frac{1}{2}} - \phi ^n_{jk,l-\frac{1}{2}}}{h} \right) , \end{aligned}$$

and the discrete divergence operator $\nabla _d \cdot \phi ^n_{ijk}$ is defined as

$$\begin{aligned} \nabla _d \cdot \phi ^n_{jkl} = \frac{\phi ^n_{j+\frac{1}{2},kl} - \phi ^n_{j-\frac{1}{2},kl}+\phi ^n_{j,k+\frac{1}{2},l} - \phi ^n_{j,k-\frac{1}{2},l}+\phi ^n_{jk,l+\frac{1}{2}} - \phi ^n_{jk,l-\frac{1}{2}}}{h}. \end{aligned}$$

From the above operators, the discrete Laplacian operator $\Delta _d$ is defined as

$$\begin{aligned} \Delta _d \phi ^n_{jkl} =&\, \nabla _d \cdot \left( \nabla _d \phi ^n_{jkl} \right) \\ =&\, \frac{\phi ^n_{j+1,kl} + \phi ^n_{j-1,kl} + \phi ^n_{j,k+1,l} + \phi ^n_{j,k-1,l} + \phi ^n_{jk,l+1} + \phi ^n_{jk,l-1} - 6 \phi ^n_{jkl}}{h^2}. \end{aligned}$$

These operators are also applied to $u^n_{i+\frac{1}{2},jk}$, $v_{i,j+\frac{1}{2},k}$, or $w_{ij,k+\frac{1}{2}}$ in a similar manner.

3.1 Fluid Motion

First, $\mathbf{u}^{n+1}$ is updated from a given $\mathbf{u}^n$. Applying the explicit scheme, the time-discrete version of Eqs. (1) and (2) is written as follows:

$$\begin{aligned}&\frac{\mathbf{u}^{n+1}-\mathbf{u}^n}{\Delta t} + \mathbf{u}^n \cdot \nabla \mathbf{u}^n = -\nabla p^{n+1} + \frac{1}{Re} \Delta \mathbf{u}^n + \frac{1}{We} \mathbf{f}^n, \end{aligned}$$

(10)

$$\begin{aligned}&\nabla \cdot \mathbf{u}^{n+1} = 0. \end{aligned}$$

(11)

Next, the Chorin’s projection method (Chorin 1968), well known as a useful solver for the Navier–Stokes equation, is used:

Step 1:

Calculate the temporal velocity $\tilde{\mathbf{u}}$ by solving the following equation:

$$\begin{aligned} \frac{{\tilde{\mathbf{u}}} - \mathbf{u}^n}{\Delta t} = - \mathbf{u}^n \cdot \nabla \mathbf{u}^n + \frac{1}{Re} \Delta \mathbf{u}^n + \frac{1}{We} \mathbf{f}^n. \end{aligned}$$

(12)

Note that $\tilde{\mathbf{u}}$ could not be divergence-free. Equation (12) can be discretized in space as follows:

$$\begin{aligned} \frac{\tilde{u}_{j+\frac{1}{2},kl} - u^n_{j+\frac{1}{2},kl}}{\Delta t} =&-(\mathbf{u} \cdot \nabla _d u)^n_{j+\frac{1}{2},kl} + \frac{1}{Re} \Delta _d u^n_{j+\frac{1}{2},kl} + \frac{1}{We} f^{x,n}_{j+\frac{1}{2},kl}, \\ \frac{\tilde{v}_{j,k+\frac{1}{2},l} - v^n_{j,k+\frac{1}{2},l}}{\Delta t} =&-(\mathbf{u} \cdot \nabla _d v)^n_{j,k+\frac{1}{2},l} + \frac{1}{Re} \Delta _d v^n_{j,k+\frac{1}{2},l} + \frac{1}{We} f^{y,n}_{j,k+\frac{1}{2},l}, \\ \frac{\tilde{w}_{jk,l+\frac{1}{2}} - w^n_{jk,l+\frac{1}{2}}}{\Delta t} =&-(\mathbf{u} \cdot \nabla _d w)^n_{jk,l+\frac{1}{2}} + \frac{1}{Re} \Delta _d w^n_{jk,l+\frac{1}{2}} + \frac{1}{We} f^{z,n}_{jk,l+\frac{1}{2}}. \end{aligned}$$

Here, the advection terms are computed with the upwind scheme. The details can be seen in Lee et al. (2016).

Step 2:

Update $\mathbf{u}^{n+1}$ using $\tilde{\mathbf{u}}$.

$$\begin{aligned} \frac{\mathbf{u}^{n+1} - \tilde{\mathbf{u}}}{\Delta t} = -\nabla p^{n+1}. \end{aligned}$$

(13)

Equation (13) can be discretized in space as follows:

$$\begin{aligned} \frac{u^{n+1}_{j+\frac{1}{2},kl} - \tilde{u}_{j+\frac{1}{2},kl}}{\Delta t} =&-\frac{p^{n+1}_{j+1,kl}-p^{n+1}_{jkl}}{h}, \\ \frac{v^{n+1}_{j,k+\frac{1}{2},l} - \tilde{v}_{j,k+\frac{1}{2},l}}{\Delta t} =&-\frac{p^{n+1}_{j,k+1,l}-p^{n+1}_{jkl}}{h}, \\ \frac{w^{n+1}_{jk,l+\frac{1}{2}} - \tilde{w}_{jk,l+\frac{1}{2}}}{\Delta t} =&-\frac{p^{n+1}_{jk,l+1}-p^{n+1}_{jkl}}{h}. \end{aligned}$$

Here, the pressure field can be calculated by solving the Poisson equation:

$$\begin{aligned} \Delta p^{n+1} = \frac{1}{\Delta t}\left( \nabla _d \cdot \tilde{\mathbf{u}} \right) . \end{aligned}$$

(14)

Note that it is derived from (13) applying the divergence operator $(\nabla _d \cdot )$ and the condition (11). Here, the multi-grid (Trottenberg et al. 2001) is used to solve (14) with V-cycles and Gauss–Seidel relaxation. See Lee et al. (2016).

3.2 Cell Membrane

Here, the numerical solver for the cell membrane equation is described with its growth term (9). Based on the convex splitting scheme of Eyre’s work (1998), Eq. (9) can be discretized in time as follows:

$$\begin{aligned} \frac{\phi ^{n+1}_{i} - \phi ^n_{i}}{\Delta t} + \mathbf{u}^n \cdot \nabla \phi ^n_{i}= & {} \frac{1}{Pe} \Delta \left( \left( \phi ^{n+1}_{i}\right) ^3 - \phi ^n_{i} - \epsilon ^2 \Delta _d \phi ^{n+1}_{i} + \beta ({\varvec{\phi }}^n) \right) \nonumber \\&\;\; + \frac{\lambda }{2} \left( 1 + \phi ^n_{i} \right) . \nonumber \\&\hbox {for} \quad i = 1, 2, \ldots , N-1. \end{aligned}$$

(15)

Theorem 1

Equation (15) is unconditionally uniquely solvable for each i.

Proof

To simplify the notation, let us omit the index i in a proof. Consider the following functional

$$\begin{aligned} \mathcal {F}(\phi ) =&\frac{1}{{2 \Delta t}}\left\| \phi - \phi ^n \right\| ^2_{-1,h} + \left\langle \mathbf{u}^n \cdot \nabla \phi ^n, \phi \right\rangle _{-1,h} - \frac{\lambda }{2} \left\langle 1 + \phi ^n, \phi \right\rangle _{-1,h}\\&+\frac{1}{Pe} \left( \frac{1}{4} \left\| \phi \right\| _4^4 - \left\langle \phi ^n, \phi \right\rangle _2 + \frac{\epsilon ^2}{2} \left\| \nabla \phi \right\| _2^2 + \left\langle \beta ({\varvec{\phi }}^n), \phi \right\rangle _2 \right) , \end{aligned}$$

where $\left\langle \phi , \psi \right\rangle _p$ is the $L_p$-inner product, $\left\| \phi \right\| _p^2 = \left\langle \phi , \phi \right\rangle _p$ is the $L_p$-norm, $\left\langle \phi , \psi \right\rangle _{-1,h} = \left\langle -\Delta \phi , \psi \right\rangle _2$ is the inner product on a Hilbert space, and $\left\| \phi \right\| _{-1,h}^2 = \left\langle \phi , \phi \right\rangle _{-1,h}$ is the norm corresponding to the inner product. Then, its first variation is

$$\begin{aligned} \delta _\phi \mathcal {F}(\phi ; \psi ) =&\left\langle \frac{\phi - \phi ^n}{\Delta t} + \mathbf{u}^n \cdot \nabla \phi ^n - \frac{1}{Pe} \Delta \left( \phi ^3 - \phi ^n - \epsilon ^2 \Delta \phi + \beta ({\varvec{\phi }}^n) \right) \right. \\&\left. - \frac{\lambda }{2} \left( 1 + \phi ^n \right) , \psi \right\rangle _{-1,h}, \end{aligned}$$

and the second variation is

$$\begin{aligned} \delta _\phi ^2 \mathcal {F}(\phi ; \psi ) = \frac{1}{\Delta t} \left\| \psi \right\| ^2_{-1,h} + \frac{3}{Pe} \left\| \phi \psi \right\| ^2_2 + \frac{\epsilon ^2}{Pe} \left\| \nabla \psi \right\| _2^2 > 0, \end{aligned}$$

where $\psi$ is in a Hilbert space $H = \left\{ \phi : \int \phi = 0 \right\}$. Since the second variation is strictly positive, $\mathcal {F}$ is a strictly convex functional and it implies that Eq. (15) is a unique minimizer of $\mathcal {F}$ from its first variation.

Here, spatial discretization is similarly defined as the previous section using $\nabla _d$ and $\Delta _d$. The detailed descriptions of numerical solver and its stability are in Lee et al. (2012).

3.3 CR

Using the updated fluid velocity $\mathbf{u}^{n+1}$ and PF functions ${\varvec{\phi }}^{n+1} = \left( {\varvec{\phi }}^{n+1}_1, \ldots , {\varvec{\phi }}^{n+1}_N \right)$ derived above, the CR velocity $\mathbf{U}^{n+1}_{i,m}$ and boundary position $\mathbf{X}^{n+1}_{i,m}$ are also updated by solving the following discrete equation:

$$\begin{aligned} \mathbf{U}^{n+1}_{i,m}= & {} -\sum _{j=1}^{N_x} \sum _{k=1}^{N_y} \sum _{l=1}^{N_z} \phi _{i,jkl} \mathbf{u}^{n+1}_{jkl} \delta ^3_h \left( \mathbf{x}_{jkl} - \mathbf{X}^n_{i,m} \right) h^3, \end{aligned}$$

(16)

$$\begin{aligned} \mathbf{X}^{n+1}_{i,m}= & {} \mathbf{X}^n_{i,m} + \Delta t \mathbf{U}^{n+1}_{i,m}, \end{aligned}$$

(17)

for $i=1, \ldots , N-1$ and $m = 1, \ldots , N_{i,s}$. Note that the motion of CR is calculated numerically when $\lambda = 0$ in Eq. 15 and the position of cell division in numerical simulation will be determined by the position of CR when the division occurs.

The following theorem proves the pointwise convergence of $\mathbf{X}^n_{i,m}$ to the zero-contours representing the cell membranes. To simplify the notation, the phase index i is omitted in the theorem. Moreover, assume that the PF function is fixed in time; hence, denote $\phi ^n_{i,jkl}$ and $\mathbf{X}^n_{i,m}$ as $\phi _{jkl}$ and $\mathbf{X}^n_m$, respectively.

Theorem 2

Given $\epsilon > 0$, $\Vert \left( x_\xi , y_\eta , z_\zeta \right) - \mathbf{X}^n_m \Vert _2 < \epsilon$ as $n \rightarrow \infty$ for some point $\left( x_\xi , y_\eta , z_\zeta \right)$ on $\{ \mathbf{x}: \phi (\mathbf{x}) = 0\}$.

Proof

Since it could be straightforwardly extended to higher-order cases, consider the problem as an one-dimensional case. If $| X^n_m - x_\xi | < 2h$, take $\epsilon = 2h$. Otherwise, (16) and (17) are first rewritten by using the notation $u^{n+1}_j = 0.5 \left( u^{n+1}_{j+\frac{1}{2}}+u^{n+1}_{j-\frac{1}{2}} \right)$ as follows:

$$\begin{aligned} X^{n+1}_m = X^n_m - \Delta t \sum _{j=1}^{N_x} \phi _j u^{n+1}_j \delta _h \left( x_j - X^n_m \right) h, \end{aligned}$$

or,

$$\begin{aligned} \frac{X^{n+1}_m - x_\xi }{X^n_m - x_\xi } = 1 - \frac{h \Delta t}{X^n_m - x_\xi } \sum _{j=1}^{N_x} \phi _j u^{n+1}_j \delta _h \left( x_j - X^n_m \right) . \end{aligned}$$

(18)

Without loss of generality, assume $u^{n+1}_j > 0$ because the CR always shrinks when the particle move happens. Clearly, h and $\Delta t$ are positive and $\delta _h$ has compact support only on four points near $X^n_m$ with a positive value. By compact supportedness, (18) is rewritten again as

$$\begin{aligned} \frac{X^{n+1}_m - x_\xi }{X^n_m - x_\xi } = 1 - \frac{h \Delta t}{X^n_m - x_\xi } \sum _{x_j \in [X^n_m - 2h, X^n_m + 2h]} \phi _j u^{n+1}_j \delta _h \left( x_j - X^n_m \right) . \end{aligned}$$

If $| X^n_m - x_\xi | \ge 2h$, then $(X^n_m - x_\xi ) \phi _j > 0$ for $\{ j: x_j \in [X^n_m - 2h, X^n_m + 2h] \}$. Moreover, it implies that

$$\begin{aligned} \left| \frac{X^{n+1}_m - x_\xi }{X^n_m - x_\xi } \right| < 1, \end{aligned}$$

and the proof is over.

4 Simulation Results

In this section, several numerical tests are described to validate our modeling in a three-dimensional domain. First, Theorem 2 is checked numerically and then some numerical simulations are performed to show the configurations of cell membrane and CR. The computational domain will be set as $\Omega _h = (0,1) \times (0,1) \times (0,2)$ unless otherwise stated. Except for comparing with experimental data, I refer the non-dimensional parameters in my previous results (Lee et al. 2016).

4.1 $\phi$-Effect in IB Velocity

The first simulation is to prove the result of Theorem 2 numerically. The parameters are chosen as $N_x = N_y = 32$, $N_z = 64$, $Re = 10$, $We = 10$, $Pe = 1/\epsilon$, $\epsilon = \epsilon _3$, $\Delta t = 0.1 Re \cdot h^2$, $L_0 = 2\pi (0.35)$, and $N_t = 1000$. Figure 4 shows the temporal evolution of differences between the radii of CR and cell membrane at $z=0.5$ until the cytokinesis occurs. Here, the black bold dotted lines represent the upper(2h) and lower(0) bounds in the hypothesis and the distances calculated from numerical results are drawn by thin lines. The distances are calculated at each Lagrangian particle. The legends min, max, and average in graph represent the minimum, maximum, and average distances, respectively. Since the differences are always bounded by [0, 2h], it has a good agreement with Theorem 2.

Fig. 4

Temporal evolution of differences between the radii of CR and cell membrane at $z=0.5$ until the cytokinesis occurs

Fig. 5

Numerical results of cell division process starting with a single cell. The isosurfaces represent cells, the blue line is the CR, and arrows describe the fluid velocities. a Initial, b $t = 300 \Delta t$, c $t = 600 \Delta t$, d $t = 1000 \Delta t$ (Color figure online)

4.2 Single Cell

Next, the numerical simulations of cell division process starting with a single cell are performed in this section. The isosurfaces represent cells, the blue line is the CR, and arrows describe the fluid velocities in Fig. 5. The same parameters as the previous simulation are chosen. Note that the topological change, i.e., cytokinesis, can be expressed by using the proposed model without complicated numerical treatment.

4.3 Comparison with Previous Model

Here, the numerical simulation for comparison with a previous model is considered to validate the proposed model. Li et al. (2012) proposed the mathematical model for simulating a single axisymmetric cell using an IB method. With the initial condition from the elongated cell in the Li’s work, I perform the numerical simulation and its results are presented in Fig. 6. The arrows and the black solid lines represent the velocity field and the cell membranes, respectively, from the previous work. Otherwise, the red dotted lines are a zero-contour of $\phi$. Note that there are no data for comparing with Fig. 6e because it is quite hard to perform the simulation after the cell is divided in the previous work.

Fig. 6

Comparison of temporal evolution with Li’s work (2012). The arrows and the black solid lines represent the velocity field and the cell membranes, respectively, in the background images, which are reprinted with permission from Springer (Li et al. 2012). Otherwise, the red dotted lines are a zero-contour of $\phi$ (Color figure online)

Fig. 7

Configuration of cell membranes from the numerical simulation and in vivo. Background images, reprinted with permission from National Academy of Sciences (Zang and Spudich 1998), and red solid lines represent the experimental data and the simulation results, respectively. a Initial, b $t = 0.2930$, c $t = 0.6006$, d $t = 1.0693$, e $t = 1.3184$ (Color figure online)

4.4 Comparison with Experiment Data

Moreover, Fig. 7 shows the configuration of cell membranes from the numerical simulation and in vivo. Background images and red solid lines represent the experimental data and the simulation results, respectively. The used parameters are $N_x = N_y = 32$, $N_z = 64$, $Re = 15$, $We = 10$, $Pe = 1/\epsilon$, $\epsilon = \epsilon _3$, $\Delta t = 0.1 Re \cdot h^2$, $L_0 = 2\pi (0.25)$, and $N_t = 1000$. Note that computational parameters are chosen in order to match the numerical result and the experimental data since the exact values for the experience are unknown. The background images are in vivo, and the red solid lines present the simulation results. Note that the times in numerical simulations are non-dimensionalized in (a)–(e) and their ratios are well matched to experimental ones. As shown in the figure, the result shows that the experiment data can be approximated well by the proposed model.

4.5 Multiple Divisions

Now, the simulation with a series of divisions is considered in this subsection. The position of cell division will be randomly chosen on the cell membrane. The parameters are the same as the first simulation, except $N_t = 3000$. Figure 8 shows the numerical results of cell division process starting with a multiple cell. Because the temporal evolution is the same as one cell until $t = 1000\Delta t$, Fig. 8a starts with the state when $t = 1000\Delta t$. In Fig. 8b, the cell membrane is growing with $\lambda _p = 1$. The cell growth was already stopped, and the second cell division starts in Fig. 8c, and the cytokinesis keeps going in Fig. 8d. At last, Fig. 8e shows that four daughter cells exist after two divisions. If the usual CH equation, not the vector-valued one, is used to model, emerging should be happened in Fig. 8b or c because the distance between each two daughter cells is too close; however, it is resolved to use the vector-valued PF method.

Fig. 8

Numerical results of cell division process starting with a multiple cell. The isosurfaces represent cells, the blue line is the CR, and arrows describe the fluid velocities. a $1000\Delta t$, b $1500\Delta t$, c $2000\Delta t$, d $2500\Delta t$, e $3000\Delta t$ (Color figure online)

5 Conclusion

Mathematical model of contractile ring-driven cytokinesis was proposed by using both PF and IB methods in this paper. To validate the model in a mathematical sense, we proved the solvability of the PF, governed the cell membrane and the convergence of the IB equation and governed the CR. Moreover, several numerical simulations were performed. The first result had a good agreement with the convergence theorem of CR, and it was also shown that the experimental data from Zang and Spudich (1998) can be approximated well by the proposed model. The multiple division simulation result was also presented. In the future work, the nucleus division could be modeled by modifying the CH equation and more detailed theories in biology would be considered.