Automated Robust Image Segmentation: Level Set Method Using Nonnegative Matrix Factorization with Application to Brain MRI

Abstract

We address the problem of fully automated region discovery and robust image segmentation by devising a new deformable model based on the level set method (LSM) and the probabilistic nonnegative matrix factorization (NMF). We describe the use of NMF to calculate the number of distinct regions in the image and to derive the local distribution of the regions, which is incorporated into the energy functional of the LSM. The results demonstrate that our NMF–LSM method is superior to other approaches when applied to synthetic binary and gray-scale images and to clinical magnetic resonance images (MRI) of the human brain with and without a malignant brain tumor, glioblastoma multiforme. In particular, the NMF–LSM method is fully automated, highly accurate, less sensitive to the initial selection of the contour(s) or initial conditions, more robust to noise and model parameters, and able to detect as small distinct regions as desired. These advantages stem from the fact that the proposed method relies on histogram information instead of intensity values and does not introduce nuisance model parameters. These properties provide a general approach for automated robust region discovery and segmentation in heterogeneous images. Compared with the retrospective radiological diagnoses of two patients with non-enhancing grade 2 and 3 oligodendroglioma, the NMF–LSM detects earlier progression times and appears suitable for monitoring tumor response. The NMF–LSM method fills an important need of automated segmentation of clinical MRI.

1 Introduction

Automated image segmentation is one of the most important and most challenging problems in medical imaging. Many applications, such as surgical planning and image-guided interventions, rely on accurate (pixel-level) delineation of the anatomical structures. However, there are many challenges that make medical image segmentation a difficult task, including the complexity of the topology of the anatomical structures, the relatively small size of regions of interest, and intensity inhomogeneity, also known as bias field, which manifests as a smooth intensity variation across the image. Intensity inhomogeneity results from imperfections in the imaging acquisition process and other artifacts, such as spatial variation in signal intensity and illumination. This bias field makes the segmentation task particularly difficult because it tends to merge the intensities of different (anatomical) regions.

The level set method (LSM) is one of the most advanced methods to extract object boundaries in computer vision. The level set approach represents the contour as the zero level of a higher-dimensional function, referred to as the level set function. The segmentation is achieved by minimizing a functional that tends to attract the contour toward the objects’ boundaries. The advantages of the level set method are that (i) the segmentation problem is formulated and solved as a mathematical optimization problem using well-established theories, such as calculus of variation, (ii) numerical computations are performed on the image grid in contrast to parametric representations of curves (Caselles et al. 1997; Cohen and Cohen 1993; Kass et al. 1987), and (iii) the contour representation is capable of representing any complex shape or surface and lends itself to a pixel-level accuracy, a highly desirable property in medical image segmentation.

Traditionally, image segmentation algorithms, including those that use the level set method, rely on modeling the intensity values across the image. In the level set approach, the functional, to be optimized, represents some error or distance between the image and its intensity model (Tsai et al. 2001; Chan and Vese 2001; Li et al. 2008, 2011; Wang et al. 2009; Chen et al. 2011). However, relying on the intensity values themselves leads to a segmentation scheme that is very sensitive to intensity artifacts, such as intensity inhomogeneity or additional noise corrupting the image. Recent applications of the level set segmentation have attempted to take into account the intensity inhomogeneity by performing a local (rather than region-wide) modeling of the image that incorporated the bias field term (Li et al. 2011; Chen et al. 2011). However, this local representation remains sensitive to noise and intensity artifacts as it relies on the intensity values in the image.

In this paper, we present a novel fully automated robust and accurate method for image segmentation; the method: (i) is robust to noise, initial condition, and intensity inhomogeneity because it includes the distribution of the pixels rather than relying solely on the intensity values, (ii) uses the probabilistic nonnegative matrix factorization (NMF) (Bayar et al. 2014) to discover and identify the image regions (their homogeneous intensities as well as their spatial distribution), (iii) introduces a novel spatial functional term that is incorporated into the equation of the LSM, and (iv) is scalable, i.e., able to detect a distinct region as small as desired. Furthermore, unlike other level set methods that handle intensity inhomogeneity, the proposed LSM-NMF approach does not introduce spurious or nuisance model parameters that have to be simultaneously estimated with the level set function and the bias field; this property increases the accuracy of the estimation of the contours.

There is an unmet urgent need of a fully automated, accurate, robust, and efficient image segmentation. Current methods for segmentation of clinical magnetic resonance images (MRI) have significant limitations (Valverde et al. 2015; Garcia-Lorenzo et al. 2013; Jain et al. 2015; Pagnozzi et al. 2015). A comparison of the software packages FSL, SPM5, and FreeSurfer to gold-standard reference brain template demonstrated that discrepancies between results reached the same order of magnitude as volume changes observed in disease (Klauschen et al. 2009). These effects limit the usability of these segmentation methods for following volume changes in individual patients over time. We compare the NMF–LSM method to the FSL and SPM12 software packages and demonstrate higher accuracy and robustness to noise.

This paper is organized as follows: Sect. 2 reviews the state-of-the-art level set approaches, describing their mathematical formulation and model parameters. Section 3 introduces the proposed NMF–LSM approach. We describe how the factors of the NMF discover and cluster the image domain into distinct regions. We introduce two external energy terms that will drive the contour to the regions boundaries. We also take into account the bias field and carry out the segmentation by minimizing the total energy functional with respect to the level set functions. In Sect. 4, we use synthetic binary and gray-scale images to compare the NMF–LSM method to two other state-of-the-art level set methods, the localized-LSM in Li et al. (2011) and the improved local Gaussian distribution fitting-LSM (LGDF–LSM) in Chen et al. (2011). In Sect. 5, we compare the NMF–LSM method to the SPM12 and FSL software packages using clinical MRI of the brain, with and without tumor; the results demonstrate the superiority of NMF–LSM in delineating the complex anatomy of the brain: gray matter, white matter, cerebrospinal fluid (CSF), edema (swelling), tumor, and necrosis (dead brain cells), especially in the presence of noise. A summary of the main contributions of this paper and future work directions are provided in Sect. 7.

2 Related Work

2.1 Mumford–Shah Model (Tsai et al. 2001)

Let $\Omega$ be the image domain and $I:\Omega \rightarrow {\mathbb {R}}$ be a gray-value image. The goal of the segmentation is to find a contour C, which separates the image domain $\Omega$ into disjoint regions $\Omega _1, \ldots , \Omega _k$, and a piecewise smooth function u that approximates the image I and is smooth inside each region $\Omega _i$. This is formulated as the minimization of the following Mumford–Shah functional:

$$\begin{aligned} {{\mathcal {F}}}^\mathrm{MS}(u, C) = \int _{\Omega }(I-u)^2 \mathrm{d}{\varvec{x}}+\mu \int _{\Omega \setminus C} |\nabla u|^2 \mathrm{d}{\varvec{x}} + \nu |C|, \end{aligned}$$

(1)

where |C| is the length of the contour C. In the right-hand side, the first term is the external energy term, which drives u to be close to the image I, and the second term is the internal energy, which imposes smoothness on u within the regions separated by the contour C. The third term regularizes the contour. The MS model is very general and does not assume a specific form for the approximating function u. It also assumes that the objects to be segmented are homogeneous.

2.2 Chan and Vese Model (Chan and Vese 2001)

Chan and Vese simplified the Mumford–Shah model by assuming that the approximating function u is a piecewise constant:

$$\begin{aligned} {{\mathcal {F}}}^\mathrm{CV}(\phi ,c_1,c_2)&=\int _{\Omega }|I({\varvec{x}})-c_1|^2 H(\phi )\mathrm{d}{\varvec{x}} \nonumber \\&\quad +\int _{\Omega }|I({\varvec{x}})-c_2|^2(1-H(\phi ))\mathrm{d}{\varvec{x}}+\nu \int _{\Omega }|\nabla H(\phi )|\mathrm{d}{\varvec{x}}, \end{aligned}$$

(2)

where H is the Heaviside function and $\phi$ is a level set function, whose zero-level contour C partitions the image domain $\Omega$ into two disjoint regions $\Omega _1 = \{{\varvec{x}}: \phi ({\varvec{x}}) > 0 \}$ and $\Omega _2 = \{{\varvec{x}}: \phi ({\varvec{x}}) < 0 \}$. Equation (2) is a piecewise constant model, as it assumes that the image I can be approximated by constants $c_i$ in region $\Omega _i$. In the case of more than two regions, two or more level set functions can be used to represent the regions $\Omega _1, \ldots \Omega _k$.

2.3 Localized-LSM Model (Li et al. 2011)

Li et al. (2011) proposed a variational level set method that deals with intensity inhomogeneity by considering the image model $I = b * J + n$ for the observed image I, where b is the bias field, J is the true image, and n is an additive noise. This approach has two assumptions: (a) The bias field is assumed to be slowly varying and (b) the true image J is approximated by a constant inside each region: $J(x)\approx c_i$ for $x \in \Omega _i$. Consider the neighborhood around pixel y, $O_y= \{x:\Vert x-y\Vert \le \rho \}$, then $b(y) \approx b(x)$ inside the neighborhood $O_y$. The energy function is then formulated as follows (Li et al. 2011):

$$\begin{aligned} {{\mathcal {F}}}(\phi ,\mathbf{b },\mathbf{c })=\int \left( \sum _{i=1}^{N} \int K(y-x)(I(x)- b(y)c_i)^2 M_i(\phi )\mathrm{d}{\varvec{x}}\right) \mathrm{d}{\varvec{y}}, \end{aligned}$$

(3)

where $K(y-x)$ is a nonnegative weighting function that defines the neighborhood $O_y$ and $M_i(\phi (x))$ is the membership function that represents each region using the Heaviside function (for two regions $M_1(\phi )=H(\phi )$ and $M_2(\phi )= 1-H(\phi )$). In the localized-LSM model, the intensity means $c_1, \ldots , c_k$ of each region are estimated iteratively along with the level set function $\phi$ and the bias field $\mathbf{b }$ using the variational principle of the level set framework.

2.4 Improved LGDF–LSM Model (Chen et al. 2011)

In the improved LGDF–LSM model (Chen et al. 2011), Chen et al. characterize the local distribution of the intensities in the neighborhood $O_x$ using a local Gaussian distribution. The segmentation is then achieved by maximizing the a posteriori probability. They used the log transform of the same image model in Li’s method ${\widetilde{I}} = \log (I) = \log (J) + \log (\mathbf{b })$ so that the bias becomes an additive factor rather than a multiplicative factor.

Let $p(x \in \Omega _i \cap O_x | {\widetilde{I}}(x))$ be the a posteriori probability of the subregions $\Omega _i \cap O_x$ given the log transform of the observed image. Using Bayes’ rule, we have $p(x \in \Omega _i \cap O_x | {\widetilde{I}}(x))\varpropto p({\widetilde{I}}(x) | x \in \Omega _i \cap O_x)$ $p(x \in \Omega _i \cap O_x)$. Assuming that the prior probabilities of all partitions are equal, and the pixels within each region are independent, the MAP estimate can be achieved by finding the maximum of $\prod _{i=1}^{N}\prod _{x\in \Omega _i\cap O_x}p_{i,y}({\widetilde{I}}(x))$. It can be shown that the MAP formulation can be converted to the minimization of the following energy functional in the level set framework (Chen et al. 2011):

$$\begin{aligned} {{\mathcal {F}}}(\phi ,\mathbf{b }, \mathbf{c },{\sigma }^2) =\int \sum _{i=1}^{N} \int -K(y-x) \log p_{i,y}({\widetilde{J}}(x)- {\widetilde{b}}(y)) M_i(\phi )\mathrm{d}{\varvec{x}} \mathrm{d}{\varvec{y}}, \end{aligned}$$

(4)

where $p_{i,y}({\widetilde{J}}(x)- {\widetilde{b}}(y))$ is modeled by a Gaussian distribution. In the improved LGDF model, the intensity means $\{c_i\}_{i=1}^k$ and variances $\{\sigma _i^2\}_{i=1}^k$ of the regions are simultaneously and iteratively estimated with the level set function $\phi$ and the bias field $\mathbf{b }$.

Observe that these approaches involved simultaneous and iterative estimation of a number of spurious model parameters ($\{c_i\}_{i=1}^k$ and $\{\sigma _i^2\}_{i=1}^k$) in addition to the bias field and the level set function, the latter being the main parameter of interest for the segmentation task. Given the high dimensionality and non-convexity of the variational optimization problem, all additional model parameters are estimated in an iterative procedure that does not guarantee convergence or optimality of the results. Hence, though they try to remedy the intensity inhomogeneity problem, they do so by introducing a large number of spurious model parameters (as a result of the local modeling) that have to be simultaneously estimated, which decreases the estimation accuracy of the main segmentation parameters, namely the level set functions. Moreover, the level set functionals rely only on a model of the intensity values and do not incorporate any other information, such as spatial distribution of the pixels, which may improve the segmentation and reduce the sensitivity to noise and other intensity artifacts.

3 The NMF–LSM Method

The basic schemes of the NMF–LSM method are summarized in Fig. 1. Specifically, the data are histograms instead of intensities and the NMF generates matrices that include key information on the number and histograms of the regions in the image and on their local distribution. The later is used to include a novel spatial term in the level set equation.

3.1 Region Discovery and Clustering Using NMF

We first consider the local information by partitioning the image into m (equally sized) blocks and computing the histogram of each block. The histograms of the blocks are then stacked to form the columns of the data matrix V. The data matrix $V = \{\upsilon _{ij}\}$ is an $n \times m$ matrix, where n is the number of intensity bins or ranges in the histograms standardized for all image blocks. Specifically, the (i, j) entry, $\upsilon _{ij}$, is the number of pixels in block j with intensity range in bin i. The rows of V describe the ranges of intensities in bin i in all the blocks.

We use the NMF algorithm in Bayar et al. (2014), which takes into account the noise in the data matrix, to perform a maximum a posteriori factorization of the histogram data matrix V into two matrices with positive entries $V \approx WH$, where W is $n \times k$ and H is $k \times m$ (see Fig. 1).

Fig. 1

Cartoon depicting the basic schemes of the NMF–LSM method. The data matrix V is built from the histograms of the blocks of the image. NMF of V generates W and H; the former, including the histograms of the regions in the image, is applied to automatically compute the number of regions. H, which includes information on the local distribution of the regions in each of the blocks, is used to modify the level set equation

Data from the factorization of V, constructed from synthetic binary and gray-scale images, demonstrate that the nonnegative matrices W and H contain key statistical and spatial information about the regions in the image. First, consider the synthetic binary image in Fig. 2. The NMF of the data matrix of this image with a specified $k=2$ results in the W and H matrices shown in Fig. 2. Plotting the entries of each column of W in Fig. 2a, we obtain two sharp peaks: one peak at the (0–1) range of intensity value, corresponding to the black region, and a second peak at the (254–255) range, corresponding to the white region. Hence, the matrix W seems to provide the histograms of the regions, which we call “basic histograms.” The normalized entries of the columns of H provide the spatial distribution of the regions within the local blocks. For instance, when the image block is entirely included in one region, we obtain the value of 1 in the entry that corresponds to that region and zero elsewhere. On the other hand, if two regions are included in a block, we obtain the fraction of each of the regions included in each block.

Fig. 2

Interpretation of the W and H matrices of a binary image. The binary image is synthetic with $16 \times 16$ pixels blocks, and the entries of H are normalized for each column. W includes the basic histograms of the binary image (black and white). H includes the fraction of the white and black regions in each of the colored tiles. Here, the number of regions k is specified. a “W” matrix interpretation. b “H” matrix interpretation

The same interpretation of the factor matrices in terms of “basic histograms” for W and spatial distribution for H applies to gray-scale images, such as the one shown in Fig. 3; Figs. 4 and 5 show the results of the factorization by NMF of the matrix V of the image in Fig. 3 using blocks of size $16 \times 16$ and $8 \times 8$ pixels, respectively. The data reveal that the blocks must be chosen to be small enough to fit entirely in the smallest region to be detected. From the plot of the columns of the matrix W in Fig. 4a, we observe that the NMF captured the four largest regions in the image, while the two smallest regions in the image with intensity values (102) and (26) were not detected. Both W and H matrices were unable to capture these two small regions with a block size of ($16 \times 16$ pixels). Even when we increase the number of regions k, we get additional zero columns in W and additional zero rows in H; thus they are still unable to capture these two small regions. However, by decreasing the size of the blocks to ($8 \times 8$ pixels), so that the block size fits into these small regions, we found that the W and H matrices of the NMF factorization specified all six regions, as shown in Fig. 5. Hence, the “resolution” of the NMF factorization, in terms of region discovery and classification, depends on the size of the blocks used to partition the image. The block size should be chosen to be as small as the smallest region that we wish to detect or segment. In particular, the resolution of the NMF approach is scalable and can be set as desired.

The analysis of the gray-scale image yields the same conclusion on the spatial information encoded in the matrix H. Note that each column of H corresponds to a block in the image. Furthermore, H includes the fraction of each of the regions, whose basic histograms are identified by the columns of the matrix W, in each of the blocks of the image (see Figs. 4b, 5b).

In summary, applying NMF on the histogram data matrix V yields two nonnegative matrices, W and H, that provide the statistical and spatial characteristics of the distinct regions in the image. The matrix W yields the histogram of each region in the image, while the matrix H provides the local spatial characteristics of each region: The fraction of each region that is included in every block. The size of the blocks should be chosen to be smaller than the smallest region of interest (see Fig. 5). Based on these statistical and spatial characteristics of the image regions, we propose to build a robust external energy or a data term that will be integrated in the level set approach. We first discuss how the NMF factors can be used to estimate the number of regions in the image.

Fig. 3

A synthetic gray-scale image. This image includes six intensity levels (0, 255, 51, 77, 26, 102) shown in the yellow rectangles

Fig. 4

Interpretation of the W and H matrices for the synthetic gray-scale image of Fig. 3 using blocks of size $16 \times 16$ pixels. a First 4 columns of W include the basic histograms of only 4 of the 6 gray regions in the image. The last two columns of W contain zeros. b Columns of H include the fractions of each block occupied by the regions; each block, represented by a column, is identified by a different color. The entries of H are normalized for each column, and the number of regions k is specified as equal to 6

Fig. 5

Small size blocks detect all six gray regions in the image of Fig. 3. a The blocks of this analysis are of size $8 \times 8$ pixels; in this case, the columns of W include the basic histograms of the six gray regions. b Columns of H include the fractions of each block occupied by the regions; each block, represented by a column, is identified by a different color. The entries of H are normalized for each column, and the number of regions k is specified as equal to 6

3.2 Automatic Estimation of the Number of Distinct Regions in the Image

We show how to use the factor matrices W and H to automatically estimate the number of distinct clusters or regions k. To illustrate the idea, we start by changing the value of k for the synthetic gray-scale image in Fig. 3 and observing the corresponding changes in the matrices W and H. We notice that when we increase k to be more than the true number of regions in the image ($k=6$ in this case), we obtain additional zero rows in H and additional zero columns in W. We, therefore, propose to use the sum of the Frobenius norms of W and H. The Frobenius norm of the matrix $A=\{a_{ij}\}$ is defined as

$$\begin{aligned} \Vert A\Vert _{F} = \sqrt{\sum _{i,j}|a_{ij}|^2}. \end{aligned}$$

(5)

We start by choosing an initial guess for the number of regions $k_0$ and apply the NMF on the histogram data matrix V with $k=k_0$. We obtain $V_{n \times m} \approx W_{n \times k_0} H_{k_0 \times m}$. We compute the sum of the Frobenius norms of $W_{n \times k_0}$ and $H_{k_0 \times m}$, $\Vert W\Vert _F + \Vert H\Vert _F$. Then, we increase k and repeat the same steps. The sum of the Frobenius norms is a non-decreasing function of k. This function platforms when $k \ge k^{*}$. The optimal number of regions is then given by $k^{*}$, which automates the estimation of the number of distinct regions in the image.

Figure 6 shows how the sum of the Frobenius norms increases with k for the synthetic gray-scale image in Fig. 3, until it stabilizes at $k=6$, which corresponds to the true number of distinct regions in the image.

The idea behind using the Frobenius norm is quite intuitive: Appending a matrix by a column of zeros and forming the matrix ${\varvec{W}}_a = [W,{\mathbf {0}}]$ will not change the Frobenius norm. Similarly, appending the matrix H by a row of zeros and forming the matrix ${\varvec{H}}_a= \bigl [ {\begin{matrix} {\varvec{H}} \\ {\mathbf {0}}^t \\ \end{matrix}} \bigr ]$ will not change its Frobenius norm. In practice, due to the image inhomogeneity, we may not have exact zeros in the additional columns and rows of the appended matrices ${\varvec{W}}_a$ and ${\varvec{H}}_a$, respectively, but we have very small values that are close to zero. If the column vector ${\mathbf {z}}_w$ and the row vector ${\mathbf {z}}_h^t$ have small entries, then the norm increase in the appended matrices is also small. In particular, the Frobenius norm will change only slightly when we append a column or a row of small values as shown in Fig. 6.

Fig. 6

The Frobenius norm saturates at the optimal number of regions. $\Vert W\Vert _F + \Vert H\Vert _F$ as a function of k from 1 to 20 for the synthetic gray-scale image in Fig. 3, which has six regions

3.3 Proposed Variational Framework

We consider the image model $I({\varvec{x}}) = J({\varvec{x}}) *b({\varvec{x}}) + n({\varvec{x}})$, where $I({\varvec{x}})$ is the observed intensity at pixel ${\varvec{x}}$, $J({\varvec{x}})$ is the “true” (noiseless/unbiased) intensity at pixel ${\varvec{x}}$, $b({\varvec{x}})$ is the bias field associated with ${\varvec{x}}$, and $n({\varvec{x}})$ is the observation and model noise at pixel ${\varvec{x}}$. We use the two matrices W and H to build the proposed energy functional. This functional codes the external energy and contains two terms: a statistical term and a spatial term. The statistical term uses the matrix W and characterizes the mean and standard deviation of each region. The spatial term relies on the matrix H and characterizes the spatial distribution of the regions inside the blocks.

In order to compute the statistical energy term, we consider the factor matrix W and model the pixel intensities within each region as a Gaussian distribution with mean and standard deviation computed from the basic histograms of W. Specifically, we consider the posterior probability $p(\{\Omega _1, \Omega _2, \ldots , \Omega _k\}| I)= p(\{\Omega \}|I)$ for the image I. Using Bayes’ rule, we have $p(\{\Omega \}| I)\varpropto p(I|\{\Omega \})$ $p(\Omega )$. Assuming that the prior probabilities of all partitions $p(\{\Omega _i\})$ are equal, and the pixels within each region are independent, the maximum a posterior (MAP) estimate of the regions reduces to finding the maximum of $\prod _{i=1}^{k}\prod _{{\varvec{x}}\in \Omega _i} p_{i}(I({\varvec{x}}))$, where $p_{i}(I({\varvec{x}}))= p(I({\varvec{x}})|\Omega _i)$, $i=1,2,\ldots ,k$.

By taking the logarithm, the maximization can be converted to the minimization of the following energy function:

$$\begin{aligned} E^\mathrm{Statistical} = \sum _{i=1}^{k} \int _{\Omega _i} - \log p_{i}(I({\varvec{x}})) \mathrm{d}{\varvec{x}}, \end{aligned}$$

(6)

where $p_{i}(I({\varvec{x}}))$ is given by the Gaussian distribution.

$$\begin{aligned} p_{i}(I({\varvec{x}}))= \frac{1}{\sqrt{2 \pi }\sigma _i}\exp \left( -\frac{(I({\varvec{x}})-\mu _i b({\varvec{x}}))^2}{2 (\sigma _i)^2}\right) , \end{aligned}$$

(7)

where $\mu _i$ and $\sigma _i$ are pre-computed form the matrix W.

To derive the spatial energy term, we consider the matrix H, which induces a local spatial clustering of the regions $\Omega _i$, $i = 1,\ldots , k$ in each block. By dividing the entries, $h_{ij}$, of H by the sum of each column, $h_{ij}$ provides the fraction of the block j that is occupied by region i. For example, if the block j is included entirely in the region i, then $h_{ij} = 1$, and $h_{lj}=0$ for $l \ne i$. We propose to represent the local area of each region i inside block j as a weighted linear combination of the block areas where the weights are given by the normalized entries of the $j^{th}$ column of the matrix H. Specifically, we propose the following spatial data term:

$$\begin{aligned} E^\mathrm{Spatial} = \sum _{i=1}^{k} \sum _{j=1}^{m} \left( \int _{\Omega _i} {{\mathcal {I}}}_{S_j}({\varvec{x}}) d{\varvec{x}} - \frac{h_{ij} a}{\sum _{i=1}^{k}h_{ij}}\right) ^2, \end{aligned}$$

(8)

where a is the area of a block (all blocks are assumed to have equal areas) and ${{\mathcal {I}}}_{S_j}({\varvec{x}})$ is the characteristic function of block $S_j$, and is defined as follows:

$$\begin{aligned} {{\mathcal {I}}}_{S_j}({\varvec{x}})= {\left\{ \begin{array}{ll} 1, \text { if}\ {\varvec{x}} \in S_j\\ 0, \text { otherwise}. \end{array}\right. } \end{aligned}$$

(9)

Observe in Eq. (8) that the integral term simply represents the area of region $\Omega _i$ that is included in block j. The total data term is then given by the sum of the statistical energy and the spatial energy terms.

$$\begin{aligned} E= & {} E^\mathrm{Statistical} + E^\mathrm{Spatial}, \end{aligned}$$

(10)

$$\begin{aligned} E= & {} \sum _{i=1}^{k} \left[ \int _{\Omega _i}(\log (\sqrt{2 \pi } \sigma _i) + \frac{(I({\varvec{x}})-\mu _i b({\varvec{x}}))^2}{2 \sigma _i^2}) \mathrm{d}{\varvec{x}}\right] \nonumber \\&+ \sum _{i=1}^{k} \sum _{j=1}^{m} \left( \int _{\Omega _i} {{\mathcal {I}}}_{S_j}({\varvec{x}}) d{\varvec{x}} - \frac{h_{ij} a}{\sum _{i=1}^{k}h_{ij}}\right) ^2. \end{aligned}$$

(11)

The energy functional E is subsequently converted to a level set formulation by generating the level set functions $\phi ({\varvec{x}})$ and representing the disjoint regions with a number of membership functions $M_i(\phi ({\varvec{x}}))$. The membership functions satisfy two constraints: (i) They are valued in [0, 1] and (ii) the summation of all membership functions is equal to 1, i.e., $\sum _{i=1}^{k}M_i(\phi ({\varvec{x}}))=1$. This can be achieved by representing the membership function as a smoothed version of the Heaviside function. For example, in the two-phase formulation, the regions $\Omega _1$ and $\Omega _2$ can be represented with their membership functions defined by $M_1(\phi )=H(\phi )$ and $M_2(\phi )=1 - H(\phi )$, respectively, where H is the Heaviside function. For a multi-phase formulation, the combination of the Heaviside functions is different. For example, in the four-phase formulation, we have two level set functions $\phi _1$ and $\phi _2$. The membership functions are given as follows: $M_1=H(\phi _1)H(\phi _2)$, $M_2=H(\phi _1)(1-H(\phi _2))$, $M_3=(1-H(\phi _1))H(\phi _2)$ and $M_4=(1-H(\phi _1))(1-H(\phi _2))$. The total energy in Eq. (11) can be equivalently expressed as the following level set energy functional:

$$\begin{aligned} E(\phi ,b)&= \sum _{i=1}^{k} \left[ \int _{\Omega }\left( \log (\sqrt{2 \pi } \sigma _i) + \frac{(I({\varvec{x}})-\mu _i b({\varvec{x}}))^2}{2 \sigma _i^2}\right) M_i(\phi ({\varvec{x}}))\mathrm{d}{\varvec{x}}\right] \nonumber \\&\quad +\sum _{i=1}^{k} \sum _{j=1}^{m} \left( \int _{\Omega } {{\mathcal {I}}}_{S_j}({\varvec{x}}) M_i(\phi ({\varvec{x}}))\mathrm{d}{\varvec{x}} - \frac{h_{ij} a}{\sum _{i=1}^{k}h_{ij}}\right) ^2. \end{aligned}$$

(12)

Equation (12) can be succinctly written as:

$$\begin{aligned} E(\phi , b)&= \sum _{i=1}^{k}\left[ \int _{\Omega }\text { } e_i({\varvec{x}}, b)M_i(\phi ({\varvec{x}}))\mathrm{d}{\varvec{x}}\right] \nonumber \\&\quad + \sum _{i=1}^{k}\sum _{j=1}^{m} \left( \int _{\Omega } {{\mathcal {I}}}_{S_j}({\varvec{x}}) M_i(\phi )\mathrm{d}{\varvec{x}} - \frac{h_{ij} a}{\sum _{i=1}^{k}h_{ij}}\right) ^2, \end{aligned}$$

(13)

where $e_i({\varvec{x}}, b)=\log (\sqrt{2 \pi } \sigma _i) + \frac{(I(x)-\mu _i b(x))^2}{2 \sigma _i^2}$. The energy term $E (\phi , b)$ represents the external energy or the data term in the total energy of the proposed variational level set formulation. The total external and internal energy is given by

$$\begin{aligned} {{\mathcal {F}}}(\phi , b) = \alpha E(\phi ,b)\text { }+\text { }\beta R(\phi )\text { }+\text { }\gamma Lg(\phi )\text { }+\text { } \nu A_g(\phi ), \end{aligned}$$

(14)

where $R(\phi )$, $L_g(\phi )$, and $A_g(\phi )$ are the regularization terms and $\alpha$, $\beta$, $\gamma$, and $\nu$ are weighting parameters. The energy term $R(\phi )$, defined by $R(\phi ){=}\frac{1}{2}\int _{\Omega }{(|\nabla \phi |-1)^2 d{\varvec{x}}}$, is a distance regularization term (Li et al. 2010) that is minimized when $|\nabla \phi |=1$, a property of the signed distance function. The second energy term, $L_g(\phi )=\int _{\Omega }{g \text { }|\nabla H(\phi ({\varvec{x}})|d{\varvec{x}}}$, computes the arc length of the zero-level set contour, ($\int _{\Omega }|\nabla H(\phi ({\varvec{x}})|d{\varvec{x}})$, and therefore serves to smooth the contour by penalizing its arc length during propagation. The contour length is weighted by the edge indication function $g=\frac{1}{1+|\nabla (G_\sigma * I)|^2}$, where $G_\sigma *I$ is the convolution of the image I with the smoothing Gaussian kernel $G_\sigma$. The function g works to stop the level set evolution near the optimal solution, since it is near zero in the variational edges and positive otherwise. Therefore, the regularization term $L_g$ serves to minimize the length of the level set curve at the image edges. The third regularization term, $A_g(\phi )=\int _{\Omega }{g \text { } H(\phi )d{\varvec{x}}}$, is the area obtained by the level set curve weighted by the edge indication function.

Finally, the total energy functional to be minimized for the purpose of segmentation is expressed as:

$$\begin{aligned} {{\mathcal {F}}}(\phi ,b)&=\alpha \sum _{i=1}^{k}\left[ \int _{\Omega }e_i({\varvec{x}},b)M_i(\phi )\mathrm{d}x \right] \nonumber \\&\quad + \alpha \sum _{i=1}^{k}\sum _{j=1}^{m} \left( \int _{\Omega } {{\mathcal {I}}}_{S_j}({\varvec{x}}) M_i(\phi )\mathrm{d}{\varvec{x}}-\frac{h_{ij} a}{\sum _{i=1}^{k}h_{ij}}\right) ^2 \nonumber \\&\quad +\frac{\beta }{2} \int _{\Omega }{(|\nabla \phi | -1)^2 \mathrm{d}x} +\gamma \int _{\Omega }{g |\nabla H(\phi )| \mathrm{d}x}+\nu \int _{\Omega }{g H(\phi )\mathrm{d}{\varvec{x}}}, \end{aligned}$$

(15)

3.4 Level Set Formulation and Energy Minimization

The minimization of the energy functional ${{\mathcal {F}}}$ in Eq. (15) can be achieved iteratively by minimizing ${{\mathcal {F}}}$ w.r.t. each of the two variables, $\phi$ and ${\varvec{b}}$, assuming that the other variable is constant. We first fix the variable ${\varvec{b}}$, and then the minimization of the energy functional ${{\mathcal {F}}}(\phi ,{\varvec{b}})$ w.r.t $\phi$ can be achieved by solving the gradient flow equation:

$$\begin{aligned} \frac{\partial \phi }{\partial t} = - \frac{\partial {{\mathcal {F}}}}{\partial \phi }. \end{aligned}$$

(16)

We compute the derivative $\frac{\partial {{\mathcal {F}}}}{\partial \phi _l}$, $l= 1, \ldots , r$ (the number of level set functions) and re-express Eq. (16) as follows:

$$\begin{aligned} \frac{\partial \phi _l}{\partial t}&= -\alpha \sum _{i=1}^{k}\left( \frac{\partial M_i\left( \phi \right) }{\partial \phi _l}e_i \right. \nonumber \\&\quad + 2 \alpha \sum _{i=1}^{k} \sum _{j=1}^{m} \left( {{\mathcal {I}}}_{S_j} \frac{\partial M_i\left( \phi \right) }{\partial \phi _l}\left( {{\mathcal {I}}}_{S_j} M_i\left( \phi \right) -\frac{h_{ij}a}{\sum _{i=1}^{k}h_{ij}}\right) \right) \nonumber \\&\quad +\beta \left( \nabla ^2 \phi _l - div \left( \frac{\nabla \phi _l}{|\nabla \phi _l|}\right) \right) +\gamma \delta \left( \phi _l\right) ~div\left( g \frac{\nabla \phi _l}{|\nabla \phi _l|}\right) +\nu g \delta \left( \phi _l\right) , \end{aligned}$$

(17)

where $\delta (\phi _l)$ is the dirac delta function obtained as the derivative of the Heaviside function. Then, for fixed $\phi _l$, the optimal bias field ${\varvec{b}}$ that minimizes the energy ${{\mathcal {F}}}$ is given by:

$$\begin{aligned} b({\varvec{x}})=\frac{\sum _{i=1}^{k}\int _{\Omega }\frac{I({\varvec{x}})\mu _i}{\sigma _i^2}M_i(\phi _l)d({\varvec{x}})}{\sum _{i=1}^{k}\int _{\Omega }\frac{\mu _i^2}{\sigma _i^2}M_i(\phi _l)d({\varvec{x}})}. \end{aligned}$$

(18)

4 Simulation Results and Discussion

In the implementation of the proposed NMF-based level set method, we choose $\alpha$, $\beta$, and $\gamma$ to be equal to 1 in Eq. (17). The smoothed version of the Heaviside function is approximated by $H_\epsilon (x)=0.5 \sin (\arctan (\frac{x}{\epsilon }))+0.5$, as in Chena et al. (2009), while the dirac delta function, $\delta (x)$, is approximated by $\delta (x) = 0.5 \cos (\arctan (\frac{x}{\epsilon }))\frac{\epsilon }{\epsilon ^2+x^2}$. In our simulations, we set $\epsilon =1$. We automate the initialization of the level set function by using the fuzzy c-means (FCM) algorithm and initiate the level set function as $\phi _o=-4\epsilon (0.5-B_k)$, where $B_k$ is a binary image obtained from the FCM result. The detailed explanation of FCM used for the initialization is provided in Chuang et al. (2006). The weighting parameter $\nu$ is defined as $\nu =2*(1- \eta *(2*B_k+1))$, for some constants $\eta$. We choose the block size to be ($8 \times 8$ pixels) as it is small enough to capture the fine details that we are interested in.

To evaluate the performance of the proposed NMF–LSM method, we compare it to two state-of-the-art level set models, namely the localized level set model (localized-LSM) (Li et al. 2011) and the improved LGDF–LSM model (Chen et al. 2011). We use ten synthetic images whose boundaries are known and used as the ground truth with different levels of noise and intensity inhomogeneities. We assay for: (i) segmentation accuracy using three different similarity measures, Jaccard similarity (JS) (Vovk et al. 2007), Dice coefficient (DC) (Babalola et al. 2008), and root mean square error (RMSE), (ii) robustness to the initial conditions, and (iii) the influence of the weighting parameters $\alpha$, $\beta$, and $\gamma$ in Eq. (14), by choosing different values for each parameter within the range [0.1, 20].

The Jaccard similarity (JS) is defined as the ratio between the intersection and the union of two regions $S_1$ and $S_2$, representing, respectively, the segmented region and the ground truth.

$$\begin{aligned} {{\mathcal {J}}}(S_1,S_2)=\frac{| S_1 \cap S_2 |}{| S_1 \cup S_2 |}, \end{aligned}$$

(19)

where | S | represents the area of region S. The closer the JS to 1 the better the segmentation result. The Dice coefficient (DC) is another metric that measures the spatial overlap between two images or two regions, defined as:

$$\begin{aligned} {{\mathcal {D}}}(S_1,S_2)=\frac{2 | S_1 \cap S_2 |}{| S_1 \cap S_2 | + | S_1 \cup S_2 |}. \end{aligned}$$

(20)

Although Jaccard and Dice coefficients are very similar, the Jaccard similarity is more sensitive when the regions are more similar, while the Dice coefficient gives more weighting to instances where the two images agree (Vovk et al. 2007). Both of the JS and DC provide values ranging between 0 (no overlap) and 1 (perfect agreement). The root mean square error RMSE is a distance measure that gives the difference between two image regions or image intensities, denoted by $R_1$ and $R_2$ as follows, where N is the total number of pixels in the region $\Omega$

$$\begin{aligned} RMSE = \sqrt{\frac{1}{N}\sum _{{\varvec{x}}\in \Omega }(R_1({\varvec{x}})- R_2({\varvec{x}}))^2}. \end{aligned}$$

(21)

The NMF–LSM approach can also be applied using a block size of one pixel (i.e., $1 \times 1$), as shown in Fig. 13. The only disadvantage of choosing a small block size is the computational cost.

4.1 Accurate Segmentation by NMF–LSM

Figure 7 shows three synthetic images (first column) and the segmentation results of NMF–LSM (second column), localized-LSM (third column), and improved LGDF–LSM (fourth column). We can see that the NMF–LSM model delineates the boundaries of the objects more accurately than the other two methods, although each image is corrupted with the same level of noise and intensity inhomogeneities. The performance of the proposed NMF–LSM is more stable as it yields higher JS and DC values than the localized-LSM and the improved LGDF–LSM models (Fig. 8). Furthermore, the mean error rate of NMF–LSM is lower than the other two models.

Fig. 7

Performance evaluation of the proposed NMF–LSM, the localized-LSM and the improved LGDF–LSM. The first column represents three synthetic images corrupted with different level of noise and intensity inhomogeneities. The second column shows the segmentation of the NMF–LSM algorithm. The third and fourth columns show the segmentation results of the localized-LSM and the improved LGDF–LSM models, respectively

Fig. 8

NMF–LSM yields high segmentation accuracy in synthetic images. The three methods, NMF–LSM, localized-LSM and LGDF–LSM, are applied to 10 synthetic images with different degrees of intensity inhomogeneities and variable levels of noise; segmentation accuracy is assayed by the JS, DC, and RMSE. a Comparison based on Jaccard similarity. b Comparison based on Dice coefficient. c Comparison based on root mean square error

4.2 Robustness to Contour Initialization

With the aforementioned similarity metrics, we can quantitatively compare the performance of the three methods to variations in the initial conditions. The methods are used to segment the synthetic image in Fig. 9a with 10 different initializations of the contour; three of the 10 initial contours (red contours) and the corresponding segmentation results (green contours) are shown in Fig. 9b–d. In these three different initializations, the initial contour encloses the objects of interest, crosses the objects, and is totally inside one of the objects as displayed in Fig. 9. Starting from these initial contours, the corresponding segmentation results are almost the same, all accurately capturing the objects’ boundaries (green lines, Fig. 9). The segmentation accuracy is quantitatively assessed in terms of the JS, DC, and RMSE. The JS, DC of these results are all between 0.78 and 0.97 pixel, while the RMSE is between 0.03 and 0.1 as shown in Fig. 10. These experiments demonstrate the robustness of the NMF–LSM model to contour initialization.

Fig. 9

Robustness of the proposed NMF-LSM segmentation to contour initializations. The NMF-LSM is applied to segment the synthetic image in (a). Different initial contours are represented by the red contours and the corresponding segmentation results are represented by the green contours (b–d)

Fig. 10

High segmentation accuracy of the NMF–LSM method for different initial contours. The segmentation accuracy is measured by the JS, DC, and RMSE

4.3 Stable Performance for Weighting Parameters

We compare the performance of the NMF–LSM model with the localized-LSM and the improved LGDF–LSM models for different weighting parameters $\alpha$, $\beta$, and $\gamma$ in Eqs. (14) and (17); the results demonstrate that NMF–LSM has better and more stable performance in terms of segmentation accuracy and robustness. Specifically, the box plots of the NMF–LSM are relatively shorter with higher JS, DC values and lower error rate for different values of $\alpha$, $\beta$, and $\gamma$ Fig. 11.

4.4 NMF–LSM is Computationally-Efficient

The NMF–LSM model converges remarkably faster than the localized-LSM and the improved LGDF–LSM models for different values of $\alpha$, $\beta$, and $\gamma$ (see Fig. 12). This property can be explained by the fact that the NMF–LSM estimates less parameters than the localized-LSM and the LGDF–LSM. In fact, only the level set functions and the bias field are estimated by NMF–LSM, whereas the localized-LSM estimates additionally the region intensity values and the LGDF–LSM estimates the regions mean intensities and variances along with the level set functions and the bias field.

Fig. 11

Comparison of the performance of NMF–LSM (NMF), localized-LSM and improved LGDF–LSM (LGDF) for different values of the parameters. Shown are box plots of the JS, DC and RMSE values for the star object in the synthetic image for parameters $\alpha$ (a), $\beta$ (b) and $\gamma$ (c)

Fig. 12

Fast convergence of NMF–LSM. The box plots of convergence times of the three models, NMF–LSM (NMF), the localized-LSM, and the improved LGDF–LSM (LGDF), for different value of the parameters $\alpha$, $\beta$, and $\gamma$. The CPU times were recorded for MATLAB programs on a Asus K53E laptop with Intel(R) Core(TM)i5-2450M CPU, 2.50 GHz, 8 GB RAM, with MATLAB R2013a on Windows 7. Convergence time is in seconds

4.5 Effects of Block Size on Segmentation Accuracy

Figures 4 and 5 demonstrate that block size plays an important role in discovering the regions of image; in the case of the image of Fig. 3, block size $8 \times 8$ pixels led to the discovery of all the regions. A titration of the block size down to the limit of $(1 \times 1)$ pixels in the image of Fig. 3 demonstrates that the segmentation accuracy of NMF–LSM improves between block size $16 \times 16$ and $8 \times 8$ pixels and then it saturates (Fig. 13). This experiment demonstrates that decreasing the block size to be very small (less than $(8 \times 8)$ pixels in this case) will not affect the segmentation accuracy of the proposed approach for this image. It also demonstrates that the NMF–LSM algorithm carries over at the limit, when the block size is equal to one pixels. We also verified that, at block size 1 pixels, the Frobenius norm stabilizes at $k = 6$, which corresponds to the true number of regions in the image (data not shown for space considerations).

Fig. 13

NMF–LSM segmentation accuracy saturates with small block sizes. The segmentation accuracy is assayed by the JS, DC, and RMSE; block sizes are in pixels

5 Application to Clinical Brain MRI Images

In this section, we apply the NMF–LSM algorithm to anonymized gadolinium-enhanced T1-Weighted MRI images of human brain with and without malignant glioblastoma multiforme, a malignant brain tumor. The results demonstrate that the NMF–LSM method accurately delineates the different structures of the brain, i.e., gray matter, white matter, cerebrospinal fluid (CSF), as well as the regions associated with the tumor, i.e., edema, tumor, and necrosis (Fig. 14). It is noteworthy that although the intensities of the gray matter, the white matter, and the edema are very close to each other and their histograms overlap (Fig. 14m), the NMF–LSM method separates them as distinct regions using an $8 \times 8$ pixels block size, which is small enough to capture the fine details in this image.

Fig. 14

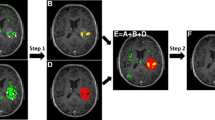
Accurate segmentation of a gadolinium-enhanced T1-Weighted MRI scan of a patient with glioblastoma multiforme by the NMF–LSM algorithm. The green contour in b indicates the growing tumor, the pink contour in c indicates the region of the brain that corresponds to necrosis and invasive tumor/edema, the red contour in d indicates the gray matter, the blue contour in e indicates the white matter, and the yellow contour in f indicates the CSF with the background. NMF–LSM retrieves the histogram of each brain structure shown in m obtained from the factor matrix W. The bias field in the MRI image is shown in g. The red and blue arrows in its binary representation (i) point to the area of necrosis and edema, respectively. The latter corresponds to high signal intensity in Fluid-Attenuated Inversion Recovery (FLAIR) sequences (not shown). h–l The binary representations of the growing tumor, the gray matter, the white matter and the CSF with the background, respectively. The image is preprocessed by histogram equalization and morphological operations. Histogram equalization improves the contrast of the image by spreading out the most frequent intensity values. Non-brain structures are removed using morphological operations. Specifically, thresholding removes the background,erosion shrinks the brain and skull, opening removes the small non-brain structures, labeling isolates the brain from the skull and non-brain structures, and dilation recovers the exact boundaries of the brain

5.1 Comparison with State-of-the-Art Software Packages for MRI Segmentation

We compare the segmentation performance of the NMF–LSM algorithm with the widely used software packages for brain MRI segmentation, SPM12 (Friston et al. 1995) and FSL (Smith et al. 2004). Both software are targeted toward brain MRI segmentation and include a set of skull stripping, intensity non-uniformity (bias) correction, and segmentation routines. To assess the performance in the presence of noise, we corrupt the MRI images with blurring and salt-and-pepper noise (28 %). The segmentation results demonstrate that the segmentation by NMF–LSM of the gray matter, white matter, and CSF is far superior than the other two methods (Fig. 15); it is also noteworthy that both FSL and SPM-12 do not discover the region that corresponds to necrosis and invasive tumor/edema, segmented by NMF–LSM (Fig. 15Ib, Ig). Furthermore, the gray natter, white matter, and CSF have not been accurately delineated by SPM12 and FSL (see Fig. 15II, III).

Fig. 15

Superior segmentation by NMF–LSM in the presence of noise. Segmentation of the MRI scan of Fig. 14 corrupted with blurring and salt-and-pepper noise (28 %) by NMF–LSM (Ia–Ii), SPM-12 (IIa–IIh), and FSL (IIIa–IIIh). The green, red, blue, and yellow regions indicate the growing tumor, gray matter, white matter, the CSF with the background, respectively. The pink region in (Ib) indicates the region, segmented by NMF–LSM, that corresponds to necrosis and invasive tumor/edema. If–Ij Binary representations corresponding to (Ia–Ie). IIe–IIh Binary representations corresponding to (IIa–IId). IIIe–IIIh Binary representations corresponding to (IIIa–IIId)

6 Potential in Early Diagnosis and Monitoring of Gliomas

Here, we illustrate the potential of the NMF–LSM method in addressing an important biological problem, the early diagnosis of progression of non-enhancing grade 2 and 3 gliomas. What follows is a presentation of two case reports and a comparison of the retrospective diagnoses rendered by the neuroradiologists who have examined the longitudinal MRIs and the conclusions from volumetric measurements by NMF–LSM. We also detail the implications of an earlier diagnosis.

Case 1

(Grade 3 oligodendroglioma $\rightarrow$ grade 3 oligodendroglioma (Fig. 16a))

In 2008, a 41-year-old male underwent gross total resection of a right frontal grade 3 oligodendroglioma, 1p/19q co-deleted. He subsequently received 12 cycles of temozolomide (Temodar), which ended on 10/12/2009 and was followed by serial MRIs. The MRIs performed on 12/30/2008 and 03/05/2009 revealed “evolving postsurgical changes.” The MRIs performed between 05/07/2009 and 01/26/2012 were interpreted as stable. The patient missed follow-up appointments. The clinical/radiological diagnosis of progression was made on 10/04/2012 (Fig. 16a, red circle); he was re-treated by Temodar on 10/29/2012 and 11/29/2012. MRI done on 01/03/2013 was interpreted as “slight interval increase in the size of the FLAIR signal in the right frontal lobe with stable pattern of enhancement” (Fig. 16a, red circle). A surgical resection on 02/06/2013 revealed a recurrent anaplastic oligodendroglioma, WHO grade 3, with deletions of 1p and 19q and positive staining for IDH1(R132H) mutant protein. He was treated by radiation therapy.

Fig. 16

The NMF–LSM method prevents delays in detecting progression of non-enhancing gliomas. a FLAIR volumes of the serial MRIs of a patient with grade 3 non-enhancing oligodendroglioma that progressed. b FLAIR volumes of the serial MRIS of a patient with grade 2 oligodendroglioma that progressed to GBM. The red circles and green arrows indicate the volumes at the dates of radiological diagnosis of progression. Stars indicate statistically significant change in tumor volumes (two-sample t test $p < 0.05$). Double arrows indicate the periods of treatment by Temodar. c, d show selected FLAIR images of cases 1 and 2, respectively; pink lines show the segmentation of the FLAIR signal. The dates are chosen to include the ones that demonstrate statistically significant increase in tumor volumes (see a, b, stars) and the MRIs immediately preceding them

The NMF–LSM segmentation method was applied to measure the tumor volumes in the MRIs done between 05/07/2009 and 01/03/2013. Figure 16a plots the volumes of the FLAIR signal vs. time. Starting from 12/10/2010, each tumor volume is compared to the sample including the volumes of the three preceding MRIs and a p value is computed (two-sample t test). The results show a statistically significant change in the volume of the tumor on 12/23/2010 and 1/26/2012 ($p < 0.05$, Fig. 16a stars). In this patient, the NMF–LSM method detects a statistically significant change in tumor volume earlier than the clinical diagnosis of recurrence on two separate dates. An earlier diagnosis could have prevented a 2-year delay in treatment with radiation therapy, which could have prolonged the overall survival time and improved the quality of life. It is noteworthy that the volume of the brain to be irradiated is derived from the volume of FLAR signal; hence, earlier detection of progression will limit the volume of irradiated brain.

Case 2

(Grade 2 oligodendroglioma $\rightarrow$ GBM (Fig. 16b))

Following a biopsy on 01/2/2007, which revealed grade 2 oligodendroglioma, the 38-year-old patient was treated by radiation therapy (01/02/2007 to 02/20/2007). Serial MRIs were interpreted as stable until 12/19/2011, when the radiological diagnosis of progression was made (Fig. 16b, red circle). The patient was treated by Temodar between 01/02/2012 and 12/02/2012. The MRI on 03/25/2013 was interpreted as stable. The MRI on 05/16/2013 showed radiological progression with new enhancement (Fig. 16b, red circle); a resection in 06/2013 revealed a GBM.

The NMF–LSM segmentation method is applied to measure the tumor volumes in all the MRIs done between 11/30/2006 and 05/16/2013. Figure 16b plots the volumes of the FLAIR signal vs. time. Starting from 11/05/2007, each tumor volume is compared to the sample including the volumes of the three preceding MRIs and a p value is computed (two-sample t test). The results show a statistically significant change in the volume of the tumor on 12/15/2008 and 3/25/2013 ($p < 0.05$, Fig. 16a stars). In this case, the NMF–LSM method can (Fig. 16b):

• 1) monitor the tumor response to radiation therapy by following the decrease in tumor volume,

• 2) facilitate a diagnosis of progression on 12/15/2008 instead of 12/19/2011,

• 3) monitor the tumor response to temozolomide, and

• 4) facilitate a diagnosis of progression on 03/25/2013 instead of 05/16/2013.

Like Case 1, early treatment of Case 2 could have prolonged the overall survival time and improved the quality of life.

7 Conclusion

Medical image segmentation is one of the most important and challenging tasks in medical image analysis. In particular, brain MRI segmentation is a difficult task, due to the complexity of the brain anatomical structures and the intensity inhomogeneity that corrupts the quality of MRI images. Great efforts have been made in this field in order to achieve automatic accurate segmentation results. In this paper, we proposed a new deformable model for image segmentation based on variational level set formulation and probabilistic nonnegative matrix factorization, termed NMF–LSM. The main advantages of NMF–LSM approach over the state-of-the-art, as well as the contributions of this work, are: (i) relying on the histogram data rather than the pixel intensity values, thus making the algorithm robust to additional noise and outliers; (ii) automating region discovery by estimating the number of regions/clusters in the image based on the Frobenius norm of the NMF factors; (iii) providing useful interpretation of the NMF as an image clustering and decomposition tool; (iv) introducing a novel spatial term in the level set equation; (vi) limiting the number of simultaneously estimated model parameters to the bias field and the level set functions, thus improving the segmentation accuracy.

In this paper, 3D versions of our approach are simply obtained by superposing 2D segmented slices and computing volumes based on 2D areas and thickness between slices (see Fig. 16). The NMF–LSM method contributes solutions to several problems in mathematical biology: (1) modeling and clustering of segments in images and (2) automated, accurate, and robust segmentation of medical images. Specific applications entertained in this paper include: (1) automated early and timely diagnosis of the recurrence of non-enhancing gliomas, (2) automated monitoring tumor response of non-enhancing gliomas, and (3) automated image segmentation in patients with GBM.