Phylogenetic Networks that Display a Tree Twice

Abstract

In the last decade, the use of phylogenetic networks to analyze the evolution of species whose past is likely to include reticulation events, such as horizontal gene transfer or hybridization, has gained popularity among evolutionary biologists. Nevertheless, the evolution of a particular gene can generally be described without reticulation events and therefore be represented by a phylogenetic tree. While this is not in contrast to each other, it places emphasis on the necessity of algorithms that analyze and summarize the tree-like information that is contained in a phylogenetic network. We contribute to the toolbox of such algorithms by investigating the question of whether or not a phylogenetic network embeds a tree twice and give a quadratic-time algorithm to solve this problem for a class of networks that is more general than tree-child networks.

1 Introduction

Although phylogenetic networks are becoming increasingly important in studying the evolution of present-day species whose past includes reticulation events, phylogenetic trees remain to play a fundamental role in phylogenetic analyses since the evolutionary history of a single gene can, in most cases, be described by a tree. It is therefore not surprising that investigating the tree-like content of phylogenetic networks is often an important first step in analyzing and interpreting such networks. For example, one might be interested in deciding whether a phylogenetic network embeds a given phylogenetic tree or in counting the number of trees embedded in a network. The latter problem is related to calculating the parsimony score of a network (Nakhleh et al. 2005) which, given the popularity of parsimony tree reconstruction algorithms, is likely to become a standard tool in computing a phylogenetic network directly from sequence data. While deciding whether a tree is embedded in a network is polynomial-time solvable for certain special classes of phylogenetic networks (van Iersel et al. 2010), the problem is NP-complete in its general form (Kanj et al. 2008). Similarly, counting the number of phylogenetic trees that are embedded in an arbitrary phylogenetic network is also known to be a computationally hard problem (Linz et al. 2013).

In this paper, we investigate a related problem. Given a phylogenetic network ${\mathcal N}$, this problem asks whether or not there exists a phylogenetic tree with the same leaf set as ${\mathcal N}$ that is embedded more than once in ${\mathcal N}$. If such a tree exists, then there are two distinct sets of edges in ${\mathcal N}$ that yield the same tree. It is known that if ${\mathcal N}$ is binary and has $k$ reticulations (detailed definitions are deferred to Sect. 2), then the maximum number of possible trees embedded in ${\mathcal N}$ is $2^k$. While it was shown independently that the upper bound of $2^k$ is sharp for so-called “normal networks” in van Iersel et al. (2010, Theorem 1) and Willson (2012, Corollary 3.4), little is known about the properties of a phylogenetic network that guarantee it embeds the maximum number of trees. Here, we present the first such characterization for a class of networks that lies strictly between tree-child and tree-sibling networks. This characterization is based on a certain type of underlying cycle in a network that will be formally introduced in Sect. 3. Moreover, we will show that such cycles are recognizable in quadratic time, leading to the following theorem, where, for now, displaying a tree twice implies that there are two distinct embeddings for the same tree.

Theorem 1

Let ${\mathcal N}$ be a rooted binary phylogenetic network with leaf set $X$ and suppose that, for each reticulation of ${\mathcal N}$, at least one of its parents is connected to a leaf of ${\mathcal N}$ via a directed path that does not contain a reticulation. Then it takes time quadratic in the size of $|X|$ to decide whether or not ${\mathcal N}$ displays a rooted phylogenetic tree with leaf set $X$ twice.

It is worth pointing out that for a network ${\mathcal N}$ with the property described in Theorem 1, the number of leaves in ${\mathcal N}$ does not bound the total number of vertices in ${\mathcal N}$. Hence, for a fixed set $X$, the class of networks with leaf set $X$ that we consider in this paper contains infinitely many networks (for example, see Fig. 1, where the directed path from the root of the network to the leaf labeled 1 can be arbitrarily long). In contrast, for a fixed set $X$, the number of tree-child networks with leaf set $X$ is finite (McDiarmid et al.).

Fig. 1

A phylogenetic network for which each reticulation has a parent connected to the leaf labeled 1 via a directed path that does not contain a reticulation

The remainder of the paper is organized as follows. The next section contains notation and terminology that is used throughout the paper. In Sect. 3, we introduce the concepts of switchings, and avoidable vertices and cycles. We also derive several lemmas and observations in this section that are important in establishing the above-mentioned characterization, which is presented in Sect. 4. In Sect. 5, we establish Theorem 1. The last section contains a remark on tree-child and normal networks.

2 Preliminaries

This section provides notation and terminology that is used in the remainder of the paper. Throughout the paper, $X$ denotes a finite set.

2.1 Phylogenetic Trees

A rooted phylogenetic $X$-tree ${\mathcal T}$ is a rooted tree in which the root has degree at least two and all other interior vertices have degree at least three, and whose leaf set is $X$. In addition, ${\mathcal T}$ is binary if, apart from the root which has degree two, all interior vertices have degree three. Since we are interested only in rooted binary phylogenetic $X$-trees throughout the paper, we will almost always refer to such a tree as a tree on $X$.

2.2 Phylogenetic Networks

A phylogenetic network ${\mathcal N}$ on $X$ is a rooted acyclic digraph that satisfies the following three properties:

• (i) the root has out-degree two,

• (ii) each vertex with out-degree zero has in-degree one, and the set of vertices with out-degree zero is $X$, and

• (iii) all other vertices either have in-degree one and out-degree two, or in-degree two and out-degree one.

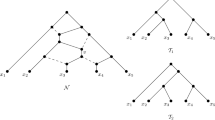
We will refer to ${\mathcal N}$ as a network on $X$ or, simply, as a network if $X$ plays no particular role. Such networks are commonly referred to as binary phylogenetic networks. An example of a network on $\{1,2,3,4\}$ is shown in the left of Fig. 2, where the vertex labels $u,\,u',\,v$, and $v'$ are ignored for the moment. Here, as well as in all other figures, edges are directed down the page. Furthermore, we will assume that networks have no parallel edges. For a network ${\mathcal N}$, vertices with in-degree two and out-degree one are called reticulations and all other vertices are called tree vertices. In addition, edges directed into a reticulation are called reticulation edges and all other edges are called tree edges. Similar to rooted phylogenetic trees, vertices with out-degree zero are referred to as leaves. Indeed, a rooted binary phylogenetic tree is a phylogenetic network with no reticulations.

Fig. 2

Left A phylogenetic network ${\mathcal N}$ that displays three trees. Middle A phylogenetic tree that is displayed twice by ${\mathcal N}$. Right A phylogenetic network ${\mathcal N}'$ that displays four trees. While ${\mathcal N}$ and ${\mathcal N}'$ are both tree-sibling, only ${\mathcal N}'$ also satisfies the stronger tree-child condition

Biologically, like phylogenetic trees, phylogenetic networks illustrate the evolutionary history of a collection of present-day species. Such species are represented by the leaves, while all other vertices represent (hypothetical) ancestors. A reticulation represents, for example, a hybrid species.

Let $u$ and $v$ be two vertices of a network ${\mathcal N}$ on $X$. If there is a directed path (resp. a directed path that contains at least one edge) from $u$ to $v$, then $u$ is an ancestor (resp. strict ancestor) of $v$, and $v$ is a descendant (resp. strict descendant) of $u$. More particularly, if $(u,v)$ is an edge in ${\mathcal N}$, then $u$ is a parent of $v$, and $v$ is a child of $u$. Furthermore, if two vertices have a common parent, then they are said to be siblings. We use $D_u$ to denote the subset of $X$ whose elements are precisely the descendants of $u$.

Let ${\mathcal T}$ be a tree on $X$, and let ${\mathcal N}$ be a network on $X$. We say that ${\mathcal N}$ displays ${\mathcal T}$ if ${\mathcal T}$ can be obtained from ${\mathcal N}$ by deleting edges and vertices, and contracting vertices with in-degree one and out-degree one. Intuitively, ${\mathcal T}$ is displayed by ${\mathcal N}$ if all of the ancestral information inferred by ${\mathcal T}$ is also inferred by ${\mathcal N}$. Note that if ${\mathcal T}$ is displayed by ${\mathcal N}$, then ${\mathcal T}$ is necessarily binary.

Tree-child and tree-sibling networks are two prominent types of networks arising in the literature. Let ${\mathcal N}$ be a network on $X$. A vertex $v$ of ${\mathcal N}$ has the tree-path property if there exists a leaf $\ell$ such that there is a directed path $P$ from $v$ to $\ell$ containing no reticulations, except for possibly $v$. If such a path exists, then each edge of $P$ is a tree edge and $P$ is the unique directed path from $v$ to $\ell$ in ${\mathcal N}$. For example, except for the parent common to $v$ and $v'$, each vertex of the network shown on the left-hand side in Fig. 2 has the tree-path property. We say that ${\mathcal N}$ is tree-child (e.g. see Cardona et al. 2009) if each vertex of ${\mathcal N}$ has the tree-path property. Equivalently, ${\mathcal N}$ is tree-child if each non-leaf vertex $u$ of ${\mathcal N}$ has a child $v$ such that $v$ is a tree vertex. Biologically, such networks guarantee that all species that arise from a speciation event (represented by a tree vertex) or a reticulation event exist for a certain period of time before evolving any further. Furthermore, ${\mathcal N}$ is tree-sibling (e.g. see Cardona et al. 2008) if each reticulation has a sibling that is a tree vertex. For example, the network shown on the left-hand side of Fig. 2 is tree-sibling but not tree-child, while the network shown on the right-hand side of the same figure is tree-child (and, hence, also tree-sibling). Observe that, for a fixed set $X$, the class of tree-child networks on $X$ is a proper subclass of tree-sibling networks on $X$. A class of networks on $X$ that is nested strictly between these two classes is the class which has the property that, for each reticulation, at least one of its parents has the tree-path property. It is this later class that is the subject of Theorem 1.

3 Switchings and Avoidability

In the first part of this section, we introduce the concept of switchings in a network to describe precisely what it means for a tree to be displayed twice. In the second part, we describe a certain type of cycle and establish several lemmas that play a role in the characterization of the next section.

3.1 Switchings

Let ${\mathcal N}$ be a network on $X$. A subset $S$ of reticulation edges of ${\mathcal N}$ is a switching of ${\mathcal N}$ if, for each reticulation $v$ of ${\mathcal N}$, the set $S$ contains precisely one of the two reticulation edges directed into $v$. Now, let $S$ be a switching of ${\mathcal N}$. If we delete each reticulation edge in ${\mathcal N}$ that is not in $S$, then the resulting directed graph contains no underlying cycle and, for each leaf $\ell \in X$, it is easily checked that there is a directed path from the root of this directed graph to $\ell$. If we now repeatedly contract each resulting vertex with in-degree one and out-degree one and delete each vertex with degree one that is not in $X$, it is easily seen that we obtain a tree ${\mathcal T}$ on $X$. We say that $S$ yields ${\mathcal T}$. Note that ${\mathcal T}$ is well defined and, by construction, ${\mathcal T}$ is displayed by ${\mathcal N}$. Conversely, observe that, if ${\mathcal T}$ is a tree on $X$ displayed by ${\mathcal N}$, then there exists a switching that yields ${\mathcal T}$. In summary, this leads to the following observation, which we will freely use throughout the paper.

Observation 1

A network ${\mathcal N}$ on $X$ displays a tree ${\mathcal T}$ on $X$ if and only if there exists a switching of ${\mathcal N}$ that yields ${\mathcal T}$.

With Observation 1 in hand, we say that ${\mathcal N}$ displays a tree twice if there exist two distinct switchings of ${\mathcal N}$ each of which yields (up to isomorphism) the same tree on $X$. For example, for the network ${\mathcal N}$ shown on the left in Fig. 2, it is easily verified that the tree shown in the middle of the same figure is displayed twice by ${\mathcal N}$. Also, referring back to a comment made in the introduction, it follows from Observation 1 that, if ${\mathcal N}$ is a network on $X$ with exactly $k$ reticulations, then ${\mathcal N}$ displays at most $2^k$ distinct trees on $X$.

3.2 Avoidable Vertices

Let ${\mathcal N}$ be a network on $X$, and let $v$ be a vertex of ${\mathcal N}$. We say that $v$ is avoidable if, for each $\ell \in X$, there exists a directed path from the root of ${\mathcal N}$ to $\ell$ that avoids $v$. Otherwise, $v$ is unavoidable. In particular, if $v$ is unavoidable, then there exists a leaf $\ell$ such that every directed path from the root of ${\mathcal N}$ to $\ell$ contains $v$. To illustrate, Fig. 3 shows a network with an avoidable reticulation $v$. Note that the definition of an unavoidable reticulation coincides with that of a so-called visible reticulation in Huson et al. (2010).

Fig. 3

A phylogenetic network that has the tree-path property for at least one parent of each reticulation and with an avoidable reticulation $v$

The next lemma gives a sufficient, but not a necessary, condition for guaranteeing that a network displays a tree twice.

Lemma 1

Let ${\mathcal N}$ be a network on $X$. If ${\mathcal N}$ has an avoidable reticulation, then ${\mathcal N}$ displays a tree on $X$ twice.

Proof

Let $v$ be an avoidable reticulation of ${\mathcal N}$, and let $e_1$ and $e_2$ be the two reticulation edges that are incident with $v$. Since $v$ is avoidable, there exists, for each $\ell \in X$, a directed path $P_\ell$ from the root of ${\mathcal N}$ to $\ell$ that avoids $v$. Let ${\mathcal T}$ be a tree on $X$ that is displayed by ${\mathcal N}$ and, up to degree-$2$ vertices, whose edge set is a subset of $\bigcup _{\ell \in X}P_\ell$. It is easily seen that such a ${\mathcal T}$ always exists. Now, let $S$ be a switching of ${\mathcal N}$ that yields ${\mathcal T}$. It follows that the two distinct switchings $(S-\{e_1,e_2\})\cup \{e_1\}$ and $(S-\{e_1,e_2\})\cup \{e_2\}$ both yield ${\mathcal T}$ and, hence, ${\mathcal N}$ displays a tree on $X$ twice.$\square$

3.3 Avoidable Cycles

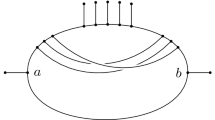
We now extend the concept of avoidability to cycles of a network. Let ${\mathcal N}$ be a network on $X$, and let $v$ be a reticulation of ${\mathcal N}$. Let $u$ be a tree vertex of ${\mathcal N}$ such that there exist two directed paths $P_1$ and $P_2$ from $u$ to $v$ whose vertex sets, apart from $u$ and $v$, are disjoint. We call the underlying cycle induced by the union of the vertex sets of $P_1$ and $P_2$ a $2$ -path cycle of ${\mathcal N}$, where $u$ is the source vertex and $v$ is the sink vertex. It is easily seen that each reticulation of ${\mathcal N}$ is the sink of at least one $2$-path cycle in ${\mathcal N}$.

Let $C$ be a $2$-path cycle of ${\mathcal N}$ with source $u$ and sink $v$. Let $H$ be a subset of the vertex set of $C$ such that, for each leaf $\ell \in X$, at least one of the following holds:

• (i) there is a directed path from the root of ${\mathcal N}$ to $\ell$ which avoids every vertex in $C$, or

• (ii) there is a directed path from the root of ${\mathcal N}$ to $\ell$ for which the last vertex in the path meeting $C$ is contained in $H$.

We refer to $H$ as a hitting set of $C$. Furthermore, $H$ is minimum if $C$ has no hitting set $H'$ with $|H'|<|H|$. If there exists a hitting set of $C$ with at most two elements, we say that $C$ is avoidable. A simplified phylogenetic network that has an avoidable cycle and summarizes the basic idea of such a cycle is shown in Fig. 4. Moreover, for a more explicit example, the network shown on the left-hand side of Fig. 2 has a $2$-path cycle $C$ with source $u$ and sink $v$ that is avoidable, and a $2$-path cycle with source $u'$ and sink $v'$ that is unavoidable. Note that $C$ is avoidable because there exist directed paths from the root of the network to leaves $3$ and $4$ that do not meet $C$.

Fig. 4

A 2-path cycle $C$ of a network ${\mathcal N}$ on $X=X_1\cup X_2\cup X_3$ with source $u$ and sink $v$. Note that $\{v,v_1\}$ is a hitting set of $C$ because $X$ can be partitioned into three sets $X_1,\,X_2$, and $X_3$ such that, for each $\ell _1\in X_1$, there exists a directed path from $\rho$ to $\ell _1$ that avoids every vertex in $C$, and, for each $\ell _2 \in X_2$ (resp. $\ell _3 \in X_3$), there exists a directed path from $\rho$ to $\ell _2$ (resp. $\ell _3$) for which the last vertex on that path that meets a vertex in $C$ is $v$ (resp. $v_1$). Thus $C$ is an avoidable cycle. Except for the edge joining $v_1$ and $v$, lines indicate directed paths in ${\mathcal N}$. Furthermore, the three triangles indicate subnetworks of ${\mathcal N}$. While omitted for the sake of simplicity, these subnetworks as well as $C$ may be further interwoven among themselves and among each other

The next lemma gives another sufficient, but again not a necessary, condition for guaranteeing that a network displays a tree twice.

Lemma 2

Let ${\mathcal N}$ be a network on $X$, and let $v$ be a reticulation of ${\mathcal N}$. If $v$ is the sink of an avoidable cycle, then ${\mathcal N}$ displays a tree on $X$ twice.

Proof

Suppose that $v$ is the sink of an avoidable cycle $C$. Then, there is a hitting set $H$ of $C$ such that $|H|\le 2$. Furthermore, for each $\ell \in X$, there is a directed path $P_\ell$ in ${\mathcal N}$ from the root to $\ell$ such that either $P_\ell$ avoids every vertex of $C$ or the last vertex of $P_\ell$ meeting $C$ is an element of $H$.

Now, let ${\mathcal T}$ be a tree on $X$ displayed by ${\mathcal N}$ whose edge set, up to degree-$2$ vertices, is a subset of $\bigcup _{\ell \in X} P_\ell$. Since $H$ contains at most two elements, ${\mathcal T}$ has a subtree that can be detached by deleting a single edge and whose leaf set contains precisely each element $\ell \in X$ for which the last vertex of $P_\ell$ meeting $C$ is an element of $H$. Let $e_1$ and $e_2$ denote the reticulation edges incident with $v$, and let $S$ be a switching of ${\mathcal N}$ that yields ${\mathcal T}$. By construction, it is now easily seen that the two switchings $(S-\{e_1,e_2\})\cup \{e_1\}$ and $(S-\{e_1,e_2\})\cup \{e_2\}$ both yield ${\mathcal T}$. Hence, ${\mathcal N}$ displays a tree on $X$ twice.$\square$

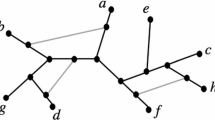
The converse of Lemma 2 does not hold. For example, Fig. 5 shows a network that has no avoidable cycle, but displays a tree twice.

Fig. 5

A phylogenetic network (left) that displays the tree shown on the right twice. Moreover, ${\mathcal N}$ has no avoidable cycle because each 2-path cycle of ${\mathcal N}$ with sink $v_i$, for $i\in \{1,2,3\}$, has a minimum hitting set of size at least three. For example, $\{h_1,h_2,v_3\}$ and $\{h_1,h_3,v_3\}$ are the two unique minimum hitting sets of the 2-path cycle of ${\mathcal N}$ with sink $v_3$

We end this section with a concept and an observation that is used in the rest of the paper. Let ${\mathcal N}$ be a network, and let $v$ be a reticulation of ${\mathcal N}$. A parent of $v$ is a distinguished parent if it has the tree-path property and, if both parents of $v$ have the tree-path property, then it is not an ancestor of the other parent. Note that, if $v$ has a parent that has the tree-path property, then $v$ has at least one distinguished parent. Moreover, if $v$ has two distinguished parents, then $v$ is not the sink of an avoidable cycle in ${\mathcal N}$. Referring back to Fig. 2, each of the two reticulations in the network shown on the left has exactly one distinguished parent, while each of the two reticulations in the network shown on the right of the same figure has two distinguished parents.

The following observation immediately follows from the definition of an avoidable cycle and recalling that such a cycle has a hitting set of size at most two.

Observation 2

Let ${\mathcal N}$ be a network with no avoidable reticulation, and let $v$ be a reticulation of ${\mathcal N}$. If $v$ has a distinguished parent, say $v_1$, and $v$ is the sink of an avoidable cycle $C$ in ${\mathcal N}$, then $\{v_1,v\}$ is the unique minimum hitting set of $C$.

4 Characterization

In this section, we characterize when a network with at least one parent of each reticulation having the tree-path property displays a tree twice. This characterization is in terms of avoidable reticulations and avoidable cycles. We will see in the next section that this result leads naturally to a quadratic-time algorithm that decides whether or not such a network displays a tree twice.

We start by describing an operation that involves a deletion of a reticulation in a network. Let ${\mathcal N}$ be a network with no avoidable reticulation and, for each reticulation, at least one of its parents has the tree-path property. Let $\rho$ be the root of ${\mathcal N}$, and let $v$ be a reticulation of ${\mathcal N}$ whose strict descendants are all tree vertices. Since ${\mathcal N}$ is acyclic such a reticulation exists. Obtain a rooted acyclic digraph ${\mathcal N}'$ from ${\mathcal N}$ by deleting $v$ and contracting any resulting vertex of in-degree one and out-degree one. Such vertices correspond to $v_1$ and $v_2$ and, provided neither is $\rho$, there are two contractions. If $v_1$ or $v_2$ is $\rho$, then delete $\rho$ as well. We say that ${\mathcal N}'$ is obtained from ${\mathcal N}$ by a reticulation deletion relative to $v$. The next lemma shows that ${\mathcal N}'$ preserves the two properties of ${\mathcal N}$ that distinguish it.

Lemma 3

Let ${\mathcal N}$ be a network on $X$ with no avoidable reticulation. Suppose that ${\mathcal N}$ has the tree-path property for at least one parent of each reticulation. Let ${\mathcal N}'$ be the rooted acyclic digraph obtained from ${\mathcal N}$ by a reticulation deletion relative to a reticulation $v$. Then ${\mathcal N}'$ is a network on $X-D_v$ with no avoidable reticulation and, for each reticulation, at least one of its parents has the tree-path property.

Proof

Let $\rho$ denote the root of ${\mathcal N}$. Furthermore, let $v_1$ and $v_2$ denote the parents of $v$. Without loss of generality, we may assume that $v_1$ is a distinguished parent of $v$. Let $m$ denote a leaf in ${\mathcal N}$ with the property that there is a tree-path from $v_1$ to $m$. Now, since each reticulation in ${\mathcal N}$ is unavoidable, $v_1$ and $v_2$ are tree vertices. Using this fact, as well as the property that at least one parent of each reticulation has the tree-path property in ${\mathcal N}$, it is easily checked that ${\mathcal N}'$ is indeed a phylogenetic network on $X-D_v$ (with no parallel edges).

We next show that each reticulation in ${\mathcal N}'$ is unavoidable, and at least one parent of each reticulation in ${\mathcal N}'$ has the tree-path property. The latter certainly holds as no such tree-path in ${\mathcal N}$ contains either $(v_1,v)$ or $(v_2,v)$. Now, let $w$ be a reticulation in ${\mathcal N}'$. If $w$ is avoidable in ${\mathcal N}'$, then, as $w$ is unavoidable in ${\mathcal N}$, there is a leaf $\ell \in D_v$ such that every directed path in ${\mathcal N}$ from $\rho$ to $\ell$ meets $w$. Moreover, there is a directed path $P_m$ from $\rho$ to $m$ in ${\mathcal N}$ avoiding $w$. Since $P_m$ extends the unique tree-path from $v_1$ to $m$, it follows that, by making use of the first part of $P_m$ from $\rho$ to $v_1$, we can construct a directed path from $\rho$ to $\ell$ that uses the edge $(v_1,v)$ and avoids $w$ in ${\mathcal N}$; a contradiction. Thus, each reticulation in ${\mathcal N}'$ is unavoidable. $\square$

The next theorem is the aforementioned characterization. For the purpose of its proof, we need an additional definition. Let ${\mathcal T}$ be a tree on $X$, and let $a,\,b$, and $c$ be three distinct elements in $X$. We say that ${\mathcal T}$ contains the triple $ab|c$ (or, equivalently, $ba|c$) if, in ${\mathcal T}$, the path connecting $a$ and $b$ does not intersect the path from the root to $c$.

Theorem 2

Let ${\mathcal N}$ be a network on $X$. Suppose that at least one parent of each reticulation in ${\mathcal N}$ has the tree-path property. Then ${\mathcal N}$ displays a tree on $X$ twice if and only if ${\mathcal N}$ contains an avoidable reticulation or an avoidable cycle.

Proof

Let $\rho$ denote the root of ${\mathcal N}$. If ${\mathcal N}$ contains an avoidable reticulation or an avoidable cycle, then, by Lemmas 1 and 2, ${\mathcal N}$ displays a tree on $X$ twice.

Now, suppose that ${\mathcal N}$ contains neither an avoidable reticulation nor an avoidable cycle. Let $k$ be the number of reticulations in ${\mathcal N}$. We will show by induction on $k$ that ${\mathcal N}$ does not display a tree on $X$ twice. If $k=0$, then ${\mathcal N}$ is a tree on $X$ and the result holds. Now assume that $k\ge 1$ and that the result holds for all networks with $k-1$ reticulations. Let $v$ be a reticulation of ${\mathcal N}$ whose strict descendants are all tree vertices, and let $v_1$ and $v_2$ be the two parents of $v$. Without loss of generality, assume that $v_1$ is a distinguished parent of $v$. Furthermore, let $m$ denote a leaf in ${\mathcal N}$ with the property that there is a tree-path from $v_1$ to $m$. Let ${\mathcal N}'$ be the rooted acyclic digraph obtained from ${\mathcal N}$ by applying a reticulation deletion relative to $v$. It follows by Lemma 3 that ${\mathcal N}'$ is a network on $X-D_v$ with no avoidable reticulation and, for each reticulation, at least one parent has the tree-path property.

To apply the induction assumption, we next show that ${\mathcal N}'$ contains no avoidable cycles. Suppose to the contrary that ${\mathcal N}'$ has an avoidable cycle $C'$ with sink $t$. Let $t_1$ and $t_2$ denote the parents of $t$ and, without loss of generality, assume that $t_1$ is a distinguished parent of $t$. By Observation 2, it follows that $\{t_1,t\}$ is the unique minimum hitting set $H'$ of $C'$. Let $C$ denote the $2$-path cycle in ${\mathcal N}$ induced by $C'$ in ${\mathcal N}'$. Since each tree vertex in ${\mathcal N}$ and ${\mathcal N}'$ has out-degree exactly $2$, and $t_1$ has the tree-path property in ${\mathcal N}'$, it follows that $t_1$ is not contained in $\{v_1,v_2\}$, so $(t_1,t)$ is an edge in $C'$ and $C$. Now, let $P_m'$ be a directed path from the root of ${\mathcal N}'$ to $m$ such that either $P_m'$ avoids $C'$ or the last vertex of $P_m'$ that meets $C'$ is contained in $H'$. As $C'$ is an avoidable cycle in ${\mathcal N}'$, such a path exists. Now, if $v_2=\rho$ and $(v_2,v_1)$ is an edge in ${\mathcal N}$, let $v_p$ denote the child of $v_1$ in ${\mathcal N}$ such that $v_p\ne v$; otherwise, let $v_p$ denote the parent of $v_1$ in ${\mathcal N}$. Note that the unique directed path from $v_p$ to $m$ in ${\mathcal N}'$ is a subpath of $P'_m$.

We next consider two cases. First, assume that the subpath of $P_m'$ in ${\mathcal N}'$ from $v_p$ to $m$ either avoids every vertex in $C'$ or $v_p\in \{t_1,t\}$. By the existence of $P_m'$ in ${\mathcal N}'$, we have that, for each leaf $\ell \in D_v$, there exists a directed path $P_\ell$ from $\rho$ to $\ell$ in ${\mathcal N}$ that uses the edge $(v_1,v)$ such that $P_\ell$ avoids every vertex of $C$ or the last vertex of $P_\ell$ that meets $C$ is contained in $\{t_1,t\}$. Furthermore, as $(t_1, t)$ is an edge in $C$, we have that $H'$ is a hitting set of $C$ in ${\mathcal N}$. In particular, as $C'$ is an avoidable cycle in ${\mathcal N}'$, it follows that $C$ is an avoidable cycle in ${\mathcal N}$; a contradiction.

Second, assume that the subpath of $P'_m$ from $v_p$ to $m$ in ${\mathcal N}'$ does not avoid every vertex in $C'$ and $v_p\notin \{t_1,t\}$. As $C$ is unavoidable in ${\mathcal N}$, $v_1$ is either a vertex of $C$ or the source of $C$ is a strict descendant of $v_1$. In the latter case, it is easily checked that, as $C'$ is avoidable in ${\mathcal N}'$, $C$ is avoidable in ${\mathcal N}$; a contradiction. We may therefore assume that $v_1$ is a vertex of $C$. If there is an element $\ell \in D_v$ for which there is a directed path in ${\mathcal N}$ from $\rho$ to $\ell$ through $v_2$ such that either it avoids $C$, or it meets $C$ and the last vertex it meets in $C$ is $t$ or $t_1$, then all elements in $D_v$ have such a path. In turn, this implies that $C$ is avoidable in ${\mathcal N}$; a contradiction. Hence, for all $\ell \in D_v$, every directed path from $\rho$ to $\ell$ through $v_2$ meets a vertex of $C$ and the last such vertex is neither $t$ nor $t_1$. Let $r$ denote such a vertex of $C$, and let $P_r$ denote a directed path from $r$ to $v_2$ in ${\mathcal N}$. We may assume that $r$ is the only vertex of $P_r$ meeting $C$. Potentially, $P_r$ may consist of the single vertex $v_2$. Now, let $D$ be the unique $2$-path cycle in ${\mathcal N}$ with sink $v$ whose vertex set is the union of $V(P_r)\cup \{v\}$ and a subset of the vertices in $C$, and whose edge set is $E(P_r)\cup \{(v_1,v), (v_2, v)\}$ , a subset of the edges in $C$, where $V(P_r)$ and $E(P_r)$ are the vertex and edge sets of $P_r$, respectively. Let $X_{v_1}$ denote the subset of $X$ such that $p\in X_{v_1}$ precisely if $p\in D_v$ or there is a path from $v_1$ to $p$ that avoids $D$ except for $v_1$. Since $v$ is not the sink of an avoidable cycle in ${\mathcal N}$, the set $X-X_{v_1}$ is non-empty. In particular, there exists a leaf $q\in X-X_{v_1}$ with the property that every directed path from $\rho$ to $q$ in ${\mathcal N}$ meets $D$ and the last vertex meeting $D$ is neither $v$ nor $v_1$. Moreover, since $C'$ is avoidable in ${\mathcal N}'$, at least one such path, say $P_q$, does not meet a vertex of $C$ in ${\mathcal N}$ or the last vertex meeting $C$ in ${\mathcal N}$ is an element in $\{t_1,t\}$. If the last vertex of $P_q$ that meets $C$ in ${\mathcal N}$ is either $t_1$ or $t$, it is easily checked that there is a path from $\rho$ to $q$ such that the last vertex on this path meeting $D$ is $v_1$; a contradiction. We may therefore assume that $P_q$ does not meet a vertex of $C$. Hence, $V(P_r)-\{r\}$ is non-empty and, in particular, $P_q$ meets $D$ in a vertex of $V(P_r)-\{r\}$. But then there is a directed path in ${\mathcal N}$ from $\rho$ to $\ell$ using $P_q$ that avoids every vertex in $C$, in which case, $C$ is avoidable in ${\mathcal N}$; a contradiction.

We now proceed with the induction. Since ${\mathcal N}'$ has $k-1$ reticulations, it follows by the induction assumption that ${\mathcal N}'$ does not display a tree on $X-D_v$ twice. Let ${\mathcal T}'$ be a tree on $X-D_v$ that is displayed by ${\mathcal N}'$, and let $S'$ be a switching that yields ${\mathcal T}'$. Now consider the two switchings $S_1=S'\cup \{e_1\}$ and $S_2=S'\cup \{e_2\}$, where $e_1=(v_1,v)$ and $e_2=(v_2,v)$. For completeness, if $S'$ contains an edge $(w_1, w)$, where $w_1$ is the parent of $v_2$ and $w$ is a child of $v_2$ in ${\mathcal N}$, then replace $(w_1, w)$ with $(v_2, w)$ in $S_1$ and $S_2$. Let $C$ be a $2$-path cycle in ${\mathcal N}$ whose sink is $v$. It is easily checked that $C$ exists. Furthermore, let $\ell$ be an element in $D_v$, and let $q$ be an element in $X$ such that the last vertex of each directed path from $\rho$ to $q$ in ${\mathcal N}$ that meets $C$ is neither $v$ nor $v_1$. As $C$ is not avoidable, such a $q$ exists. Then, $S_1$ yields a tree ${\mathcal T}_1$ on $X$ that contains the triple $\ell m|q$ while $S_2$ yields a tree ${\mathcal T}_2$ on $X$ that contains the triple $\ell q|m$ or $qm|\ell$ and, thus, ${\mathcal T}_1\ncong {\mathcal T}_2$. Applying this argument to each of the trees on $X-D_v$ displayed by ${\mathcal N}'$, it follows that ${\mathcal N}$ does not display a tree on $X$ twice; thereby completing the proof of the theorem. $\square$

5 Quadratic-Time Algorithm

Making use of the characterization Theorem 2, in this section, we establish Theorem 1. If ${\mathcal N}$ is a network with $n$ vertices, then, as each vertex of ${\mathcal N}$ has degree at most three, the number of edges in ${\mathcal N}$ is at most $\frac{3}{2}n$. We will implicitly use this fact throughout the section.

We start by showing that the total number of vertices in a certain type of network ${\mathcal N}$ on $X$ is bounded by a function that is linear in the size of $X$. Eventually, this will enable us to get the overall running time to be quadratic in $|X|$.

Lemma 4

Let ${\mathcal N}$ be a network on $X$ with no avoidable reticulation, and suppose that ${\mathcal N}$ has the tree-path property for at least one parent of each reticulation. Let $k$ be the number of reticulations in ${\mathcal N}$, and let $n$ be the total number of vertices in ${\mathcal N}$. Then $k\le |X|$ and, in particular, $n < 4|X|$.

Proof

If $k=0$, then the result clearly holds. So assume that the result holds for all networks with fewer than $k$ reticulations. Let ${\mathcal N}'$ be a network obtained from ${\mathcal N}$ by applying a reticulation deletion relative to a reticulation $v$ in ${\mathcal N}$. It follows by Lemma 3 that ${\mathcal N}'$ is a network on $X-D_v$ with no avoidable reticulation and, for each reticulation, at least one parent has the tree-path property. Moreover, ${\mathcal N}'$ has $k-1$ reticulations and at most $|X|-1$ leaves. Therefore, by induction,

$$\begin{aligned} k-1\le |X-D_v|\le |X|-1, \end{aligned}$$

and so $k\le |X|$. To establish the second part, we use a result from (McDiarmid et al., Equation 5) whose authors have shown that $|X|+k=\frac{n+1}{2}$. Since $k\le |X|$, it follows that

$$\begin{aligned} n=2(|X|+k)-1\le 4|X|-1<4|X|, \end{aligned}$$

thereby establishing the second inequality of the lemma. $\square$

Corollary 1

Let ${\mathcal N}$ be a network on $X$ that has the tree-path property for at least one parent of each reticulation. If ${\mathcal N}$ has at least $4|X|$ vertices, then ${\mathcal N}$ displays a tree on $X$ twice.

Proof

It follows by the contrapositive of Lemma 4 that ${\mathcal N}$ has an avoidable reticulation. Hence, by Lemma 1, ${\mathcal N}$ displays a tree on $X$ twice. $\square$

Following on from Corollary 1, the next lemma shows that we can decide quickly if a network on $X$ has at least $4|X|$ vertices.

Lemma 5

Let ${\mathcal N}$ be a network on $X$. It takes time linear in $|X|$ to decide whether ${\mathcal N}$ has at least $4|X|$ vertices.

Proof

The result follows by applying a breadth-first search traversal to ${\mathcal N}$ that keeps track of the number of previously visited distinct vertices in ${\mathcal N}$ and either returns the number $n$ of vertices in ${\mathcal N}$ if $n<4|X|$ or stops if $4|X|$ distinct vertices have been traversed. Since the running time of a breadth-first search algorithm applied to ${\mathcal N}$ is $O(\frac{3}{2}n+n)$ (Cormen et al. 2001), the lemma now follows. $\square$

We next establish a lemma on avoidable cycles and then state an algorithm that recognizes whether or not a reticulation is the sink of an avoidable cycle in a network with no avoidable reticulations and, for each reticulation, at least one parent has the tree-path property.

Lemma 6

Let ${\mathcal N}$ be a network with no avoidable reticulation, and suppose that at least one parent of each reticulation in ${\mathcal N}$ has the tree-path property. Let $v$ be a reticulation in ${\mathcal N}$ with parents $v_1$ and $v_2$ say, where $v_1$ is a distinguished parent of $v$. If $v$ is the sink of an avoidable cycle $C$, and $P_1$ and $P_2$ are the two directed paths whose union is $C$ with $v_i$ lying on $P_i$, then, apart from $v$, the path $P_1$ contains at most one reticulation and the path $P_2$ contains no reticulations. Moreover, $C$ is the unique avoidable cycle with sink $v$.

Proof

Let $\rho$ denote the root of ${\mathcal N}$. It follows by Observation 2 that $\{v, v_1\}$ is the unique hitting set of $C$. We first show that $P_2$ contains no reticulations except for $v$. Assume that $w$ is a reticulation lying on $P_2$ such that $w\ne v$. Among all such reticulations, choose $w$ so that the only reticulation in $P_2$ after $w$ is $v$. Since $w$ is unavoidable, there exists a leaf $q$ such that every directed path from $\rho$ to $q$ contains $w$. In particular, there exists a directed path from $\rho$ to $q$, say $P_q$, such that, as $C$ is avoidable, the last vertex of $P_q$ meeting $C$ is either $v$ or $v_1$. But then, as $w$ is not the source of $C$, there is a directed path from $\rho$ to $q$ using $P_1$ that avoids $w$; a contradiction. Thus, $P_2$ contains no reticulations except $v$.

We next show that $P_1$ contains at most one reticulation except for $v$. Assume that $w$ is a reticulation lying on $P_1$ such that $w\ne v$. Like above, choose $w$ so that among all such reticulations the only reticulation after $w$ in $P_1$ is $v$. Let $w_1$ and $w_2$ be the parents of $w$ in ${\mathcal N}$. Without loss of generality, we may assume that $w_1$ is a distinguished parent of $w$. Since $w_1$ has the tree-path property, there is a leaf $q$ with the property that there is a tree-path from $w_1$ to $q$. Since $C$ is avoidable and $\{v, v_1\}$ is the unique hitting set of $C$, it follows that $w_1$ does not lie on $P_1$; otherwise, a hitting set of $C$ has size at least three. Thus, $w_2$ lies on $P_1$. Now assume that $P_1$ contains a reticulation $t$ other than $v$ and $w$. Choose $t$ so that the only reticulations after $t$ in $P_1$ are $w$ and $v$. Since $t$ is unavoidable, there exists a leaf $r$ such that every directed path from $\rho$ to $r$ contains $t$. Moreover, as $C$ is avoidable, there exists at least one such path, say $P_r$, such that the last vertex of $P_r$ meeting $C$ is either $v$ or $v_1$. Now, let $P_q$ be a directed path from $\rho$ to $q$ and observe that $P_q$ contains as a subpath the tree-path from $w_1$ to $q$. Since ${\mathcal N}$ is acyclic and $C$ is avoidable, $P_q$ does not meet $C$. But then there is a directed path from $\rho$ to $r$ using $P_q$ to $w_1$, the unique path from $w_1$ to $v_1$, and the subpath of $P_r$ from $v_1$ to $r$. In particular, this path avoids $t$; a contradiction. Hence, $P_1$ contains at most one reticulation other than $v$.

To see that $C$ is the unique avoidable cycle with sink $v$ in ${\mathcal N}$, first note that $P_2$ contains no reticulations except $v$. Furthermore, $P_1$ contains at most one reticulation (other than $v$) and, if it contains such a reticulation $w$, then $P_1$ has no choice with regard to which parent of $w$ it meets. Since no 2-path cycle of ${\mathcal N}$ with sink $v$ that contains $v$, $v_1$, and a parent of $w$ that has the tree-path property is avoidable, the uniqueness of $C$ now follows.$\square$

The previous lemma provides insights into how to decide whether or not a reticulation is the sink of an avoidable cycle in a network ${\mathcal N}$ on $X$ with no avoidable reticulation and for which the tree-path property holds for at least one parent of each reticulation. We next summarize these insights in the form of an algorithm, called AvoidableCycle. Subsequently, we will establish that AvoidableCycle works correctly and that its running time is linear in the size of $X$.

Algorithm: AvoidableCycle

Input: A network ${\mathcal N}$ on $X$ with no avoidable reticulation and, for each reticulation, at least one parent has the tree-path property. A reticulation $v$ of ${\mathcal N}$ with parents $v_1$ and $v_2$ say, where $v_1$ is a distinguished parent of $v$.

Output: Return ‘yes’ if $v$ is the sink of an avoidable cycle in ${\mathcal N}$; otherwise, return ‘no’.

Step 1 :

Set $P_2=u_1, u_2, \ldots , u_l$ to be the (unique) maximal directed path in ${\mathcal N}$ with $u_{l-1}=v_2$ and $u_l=v$ such that, except for $v$, each vertex on $P_2$ is a tree vertex.

Step 2 :

Set $P_1=w_1, w_2, \ldots , w_m$ to be the (unique) maximal directed path in ${\mathcal N}$ with $w_{m-1}=v_1$ and $w_m=v$ such that the following three properties are satisfied: (i) $w_1$ is a tree vertex, (ii) $P_1$ contains at most one reticulation other than $v$, and (iii) except for $v_1$ and, possibly $v_2$, no vertex on $P_1$ that is a parent of a reticulation in ${\mathcal N}$, has the tree-path property.

Step 3 :

If $P_1$ and $P_2$ have no common tree vertex, then return ‘no’. Otherwise, let $C$ be the $2$-path cycle of ${\mathcal N}$ induced by subpaths of $P_1$ and $P_2$ with source $u$ and sink $v$, where $u$ is the last tree vertex in $P_1$ and $P_2$ common to both paths.

Step 4 :

Let $X'$ be the subset of $X$ such that $\ell \in X'$ if and only if there is a directed path from either $v_1$ or $v$ to $\ell$ avoiding all other vertices of $C$.

Step 5 :

For each leaf $q$ in $X-X'$, check whether there is a directed path from the root of ${\mathcal N}$ to $q$ avoiding all vertices of $C$. Return ‘yes’ if there exists such a path for all $q$; otherwise, return ‘no’.

Lemma 7

Let ${\mathcal N}$ be a network on $X$ with no avoidable reticulation. Suppose that at least one parent of each reticulation in ${\mathcal N}$ has the tree-path property. Let $v$ be a reticulation in ${\mathcal N}$. Calling AvoidableCycle for ${\mathcal N}$ and $v$ returns ‘yes’ if and only if $v$ is the sink of an avoidable cycle. Furthermore, the running time of AvoidableCycle in this call is linear in the number of vertices in ${\mathcal N}$.

Proof

Let $\rho$ denote the root of ${\mathcal N}$, and let $v_1$ and $v_2$ denote the parents of $v$. Without loss of generality, we may assume that $v_1$ is a distinguished parent of $v$. Furthermore, let $n$ denote the number of vertices in ${\mathcal N}$. Throughout the proof, we use the same notation as in the description of AvoidableCycle.

We first show that AvoidableCycle works correctly. Suppose that $C'$ is an avoidable cycle of ${\mathcal N}$ with sink $v$. Then, by Lemma 6, $C'$ is unique. Applying AvoidableCycle to ${\mathcal N}$ and $v$, it follows by Lemma 6 and the construction described in AvoidableCycle that $C'$ is the $2$-path cycle $C$ constructed in Step 3 of the algorithm. By the definition of an avoidable cycle, Step 5 returns ‘yes’. Now suppose that ${\mathcal N}$ has no avoidable cycle with sink $v$. Applying AvoidableCycle to ${\mathcal N}$ and $v$, there are two cases to consider depending on whether or not $P_1$ and $P_2$ meet in Step 3. If $P_1$ and $P_2$ do not meet at a tree vertex, then Step 3 returns ‘no’. Therefore, assume that $P_1$ and $P_2$ do meet at a tree vertex. Then, as $v$ is not the sink of an avoidable cycle in ${\mathcal N}$, there is some leaf $q\in X-X'$ such that every path from $\rho$ to $q$ meets $C$, in which case Step 5 returns ‘no’. Hence, AvoidableCycle correctly determines whether $v$ is the sink of an avoidable cycle in ${\mathcal N}$.

We now turn to the running time of AvoidableCycle. Starting at $v_2$ and traversing edges in the opposite direction to determine $P_2$ takes time linear in $n$. Similarly, determining $P_1$ takes time linear in $n$. However, if $P_1$ contains a reticulation $v'$, distinct from $v$, then one has additionally to determine which of its two parents, say $v_1'$ and $v_2'$, have the tree-path property. A naive way to do this is the following. Let $(r_1,r_2,\ldots ,r_{|X|})$ be an ordering on the leaves of ${\mathcal N}$. In turn, for each $r_i$, let $P_{r_i}$ be the unique maximal directed path in ${\mathcal N}$ that ends in $r_i$ such that each vertex on $P_r$ is a tree vertex and, except for the first vertex of $P_{r_i}$, no vertex is contained in a path $P_{r_j}$ with $1\le j<i\le |X|$. If there exists an $r_i$ such that $P_{r_i}$ meets $v_k'$ with $k\in \{1,2\}$, then $v_k'$ has the tree-path property. Collectively, this takes time linear in $n$. Clearly, Step 3 can be done in time linear in $n$ and, so, it remains to check the running time of Steps 4 and 5. For Step 4, delete the vertices in $C$ that are neither $v$ nor $v_1$, and then determine, for each leaf $\ell$, if there is a directed path from $v_1$ to $\ell$ in the resulting directed graph, in which case, $\ell \in X'$. Here, we can, for example, use a depth-first search traversal (Cormen et al. 2001) starting at $v_1$ and, so, this step takes time linear in $n$. An analogous approach can be done for Step 5. We conclude that the running time of AvoidableCycle is linear in $n$. $\square$

We are now in a position to prove Theorem 1 which we restate in the language of Sect. 2.

Theorem 1

Let ${\mathcal N}$ be a network on $X$ and suppose that ${\mathcal N}$ has the tree-path property for at least one parent of each reticulation. It takes time quadratic in the size of $X$ to decide whether ${\mathcal N}$ displays a tree on $X$ twice.

Proof

First, by Lemma 5, we can decide in time linear in $|X|$ if ${\mathcal N}$ has at least $4|X|$ vertices. If ${\mathcal N}$ has at least that many vertices, then, by Corollary 1, ${\mathcal N}$ displays a tree on $X$ twice. We may therefore assume that ${\mathcal N}$ has at most $4|X|$ vertices.

We complete the proof by showing that it takes time quadratic in $|X|$, to decide whether or not ${\mathcal N}$ has an avoidable reticulation or an avoidable cycle which is, by Theorem 2, a necessary and sufficient condition for ${\mathcal N}$ to display a tree on $X$ twice. Let $v$ be a reticulation in ${\mathcal N}$. Deciding if $v$ is avoidable is easily checked in time that is linear in the size of ${\mathcal N}$, which is at most $4|X|$. For example, one way is to simply delete $v$ from ${\mathcal N}$ and then use a depth-first search (Cormen et al. 2001), whose running time is linear in $|X|$, to decide whether there is a directed path from the root to each vertex in $X$ in the resulting directed graph. Since the number of reticulations in ${\mathcal N}$ is at most $|X|$ (see Lemma 4), deciding whether or not ${\mathcal N}$ has an avoidable reticulation takes time quadratic in $|X|$. Now we may assume that ${\mathcal N}$ has no avoidable reticulation. It then follows by Lemma 7 that it takes time linear in the number of vertices in ${\mathcal N}$ and, hence, by Lemma 5, time linear in $|X|$, to decide if $v$ is the sink of an avoidable cycle in ${\mathcal N}$ using AvoidableCycle. Applying this algorithm to each reticulation in ${\mathcal N}$ to decide if there exists a reticulation that is the sink of an avoidable cycle takes time quadratic in $|X|$. The theorem now follows. $\square$

6 Remark on Tree-Child and Normal Networks

As tree-child networks are a subclass of the networks in which each reticulation has at least one parent that satisfies the tree-path property, it immediately follows by Theorem 1 that it can be decided quickly whether or not a tree-child network displays a tree twice. Curiously, since each vertex of a tree-child network ${\mathcal N}$ has the tree-path property, it is tempting to assume that ${\mathcal N}$ never displays a tree twice and therefore has no avoidable cycles. However, this is not necessarily true. To see this, consider a reticulation $v$ of ${\mathcal N}$ and its two parents $v_1$ and $v_2$. If $v_1$ has the tree-path property and $v_2$ is an ancestor of $v_1$, then it is possible for $v$ to be contained in an avoidable cycle. In Willson (2010), refers to a tree-child network that does not have a reticulation for which one parent is an ancestor of the other parent as a normal network. Noting that a normal network does not have an avoidable cycle as every $2$-path cycle has a minimum hitting set of size at least three, the next corollary is now an immediate result of Theorem 2.

Corollary 2

Let ${\mathcal N}$ be a normal network on $X$. Then ${\mathcal N}$ does not display a tree on $X$ twice.