Revising the Role of Species Mobility in Maintaining Biodiversity in Communities with Cyclic Competition

Abstract

One of the most crucial tasks faced by biologists today is revealing the mechanisms which account for biodiversity, yet we are still far from a full understanding of these mechanisms, and in particular the role of spatially heterogeneous population distributions. Recently, the spatially heterogeneous coexistence seen in cyclic competition models—in which species compete as in the game rock-paper-scissors—has brought them to the fore as a paradigm for biodiversity. Research into cyclic competition has so far been focused almost exclusively on stochastic lattice models with discrete space, which ignore several key dynamical aspects. In particular, such models usually assume that species disperse at the same speed. This paper aims to extend our understanding of cyclic competition by applying a reaction–diffusion Lotka–Volterra scheme to the problem, which allows us to vary the mobility of each species, and lets us take into account cyclic competition with more complex underlying mechanisms. In this paper we reveal an entirely new kind of cyclic competition—‘conditional’ cyclic competition, with a different underlying mechanism to ‘classic’ cyclic competition—and we show that biodiversity in communities with cyclic competition in fact depends heavily on the ratios between the species mobilities. Furthermore, we show that this dependence can be completely different for conditional and classic cyclic competition. We also present a wide range of spatiotemporal patterns which are formed in the system, including spiral and target waves, spiralling patches, and irregular chaotic patches. We show that the previously unknown case of conditional cyclic competition is host to a scenario of patchy co-invasion, where the spread of the population front takes place via the formation, splitting and propagation of patches of high species density. This is also an example of invasional meltdown because one competitor facilitates the invasion of the other, but unlike well-known cases of invasional meltdown the co-invaders in this system are not mutualists but antagonistic competitors, and the overall result mitigates, rather than amplifies, the damage done to the native ecosystem.

1 Introduction

One of the major challenges in mathematical ecology today lies in discovering the mechanisms that account for the high degree of species diversity seen in the natural world (Ives and Carpenter 2007; Tilman 1982; Tilman et al. 1994; Levine and Hille Ris Lambers 2010; Chesson 2000). A large volume of research has made it increasingly apparent that competition displaying the ‘competitive exclusion principle’ (Gause 1934; Hardin 1960; MacArthur and Levins 1967) cannot alone account for the rich assortment of species our ecosystems contain. As a classic example, the ‘paradox of the plankton’ (Hutchinson 1961) concerns a situation in which many species of plankton coexist in the same ecological niche. Several possible explanations have been put forward for the diverse range of plankton species found in nature; these include spatial and temporal heterogeneity of the environment, environmental fluctuations or turbulence, oscillations or chaos in the competition dynamics and non-competition interactions with other species in the environment (Huisman et al. 2001; Scheffer et al. 2003; Roy and Chattopadhyay 2007). One of the more important proposed mechanisms is spatial partitioning of the species, in which they occupy distinct areas of the habitat. Often, this is due to heterogeneity in the environment creating spatial niches (Ryabov and Blasius 2011), but there are also many models which exhibit such spatial heterogeneity in a completely homogeneous physical environment—usually with partitioning of the species being dynamic in time (Amarasekare 2003; Reichenbach et al. 2007). In this paper we will continue to explore species diversity in homogeneous environments by considering a particular type of multispecies competition called ‘cyclic’ competition.

Cyclic competition is an example of a non-transitive competition (Moen 1989) characterised by a cyclic ordering of competitive dominance. The simplest case involves only three species: species 1, 2 and 3, and the ordering of the competition is analogous to the popular game ‘rock-paper-scissors’: that is, species 1 outcompetes species 2, which outcompetes species 3, which in turn outcompetes species 1. There are several well-documented examples of cyclic competition in nature, perhaps the most famous concerning the different mating strategies of male side-blotched lizards of the species Uta stansburiana (Sinervo and Lively 1996). There has also been evidence found for the presence of cyclic competition in several other cases, including competition between certain species of coral reef invertebrates (Jackson and Buss 1975; Buss and Jackson 1979), some yeast strains (Paquin and Adams 1983) and competing strains of bacteria (Kerr et al. 2002; Kirkup and Riley 2004). There are also several non-biological situations which can be modelled by similar competition with cyclic competitive advantage, as in certain many-player prisoner’s dilemma games (Szabó 2002; Hauert et al. 2002) and in some types of voter model (Tainaka 1993). We should note that although we use the term ‘species’ to refer to the competitors in general, examples of cyclic competition are not limited to either inter-species or intra-species competition, and our investigation is equally valid for ‘strains’ or ‘types’ of different species since we are concerned with the general conditions under which cyclic competition can allow for the coexistence of all three participants (e.g. Prado and Kerr 2008).

While models of cyclic competition without space usually forecast the extinction of one or more species (May and Leonard 1975; Gilpin 1975), considering the same interactions in space can allow all three types to coexist (Durrett and Levin 1998; Frean and Abraham 2001; Reichenbach et al. 2007). Durrett and Levin (1998) and Frean and Abraham (2001) consider a cyclic system which exhibits neutral limit cycles under the assumption that each individual has an equal possibility of interacting with any other individual, regardless of the distance between them. In this case the long-term persistence of all competitors is impossible, but by considering only local interactions they show that the same system exhibits coexistence due to spatial partitioning. Using a similar modelling approach based on stochastic lattice models, Reichenbach et al. (2007) show that coexistence of the three species is subject to limitations on the species migration rate: there exists a critical mobility, M _c , such that higher values of mobility cause a rapid degradation of persistence. This result can be intuitively understood in the following way: the faster the species move, the more the system approximates the mean-field case with full mixing and no explicit space, thus resulting in extinction (May and Leonard 1975).

One significant limitation to the previous investigations is that they are all restricted to the case in which all species have equal mobility. In nature, however, it is evident that in the majority of such interactions the competing species will disperse at different rates. Furthermore, previous studies have shown that differences in the dispersal distributions of competing species can fundamentally alter the outcome of competition: Durrett and Levin (1998) show that in a two-species model, a longer-range dispersal can allow a type to overcome a superior competitor. For this reason the absence of any investigation into the possibility of coexistence in systems of cyclic competitors with unequally mobile competitors represents a significant gap in the literature, and this paper aims to provide further research in this direction by explicitly considering disparity in the dispersal rates of the species, and investigating the resulting behaviour of the system.

We have chosen to undertake our study using a reaction–diffusion modelling framework. This is a rather popular approach in ecological modelling (Sherratt 2001; Cantrell and Cosner 2003), but surprisingly this approach has not been used in the previous studies of cyclic competition systems in space—with Merino (1996), Petrovskii et al. (2001) and Ikeda (2001) being notable exceptions—instead, the conventional approach in considering cyclic competition in space is to use stochastic individual-based cellular automata models. However, using a reaction–diffusion scheme has several benefits when we model dynamics of highly mobile species: as the spatial position of individuals can change quickly on the timescale of reproduction, we can only describe the population dynamics in terms of population densities averaged over time and space. This is the case, for instance, in the competition between male side-blotched lizards (Sinervo and Lively 1996). Another advantage of the reaction–diffusion framework is that we can explicitly consider local interactions between individuals of all three species, which is rather difficult to do using lattice models where we only consider interactions between pairs of individuals (Durrett and Levin 1998; Frean and Abraham 2001; Reichenbach et al. 2007). Additionally, under the reaction–diffusion framework it is very straightforward to vary the species’ mobility without affecting the local competition dynamics—we can simply change the diffusion coefficients at will. Our results reveal several other important benefits of using a reaction–diffusion framework in modelling movement of cyclic competitors, which we shall discuss in Sect. 4.

In this paper we examine several aspects of the relationship between biodiversity in a cyclic competition community and the dispersal rates of the competitors. Firstly, we find the range of dispersal rates which actually admit coexistence of all three species—we show that small variations in the competition parameters can completely change the range of dispersal rates which admit coexistence by presenting an instance in which small parameter variations cause a shift from a situation where highly disparate species mobilities are detrimental to persistence to one in which disparity is necessary for coexistence. Secondly, we consider several variations in the competition parameters to determine how such variation affects the extent of species coexistence and the spatiotemporal patterns observed. We show that the competition parameters also have a substantial influence on the spatial patterns observed in the system, and that the system exhibits a large range of spatiotemporal dynamics, including spiral/target waves, spatiotemporal chaos, and patchy invasion. Thirdly, we emphasise the importance of both the relative and the absolute values of species mobility to guarantee biodiversity in the community and we estimate the size of the habitat which can allow the coexistence of all species. Finally, we use cyclic competition in space as a paradigm to model the phenomenon of mutual invasion—which is a hot topic in the ecological literature—and reveal a regime of patchy co-invasion in which one invasive competitor facilitates the invasion of another in a similar way to a scenario of invasional meltdown.

2 Modelling Framework

We model the spatiotemporal interaction of three competing species using a reaction–diffusion scheme based on the three-species Lotka–Volterra competition approach, as considered by May and Leonard (1975) (see also Petrovskii et al. 2001):

(1)

(2)

(3)

where u ₁, u ₂, and u ₃ are the densities of species 1, 2 and 3, respectively, a ₁, a ₂ and a ₃ are the intrinsic growth rates of the three species, and each coefficient α _i,j represents the limiting effect that the presence of species u _j has on species u _i . In this sense, $\frac{1}{\alpha_{i,i}}$ can be interpreted as the carrying capacity of species i. The diffusion coefficients D ₁, D ₂ and D ₃ describe the dispersal rate/mobility of each species.

Since system (1)–(3) contains 15 parameters, it is natural to scale each species’ density according to its carrying capacity: $\hat{u}_{i}=\alpha_{i,i}u_{i}$, and then rescale both time and space to obtain the simplified three-species competition system:

(4)

(5)

(6)

and so reducing the number of parameters to 10. Secondly, we can assume without loss of generality that ε ₂,ε ₃≤1 since we can always choose to scale the system to the largest diffusion coefficient, and consider the corresponding species as u ₁.

Before we proceed further, we ought to determine exactly what we mean when we refer to ‘cyclic competition’ in model (4)–(6). Our definition is based on the arrangement of outcomes in the competition between each pair of species in space: we consider competition between the two species in 1D space with initial conditions such that at infinity the species densities are equal to the carrying capacities, and the species boundary forms a travelling wave as shown in Fig. 1A. The direction of the wave determines which species outcompetes the other, i.e. competitive dominance is defined by spatial displacement. We define cyclic competition as having such competitive advantage ordered in a cycle, i.e. 1>2>3>1. We require that this order should hold for any ratio between the diffusion coefficients.

Fig. 1

Defining cyclic competition. (A) A solution of the 1D reaction–diffusion competition between species u _i and species u _i+1 in our definition of cyclic competition. We require that species u _i displaces u _i+1 in space. (B) Phase trajectories for the local dynamics of our model, starting from near the unstable coexistence state $(u_{1}^{*},u_{2}^{*},u_{3}^{*})$. The trajectories are truncated to exclude biologically meaningless heteroclinic cycling. (C) Isocline diagram for the competition between two species in the case of classic cyclic competition. Filled dots represent stable steady states and unfilled dots represent unstable ones. The arrows show the directions of the phase trajectories. (D) Isocline diagram for the competition between species 1 and 3 in the case of conditional cyclic competition. The dots and arrows have the same meaning as in Fig. 1C

Interestingly, our spatial-displacement definition of cyclic competition can hold for two types of competition with very different underlying mechanisms in the local dynamics.

• (i) Classic cyclic competition

The local interactions between each pair of species u _i and u _i+1 (i+1 always being considered to refer to $i+1\operatorname {mod}3$) involve only one stable steady state, which lies on the u _i axis, so u _i always prevails over u _i+1 for nonzero initial conditions. The isocline diagram and phase trajectory directions for such a case of competition between two species are shown in Fig. 1C. We should note that the $\dot{u}_{i}=0$ and $\dot{u}_{i+1}=0$ nullclines can intersect on the u _i+1-axis (at u _i+1=1) without altering the number and stability of the steady states. For the competition coefficients we have α _i,i+1≤1 and α _i+1,i >1. Adding space to the local interaction does not alter the outcome of competition: the resultant travelling wave will always be directed from the area occupied by u _i to the area occupied by u _i+1 (Hosono 1998; Lewis et al. 2002).

• (ii) Conditional cyclic competition

To illustrate the concept of conditional cyclic competition, let us suggest that the local interactions between two of the pairs of species—which we will assume without loss of generality to be u ₁,u ₂ and u ₂,u ₃—are the same as in case (i) but the local competition between species u ₃ and u ₁ is bistable: there is an unstable nontrivial equilibrium, and both of the axial steady states are locally stable. In ecology such competition is called pre-emptive. This will be the case if both a _1,3>1 and a _3,1>1 hold—in other words, if the interspecies competition is ‘strong’ in both directions. The corresponding isoclines and phase trajectory directions for such a situation are shown in Fig. 1D. Unlike in case (i), the outcome of the local competition between species 3 and 1 is now dependent upon the initial conditions: in other words, we have bistability. When we add a spatial dimension to the local interaction, the direction of the travelling wave can be either from the area occupied by 3 to the area occupied by 1 or vice-versa, since the outcome depends both on local interaction parameters and the diffusion coefficients (Alzahrani et al. 2010, 2011). In the case where species 3 displaces species 1 in space (see Fig. 1A) we call such cyclic competition ‘conditional’, since local pairwise interactions of some species can show bistability but this does not alter the order of spatial displacement schematically given by 1>2>3>1.

Note that Alzahrani et al. (2010) derive the relevant analytical conditions for the direction of a travelling wave in the case of local bistability when there is a low ratio between the diffusion rates of the competitors. However, for intermediate and large diffusion coefficients we always need to check numerically that the same direction of displacement in space still holds, ensuring that we have cyclic pairwise competition.

In cases (i) and (ii) the mathematical properties of model (4)–(6) without diffusion are qualitatively quite different but behave much the same when we ignore biologically meaningless behaviour. In all cases, the system may have at most one interior stationary state $(u_{1}^{*},u_{2}^{*},u_{3}^{*})$ with all species densities being above zero; there are always semi-trivial stationary states where one species density is zero and the trivial stationary state (0,0,0) always exists and is always unstable. Depending on parameters the state $(u_{1}^{*},u_{2}^{*},u_{3}^{*})$ can be either stable or unstable (May and Leonard 1975), but in this paper we consider the most interesting case of cyclic competition where no stable limit cycle exists in the system and the persistence of all three species becomes impossible (May and Leonard 1975). In this case the system can show heteroclinic behaviour—trajectories cycle between the three one-species unstable steady states ((1,0,0),(0,1,0),(0,0,1)), spending longer in the vicinity of each steady state with every orbit, but never converging. Another type of behaviour is possible in the case of conditional cyclic competition: consider, for instance, that interactions between species 1 and 3 show bistability (see Fig. 1D). The u ₁-only state is now locally asymptotically stable (this requires α _2,1,α _3,1>1) and the trajectories unwinding from $(u_{1}^{*},u_{2}^{*},u_{3}^{*})$ will be attracted by this state. In this paper, however, we truncate the trajectories at very small densities (less than 10⁻⁵ in our simulations) to reflect biologically relevant dynamics and as a result; the local cyclic competition dynamics in both cases becomes qualitatively similar: typical phase trajectories for both cases are shown in Fig. 1B. Depending on initial conditions trajectories will go to one of the stationary states ((1,0,0),(0,1,0),(0,0,1)). This can be explained by the fact that in the case where the u ₁-only state is stable, the trajectory can reach unrealistically low densities of u ₂ and u ₃ before eventually converging to this state, thus we may need to truncate it near the other states (0,1,0) and (0,0,1).

Although system (4)–(6) can be partially studied analytically (Petrovskii et al. 2001), it is not possible to perform a complete analytical investigation in the two-dimensional case, where the spatial patterns have irregular shape. We have used numerical methods and have mostly used an explicit Euler finite-difference scheme, whilst checking that our results are consistent with those obtained using more advanced implicit schemes (see Thomas 1995 for details). In order to avoid unrealistic heteroclinic cycling behaviour as observed in the mean-field case, we truncate population densities lower than u _i =10⁻⁵. We should note that the system with and without such truncation is quite consistent in terms of both spatiotemporal patterns and persistence provided that the truncation threshold is quite low (we considered the integration time to be T≈3000). For truncation thresholds of ∼0.01 (i.e. 1/100th of the carrying capacity of the species), the spatiotemporal patterns are affected and persistence becomes somewhat more tentative. Finally, we have assumed a square habitat, and used zero-flux Neumann boundary conditions.

The solutions to system (4)–(6) largely depend upon the choice of initial conditions; and, so here we use the following four types of initial condition sets in order to perform a thorough investigation of various dynamical patterns in a 2D environment: (i) the simplest initial condition: from the centre of the habitat, we extend three boundary lines at angle 2π/3 from each other, thus dividing the habitat into three ‘triangular’ sub-domains, and we start with one—and only one—species present in each of these sub-domains, initially at its equilibrium density; (ii) the initial condition set consists of the same arrangement as above, but with M=10 such ‘triangulations’; (iii) for the given parameter set we use the eventual spatial dynamics formed in the system with nearby parameters (if coexistence for nearby parameter is possible); in the case the two parameter sets are not close, we can take appropriately small steps through the parameter space, each time updating the initial conditions to the new asymptotic spatial distribution; (iv) we consider that the two species are initially distributed in a pair of overlapping rectangles in the middle of the habitat, with the other species occupying the rest of the habitat in its entirety. The initial condition of type (iv) is used to explore patterns of co-invasion in the system where the density of the native species is at its carrying capacity. Finally, the scale of the investigation should be emphasised: in order to construct the parametric diagrams (see the following sections) we have had to perform a substantial number (over 2000) of simulations.

3 Results

Our main goal is to explore community biodiversity in a two-dimensional environment, but it is convenient to start with the simpler one-dimensional case. An understanding of the mechanisms of persistence and extinction, and the role of varying dispersal rates in the simplified case, can then form our understanding of the corresponding mechanisms in the two-dimensional case. We are mainly interested in the dependence of species persistence on variation in the species’ mobility, and so it is convenient to plot regions of coexistence and extinction in the ε ₂–ε ₃ dispersal-rate space for system (4)–(6). The results for a one-dimensional environment are shown in Fig. 2. To check the possibility of coexistence of all species in the system we consider the invasion-type initial conditions: the whole habitat is initially occupied by species 3 except for two non-overlapping domains occupied by species 2 and 1 where the initial density of the species is equal to the carrying capacities. We consider the boundary conditions to be of Neumann form.

Fig. 2

Domains of coexistence and extinction for model (4)–(6) in an unbounded 1D habitat in terms of the diffusion coefficients ε ₂ and ε ₃. Black regions indicate that coexistence is impossible, and light grey regions indicate coexistence is possible. (A) Cyclically symmetrical parameters: α _i,i+1=1; α _i,i−1=2 for i=1,2,3; a ₂=1, a ₃=1. The dashed line denotes the boundary of coexistence for an intermediate domain length L=400, and the dotted line denotes the boundary of coexistence for small domains, L=150. (B) Increased pressure exerted on species u ₂ by u ₁: α _2,1=4, all other parameters are the same as in (A). (C) Conditional cyclic competition: α _3,1=1.3, all other parameters are the same as in (A). In this case, the local interactions between u ₁ and u ₃ display bistability, as seen in Fig. 1D

In Fig. 2A, we show the case where we have classic cyclic competition (see Sect. 2); in particular, we consider cyclically symmetrical competition parameters (α _i,i =1, α _i,i+1=1, α _i,i−1=2 for i=1,2,3). The grey domain corresponds to the coexistence of all species in an ‘unbounded’ habitat: i.e. the size of the domain, L, was taken to be as large as necessary. The meaning of the dashed and the dotted curves will be explained later. We can see from the figure that most of the diffusion space allows for coexistence, except for small values of ε ₂ or ε ₃. One can also see that although the parameters are cyclically symmetrical, the domain of coexistence is not symmetrical with respect to the line ε ₂=ε ₃. We have also examined a more realistic situation of classic cyclic competition (see Fig. 2B) where we do not have exact cyclic symmetry in the parameters: we increased the parameter α _2,1 so that species u ₁ exerts more competitive pressure on species u ₂. The main effect of this is that the domain of coexistence moves away from the ε ₃-axis, and so extinction will occur for small values of ε ₂—that is, the extra competitive pressure on species u ₂ requires it to be faster if all the three species are to coexist. On the whole, however, the coexistence region is qualitatively quite similar to the symmetrical case.

On the other hand, the structure of the diagram changes if we consider parameters for conditional cyclic competition. When species u ₁ is able to ‘retaliate’ more to competition from u ₃ (the parameter α _3,1 is increased), we get the case of u ₃,u ₁-bistable competition as discussed in Sect. 2. As shown in Fig. 2C, in this case the regions of coexistence and extinction change drastically from those in Figs. 2A and 2B: all three species can only coexist in a thin strip near (but not including) the ε ₃-axis—exactly the contrary to the classical cyclic competition case. Full coexistence places very specific demands on the mobility of species u ₂, and will not be possible for medium or small dispersal rates, but is flexible with regard to the third species—only a small dispersal rate of species u ₃ will necessarily result in extinction of one or more species.

To gain an informative insight into how spatial coexistence is maintained, we can follow the population densities of three species at different times, giving us a ‘profile’ of coexistence. Figure 3 represents patterns of the coexistence in the community with cyclically symmetrical parameters (constructed for ε ₂=0.2, ε ₃=0.3). The plots at times t=20, 60, 80 show the basic underlying mechanism of coexistence: since species 1 is faster, it can ‘catch up to’ species 2 (which it outcompetes), causing the habitat occupied by species 2 to become attenuated (t=20). Eventually, the species 2 distribution becomes so narrow that species 3 can invade the encroaching species 1 population, allowing species 2 to recover (t=60). Once the species 2 population has recovered, it resumes pressing on the species 3 population and this allows species 1 to recover, eventually resulting in a return to the scenario we started with, but now with two such travelling waves (t=80). Through variations on this mechanism, the travelling waves multiply until there are many travelling patches of various sizes intermingled in a complicated way (t=500, 900).

Fig. 3

Patchy coexistence in the one-dimensional model. The distribution of the three species is shown at 5 different points of time. Species u ₁ is indicated by the thin solid line, u ₂ is indicated by the thick solid line and the dashed line represents species u ₃. The diagrams are plotted for the same parameters as in Fig. 2A, with ε ₂=0.3 and ε ₃=0.2

For certain arrangements of the species mobility, all the species can interact (as opposed to a situation where two of the species are constantly separated by the third), but eventually extinction will still take place, rather than coexistence as is observed in Fig. 3. We display a portrait of such a scenario in Fig. 4, constructed for the same parameters as were used for Fig. 3, except with ε ₃ much lower (ε ₃=0.05). Here the dynamics start off as in Fig. 3, but since species 3 is slower it cannot invade species 1 as quickly, and this allows the species 1 population to recover before species 2 can establish itself on the other side of the species 1 peak. Because of this, we do not have local persistence of species 2, as it is constantly forced towards the boundary by the other species, which eventually results in extinction. In the same way one can observe that for a slow-moving species 2, coexistence of all three species is impossible (for the sake of brevity we do not show the corresponding diagrams).

Fig. 4

Dispersal-induced extinction in the one-dimensional model. Species u ₁ is indicated by the thin solid line, u ₂ is indicated by the thick solid line and the dashed line represents species u ₃. The diagrams are plotted for ε ₃=0.05, with all other parameters the same as in Fig. 3. As a result of this single change, two of the species will be driven to extinction when the travelling wave fronts reach the boundary

Considering spatiotemporal dynamics in the case of conditional cyclic competition (with bistability between species 1 and 3) allows us to give a reason why coexistence is only possible for a narrow range of ε ₂ in this case. If species 3 is to invade species 1, it requires a supercritical density to successfully establish itself (a small density will result in extinction). For this to happen, the population of species 2 must become sufficiently attenuated so that species 3 can disperse across it in high enough volume, but not become attenuated so quickly that it is overwhelmed by the encroaching species 1 population. For this reason, coexistence is largely determined by the speed of spread of the species 2 population, which is determined by ε ₂. Interestingly, in some cases species 3 is unable to disperse across species 2 in high enough volume to establish itself, but the three-species wave keeps on moving following such an interaction, with the whole scenario repeating and the invasion of species 3 always failing. As before, this also results in geographical spread (propagation of a pulse of population density of species 2 in space), but without local persistence, which will end in extinction when the habitat boundary is eventually reached. Curiously, the geographical spread results in replacement of species 3 by species 1, i.e. the inferior competitor will eventually replace the superior. This becomes possible due to species 2 acting as a biological ‘buffer’ between species 1 and 3. Since we do not have local persistence in the system, we do not include the regions corresponding to propagation of pulses in the domain of existence in Fig. 2C.

We can reasonably suppose that, since the inclusion of an additional spatial dimension usually allows more complex patterns of dynamics, some scenarios of extinction in one-dimensional habitats can be avoided in two-dimensional ones (e.g. Morozov and Li 2007). Therefore we should extend our investigation to consider the role of species mobility in biodiversity in two-dimensional landscapes. The regions of coexistence and extinction in two dimensions for the same three sets of parameters as we plotted in Fig. 2 are shown in Fig. 5. Initial conditions of types (i) and (ii) were used to determine coexistence in the middle of the domains, and regions near the boundary of coexistence were explored using type (iii) initial conditions—obtained from the asymptotic dynamics of the system with nearby parameters—since in these regions type (i) and (ii) initial conditions may result in extinction as they are too far removed from the eventual dynamics.

Fig. 5

Domains of coexistence and extinction for model (4)–(6) in a 2D habitat in terms of the diffusion coefficients ε ₂ and ε ₃, with the habitat length, L=300. Black regions indicate that no coexistence is possible. (A) Cyclically symmetrical parameters: the model parameters are the same as in Fig. 2A. In the white region the species coexist through spiral and target waves, the region in which the system exhibits intermingled spirals are coloured dark grey, and the region in which the system displays chaotic patchy behaviour is coloured light grey. (B) Increased pressure exerted on species u ₂ by u ₁: all parameters are the same as in Fig. 2B. The grey region indicates the region in which the species can coexist through chaotic patches. (C) Conditional cyclic competition: all parameters are the same as in Fig. 2C. The grey region again indicates the possibility of coexistence through chaotic patches

Comparing Figs. 2A and 5A shows us that, when the competition parameters are cyclically symmetrical, including a second spatial dimension causes the domain of coexistence to increase to take up almost all of the mobility space of the system, with extinction being unavoidable only for extremely small relative motilities of ε ₂ or ε ₃. The dynamics through which coexistence takes place, however, become much more rich and varied. In Fig. 5A we have divided up the coexistence domain into the regions in which the three main types of nontrivial dynamics are observed. Firstly, when all the dispersal rates are close to each other (white region in Fig. 5A), the coexistence takes place through spiral waves such as those in Fig. 6A (plotted for type (i) initial conditions), or through target waves (not shown here), depending on whether initial conditions of type (i) or (ii) are used, respectively. This observation is consistent with previous studies which have reported spiral dynamics in cyclic competition when the species all have equal mobility (Reichenbach et al. 2007; Jiang et al. 2011). These spiral dynamics do not take place for all mobility configurations, however: if the species have more unequal motilities, the spirals start to break up (dark grey region in Fig. 5A). The greater the disparity in the dispersal rates, the shorter the distance from the origin at which the spiral waves break down, and the dynamics begin to resemble several intermingled spirals which no longer form waves, as is seen in Fig. 6B (plotted for type (ii) initial conditions). Eventually, when the first species is very much faster than one or more of the others, the spiral behaviour disappears, except for a few temporary spiral heads (light grey region in Fig. 5A). In this region the species coexist in the manner seen in Fig. 6C (plotted using type (iii) initial conditions)—through a convoluted and constantly shifting arrangement of irregular patches of varying size and character, from small island-like patches to large, contiguous patches.

Fig. 6

Three types of spatiotemporal dynamics displayed by system (4)–(6) in a 2D habitat. Blue regions represent a prevalence of species u ₁, yellow regions mostly contain species u ₂, and red regions indicate that the predominant species is u ₃. (A) Spiral waves, plotted here for diffusion coefficients ε ₂=ε ₃=1, all other parameters are the same as in Fig. 5A. (B) Intermingled spirals, plotted for diffusion coefficients ε ₂=0.6, ε ₃=0.5, all other parameters kept the same. (C) Chaotic patches, shown for coefficients ε ₂=0.2, ε ₃=0.3, all other parameters are the same (Colour figure online)

To gain an insight into the dynamical properties and spatiotemporal complexity of the system dynamics observed, we can fix a point in the habitat and follow the change in the densities of the species as they interact. Since the model displays three apparently very different kinds of dynamics, we have examined the local population dynamics for each of them: the results are shown in Fig. 7, plotted using the same parameters and initial conditions as Fig. 6. In the case of spiral waves (Fig. 7A)—as might be expected—the local species densities display perfect periodicity, with constant amplitudes and frequencies. More surprisingly, however, are the local dynamics seen in the dark grey transition region, which are plotted in Fig. 7B: here we still observe periodicity with constant amplitudes, despite the observed spatiotemporal dynamics being complicated and irregular in space. Also of interest are the population densities attained: the species having maximal total biomass is the one which is the inferior competitor of the species with the smallest mobility, and the species having the minimal total biomass is the inferior competitor of this species. When we consider the region of irregular patches (Fig. 7C), the periodicity of the local population densities quickly disappears resulting in chaotic dynamics, as can be seen by either considering trajectories in the local phase plane (Fig. 7D) or by calculating the leading Lyapunov exponent for the spatial model and showing that it is positive.

Fig. 7

Local population densities for the types of spatiotemporal dynamics seen in Fig. 6. Species u ₁ is indicated by the thin solid line, u ₂ is indicated by the thick solid line and the dashed line represents species u ₃. (A) Spiral waves: plotted for the same parameters as in Fig. 6A. The local population densities show periodic cycling. (B) Intermingled spirals: plotted for the same parameters as in Fig. 6B. Local population densities still show periodic cycling. (C) Chaotic patches: plotted for the same parameters as in Fig. 6C. Periodicity in the local population densities disappears, resulting in chaotic dynamics. (D) Local phase portrait for chaotic patches: plotted for the same parameters as in Fig. 6C

In the other two diagrams of coexistence in 2D space (corresponding to 1-D diagrams in Fig. 2) we do not observe any spiral behaviour at all—we can only have coexistence through irregular patches as in Fig. 6C. For example, Fig. 5B shows the regions of coexistence and extinction in two dimensions when we increase the coefficient α _2,1, which is analogous to the case shown in Fig. 2B for one spatial dimension. In this case, even when all diffusion coefficients are equal, there is no possibility of long-term spiral behaviour. However, this shift in the dynamics is not accompanied by a significant change in the domains of coexistence and extinction: comparing Figs. 5B and 5A, the region of coexistence dominates most of the mobility space in both cases, and the only notable difference is that the extinction domain in Fig. 5B does expand substantially in the regions near the origin and the ε ₃-axis.

Note that in both diagrams constructed for the classical cyclic competition scenario we considered the particular case α _i,i+1=1. Our numerical simulations show that considering the case α _i,i+1<1 will not affect qualitatively the conditions of maintaining the biodiversity in the system: the location and the shape of the domains of coexistence of all species will be similar to those shown in Figs. 5A, B as well as Figs. 2A, B (we have checked the robustness of the results by decreasing the parameters α _i,i+1 up to 1/2). However, we found that for smaller α _i,i+1, formation of spiral waves (as shown in Fig. 6A) becomes hampered: in the case α _i,i+1 is close to 1 the spiral waves are still possible; finally, for smaller α _i,i+1 (e.g. α _i,i+1<0.75) only intermingled spirals can be observed even for the equal diffusion coefficients.

An entirely different structure of the mobility space which provides coexistence is shown when we consider conditional competition (involving u ₃, u ₁-bistability), with parameters the same as the symmetrical parameter set except for α _3,1, which is increased—allowing species 1 to ‘retaliate’ against the competitive pressure of species 3. In a similar way to the system with a one-dimensional habitat, when the competition is altered like this, the distribution of the coexistence and extinction domains completely changes. The new scenario is shown in Fig. 5C, plotted for α _3,1=1.3. The coexistence domain is shifted towards the ε ₃-axis, while the extinction region near the ε ₂-axis grows, so that rather than coexistence being possible for most of ε ₂–ε ₃ space—with extinction only guaranteed in proximity to the axes—the coexistence region is instead constrained to the left-hand side of ε ₂–ε ₃ space, with overly large values of ε ₃ necessarily resulting in extinction. Comparing Fig. 5C with Fig. 2C reveals that this is effectively an extension of the analogous coexistence domain in the one-dimensional case: the inclusion of the second dimension allows coexistence in a relatively large area around the initial small strip of 1D coexistence. We can also note that most of the region in Fig. 2C which features the propagation of pulses without local coexistence (in the 1D case ending in extinction when the boundary is reached) seems to contribute to this coexistence region—implying that this mechanism can result in full coexistence when a second spatial dimension is included. A similar mechanism was reported in Morozov and Li (2007). An open question regarding the results shown in Fig. 2C concerns coexistence in the regions lying extremely close to the ε ₃-axis and ε ₂-axis—while we can say that any regions of extinction in these areas must be very small, we cannot rule them out completely due to extreme demands on the computation in these areas.

The boundary region of the coexistence domain in the case of conditional cyclic competition is host to a rather interesting phenomenon: a scenario of patchy biological invasion. Biological invasion is the name given to the process by which one or more alien species are introduced to a native ecosystem, establish themselves and then spread out in space. In reaction–diffusion models of biological invasion the population front that arises is often continuous. However, recently the population front in some predator–prey systems has been found to break down and become discontinuous (Petrovskii et al. 2002; Morozov et al. 2006). Interestingly, we found that invasion in our cyclic competition model (4)–(6) can exhibit this behaviour.

An example of such an invasion is given in Fig. 8. We model the scenario of biological invasion where two cyclic competitors invade an ecosystem in which the third competitor is native. Starting from initial conditions of type (iv)—small overlapping rectangles of species 2 and 3 in the middle of a habitat dominated by the resident species 1—we can see species 2 and 3 co-invade the domain, with the initially continuous invasion front becoming discontinuous, until patches of all three species can be found across the whole habitat. This situation is closely related to the scenario known as invasional meltdown, where one invasive species facilitates the invasion of another invasive species (Simberloff and Von Holle 1999; O’Dowd et al. 2003; Simberloff 2006). Similarly, in our system, species 2 would be unable to establish itself in the habitat at all were it not for species 3. However, the joint invasion of species 2 in fact prevents species 3 from driving species 1 to extinction, and maintains biodiversity, thus potentially reducing the damage caused to the native ecosystem by the invasion. Such patchy invasion scenarios were found to take place within a large range of model parameters.

Fig. 8

Patchy invasion in a cyclic competition system. The distributions of the invasive species u ₂ and u ₃ are plotted in space at three different times with species u ₂ shown in the left column and u ₃ in the right column: starting from two small overlapping rectangles, the continuous invasion front breaks down, and eventually dynamic patches of all three species are present across the whole domain. The resident species u ₁ is not shown here. The diagrams were plotted for the diffusion coefficients ε ₂=0.35, ε ₃=0.4, with all other parameters the same as in Fig. 5C

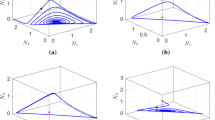
Finally, we investigate one more crucial constraint on the coexistence of competitors in spatial systems: the size of the habitat. Note that previously we assumed that the habitat was large compared to the characteristic sizes of spatial patterns—we now relax this assumption. It is easy to see that varying the size of the habitat is equivalent to varying the absolute values of the mobility of all three species while keeping the habitat size fixed. To show the results of variation of habitat size in the case of symmetrical cyclic competition, the boundaries between coexistence and extinction for several sizes of one-dimensional habitat are plotted as dashed lines in the coexistence domain in Fig. 2A. We see that when the habitat size becomes restricted, full coexistence is impossible for values of ε ₂ and ε ₃ close to 1, and with a further decrease in habitat size the domain of coexistence is quickly pushed to the interior of the diffusion space until it is extremely small and eventually disappears (for L=100). The same analysis in the two-dimensional case (considering a square spatial domain) is plotted in Fig. 9. From this figure it is apparent that as in the one-dimensional case, decreasing the habitat size causes the coexistence domain to decrease monotonically. This is consistent with the results of Reichenbach et al. (2007), but interestingly, for fast enough species, the point (1,1) representing equal species mobility does not admit coexistence, whereas there is still an interior coexistence domain. If the habitat domain is decreased further (until approximately L=20—much lower than the threshold observed in a 1D environment), then this interior coexistence domain disappears in a discontinuous manner, meaning that one or more species will always go extinct in a habitat of this size, regardless of the arrangement of their dispersal rates.

Fig. 9

Dependence of the boundary of coexistence upon the habitat size in two spatial dimensions. The boundary of coexistence in the system is plotted for three different habitat sizes, with cyclically symmetrical parameters used in each case. The solid line is the boundary in a habitat length of 150, the dashed line is constructed for a habit length of 25, and the dotted line is constructed for a habitat length of 20. For smaller habitats, the coexistence domain rapidly disappears

4 Discussion

In this paper we have revisited the spatiotemporal dynamics of a community of three species showing a particular type of non-transitive competition: cyclic competition. Two main features set our investigation apart from previous studies: we have allowed the species to have disparate dispersal rates, while previous papers have assumed the species have equal mobility, and we have used a reaction–diffusion framework, whereas previous papers have mostly studied coupled lattice models. Aside from the clear benefit of relaxing the previous assumption on equal mobility—which allows us to extend the model to include interacting competitors as distinct from another as, for instance, parasite–grass–forb interactions in which the competitors have substantially different dispersal rates (Cameron et al. 2009)—these two factors of our approach also allow us to reveal a number of new features of spatial cyclic competition systems in general. In addition, it should be stressed that a tremendous number of simulations (>2000) were performed in order to complete the current work.

A critical conclusion we can draw from our results is that we should strongly emphasise the role which disparity in the mobilities of the species plays in the level of diversity in systems of cyclic competitors. Depending on the parameters representing the strength of competition, we can see that disparity in dispersal rates can induce diversity loss in an otherwise healthy system (as in the classical cyclic competition, see Fig. 5A and B), and furthermore, in some cases biodiversity can be threatened by a disparity in the mobilities as small as D ₂/D ₁=D ₃/D ₁≈0.5 (see Fig. 5B). On the other hand, there are also cases where species with unequal dispersal rates can coexist, while the same situation with equally mobile species would end in extinction, as in the case of conditional cyclic competition (see Fig. 5C). Assuming that all species have equal mobility in a cyclic competition system ignores this (e.g. Reichenbach et al. 2007), and so may give misleading predictions with regard to biodiversity enhancement or loss. Interestingly, the set of mobility rates defines the critical habitat size and, consequently, the magnitude of the dispersal rates for which biodiversity can be maintained: our results show that once a critical habitat size is reached, coexistence becomes impossible for equal dispersal rates in smaller habitats, but remains possible for disparate dispersal rates (see Fig. 2A and Fig. 9). In a study which only considers equal dispersal rates this possibility of coexistence in smaller habitats would be simply missed.

An important question concerns the mechanisms allowing for biodiversity observed for different species mobilities, and the reasons why those mechanisms stop working for small or large values of ratios of the dispersal rates. The complete understanding of this fundamental issue is still an open question—the large number of simulations performed tell us that the persistence of interactions in a 2D environment combines several mechanisms and does not allow a simple qualitative explanation. In particular, complex shapes taken by the boundaries separating areas occupied by different species in 2D space can play a major role, and this can be estimated only numerically. The spatial patterns observed include spiral and target waves, intermingled spirals and irregular patches, with the observed patterns depending on the ratios between the dispersal rates considered.

For example, we found that the parametric region corresponding to the formation of spiral waves is rather narrow and requires exact cyclic symmetry of the competition coefficients, whereas for slightly different mobility rates and/or competition coefficients no spirals are formed (cf. Reichenbach et al. 2007 and Jiang et al. 2011). In fact, for our system to exhibit ‘true’ spiral waves which propagate forever, we require exact cyclic symmetry in both competition and diffusion parameters—any other parameters will result in the spiral wave breaking up eventually—so we have considered a spatial pattern a ‘spiral wave’ if the spiral wave occupies most of the habitat. This result can partially explain the paradoxical fact that we do not usually observe spiral waves of population densities in real ecosystems (Hanski 1994; Rohani et al. 1997), whereas such waves are observed in a large number of models (Boerlijst et al. 1993; Gurney et al. 1998; Sherratt and Smith 2008)—indeed, in Reichenbach et al. (2007) it was shown that spirals in cyclic competition systems are even robust to perturbation by noise. In our case, the absence of spirals in our model is due to the symmetry breaking in the model parameters and the diffusion coefficients, and this may be the case with real ecosystems: the heterogeneity of species’ life traits might be the reason for the absence of spirals.

We suggest that the formation of complex 2D spatial patterns is an important mechanism that allows biodiversity to be maintained in the system, and that they need the additional degree of freedom that an extra spatial dimension allows (Morozov and Li 2007). For instance, in regions of mobility space where in 1D we have a geographical spread without local persistence (e.g. on the right-hand side of the boundary of the coexistence domain in Fig. 2C), in the 2D case we will have target waves, intermingled spirals and patchy invasion allowing for coexistence. It is for this reason that dimensionality of the environment is key to the understanding of coexistence of the competitors. In particular, we showed that the range of dispersal rate ratios which permit coexistence significantly increases with dimensionality from a one-dimensional habitat to a two-dimensional one, which implies potential biodiversity loss for cyclically competing species which are confined to narrow habitats through habitat loss or fragmentation. Overall, the main difference between 1D and 2D coexistence patterns is that in the latter case the competition between each pair of species becomes less harsh: often each patch of species i has the other two species in its neighbourhood, thus the pressure on species i from the superior competitor becomes mitigated by its own superior competitor. Such a situation is, obviously, less probable in 1D space.

Considering species interaction in the 1D case can also give us some clue regarding the loss of biodiversity for very small relative mobilities of species in the case of classical cyclic competition (see Fig. 2A and B). The first major constraint seems to be the impossibility of species with low mobility to be able to pass through the domain occupied by their superior competitors. To illustrate this idea let us suggest, for instance, that we have the situation—illustrated in Fig. 3—where species 2 is surrounded from the left by species 1 and from the right by species 3, so that the population fronts of species 1, 2 and 3 are moving from the left to the right. If the mobility of species 3 is high enough, and the domain occupied by species 2 becomes thin enough due to pressure from the faster species 1, diffusion allows a number of individuals to pass through the domain occupied by species 2 and further split the population front of species 1 (which is the inferior competitor of species 3) into two pieces, with one of these new pieces splitting the population front of species 2 into two pieces. From the new arrangement of species 1, 2 and 3, splitting of the population front can repeat again, with repetition leading to the whole habitat being occupied by splitting population fronts. In the case of low mobilities this ‘infiltration’ through the domains occupied by competitors happens too slowly for the population front to split properly: as shown in Fig. 4, if species 3 is too slow in the previous case, then it only disperses across the population front gradually, and so by the time the species 1 domain has split into two, the front occupied by species 2 has moved on, and so we will only have a joint propagation of non-splitting population fronts which will hit the boundary and disappear.

If the mobility of species 2 is too low compared to that of species 1, a second major constraint emerges: the pressure from its superior competitor, species 1, will be high enough to drive the species 2 population to too low a level to recover—even if species 3 is able to successfully disperse across the population front. In the case of conditional cyclic competition, if this mechanism of coexistence is to work, species 3 must disperse across the species 2 population abruptly—a gradual infiltration will be suppressed because while its density is low, species 3 is an inferior competitor of species 1 (i.e. due to the bistability between the two species). The abruptness of the infiltration is largely determined by the rate at which the species 2 population attenuates, which is in turn determined by ε ₂, which must be sufficiently small, but as before, the mobility of species 2 or species 3 cannot be too small or else species 3 will not be able to disperse across the species 3 population at all.

Using cyclic competition as a modelling paradigm, we considered mutual biological invasion of two exotic species into a habitat occupied by a native species. In theoretical ecology, this phenomenon is known as invasional meltdown (Simberloff and Von Holle 1999)—one non-indigenous species facilitates invasion of another non-indigenous species. At present, invasional meltdown is usually considered to take place in the case where the co-invaders are mutualists (Crosby 1986; Richardson et al. 2000; O’Dowd et al. 2003), or one invader facilitates the invasion of another without receiving either any substantial gain or penalty (Wonham et al. 2005). In both cases, the overall effect is to accelerate the impact on the native ecosystem. In our system, the introduced invasive species are antagonistic competitors, but we still see a scenario of invasional meltdown. This differs from a traditional invasional meltdown scenario, however, because here the co-invader allows the native species to survive, and prevents, rather than amplifies, the damage done to the native ecosystem. Therefore this result represents a significant extension of the original concept of invasional meltdown originally suggested by Simberloff and Von Holle (1999).

Also of interest is the pattern of spread in the observed co-invasion. The invasion takes place not through the formation of a smooth population front but instead through the spread of irregular patches of high density. Such a pattern of biological invasion is rather typical in nature (Shigesada and Kawasaki 1997; Davis et al. 1998; Kolb and Alpert 2003), and various mechanisms have been suggested so far to explain the observed patterns of patchy invasion—including landscape fragmentation (Murray 1989; With 2001) and/or pronounced environmental and demographic stochasticity (Lewis 2000; Lewis and Pacala 2000). In our model, we show the possibility of patchy invasion in a deterministic system with a completely homogeneous environment. The possibility of patchy invasion scenarios in fully deterministic models is only a very recent discovery, and has previously only been observed in predator–prey or host–pathogen type interactions with the prey subject to a strong Allee effect (Petrovskii et al. 2002; Morozov et al. 2006)—this is the first example of such an invasion in a competition system, and therefore this finding is an important extension of recent works. It is of note that we found patchy invasion only in the case of conditional cyclic competition.

The observed patterns of patchy invasion (see Fig. 8) can potentially describe the experimental case study of mutual invasion of green alga Codium and encrusting bryozoan Membranipora membranacea into the area originally occupied by native kelps in southern Maine (Levin et al. 2002). Codium can replace kelp by colonizing gaps in kelp beds inhibiting kelp recruitment, but established kelp populations can resist Codium invasion by monopolizing available space. Meanwhile, the bryozoan grows on kelp and reduces its growth and survivorship, but dominance of Codium will result in a drop of density of bryozoans, which cannot grow on Codium. As a result, the community of these three species can be considered to show non-transitive cyclic competition. Since it is been reported that depending on initial densities either the dominance of kelp or the dominance of Codium is possible (Levin et al. 2002), we can suggest that this study case be described as conditional cyclic competition (see Sect. 2), which would explain the complex patterns of patchy invasion seen in the system.

Finally, our theory of invasional meltdown due to invasive antagonistic competitors could potentially be applied to the invasion of grey squirrels in the UK. It is well known that the exotic grey squirrel species Sciurus carolinensis has replaced the native red squirrel species S. vulgaris across most of the UK, the main reasons being competitive superiority with regard to resources as well as the susceptibility of the red squirrel to parapoxviruses carried by the grey squirrel (Okubo et al. 1989; Rushton et al. 2000; Tompkins et al. 2003). Recently, populations of the black squirrel—a melanistic subgroup of S. carolinensis—have been found to have established themselves in parts of the UK and now are spreading across the country (for details, see the site http://blacksquirrelproject.org/). Little is known yet regarding the possible competition outcome between red and black squirrels, but black squirrels have been found to store heat with much greater efficiency than grey squirrels (Ducharme et al. 1989) and therefore enjoy a competitive advantage in the northern range of S. carolinensis, where they are predominantly found. In the case that red squirrels turn out to be superior competitors of black squirrels, we may expect to find similar patterns of patchy invasion amongst the competing squirrels—particularly in the colder northern regions of the UK such as Scotland, in which the vast majority of the UK’s red squirrel population is presently located.

The most important distinction between our study and the majority of the cyclic competition literature is that we consider continuous space and describe the movement of animals based on macroscopic diffusion—somewhat different from the approach taken in previous works using stochastic coupled lattice models in a discrete space (Frachebourg et al. 1996; Durrett and Levin 1998; Frean and Abraham 2001; Kerr et al. 2002; Károlyi et al. 2005; Reichenbach et al. 2007; Müller and Gallas 2010). Firstly, assuming space to be continuous can result in different predictions regarding the coexistence of species: it was shown that in the case of equal mobility rates of cyclic competitors in continuous space, an intermediate level of mobility produces the maximal likelihood of biodiversity (Ni et al. 2010). Moreover, coupled lattice models can be rather restricted when incorporating disparity in mobility rates if, for instance, we describe movement of individuals in a ‘stirring’-like manner by simply swapping between organisms (or patches) occupying the nearest cells in cellular automata models (e.g. Reichenbach et al. 2007). This kind of movement of organisms in space is rather exotic from a biological point of view unless we consider some sessile organisms or we are in the situation where animals fill the physical environment in such a dense manner that they cannot move without bumping into each other. The above problem can be partially solved in discrete lattice models where we consider interaction by randomly choosing a pair of individuals (patches) located within a certain distance R (e.g. Durrett and Levin 1998). This situation can apply, for instance, when considering the dispersal of seeds. However, such a modelling framework considers dispersal as a by-product of species interactions and does not take into account the possibility of individuals dispersing without interacting with other species, a process which is often observed in real ecosystems.

Implementation of the reaction–diffusion framework, on the other hand, allows us both to easily incorporate the disparity in mobility/dispersal rate of species and to separately vary the parameters accounting for competition (α _i,j ). Furthermore, a reaction–diffusion system allows us to define competitive dominance by the actual displacement in space, rather than by a single probability (as in lattice models)—this, for instance, permits us to distinguish between ‘classical’ cyclic competition and conditional cyclic competition. An important property of reaction–diffusion models is that populations are described in terms of densities and temporary local coexistence of all three species is possible. The latter has a crucial effect on the coexistence of species in the model: even if the local fitness is negative, a population can migrate through a large unfavourable habitat (a domain largely occupied by the superior competitor) and reach a favourable domain (occupied by the inferior competitor). This behaviour is vital for the coexistence of all three species in the case of conditional cyclic competition in model (4)–(6) (see Fig. 5C), but this type of behaviour is hardly possible in any lattice models which consider interactions in the nearest neighbourhood only (Frean and Abrams 2001; Kerr et al. 2002; Müller and Gallas 2010). Finally, the existence of conditional cyclic competition in (4)–(6) requires a revisiting of the phenomenon called the ‘survival of the weakest’, previously found in discrete models of cyclic competition: certain studies have found that the competitor with the weakest competitive ability (measured in terms of pairwise invasion probability) is more likely to survive when the parameters are close to the edge of extinction region (e.g. Frean and Abraham 2001). In the case of conditional cyclic competition, however, the strength of the competition between species 1 and 3—which shows local bistability—and that of the competition between the species pairs 1,2 and 2,3—which results in the unconditional local exclusion of species 3—are simply incomparable, and the previous definition of the weakest/strongest competitor does not makes sense.

Among the open questions in cyclic competition theory in space we would like to emphasise the following. First, it will be interesting to follow spatial interactions in a three-component cyclic system involving more complicated conditional competition, for instance, where the competition between both species pairs 1,2 and 2,3 exhibits pairwise local bistability whilst still following cyclic competition in space (with the same ordering as before: 1>2>3>1). Another important future direction is the consideration of non-transitive competition in systems with n>3 species in space. It is well known that real ecosystems often show patterns of complex competitive relations involving multiple species (Buss and Jackson 1979; Silvertown et al. 1992; Tanner et al. 1994; Laird and Schamp 2008), and these include non-transitive competition patterns. Additionally, it would be interesting to consider the influence of disparity in dispersal rates on the spatial dynamics of evolutionary hypercycles where the species i catalyzes the replication of species i+1, and finally, species n catalyses species 1 (Boerlijst and Hogeweg 1995; Kim and Jeong 2005). Finally, it will be interesting to include into the initial model (4)–(6) evolution of some life traits (e.g. mobility or competition parameters) which can be related by some trade-off relations between the life traits and follow a possible convergent stable strategy, for instance, using the standard adaptive dynamics principals (Metz et al. 1992). Such an analysis may be particularly interesting, for instance, when considering animal mobility, since our investigation has revealed that slowing down a species actually drives the biomass of its superior competitor down at no cost to itself, which may lead to some particularly surprising evolutionary dynamics—especially when considering a trade-off which reflects the energy cost of mobility.