1 Introduction

Physiological models are used to mathematically describe, replicate or predict the dynamics or mechanics of biological phenomenon. Suitable models accurately describe or re-create observed behaviour of an appropriate range of subjects by varying the value of key model parameters. The values of these model parameters can then be used to characterise the observed behaviour with respect to the model configuration. Most frequently, the optimal model parameter values are considered those that minimise the difference between the observed data and a response simulated by the model. Numerous algorithms have been postulated for the purpose of identifying the optimal model parameter values as a function of the model formulation and observed data [3].

However, parameter identification is intrinsically complex. An insufficient ability to effectively apply parameter identification methods or diagnose and remedy their failure can become an insurmountable research obstacle. Thus, there is some significant demand for a parameter identification method that is robust, convex and relatively intuitive and straightforward to apply.

Most algorithms attempt to identify the optimal parameter values by characterising the error change as a function of variances in the model parameters. For example, the Levenberg–Marquardt algorithm is a very commonly used form of nonlinear-least-squares that optimise model parameters in the direction of descending simulation error [11, 15]. The algorithm steps towards convergence by measuring the derivative of an error-surface with respect to changes in model parameters and defines a parameter change that is a function of the derivative and a manually defined proportional driver. Thus, the method can be used for numerous model configurations, and has been accepted as a preferred method in a number of fields. However, the method is susceptible to instability when there is an insufficient error gradient at the initial conditions, or the proportional driver value is over-estimated. Under-estimation of the driver will slow the rate of convergence. Furthermore, the method is non-convex and can converge to false local minima giving incorrect parameter values. Thus, the method requires some operator experience and care for best results, which cannot necessarily be provided by some research groups.

The single integral parameter identification method has been proposed as a simple-to-use, convex algorithm that is robust to sample error [8]. It has been used in a number of applications [4, 10, 13, 14, 16, 18]. However, the single integral method does not necessarily converge to a minimal least-square error. The iterative integral method (IIM) is an extension of the single integral method and has previously been presented in application [5, 7], but without formal validation or comparison. This article presents IIM methodology, and compares it to the frequently used Levenberg–Marquardt nonlinear-least-squares method [11, 15].

2 Methods

2.1 Steps of the iterative integral method

A general coupled first order differential equation will be used to define the overall IIM algorithm. We may write this in a general form such that for a vector of measured species variables x with \( {\mathbf{x}} \in \mathbb{R}^{n} \) then the kth differential equation can be written as:

$$ \dot{x}_{k} = \sum\limits_{j = 1}^{M} {\xi_{jk} f_{j} \left( {{\mathbf{x}},t,{\varvec{\theta}}} \right)} $$
(1)

where x n is a co-dependent species of the subset of x, \( {\mathbf{x}} \in \mathbb{R}^{n - 1} \), f j are functions of x and a priori known parameters and/or known external time-variant inputs (θ), while ξ jk are the matrix of unknown parameters to be identified. To illustrate the method, we simplify the system of o.d.e.s to a pair of coupled equations given by:

$$ \begin{gathered} \dot{x} = \sum\limits_{j = 1}^{M} {\xi_{j} f_{j} \left( {{\mathbf{x}},t,{\varvec{\theta}}} \right)} \hfill \\ \dot{y} = f_{M + 1} \hfill \\ \end{gathered} $$
(2)

with the constraints

$$ \begin{gathered} f_{i} \ne f_{j} \,{\text{ for }}i \ne j \hfill \\ \xi_{M} = 1 \hfill \\ \end{gathered} $$

These constraints enable a priori model identifiability and unique identification of all the ξ j ’s [7, 17].

If none of f i are functions of x, the first iteration of IIM will produce the optimal parameter values and further iterations would not improve the outcome. In this case, the single integral method is sufficient. However, if any of the f i are functions of x, then IIM is needed to converge to the solution. The IIM algorithm is defined in Steps 1–7:

  1. 1.

    The governing equation is integrated over time

    $$ x\left( t \right) - x\left( 0 \right) = \sum\limits_{j = 1}^{M} {\left[ {\xi_{j} \int\limits_{0}^{t} {f_{j} \left( {{\mathbf{x}},t,\theta } \right){\text{d}}\tau } } \right]} $$
    (3)
  2. 2.

    The equation is re-arranged with unknown coefficients (ξ jk ) on the RHS and the remaining terms on the LHS with x(t) = x t and x(0) = x 0, we have that

    $$ x\left( t \right) - x\left( 0 \right) - \int\limits_{0}^{t} {f_{M} \left( {{\mathbf{x}},t,\theta } \right)d\tau } = \sum\limits_{j = 1}^{M - 1} {\left[ {\xi_{j} \int\limits_{0}^{t} {f_{j} \left( {{\mathbf{x}},t,\theta } \right){\text{d}}\tau } } \right]} $$
    (4)
  3. 3.

    The LHS and the coefficients of the model parameters are evaluated over a series of periods between t 0 and the sample times t 1, t 2,…,t n where x t and x 0 are the measured data. In contrast, functions f i are evaluated by simulations of x n . The initial f i simulations can be evaluated using simple linear interpolations of the measured data or a vector of zeros.

  4. 4.

    The values evaluated in Step 3 are arranged in the matrix formulation over all evaluated periods:

    $$ \begin{gathered} {\mathbf{A\xi }} = {\varvec{\psi}} \hfill \\ {\mathbf{A}} = \left\{ {A_{ij} } \right\};\quad A_{ij} = \int\limits_{0}^{{t_{i} }} {f_{j} \left( {{\mathbf{x}},\tau ,{\varvec{\theta}}} \right)\;{\text{d}}\tau } \hfill \\ {\varvec{\psi}} = \left\{ {\psi_{i} } \right\};\quad \psi_{i} = x_{t} - x_{0} - \int\limits_{0}^{{t_{i} }} {f_{M} \left( {{\mathbf{x}},\tau ,{\varvec{\theta}}} \right)\;{\text{d}}\tau } \hfill \\ \end{gathered} $$
    (5)

    Since the matrix is non-square, the system is over-determined and A −1 does not exist and careful analysis is needed to find the modelling parameter vector (ξ). To solve the matrix system, the Moore–Penrose pseudo inverse is used. However, this approach does not automatically produce a unique solution and there is no indication that the matrix is necessarily of full rank. A solution may be obtained in the least squares sense by minimising the error (E):

    $$ E = \left\| {{\mathbf{A\xi }} - {\varvec{\psi}}} \right\|_{2} $$
    (6)

    where we assume that the M columns of A are linearly independent.

  5. 5.

    x is re-simulated using the identified vector ξ and the governing Eqs. 1 and 2.

  6. 6.

    Equation 5 can be re-defined using the updated f i to re-evaluate ξ

  7. 7.

    Steps 5 and 6 are iterated until convergence is declared.

It should be noted that this process is mechanistic. Neither does it require initial starting values to be estimated nor does it require the calibration of the proportional driver functions to stabilise or accelerate convergence. Hence, the method is operator independent.

2.2 Insulin pharmacokinetic example

The iterative method will be used to identify insulin pharmacokinetic parameters from the dynamic insulin sensitivity and secretion test (DISST) model [14] defined in Eqs. 7 and 8. This coupled model is indicative of a number of physiological models. The DISST model fits to the insulin data by finding the optimal values of the first pass (x L) and proportional (n T) insulin clearance rates [14].

$$ \dot{I} = - n_{\text{T}} \frac{I}{{1 + \alpha_{\text{I}} I}} + \frac{{n_{\text{T}} }}{{V_{\text{p}} }}(Q - I) + \frac{{x_{\text{L}} U_{\text{N}} + U_{\text{X}} }}{{V_{\text{P}} }} $$
(7)
$$ \dot{Q} = \frac{{n_{\text{I}} }}{{V_{\text{Q}} }}I - \left( {n_{\text{C}} + \frac{{n_{\text{I}} }}{{V_{\text{Q}} }}} \right)Q $$
(8)

where I and Q are the plasma and interstitial insulin concentrations [x n in Eq. 1]; V P and V Q are the distribution volumes of plasma and interstitium [θ]; U N and U X are the endogenous and exogenous insulin inputs [θ]; n I is the a priori known rate of transfer between plasma and interstitium [θ]; n C is the a priori known clearance rate in the interstitium [θ]; α I is the saturation of insulin clearance [θ]; n T is the proportional plasma clearance rate [ξ 1]; and x L is the proportion of endogenous insulin that is not extracted on the first hepatic pass [ξ 2].

$$ {\text{if}}:\xi_{1} = n_{\text{T}}\, \therefore\, f_{1} = \frac{ - I}{{1 + \alpha_{\text{I}} I}} $$
$$ {\text{if}}:\xi_{2} = x_{\text{L}}\, \therefore\, f_{2} = \frac{{U_{\text{N}} }}{{V_{\text{P}} }} \, $$
$$ \xi_{3} = 1\,\therefore\, f_{3} = \frac{{n_{1} }}{{V_{\text{P}} }}(Q - I) + \frac{{U_{\text{X}} }}{{V_{\text{P}} }} $$
$$ f_{4} = \frac{{n_{1} }}{{V_{\text{Q}} }}(I - Q) - n_{\text{C}} Q $$

2.3 Analysis

Clinical data obtained from one insulin resistant (IR) and one healthy, normo-glucose tolerant (NGT) participant of the DISST pilot investigation [14] are used to characterise the range of test responses that may be expected from a general cohort. Participant characteristics are summarised in Table 1. Parameter values from these participants are used to simulate 60-min insulin response to the DISST test stimulus in silico. The DISST stimulus includes 10 g intravenous (IV) glucose bolus at t = 10 and 1 U IV insulin bolus at t = 20 min. The endogenous insulin production response (U N ) will be modelled as a three-stage block step infusion with three rates: the basal rate (U B) from t = 0–10, the first phase (U 1) response to glucose stimulus from t = 10 to 15 and the second phase response (U 2) t = 15–60 min. Data in terms of I will be ‘sampled’ from the synthetic profiles at 5-min interval.

Table 1 Summary characteristics of participant physiology
Full size table

In order to provide context and comparison, IIM and the frequently used nonlinear least-squares method are used to identify the true values of n T and x L from the ‘sampled’ data using 16 starting points. The 16 initial conditions are within the values that may be reasonably assumed [14] and are shown in Fig. 1. Convergence is declared when both model parameters are within 1% of the true values, while non-convergence is declared if at least 1 parameter is outside 1% after 100 iterations.

Fig. 1
figure 1

Starting conditions and true values of n T and x L for the IR and NGT participants

Full size image

Nonlinear least-squares will be applied with the proprietary Matlab™ (version 7.10.0, R2010a) function lsqnonlin.m. The IIM method is also applied in Matlab™ (version 7.10.0, R2010a).

Step 3 of IIM states that the method does not necessarily require accurate simulations for the initial estimate. Thus, six initial condition cases are tested:

  1. 1.

    I t  = interpolation of measured data. This is the typical approach used in application,

  2. 2.

    I t  = interpolation of measured data I t  × 0.5,

  3. 3.

    I t  = interpolation of measured data I t  × 2,

  4. 4.

    I t  = interpolation of measured data I t  × 5,

  5. 5.

    I t  = 0,

  6. 6.

    I t  = I(0).

Finally, if the nonlinear least-squares method converges to local minima, the local minima values will be used to simulate I t and Q t profiles that will be used as initial conditions of IIM.

3 Results

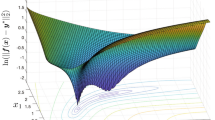
Figure 2 presents the error distribution as a function of model parameter variances across the axis shown in Fig. 1. Note that the in silico data used in this analysis does not include simulated noise to represent assay error. Hence, there are ‘zero error’ conditions at the true values which would not occur in real clinical data.

Fig. 2
figure 2

Error distribution across the identified model parameters. (NGT left, IR right)

Full size image

Iterative integral method successfully iterated to the true values from every starting condition. The nonlinear least-squares method failed to converge on 7 of the 32 cases tested (22% failure). Table 2 indicates the initial conditions that caused failure of nonlinear least-squares and provides an indication of the nature of the failure.

Table 2 Cases of nonlinear least-square failure
Full size table

Table 3 shows that while IIM typically requires more iterations than nonlinear least-squares, those iterations are less computationally expensive, and convergence is achieved faster. Figure 3 shows the convergence patterns of the two methods as a function of time.

Table 3 Convergence of methods and indicative identification times from the respective methods
Full size table
Fig. 3
figure 3

Convergence of parameters as a function of time. (NGT left, IR right)

Full size image

The convergence paths from the 16 starting positions for both participants and both identification methods are shown in Fig. 4. Note that IIM followed distinct convergence patterns for each participant, and while some initial iterations actually produced parameter values that diverged from the true values, the convergence path always reduced in I t simulation error. In contrast, nonlinear least-squares converged in the direction of descending error gradient.

Fig. 4
figure 4

Convergence paths for IIM and nonlinear least-squares for both participants and all 16 starting conditions tested. (NGT left, IR right)

Full size image

The starting point analysis was undertaken to directly compare the performance of IIM and nonlinear-least-squares. However, typical application of the IIM uses interpolation of the measured data as an initial condition rather than initial parameter estimates. Figure 5 shows the convergence of the parameters when the different initial I t and Q t profiles are tested. Note that for most cases, the initial parameter estimation using the simple initial simulation is within the range of expected values, and converges quickly to the true values. However, for the NGT I t  = I(0) case, the parameter values identified in the initial iteration were very erroneous, and while it eventually converged to the simulation values, the rate of convergence was slow. Hence, placing bounds that limit parameters to realistic values significantly increased the rate of convergence. The effect of such bounding shown in Fig. 5, where n T is bound below 1 min−1.

Fig. 5
figure 5

Convergence of IIM from the simple initial simulations of the analytes and the local minima identified by nonlinear least-squares. Paths are numbered according to the initial simulation conditions listed in Sect. 2.3, and the local minima listed in Table 3. (NGT left, IR right)

Full size image

Figure 5 also shows successful convergence when the local minima identified by nonlinear least-squares (listed as failures numbered 2–4 in Table 2) are used to simulate I t and Q t profiles which are then used as initial conditions for the IIM.

4 Discussion

Iterative integral method is a robust and relatively fast method of parameter identification. For each of the initial and local minima conditions tested, the method successfully converged to the true values. The convergence path of IIM consistently reduced the I t simulation error. Although model parameter values from the initial iterations of the method actually diverged from the true values in some cases, convergence ultimately occurred and the true parameter values were always identified. IIM is comparatively simple to apply, starting point independent (Fig. 3), and requires no special operator input or care. In particular, the method can use arbitrary initial simulations of the observed analytes (Fig. 5), which are significantly advantageous over non-convex starting-point-dependent methods.

For the cases presented, IIM is more robust than nonlinear least-squares. Seven of the 32 cases failed to converge to the true parameter values when the nonlinear least-squares method was used (Tables 2, 3). A very low gradient of the error-surface at four of the starting conditions meant that nonlinear least-squares failed to initialise iteration towards the true values. Three of the failed cases resulted in iteration towards local, rather than global, minima. While the cases which failed to initialise may be quickly recognised by the researcher and could be potentially remedied via alternative initial conditions, the cases of convergence to local minima would not be as easily observed, and thus, non-optimal parameter values would generally be reported.

The median convergence time for IIM was faster than for nonlinear least-squares. Table 2 and Fig. 4 show that the median required iterations for convergence of the nonlinear least-squares method was less than the iterative integral method. However, the overall computational requirement of IIM was significantly less than nonlinear least-squares. This result is due to the different number of forward simulations required by the two methods. While IIM requires only one simulation per iteration, the nonlinear least-squares method requires numerous simulations at each iteration to compute a Jacobian. As the model of Eqs. 7 and 8 had a saturation term, analytical solutions were not possible. Thus, comparatively computationally expensive Picard iterations [9, 19] were used to simulate I t and Q t . Importantly, such non-linearity features in many physiological models and identification problems. Hence, much of the computational cost of each method is attributable to the number of forward simulation processes.

Nonlinear least-squares seem to be slightly more complex than IIM and thus could be more difficult to write into computational code form. However, there are numerous proprietary nonlinear least-squares computational packages that require the user to define the model error given certain parameter values. These packages then perform the more complex iterative steps. However, when the proprietary nonlinear least-squares packages fail to converge, an in-experienced user may not be able to correctly diagnose and overcome the cause. Hence, the lack of robustness or transparency can result in subpar results.

Iterative integral method has a major limitation in comparison to the nonlinear least-squares method. Specifically, it cannot be used to identify non-separable parameters. While this issue is not problematic for a wide variety of models and research applications, it is impossible to use in some situations. For example, the proportional and saturation terms in Michalis–Menton formulations cannot be concurrently identified with IIM [6].

Furthermore, IIM requires the identified model parameters to be functions of the observed species (i.e. x in Eq. 1). Most often, model parameters are direct functions of the measured species. However, when the identified model parameters are functions of unobserved species, re-arrangement of the model equations generally enables an expression of the model variables in terms of the observable species. Indeed, if the model parameters were not dependent on the observed species, then the model would not be a priori identifiable [1, 7, 17].

For example, the widely used Minimal Model (Equations 9 and 10) of insulin/glucose pharmacodynamics utilises three model parameters, two of which are not a direct function of glucose, the typically observed species (p 2 and p 3) [1, 2].

$$ \dot{G} = p_{1} \left( {G_{\text{B}} - G} \right) - XG $$
(9)
$$ \dot{X} = p_{3} \left( {I - I_{\text{B}} } \right) - p_{2} X $$
(10)

where G is the measured glucose (G B denotes basal glucose); I is the interpolation of measured plasma insulin data (I B denotes basal plasma insulin); X is a lumped insulin action and concentration parameter [X(0) = 0 assumed]; and p 1–3 are identified model parameters with p 1 representing glucose-related inhibition of endogenous glucose production, and insulin sensitivity defined as p 3/p 2.

In order to identify p 1–3 as model parameters, Eq. 10 must be incorporated into Eq. 9 to make p 2 and p 3 functions of G. Equations 11–13 show how the Minimal Model can be defined as a single equation in terms of G with separated coefficients of the model parameters, thus enabling the IIM approach.

$$ X = p_{3} \int {I - I_{\text{B}} {\text{d}}t - p_{2} \int {X{\text{d}}t} } \, $$
(11)
$$ \dot{G} = p_{1} \left( {G_{\text{B}} - G} \right) - G\left( {p_{3} \int {I - I_{\text{B}} {\text{d}}t - p_{2} \int {X{\text{d}}t} } } \right) $$
(12)
$$ G - G_{\text{B}} = p_{1} \int {G_{\text{B}} - G{\text{d}}t} + p_{2} \int {G\int {X{\text{d}}\tau {\text{d}}t} } - p_{3} \int {G\int {I - I_{\text{B}} {\text{d}}\tau {\text{d}}t} } $$
(13)

Hence, when the Minimal Model parameters are identified with IIM, both G and X must be simulated between iterations, these equations demonstrate the flexibility of the presented method.

This article presented the IIM approach in general and evaluated it in comparison to the nonlinear-least-squares method for a validated insulin pharmacokinetic model [12] and two indicative individuals. A two-variable case was used in this analysis to allow the convergence paths to be easily visualised. However, IIM is capable of identifying models with a greater number of parameters. This analysis enabled two distinct error-surfaces to be defined. These distinct error-surfaces showed the different iterative paths of IIM (Fig. 3). They also showed how the nonlinear least-squares methods can fail when the initial parameter estimations are located in areas of limited error gradient (Fig. 3). Furthermore, the analysis showed how the nonlinear-least-squares method located local minima in the IR participant’s error-surface (Fig. 3). Convergence to these local minima was due to the sharp valley in the error-surface limiting the efficacy of the Jacobian to identify the dominant error gradient. In effect, nonlinear-least-squares had reached convergence criteria. Equally, Fig. 5 (right) shows that the IIM overcame these issues in the cases tested.

Most importantly, IIM is robust to starting conditions, and is not susceptible to locating local minima. IIM could potentially be implemented in a wide range of physiological models as the method is quicker, more stable and more operator independent than the frequently used Levenberg–Marquardt gradient decent method.