1 Introduction

Diabetes is a disorder of the metabolism where insufficient insulin is secreted by the pancreas, resulting in blood glucose concentration chronically elevated beyond normal levels (hyperglycaemia), a situation that can lead to microvascular and macrovascular complications [2, 30]. Type-1 diabetes is the most severe diabetic disorder, being characterized by an absolute deficiency of insulin secretion; therefore, people affected by type 1 diabetes require insulin therapy to control hyperglycaemia and sustain life. In the development of an insulin therapy, the importance of dynamic models describing the complex mechanisms of glucose homeostasis cannot be overestimated. Whereas “minimal” (coarse) models describe the basic components of the system functionality and can measure the crucial processes of glucose metabolism and insulin control in health and diabetes, “maximal” (detailed) models are required to capture the full body of knowledge on metabolic glucose regulation and are capable to simulate the glucose–insulin system in diabetes [7, 25]. Furthermore, maximal models may be used to design in silico preclinical trials as recently suggested by the U.S. Food and Drug Administration (FDA) [24]. Therefore, maximal models provide an extremely useful simulation scenario where personalised treatments can be initially developed and assessed. Successful procedures can (and should) then be tested experimentally.

Maximal models result in a large system of nonlinear differential–algebraic equations (DAEs) with several parameters. For in silico experimentation purposes, the use of an average population-based maximal model is not realistic, because the model parameters must be able to characterise the metabolic portrait of each single diabetic individual [7, 29]. Therefore, parametric identification represents a fundamental step for the effective use of detailed models. Unfortunately, maximal models are known to be difficult to identify, unless massive experimental investigation on a single individual is carried out [4, 7].

In the process systems engineering community, techniques of model-based design of experiments (MBDoE) for parameter identification [14] have proved to be very useful to increase the information content of an experimental trial devoted to parameter identification of constrained nonlinear dynamic systems. Based on a preliminary model of a system (a diabetic subject in our case), the goal of MBDoE is to design an experiment (or a series of experiments) capable of providing as much information as possible on the model parameters. The information embedded in the experimental data is exploited at the end of the experiment, when improved values of the parameters are estimated in a parameter identification session. Basically, information maximisation is accomplished by appropriately designing the time-profile of the control inputs and the time-schedule of measurements, whilst explicitly accounting for any input and output constraints that the system being investigated may be subject to.

Recently, MBDoE techniques have been proposed to design clinical tests for the subject-specific identification of a detailed type 1 diabetes model in the presence of parametric mismatch [17], i.e. in a condition where the difference between the true and modelled blood glucose responses is due only to incorrect initial estimates of the model parameters. Although this MBDoE approach demonstrated that there is the potential to tune up a maximal model to the specific physiological behaviour of a single individual using limited experimental investigation, the assumption of parametric-only mismatch is quite simplistic. In fact, for a given profile of the inputs, the subject response and the modelled one are always structurally different [13]. This is due to the fact that any model is only a proxy of reality, and is therefore (to some extent) structurally different from reality itself. This occurrence is called structural mismatch or model mismatch. Designing a clinical test with no concern about the existence of model mismatch may have dramatic impacts on the effectiveness of the test. In fact, the result of an MBDoE session might be the design of a sub-optimal (scarcely informative) test or even of an unsafe test (e.g. the actual response of the subject might be hypoglycaemic or strongly hyperglycaemic). An advanced MBDoE approach accounting for model mismatch would allow developing a much safer and more effective strategy for the parametric identification of detailed glucose–insulin models. This article is concerned with the development of such an approach.

Recent advances in MBDoE techniques have addressed two important issues. On the one hand, adaptive optimal input design [34] and online model-based redesign of experiments (OMBRE) [16] have provided a way to exploit in real time the information acquired during an experimental trial. This can be done through intermediate parameter estimation sessions, which in turn allow updating the optimally designed experimental conditions whilst the experiment is still running. In this way, the uncertainty on the model parameters can be reduced progressively, thus implicitly reducing the risk of constraint violation during the execution of the experiment. From a different perspective, MBDoE techniques that ensure experiment optimality as well as feasibility by design have been proposed [18]. These techniques use the concept of backoff from the nominal constraints, which is used in the experiment design session to keep the system within a feasible region with specified probability, regardless of the initial uncertainty on the model parameters or the accuracy of model structure itself. Therefore, in backoff-based MBDoE, the issue of constraint violation during the execution of an experiment is addressed explicitly (rather than implicitly).

In this simulation article, the integrated use of OMBRE and backoff-based MBDoE is proposed to tackle the issue of model mismatch in the optimal design of clinical tests for single-individual parameter identification of detailed models of type 1 diabetes. Model mismatch is deliberately introduced using two distinct, structurally different, state-of-the-art maximal models of glucose homeostasis: a detailed model [9, 10] for simulating the subject behaviour (this model will be referred to as the “simulated subject”) and another detailed model [21, 22] (which will be referred to as the “model”) for MBDoE identification. An identification test is designed first using the “model” (with some initial estimate of its parameters) by means of advanced MBDoE techniques; then, the designed test is executed on the “simulated subject” to obtain the “experimental” data for improved parameter identification so as to tailor the “model” to the “simulated subject”.

After a short description of the glucose homeostasis models used in this study, some background material on the standard and advanced MBDoE techniques exploited in this study is provided. Then, the general procedure to design a clinical test using MBDoE techniques is illustrated, and the performance of three different experiment design strategies (standard MBDoE, OMBRE and OMBRE including backoff) is compared and discussed. Some final remarks on the results conclude the article.

2 Methods

2.1 Glucose homeostasis models

A detailed model of glucose homeostasis may be viewed as a multiple-input single-output system described by a system of DAEs where the measured output is the glucose concentration and the manipulated inputs are the amount of carbohydrates in the meal(s) and the subcutaneous insulin infusion rate.

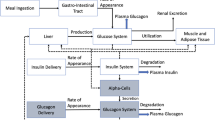
The meal ingestion and the insulin infusion are modelled by a glucose absorption submodel (providing the rate of appearance of glucose in plasma, R a) and an insulin infusion submodel (providing the rate of appearance of insulin in plasma, R i). The connections between functional blocks for a model of glucose homeostasis are shown in Fig. 1. The relationships between the glucose/insulin system, the endogenous glucose production (EGP), and the glucose utilisation and elimination define the metabolic portrait of the individual and are inherently related to the mathematical structure of a specific model and the set of its parameters. Several submodels have been proposed to define the rate of appearance of glucose in plasma (e.g. [8]) and the kinetics of subcutaneous insulin absorption (e.g. [28, 36]).

Fig. 1
figure 1

Relationships between functional blocks for a generic model of glucose homeostasis. The insulin infusion submodel and the glucose absorption submodel are evidenced with dashed boxes

Full size image

To mimic a subject affected by type 1 diabetes mellitus, the model developed by Cobelli and coworkers (here denoted as Cobelli Model, CM) is adopted as the simulated subject, as done in several simulation [9] and control [24, 26] studies. In this model, the subcutaneous insulin infusion is represented by a variation of a model described in [25]. As discussed in [24], CM served as the foundation for a model and simulation environment approximating the human glucose/insulin utilisation which was recently accepted by FDA [23]. Accordingly, it has been chosen as a representative in silico subject to be used in initial tests for the assessment of the approach proposed here.

The model developed by Hovorka et al. [21] (denoted as Hovorka model, HM), with the same insulin infusion submodel as CM, is used as the model to be identified. Although HM is known to suffer from some drawbacks [12], it has been applied in several in silico experimentations [11, 22, 27, 31] and has been shown to be identifiable when a proper reparameterisation is realised [17]. Accordingly, it has been chosen as a suitable identification model candidate to assess the performance of MBDoE techniques. Details about these models can be found in the original references. In general, it is expected that the model mismatch between CM and HM will result in a structural difference ɛ MM(t) between the simulated subject’s actual response and the identified model predicted response. It is stressed that it is not the purpose of this article to endorse one model or another, but rather (acknowledging that all models are approximations to reality) to test the effect of mismatch and ways to cope with it.

The glucose response of the simulated subject refers to a 56-year-old male subject with a body weight of 78 kg, affected by type 1 diabetes. The goal of the study is to identify in a statistically sound way the parameters defining the identification model (described by HM), by carrying out on the simulated subject (described by CM) a clinical test designed using standard and advanced MBDoE techniques.

2.2 MBDoE techniques for the identification of physiological models

This section presents a quick overview of standard and advanced MBDoE techniques suitable for the design of a clinical test for physiological models identification.

2.2.1 Standard MBDoE

Standard model-based experiment design procedures aim at decreasing the model parameter uncertainty region predicted a priori by the model by acting on the experiment design vector \( {\varvec\upvarphi} \in \Re^{{n_{\phi } }} \) and solving the following set of equations

$${\varvec \upvarphi}^{\text{opt}} = \arg \mathop {\min }\limits_{\varvec\upvarphi } \left\{ {\psi \left[ {{\mathbf{V}}_{\theta } \left( {\varvec\uptheta ,\varvec\upvarphi } \right)} \right]} \right\} = \arg \mathop {\min }\limits_{\varvec\upvarphi } \left\{ {\psi \left[ {{\mathbf{H}}_{\theta }^{ - 1} \left( {\varvec\uptheta ,\varvec\upvarphi } \right)} \right]} \right\} $$
(1)

subject to

$$ {\mathbf{f}}\left( {{\dot{\mathbf{x}}}\left( t \right),{\mathbf{x}}\left( t \right),{\mathbf{u}}\left( t \right),{\mathbf{w}},{\varvec\uptheta} ,t} \right) = 0 $$
(2)
$$ {\hat{\mathbf{y}}}\left( t \right) = {\mathbf{g}}\left( {{\mathbf{x}}\left( t \right)} \right) $$
$$ \user2 {\text {C}} = {\mathbf{x}}\left( t \right) - {\varvec\Upgamma} \left( t \right) \le 0 $$
(3)

with the set of initial conditions x(0) = x 0. In these equations, V θ and H θ are the variance–covariance matrix of model parameters and the dynamic information matrix, respectively; \( {\mathbf{x}}(t) \in \Re^{{N_{x} }} \) is the vector of time-dependent state variables, \( {\mathbf{u}}(t) \in \Re^{{N_{u} }} \) and \( {\mathbf{w}} \in \Re^{{N_{w} }} \) are the time-dependent and time-invariant control variables (manipulated inputs), \( {\varvec\uptheta} \in \Re^{{N_{\theta } }} \) is the set of unknown model parameters to be estimated and t is time. The symbol ^ is used to indicate the estimate of a variable (or a set of variables): thus, \( {\mathbf{y}}(t) \in \Re^{{N_{y} }} \) is the vector of measured values of the outputs, whilst \(\user2{ \hat{y}}(t) \in \Re^{{N_{y} }} \) is the vector of the corresponding values estimated by the model. C is an N c-dimensional set of constraint functions expressed through the set \( {\varvec\Upgamma} \left( t \right) \in \Re^{{N_{\text{c}} }} \) of (possibly time-varying) constraints on the state variables. In this study, vector \(\varvec\uptheta\) in HM comprises five parameters [17], representing the insulin sensitivity of distribution/transport (S fIT ), the insulin sensitivity of disposal (S fID ), the insulin sensitivity of EGP (S fIE ), the EGP extrapolated to zero insulin concentration (EGP0) and the non-insulin dependent flux (F 01).

The design vector

$$ {\varvec\upvarphi} = \left\{ {{\mathbf{y}}_{0} ,{\mathbf{u}}(t),{\mathbf{w}},{\mathbf{t}}^{\text{sp}} ,\tau } \right\} $$
(4)

includes the N y -dimensional set of initial conditions of the measured variables (y 0), the manipulated input variables, the duration of the single experiment (τ) and the N sp-set of time instants at which the output variables are sampled t sp = \( \left[ {\begin{array}{*{20}c} {t_{1} } & \ldots & {t_{{N_{\text{sp}} }} } \\ \end{array} } \right]^{T} \).

Function ψ in Eq. (1) is an assigned measurement function of the variance–covariance matrix of model parameters, and represents the design criterion. Different design criteria have been proposed in the literature, such as the D-, A-, E-optimal criteria, considering the determinant, the trace and the maximum eigenvalue of V θ , respectively [33], or, more recently, the SV-based [15] or P-based [37] ones.

In the case under investigation, the design vector is

$$ {\varvec\upvarphi} = \left\{ {u(t),{\mathbf{w}},{\mathbf{t}}^{\text{sp}} } \right\} $$
(5)

where the time-dependent manipulated input u(t) is the insulin subcutaneous infusion, whilst the glucose intake and the subcutaneous bolus administration are comprised within the time-invariant control vector w. To facilitate the dynamic optimisation task [35], the manipulated input u(t) is approximated with a piecewise constant function (defined by n z levels and n sw switching times to be optimised). There is only one measurable output y(t), which is constituted by the blood glucose concentration G. The blood sampling schedule is a design variable itself and is expressed through the vector t sp of sampling times. Recent sampling techniques, such as continuous glucose monitoring systems (CGMSs), could enrich the information content of the glucose test. Although CGMSs represent a promising technique [20], a traditional discrete sampling followed by an off-line analysis is assumed in this study.

The set of constraints on the state variables given by Eq. (3) aims at retaining normoglycaemia:

$$ C_{1} = y\left( {{\varvec\uptheta} ,{\varvec\upvarphi} ,t} \right) - {\Gamma}_{1} \le 0\quad {\text{and}}\quad C_{2} = {\Gamma}_{2} - y\left( {{\varvec\uptheta} ,{\varvec\upvarphi} ,t} \right) \le 0 $$
(6)

so that the blood glucose concentration is kept within an assigned range. A standard MBDoE procedure involves a sequential interaction between three key activities:

  1. 1.

    design of the clinical test;

  2. 2.

    execution of the test;

  3. 3.

    estimation of the parameters.

The procedure starts with the design of the first experiment, given an initial guess of parameters (say \(\varvec\uptheta\)) and related statistics, and the (expected) features of the measurement noise of the glucose sensor. The identification test is then executed using the designed experimental settings. Finally, the information within the set of acquired experimental data is extracted through a parameter estimation step. The procedure 1–3 can be iterated until sufficiently precise parameter estimation is reached.

2.2.2 Online model-based redesign of a clinical test

OMBRE exploits intermediate parameter estimation sessions to narrow the confidence interval of the estimated model parameters, and to partially redesign the clinical test whilst it is being executed. This implicitly makes the test safer and more informative. Different OMBRE configurations can be exploited depending on the online updating policy [16]. In this study, we consider the following updating rationale: the test is divided into a number of equally lasting sub-tests and within each sub-test the manipulated input is discretised with the same number of switching times and switching levels. Furthermore, the same number of blood samples is taken within each sub-test. An update of the design variables is scheduled at the end of each sub-test, when a parameter estimation session and a sub-test redesign are carried out in sequence. Each sub-test redesign is carried out by solving the optimisation problem given by Eqs. (1)–(3). Note that the complexity of the design optimisation problem is greatly reduced with respect to standard MBDoE (the predicted information is maximised within the single sub-test, which is a fraction of the complete test), with great benefit on the overall computational burden. On the other hand, too frequent an update may lead to suboptimal solutions and even to issues in the convergence of the successive online updating scheme (see also [16]).

2.2.3 MBDoE with backoff

In an OMBRE approach, an experimental test can be adjusted as soon as experimental evidence about the system being modelled becomes available. Although in a clinical setting this can implicitly reduce the risk of unsafe or uninformative experimental conditions, it should be remarked that the model mismatch is not dealt with explicitly by OMBRE. In the process systems design area, the problem of constrained optimisation under uncertainty, seen as a trade-off between feasibility and optimality, has long been recognised as a key issue. As discussed by Chachuat et al. [5], when model uncertainty is present, feasibility is often of greater importance than optimality. Following a recently proposed approach [18], to avoid unfeasible solutions by design, a backoff from active constraints can be introduced within a standard MBDoE framework. In this study, the only variable being constrained is the glucose concentration, and the MBDoE optimisation problem with backoff is the solution of Eqs. (1), (2) with the feasibility conditions

$$ C_{1} = y\left( {\varvec{\uptheta},{\varvec\upvarphi} ,t} \right) + \beta \left( t \right) - \Gamma_{1} \le 0\quad {\text{and}}\quad C_{2} = \Gamma_{2} - y\left( {\varvec{\uptheta},{\varvec\upvarphi} ,t} \right) + \beta \left( t \right) \le 0. $$
(7)

Thus, the backoff strategy allows the designer to enforce or relax the active constraints to meet the safety requirements when the test is performed on the subject. More details on the method and the procedure to define the backoff can be found in Ref. [18].

In this study, backoff-based MBDoE is integrated within OMBRE to provide inherent effectiveness and safety to an experiment designed under model mismatch. Accordingly, after each OMBRE sub-test is performed, a parameter estimation session and a sub-test redesign are carried out in sequence, updating both the uncertainty domain of model parameters (necessary to describe a new backoff) and the optimal experimental conditions (in order to maximise the information content within the subsequent sub-test).

Note that when a model mismatch is present, to preserve feasibility during the execution of the planned test the conditions given by Eq. (7) on constrained variables should be modified including the bias term ε MM. Although ε MM cannot be explicitly evaluated (the subject model is obviously unknown), it can be bracketed within a backoff formulation of the active constraints:

$$ C_{1} = y\left( {\varvec{\uptheta},{\varvec\upvarphi} ,t} \right) + \beta^{\prime}\left( t \right) - \Gamma_{1} \le 0\quad {\text{and}}\quad C_{2} = \Gamma_{2} - y\left( {\varvec{\uptheta},\varvec\upvarphi ,t} \right) + \beta^{\prime}\left( t \right) \le 0 $$
(8)

where \( \beta^{\prime}\left( t \right) = \beta \left( t \right) + \varepsilon^{MM} \left( t \right) \) is a generalised backoff term that takes into account both model mismatch (through ε MM) and parameter mismatch (through β, which is a function of the expected uncertainty domain of model parameters).

For the representation of the bias term ε MM, a conservative approach (adopted in this study) is to assume a fixed value for ε MM, representing the maximum expected difference between the model and the subject’s responses due to a model mismatch. If prior knowledge and/or preliminary data are available about the subject’s behaviour, then more sophisticated approaches can be used including bias modelling [19].

2.3 Implementing an MBDoE strategy

Three MBDoE strategies will be considered in the Results section: standard MBDoE, OMBRE and OMBRE with an embedded backoff policy (OMBRE-B). The goal of a designed test is to enable a statistically sound estimation of the model parameters when a single day-long test is performed on the subject. The identification test plans the amount of carbohydrates ingested during breakfast, lunch and dinner; schedules the blood glucose measurements concentrations; and fully manages the multiple insulin boluses and insulin infusion (in terms of amount/rates and scheduling).

The insulin infusion rate u(t) (mU/min) is expressed as

$$ u\left( t \right) = u_{\text{bas}} + u_{S} \left( t \right) + \delta \left( t \right)u_{\text{bol}} $$
(9)

where u bas is the basal insulin infusion rate (u bas = 12.9 mU/min), u S (t) is the time-dependent rate of subcutaneous infusion of insulin (approximated with a piecewise constant discrete function), whilst the last term is the subcutaneous bolus administration with the time-invariant bolus amount u bol (mU) released at meal time and modelled through a Dirac impulse δ(t). The amount of each subcutaneous insulin bolus is adjusted according to the following empirical rule:

$$ u_{\text{bol}} = \alpha kD_{g} $$
(10)

where α = 52.63 mU/gCHO is an approximated value for the optimal insulin/CHO ratio and D g is the amount of carbohydrates of a meal [gCHO]. The amount of the bolus is optimised by varying the relaxing factor k during the MBDoE procedure [17].

It is assumed that the design must fulfil the following constraints:

  1. 1.

    interior constraints on the glycaemic curve (the upper and lower bounds are Γ 1 = 60 mg/dl and Γ 2 = 180 mg/dl at all times);

  2. 2.

    end point constraints on the glycaemic curve—i.e. at the end of the test the glucose concentration must be within a narrower range (100–140 mg/dl).

Finally, it is assumed that blood glucose concentration measurements are available with a constant relative variance of 0.03 from the reading and a minimum time distance between two consecutive samples of 2 min. Here, the measurements errors are assumed to be Gaussian and uncorrelated, which, in general, may be a rough approximation. A correct description of the measurement errors would depend on the sensor system; however, assuming that the errors be uncorrelated [4] is a rather widely adopted simplification, even for CGMSs [6].

A type 1 diabetic subject is expected to have a higher (vs. normal) basal glucose concentration. For example, at the beginning of the test the blood glucose concentration might be close to the upper hyperglycaemic threshold (G = 175 mg/dl). Therefore, in this case an immediate insulin infusion treatment would be required to keep the subject in the feasible glycaemic range.

Taking all of the above issues into account, a day-long test is articulated into three phases: (i) an overnight preliminary phase, in which the subject’s glycaemia is normalised at around 140 mg/dl from midnight until 8:00 AM (during this phase a sample is collected every hour); (ii) a phase (phase 1) lasting 10 h and comprising two meals (at 8:00 AM and at 1:00 PM); (iii) a subsequent phase (phase 2) lasting 6 h with one meal at 6:00 PM. A parameter estimation session is carried out at the end of each phase in every design configuration (standard MBDoE; OMBRE; OMBRE-B). During the preliminary phase, the insulin infusion rate is kept constant, and at the end of the phase a parameter estimation is carried out to achieve an initial rough estimate of the model parameters. Therefore, the preliminary phase will be the same for all design configurations. On the other hand, in phase 1 and 2, the profile of the insulin infusion rate is optimised by design. The details of the experiment procedure are summarised in Table 1.

Table 1 Clinical test scheduling and design variables distribution for parameter identification
Full size table

The MBDoE optimisation is carried out with simple bounds on design variables using the gPROMS® [32] modelling environment and an SRQPD optimisation solver to solve the nonlinear optimisation problem, adopting a two-step multiple shooting technique [3] to mitigate the risk of incurring into local minima. In the first step, the design problem is solved by maximizing the trace of the dynamic information matrix; in the second step, the elements of the optimal design vector obtained in the first step are randomised providing new initial points for the following multiple shooting optimisation. The benefit in terms of convergence of such an approach is that, unlike direct optimisation methods, in the first step an approximate solution to the design problem is always found avoiding singularity points for the dynamic information matrix (since no matrix inversion is involved) and facilitating the detection of the optimum in the second step of the design procedure. Notwithstanding this, the approach cannot ensure that a global optimum is always found. This is still an open question, and its solution is beyond the scope of this study.

In all design configurations, the selected design criterion is the D-optimal one, which minimises the determinant of the variance–covariance matrix of model parameters.

2.3.1 Estimation procedure and quality of the estimates

Both the design step and the estimation step are deeply influenced by the choice of the model parameterisation. For numerical robustness, a normalisation procedure is carried out by dividing each parameter by a normalising factor, whose value is found in the literature (Table 2). The set of normalised parameters is indicated by symbol Θ. As discussed in Ref. [17], only four parameters are identifiable (Θ 1, Θ 2, Θ 3 and the ratio Θ 4/Θ 5). However, in order to increase the HM flexibility and to explicitly include the effect of the renal clearance (related to Θ 5) on the glucose response, a two-step maximum likelihood parameter estimation procedure is carried out. First, maximum likelihood estimation is performed on the parametric set Θ T1–4 , whilst Θ 5 is kept fixed. Then, only Θ 5 is estimated whilst keeping Θ 1–4 fixed (the objective is to provide a meaningful estimate for Θ 5, consistent with the simulated subject’s renal clearance). The procedure is iterated until the maximum likelihood condition is satisfied. Note that a poor estimate of Θ 5 represents the impossibility to obtain the ratio Θ 4/Θ 5 in a statistically sound way.

Table 2 Parameterisation of HM, initial guess of model parameters and normalising factors
Full size table

Given the assumptions on the distribution of measurements errors, the maximum likelihood approach provides a set of a posteriori statistics, calculated from the variance–covariance matrix of model parameters (V θ ), which may be used to evaluate the quality of the estimates. Thus, the effectiveness of an MBDoE strategy can be assessed in the usual way in terms of confidence intervals analysis and t-test on the identified parameters. The t-values are calculated from the formula

$$ t_{i} = {\frac{{\Theta_{i} }}{{\kappa_{i} }}}\quad i = 1 \ldots N_{\theta } $$
(11)

where the κ i are the 95% confidence intervals and compared with a tabulated reference t-value from the Student’s t distribution with N sp − N θ degrees of freedom.

3 Results

3.1 Preliminary parameter estimation

During the overnight fast (preliminary phase of the test), it is supposed that the subject is kept under a continuous insulin infusion of u = 6.4 mU/min to normalise his/her glycaemia. Glycaemic levels are checked every hour and at the end of this phase parameter estimation is performed to obtain preliminary parameter estimates (Table 3). After the preliminary phase only rough parameter estimates are achieved, as may be noticed from the a posteriori statistics. However, it may be observed from Fig. 2a that the fit of the model to the simulated subject response data is satisfactory (as was verified through a χ 2-test), and the residuals are randomly distributed (Fig. 2b).

Table 3 Parameter estimation after the preliminary phase
Full size table
Fig. 2
figure 2

Dynamics of the blood glucose concentration during an overnight fast. a Glucose response of the simulated subject (diamonds) and as predicted by the model after preliminary identification (solid line). The bars on the collected samples represent the maximum error on the blood glucose measurements. b Distribution of the residuals where the ±10 mg/dl range is identified by dotted lines

Full size image

3.2 Clinical test design using standard MBDoE

The results of a standard MBDoE approach for the design of phase 1 and 2 of the test are discussed in this section. The two designed experiments for these phases will be denoted as STD1 and STD2, respectively.

The optimised CHO content of the three meals administered to the simulated subject during the whole test is D T g  = [17.9 30.5 5.0] [gCHO], and the insulin bolus is u Tbol  = [10.4 11.3 359.5] (mU). Figure 3a shows the profile of the optimal insulin infusion rate, whereas Fig. 3b shows three glucose concentration trends: the profile predicted by the model during the design of the experiment (i.e. before the parameters are identified, broken line), the actual measurements taken on the simulated subject at the designed time instants during the execution of the experiment (diamonds), and the profile predicted by the model after the parameters have been identified (i.e. after the execution of the experiment, solid line). The great uncertainty on the parameters estimated during the preliminary phase, coupled to model mismatch, make the actual glucose measurements during STD1 differ very markedly from the expected profile, to a point that the actual blood glucose level violates the hyperglycaemic constraint. Note that the upper constraint on glycaemia is treated here as a hard constraint but, generally speaking, only hypoglycaemic conditions represent a hard constraint that must never be violated. Also note that at t ≈ 13 h, the predicted glucose concentration profile gets very close to the hypoglycaemic threshold. When this experiment is executed, the actual response happens to be substantially above this threshold. However, with such a large uncertainty in response due to the presence of parameter and model mismatch, in practice it would be extremely risky to implement the designed experiment on a type 1 subject without accepting the possibility of a hypoglycaemic episode during the test execution.

Fig. 3
figure 3

Standard MBDoE. a Optimised profile of insulin infusion rate. b Profiles predicted by a standard design (broken line) and after identification (solid line); the simulated subject actual response is indicated by diamonds. The bars on the collected samples represent the maximum error on the blood glucose measurements

Full size image

Table 4 shows that at the end of STD1, the parameter estimation is not statistically satisfactory (four out of five estimated parameters fail the t-test). However, the parameters estimated after the conclusion of STD1 are sufficiently precise to make the expected glucose concentration profile somewhat closer to the actual measurements during STD2 (Fig. 3b). Although experiment STD2 provides a source of additional information for the subsequent parameter estimation, after the execution of STD2 two parameters are still poorly estimated (Table 5).

Table 4 Standard MBDoE: parameter estimation after STD1
Full size table
Table 5 Standard MBDoE: parameter estimation after STD2
Full size table

Figure 4 shows the distribution of residuals during the entire experiment. It can be seen that during STD1 and STD2, the absolute residuals are neither independent nor randomly distributed (they are following a deterministic behaviour driven by ε MM) because of model mismatch.

Fig. 4
figure 4

Standard MBDoE: distribution of residuals (black squares) along the experimental horizon

Full size image

3.3 Clinical test design using OMBRE and backoff-based MBDoE

The results of two advanced methods for the design of phase 1 and 2 of the test are discussed in this section. One approach is based on OMBRE alone, whereas the other one integrates OMBRE with a backoff-based MBDoE. Therefore, in both cases an online redesign policy is exploited to update the designed experimental conditions as the test is running, next to an intermediate parameter estimation session.

A schematic of the time scheduling of the experiment design updates and of the intermediate parameter estimation sessions is shown in Fig. 5. Phase 1 and 2 can be regarded as a sequence of eight (5 + 3) separately designed sub-tests lasting 2 h each. During each sub-test, five blood samples are taken (at optimally designed instants), and the insulin infusion profile is optimised by acting on three switching levels (hence two switching times).

Fig. 5
figure 5

Time scheduling for design updates and parameter estimations in the redesign strategies

Full size image

The two redesign configurations considered in the following will be denoted by OMBRE (no backoff from the constraints) and OMBRE-B (OMBRE with integrated backoff from the constraints).

3.3.1 OMBRE without backoff

Figure 6a shows the optimal insulin infusion profile for the OMBRE approach. The profiles of the glucose concentration before and after the identification of the model parameters are shown in Fig. 6b along with the actual glucose concentration measurements. It is apparent that, thanks to the intermediate parameter estimations and the subsequent sub-test redesigns, the predicted glucose concentration (broken line) is much closer to the actual measurements (diamonds) during almost the entire test. Only at the beginning of phase 1 (8 h ≤ t ≤ 10 h) the predicted glucose concentration profile is somewhat different from the actual one; however, soon after the first redesign (t ≥ 10 h), the difference gets smaller, and becomes very small during the whole phase 2 (t ≥ 18 h). The fact that the expected glucose concentration profile matches more closely the actual one implicitly indicates that the risk for hypo- and hyperglycaemic episodes is much smaller than in a standard MBDoE test design. For example, although at t ≈ 13 h the predicted glucose concentration approaches the hypoglycaemic threshold, the parameter uncertainty at this time instant is much smaller than that of an experiment carried out on the basis of a standard MBDoE approach. Differently stated, the OMBRE approach can return a test that is implicitly safer than what a standard MBDoE approach can do.

Fig. 6
figure 6

OMBRE. a Optimised profile of insulin infusion rate and b profiles predicted by a redesign (broken line) and after identification (solid line); the simulated subject actual response is indicated by diamonds. The bars on the collected samples represent the maximum error on the blood glucose measurements

Full size image

To achieve this result, the optimal insulin infusion profile (Fig. 6a) is very different from the one obtained with the standard MBDoE approach. The optimal meal contents and insulin boluses are also different from those from the standard MBDoE method, being (respectively) D T g = [12.6 30.5 12.3] [gCHO] and u T b  = [66.3 1.4 0.2] (mU). Therefore, the redesign strategy dictates a lower bolus amount and a higher CHO content for the dinner.

The results for parameter estimation after phase 1 (t = 18 h) and at the end of the test are shown in Tables 6 and 7, respectively. After phase 1, the parameter estimation is fully satisfactory for three parameters (not that the final values may be very different from one because of model mismatch). Therefore, from a parameter estimation viewpoint, this 18-h OMBRE test is at least as satisfactory as the previous 24-h standard MBDoE test. The additional 6-h test (phase 2) results in a dramatic improvement in the estimation of parameter Θ 5. Therefore, not only is this OMBRE test safer than the standard MBDoE one, but it is also more informative. Note that at the end of phase 2 parameter, Θ 3 is still poorly estimated, but this has a limited impact on the variability of the predicted glucose response as shown in Fig. 7, where the effect of the uncertainty on Θ 3 is displayed. The incapability of estimating Θ 3 in a statistically satisfactory way is related to the effect of model mismatch, which makes a full match between the simulated subject and the model responses impossible. In fact, if only a parametric mismatch was presented, then the identification of Θ 3 would be feasible [17].

Table 6 OMBRE: parameter estimation after phase 1
Full size table
Table 7 OMBRE: parameter estimation after phase 2
Full size table
Fig. 7
figure 7

OMBRE: uncertainty on glucose concentration as predicted by the model for the estimated 95% confidence on Θ 3

Full size image

These results clearly show that, with respect to a test designed by a standard MBDoE approach, an OMBRE strategy can handle model mismatch much more effectively: the test is safer for the simulated subject and more informative from the parameter estimation point of view. However, safety (i.e. feasibility) of the test is obtained only indirectly, i.e. it comes as a result of reduced parameter uncertainty. Yet, parameter uncertainty (which in turn derives from model mismatch) is not explicitly accounted for in the design of the test, and therefore no a priori guarantee exists that hypo- or hyperglycaemia episodes are not encountered during the execution of the experiment. This is the reason why we propose to integrate an online redesign strategy like OMBRE with a technique ensuring by design the feasibility of an experiment under parametric uncertainty in the presence of model mismatch. This is addressed in the next section.

3.3.2 OMBRE with integrated backoff

To take model mismatch into account by design, a backoff strategy is integrated into the OMBRE procedure by means of the generalised backoff vector β′(t). The bias ε MM(t) in Eq. 8 is set assuming a deviation of 5% from the model predicted response (higher values will result in more conservative designs, i.e. with responses staying further away from the constraints). The formulation of backoff β(t) first requires a characterisation of the parameter uncertainty: the expected uncertainty region of the model parameters is represented by a multidimensional uncertainty domain T that needs describing according to some assumptions on the set of model parameters [16]. In this case, T is defined by a family of uniform distributions \( R_{{\Uptheta_{i} }} \) in the estimated values of model parameters, centred on the current values of model parameters, with a 30% deviation:

$$ \user2{T} = \left[ {\left. {\Theta_{ij}} \right|\Theta_{ij} \in R_{{\Theta_{i} }} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{i} - 0.3\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{i} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{i} + 0.3\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\Theta }_{i} } \right), i = 1 \ldots N_{\theta },\;j = 1 \ldots N^{\prime} } \right] $$
(12)

Then, it is necessary to map the uncertainty of the parameters onto the uncertainty region of the model responses. To this purpose, a large number N′ (here 200) of simulations are carried out at perturbed values of model parameters (sampled from the expected uncertainty region T). A subsequent statistical analysis of the N′ profiles of the state variables is used to provide a probabilistic description of the uncertainty region of each model response. Finally, β(t) is evaluated from a 95% confidence uncertainty region of model responses.

After phase 1 of the test, the uniform parameter distributions are adjusted according to the a posteriori variance–covariance matrix of model parameters V θ evaluated by the maximum likelihood estimator. This ensures that the backoff for phase 2 is adjusted according to the (usually increased) confidence in the predicted responses.

The results of the OMBRE-B approach are illustrated in Fig. 8. Namely, Fig. 8a shows the optimal insulin infusion profile; Fig. 8b shows the original profiles of the constraints on glucose concentration (horizontal dotted lines), the actual constraint profiles after application of the backoff (solid lines) and the glucose concentration profile as expected from the experiment design (dashed line); Fig. 8c shows the actual glucose concentration measurements obtained during the execution of the test (diamonds) and the predicted blood glucose response after the final parameter identification (solid line). Note that the backoff is updated after each new estimation of the parametric uncertainty, i.e. after each sub-test has been completed. After the preliminary 8 h, the backoff starts taking into account the parameter uncertainty and effectively constrains the designed test within the 80–165 mg/dl glucose concentration range (which is narrower than the 60–180 mg/dl range originally requested), thus ensuring by design the test feasibility. As a result, the actual glucose response (Fig. 8c) remains well clear of the hypo- and hyperglycaemic thresholds for the entire duration of the test.

Fig. 8
figure 8

OMBRE-B. a Optimised profile of insulin infusion rate and b profiles predicted by a redesign (broken line) including the backoff effect on constraints. c Profile predicted by the model after identification (solid line); the simulated subject actual response is indicated by diamonds. The bars on the collected samples represent the maximum error on the blood glucose measurements

Full size image

The excitation pattern, as well as the distribution of information along the test, is very different from those obtained by a simple OMBRE approach. The insulin bolus is u Tbol  = [4.6 1300.0 78.9] (mU), whilst the glucose amount of the three meals is D T g = [6.6 32.9 15.0] [gCHO]. Due to the narrower design space allowed, the parameter estimation after phase 1 of the test is not as good as the one provided by OMBRE (Table 8), with three parameters (instead of two) estimated with a large uncertainty. Although safer, the OMBRE-B phase 1 test is slightly less informative than the corresponding OMBRE phase 1. However, when phase 2 is carried out, the parameter estimation is substantially improved (Table 9) and is comparable to the one obtained by the OMBRE test.

Table 8 OMBRE-B: parameter estimation after phase 1
Full size table
Table 9 OMBRE-B: parameter estimation after phase 2
Full size table

It is worth stressing that in the OMBRE-B approach the parameter uncertainty is accounted for by design, and the designed test is inherently safer than in OMBRE. Therefore, the results indicate that, even if the backoffs may shrink the available experimental space, the possibility to update the design together with the intermediate parameter estimations allows decreasing the parameter uncertainty region, whilst providing the experiment with enough information for a statistically satisfactory estimation of the model parameters through a safe experiment. The drawback is that a significantly higher computational effort is needed (although this effort is concentrated mainly at the beginning of the test to map the uncertainty region and several techniques for dynamic stochastic optimisation have been proposed recently, e.g. [1]).

It is worth mentioning that a design with backoff (but without OMBRE) was assessed, too. However, when the available information was not exploited continually (like in OMBRE), the narrowing of the design space (which is inherent to the backoff strategy) made the clinical test safe, but less informative, i.e. the quality of the parameters estimation was (slightly) worse than the one obtained after a standard MBDoE.

3.3.3 Residuals analysis

The residuals distributions from OMBRE and OMBRE-B are compared in Fig. 9 and Table 10. Both distributions show a high autocorrelation between residuals, but OMBRE overall results in a better fit of the test data, providing absolute residuals all within a ±14 mg/dl interval. It should be noted that OMBRE provides a better prediction of the glucose concentration also because the insulin infusion profile has less drastic changes, avoiding significant releases of insulin in a short period, which keeps the test in a region where the model response differs less markedly from the simulated subject’s one. In fact, it may be observed in Fig. 9 that the model identified through OMBRE-B is not able to fit the data precisely when a large insulin bolus is administered (t ≈ 13 h).

Fig. 9
figure 9

Distribution of residuals (black squares). a OMBRE designed test and b OMBRE-B designed test

Full size image
Table 10 Statistics on distributions of absolute residuals for the OMBRE and OMBRE-B methods
Full size table

Although the residuals are neither independent nor normally distributed in both redesign strategies, the OMBRE-B distribution shows a greater mean (i.e. on average the simulated subject response is underestimated) and a higher dispersion around the mean value, when compared to the distribution obtained in the OMBRE approach with no backoff.

4 Discussion

Table 11 summarises the results and main inputs resulting from through the adoption of various strategies of MBDoEs for the identification of a detailed model of glucose homeostasis in type 1 diabetes when model mismatch is present.

Table 11 Summary of results and design inputs for different protocols for HM identification
Full size table

When a day-long identification test is designed through a model-based strategy, a standard MBDoE approach cannot ensure a feasible test, leading the simulated subject to a state of prolonged hyperglycaemia. In addition, after 18 h the test is still scarcely informative, and the parameter estimates are not statistically satisfactory.

The online redesign approach (OMBRE) is capable of planning an informative test, so that a statistically sound estimation of all but one (Θ 3 ) parameters is eventually obtained. After 18 h, the test is significantly more informative than one designed through standard MBDoE. Furthermore, due to the reduction of model parameter uncertainty, the test is also implicitly safer than the standard one. Yet, no guarantee exists (in a statistical sense) that the simulated subject response to the optimal insulin infusion profile will not cross the upper or lower glucose concentration limits. The amount of glucose delivered to the patient is 4% higher than in standard MBDoE, but even higher (+14%) is the insulin administration.

When a backoff from active constraints is realised and embedded within an OMBRE framework (OMBRE-B), the information is extracted in a slower way from the test with respect to the OMBRE approach, because the simulated subject’s glycaemic response is constrained to be within a narrower range. However, the test turns out to be safe by design and still sufficiently informative. Although the amount of glucose delivered to the patient is similar to standard MBDoE (+2%), a higher amount of insulin administration is designed (+20%). To conclude, OMBRE-B provides a very effective way to design a clinical test by combining test optimality and test feasibility through limited experimental effort. In effect, OMBRE-B can simultaneously exploit the potential of online redesign strategies to make a designed experiment more informative, as well as the potential of backoff strategies to make the experiment feasible by design.