1 Introduction

Hyperthermia has been widely used as a therapeutic procedure for cancer treatment due to its simple implementation, low cost, and reduced complication. Different techniques have been used in hyperthermia to generate thermal energy in malignant tumors, including microwave, radiofrequency induction, magnetic field, and ultrasound. The heat distribution induced by each method in the tumor has been extensively studied with both experimental and numerical methods [5, 7, 42]. D’Ambrosio and Dughiero performed a numerical study that predicts the power density and temperature distributions during RF-capacitive hyperthermia treatment [5]. Teixeira et al. presented a model for estimating the temperature profile in a special region of a glycerine reservoir submitted to ultrasound [42]. Dughiero and Corazza conducted FEM simulation to provide useful information on power distribution during hyperthermia under a pulsating magnetic field [7]. Recently, magnetic nanoparticle hyperthermia has attracted growing research interests in malignant tumor treatment. In this method, magnetic particles delivered to the tissue or blood vessels induce localized heating when exposed to an alternating magnetic field, leading to thermal damage to the tumor [8]. Magnetic nanoparticle hyperthermia is superior to traditional non-invasive heating approaches because it is able to generate sufficient heating in deep-seated/irregular shaped tumors without necessitating heat penetration through the skin surface, thus eliminating the consequent side effects of excessive collateral thermal damage. Iron oxides magnetite Fe3O4 and maghemite γ-Fe2O3 nanoparticles have been extensively used in this application [13, 21, 27]. Previous studies suggest that smaller particles (10–40 nm) are able to produce more heating in relatively low magnetic fields than larger ones, and thus are preferred in the hyperthermia application [18].

One technique for nanoparticle delivery in solid tumors is intratumoral infusion [12, 13, 24, 26]. After injection, the spatial distribution of the particles in tissue is a main factor that determines nanoparticle-induced heat generation distribution and temperature elevation [38]. However, understanding nanoparticle transport behavior during an injection process is very limited due to the difficulty of quantitative characterization of the nanoparticle concentration distribution in the tissue. Salloum et al. [37, 38] measured the Specific Absorption Rate (SAR) generated by ferrofluid injected in gels and in the hind limbs of rats subjected to an external magnetic field. The results show that the SAR distribution is not uniform, which suggests a heterogeneous nanoparticle distribution in gels/tissues [37, 38]. Also, the injection rate and injection volume were observed to have substantial influence on the SAR distributions. The relationship between the particle concentration distribution and the injection parameters, such as injection rate, injection volume, nanofluid concentration, nanoparticle properties, and porous structures, remains unclear.

A tumor with an irregular shape can be treated more efficiently with multiple-site injections to cover the entire target region. Salloum et al. [39] has proposed an optimization algorithm for multi-site injection to maximize the damage of a tumor while minimizing heating in the surrounding tissue. The optimized parameters in this algorithm are the Gaussian type SAR distributions at each injection site, which supposedly can be achieved by manipulation of the injection parameters. Thereby, the successful implementation of this method requires an in-depth understanding of the effects of the injection parameters on the SAR distribution and the mechanism of the nanoparticle transport and dispersion in biological tissues.

The delivery of large therapeutic agents such as antibodies and nucleotides by pressure-driven intratumoral infusion has been extensively studied in the past decade [2, 6, 16, 25, 47]. However, the existing theory is not readily applicable to nanoparticles because the small size of the particles results in strong surface interactions that could lead to particle deposition on the cell surface. The deposition is dependent on many factors including local fluid velocity, particle size, particle properties, surface properties and structure of the medium, and physicochemical properties of the aqueous environment.

The objective of the current study is to understand the effect of particle deposition on cellular structures and its impact on the nanoparticle penetration during an injection process. A multi-scale model is developed consisting of two components: (a) a particle trajectory tracking model that considers particle dynamics in aqueous solution and interactions of the particles with a spherical surface and (b) nanoparticle transport in porous media considering convection, diffusion, and surface deposition. The integration of the two components allows one to study the effect of particle deposition on the spatial distribution of nanoparticles under a variety of process conditions regarding infusion rate, concentration, injection volume, and velocity fields. Parametric studies are also performed to examine the effects of injection parameters and particle properties on the particle distribution.

2 Methods

2.1 Mathematical model

2.1.1 Nanofluid convection in porous tissues

During an injection of a nanofluid into gels or tissues, the flow pattern of the carrier solution is central to the transport and deposition behavior of nanoparticles. The injection process is inherently transient. The characteristic time for achieving a steady state can be estimated as τ = LU −1, where L is the characteristic length and U is the infusion velocity. Based on the typical operational parameters used in this study, τ is estimated to be in the range of 2–51 s, which is much shorter than the injection duration of 8 min to 4 h. Thereby, the injection process is approximated as steady state.

Both human tissues and gels have deformable porous structures whose elastic deformations affect the flow pattern [3, 26]. Since the central focus of this study is to examine the effect of particle deposition on particle transport, we assume the porous structure as homogenous and non-deformable. The fluid with a volumetric concentration of <5% is considered dilute fluid [48], where the presence of the particles does not significantly affect the transport properties of the fluid. The particle agglomeration on fluid transport is not considered in this study.

With these assumptions, the nanofluid flow in a porous medium during an injection process is modeled by using the continuity and Darcy’s equations which are regarded suitable for modeling fluid flow in tumors and tissues [19]:

$$ \begin{aligned} \nabla \cdot (\rho {\mathbf{u}}) & = 0 \\ \nabla P_{\text{f}} & = - {\frac{\mu }{K}}{\mathbf{u}}, \\ \end{aligned} $$
(1)

where ρ is the density of the nanofluid, u is the local volume average velocity vector, P f is the fluid pressure, μ and K are the fluid viscosity and the permeability of the porous medium, respectively.

2.1.2 Nanoparticle transport and deposition in tissues

The interactions of nanoparticles with a cell surface lead to nanoparticle deposition on the solid structure, which subsequently reduces the concentration of the nanoparticles in the fluid phase and affects the penetration depth of the nanoparticles in tissues. The transport of colloids through a saturated porous medium is often treated via the application of the classical Colloid Filtration Theory (CFT). In this theory, the convection and diffusion of colloidal particles are hypothesized analogous to molecular solutes; the retention of colloids by the solid structure is treated as a concentration-dependent reaction that consumes colloidal particles in the fluid phase [43]. The resulting colloid transport equation is a convective mass transfer equation with an additional source term representing the rate of particle deposition on the solid phase.

Stemming from the CFT, the equation for macromolecular transport in tissues is slightly modified to describe the convection, diffusion, and deposition of nanoparticles in tissues [28]. The original equation considers multiple mechanisms such as convection, diffusion, internalization of drugs by cells, and collection of macromolecules by circulation. In this study, the leakage of nanoparticles through a capillary wall and collection by circulation are neglected due to the short injection duration. The nanoparticles internalization is not considered because it does not affect the macroscale particle concentration profile. We also assume that the deposition is irreversible. The modified equation for nanoparticle transport in a porous tissue is

$$ {\frac{\partial C}{\partial t}} + \nabla \cdot ( \, {\mathbf{u}}C) = \nabla \cdot \left[ {D_{\text{e}} \nabla C} \right] - k_{\text{f}} C, $$
(2)

where C is the molar concentration of the particles in the fluid, the term k f C represents the volumetric deposition rate of the particles on the solid phase, and k f is the deposition rate coefficient of the particles. k f reflects the dependence of the volumetric deposition rate of the particles on particle size and properties, local velocity, porous structure, etc. The effective diffusivity D e of nanoparticles in tissues is calculated as [9]:

$$ D_{\text{e}} = D_{0} {\frac{L(\lambda )}{F\tau (\varepsilon )}},\quad {\text{and}}\quad D_{0} = {\frac{{k_{\text{B}} T}}{{3\pi \mu d_{\text{p}} }}}, $$
(3)

where D 0 is the diffusion coefficient in an unbounded liquid phase, k B is the Boltzmann’s constant, T is the absolute temperature, d p is the particle diameter, L(λ) is the factor responsible for hydrodynamic reduction of the diffusion coefficient in the pore, τ(ε) is the tortuosity which is the function of porosity ε, and F is a shape factor valued from one to four [33, 40]. The volumetric concentration of the nanoparticles attached to the solid structure S can be calculated by the equation:

$$ {\frac{\partial S}{\partial t}} = k_{\text{f}} C. $$
(4)

For a porous medium consisting of spherical bodies with a diameter of d c, the local deposition rate coefficient k f can be calculated using the unit cell collector efficiency ηs [43]

$$ k_{\text{f}} = {\frac{{3\left( {1 - \varepsilon } \right)}}{{2\varepsilon d_{\text{c}} }}}\eta_{\text{s}} \left| {\mathbf{u}} \right|, $$
(5)

where |u| is the magnitude of the local velocity calculated by Darcy’s equation, and ηs is the collector efficiency defined as the ratio of the particles captured by the solid surface to those brought into a unit structural cell of the porous medium. ηs measures the probability of particle interception by the solid structure. The collector efficiency ηs in the absence of the electrostatic double layer force is termed η0. In this study, ηs and η0 are acquired through a particle trajectory tracking model.

2.1.3 Particle trajectory tracking model

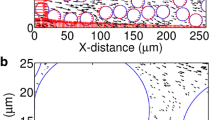
In the trajectory tracking analysis, the suspended particles are treated as individual entities. Given the particle properties, flow field, and the unit cell structure of a porous medium, the forces acting on these particles can be calculated to determine their trajectories. A deposit is counted when a particle is in contact with the solid surface [30]. In the theoretical study of flow and colloidal filtration in porous media, Happel’s sphere-in-cell model [11] is widely used as the unit structural cell of granular porous media [30, 32, 45]. Since tissues are typically conceptualized as porous structures consisting of nearly spherical cells in the study of drug delivery [3], Happel’s model was employed in the trajectory tracking analysis. As schematically shown in Fig. 1a, it consists of a solid spherical body representing a cell and a uniform layer of fluid that envelops the sphere. The thickness of the fluid layer is calculated as γ = d c[(1 − ε)−1/3 − 1]/2, where d c is the diameter of the solid sphere [30].

Fig. 1
figure 1

a Happel’s sphere-in-cell for the particle trajectory tracking analysis, b = ac(1 − ε)−1/3, where ε is porous porosity. Black dots refer to nanoparticles [30]; b forces acting on a particle traveling near a solid surface immersed in the fluid

Full size image

We assume that the particles are small (nanosized particles), spherical, chemically inert, solid, and very dilute in a liquid that flows at low Re number in the laminar regime. Hydrodynamic interactions among the particles are neglected. Typically the particles are properly coated to prevent agglomeration.

The forces that act on a particle near a solid surface immersed in the moving fluid are shown in Fig. 1b, including van der Waals attractive force, electrostatic double layer force, hydrodynamic drag force, lift force, buoyancy force, and Brownian motion. The van der Waals force and electrostatic double layer force act along the normal direction of a surface and only become significant at close separation distance between the particles and a surface. The lift force pushes particles away from the surface toward the direction of increasing velocity [17, 23]. A particle fully immersed in a fluid also experiences an upward buoyancy force. For a nanoparticle, buoyancy force is insignificant when compared with other forces due to its small size. Basset force which is important for a particle accelerated at a high rate is neglected due to the laminar flow conditions used in the current study [17]. Magus force is considered negligibly small when compared to the drag force because of the small particle size [17].

For submicron-sized colloids whose relaxation time is small, one could neglect the inertia force and assume that the particles relax to the fluid velocity instantaneously. The colloidal particle trajectory is then governed by the Stochastic Langevin equation [22, 30, 46]

$$ d{\mathbf{r}}_{j} = \left( {{\frac{D}{{k_{\text{B}} T}}}\sum\limits_{i} {{\mathbf{F}}_{i} } + {\mathbf{u}}_{\text{f}} } \right)\Updelta t + (\Updelta {\mathbf{r}})_{j}^{\text{B}} , $$
(6)

where d r j is the displacement vector of jth particle, D is the particle diffusivity, F i represents the forces acting on the particle, u f is the fluid velocity, and (Δr) B j is the random Brownian displacement. Δt is the time interval used in the integration.

The velocity expressions in a Happel’s sphere-in-cell shown in Fig. 1a are obtained directly from the stream function of Stokes flow in the Happel’s model. The azimuthal and radial velocities, respectively, are [11]

$$ \begin{array}{*{20}c} {v_{\text{f,r}} = - U_{\infty } \cos \theta \left( {{\frac{{K_{1} }}{{r*^{3} }}} + {\frac{{K_{2} }}{r*}} + K_{3} + K_{4} r*^{2} } \right),\quad {\text{and}}} \\ {v_{{{\text{f}},\theta }} = \frac{1}{2}U_{\infty } \sin \theta \left( { - {\frac{{K_{1} }}{{r*^{3} }}} + {\frac{{K_{2} }}{r*}} + 2K_{3} + 4K_{4} r*^{2} } \right),} \\ \end{array} $$
(7)

where K 1 = 1/w, K 2 = −(3 + 2p 5)/w, K 3 = (2 + 3p 5)/w, K 4 = −p 5/w, w = 2 − 3p + 3p 5 − 2p 6, p = (1 − ε)1/3, and r* = r/a c.

When a freely moving particle travels near a rigid surface, the extra viscous resistance exerted by the wall and the rotation of the particle can substantially modify both the velocity and mobility of the particle. This is referred to as hydrodynamic retardation. The correction factors used in this study are given in the Appendix A—Supplementary material.

2.1.3.1 Viscous lift force

Particles traveling across a velocity gradient caused by the presence of a wall can experience a lift force that directs a particle away from the wall. Saffman force is a well known lift force for inertial particles. However, it is insignificant for nanoparticles having a very small Stokes number [36]. It has been found that other factors such as the pressure difference across the particle and particle rotation can cause an appreciable lift force on a non-inertia particle [23]. Cox and Hsu derived the following expression to calculate the lift velocity for non-inertia spherical particles in a laminar parabolic flow field near a single vertical plane [4]:

$$ {\mathbf{u}}_{\text{lift}} = \frac{55}{144}{\frac{{\rho d_{\text{p}} u_{{{\text{f}},\max }}^{2} }}{2\mu }}\left( {{\frac{{d_{\text{p}} }}{{2h_{\max } }}}} \right)^{2} \left( {1 - {\frac{h}{{h_{\max } }}}} \right)\left( {1 - \frac{73}{22}{\frac{h}{{h_{\max } }}}} \right), $$
(8)

where h is the distance between the particle center and the wall, h max is the distance at which the velocity profile reaches its maximum u f,max. More details about the calculation of the lift force can be found in the reference [1]. Given the lift velocity u lift, the lift force can be obtained accordingly:

$$ {\mathbf{F}}_{\text{lift}} = 3\pi \mu d_{\text{p}} {\mathbf{u}}_{\text{lift}} . $$
(9)
2.1.3.2 van der Waals force and electrostatic double layer force

The potential for particle–surface interactions within the interaction range is calculated according to the Derjaguin, Landau, Verwey, and Overbeek (DLVO) theory [35]. The DLVO potential interaction forces can be derived through the differentiation of the potential interaction energies [14]

$$ {\mathbf{F}}_{\text{potential}} = - {\frac{\partial }{\partial h}}(A_{\text{elec}} + A_{\text{vdW}} ), $$
(10)

where A elec is the potential due to electrostatic interaction and A vdW is the potential due to van der Waals force between particles and a surface. Since the size of a nanoparticle is much smaller than that of a cell, their interactions can be approximated as those between a particle and a flat wall.

The van der Waals interaction energy between a sphere and a wall at a distance of h is expressed as [14]

$$ A_{\text{vdW}} = - A_{\text{H}} d_{\text{p}} /(12h), $$
(11)

where A H is the Hamaker constant, which can be calculated by an empirical formulation provided by the reference [35].

According to the Gouy–Chapmann model of a diffuse double layer and electrostatic Poisson–Boltzmann equation, A elec between a spherical particle and a flat surface with the zeta potentials of ψ1 and ψ2, respectively, is given by the following equation:

$$ A_{\text{elec}} = 64\pi \varepsilon_{\text{r}} \varepsilon_{0} \left( {{\frac{{k_{\text{B}} T}}{zE}}} \right)^{2} {\frac{{d_{\text{p}} }}{2}} \times \left[ {\tanh \left( {{\frac{{zE\psi_{1} }}{{4k_{\text{B}} T}}}} \right)\tanh \left( {{\frac{{zE\psi_{2} }}{{4k_{\text{B}} T}}}} \right)} \right]{\text{e}}^{ - \kappa h} , $$
(12)

where ε0 is the vacuum permittivity, εr is the relative dielectric constant of the water, E is the electron charge, and z is the valence of the electrolyte. The effect of the aqueous environment is reflected by the Debye–Hückel parameter κ.

2.1.3.3 Brownian motion

Brownian motion is formulated through Brownian displacement (Δr)B, a random value taken from a Gaussian white noise distribution with a zero mean W(t) and a specific intensity that relates to the Mean Square Displacement (MSD). Stokes–Einstein equation is used to calculate the MSD [14]:

$$ {\text{MSD}}^{2} (t) = \left\langle {\left( {\Updelta {\mathbf{r}}} \right)^{2} } \right\rangle = {\frac{{2k_{\text{B}} T}}{f}}\left| {\Updelta t} \right| = 2D\left| {\Updelta t} \right|,\quad f = 3\pi \mu d_{\text{p}} . $$
(13)

A freely moving particle may experience rotations near a solid surface. In the case of spheroid and ellipsoidal particles, the determination of the rotational velocity is essential because the interaction energy is dependent on the particle orientation. However, spherical particles are symmetric and hence are less likely to be affected by the particle rotation [46]. Therefore, the particle rotational velocities are neglected in the trajectory tracking analysis. The effect of particle rotation on the motion of a particle near a surface is considered through the lift force and corrections of the fluid velocity and particle mobility.

The particle trajectories are determined by integrating Eq. 6 using the predictor–corrector method [20]. At the beginning of a particle trajectory analysis, a large number of particles are distributed randomly over the curved segment extending from y = 0 to y = b as shown in Fig. 1a [34]. The vertical position of a particle is determined by

$$ y_{0} = \xi_{i} b, $$
(14)

where ξ i is a sequence of uniformly distributed random numbers in the range of zero to unit, and b is the radius of the fluid shell shown in Fig. 1a. Once its vertical position is determined, the x coordinate of an entering particle can be determined as

$$ x_{0} = - (b^{2} - y_{0}^{2} )^{1/2} . $$
(15)

A particle deposition is counted if the calculated trajectory of a particle reaches the solid surface. Through calculating the trajectories of a number of particles, the collector efficiency can be determined for various combinations of parameters such as particle size, surface properties, local fluid velocity, etc. Note that the number of particles used in the simulation should be sufficiently large to ensure that the collector efficiency is independent of the particle number and the result is statistically meaningful.

The time step Δt should be sufficiently small such that the deterministic forces remain constant during each time interval. Also, the assumption of negligible particle inertia requires that the time step should be much greater than the particle relaxation time τ p = m p f −1. Thus, the requirement of the time step may be written as τ p ≪ Δt ≪ τ u , where τ u is the time increment at which deterministic velocity is considered constant. This study used a Δt of 10−5 s.

The particle trajectory tracking model is verified by comparing our simulation results with the experimental data [44] and two existing correlations [32, 45] as shown in Figs. 2 and 3. Detailed information can be found in Appendix B—Supplementary material. To model the injection of nanoparticles in tissues, the particle transport and particle trajectory models are integrated through k f. Equation 1 is first solved to determine the velocity field of the fluid in the tissue. For a given set of operational parameters, the local deposition rate coefficient k f for different fluid velocities can be calculated using the particle trajectory tracking model. k f is then fed into Eqs. 2 and 4 to predict the particle concentration distributions.

Fig. 2
figure 2

The comparison of collector efficiency (η0) predicted by the simulation and experimental measurement for various particle sizes at various velocities

Full size image
Fig. 3
figure 3

The comparison of collector efficiency (η0) predicted by the simulation and correlations (RT and TE) at various velocities (d c = 20 μm, ε = 0.36, μ = 0.001 kg m−1 s−1, A H = 4 × 10−20 J, ρp = 1,060 kg m−3, ρf = 997 kg m−3)

Full size image

2.2 Simulation setup and numerical issues

The simulation of nanofluid injection in tissues is performed in a configuration shown in Fig. 4 consisting of a spherical domain with a diameter of 4 cm and a 26 gauge needle. The nanofluid and injection-related parameters were taken from the experimental study of Salloum et al. [37, 38].

Fig. 4
figure 4

Simulation configuration for nanofluid injection in tissues

Full size image

At the inlet of the needle, the boundary conditions are constant velocity and nanoparticle concentration. At the surrounding boundaries, ∂C/∂r = 0 is applied. Unless specified, the nanofluid is 3 vol% of Fe3O4 nanoparticles dispersed in DI water and the injection volume of the nanofluid is 0.3 cc. The infusion rates vary from 1.25 to 40 μl min−1 with the corresponding velocities in the range of 3.9 × 10−4 to 1.26 × 10−2 m s−1. A surface zeta potential of −20 mV was employed for a tumor cell in the simulation [10]. Important tissue and particle-related parameters used in the simulation are shown in Table 1. As available information on the surface properties of the magnetic nanoparticles is limited to a negative surface zeta potential, we used a surface potential ranging between 0 and −60 mV to examine the effect of surface potential on the particle deposition behavior.

Table 1 Main tissue parameters used in the study
Full size table

COMSOL Multiphysics 3.5a® software package was used to solve the equations that govern fluid flow and particle transport in porous media. Triangular elements were used in the simulation with fine elements near the injection site. Grid dependency study was performed to ensure that the final results are independent of the grid numbers. 22,792 elements were used in the simulation and doubling the number of the elements results in a <5% change in the velocity and concentration.

3 Results

3.1 Effect of injection volume

Previous experimental study [38] measured the magnetic nanoparticle-induced temperature elevation and its distribution in the hind limbs of rats. The SAR distributions in the form of Gaussian distribution were obtained through an inverse analysis, which is

$$ {\text{SAR}} = B{\text{e}}^{{ - r^{2} /R^{2} }} , $$
(16)

where r is the radial distance from the injection site, B and R are constants. Depicted in Fig. 5a are the variations of the SAR with distance from the injection site for the injection volumes of 0.1 and 0.2 cc. Given that the properties of the particles, tissue, and magnetic field were preset, the heating distribution is solely dependent on the distribution of nanoparticle concentration. Thereby, the SAR distribution can be viewed as an index of the nanoparticle concentration when quantitative information on the nanoparticle concentration is not available. Currently, it is not feasible to compare the simulation results with the experimental measurement quantitatively due to uncertainty in tissue properties and several unknown parameters such as surface potential and heating capacity of the nanoparticles. We attempted to make a qualitative comparison of the varying trends and nanoparticle-influenced area. The nanoparticle size of 10 nm and the injection rate of 10 μl min−1 used in the simulation were taken from the experimental study [38]. The surface charge of the nanoparticles is −30 mV. Figure 5b, c show the simulated nanoparticle concentration distributions with and without particle deposition on the surface, respectively. It is observed that convection and diffusion without deposition lead to a nearly uniform nanoparticle concentration in the vicinity of the injection site due to the low effective diffusivity of the nanoparticles in the extracellular space of tissues. With surface deposition being considered, the nanoparticle concentration varies similarly to that indicated by the SAR, decaying quickly with the distance from the injection site. Also, both the SAR and nanoparticle distribution show that increasing the injection volume can significantly elevate the number of particles confined near the injection site without causing appreciable difference in the penetration depth. The modeling results with surface deposition predict a nanoparticle-covered area the same order of those illustrated by the SAR. It is reasonable to conclude that nanoparticle deposition on the cellular structure plays an important role in the nanofluid injection process, and the modeling framework presented in this study captures the main features of the complex process of nanoparticle transport in tissues.

Fig. 5
figure 5

Distributions of a Specific Absorption Rate (SAR) [38]; b nanoparticle concentration with surface deposition (d p = 10 nm, ψp = −30 mV); and c nanoparticle concentration without surface deposition for various injection volumes

Full size image

Although the simulations are performed on rats, the relevant transport parameters of rats and human tissues fall into similar ranges [10, 31, 41, 50]. Therefore, we believe that the current study can be used to provide insight in future investigation of nanofluid transport in human tissues.

3.2 Effect of particle surface potentials

The collector efficiency ηs is a quantity that measures the probability of the particle deposition on the solid structure within a unit structural cell of a medium. Figure 6a shows that for given sizes of particles and cells, the collector efficiency decreases with the local fluid velocity. This can be explained by two reasons. First, a high velocity reduces the time needed for particles to pass a cell, hence reducing the chance of the particles to migrate to the cell surface. Also, a high fluid velocity creates a large velocity gradient on the surface, resulting in the particle rotation and lift force that direct a particle away from the surface. An interesting observation in Fig. 6a is that the deposition rate coefficient k f increases with the velocity. As indicated by Eq. 5, k f depends on the structural properties of the medium, local velocity, and collector efficiency. The local velocity determines the rate of the particles approaching a cell. While a high fluid velocity reduces the probability of a particle captured by the cell surface, it increases the number of the particles approaching the cell. For particles with zero surface potential, the latter dominates the particle deposition, leading to an elevated k f at the high local fluid velocity. On the other hand, for the particles with a negative surface charge, there exists a repulsive force as the tumor cell surface also has a negative zeta potential [10]. This repulsive electrostatic double layer force causes such a substantial decrease in ηs that leads to a reduced k f with increased velocity as shown in Fig. 6b. Note that doubling the particle surface potential leads to a reduction of k f by several orders of magnitude.

Fig. 6
figure 6

Variations of a deposition rate coefficient (k f) and collector efficiency (η0) with velocity (zero surface charge) and b deposition rate coefficient (k f) with velocity for negatively charged particle and cell surfaces (d p = 10 nm, d c = 15 μm)

Full size image

The distribution of nanofluid concentration in the fluid near the injection site is shown in Fig. 7a and the overall nanoparticle concentration distribution in the medium (S + C) right after an injection is depicted in Fig. 7b. While most particles with zero surface potential are observed to concentrate at the injection site, the charged particles demonstrate a penetration depth of several millimeters. It is also observed that that most particles have been deposited on the solid structure at the end of the injection.

Fig. 7
figure 7

a Distributions of nanoparticle concentration in fluid and b overall particle distributions for various particle surface charges (dp = 10 nm, dc = 15 μm)

Full size image

3.3 Effect of injection rate

Infusion rate is an important factor that not only determines the duration of an injection, but also affects the nanofluid distribution in gels/tissues [37]. Since particle deposition is closely related to fluid flow, we investigated the effects of the infusion rate on the deposition process. For particles that carry negative surface charge of −30 mV, increasing velocity reduces the deposition rate, and results in a wider spreading of nanoparticles in tissues as shown in Fig. 8a. However, a high infusion rate may cause an irregular nanoparticle distribution, or abnormal breakage of tumor tissues [47]. The infusion rate should be selected carefully to achieve desired particle distribution.

Fig. 8
figure 8

Overall nanoparticle concentration distributions in the medium for: a various injection rates and b for various nanofluid concentrations

Full size image

3.4 Effect of particle concentration

In addition to the infusion rate, the effect of the nanoparticle concentration on nanoparticle transport is also investigated. To ensure that the assumption of dilute nanofluid and negligible interactions among the particles are still valid, we simulate the nanoparticle distributions with three low volumetric concentrations: 1.5, 3, and 5%. The injection volumes are subsequently changed to 0.6, 0.3, and 0.18 cc, respectively, so that the amounts of nanoparticles delivered remain the same. Figure 8b shows the nanoparticle concentration profiles for 10 nm nanoparticles with a surface potential of −30 mV. The injection rate was 10 μl min−1. Note that the difference in the overall particle distributions is not obvious. This simulation suggests that further reduction of nanofluid concentration will not affect the nanoparticle distribution profile substantially if the nanofluid is already dilute. Shown in the same figure are the nanoparticle distributions resulted from the injection of nanofluid of 0.3 cc with three volumetric concentrations of 1.5, 3, and 5%. It is observed that a high volumetric concentration causes a high nanoparticle concentration near the injection site. However, increasing the volumetric concentration does not facilitate particle penetration into the tissue.

4 Discussion

In this study, we present a numerical investigation of nanoparticle transport in tissues involving depositions of nanoparticles on the cellular structure during an injection process. To the authors’ best knowledge, it is the first theoretical study that considers detailed colloidal interactions between nanoparticles and cellular structures in a convection process. The varying trends of nanoparticle distribution from the injection site and the predicted nanoparticle penetration depths agree qualitatively with those indicated by the SAR distributions obtained by an in vivo experiment. This renders the assumptions made in this study justified. It also suggests that the modeling framework presented in this study captures the main features of the complex process of nanoparticle transport in tissues. However, as the first stage of a systematical study of a highly complicated process, some simplifications are introduced in the modeling. For instance, the heterogeneous tissue structure and tissue deformation are not considered in the modeling of the fluid flow in tissues. The physicochemical theory underlying the calculation of collector efficiency applied to cells insofar as shares the general properties of all colloidal particles. However, the interaction of particles with the living cells is of course more complex than that of non-living, inert, smooth, and spherical bodies. In addition, the resistance of the extracellular structure to particle transport is only considered in the evaluation of the particle diffusivity. In fact, collagen fibers may also capture nanoparticles and thus hinder the transport of nanoparticles throughout tissues. Besides, the complex cellular structure renders the flow path tortuous and the random packing of the cells causes some volume fraction inaccessible to nanoparticles. It should also be noted that in the currently model, dilute nanofluid is employed and particle agglomeration is not considered. It is unclear to what extent the particle–particle interactions affect the particle transport, especially when highly concentrated nanofluids are employed.

While the current study shows the pronounced effect of particle deposition on particle distribution, neglecting these phenomena may cause an overestimated penetration depth of the nanoparticles. To include these phenomena into a model presents a formidable task; however, it is still feasible to add a correction factor to the deposition rate coefficient to address the above mentioned limitations. Our research plan for the next stage is to conduct in vivo studies on tumors implanted on mice. The SAR distributions can be obtained with different combinations of injection parameters, nanoparticle properties, and nanofluid concentrations. We anticipate that the interplay of the experimental study and theoretical modeling will allow one to better understand the nanoparticle transport mechanism and further improve the theoretical model.

The current study will continue by progressively adding further considerations such as heterogeneous porous structure, poroelastic deformation, and correction factors for the deposition rate coefficient to address the limitations of the current model. We anticipate that the model in its final form can be used to advance current understanding of the nanoparticle transport behavior with different injection-related parameters, particle properties, and types of tissues.

This study endeavors to develop a multi-scale theoretical model for the purpose of investigating nanoparticle transport in tissues during an injection process. The results demonstrate that for a dilute nanofluid, the deposition is dependent on particle surface properties and infusion rate, but relatively insensitive to nanofluid concentration. While increasing the injection volume changes the maximum nanoparticle concentration at the injection site, it does not affect the nanoparticle penetration depth appreciably.