INTRODUCTION

Intratumoral infusion provides a viable technique for drug and gene delivery in solid tumors, especially for large therapeutic agents such as antibodies, nucleotides, and nanoparticles. Large therapeutic agents hardly distribute throughout tissues via passive transport after systemic delivery because of the heterogeneous vasculature and blood supply, elevated interstitial fluid pressure (IFP), and transport barriers commonly found in solid tumors.14,15,20,37 Local delivery of large therapeutic agents based on polymeric devices is also hampered by cells and extracellular matrix.8,12,32 Therefore, intratumoral infusion is so far the best method available for distributing large therapeutic agents in tumors. The method allows therapeutic agents to bypass or overcome some of the obstacles, including the elevated IFP, by creating a hydrostatic pressure gradient for enhancing convective transport in tumors.4,5,9,14,18,19,34,35,41 Furthermore, direct infusion may reduce systemic toxicity because localized delivery can significantly decrease the plasma concentration of drugs.18 The infusion method can also be combined with surgery in cancer treatment. Preoperative drug infusion may reduce the size of tumors so that they can be removed more easily and less destructively. Postoperatively, intratumoral infusion may be used to deliver therapeutic agents to surrounding tissues to kill residue tumor cells that are missed during surgery.

The efficiency of drug delivery via intratumoral infusion depends largely upon transport parameters that are determined by interstitial structures and cell density as well as molecular properties of drugs.3,7,11,14,21,23,25,30 More specifically, the rate of fluid flow during the infusion depends on the hydraulic conductivity of tumor tissues. This parameter is a constant in rigid porous materials but a function of deformation in gels and tissues.2,13,17,19,27,36,40,41 During the intratumoral infusion, we have demonstrated that a four-fold increase in the infusion pressure can alter the hydraulic conductivity by several orders of magnitude.41 The mechanism of alteration is related to tissue deformation-induced changes in the size and connectedness of aqueous pathways.19,38,41 Tissue expansion may increase the size and improve the connectedness of the pathways, thereby reducing the resistance to both fluid and solute transport. Conversely, tissue compression may close and/or disconnect aqueous pathways and thus lead to a significant increase in the interstitial resistance to diffusion and convection. The extent of deformation depends upon mechanical properties of tissues, which in turn are functions of extracellular matrix (ECM) structures and cell density.24 In general, the extracellular matrix and cells can affect intratumoral infusion through both hindering transport and controlling mechanical deformation of tumors. To this end, we infused fluid into three types of tumors with different collagen concentrations and compared the flow rates in these tumors under the same infusion conditions. We observed that the infusion pressure must be higher than a threshold level in order to initiate the infusion in all tumors. In addition, there existed two distinct relationships between infusion rate and infusion pressure. In tumors with relatively low collagen concentrations, the flow rate was high and increased monotonically with the infusion pressure. In the tumor with relatively high collagen concentration, the flow rate was a bell-shaped function of the infusion pressure. To interpret the experimental data and understand mechanisms of fluid transport during the infusion, we developed a poroelastic model. The model predictions were consistent with the data, suggesting that both the existence of the threshold pressure and the nonlinear relationships between the flow rate and the infusion pressure could be due to infusion-induced tissue deformation that anisotropically affected the hydraulic conductivity of tumor tissues.

MATERIALS AND METHODS

Tumor Models

Three tumor cell lines were used in the study. B16.F10 was a murine melanoma, 4T1 was a murine mammary carcinoma, and U87 was a human glioma. These cell lines were maintained at 37°C with 95% air and 5% CO2 in DMEM supplemented with 10% fetal bovine serum, 1% penicillin, and 1% streptomycin. Cells were harvested from culture flasks with 0.25% trypsin/EDTA, and rinsed twice with sterile PBS. Suspensions of B16.F10, 4T1, and U87 cells (106 in 50 μl of PBS) were injected subcutaneously into the left hind limbs of female Balb/c, C57BL/6, and NCr-nu Athymic mice (4–6 weeks old, Charles River, Raleigh, NC, USA), respectively. During the tumor cell implantation, mice were anesthetized with intraperitoneal injection of ketamine/xylazine (80 mg and 9 mg, respectively, per kg body weight). Tumors were allowed to grow until they reached ∼1 cm in diameter, which typically took 8– 10 days for B16.F10 and 4T1 tumors and 3 weeks for U87 tumors. The animal protocol has been approved by the Duke University Institutional Animal Care & Use Committee.

Flow Rate and Hydraulic Conductivity During Intratumoral Infusion

Mice were anesthetized as described above. A solution of Evans blue-labeled albumin (EBA), prepared by mixing 0.04% Evans blue and 0.1% albumin in 0.9% saline, was infused into the center of the tumor via a 28 G needle connected to a reservoir of Evans blue-labeled albumin solution via a 0.52-mm diameter tubing. The infusion pressure (P inf) was defined by the height of the top of the reservoir relative to the needle tip. The initial pressure was ∼5 cmH2O, then the pressure was raised in 5-cmH2O increments until a bubble introduced into the tubing began to move. At this moment, the pressure minus 5-cmH2O was defined as the threshold pressure. Based on this definition, the uncertainty for the measured threshold pressure was less than 5 cmH2O (i.e., 3.7 mmHg) in all tumors. The flow rate (Q) was determined by measuring the velocity of the bubble.41 Periodic flow rate measurements were made throughout the infusion period to determine the time-dependence of the flow rate. The volume of infusion in all experimental groups was approximately 10 μl because this volume could be well contained within the tumor. The flow rate measured at the end of the infusion was reported in the Results section and also used to calculate the apparent hydraulic conductivity (K app) based on the Darcy’s law for unidirectional flow in an infinite region around a spherical fluid cavity: K app=Q/(4πa 0 P inf), where a 0 was the initial radius of fluid cavity that was approximately equal to the radius of the 28 G needle (0.18 mm). All measurements were repeated five times in different tumors.

After the infusion, we sacrificed the mice, removed the tumors, and then examined the distribution of EBA by cutting the tumor in half through the infusion site and visually inspecting the dyed region. If the distribution of EBA was not approximately spherical around the tip of the infusion needle, the sample was discarded for the following reasons. First, the method of analysis used in this study was invalid for non-spherical distributions caused by the presence of cracks and/or necrotic regions in tumors. Second, infusion into a necrotic region or macroscopic cracks encountered minimal resistance compared with that into a viable region of tumors. In this case, the infusion rate was too fast to be accurately measured in our experiments. Cracks and necrotic tissues are common features in large tumors.19 In this study, approximately half of the samples were discarded due to these problems.

Collagen Concentration in Tumors

The collagen concentration was measured using a method adopted from the literature.39,42 Small samples (∼100 mg) of tumors were incubated in a 1-ml papain digest buffer (125 μg/ml papain in 0.1 M sodium phosphate, 5 mM Na2EDTA, and 5 mM l-cysteine-HCL at pH 6.0) for 16–24 h in a 60°C water bath. 100 μl samples from each digest were hydrolyzed in 6 N HCl for 16–24 h at 115°C. The solutions were then cooled to the room temperature and 2 drops of methyl red indicator were added to tritrate the samples with 2.5 N NaOH followed by 0.5 N HCl, and finally 0.5 N NaOH until the samples were in a faint yellow color. Solutions were then diluted with distilled water to approximately 7 ml total volume. A hydroxyproline standard solution (10 mg of hydroxyproline in 100 ml distilled water) was diluted to concentrations of 0.5, 1, 2, 3, and 4 μg/ml, respectively, in separate tubes for generating a standard curve of hydroxyproline. 1 ml of each test sample and standard solution were mixed in glass tubes, at the room temperature, with 0.5 ml chloramine-T solution (0.705 g Chloramine-T, 40 ml of pH 6 buffer (17 g, sodium hydroxide, 25 g citric acid monohydrate, 60 g sodium acetate trihydrate, and 6 ml glacial acetic acid in 250 ml distilled water), and 5 ml isopropanol). 20 min later, 0.5 ml of pDAB solution (7.5 g p-Dimethylaminobenzaldehyde and 30 ml isopropanol) was added to all tubes while vortexing. All tubes were then incubated in a 60°C water bath for 20 min. The absorbencies of each sample and standard at 550 nm were then measured with a spectrophotometer. The amount of hydroxyproline in each sample was determined by using the standard curve. Hydroxyproline is unique to collagen and comprises ∼7% of its total weight. For each model, three tumors were prepared and three samples were collected from different regions in each tumor. Therefore, the experiment was repeated 9 times for each model and the mean ± standard deviation are reported in the Results section.

FIGURE 1.
figure 1

Schematic of intratumoral infusion of EBA solution. The block arrow indicates the flow of EBA solution from the reservoir into the infusion needle at a pressure P inf and flow rate Q. The arrows indicate solid displacement of tumor tissue u(r), fluid velocity v(r), or gradient of interstitial fluid pressure dP/dr in the radial direction at individual locations. The dashed arrow indicates the radial distance r from the center of fluid cavity.

Full size image

Mathematical Modeling of Intratumoral Infusion

The schematic of intratumoral infusion is shown in Fig. 1. We assumed that tumor tissue was a deformable porous material and that the deformation during the infusion was infinitesimal. Therefore, the poroelastic model could be used to simulate the intratumoral infusion. The details of the model have been described in the literature.33 In brief, the model assumes that the solid phase of the medium is a Hookian material, i.e., the stresses are linear functions of strains, and the momentum balances in both fluid and solid phases are governed by the generalized Biot’s law. During the infusion, the fluid flow in tumors was assumed to be spherically symmetric about the tip of the infusion needle and at the steady state. Based on these assumptions, the governing equations in spherical coordinates are

$$(2G + \lambda )\frac{d}{{dr}}\left( {\frac{{du}}{{dr}} + \frac{{2u}}{r}} \right) - \frac{{dP}}{{dr}} = 0$$
(1)
$$v = - K\frac{{dP}}{{dr}}$$
(2)

where P is the interstitial fluid pressure, u and v are the components of solid displacement and fluid velocity, respectively, in the r direction, and K is the intrinsic hydraulic conductivity. G and λ are the Lamé constants. They are related through the Poisson ratio ν: G=λ(1−2ν)/(2ν).

The mass conservation in the fluid phase at the steady state requires

$$\frac{1}{{r^2 }}\frac{{d(r^2 v)}}{{dr}} = 0$$
(3)

where we had neglected the fluid exchange between the interstitial space and the blood or lymph vessels, because the microvascular pressure is approximately equal to the interstitial fluid pressure at the steady state and there are no functional lymph vessels in tumors.6,14,22 As a result, we could treat vascular and interstitial fluid spaces as a single liquid phase and cellular and extracellular matrix as a single solid phase in tissues.

The hydraulic conductivity is generally dependent on tissue deformation. Various empirical relationships between K and tissue deformation have been proposed.1,16,17 A commonly used equation was proposed by Lai and Mow in 1980,17 in which K is an exponential function of the volume dilatation e, K=H exp(Me/3), where H and M are constants. The Lai and Mow equation assumes that K depends only on e and is independent of the way of tissue deformation. This assumption may not be valid in tissues with a high volume fraction of ECM and cells. To simplify the discussion, we might consider two hypothetical situations of cell arrangement in tissues. In both situations, the cells were identical and arranged in ordered periodic arrays. The only difference was that cells were aligned in the first situation and staggered in the second one.10 If the cells were aligned in all directions and the space between cells was much smaller than the size of cells, then the deformation in the flow direction would have only minor effects on K. If the cells were staggered, however, K would be sensitive to the same deformation. The value of K could approach to zero if the tissue with staggered cells was adequately compressed, because the cells would block all pathways for the flow of interstitial fluid. The same discussion may also be applied to fibers in ECM. Therefore, we proposed that K depended on tissue deformation in an anisotropic manner. To model the anisotropic effect, we modified the Lai and Mow equation as,

$$K = H \exp \{ M[\alpha E_{{\rm rr}} + (1 - \alpha )E_{\theta \theta } ]\}$$
(4)

where E rr and E θθ are the rr and θθ components of the strain tensor, respectively. They are related to the solid displacement u by\(E_{{\rm rr}} = du/dr\) and \(E_{\theta \theta } = u/r\). α is introduced as a parameter that accounts for the relative contribution of tissue deformation in the radial direction (E rr) to changes in K. When α = 1/3, Eq. (4) reduces to the Lai and Mow equation. In this case, K depends on tissue deformation isotropically. When α ≤ 1/3, K is dominantly determined by the circumferential expansion. When α > 1/3, the radial compression becomes a dominant factor. Furthermore, it is possible that the value of α is related to densities of cells and ECM. Consequently, α depends on mechanical properties of tissues (i.e., λ and G). Since these relationships are still unknown, we assumed that α and λ were independent parameters in the model.

Previous studies one have shown that there exists a threshold pressure P t below which the infusion cannot be initiated.19,41 To model the threshold pressure, we hypothesized that the insertion of infusion needle caused compression of a thin layer of tissues around the needle tip, which immediately closed all aqueous pathways. The thickness of this layer (Δx) was much smaller than the radius of the needle so that it could be treated as a membrane. The hydraulic conductivity of the membrane (L P) was zero if the infusion pressure P inf was lower than P t. When P inf > P t, L P was assumed to increase exponentially with increasing P inf,

$$L_{\rm P} = \left\{ {\begin{array}{@{}l@{\quad}l@{}}0 & {P_{\inf } < P_{\rm t} } \\ {L_{{\rm P}0} \left\{ {{\rm exp} \left[ {\frac{{P_{{\rm inf}} - P_{\rm t} }}{{\beta (2G + \lambda )}}} \right] - 1} \right\}} & {P_{\inf } \ge P_{\rm t} } \\\end{array}} \right.$$
(5)

where L P0 and β are constants. The boundary conditions in the model were

$$v = L_{\rm P} (P_{\inf } - {\rm }P)\quad {\rm at}\quad r = a_0$$
(6)
$$P = 0\quad {\rm at}\quad {\rm }r = R$$
(7)
$$(2G + \lambda )\frac{{du}}{{dr}} + 2\lambda \frac{u}{r} = P_{\inf } \quad {\rm at}\quad r = a_0$$
(8)
$$(2G + \lambda )\frac{{du}}{{dr}} + 2\lambda \frac{u}{r} = 0\quad {\rm at}\quad r = R$$
(9)

where a 0 and R are the initial radius of the fluid cavity around the needle tip and the radius of the tumor, respectively. Equation 9 assumed that there were no contact stresses in the r direction on the tumor surface.3

Equations 1 through 3 under the boundary conditions described in Eqs. (6) through (9) were solved simultaneously by first converting the differential equations into the integral ones. Then, the nonlinear integral equations were solved numerically using an iteration method. Once the velocity (v a) at r = a 0 was solved, the infusion rate Q was calculated as \(4\pi a_0^2 v_a\). A list of all variables and constants used in the study is shown in Table 1.

TABLE 1. A list of variables and constants used in the study.
Full size table

Baseline Values of Model Constants

a 0 and R were equal to 0.18 mm and 0.5 cm, respectively. In the study, we chose M to be 10 mmHg17 and the Poisson ratio ν to be 0.35.31 H might be tumor- and collagen concentration-dependent. However, we did not have enough data to determine H. Therefore, we assumed H to be 3×10−5 cm2/mmHg/s, which was estimated by the average value of K in our experiments. The value of β was assumed to be unity. L P0 was estimated by H/Δx, in which Δx was assumed to be 20 μm. The values of α and λ varied in the simulation. They were determined through nonlinear curve fitting of simulation results to experimental data.

FIGURE 2.
figure 2

Flow rate as a function of the pressure P inf during the infusion into (a) B16.F10 tumors (n=5), (b) 4T1 tumors (n=5), and (c) U87 tumors (n=5). The symbols represent data from individual tumors.

Full size image
FIGURE 3.
figure 3

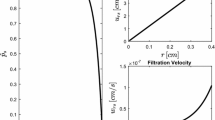
Apparent hydraulic conductivity (K app) as a function of the pressure P inf in (a) B16.F10 tumors (n=5), (b) 4T1 tumors (n=5), and (c) U87 tumors (n=5). It was calculated using the data shown in Fig. 2.

Full size image
FIGURE 4.
figure 4

Nonlinear curve fitting of flow rate versus pressure data during the infusion into (a) B16.F10 tumors, (b) 4T1 tumors, and (c) U87 tumors, using the poroelastic model. The symbols represent the mean of Q at each pressure shown in Fig. 2; and the curves are the model predictions when the best fits were achieved.

Full size image

Statistical Analysis

The Mann-Whitney U test was used to compare the difference between two unpaired groups. The difference was considered to be significant if the p-value was less than 0.01.

RESULTS

The concentrations of collagen in B16.F10, U87, and 4T1 tumors (mean ± standard deviation) were 2.9±1.2, 12.2±0.9, and 18.1±3.5 μg/mg wet wt. of tissue, respectively. The concentration difference between any pair of tumors was statistically significant (p < 0.01). When the solution of EBA was infused into the tumors at constant infusion pressure (P inf), we observed that there existed a threshold infusion pressure (P t), below which the infusion could not be initiated. The values of P t were 7.36, 36.8, and 29.4 mmHg in B16.F10, U87, and 4T1 tumors, respectively. The value of P t had no correlation with the collagen concentration. When P inf was approximately 4 mmHg larger than P t, the infusion could be started in all tumors. The infusion rate (Q) was measured for P inf being maintained at 36.8, 51.5, or 69.2 mmHg. The data shown in Fig. 2 demonstrated that Q was a nonlinear function of P inf and the shape of the function was tumor-dependent. In 4T1 tumors that had the highest collagen concentration among the three tumor lines, Q was a bell-shaped function of P inf. In B16.F10 and U87 tumors, Q increased monotonically with increasing P inf. Comparing the values of Q in these tumors, Q decreased with increasing the concentration of collagen (see Fig. 2). The flow rates shown in Fig. 2 were used to calculate the apparent hydraulic conductivity (K app) at each infusion pressure. The results are shown in Fig. 3. The pressure-dependence of K app was similar to that of Q in individual tumors.

Using the mathematical model described in the Materials and Methods section, we numerically simulated Q for different P inf and fit the simulation results to the experimental data shown in Fig. 2 by varying the values of α and λ. The best fits were achieved when (α, λ) were equal to (0, 57 mmHg), (0, 95 mmHg), and (0.733, 175 mmHg) for B16.F10, U87, and 4T1 tumors, respectively (see Fig. 4). We also performed a sensitivity analysis of the model predictions by varying α from 0 to 2.5/3.0 and λ from 10 to 800 mmHg (see Fig. 5). The range of λ covered the values reported in the literature that are between 14 and 675 mmHg.3,23,25,26,31 The threshold pressure P t in the simulations was fixed at 25 mmHg, i.e., the average value of the experimental data. It can be shown mathematically that the necessary condition for Q being a bell-shaped function of P inf is α > 1/3. To illustrate how Q changed with λ at fixed values of α and P inf, the data shown in Fig. 5 were re-plotted in Fig. 6.

DISCUSSION

The collagen concentrations, the threshold pressures, and the infusion rates at different infusion pressures were quantified in three different tumors. The data suggested that the collagen concentration might have significant effects on both the infusion rate and the relationship between infusion rate and infusion pressure. To analyze the experimental data, a new poroelastic model was also developed in the study. The model predictions suggested that the hydraulic conductivity depended on intrinsic structures of tissues as well as infusion-induced tissue deformation in an anisotropic manner.

The amount of collagen contained in a tissue is generally a predictor of deformability of tissues; the latter decreases with increasing the former.24 In this study, we observed qualitatively that B16.F10 tumors were almost like a viscous gel while U87 and 4T1 tumors were more structurally stable. In addition, 4T1 tumors, noticeably more rigid than U87 tumors, formed tight spheres under the skin after subcutaneous implantation. In addition to the deformability, the amount of collagen correlates to molecular diffusivity in tissues because the network of collagen fibers is a major transport barrier. Netti et al. have shown that collagen can significantly hinder diffusion of large molecules in tumors.24 In collagen solutions or gels, the diffusion coefficients of molecules with different sizes all decrease with increasing the collagen concentration.29 Furthermore, the location of collagen fibers dictates size distribution of hydrophilic pores that are available for molecular transport within the tissue. Pluen et al. have shown a drastic decrease in the diffusivity of non-flexible molecules when the ratio of pore size versus molecular hydrodynamic radius (a/R H) is less than ∼6.8.28 Therefore, the distribution of collagen fibers may affect drug distribution as well.

The relationship between the collagen concentration and the hydraulic conductivity is still uncertain since other components in tissues (e.g., cells and glycosaminoglycans (GAG)) may also hinder fluid flow. However, we hypothesized that the collagen concentration was a dominant factor for determining tissue deformation-induced changes in hydraulic conductivity. The hypothesis was based on the following observations. First, our preliminary data showed that there was no significant difference in cell volume fractions between B16.F10 and 4T1 tumors. Second, Netti et al. have examined four types of tumors implanted in mice. They demonstrated that the maximum difference in the extracellular matrix was less than 50% in terms of the total GAG concentration but more than 4-fold in terms of the collagen concentration.24 These observations suggest that cells and GAG may affect the hydraulic conductivity but these effects are likely to be qualitatively the same in all tumors if the amount of tissue deformation is the same. On the other hand, 4T1 tumors were less deformable than the other two tumors. As a result, tissue deformation-induced changes in hydraulic conductivity would be smaller in 4T1 tumors if cells and GAG were dominant factors in the determination of flow resistance. This conclusion was inconsistent with the observations shown in Fig. 3, indicating that the opposite was likely to be true.

FIGURE 5.
figure 5

Numerical simulations of flow rate as a function of infusion pressure for different values of α and λ. In each panel, λ (mmHg) is equal to 10, 20, 50, 150, 500, or 800 whereas α is fixed at (a) 0, (b) 1/3, (c) 1.5/3.0, or (d) 2.5/3.0. The threshold pressure P t in all panels is equal to 25 mmHg. In Panel (d), the curves for λ being 10, 20, and 50 collapse onto a single curve closed to Q=0 and thus cannot be shown separately in the figure.

Full size image
FIGURE 6.
figure 6

Numerical simulations of flow rate as a function of λ for different values of α and infusion pressure P inf. In each panel, P inf (mmHg) is equal 28, 32, 40, 50, 60, 70, 85, or 100 whereas α is fixed at (a) 0, (b) 1/3, (c) 1.5/3.0, or (d) 2.5/3.0. The threshold pressure P t in all panels is equal to 25 mmHg.

Full size image

Collagen could affect the hydraulic conductivity through two mechanisms. One was to limit mechanical deformation as mentioned above. Another was to hinder fluid flow. Although 4T1 tumors were less deformable than the other two tumors, the distance between collagen fibers in these tumors was smaller due to the higher concentration of collagen. Under these conditions, a small deformation could cause a large relative change in the volume fraction of interstitial fluid space or even cause disconnectedness of a large fraction of interstitial fluid space if the fibers in certain regions were densely packed. Consequently, the hydraulic conductivity could be decreased significantly due to the small deformation.

To understand quantitatively how tissue deformation affects K and Q-P inf relationship, we developed a poroelastic model of fluid transport in tumors. The model predicted that the strain was positive (i.e., expansion) in the circumferential directions but negative (i.e., compression) in the radial direction. The model also predicted that the dependence of K on tissue deformation was anisotropic (i.e., α≠1/3) (see Fig. 4). The extent of tissue deformation was a function of α and λ that could affect both the magnitude of Q and the shape of Q-P inf curves. When α ≤ 1/3, Q increased with increasing P inf but the amount of increase was low if λ was large (Figs. 5a and 5b). If P inf was fixed, Q decreased with increasing λ (Figs. 6a and 6b). When α > 1/3, Q was a bell-shaped function of P inf (see Figs. 5c and 5d). The curve was shifted to the right when λ was increased. If the value of λ was large (e.g., 800 mmHg), the decrease portions of the curves could be shifted out of the figure frames (see Figs. 5c and 5d). This nonlinear behavior of Q versus P inf was mainly caused by the increase in the relative contribution of radial compression of tissues to K in Eq. (4). If P inf was fixed and α > 1/3, Q was also a bell-shaped function of λ and the curve was shifted to the right when P inf or α was increased (Figs. 6c and 6d). For all values of α, Q → 0 as λ→∞.

The value of K either increased (if α > 1/3) or decreased (if α≤1/3) with the radial distance (data not shown), indicating that tissue deformation could change K in both directions. The value of K was close to H (a constant in Eq. 4) at a large distance where the deformation was negligible. The apparent hydraulic conductivity (K app), defined in the Materials and Methods section, was a sigmoidal function of λ if α > 1/3 but decreased rapidly with increasing λ if α≤1/3 (data not shown). For all values of α, K app → H as λ → ∞.

The threshold pressure (P t) is another important factor in characterizing the intratumoral infusion. Fluid cannot be infused into the tissue until P inf > P t. This phenomenon has also been observed in previous studies.19,41 Mechanisms for the existence of threshold pressure are still unknown although we hypothesized in the poroelastic model that the needle insertion-induced tissue compression around the needle tip could be a potential mechanism. Other mechanisms were likely to be related to the elevated IFP14 and disconnectedness of aqueous pathways in tumor tissues.38 These mechanisms need to be investigated systematically in future studies.

In summary, our data demonstrated that structures of tumor tissues have significant effects on intratumoral infusion. A threshold pressure must first be overcome to open aqueous pathways for convective transport. The nonlinearity in the relationship between infusion rate and infusion pressure was caused by tissue deformation-induced changes in hydraulic conductivity. The collagen concentration might be a dominant factor for determining tissue deformation-induced changes in hydraulic conductivity. In tumors with higher collagen concentrations, infusion at a higher pressure might not necessarily result in more drug delivery, but would in fact, decrease it. These results may be useful for further investigations of intratumoral infusion of drugs and genes.