1 Introduction

Stroke is one of the most important causes of disablement among elderly people. In the UK, around 130,000 people each year suffer a stroke, and one-third of them have a severe disability due to the deteriorated motor function in arms and legs. Evidence shows that additional early exercise training may be beneficial [4]. Independent and repetitive exercises could directly strengthen arms and legs, and may help patients recover more quickly.

Classical treatments primarily rely on the use of physiotherapy, which depends on the trained therapists and their past experience. This suggests that traditional methods lack objective standardised analysis for evaluating a patient’s performance and assessment of therapy effectiveness. To address this problem, trajectories during the rehabilitation course after stroke have to be quantified, and hence appropriate instruments for quantitative measurements are desirable to capture motion trajectories and specific details of task execution. Recently, research has commonly addressed on measurements of upper limb movements. Since upper limbs are frequently used to contact and manipulate objects [5], stroke recovery of functional use of upper limbs is a primary goal of rehabilitation.

Successful examples have existed in literature for the applications of inertial sensor based systems in the measurements of upper limb movements [12, 14]. Inertial sensors are sourceless and are able to provide accurate readings without inherent latency. Hence, they are a better option than other sensors in our application. For example, they are able to cope with the occlusion problem bound in the optical tracking systems. However, accumulating errors (or drifts) are usually found in the measurements by inertial sensors. Therefore, in this study, we intend to develop an inertial based motion detector, which can be used to properly locate the position of the upper limb in space without or with less drifts.

2 Methods

2.1 System description

We here propose a portable motion tracking system that uses a commercially available MT9-B inertial sensor (Xsens Dynamics Technologies, Netherlands). This approach actually is the combination of sensor fusion and optimisation techniques. This design enables us to estimate the arm motion in a rehabilitation program with a minimum requirement of inertial sensors (low costs) and higher accuracy. The system is implemented in the environment of Visual C++, where the computer is a Media PC with a VIA Nehemiah/1.2 GHz CPU. The connection between the computer and MT9 sensors is wireless (using Bluetooth devices) via a digital data bus called “XBus” (placed on the waist). The designed motion tracking system will be integrated within a home-based rehabilitation system illustrated in Fig. 1.

Fig. 1
figure 1

Illustration of the designed rehabilitation system

Full size image

The positioning algorithm is summarised as follows: using the double buffers on-board, inertial measurements corresponding to human arm movements are consistently generated and then filtered to remove high frequency noise. The wrist position can be obtained by double integrating the measured accelerations. A kinematic model will exploit this outcome, combining the computed Euler angles, and then provide the position of the elbow joint. Since the positioning of the wrist and elbow joints is conducted in a sense of integration, the drift problem will unlikely be avoided. Therefore, a Monte Carlo Sampling based optimisation technique, simulated annealing, is adopted in order to attract the estimates near to the true positions given a physical constraint equation.

2.2 Kinematic modelling

The human arm motion could be approximated as an articulated motion of rigid body parts. Regardless of its complexity, one still can characterise human arm motion by a mapping describing the generic kinematics of the underlying mechanical structure. In this paper, we mainly focus on the design of a two-joint (shoulder and elbow) model. However, to respond the request of learning dynamics of fingers, a more complicated model with the finger joints will be launched in a future study.

Human arm motions can be represented by kinematic chains. The kinematic chain of our concern consists of four joint variables, i.e. three for the shoulder joint and one for the elbow joint. Our system is different from other existing 7 degree-of-freedom (DOF) limb models, i.e. [11]. To obtain the positions of the joints, an analytic formulation will be sought, followed by optimal numerical rendering. For the purpose of clarification, forward kinematics of the arm motion will be discussed next.

The forward kinematics specify the Cartesian position and orientation of the local frame attached to the human arm relative to the base frame which is attached to the still joint (shoulder). They are provided by multiplying a series of matrices parameterised by joint angles. Figure 2 illustrates a three-joint human arm, where there are two segments linking these three joints.

Fig. 2
figure 2

Kinematics of a three-joint human arm

Full size image

An inertial sensor is placed near to the wrist joint. To simplify the position estimation, we further assume that the distance (L 1) between the shoulder and elbow joints has been known. The same assumption is also applied to the distance (L 2) between the elbow and wrist joints. In practice, these two parameters can be obtained with careful anthropometric measurements.

Consider a rigid body moving in the world (or earth) frame. The world frame is n, and the sensor body frame is b. D represents the position displacement vector between the origin of the n-frame and that of the b-frame. Let the coordinates of the elbow joint and the sensor be denoted by (x 1, y 1, z 1) and (x 2, y 2, z 2), respectively. Also, we suppose that \(\omega^{b}\) is the angular rate vector transformed from the n-frame to the b-frame, and a b is the tri-axial non-gravitational acceleration of the b-frame.

R n b , a 3×3 rotation matrix, represents the orientation transformation from the b-frame to the n-frame v n=R n b v b, where v n and v b stand for the linear velocity vector of the sensor in the n- and b-frames, respectively. It is recognised that R n b at the next instant, namely R n′ b , can be updated using the continuous-time differential equation [2]: \({\dot{\mathbf{R}}}_{b}^{n} = {\bf R}_{b}^{n} S\left(\omega^{b} \right),\ \hbox{where}\ S\left(\omega^{b} \right) \equiv\left[\omega^{b}\times\right]\) is the skew-symmetric matrix that is formed using the cross-product operation. In fact, the new rotation matrix R n′ b will be equivalent to the previous R n b plus \({\dot{\mathbf{R}}}_{b}^{n}\) multiplied by a time interval.

Once the rotation matrix has been updated, then the acceleration readings in the n-frame will be obtained as follows a n=R n b a b+G n, where G n=[0, 0, 9.81]T m/s2 is the local gravity vector whose effect on the acceleration needs to be eliminated [3].

Finally, we have the sensor’s velocity and position in the n-frame by integrations as \({\bf v}^{n} = \int_{0}^{t_1} {\bf a}^{n}{\text{d}}t\ \hbox{and}\ {\bf D}^{n} = \int_{0}^{t_1} \int_{0}^{t_1} {\bf a}^{n}{\text{d}}t\) where t is time and t 1 is the present instant.

Using the kinematic models proposed in [13], we can derive the positions of the elbow joint and the sensor. Suppose that ϕ x , ϕ y and ϕ z are the Euler angles of the sensor around x-, y- and z-axis (in the frame originated at the elbow joint), respectively. The position of the sensor is represented as follows

$$\left.\left[ x_2, y_2, z_2 \right]^{\text{T}}\right|_{t_{i+1}} = \left.\left[x_2,y_2, z_2\right]^{\text{T}}\right|_{t_{i}} + \int\limits_{t_{i}}^{t_{i+1}}\int\limits_{t_{i}}^{t_{i+1}}{{\bf a}_{w}}{\text{d}}t$$
(1)

where t i and t i+1 are two instants, and a w is a linear acceleration vector from the inertial sensor attached to the forearm and 1 cm away from the wrist joint (see Fig. 3).

Fig. 3
figure 3

Experimental set-up in evaluation (the sensor and markers are attached to the arm using adhesive tapes)

Full size image

The solution for the position of the elbow joint is obtained as a “piecewise” function [13], which can be presented as follows: if\(\phi_{y} = \pm \frac{\pi}{2},\) then

$$x_1 = x_2$$
(2)

When \(-\frac{\pi}{2} < \phi_{y} < \frac{\pi}{2},\;\hbox{or}\;\frac{3\pi}{2} <\phi_{y} < {2\pi}\)

$$x_1 = x_2 - L_{2}\sqrt{\frac{\cos^{2} (\phi_{z}) + \sin^{2}(\phi_{x})\sin^{2} (\phi_{z})}{\sin^{2}(\phi_{x})\sin^{2}(\phi_{z}) +\frac{1}{\cos^{2}(\phi_{y})}}}$$
(3)

Otherwise, if \(\frac{\pi}{2} < \phi_{y} < \frac{3\pi}{2},\;\hbox{or}\;-\frac{3\pi}{2} < \phi_{y} < -\frac{\pi}{2}\)

$$x_1 = x_2 + L_{2} \sqrt{\frac{\cos^{2} (\phi_{z}) + \sin^{2} (\phi_{x})\sin^{2} (\phi_{z})}{\sin^{2} (\phi_{x}) \sin^{2} (\phi_{z}) +\frac{1}{\cos^{2} (\phi_{y})}}}$$
(4)

The solutions for y 1 and z 1 will be available as

$$\left\{ \begin{array}{*{20}c}y_1 = y_2 - \sqrt{L_{2}^{2} - (x_2-x_1)^2} \cos(\phi_{x})\\z_1 = z_2 - \sqrt{L_{2}^{2} - (y_2-y_1)^2} \sin(\phi_{y})\\\end{array}\right. $$
(5)

Clearly, the estimation of the elbow position relies on the estimated position of the sensor. Empirical evidence shows that the estimated 3-D positions using Eq. 1 usually suffers from drifts [12]. Therefore, we here need to launch a study to eliminate or minimise the unexpected errors.

2.3 Error minimisation by fast simulated annealing

We here attempt to challenge the problem where the used accelerometers and gyros are sensitive to translational accelerations. If an erroneous acceleration or orientation is sampled, then the error will be accumulated due to the required integration and eventually deteriorates the accuracy of the later episodes. This has happened if errors occur in the estimation of the wrist position, then they will be brought forward to the computation of the elbow-joint position. Classically, model based optimal filtering approaches, e.g. Kalman filter, can be used to estimate the arm position by fusing the detected accelerations and orientations with physical restrictions. However, these methods cannot be justified in the presence of non-Gaussian errors. Further, parameters of the filters need to be tuned in order to fit different circumstances. Hence, our aim is to develop a motion detector that is adaptive to different environments and automatically runs with stable performance in accuracy and reliability.

Recall that the distance between the elbow and shoulder joints has been known as L 1. Assuming that the shoulder joint is the origin of the base frame, then we shall have the Euclidean distance constraint as x 21 +y 21 +z 21 − L 21 → 0. A similar constraint equation can be deduced for x 2, y 2, and z 2 (L 2 is used instead). Irregular overestimates or underestimates due to noise or erroneous measurements can lead to \(\left| x_{1}^2 + y_{1}^2+ z_{1}^2 - L_{1}^2 \right| \gg 0.\) Indeed, a generic generalised format for the distance constraint is yielded as follows:

$$E \left( {x}_{1}, {y}_{1}, {z}_{1} \right) \propto {\text{argmin}} \left({x}_{1}^2 + {y}_{1}^2 + {z}_{1}^2 - L_{1}^2 \right)$$
(6)

To pursue a global solution to Eq. 6, an efficient simulated annealing by Penna [10] is adopted with the given set of measurements and the physical constraint. Simulated annealing is analogue to a thermodynamic process. The technical key for annealing is to ensure a low energy state to be reached. The search of a global minima involves the comparison of the energies of two consecutive random conformations [6]. The states at steps i+1 and i are given by v i+1 and v i , respectively, where v i is a 6-D vector that includes the tri-axial position of the wrist and the tri-axial angular changes to be optimised. v i+1 and v i are linked together by v i+1=v i +Δv i , where Δv i is a random perturbation of the six variables (coordinates of the two joints). This random perturbation allows v i to gradually approach to the desired state \({\tilde{\mathbf{v}}}_{i+1}.\) In practice, a proper random perturbation falls in the range of |0.01, 0.1| cm.

The optimisation of using simulated annealing starts from a set of initial estimates of parameters (here positions of the elbow joint and the sensor), and then adjusts their values during the iterative process. It is helpful to improve convergence speed if the initial estimates are close to the finals.

To reach this purpose, we use the iterative Levenberg–Marquardt (L–M) algorithm to find proper starting positions (x 2_0, y 2_0, z 2_0): we can take the derivative of E(x 1, y 1, z 1) with respect to each of the parameters, e.g. x 2, y 2, and z 2, and sets each to zero. The required derivatives in the iteration of L–M are yielded as

$$\left\{ \begin{array}{*{20}l}\frac{\partial E}{\partial {x_2}} = 2x_1 + \frac{2y_1 \left( x_2 - x_1\right) \cos \left(\phi_x\right)}{\sqrt{L_{2}^{2} - \left(x_2 - x_1\right)^2}}\\\frac{\partial E}{\partial{y_2}} = 2y_1 + \frac{2 z_1 \left( y_2 - y_1\right) \sin (\phi_y)}{\sqrt{L_{2}^{2} - \left( y_2 - y_1 \right)^2}}\\\frac{\partial E}{\partial {z_2}} = 2z_1\end{array}\right.$$
(7)

Once the starting positions have been found, we are then able to perform the optimisation using the established simulated annealing strategy. The entire optimisation algorithm is shown in [13]. This combination expectedly leads to final results accurately and faster as the initial estimates have been driven towards the final settlement. In practice, iteration numbers are normally less than 50 before the convergence is reached.

3 Experimental work

In this section, the performance of the proposed monitoring system consisting of kinematic models and the simulated annealing algorithm is in comparison to that of the standard motion tracking system, CODA CX1. As a vision based system, CODA picks up emitted signals from the active markers mounted on the objects. At a 3-m distance, this system has less than 3 mm in all axes for peak-to-peak deviations from actual position.

3.1 Experimental set-up

Before the evaluation starts, an experimental environment needs to be set-up. Figure 3 illustrates a subject sitting in front of the CODA system, while a MT9 sensor and three CODA markers are rigidly attached to his arm. The distance between the subject and the CODA system is 2 m. The viewing direction of the cameras is aligned with the z-axis of the world coordinate system, and the x-axis is vertical to the floor. In order to avoid relative motion, a marker is fixated on the MT9 sensor while facing the cameras. For direct comparison, two engaged systems use the sampling rate of 100 Hz. In order to properly interpret the outcomes, it is desirable to align these two systems in the world coordinate system. Alternatively, the transformation between the two trackers needs to be discovered. Once the measurements from these two tracking systems have been registered, then the estimation using the proposed tracker will directly represent the real movements of the human upper limb in 3-D space.

To conduct this system alignment or calibration, we consider a 3-D coordinate transformation between these two systems:

$${\mathbf {P}}_{{\text{MT9}}_{(k)}}={\mathbf {P}}_{{\text{CODA}}_{(k)}}{\bf R}+{\bf T}$$
(8)

where k is the trial number, P CODA is the sensor position estimated by the CODA system, P MT9 by our proposed system, R is a rotation matrix and T is a translation vector (R and T are to be estimated). The following strategy is thus applied: with the set-up shown in Fig. 3, a male subject is asked to move his arm nearer-to-further by following a straight line (about 15 cm) on the surface of a desk in front of him. We then collect ten samples from the whole trajectory in averaging time. This motion-sampling process is repeated for five times. To reduce errors in different motion directions, movements in four axial directions (like a “+” symbol) are subsequently conducted and sampled as introduced above. We then use the estimated position of the overall samples by the two trackers to solve Eq. 8 for R and T using the singular value decomposition (SVD) technique. Once R and T have been obtained, then the proposed tracking system is calibrated.

The overall experiments are carried out using two methods. In the first method, we use the proposed analytic model to estimate the movements of the human arm without any further optimisation. In the second method, based on the outcomes of method 1, we apply the simulated annealing optimisation to reduce the errors existing in the measurements.

In general, we collect three sequences that represent three different motion manners (Fig. 4): (1) the forearm moves up–down repeatedly but the elbow joint is kept stationary; (2) the whole arm is allowed to perform up–down motion; and (3) the whole arm conducts left–right movements. The individual motion styles and their corresponding results, the estimated 3-D wrist- and elbow-joint positions, will be subsequently introduced in the rest of this section. Before the overall tests start, each subject has been informed to keep his/her shoulder still during the motion session. However, it is still likely that the shoulder position can be changed, e.g. forward or backward. This leads to over- or under-estimation of the wrist and elbow position. To avoid this, the position of the CODA marker placed nearby the shoulder is used as a compensation to the estimates by the proposed tracking system.

Fig. 4
figure 4

Movement patterns of the human arm

Full size image

Four male subjects have been involved in the evaluation experiments, and the lengths of their arm segments are given in Table 1. In our application, computational errors less than 10% of the entire travelling distance is subjectively permitted. In other words, errors less than ∼ 3 cm will be acceptable in trials.

Table 1 Segment lengths of individual subjects in the experiments (units: cm)
Full size table

4 Results

Motion pattern 1

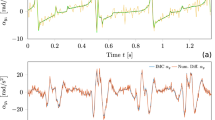
The motion style has been illustrated in Fig. 4a. Figure 5 illustrates examples of the detected accelerations and Euler angle z (the forearm), which show stable consistency. Figure 6 clearly shows that in this circumstance the simulated annealing (the second method) improves system performance dramatically: (a) in the estimation of the wrist position along the x-axis, the first method has the RMS errors of 9.1 cm against 1.36 cm by the second method. (b) Wrist position along the y-axis. The first method has the RMS errors of 5.11 cm, and the second method has the RMS errors of 0.94 cm. In (c), (d), (e) and (f), it has been found that the results from these two methods are close but obviously the second method is better.

Fig. 5
figure 5

Motion pattern 1: accelerations and Euler angles (forearm)

Full size image
Fig. 6
figure 6

Motion pattern 1: measurement plotting of human arm movements (solid lines by the CODA system, dotted lines by the proposed kinematic models only, and dashed lines by the proposed kinematic models and simulated annealing)

Full size image

Motion pattern 2

The motion style has been shown in Fig. 4b. Partial measurements of accelerations and Euler angles are shown in Fig. 7. We here focus on the measurements of the z coordinates of the wrist and elbow joints, illustrated in Fig. 8. In Fig. 8a, the RMS errors in the second method have been limited to be 3.1 cm. This accuracy is much better than that of the first method, where the RMS errors are 8.1 cm. Similar conclusion can be drawn from Fig. 8b.

Fig. 7
figure 7

Motion pattern 2: accelerations and Euler angles (forearm)

Full size image
Fig. 8
figure 8

Motion pattern 2: measurement plotting of human arm movements (solid lines by the CODA system, dotted lines by the proposed kinematic models only, and dashed lines by the proposed kinematic models and simulated annealing)

Full size image

Motion pattern 3

The motion style is shown in Fig. 4c. Instead of showing the results in figures, we rather demonstrate the animation of the motion estimation using the proposed simulated annealing method, which is shown in Fig. 9. It reveals that the estimated parameters have matched the actual movements. For example, the graph on the first column and the second row shows the current position of the left arm. Due to the flexion of the elbow (refer to the graph on the third column and the second row), the real elbow angle is reduced. The estimated joint positions by our model (simulated annealing based) properly reflect this variation in the same graph.

Fig. 9
figure 9

Illustration of the tracking performance in “motion pattern 3” by the kinematic models plus simulated annealing method

Full size image

4.1 Experimental statistics

This section allows us to summarise the statistics, based on long trial experiments and their corresponding results. The trials have been continuously conducted for 120 s. The Euclidean distance between the estimated positions of the wrist and elbow joints by the proposed systems and the ground truth by the CODA system, including means and standard deviations, will be subsequently tabulated in Table 2. In a general sense, the kinematic models plus simulated annealing method is favourable against the case of the kinematic models only due to smaller means and standard deviations. For example, in “pattern 1 (wrist)” we discover that the simulated annealing method holds the mean errors of 1.6 cm against 7.7 cm by the kinematic models only method (absolute means are considered). However, it is also noticed that both methods have approximate accuracy in estimating the elbow-joint position in “pattern 1 (elbow)”. This happens because these two methods have respectively reached their maximum limitations of accuracy, and the travelling distance (peak-to-peak) is fairly short (only 3.5 cm).

Table 2 Statistic errors in motion estimation of the upper limb (units: cm)
Full size table

5 Discussion

In this paper, we have achieved a fast and accurate estimation of the arm position using a combination of sensor fusion and optimisation techniques. Classical sensor fusion methods (i.e. [9]) demand a complicated system set-up, while optimisation only methods (i.e. [1]) may lead to over- or under-estimate of the arm position. Our method integrates the measurements from the accelerometers and gyroscopes, and then uses a simulated annealing based optimisation technique to render the position of the upper limb. The theoretical and experimental work has clearly indicated that the proposed scheme is able to achieve accurate and reliable arm location.

Our system allows the subjects to freely move their upper limbs in the experiment. This releases the constraint of the classical robot-assisted systems, where robotic arms were physically attached with the upper limbs of the stroke patients in order to locate the latter in motion exercises [8]. In addition, our system is able to perform real track in the presence of “self-occlusion” [7] due to the sourceless features of the inertial sensors. It also shows that no drift appears in the estimates. This indicates that the proposed fusion strategy successfully handles the drift problem in the reported experiment.

However, some errors or noise have been observed in the estimates: less than 1.8 cm (mean values) errors existed in the estimated joint position. To reduce errors, in the future work we will launch a further study to improve the optimisation approach. This is mainly related to the convergence properties and possible solutions. At present, we strictly keep the assumption of a still shoulder joint during arm movements. In a real case, the movements of the upper limb are not restricted to this assumption. In other words, both translation and rotation of the shoulder joint are varied. In the future work, we attempt to develop a trunk model that is an extension of the proposed kinematic model herein. This permits us to release this assumption and to consider the case of free movements of the shoulder joint.