Introduction

Surface plasmon polaritons (SPPs) are evanescent waves that exist at a metal-dielectric interface. They are generated by the interaction of incident electromagnetic waves with free electrons in the metal, and amplitudes decay exponentially in the vertical direction of the metal-dielectric interface [1, 2]. SPPs play a vital role in many aspects because of breaking through the classic diffraction limit and manipulation on subwavelength scales, such as biomedicine, optical system [3] etc. In optical integrated devices based on SPPs, filters have captured more attention from researchers because of the high importance in high-density plasmonic integrated optical circuits for optical processing. MIM waveguide structure is composed of two metal layers and a dielectric layer sandwiched between them, which effectively confine surface plasmons in the waveguide. Therefore, MIM waveguides are very suitable for making surface plasmon filters. In recent years, MIM waveguide structure devices based on SPPs have been widely studied, such as Mach-Zehnder interferometer [4], switch [5, 6], multiplexer and demultiplexer [7, 8], Bragg reflector [9], plasma filter [10] etc.

Currently, numerous resonators, including disk resonators [11,12,13] and ring resonators [14, 15] based on MIM waveguides have been proposed. Modulation of a specific mode or multiple modes is implemented in these works. The multimode interference coupled mode theory (MICMT) and degenerate interference coupled mode theory (DICMT) based on the Fano resonance were proposed by Li et al. [16, 17]. The filtering effect is not reinforced despite the independent adjustment of the resonance peak. Rectangular cavities were placed at specific locations by Zheng et al to achieve more modes exploiting the MICMT [18]. The method, however, is theoretically unable to determine the geometric parameters and locations of the added rectangle cavities.

In light of this, a MIM waveguide structure filter with a main waveguide and a resonator composed of four rectangular cavities that are perpendicular to one another is proposed. One or more rectangular cavities are then placed on the proposed cavity. According to the standing wave theory and the MICMT, the filtering effect can be optimized or the number of modes can be increased by appropriately altering the parameters of the additional cavities. Moreover, the fitting of the finite-difference time-domain (FDTD) simulation graph and the MICMT is realized. The filter may exert a significant impact on the device design in highly integrated optical circuits.

Structure and Theory

Fig. 1
figure 1

The schematic diagram of the structure 1

Full size image

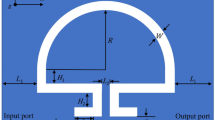
The structure 1 (S1) in Fig. 1 is composed of a main waveguide and a resonant cavity. The width of the waveguide is represented by the parameter \(w=50\, \text {nm}\) in the figure. The distance between the resonant cavity and the main waveguide is set to \(d=35\, \text {nm}\). The lengths of the rectangular cavities in the vertical and horizontal cavities are defined as \({{L}_{1}}=210\, \text {nm}\) and \({{L}_{2}}=600\, \text {nm}\), respectively. The separation of the two vertical rectangular cavities is \({{L}_{3}}=180\, \text {nm}\). The simulation is done using FDTD solutions. The calculation region is subjected to the perfect matching layer absorption boundary conditions. At the same time, the space step and the time step are designed \(~\Delta x=\Delta y=5\, \text {nm}\) and \(~\Delta t=\Delta x/2c\) (c is the velocity of light in a vacuum) in order to ensure the stable and accurate process of the numerical simulation. In addition, the incident light along the positive x-axis is TM polarized wave.

The white part of the diagram indicates air (n=1), whereas the light blue part represents silver. The dielectric constant of the metal silver is characterized by Drude model [19]:

$$\begin{aligned} {{\varepsilon }_{m}(\omega )}={{\varepsilon }_{\infty }}-\frac{\omega _{p}^{2}}{{{\omega }^{2}}+i\gamma \omega } \end{aligned}$$
(1)

where \(\varepsilon _m\) is the permittivity of the metal, \(\varepsilon _\infty =3.7\) is the relative permittivity at infinite frequency, \(\omega\) stands for the angular frequency of the incident electromagnetic radiation, \(\omega _p=1.38\times 10^{16}\,\)rad/s reflects the resonance frequency of the plasma, and \(\gamma =2.73\times 10^{13}\,\)rad/s represents the damping attenuation frequency at resonance.

Surface plasmons are stimulated after light enters the main waveguide. Then, standing waves are formed when surface plasmon waves are coupled into the cavity. The light wave is confined in the resonant cavity, resulting in the filtering function. In order to create a standing wave in a rectangular cavity, the light must meet the formula below [20]:

$$\begin{aligned} 2k(\omega )\cdot {Re}({{n}_{eff}}){{L}_{eff}}+2\Delta \varphi =2m\pi \end{aligned}$$
(2)

where m is an integer, which represents the number of antinodes of the standing wave. \(k(\omega )={2\pi }/{{{\lambda }}}\) is the wave vector in free space, and \(L_{eff}\) is the effective length of the electromagnetic wave propagating once in the resonant cavity. The effective length is not a definite parameter but varies with the resonance position [21]. And \(\Delta \varphi\) is the phase difference generated by the reflection of SPPs at the end of the rectangular cavity.

Through the above equations, the resonance wavelength can be solved as:

$$\begin{aligned} {{\lambda }_{m}}=\frac{2{{L}_{eff}}{Re}({{n}_{eff}})}{m} \end{aligned}$$
(3)

where \(n_{eff}\) is the effective refractive index of MIM waveguide structure. According to the dispersion relationship of SPPs, the \(n_{eff}\) can be derived that [22]:

$$\begin{aligned} \frac{{{\varepsilon }_{i}}{{k}_{m}}}{{{\varepsilon }_{m}}{{k}_{i}}}=\frac{1-{{e}^{{{k}_{i}}w}}}{1+{{e}^{{{k}_{i}}w}}} \end{aligned}$$
(4)
$$\begin{aligned} {{k}_{i}}={{k}_{0}}\sqrt{{{\left( \frac{{{\beta }_{spp}}}{{{k}_{0}}} \right) }^{2}}-{{\varepsilon }_{i}}},\quad {{k}_{m}}={{k}_{0}}\sqrt{{{\left( \frac{{{\beta }_{spp}}}{{{k}_{0}}} \right) }^{2}}-{{\varepsilon }_{m}}} \end{aligned}$$
(5)
$$\begin{aligned} {{\beta }_{spp}}={{n}_{eff}}{{k}_{0}}={{n}_{eff}}\frac{2\pi }{\lambda } \end{aligned}$$
(6)

where \({{\varepsilon }_{i}}\) and \({{\varepsilon }_{m}}\) are the permittivities of the insulator and metal, respectively; \({{\beta }_{spp}}\) is the propagation constant of SPPs wave; \({{k}_{0}}\), \({{k}_{i}}\), and \({{k}_{m}}\) are the wave vectors in vacuum, insulator and metal, respectively.

In coupled cavity systems, the overall field transmission can be viewed as interference between multiple modes. Therefore, based on the single-mode coupled mode theory, the MICMT is derived, and the amplitude of any mode can be expressed as follows [16, 23]:

$$\begin{aligned} \frac{d{{A}_{n}}}{dt}=(i{{\omega }_{n}}-\frac{1}{{{\tau }_{in}}}-\frac{1}{{{\tau }_{cn}}}){A_n}+\sqrt{\frac{1}{{{\tau }_{cn}}}}{{S}_{n,1+}}+\sqrt{\frac{1}{{{\tau }_{cn}}}}{{S}_{n,2-}} \end{aligned}$$
(7)
$$\begin{aligned} {{S}_{2+}}={{S}_{1+}}-\sum \limits _{n}^{{}}{\sqrt{\frac{1}{{{\tau }_{cn}}}}{{A}_{n}}} \end{aligned}$$
(8)
$$\begin{aligned} {{S}_{n,1+}}=C{{e}^{i{{\varphi }_{n}}}}{{S}_{1+}},\quad {{S}_{n,2-}}=C{{e}^{i{{\varphi }_{n}}}}{{S}_{2-}} \end{aligned}$$
(9)

\(S_{i\pm } (i=1,2)\) represents the amplitude in each waveguide, where positive sign represents the forward amplitude, and negative sign represents the backward amplitude. \(S_{n,i\pm } (i=1,2)\) is the forward and backward amplitude for nth order resonant mode. \(C{{e}^{i{{\varphi }_{n}}}}\) is the normalization coefficient, where \(\varphi _n\) is total coupled phase difference and \(C=1\). \(1/{{\tau }_{cn}}=\omega /{2Q_c}\) and \(1/{{\tau }_{in}}=\omega /{2Q_i}\) [24] represent the decay rate of external losses and internal losses, respectively.

The ratio of the normalized amplitude of the output to the normalized amplitude of the input is defined as the transmission coefficient of the SPPs, so the simultaneous Eqs. (7–9) can be derived as:

$$\begin{aligned} {{t}_{n}}=\frac{{{S}_{2+}}}{{{S}_{1+}}}=1-\sum \limits _{n}^{{}}{\frac{\frac{1}{{{\tau }_{cn}}}C{{e}^{i{{\varphi }_{n}}}}}{i(\omega -{{\omega }_{n}})+\frac{1}{{{\tau }_{in}}}+\frac{1}{{{\tau }_{cn}}}}} \end{aligned}$$
(10)
$$\begin{aligned} T={{ |{ {{t}_{n}}} |}^{2}}={{ |{1-\sum \limits _{n}^{{}}{\frac{\frac{1}{{{\tau }_{cn}}}C{{e}^{i{{\varphi }_{n}}}}}{i ( \omega -{{\omega }_{n}} )+\frac{1}{{{\tau }_{in}}}+\frac{1}{{{\tau }_{cn}}}}}} |}^{2}} \end{aligned}$$
(11)

The total coupled phase difference \(\varphi _n\) can be approximated as a constant for the convenience of calculation [17].

Simulation Results and Discussions

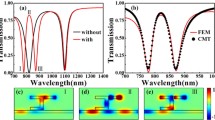
The transmission spectrum obtained by the FDTD simulations is shown in Fig. 2(a) as a black solid line. It reveals that the structure exhibits three resonance peaks in 800–1600\(\, \text {nm}\), positioned at 864\(\, \text {nm}\) (mode 1), 966\(\, \text {nm}\) (mode 2), and 1481\(\, \text {nm}\) (mode 3), with the corresponding transmittance of 5.6%, 10.7%, and 21.3%, respectively. The transmission response exhibits evidently Lorentz line shape. Furthermore, the simulation results are approximated using MICMT theory, with the amplitude coefficient of each mode being described by Eq. (10), and the overall amplitude value obtained from \(t=\sum \limits _{n=1}^{3}{{{t}_{n}}}\). When the parameter is set to \({{\tau }_{i1}}=244\,\text {fs}\), \({{\tau }_{i2}}=226.7\,\text {fs}\), \({{\tau }_{i3}}=248\,\text {fs}\), \({{\tau }_{c1}}=74.4\,\text {fs}\), \({{\tau }_{c2}}=108.6\,\text {fs}\), and \({{\tau }_{c3}}=212.4\,\text {fs}\), the fitting structure can be obtained as shown by the red dash line in Fig. 2(a). The lines show good fitting between results from FDTD and MICMT theory.

Fig. 2
figure 2

a The transmission spectra (black solid line) for S1 and theoretical fitting based on the MICMT (red dash line). b–d Normalized magnetic field distributions at resonance wavelengths of 864\(\, \text {nm}\), 966\(\, \text {nm}\) and 1481\(\, \text {nm}\), respectively

Full size image

The normalized magnetic field diagrams at the three peaks are displayed in Fig. 2(b)–(d), respectively. The propagation process of SPPs can be clearly seen in the figure. The SPPs propagate into the main waveguide and are coupled to the resonator where is reflected back and forth. If the resonance conditions are met, two light waves in opposite directions with phase differences meet to form a standing wave, thereby confining the light waves in the resonant cavity. Therefore, the resonance peak appears in the transmission spectrum.

Fig. 3
figure 3

a–d Transmission spectra of different \(L_1\), \(L_2\), \(L_3\) and \(d_1\) with constant other parameters and the influence on the resonance peak of mode 1

Full size image

Moreover, the influences of the length of the resonator and the distance between the waveguide and the resonator on the transmission spectra are studied. Firstly, variety in \(L_1\) from 190\(\, \text {nm}\) to 230\(\, \text {nm}\) and \(L_2\) from 580\(\, \text {nm}\) to 620\(\, \text {nm}\) is researched in Fig. 3(a)–(b), which demonstrate the red-shift phenomenon. The transmittance of other modes is basically steady, and merely that of mode 2 in Fig. 3(a) is slightly increased. The reason for the red-shift is the positive correlation between the length of the rectangular cavity and the effective length. Besides, according to Eq. (3), the increase of the effective length shift red the resonance wavelength. Subsequently, as shown in Fig. 3(c), with \(L_3\) from 140\(\, \text {nm}\) to 220\(\, \text {nm}\), mode 1 is red-shift and mode 2 and mode 3 are blue-shift. Finally, the coupling distance \(d_1\) is varied from 30\(\, \text {nm}\) to 40\(\, \text {nm}\) in 5\(\, \text {nm}\) steps, while keeping the other parameters constant. According to the simulation results displayed in Fig. 3(d), \(d_1\) substantially affects the resonance peaks: the transmission spectrum becomes blue-shifted as \(d_1\) increases, and the transmittance at the resonance peaks decreases seriously. This results from the phenomenon that the attenuation rises as the coupling distance increases so as to most of the light is lost from the main waveguide. As demonstrated in Eq. (11), the output transmittance will increase as the delay rate increases. All in all, the transmittance and resonant wavelength can be controlled by modifying the structural parameters.

Variations in transmittance due to fabrication errors inevitably affect the resonance peak of the filter. Accordingly, fabrication tolerance [25] should be considered. In the inserted pictures in Fig. 3, we measure the resonance peak of mode 1 as a function of geometric parameters (\(L_1\), \(L_2\), \(L_3\), \(d_1\)). When \(L_1\) and \(L_3\) change in a large range of 80\(\, \text {nm}\), the resonance peaks change by 24\(\, \text {nm}\) and 52\(\, \text {nm}\), respectively. It means that the wavelength error induced by \(L_1\) and \(L_3\) errors in fabrication has little impact. And the resonance peak is not sensitive to \(d_1\). Besides, the structure is more sensitive to \(L_2\), and the change of 40\(\, \text {nm}\) causes the resonance peak to shift by 39\(\, \text {nm}\). It may be solved by some high-precision fabrication methods, such as focused ion beams (FIB).

The Physical Mechanism of the Mode Increase

Fig. 4
figure 4

a The schematic diagram of the S2. b The transmission spectra (black solid line) for S2 with \(L_4=500\, \text {nm}\) and theoretical fitting based on the MICMT (red dash line)

Full size image

Figure 4(a) depicts a new structure (S2) which is added rectangular resonant cavity B with length \(L_4=500\, \text {nm}\), width \(w=50\, \text {nm}\), and separating distance from the main waveguide \(d_2=40\, \text {nm}\). The black line in Fig. 4(b) is the simulated transmission spectrum of S2. The number of resonance peaks within 750\(\, \text {nm}\) to 1600\(\, \text {nm}\) has increased from three to five, which are located at 789\(\, \text {nm}\), 864\(\, \text {nm}\), 966\(\, \text {nm}\), 1479\(\, \text {nm}\) and 1541\(\, \text {nm}\), respectively. The corresponding transmittance are 4.08%, 5.54%, 10.31%, 21.43%, and 25.40%, respectively. Comparing Fig. 5(a), (d) and (g), it can be concluded that the resonance wavelength and transmittance of the five modes in Fig. 5(d) correspond to Fig. 5(a) (cavity A) and Fig. 5(g) (cavity B).

Here, the physical mechanism of the mode number increase is investigated in terms of the magnetic field distribution map. There is a simulation in the transmission spectrum and electric field as the two cavities work separately. From Fig. 5(b, e, h) and Fig. 5(c, f, i), when cavity A and cavity B are existence, the mutual interference between them is very weak, so that it can approximately present their respective resonance peak properties. Figure 5(b), (e), and (h) show that most of the energy is not coupled into cavity A but propagates out of the main waveguide. After adding cavity B, however, the energy that is not coupled by cavity A can form a standing wave in cavity B, causing the output to drop sharply. The opposite is true for Fig. 5(c), (f), and (i). Therefore, it is clear from the analysis of the magnetic field that these two sets of peaks are caused by different factors and thus can be adjusted independently.

Furthermore, the phenomenon can be fitted by MICMT in the Eq. (10) with the number of modes \(n=5\), as shown by the red dash line in Fig. 4(b). At this time, the external loss, internal loss and phase difference of each mode are obtained as \({{\tau }_{c1}}=74.4fs\), \({{\tau }_{c2}}=108.6\,\text {fs}\), \({{\tau }_{c3}}=212.4\,\text {fs}\), \({{\tau }_{c4}}=52.9\,\text {fs}\), \({{\tau }_{c5}}=224\,\text {fs}\), \({{\tau }_{i1}}=244\,\text {fs}\), \({{\tau }_{i2}}=226.7\,\text {fs}\), \({{\tau }_{i3}}=248\,\text {fs}\), \({{\tau }_{i4}}=205.6\,\text {fs}\), \({{\tau }_{i5}}=234.6\,\text {fs}\), \({{\varphi }_{1}}=0\), \({{\varphi }_{2}}=-0.05\pi\), \({{\varphi }_{3}}=0.05\pi\), \({{\varphi }_{4}}=0.01\pi\), \({{\varphi }_{5}}=-0.07\pi\). It is consistent with the black solid line, thus proving the correctness of the previous analysis.

Fig. 5
figure 5

a, d, g The transmission spectra of S1, S2 and cavity B. b, e, h The normalized magnetic field distribution at 789\(\, \text {nm}\) for S1, S2 and cavity B. c, f, i The normalized magnetic field distribution at 966\(\, \text {nm}\) for S1, S2 and cavity B

Full size image

Transmission Optimization for One Mode

The filtering effect of S1 is far from the ideal. Therefore, another cavity of specific length is added below the main waveguide. According to the analysis in the “Structure and Theory’’ section, as long as the wavelength of the incident light satisfies the standing wave conditions of the upper and lower cavities at the same time, the transmittance at the resonance wavelength can be markedly reduced. As shown in Fig. 6(a), when the length of the rectangular cavity is \(L_4=264\, \text {nm}\), the transmittance of mode 1 drops sharply from 5.6% to nearly 0.

In fact, given the known resonance wavelength, the theoretical length of \(L_4\) can be calculated by standing wave theory. For mode 1, the effective refractive index is known to be \(n_{eff}=1.436\). According to Eq. (3), the theoretical length of cavity B is \(301\, \text {nm}\), while the actual value is \(264\, \text {nm}\). This is because standing wave theory only deals with the effective length \(L_{eff}\) and effective refractive index \(n_{eff}\), but the waveguide width w and distance \(d_2\) which are ignored also have effects on the resonant wavelength [20].

Fig. 6
figure 6

The transmission spectra (black solid line) for S1 and theoretical fitting based on the MICMT (red dash line) with \(L_4=\) 264\(\, \text {nm}\), \(L_4=\) 295\(\, \text {nm}\), and \(L_4=\) 480\(\, \text {nm}\), respectively

Full size image

Then, the other two modes are optimized by changing the length of \(L_4\). When \(L_4=295\, \text {nm}\) (the standing wave theoretical value is 338\(\, \text {nm}\)), the transmittance of mode 2 is optimized, falling from 10.3% to 0.27% at 968\(\, \text {nm}\); when \(L_4=480\, \text {nm}\) (the standing wave theoretical value is 523\(\, \text {nm}\)), mode 3 is optimized, dramatically reducing the transmittance from 21.3% to 12.4% at 1481\(\, \text {nm}\), as illustrated by the black line in Fig. 6(b)–(c). The MICMT is also used to analyze the above results as shown by the red dash line in Fig. 6(a)–(c), and the MICMT results are in agreement with the simulation results.

Transmission Optimization for Two Modes

Fig. 7
figure 7

a The schematic diagram of the S3. The transmission spectra (black solid line) for S3 and theoretical fitting based on the MICMT (red dash line) with b \(L_5=\) 264\(\, \text {nm}\) and \(L_6=\) 295\(\, \text {nm}\), c \(L_5=\) 295\(\, \text {nm}\) and \(L_6=\) 480\(\, \text {nm}\), d \(L_5=\) 264\(\, \text {nm}\) and \(L_6=\) 480\(\, \text {nm}\), respectively

Full size image

To enhance both modes at the same time, two rectangular cavities are placed below the main waveguide. This structure is called S3. Despite the fact that a cavity can generate multiple modes, the principle of their resonance is the same. As a result, altering the parameters results in all modes moving simultaneously, making it difficult to enhance two specific modes. Therefore, the simplest solution is to place two cavities underneath, each independently controlling a mode, allowing for dual-mode simultaneous enhancement. At the same time, the distance \(d_3\) between the cavities should be sufficient to avoid the plasma induced transparency effect generated by the coupling between the cavities. Here, it is set to 100 \(\, \text {nm}\).

In S3 of Fig. 7(a), the lengths of the additional resonant cavity are \(L_5\) and \(L_6\), respectively; the distance between the main waveguide and the rectangle cavity is \(d_1=d_2=40\, \text {nm}\). A new parameter, the degree of deviation from the symmetry axis of cavity A is \(t=56\, \text {nm}\). As shown in Fig. 7(b)–(d), mode 1 and mode 2 are optimized when the length of the additional resonant cavity is \(L_5=264\, \text {nm}\), and \(L_6=295\, \text {nm}\). Mode 3 and mode 1 are improved with \(L_5=480\, \text {nm}\), and \(L_6=264\, \text {nm}\). Moreover, mode 2 and mode 3 are enhanced when the parameters are \(L_5=295\, \text {nm}\), and \(L_6=480\, \text {nm}\). In addition, the simulation results (solid black line) are consistent with the theoretical fit curve of MICMT (dashed red line). Table 1 presents the transmittance changes after adding different resonators.

Table 1 Transmittance change at the resonant wavelength before (T) and after (\(T'\)) adding the cavities shown in Fig. 7(b)–(d)
Full size table

Transmission Optimization for Three Modes

Fig. 8
figure 8

a The schematic diagram of the S4. b The transmission spectra (black solid line) for S4 and theoretical fitting based on the MICMT (red dash line)

Full size image
Fig. 9
figure 9

a The transmission spectra of S4 with different refractive indices of the insulator. b The FOM curve of the S4

Full size image

It is inferred from the above analysis that inserting three rectangular cavities beneath the main waveguide can concurrently enhance all three modes of S1. However, the three rectangular cavities arranged side by side dramatically expand the width of Structure 4 (S4). Therefore, symmetry is introduced to enhance all modes of the S1 [11]. S1 is symmetrical around the x-axis to obtain S4 as depicted in Fig. 8(a). The theoretical fitted transmission spectrum of MICMT (red dash line) and the FDTD simulated transmission spectrum (black solid line) are presented in Fig. 8(b). After optimization, the transmittance of mode 1 drops from 5.5% to 1.3%, mode 2 decreases from 10.3% to 4.2%, and mode 3 falls from 21.3% to 8.8%.

Biosensing Properties of Structures

The application of structure in sensing is investigated. Figure 9(a) exhibits that the refractive index of the insulator of S4 transforms in the range of 1 to 1.06, and the transmission spectrum is red-shift. According to the sensitivity formula [26]: \(S={\Delta \lambda }/{\Delta n}\), where \(\Delta \lambda\) and \(\Delta n\) present the variation in resonance wavelength and refractive index relative to those of air, the sensitivity of S1 at 864 \(\, \text {nm}\) is calculated to be 873 \(\, \text {nm}\)/RIU, 964 \(\, \text {nm}\)/RIU at 966 \(\, \text {nm}\) and 1435 \(\, \text {nm}\)/RIU at 1481 \(\, \text {nm}\). Then the sensitivities of the four structures are measured as indicated in Table 2.

Table 2 The sensitivity of S1, S2 (\(L_4=295\, \text {nm}\)), S3 (\(L_5=264\, \text {nm}, L_6=295\, \text {nm}\)), and S4
Full size table

In addition, the figure of merit (FOM) is a crucial factor for evaluating the structure, the quality factor with wavelength can be calculated by [27]:

$$\begin{aligned} FOM=\frac{2({{T}_{2}}-{{T}_{1}})}{({{T}_{2}}+{{T}_{1}})({{n}_{2}}-{{n}_{1}})} \end{aligned}$$
(12)

The FOM curves are depicted in Fig. 9(b). The FOM at the three peaks is 87.31, 78.67, and 61.58, respectively. Subsequently, the FOM of the four structures mentioned in this paper is probed and listed in Table 3. What is striking in Tables 2 and 3 is that S and FOM are optimized.

Table 3 The FOM of S1, S2 (\(L_4=295\, \text {nm}\)), S3 (\(L_5=264\, \text {nm}\), \(L_6=295\, \text {nm}\)), and S4
Full size table
Table 4 The material name, refractive index (n), the resonance wavelength of mode 3, and maximum sensitivity (\(S_{max}\)) of S4
Full size table

Finally, the biosensing property of the proposed structure is as well researched. The sensitivity of S4 to four materials (pepsin, plasma, hemoglobin, and glucose) is investigated. The refractive index of the sample can be obtained from the literature [28,28,30]. Table 4 describes the material name, refractive index (n), the resonance wavelength of mode 3, and the maximum sensitivity (\(S_{max}\)) of S4 when filled with different biomaterials. According to the sensitivity formula, the sensitivity of S4 for detecting four biological samples is 1487\(\, \text {nm}\)/RIU, 1489\(\, \text {nm}\)/RIU, 1482\(\, \text {nm}\)/RIU, and 1483\(\, \text {nm}\)/RIU. The sensitivity of the filter is high enough for biosensing.

Conclusion

A unique three-channel filter made up of four mutually perpendicular rectangular cavities and the main waveguide is presented in this paper. Investigation results display that filtering can be optimized and the number of modes can be increased by adding a particular structure below the main waveguide. This phenomenon can be calculated by the multimode interference coupling theory and standing wave theory, and the theoretical results fit well with the FDTD solutions. Furthermore, the sensitivities and FOM of the four structures are measured and the biosensing properties of the S4 are analyzed. This structure which can achieve transmission optimization and mode enhancement effects can be fully utilized in highly integrated optical circuits.