A Tunable Slow Light Device with Multiple Channels Based on Plasmon-Induced Transparency

Abstract

Slow light devices with buffering capability play a critical role in all-optical signal processing. In this paper, multiple slow light phenomena are implemented based on plasmon-induced transparency (PIT) in our device. The device mainly consists of dual tooth cavities coupled with stub resonators, respectively. Temporal coupled-mode theory model illustrates that the triple PIT phenomena can be achieved based on different formation mechanisms. The simulation results calculated by the finite-difference time-domain method reveal that significant slow light response occurs at two wavelength regions. In addition, the parameters of structure have an important influence on PIT response and slow light characteristics. Moreover, the separate manipulation of wavelength, transmission and group index at transparency peak can be achieved in different slow light channels by adjusting the structural parameters. This plasmonic device is of great significance for the design of optical networks on chips.

Introduction

Electromagnetically induced transparency (EIT) is a quantum interference phenomenon between two different excitation pathways in a three-level atomic system, which can generate a narrow transparency window [1, 2]. It is generally accompanied with sharp dispersion near the transparency window [3]. This attractive phenomenon has various potential applications in the areas of optical data storage, ultrafast switching and slow light devices [4,5,6]. In particular, slow light devices can slow down the propagation speed of optical signals, temporarily store blocked optical signals and resolve resource conflicts in signals transmission [7, 8]. Moreover, the buffering is also required for synchronization, optical time-division multiplexing and optical beamforming [9]. Therefore, slow light propagation has been extensively studied [10, 11]. However, practical implementation of EIT is limited by strict conditions, such as low-temperature environments and stable gas lasers [12,13,14]. Fortunately, plasmon-induced transparency (PIT), an analogous EIT effect, has attracted the attention of researchers [15,16,17]. Compared with EIT, the PIT can remove rigorous implementation conditions. Furthermore, since surface plasmon polaritons (SPPs), a special kind of electromagnetic wave, have the capability of breaking classical diffraction limit, the PIT can be implemented in nanoscale structures [18,19,20,21].

Therefore, many slow light devices based on the PIT have been proposed to achieve slow light phenomena [22,23,24,25]. Among these devices of implementing PIT and slow light effects, for the metal-insulator-metal (MIM) waveguides having the advantages of ease fabrication, strong confinement to SPPs and acceptable propagation length, the MIM waveguides are widely employed [26,27,28]. For example, tunable slow light was analyzed in dual stubs coupled with MIM waveguide [2]. Slow light response was achieved in dual-ring resonator-coupled MIM waveguide system [22]. A stub MIM waveguide coupled with a nanodisk resonator for PIT and slow-light effect was proposed [23]. Although these plasmonic devices have great performance, they can only be used to implement the PIT and slow light effect at a single wavelength. In order to solve the above problem, many plasmonic structures that can implement PIT response and slow light effect with multiple channels are investigated, such as dual coupled stub-nanodisks system [5], MIM stub coupled with two Fabry–Perots structure [24] and aperture-coupled cascade resonators [25]. These structures proposed further improve the integration of the device. However, how to individually manipulate the slow light characteristics at one of the channels without affecting the other channels, which is urgently needed in practical applications, is not discussed in detail.

To meet these demands, a slow light device mainly consisting of two tooth cavities coupled with stub resonators is proposed in this paper. The triple PIT responses are achieved at different wavelengths in the proposed device. The physical mechanisms of their formation are analyzed in detail using temporal coupled-mode theory (CMT) model. The simulation results calculated by finite-difference time-domain (FDTD) method reveal that significant slow light characteristics occurs at two of the wavelengths. Depending on the cause of the formation, we illustrate the methods of manipulating wavelength, transmission and group index at transparency peak for different slow light areas separately. The device proposed will pave the way for buffer technique in highly integrated optical systems.

Structure Model and Theoretical Analysis

Fig. 1

Schematic diagram of the proposed plasmonic slow light device

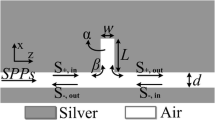
A two-dimensional schematic diagram of the proposed plasmonic structure which mainly consists of dual tooth cavities coupled with stub resonators separately is shown in Fig. 1. The geometric parameters of the structure $l_\mathrm{t1}$, $l_\mathrm{t2}$, $l_\mathrm{s1}$ and $l_\mathrm{s2}$ are the lengths of the tooth$_1$, tooth$_2$, stub$_1$ and stub$_2$ resonators, respectively. The widths of waveguide, tooth cavities and stub resonators are denoted as w. Parameter D means the core-core separation between two tooth resonators, $d_1$ ($d_2$) represents the coupling distance between tooth$_1$ (tooth$_2$) cavity and stub$_1$ (stub$_2$) resonator. The refractive index of dielectric in waveguide and resonators is n. The background metal is supposed to be silver whose frequency-dependent relative permittivity can be characterized by the well-known Drude model [29]:

$$\begin{aligned} \varepsilon _m(\omega )=\varepsilon _\infty -\omega ^2_p/[\omega (\omega +j\gamma )] \end{aligned}$$

(1)

where $\varepsilon _\infty =3.7$, $\omega _p=9.1$ eV and $\gamma =0.018$ eV are the dielectric constant of the infinite frequency, the bulk plasma frequency and the electron collision frequency, respectively. (Drude model with these parameter values can well describe the permittivity at infrared frequencies [30].) The angular frequency of the incident wave is denoted by $\omega$. In this model, since the width of the plasmonic waveguide is much smaller than the wavelength of the incident light, only the TM$_0$ waveguide mode can propagate and dispersion relation for TM$_0$ mode in the MIM waveguide can be obtained by the following equations[31]:

$$\begin{aligned} (\varepsilon _m k_d)tanh(\frac{w k_d}{2})+\varepsilon _d k_m=0 \end{aligned}$$

(2)

$$\begin{aligned} k_{d,m}=\sqrt{\beta ^2-\varepsilon _{d,m}k_0^2} \end{aligned}$$

(3)

where $\varepsilon _d$, $\varepsilon _m$, $k_d$, $k_m$, respectively, represent the permittivities and propagation constants of the dielectric and metal. The wave vector $\beta$ in the waveguide can be expressed as $\beta$ = $k_0$ $n_{eff}$, in which $k_0$ = $2\pi /\lambda$ stands for the wave vector in vacuum and $n_{eff}$ is the effective refractive index in plasmonic waveguide.

When the incident light is injected, the SPPs are formed on the metallic surfaces and propagate along bus waveguide. When resonance condition is satisfied, SPPs can be coupled directly to the tooth cavities from bus waveguide and coupled indirectly into the stub resonators through the tooth cavities. The resonance condition of tooth$_\mathrm{i}$ cavity and stub$_\mathrm{i}$ resonator ($i=1,2$) can be, respectively, described as[32, 33]:

$$\begin{aligned} 2Re(N_{eff})l_\mathrm{ti}\frac{2\pi }{\lambda _{tim}}+\Delta \phi _{ti}=&(2m+1)\pi \end{aligned}$$

(4)

$$\begin{aligned} 2Re(N_{eff})l_\mathrm{si}\frac{2\pi }{\lambda _{sin}}+\Delta \phi _{si}=&2n\pi \end{aligned}$$

(5)

where $Re(N_{eff})$ means the real part of the effective refractive index in the tooth and stub cavities, $\lambda _{tim}$ and $\lambda _{sin}$ are resonance wavelengths of tooth$_\mathrm{i}$ cavity and stub$_\mathrm{i}$ resonator, m is a non-negative integer and n is a positive integer. The additional phase shifts $\Delta \phi _{ti}$ and $\Delta \phi _{si}$ are caused by reflection on the interface of dielectric and metal in the tooth$_\mathrm{i}$ cavity and stub$_\mathrm{i}$ resonator, respectively.

Transmission characteristics of the structure can be investigated according to the CMT model. As shown in Fig. 1, $t_1$, $r_1$, $t_2$ and $r_2$ represent the transmission and reflection coefficients of the tooth$_1$ and tooth$_2$. For obtaining the transmission coefficients $t_\mathrm{i}$ and reflection coefficients $r_\mathrm{i}$ of the device, we first analyze the transmission characteristics of a single tooth cavity coupled with stub resonator. Figure 2 illustrates the cross section schematic diagram of single tooth cavity coupled with stub resonator.

Fig. 2

Schematic diagram of single tooth cavity coupled with stub resonator

The temporal evolution of the normalized amplitude $a_i$ of the tooth$_\mathrm{i}$ resonator can be written as[34]:

$$\begin{aligned} \begin{aligned} \frac{da_i}{dt}=&(j\omega _i-k_{oi}-k_{wi}-k_{si})a_i+e^{j\varphi _{wi}}\sqrt{k_{wi}}(S^{i}_{+in}\\ {}&+S^{i}_{-in})+e^{j\varphi _{si}}\sqrt{2k_{si}}S^{i}_{+si} \end{aligned} \end{aligned}$$

(6)

where $\omega _i$ means the resonance frequency of tooth$_\mathrm{i}$ resonator, $k_{oi}$, $k_{wi}$ and $k_{si}$ stand for decay rate due to internal loss in the tooth$_\mathrm{i}$, the decay rate induced by the energy escape into the bus waveguide and stub$_\mathrm{i}$ resonator, respectively. The phases of the coupling coefficients are denoted by $\varphi _{wi}$ and $\varphi _{si}$. As shown in Fig. 2, $S^{i}_{\pm {in}}$ represent the amplitudes of the inputting waves in the MIM waveguide, subscript ± mean two propagating directions of waveguide modes. In addition, the amplitudes $S^{i}_{\pm si}$ of inputting and outgoing waves in the stub$_\mathrm{i}$ resonator should satisfy a steady-state relation:

$$\begin{aligned} S^{i}_{-si} = -S^{i}_{+si} + e^{-j\varphi _{si}}\sqrt{2k_{si}}a_i \end{aligned}$$

(7)

$$\begin{aligned} S^{i}_{+si} = \delta _i e^{j\phi _i}S^{i}_{-si} \end{aligned}$$

(8)

where $\delta _i$ and $\phi _i=2l_\mathrm{si}\omega Re(N_{eff})/c+\theta _i$ represent the amplitude attenuation and the phase difference between the incoming and outgoing waves of the stub$_\mathrm{i}$ resonator, $\theta _i$ means the additional phase shift in the stub$_\mathrm{i}$ resonator. In the linear system, the field everywhere oscillates as $e^{j\omega _it}$ and $da_i/dt = j\omega _ia_i$. Since the light is only inputted into bus waveguide from the left port ($S^{i}_{-in}=0$), according to the above equations, amplitude $a_i$ of the stub$_\mathrm{i}$ resonator is derived as:

$$\begin{aligned} \begin{aligned} a_i=\frac{e^{j\varphi _{wi}}\sqrt{k_{wi}}S^i_{+in}}{j(\omega _i-\omega )+k_{oi}+k_{wi}+k_{si}-\frac{2k_{si}\delta _ie^{j\phi _i}}{1+\delta _i e^{j\phi _i}}} \end{aligned} \end{aligned}$$

(9)

Based on energy conservation, the amplitudes $S^{i}_{\pm out}$ of the outgoing waves can be expressed as:

$$\begin{aligned} S^{i}_{-out} = S^{i}_{-in} - e^{-j\varphi _{wi}}\sqrt{k_{wi}}a_i \end{aligned}$$

(10)

$$\begin{aligned} S^{i}_{+out} = S^{i}_{+in} - e^{-j\varphi _{wi}}\sqrt{k_{wi}}a_i \end{aligned}$$

(11)

According to the above equations, the transmission $T_{i}$ of the single tooth cavity coupled with stub resonator structure can be deduced as:

$$\begin{aligned} \begin{aligned} T_i&=\left| \frac{S^i_{+out}}{S^i_{+in}}\right| ^2=\left| \frac{j(\omega _i-\omega )+k_{oi}+k_{si}\frac{1-\delta _i e^{j\phi _i}}{1+\delta _i e^{j\phi _i}}}{j(\omega _i-\omega )+k_{oi}+k_{wi}+k_{si}\frac{1-\delta _i e^{j\phi _i}}{1+\delta _i e^{j\phi _i}}}\right| ^2 \end{aligned} \end{aligned}$$

(12)

Obviously, as coupling distance $d_\mathrm{i}$ increases, $k_{si}$ will gradually decrease. When tooth$_\mathrm{i}$ cavity and stub$_\mathrm{i}$ resonator are no longer interaction ($k_{si} = 0$), equation (12) is modified as:

$$\begin{aligned} \begin{aligned} T_s=\left| \frac{j(\omega _i-\omega )+k_{oi}}{j(\omega _i-\omega )+k_{oi}+k_{wi}}\right| ^2 \end{aligned} \end{aligned}$$

(13)

When $\omega =\omega _i$, transmission $T_s$ approximately equals 0 under the condition of $k_{oi}$ $\ll$ $k_{wi}$, which is consistent with the transmission of the band-stop filter based on SPPs. By comparing equation (12) and (13), it can be seen that due to the interaction between tooth$_\mathrm{i}$ cavity and stub$_\mathrm{i}$ resonator, the EIT-like response occurs, which means that a recess is generated at the original absorption peak and a transparency window is formed. Moreover, based on the above analyses, we can obtain the transmission and reflection coefficients of the single tooth$_\mathrm{i}$ cavity coupled with stub$_\mathrm{i}$ resonator as follows:

$$\begin{aligned} \begin{aligned} t_i=\frac{j(\omega _i-\omega )+k_{oi}+k_{si}\frac{1-\delta _i e^{j\phi _i}}{1+\delta _i e^{j\phi _i}}}{j(\omega _i-\omega )+k_{oi}+k_{wi}+k_{si}\frac{1-\delta _i e^{j\phi _i}}{1+\delta _i e^{j\phi _i}}} \end{aligned} \end{aligned}$$

(14)

$$\begin{aligned} \begin{aligned} r_i=\frac{k_{wi}}{j(\omega _i-\omega )+k_{oi}+k_{wi}+k_{si}\frac{1-\delta _i e^{j\phi _i}}{1+\delta _i e^{j\phi _i}}} \end{aligned} \end{aligned}$$

(15)

Consequently, feedback and transmitted waves of the ith tooth cavity can be expressed as following matrix:

$$\begin{aligned} \begin{bmatrix}S^i_{-in}\\ S^i_{+out}\end{bmatrix}=\begin{bmatrix}-\frac{r_i}{t_i}\quad \frac{1}{t_i}\\ \\ {1+\frac{r_i}{t_i}}\quad \frac{r_i}{t_i}\end{bmatrix}\begin{bmatrix}S^i_{+in} \\ S^i_{-out}\end{bmatrix} \end{aligned}$$

(16)

According to the above equation, the feedback and transmitted waves of the proposed device can be obtained as:

$$\begin{aligned} \begin{bmatrix}S_{-in}\\ S_{+out}\end{bmatrix}=\begin{bmatrix}-\frac{r_2}{t_2}\quad \frac{1}{t_2}\\ \\ {1+\frac{r_2}{t_2}}\quad \frac{r_2}{t_2}\end{bmatrix}\begin{bmatrix}0\quad e^{j\theta '}\\ \\ e^{-j\theta '}\quad 0\end{bmatrix}\begin{bmatrix}-\frac{r_1}{t_1}\quad \frac{1}{t_1}\\ \\ {1+\frac{r_1}{t_1}}\quad \frac{r_1}{t_1}\end{bmatrix}\begin{bmatrix}S_{+in} \\ S_{-out}\end{bmatrix} \end{aligned}$$

(17)

where $\theta '=\omega Re(n_{eff})D/c$ is the phase difference between the 1st and 2nd tooth cavities. When the incident light is launched only from the left port in device ($S_{-in} = 0$), the transmission efficiency T at the output port can be derived as:

$$\begin{aligned} T=\left| \frac{S_{+out}}{S_{+in}}\right| ^2=\left| \frac{t_1t_2}{1-r_1r_2e^{j2\theta '}}\right| ^2 \end{aligned}$$

(18)

When the separation D is set to 0, the smallest device size and the maximum transmission can be obtained. The maximum transmission can be written as:

$$\begin{aligned} T_{max}=\left| \frac{S_{+out}}{S_{+in}}\right| ^2=\left| \frac{t_1t_2}{1-r_1r_2}\right| ^2 \end{aligned}$$

(19)

According to the above analyses, we know that transmission characteristics of proposed device are not only related to interference between radiative (directly coupled to waveguide) resonators and subradiant (indirectly coupled to waveguide) resonators but also include phase coupling mechanism. In addition, from the previous derivation, working wavelengths can be selected by changing the lengths of tooth and stub cavities as shown in equation (4) and (5). Transmission of device can be manipulated by adjusting the coupling distance $d_\mathrm{i}$ since the coupling distances $d_\mathrm{i}$ are related to the transmission coefficients $t_{i}$ and reflection coefficients $r_{i}$ as illustrated in equation (12) and (13).

Fig. 3

(a) Transmission spectra at output port of proposed device calculated by the CMT and FDTD methods. Filed distributions of $H_Z$ in the proposed device with the incident light wavelength of (b) 819.1 nm, (c) 855.9 nm, (d) 897.6 nm, (e) 1114.5 nm, (f) 1260.6 nm, (g) 1314.3 nm and (h) 1364.9 nm

Fig. 4

(a) Transmission phase shift, (b) delay time and (c) group index at the PIT$_1$ window. (d) Transmission phase shift, (e) delay time and (f) group index at the PIT$_2$ window

Results and Discussions

Transmission Characteristics

We take 2-D FDTD method to further investigate the transmission characteristics of the device. The mode source is introduced to excite fundamental TM mode of the waveguide and perfectly matched layer (PML) is utilized as boundary conditions. The spatial steps and temporal step are set as $\Delta x=\Delta y=4$ nm and $\Delta t=\Delta x/1.43c$. First of all, the parameters of structure are set as $l_\mathrm{t1}=120$ nm, $l_\mathrm{s1}=260$ nm, $l_\mathrm{t2}=200$ nm, $l_\mathrm{s2}=420$ nm, $d_1=25$ nm and $d_2=20$ nm. In order to fix the characteristics of guided modes, the widths of waveguide and resonators are set as a constant (50 nm) in this paper. The dielectric embedded in the waveguide and resonators is regarded as air. Figure 3a shows the transmission spectra of the device calculated by the theory and simulation. As drawn in Fig. 3a, triple PIT windows can be observed and central wavelengths, respectively, are located at $\lambda _B$ = 855.9 nm, $\lambda _D$ = 1114.5 nm and $\lambda _F$ = 1314.3 nm. The transmission efficiencies of transparency peak reach 50%, 90% and 42%, respectively, between the four resonance dips at $\lambda _A$ = 819.1 nm, $\lambda _C$ = 897.6 nm, $\lambda _E$ = 1260.6 nm and $\lambda _G$ = 1364.9 nm, which are typical representation of PIT.

The field distributions of $H_Z$ at the transmission peaks and resonance dips represented by A, B, C, D, E, F and G are sketched in Figs. 3b-h. According to the previous theoretical analysis and field distributions, two transparency windows are formed by interaction between tooth$_\mathrm{i}$ cavity and stub$_\mathrm{i}$ resonator: transparency window with a central wavelength at 855.9 nm (PIT$_1$ window) and transparency window with a central wavelength at 1314.3 nm (PIT$_2$ window). The formation of transparency window with a central wavelength at 1114.5 nm (PIT$_3$ window) originates from the phase interference between the two tooth cavities. Moreover, PIT$_1$ (PIT$_2$) is mainly formed by the interaction of tooth$_1$ (tooth$_2$) cavity and stub$_1$ (stub$_2$) resonator. Therefore, the transmission characteristics of PIT$_1$ window or PIT$_2$ window can be individually manipulated by adjusting the structural parameters.

Slow Light Effect

The results calculated by FDTD method reveal that phase shift exhibits a sharp dithering at PIT$_1$ and PIT$_2$ windows, which means that obvious slow light phenomenon appeared at the two transparency windows. The group index $n_g$ of the device affects buffering time of signal, and physical significance of group index not only includes the meaning of refractive index but also reflects the dispersion properties. Therefore, the slow light characteristic can be expressed by the group index, which is denoted by following equation:

$$\begin{aligned} n_g=\frac{c}{v_g}=\frac{c}{L}\tau _g=\frac{c}{L}\frac{d\psi (\omega )}{d\omega } \end{aligned}$$

(20)

where $v_g$, $\tau _g$ and L are group velocity, optical delay time and the length of the plasmonic structure, respectively. The transmission phase shift $\psi (\omega )$ is a function of angular frequency $\omega$, which can be obtained by $\psi (\omega )$ = angular $(S_{+out}/S_{+in})$.

We numerically investigated the slow light behavior of the device with the length L is set to 500 nm. Figure 4a shows the transmission phase shift at PIT$_1$ window. The phase jitter at PIT$_1$ window results in delay time at PIT$_1$ window and the delay time of peak B reaches maximum value 0.06 ps, as depicted in Fig. 4b. Based on equation (20), the group index at PIT$_1$ window is plotted, as shown in Fig. 4c. The strong dispersion around the transparency window leads to high group indices and maximum group index at peak of PIT$_1$ window is over 34. Similarly, Figs. 4d-f illustrate the phase shift, delay time and group index at PIT$_2$ window. The results show that the maximal group delay time and group index reach 0.074 ps and 44 at peak of PIT$_2$ window, respectively. Therefore, different slow light areas are achieved at commonly used wavebands.

Influence of Structural Parameters

As we have analyzed in the previous theory, the controllability of the transmission characteristics can be achieved by adjusting the lengths of resonators and coupling distances, for example, selected operating wavelengths and variable transmissions. For verifying the previous analyses, sweeps of the numerical parameters are performed. Above all, the impacts of the length $l_\mathrm{t1}$ and length $l_\mathrm{s1}$ on the transmission characteristics are analyzed. The length $l_\mathrm{t1}$ is taken from 110 nm to 130 nm with an interval of 5 nm. In order to ensure the detuning state of the resonant wavelength between tooth$_1$ and stub$_1$ resonator remains invariable, the length $l_\mathrm{s1}$ satisfies the formula $l_\mathrm{s1} = 2l_\mathrm{t1} + a$. The parameter a is set to 20 nm, and other parameters are fixed to $l_\mathrm{t2}=200$ nm, $l_\mathrm{s2}=420$ nm, $d_1=25$ nm and $d_2=20$ nm. As the length $l_\mathrm{t1}$ and length $l_\mathrm{s1}$ increase, the variation of transparency peak wavelengths at PIT$_1$ and PIT$_2$ windows is plotted in Fig. 5a. It is noteworthy that the central wavelength of PIT$_1$ window exhibits a red-shift with the increase of length $l_\mathrm{t1}$ and length $l_\mathrm{s1}$, which is basically a linear relationship. Meanwhile, the resonance wavelength of PIT$_2$ is barely changed. So, we can manipulate the central wavelength of PIT$_1$ window without affecting PIT$_2$ by changing the length $l_\mathrm{t1}$ and length $l_\mathrm{s1}$.

Then, we investigate the influence of the length $l_\mathrm{t2}$ and length $l_\mathrm{s2}$ on the transmission characteristics. Length $l_\mathrm{t2}$ increases from 190 nm to 210 nm with the step size of 5 nm. The length $l_\mathrm{s2}$ is expressed as $l_\mathrm{s2} = 2l_\mathrm{t2} + a$ and the other parameters remain unchanged. Figure 5b illustrates the variation of central wavelengths at PIT$_1$ and PIT$_2$ windows. As the Length $l_\mathrm{t2}$ and Length $l_\mathrm{s2}$ increase, central wavelength of PIT$_2$ window exhibits red-shift while resonance wavelength of PIT$_1$ has almost no movement. Therefore, by adjusting the length $l_\mathrm{t2}$ and length $l_\mathrm{s2}$, the transparency peak wavelength of PIT$_2$ can be individually manipulated.

Fig. 5

(a) Variation tendency of the transparency peak wavelengths at PIT$_1$ and PIT$_2$ windows as length $l_\mathrm{t1}$ and length $l_\mathrm{s1}$ increase. (b) Variation tendency of the transparency peak wavelengths at PIT$_1$ and PIT$_2$ windows as length $l_\mathrm{t2}$ and length $l_\mathrm{s2}$ increase

Fig. 6

(a) The transmission at peak of PIT windows as functions of coupling distance $d_1$. (b) The relationship between group index at peak of PIT windows and the coupling distance $d_1$

Fig. 7

(a) The transmission at peak of PIT windows as functions of coupling distance $d_2$. (b) The relationship between group index at peak of PIT windows and the coupling distance $d_2$

As we all know, transmission and group index are important indicators for a slow light device. Next, we explore the effects of coupling distance $d_1$ on the transmission and group index. The coupling distance $d_1$ is varied from 10 nm to 35 nm in steps of 5 nm whereas other parameters are kept fixed. Figure 6a depicts the relationship between transmission of transparency peak at PIT$_1$ and coupling distance $d_1$. As the coupling distance $d_1$ increases, the transmission at transparency peak of PIT$_1$ gradually decreases. However, the group index at transparency peak of PIT$_1$ gradually increases, as drawn in Fig. 6b. There is a trade-off problem between the group index and the transmission through calculation. In order to achieve appropriate transmission and higher group index at the same time, the coupling distance $d_1$ is set to 25 nm in this paper. In addition, it can be observed from Figs. 6a, b that the transmission and the group index at central wavelength of PIT$_2$ window are hardly affected when coupling distance $d_1$ increases. This provides a method of manipulating the transmission and group index of central wavelength at PIT$_1$ window without affecting the slow light characteristics of PIT$_2$ window.

Finally, the relationship between the coupling distance $d_2$ and slow light characteristics are researched. The coupling distance $d_2$ is taken from 10 nm to 35 nm with an interval of 5 nm, while the other parameters remain invariable. As the coupling distance $d_2$ increases, the variation in the transmission and group index at transparency peak of PIT$_1$ and PIT$_2$ is shown in Figs. 7a, b. Contrary to the consequence of adjusting coupling distance $d_1$, when the coupling distance $d_2$ increases, the transmission and group index at transparency peak of PIT$_1$ are barely influenced. Meanwhile, the transmission and group index at central wavelength of PIT$_2$ window present a tendency to decrease and increase, respectively. Therefore, we can manipulate the transmission and group index at transparency peak of PIT$_2$ separately. The coupling distance $d_2$ is set to 20 nm for obtaining higher transmission and group index simultaneously in this paper.

Conclusion

In summary, we proposed a novel plasmonic structure mainly consisting of two tooth cavities coupled with stub resonators, respectively. Triple PIT windows are implemented based on different formation mechanisms and the reasons of formation are analyzed in detail using CMT model. Simulation results calculated by the FDTD method demonstrate that the obvious slow light responses at PIT$_1$ and PIT$_2$ windows are achieved. In addition, we can separately manipulate the transmission characteristics of PIT$_1$ and PIT$_2$ windows, including the wavelength, transmission and group index of transparency peak. The proposed plasmonic slow light device has many potential applications in highly integrated photonic loop.