Assessment and calibration of two models for estimation of soil nail loads and system reliability analysis of soil nails against internal failures

Abstract

This study first presents accuracy assessments of two default models proposed in two popular soil nail wall design specifications and their calibrated versions for estimation of maximum soil nail loads under operational conditions. The assessments are based on a general nail load database reported in the literature. Evaluation results showed that predictions using the default and calibrated models are unsatisfactory as the dispersions are high to extremely high. Simple calibration terms are introduced to the calibrated models for performance enhancement. The recalibrated models are shown to be accurate on average, and the prediction dispersions are significantly reduced. The model biases for the above six models are demonstrated to be lognormal random variables. Individual reliability-based designs for the nail pullout and nail-in-tension limit states using the six models are carried out. System reliability of nails against internal failures is also explored. The correlation between the two limit states is investigated, and its influences on system reliability evaluation are discussed. The practical value of model calibration is demonstrated as using the recalibrated models for nail designs leads to the most cost-effective design outcomes. This study represents a solid step toward development of reliability-based design framework for soil nail walls.

1 Introduction

Estimation of the maximum tensile load that a soil nail would sustain during its service life is an important step for design of soil nail walls against internal failures, including nail pullout and nail-in-tension limit states. In China, soil nail walls are usually designed according to either one of the two national specifications: Technical Specification for Retaining and Protection of Building Foundation Excavations by China Academy of Building Research (CABR) [7] or Specifications for Soil Nailing in Foundation Excavations by China Association for Engineering Construction Standardization (CECS) [10]. Each specification proposes a default model for estimation of soil nail loads. In this study, the nail load models in the two specifications are referred to as the default CABR and CECS models, respectively.

The current design practice for soil nail walls is still based on deterministic allowable stress methods, e.g., [7, 10, 19, 33]. However, reliability-based design approaches have been advocated in recent years, e.g., [13, 18, 21, 23, 38, 50, 52, 55]. Characterizing nail load model uncertainty is a precursor for reliability-based design of soil nail walls against internal failures. Model uncertainty has been widely recognized as one of the primary sources of uncertainty in geotechnical reliability-based designs, e.g., [12, 14, 15, 35]. Usually, the model uncertainty of a model can be quantitatively characterized by comparing measured values against its predicted values. By defining the ratio of measured to predicted value as model bias, the mean and coefficient of variation (COV) of a model bias represent the on-average prediction accuracy and prediction dispersion of the model, respectively. Obviously, it is preferred to have as many measured values as possible for estimating the statistics of a model bias. That is to say, as more measured values are cumulated, statistics of a model bias should be updated from time to time.

The prediction accuracy of the default CABR and CECS nail load models was evaluated by Yuan et al. [45] using 144 measured nail loads they collected from the literature. They concluded that overall the default CABR and CECS are conservative as they would overestimate nail loads by about 40% on average. In addition, the dispersion in prediction using the two default models is very high. They then proposed empirical correction terms to the two default models for accuracy improvement. In this study, their corrected models are referred to as the calibrated CABR and CECS models, respectively. Recently, Lin et al. [28] compiled a general nail load database containing a total of 312 measured nail load data they collected from the literature, including the 144 data reported by Yuan et al. [45]. They first utilized the broad database to both evaluate and calibrate the default Federal Highway Administration (FHWA) simplified soil nail model. Then, they developed an artificial neural network model for mapping soil nail loads. Through that, the opportunity of applying machine learning approaches in design of soil nail walls was demonstrated. Reviews of prediction models for soil nail loads can be found in Yuan et al. [45] and Lin et al. [28].

The first research task this study takes on is to reevaluate the accuracies of the default and calibrated CABR and CECS models using the general nail load database established by Lin et al. [28]. It is found that both the default and calibrated models are unsatisfactory due to excessively high dispersions in prediction. Simple empirical correction terms are then introduced to the calibrated models for performance enhancement. The recalibrated models are shown to be accurate on average and have much less prediction dispersions.

As the model uncertainty on the load side is characterized, the second research task in this study is to perform thorough reliability analysis and design of soil nail walls against internal failures (i.e., nail pullout and nail-in-tension limit states) using the default, calibrated, and recalibrated models. Reliability analyses of individual internal limit states of soil nail walls and similar reinforced soil walls have been extensively reported, for example Chalermyanont and Benson [11], Low [30], Basha and Sivakumar Babu [2], and Kim and Salgado [16, 17]. Nevertheless, none has used the CABR and CECS nail load models for reliability analyses. Hence, previous results may not be straightforwardly indicative to soil nail wall design engineers in China. In addition, only a few previous studies considered model uncertainty in the analyses.

Another point of interest is the system reliability of nail internal stability. Here, system reliability is defined as the reliability that neither of the nail pullout and nail-in-tension failures occurs. This definition is consistent with those by Zevgolis and Daffas [50], and Yuan and Lin [44]. Zevgolis and Daffas [50] presented system reliability analyses of soil nail walls; however, model uncertainty was not addressed in their study. Yuan and Lin [44] investigated the internal system reliability of nails designed in USA, where the nail load model is very different from the CABR and CECS models used in China. System reliability analyses were also reported for other reinforced soil walls, e.g., Zevgolis and Bourdeau [47,48,49]. In this study, the system reliability of nail internal stability using the CABR and CECS models is investigated. The two internal limit states are shown to be correlated as their performance functions share same nail load terms. The correlation is presented in detail based on an example wall, including its magnitude and influences on evaluation of system reliability. Through the example analysis, the practical value of using the recalibrated CABR and CECS models for soil nail design is demonstrated.

2 Performance functions for internal stabilities of soil nails

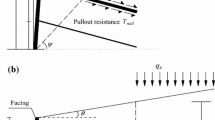
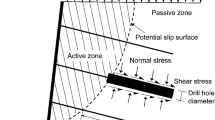
A soil nail wall system typically consists of three main components, including nails, in situ soils, and the wall facing. Figure 1 shows the cross-sectional profile of a typical soil nail wall, which is usually divided into two zones, i.e., a passive zone and an active zone, by a potential slip surface. In the two soil nail wall design specifications in China [7, 10], the potential slip surface is assumed to be planar. The same assumption is adopted in the Federal Highway Administration (FHWA) soil nail wall design manual [19] and many studies (e.g., [21, 25, 36, 38, 44]) reported in the literature. The soil mass in the active zone tends to slide along the slip surface, which exerts active earth pressure to the facing of the wall. As nails are structurally connected to the facing, the earth pressure acting on the facing propagates to nails, resulting in tensile loads along soil nails under operational conditions. As such, two limit states must be considered for the internal stability of soil nails, as described in the following.

Fig. 1

Cross-sectional profile of a typical soil nail wall

2.1 Nail pullout limit state

When the maximum tensile load that a nail carries exceeds its ultimate pullout capacity, the nail fails due to pullout. Suppose a nail is subjected to both dead load and live load, then the performance function for the pullout limit state, $g_{p}$, can be formulated as (e.g., [44]):

$$g_{p} = \lambda_{p} P_{n} - \lambda_{D} T_{D} - \lambda_{L} T_{L}$$

(1)

where $P_{n}$, $T_{D}$, and $T_{L}$ are predicted pullout capacity, dead load, and live load of a nail, respectively, and $\lambda_{p}$, $\lambda_{D}$, and $\lambda_{L}$ are model biases accounting for discrepancies in $P_{n}$, $T_{D}$, and $T_{L}$ from their true values, respectively. Commonly, model bias is defined as the ratio of measured to predicted value of the variable of interest.

For the ultimate pullout capacity, it can be computed as [7, 10, 19, 33]:

$$P_{n} = \pi DL_{e} q_{u}$$

(2)

where $D$ is nail drill hole diameter; $L_{e}$ is effective nail length as shown in Fig. 1, and $q_{u}$ is ultimate bond strength at the nail–soil interface. Both the CABR and CECS soil nailing design specifications suggest preliminary values for $q_{u}$ based on soil type and provide guidance on how to select the $q_{u}$ value for nail design.

For nail dead load, $T_{D}$, different default computation models are adopted in the CABR and CECS design specifications. For CABR, the default nail load model is expressed as [7]:

$$T_{D} = \zeta \eta P_{a} S_{h} S_{v} /\cos i$$

(3)

where $\zeta$ is a load reduction factor accounting for wall facing inclination and overall soil stiffness; $\eta$ is a load adjustment factor accounting for the overall effect of wall height, nail depth, nail tributary area, and total number of nail rows; $P_{a}$ is active earth pressure using Rankine’s theory; $S_{h}$ and $S_{v}$ are horizontal and vertical nail spacing, respectively, and $i$ is nail inclination angle. For the load reduction factor, $\zeta$, it is computed as

$$\zeta = \frac{{\tan \left( {45^{\circ} - \frac{{\alpha + \phi_{m} }}{2}} \right)\left[ {\frac{1}{{\tan \left( {45^{\circ} - \frac{{\alpha - \phi_{m} }}{2}} \right)}} - \frac{1}{\cot \left( \alpha \right)}} \right]}}{{\tan^{2} \left( {45^{\circ} - \frac{{\phi_{m} }}{2}} \right)}}$$

(4)

where $\alpha$ is wall face batter angle from the vertical and $\phi_{m} = \mathop \sum \nolimits_{j = 1}^{j = k} h_{j} \phi_{j} /\mathop \sum \nolimits_{j = 1}^{j = k} h_{j}$ is the weighted average soil friction angle for soil layers within the height of the wall. Here, $h_{j}$ and $\phi_{j}$ are thickness and soil friction angle of the $j$th soil layer, respectively, and $k$ is the number of soil layers within the wall height. Yuan et al. [45] showed that for vertical walls where $\alpha = 0^{\circ}$, $\zeta$ is equal to 1, irrespective of $\phi_{m}$, while for inclined walls where $\alpha > 0^{\circ}$, the more inclined the wall, the stiffer the soil, the smaller the $\zeta$ value.

The load adjustment factor, $\eta$, is a nail-specific parameter. For nails in the $j$th row from the top of the wall, the load adjustment factor, $\eta_{j}$, is computed as

$$\eta_{j} = \eta_{a} - \left( {\eta_{a} - \eta_{b} } \right)\frac{{z_{j} }}{H}$$

(5)

where $\eta_{b}$ is an empirical constant that can be selected between 0.6 and 1.0 by the design engineer; $z_{j}$ is the depth of the $j$th row nails; $H$ is wall height; and $\eta_{a}$ is another empirical factor calculated as:

$$\eta_{a} = \frac{{\mathop \sum \nolimits_{j = 1}^{j = N} \left( {H - \eta_{b} z_{j} } \right)P_{aj} A_{j} }}{{\mathop \sum \nolimits_{j = 1}^{j = N} \left( {H - z_{j} } \right)P_{aj} A_{j} }}$$

(6)

where $A_{j}$ is the tributary area of the $j$th nail and $N$ is the total number of nail rows. In practice, for simplification purposes, $\eta_{b}$ is commonly taken as 1.0 [45]. This results in $\eta_{a} = 1.0$ and thus $\eta = 1.0$. In this study, $\eta = 1.0$ is adopted.

In the CECS specification, the default model to calculate the nail load $T_{D}$ is:

$$T_{D} = \mathop \int \limits_{{z - S_{v} /2}}^{{z + S_{v} /2}} P_{z} S_{h} {\text{d}}z + K_{a} q_{s} S_{h} S_{v}$$

(7)

where $P_{z}$ is the empirical earth pressure at depth $z$; $K_{a}$ is the active earth pressure coefficient; and $q_{s}$ is the surcharge dead load if exists. For $0 \le z \le 0.25H$, $P_{z} = \frac{z}{0.25H}P_{m}$, whereas for $z > 0.25H$, $P_{z} = P_{m}$. Parameter $P_{m}$ is an empirical term relating to soil types (i.e., cohesive or cohesionless) that are classified based on $c/\gamma H$ with $c$ being soil cohesion. If $c/\gamma H > 0.05$, the soil is conceived as “cohesive” and $P_{m}$ is calculated as

$$0.2\delta \gamma H \le P_{m} = \delta K_{a} \left( {1 - \frac{2c}{{\gamma H\sqrt {K_{a} } }}} \right)\gamma H \le 0.55\delta K_{a} \gamma H$$

(8)

where $\delta$ is a depth factor equal to $z/0.25H$ if $z < 0.25H$, and 1 if $z \ge 0.25H$. On the other hand, if $c/\gamma H \le 0.05$, the soil is conceived as “cohesionless” and the corresponding $P_{m}$ is

$$P_{m} = 0.55\delta K_{a} \gamma H$$

(9)

Yuan et al. [45] compiled a database containing 147 measured maximum nail loads from fully instrumented soil nail walls built and monitored in China. They then evaluated the accuracies of the default CABR [Eq. (3)] and CECS [Eq. (7)] models based on their database. The two default models were shown to overestimate the maximum nail loads by about 40% on average with high to very high dispersions in the predictions. Here, the level of dispersion is based on the four-tier classification scheme proposed by Phoon and Tang [35]. To improve the prediction accuracy, Yuan et al. [45] introduced correction factors, $M_{1}$, to each of the two default models for calibration. For the CABR model, the correction factor is $M_{1} = C_{0} \ln \left( {z/H} \right) + C_{z}$, while for the CECS model, $M_{1} = C_{0} \exp \left( {C_{z} z/H + C_{\alpha } \alpha /\alpha_{0} } \right)$. Here, $C_{0}$, $C_{z}$, and $C_{\alpha }$ are all empirical constants, which can be determined through optimization using the compiled database and $\alpha_{0}$ is a constant used to normalize wall face batter angle $\alpha$. As such, their calibrated CABR and CECS models are, respectively, expressed as [45]:

$$T_{D} = M_{1} \zeta \eta P_{a} S_{h} S_{v} /\cos i = \left[ {C_{0} \ln \left( {\frac{z}{H}} \right) + C_{z} } \right]\zeta \eta P_{a} S_{h} S_{v} /\cos i$$

(10)

$$\begin{aligned} T_{D} = & M_{1} \mathop \int \limits_{{z - S_{v} /2}}^{{z + S_{v} /2}} P_{z} S_{h} {\text{d}}z + K_{a} q_{s} S_{h} S_{v} \\ = & \left[ {C_{0} \exp \left( {C_{z} z/H + C_{\alpha } \alpha /\alpha_{0} } \right)} \right]\mathop \int \limits_{{z - S_{v} /2}}^{{z + S_{v} /2}} P_{z} S_{h} {\text{d}}z + K_{a} q_{s} S_{h} S_{v} \\ \end{aligned}$$

(11)

When a soil nail wall is subjected to uniformly distributed surcharge live load, $q_{L}$, on the top of the wall in addition to gravitational dead loads, the term $T_{L}$ in Eq. (1) can be computed as [7, 10]:

$$T_{L} = K_{a} q_{L} S_{h} S_{v}$$

(12)

It is re-clarified here that Eqs. (3) and (10) are referred to as the default and calibrated CABR models, respectively; Eqs. (7) and (11) are referred to as the default and calibrated CECS models, respectively, for the estimation of maximum nail loads under operational conditions.

2.2 Nail-in-tension limit state

The same load terms apply to the nail-in-tension limit state. When the maximum tensile load in a nail exceeds its tensile yielding capacity, the nail is said to fail due to tension. The performance function for nail-in-tension limit state, $g_{t}$, is written as (e.g., [44]):

$$g_{t} = \lambda_{t} T_{t} - \lambda_{D} T_{D} - \lambda_{L} T_{L}$$

(13)

where $T_{t}$ is nail tensile yielding capacity; $\lambda_{t}$ is model bias for $T_{t}$; and $T_{D}$, $T_{L}$, $\lambda_{D}$, and $\lambda_{L}$ are the same as those in Eq. (1) for the pullout limit state. The term $T_{t}$ can be computed as (e.g., [7, 10, 19, 21]):

$$T_{t} = \pi d^{2} f_{y} /4$$

(14)

where $d$ is nail bar diameter and $f_{y}$ is tensile yielding strength of the steel bar. Note that the grout column also contributes to the total tensile yielding capacity of a nail; nevertheless, the contribution from the grout column is far less than that from the steel bar (nail tendon), and as a result, it is commonly neglected in practice [21].

2.3 System reliability of internal stability

A nail is said to fail due to pullout when the maximum tensile load exceeds the ultimate pullout capacity. In this case, we have $g_{p} < 0$. Therefore, the probability of failure due to pullout is the probability of $g_{p}$ smaller than 0, which is denoted as ${ \Pr }(g_{p} < 0)$ in this study. Correspondingly, the reliability index for the nail pullout limit state can be calculated as $\beta_{p} = - {{\varPhi }}^{ - 1} \left( {{ \Pr }(g_{p} < 0)} \right)$, where ${{\varPhi }}^{ - 1} ()$ is the inverse of the standard normal cumulative distribution function. Similarly, with performance function Eq. (13), we can define the probability of failure and the reliability index for the nail-in-tension limit state as ${ \Pr }(g_{t} < 0)$ and $\beta_{t} = - {{\varPhi }}^{ - 1} \left( {{ \Pr }(g_{t} < 0)} \right)$.

For system reliability of nail internal stability, it requires that neither nail pullout nor nail-in-tensile failures take place. As such, the system reliability index can be computed as:

$$\beta_{sys} = - {{\varPhi }}^{ - 1} \left( {1 - { \Pr }(g_{p} > 0 \cap g_{t} > 0)} \right)$$

(15)

Note that the same definition of soil nail internal system reliability was adopted by Zevgolis and Daffas [50], and Yuan and Lin [44]. As the performance functions $g_{p}$ (Eq. 1) and $g_{t}$ (Eq. 13) share the same load terms, they are expected to correlate with each other. This correlation might have an influence on $\beta_{sys}$, which will be investigated later in this study.

3 Databases of measured nail loads

The section presents a brief review of a large database of measured nail loads compiled by Lin et al. [28]. Their database is used in this study for twofold: (1) to reassess the accuracies of both the default and calibrated CABR and CECS nail load models and (2) to recalibrate these models for accuracy improvement.

The database by Lin et al. [28] contains a total of 312 measured maximum nail load data they collected from fully instrumented soil nail walls reported in the literature. Note that the load data were for nails under working conditions, rather than failure conditions. Also contained in the database are design parameters such as soil type, wall geometry, soil shear strength property, nail configuration, and external loading condition. The wall geometry mainly refers to wall height ($H$), face batter angle ($\alpha$), and back slope angle ($\theta$). The soil shear strength property data include soil friction angle ($\phi$), soil cohesion ($c$), and soil unit weight ($\gamma$). The nail configuration data are nail length ($L$), drill hole diameter ($D$), nail depth ($z$), nail horizontal and vertical spacing ($S_{h}$ and $S_{v}$), and nail inclination angle ($i$). The external loading condition mainly refers to the surcharge load ($q_{s}$) on the top of a wall. The cumulative percentage distributions of these parameters are shown in Fig. 2. Table 1 summarizes the minimum, mean, median, maximum, and typical values of the above 12 design parameters.

Fig. 2

Cumulative percentage distributions of design parameters in the nail load database compiled by Lin et al. [28]

Table 1 Summary of the minimum, mean, median, maximum, and typical values of the soil nail wall design parameters in the general database compiled by Lin et al. [28]

In the database, nails were installed in a wide variety of soils, including sand, silty sand, silt, silty clay, clayey soils, and even soft clays and pebble boulders or weathered sandstones. For wall geometry, most of the walls were from 6 to 15 m high with steep or vertical facing structures and horizontal back slopes. For soil strength properties, the soil friction angles ranged widely from 0° to 40° with both the mean and median about 30°. The soil cohesions were typically less than 20 kPa; few were up to 40 kPa. For nail design configurations, the normalized nail length ($L/H$) ranged from 0.13 to 2.0, with a typical range of 0.7 to 1.2. The nail drill hole diameters ($D$), nail tributary areas ($S_{h} S_{v}$), and nail inclination angles ($i$) typically ranged from 100 mm to 150 mm, 1.5 m² to 2.5 m², and 10° to 15°, respectively. A few walls were subjected to surcharge loads larger than 60 kPa; the rest were under self-weight loading conditions, i.e., $q_{s} = 0$ kPa. In addition, the database also specifies the wall type, i.e., traditional or hybrid soil nail walls. Traditional soil nail walls refer to walls with soil nails as the sole reinforcing elements, whereas hybrid walls jointly use soil nails and other reinforcing elements such as geosynthetics or ground anchors for reinforcement.

It is possible to split the entire dataset into several data subsets based on wall working conditions, i.e., traditional or hybrid wall types, cohesionless or cohesive soils, and with surcharge or without surcharge. Nevertheless, Yuan et al. [45] examined the accuracy of the default and calibrated CABR and CECS nail load models under different wall working conditions and concluded that overall the prediction accuracy of these models is not significantly influenced by wall working conditions. Therefore, this study takes all the nail load data as one dataset for the reassessment and recalibration of the CABR and CECS models. This opportunity is left for future study. Readers are directed to Lin et al. [28] for detailed description of the nail load database.

4 Reassessment and recalibration of current models

In this study, the accuracy of a model is characterized as a model bias, which is defined as the ratio of measured to predicted maximum nail load, i.e., $\lambda_{D} = T_{m} /T_{D}$. The measured nail load (T_m) is directly taken from the database by Lin et al. [28], while the predicted nail load (T_D) is computed using the CABR and CECS models. The accuracy of the default and calibrated CABR and CECS models is firstly reassessed in Sect. 4.1, followed by recalibration of the models in Sect. 4.2. Section 4.3 characterizes the statistical distributions of the model biases.

4.1 Model reassessment

The measured nail loads, T_m, are plotted against predicted loads, T_D, in Fig. 3a and b using the default CABR and CECS models, respectively. Overall, the data points in the figures scatter widely from less than $T_{m} /T_{D} = 0.1$ to over $T_{m} /T_{D} = 10$. The majority fall between $T_{m} /T_{D} = 0.2$ and $T_{m} /T_{D} = 2$. This suggests that predictions using both models are dispersive. The second visual observation is that the scattering of predictions using the default CECS model is less than that using the default CABR.

Fig. 3

Measured nail load (T_m) versus predicted nail load (T_D) using default, calibrated, and recalibrated models: a CABR, and b CECS

The means and coefficients of variation (COV) of model biases ($\lambda_{D}$) are computed as 1.26 and 1.453 for the default CABR model, respectively, and 0.97 and 0.846 for the default CECS model, respectively. This is interpreted as that the default CABR model underestimates the maximum nail load by about 26% on average; moreover, the dispersion in its predictions is extremely high (i.e., bias COV equal to 1.453 > 0.9) according to the ranking scheme proposed by Phoon and Tang [35]. However, for the default CECS model, it is slightly conservative on average and the prediction dispersion is high (i.e., bias COV between 0.6 and 0.9). These computation outcomes quantitatively confirm the earlier visual observation that the default CECS model has a better prediction accuracy than that of the default CABR model.

The very high dispersion in predictions using the two default models is neither unexpected nor uncommon. Allen and Bathurst [1] showed that the default AASHTO simplified method for estimation of geosynthetic loads has a bias COV ranging from 0.919 to 1.46, depending on soil type. Note that for mechanically stabilized earth walls, the soil to be reinforced is engineered and thus can be expected to have much less variability than the case for soil nail walls where the soil is in natural conditions. In general, as have been pointed out by Lin et al. [24, 28] and Yuan et al. [45, 46], the dispersion could be attributed to underlying model uncertainty, wide variety of soil types, in situ soil spatial and temporal variability, state of in situ soils, variation in time to collect the load data, workmanships in wall construction and monitoring instrument setup, designed margins of safety, etc.

Figure 4 shows the plots of $\lambda_{D}$ versus $T_{D}$ using the two default models. Visually, $\lambda_{D}$ tends to decrease as $T_{D}$ increases. The same observation is made for both models. Typically, the default models tend to underestimate $(\lambda_{D} > 1)$ the nail load if $T_{D}$ is small, but overestimate $(\lambda_{D} < 1)$ it if $T_{D}$ is large. Spearman’s rank correlation tests are applied to the datasets in Fig. 4. The results show that the Spearman’s $\rho$ and the p values are − 0.714 and 0.000, respectively, for the default CABR model, and − 0.355 and 0.000, respectively, for the default CECS model. Both the p values are less than 0.05, indicating that at a level of significance of 0.05, $\lambda_{D}$ is negatively correlated with $T_{D}$. This type of correlation has been widely reported for various geotechnical models, e.g., [26, 27, 32, 34, 39,40,41,42, 45, 46]. Lin and Bathurst [22] and Yuan and Lin [44] demonstrated that ignoring the negative correlation between $\lambda_{D}$ and $T_{D}$ will result in underestimation of the design reliability, and thus the error is on the safe side.

Fig. 4

Plots of model bias, $\lambda_{D}$, against predicted nail load, T_D, using default, calibrated, and recalibrated nail load models: a CABR and b CECS

The same database is used to reassess the accuracy of the previously calibrated CABR and CECS models, i.e., Equations (10) and (11), respectively. Although the values of the constants ($C_{0}$, $C_{z}$, and $C_{\alpha }$) that appear in the equations were reported by Yuan et al. [45], those values were determined using 144 measured nail load data that are now a part of the general database that is adopted in this study. To allow fair assessments and comparisons, the values of the constants are first re-determined using the general database; then, with the re-determined constants, accuracies of Eqs. (10) and (11) are evaluated. The re-determination of the values for $C_{0}$, $C_{z}$, and $C_{\alpha }$ is carried out to simultaneously meet two requirements: (1) mean of $\lambda_{D}$ is equal to 1 and (2) COV of $\lambda_{D}$ is minimized. The optimal values are found to be $C_{0} = - 1.267$ and $C_{z} = 0.138$ for the CABR model [Eq. (10)], and $C_{0} = 2.104$, $C_{z} = - 1.326$, and $C_{\alpha } = - 2.601$ for the CECS model [Eq. (11)]. Note that $\alpha_{0}$ in Eq. (11) is taken to be 10°.

With these optimal values for the constants, Eqs. (10) and (11) are then used to compute the $T_{D}$ values. For comparison purposes, the $T_{m}$ versus $T_{D}$ plots using the two calibrated models are also shown in Fig. 3a and b. Visually, in the figures, the data points by the two calibrated models are moved toward the 1:1 correspondence lines and thus the spreads are much less than those by the two default models. Quantitatively, the mean and COV of $\lambda_{D}$ are calculated to be 1.00 and 0.843, respectively, for the calibrated CABR, and 1.00 and 0.678, respectively, for the calibrated CECS. Both the calibrated CABR and CECS models are now accurate on average. Moreover, the prediction dispersions of both calibrated models are greatly reduced, especially for the CABR models, i.e., 1.453 (default) versus 0.846 (calibrated). These outcomes demonstrate that introducing a simple calibration could remarkably enhance the prediction accuracy of a model.

Again, Spearman’s rank correlation tests are applied to investigate the statistical correlations between $\lambda_{D}$ and $T_{D}$ datasets for the two calibrated models. The Spearman’s ${{\rho }}$ and p values are − 0.535 and 0.000 for the calibrated CABR model, respectively, and − 0.177 and 0.002 for the calibrated CECS model, respectively. The correlation between $\lambda_{D}$ and $T_{D}$ still exists for both calibrated models. This is an undesirable calibration outcome.

The reassessment outcomes for the default and calibrated CABR and CECS models are summarized in Table 2. Both models, regardless of default or calibrated, are concluded to be unsatisfactory due to biased on-average prediction accuracy, high to very high prediction dispersion, and presence of correlation between model bias and predicted value. A further calibration is thus warranted.

Table 2 Summary of reassessment and recalibration outcomes for the CABR and CECS models

4.2 Model recalibration

Two methods have been widely adopted for model calibration in the geotechnical literature. Both introduce a correction factor to the model. The first approach, referred to as the general model factor approach, is to regress the model bias against the final predicted value, while the second approach is to regress the model bias against each model input parameter. This study adopts the second approach for recalibration of the previously calibrated CABR and CECS models. Technical details of these two calibration methods can be referenced to, e.g., Dithinde et al. [12]. With a broad nail load database, we can test the bias of a model equation not only against its input parameters, but also against those that do not appear in the equation formulation. This provides us a precious opportunity to go beyond the existing model structure and look at the model accuracy within a broader context.

Figures 5 and 6 show the plots of model bias versus 12 design parameters (i.e., $H$, $\alpha$, $\theta$, $\phi$, $c$, $\gamma$, $L$, $D$, $z$, $i$, $S_{h} S_{v}$, and $q_{s}$) for the calibrated CABR and CECS models, respectively. Spearman’s rank correlation tests are applied to the data in the figures. The test outcomes are summarized in Table 3. For the calibrated CABR model case, the model bias, $\lambda_{D}$, is statistically correlated to design parameters such as $H$, $\theta$, $\phi$, $c$, $\gamma$, $L$, $D$, $i$, and $S_{h} S_{v}$ at a level of significance of 0.05. However, for the calibrated CECS model case, $\lambda_{D}$ is correlated with design parameters such as $\theta$, $\phi$, $\gamma$, and $i$ at the same level of significance. Therefore, extra correction factors, $M_{2} = f\left( {H, \theta , \phi , c, \gamma , L, D, i, S_{h} S_{v} } \right)$ and $M_{2} = f\left( {\theta , \phi , \gamma , i} \right)$, can be introduced to the calibrated CABR (Eq. 10) and CECS (Eq. 11) models, respectively, for accuracy improvements.

Fig. 5

Plots of model bias $\lambda_{D}$ for the calibrated CABR model against different design parameters

Fig. 6

Plots of model bias $\lambda_{D}$ for the calibrated CECS model against different design parameters

Table 3 Summary of Spearman's rank correlation test results and determination of coefficients between model bias $\lambda_{D}$ and different design parameters using the calibrated CABR and CECS models

Three further steps are taken in this study to avoid developing overly complicated formulations for $M_{2}$. First, it is assumed that $M_{2}$ can be simplified as $M_{2} = f\left( H \right)f\left( \theta \right)f\left( \phi \right)f\left( c \right)f\left( \gamma \right)f\left( L \right)f\left( D \right)f\left( i \right)f\left( {S_{h} S_{v} } \right)$ and $M_{2} = f\left( \theta \right)f\left( \phi \right)f\left( \gamma \right)f\left( i \right)$ for the calibrated CABR and CECS models, respectively. Second, the form of each $f\left( x \right)$ is taken as one of the following four simple equations, including exponential ($f\left( x \right) = ae^{bx}$), linear ($f\left( x \right) = ax + b$), logarithm ($f\left( x \right) = alnx + b$), and power ($f\left( x \right) = ax^{b}$). Third, model bias $\lambda_{D}$ is regressed against each correlated design parameter using the above four simple equations. The coefficient of determination, $R^{2}$, for each regression is computed; the result is summarized in Table 3. As shown, for the calibrated CABR case, the $R^{2}$ values are 0.35 (Linear) and 0.13 (Exponential) for $\lambda_{D}$ against back slope angle $\theta$ and soil cohesion $c$, respectively; both are greater than 0.10. However, the $R^{2}$ values for other scenarios are small. This indicates that $M_{2}$ in this case can be further simplified as $M_{2} = f\left( \theta \right)f\left( c \right)$ without losing significant correction precision practically, where $f\left( \theta \right)$ and $f\left( c \right)$ are the simple linear and exponential functions, respectively. Similarly, $M_{2}$ for the calibrated CECS model case can be taken as $M_{2} = f\left( \theta \right)$ where $f\left( \theta \right)$ in this case is also the simple linear function. Taking $M = M_{1} \times M_{2}$, the recalibrated CABR and CECS models can be, respectively, formulated as:

$$\begin{aligned} T_{D} = & \frac{{M\zeta \eta P_{a} S_{h} S_{v} }}{\cos i} \\ = & \left[ {C_{0} \ln \left( {\frac{z}{H}} \right) + C_{z} } \right]\left( {\frac{\theta }{{\theta_{0} }} + C_{\theta } } \right){ \exp }\left( {\frac{{C_{c} c}}{{c_{0} }}} \right)\zeta \eta P_{a} S_{h} S_{v} /\cos i \\ \end{aligned}$$

(16)

$$\begin{aligned} T_{D} = & M\mathop \int \limits_{{z - S_{v} /2}}^{{z + S_{v} /2}} P_{z} S_{h} {\text{d}}z + K_{a} q_{s} S_{h} S_{v} \\ = & C_{0} \left( {\frac{\theta }{{\theta_{0} }} + C_{\theta } } \right)\exp \left( {\frac{{C_{z} z}}{H} + \frac{{C_{\alpha } \alpha }}{{\alpha_{0} }}} \right)\mathop \int \limits_{{z - S_{v} /2}}^{{z + S_{v} /2}} P_{z} S_{h} {\text{d}}z + K_{a} q_{s} S_{h} S_{v} \\ \end{aligned}$$

(17)

where $C_{0}$, $C_{z}$, $C_{\theta }$, $C_{c}$, and $C_{\alpha }$ are model parameters to be determined, and $\alpha_{0} = 10^{\circ}$, $\theta_{0} = 10^{\circ}$, and $c_{0} = 10$ kPa are empirical constants used to make the correction term $M$ dimensionless.

Following the same criteria as clarified earlier, the empirical model parameters in Eqs. (16) and (17) are determined as those minimizing the COVs of $\lambda_{D}$ while maintaining means of $\lambda_{D}$ of one. All the 312 nail load data are randomly divided into two data groups: a training data group and a validation data group. The training data group is used to calibrate the model parameters in Eqs. (16) and (17), while the validation data group is used to validate the recalibrated models. Figure 7 shows the plots of $T_{m}$ versus $T_{D}$ for both data groups where the training data group takes up 70% of the total data and the remaining 30% are for the validation data group. Note that $T_{D}$ for the validation data case is computed using Eqs. (16) and (17) with model parameters determined using the training data group. The scatter plots in Fig. 7 for both data groups visually follow the same trends and are highly comparable; thus, the recalibrated models are visually validated. To further validate the recalibrated models, $\lambda_{D}$ values based on the training and validation data groups are compared. For the recalibrated CABR model, the mean and COV of $\lambda_{D}$ are computed to be 1.00 and 0.636, respectively, based on the training data group, and 0.96 and 0.844, respectively, based on the validation data group. For the recalibrated CECS model, these values are 1.00 and 0.691, and 1.08 and 0.486. The Mann–Whitney tests are applied to the training and validation bias datasets, and the results show that the two datasets do not significantly differ from each other at a level of significance of 0.05. Therefore, the two recalibrated models are quantitatively validated.

Fig. 7

Measured nail loads T_m versus predicted nail loads T_D using the training and validation data groups: a the recalibrated CABR model and b the recalibrated CECS model

Figure 7 only represents one realization of randomly splitting the measured data. Now, the analyses are extended in two aspects. First, four data-splitting scenarios are considered, i.e., training versus validation data percentages are, respectively, set to be 60% versus 40%, 70% versus 30%, 80% versus 20%, and 100% versus 0%. Second, for each data-splitting scenario, one thousand realizations are carried out. The analysis results of the determined model parameters and the corresponding biases with respect to different training and validation data scenarios are summarized in Tables 4 and 5, respectively, for both the recalibrated CABR and CECS models. The corresponding histograms of the determined model parameters and the biases are plotted in Figs. 8 and 9. Clearly, the means of the determined model parameters and the biases for the three data-splitting scenarios, i.e., 60% versus 40%, 70% versus 30%, and 80% versus 20%, are very close to those for the 100% versus 0% data scenario. This again validates the two recalibrated models. Therefore, from hereafter, only the model parameters based on the 100% versus 0% data scenario are used for further analyses.

Table 4 Calibrated outcomes of the optimal model constants with respect to different training and validation data scenarios

Table 5 Bias statistics estimated using the training and validation datasets under different data percentage scenarios with the recalibrated CABR and CECS models

Fig. 8

Histogram plots of the determined model parameters for different data-splitting scenarios: a the recalibrated CABR model and b the recalibrated CECS model

Fig. 9

Histogram plots of the biases for different data-splitting scenarios: a the recalibrated CABR model and b the recalibrated CECS model

For the two recalibrated models, the optimal values are determined as $C_{0} = - 0.616$, $C_{z} = 0.126$, $C_{\theta } = 1.772$, and $C_{c} = - 0.171$ for the CABR case, and $C_{0} = 0.807$, $C_{z} = - 1.199$, $C_{\theta } = 2.143$, and $C_{\alpha } = - 0.260$ for the CECS case. With these values, the recalibrated CABR and CECS models are used to predict the nail loads $T_{D}$, which are plotted against the measured values $T_{m}$ in Fig. 3. Visually, the recalibrated models have the least dispersions among all models. The means and COVs of $\lambda_{D}$ are 1.00 and 0.689 for the recalibrated CABR model (Eq. 16), respectively, and 1.00 and 0.630 for the recalibrated CECS model (Eq. 17), respectively. For the convenience of comparisons, the recalibration outcomes are also shown in Table 2. The COVs of $\lambda_{D}$ are significantly reduced, especially for the CABR case. Figure 4 shows the plots of $\lambda_{D}$ versus $T_{D}$ using the two recalibrated models. Again, Spearman’s rank correlation tests are carried out and the results show that the Spearman’s $\rho$ and p values between $\lambda_{D}$ and $T_{D}$ are − 0.284 and 0.03 for the recalibrated CABR model, respectively, and − 0.070 and 0.22 for the recalibrated CECS model, respectively. The statistical correlation between $\lambda_{D}$ and $T_{D}$ is removed for the recalibrated CECS model, but is still present for the recalibrated CABR model. Nevertheless, in that case, the p value is 0.03, which is close to 0.05 and thus a recalibration of the CABR model by introducing more design parameters into the formulation is not conducted in this study. Obviously, from Table 2, it is concluded that the recalibrated models are superior to the default and calibrated models.

4.3 Distribution of model bias

The means and COVs of $\lambda_{D}$ for the default, calibrated, and recalibrated CABR and CECS models have been characterized in previous sections. In this section, we investigate the statistical distribution of $\lambda_{D}$ for each model. Figure 10a and b plots the cumulative distributions for the CABR and CECS models, respectively. The vertical axis is the standard normal variable; the horizontal axis is on log scale. The cumulative distributions appear to be linear, implying that they follow lognormal distributions. Kolmogorov–Smirnov (K–S) tests are applied to the datasets, and the results show that the p values are 0.81, 0.98, and 0.46 for the default, calibrated, and recalibrated CABR model cases, respectively, and 0.49, 0.63, and 0.66 for the default, calibrated, and recalibrated CECS model cases, respectively. All far exceed 0.05. As a result, $\lambda_{D}$ for the six models can be taken as lognormal random variables.

Fig. 10

Cumulative distribution plots of model bias λ_D for the default, calibrated, and recalibrated models: a CABR and b CECS

5 Reliability-based design of internal limit states

The application of the six models to reliability-based design of soil nail walls against internal limit states is presented in this section. Reliability analyses are conducted first for individual limit states, i.e., nail pullout and nail-in-tension limit states; then, the system reliability of nail internal stability is studied, with consideration of the correlation between the two limit states.

5.1 Basics of the design example

The example wall in [28] is adopted here for reliability-based design of soil nail internal stabilities. The basic information of the wall is summarized in Table 6. The wall is 10 m in height with a horizontal back slope and a vertical facing. Nails are installed in a homogenous soil, which has a friction angle of $\phi = 33^{\circ}$ (mean value) and a unit weight of ${{\gamma }} = 18$ kN/m³ (mean value). The variations in $\phi$ and $\gamma$ are 0.10 and 0.05, respectively, in terms of COV. For nail configuration, in total seven rows of nails are placed, at depths of z = 0.5, 2.0, 3.5, 5.0, 6.5, 8.0, and 9.5 m. The nails are inclined at an angle of 15° to the horizontal and spaced 1.5 m horizontally and vertically, with drill hole diameter of 150 mm. The bond strength at the nail–soil interface is taken as $q_{u} = 100$ kPa. The tensile yield strength of nail bar is taken as $f_{y} = 520$ MPa. The wall is assumed to be subjected to a surcharge live load of $q_{L} = 12$ kPa at the top. The nail length ($L$) and bar diameter ($d$) are the two primary design parameters.

Table 6 Summary of values of parameters in the performance functions Eqs. (1) and (13) used for the example design of nail pullout and nail-in-tension limit states (after [28])

The model biases include $\lambda_{p}$ in prediction of nail ultimate pullout capacity $P_{n}$, $\lambda_{t}$ in prediction of nail bar tensile yielding strength $T_{t}$, $\lambda_{D}$ in prediction of nail dead load component $T_{D}$, and $\lambda_{L}$ in prediction of nail live load component $T_{L}$. The means and COVs are, respectively, assumed to be 1.05 and 0.24 for $\lambda_{p}$, 1.10 and 0.10 for $\lambda_{t}$, and 1.20 and 0.205 for $\lambda_{L}$. The justification of these statistics can be found in, e.g., [13, 16,17,18, 21, 44]. The statistics of $\lambda_{D}$ can be seen in Table 2. All random variables are taken to be lognormally distributed.

Figure 11 shows the means and 95% prediction intervals of the total nail loads ($\lambda_{D} T_{D} + \lambda_{L} T_{L}$) computed using different models. For the default CABR model case, both the mean and 95% prediction intervals of the predicted nail load increase monotonically with increasing depth. For example, the mean of ($\lambda_{D} T_{D} + \lambda_{L} T_{L}$) is about 20 kN for the first row of nails, but increases to about 160 kN for nails at the last row. For the default CECS model case, the mean and the 95% intervals increase first and then keep constant for nails at depths greater than $z/H = 0.25$. For example, the mean in this case stays at about 75 kN from the third row of nails and after. Nail loads computed by the two default models exhibit monotonic trends with depth. However, for the calibrated and recalibrated model cases, the nail load ($\lambda_{D} T_{D} + \lambda_{L} T_{L}$) exhibits a nonmonotonic trend, i.e., first increases until reaching a certain depth and then decreases thereafter. Figure 11 demonstrates that calibrating a default model would change not only the predicted magnitude of nail load, but also the trend in prediction.

Fig. 11

Means and 95% prediction intervals for total predicted nail load ($\lambda_{D} T_{D} + \lambda_{L} T_{L}$) using different CABR and CECS models

5.2 Nail pullout limit state

The nonuniform nail length pattern is considered for this design example. The Monte Carlo simulation technique is adopted for reliability analysis. Nails at each depth are designed to have a length ($L$) satisfying a prescribed target pullout reliability, $\beta_{p}$. In this study, $\beta_{p}$ values are chosen to be 2.33, 3.09, and 3.54, corresponding to probabilities of failure of 1/100, 1/1000, and 1/5000, respectively. Note that $\beta_{p} = 2.33$ is the most commonly adopted target pullout reliability index in the literature for reinforced soil walls, e.g., [4, 5, 13, 21, 23, 44]. Table 7 summarizes the determined nail lengths ($L/H$) at different depths satisfying target reliability of $\beta_{p}$ = 2.33, 3.09, and 3.54 using default, calibrated, and recalibrated CABR and CECS models. The case of $\beta_{p} = 2.33$ is plotted in Fig. 12 for visual convenience of discussion.

Table 7 Summary of nail lengths ($L/H$) at different depths satisfying target reliability of $\beta_{p}$ = 2.33, 3.09, and 3.54 using default, calibrated, and recalibrated CABR and CECS models

Fig. 12

Nail lengths $L/H$ at different depths satisfying target reliability $\beta_{p} = 2.33$ using the default, calibrated, and recalibrated CABR and CECS models for the pullout limit state

Figure 12 shows that, on the one hand, for the default CABR model case, the length of nails should increase with nail depth in order to maintain the same pullout reliability ($\beta_{p} = 2.33$) throughout the entire wall height. For example, the length is about $L/H = 0.63$ for nails at the first row $z/H = 0.05$, but increases to $L/H = 2.34$ for nails at the bottom $z/H = 0.95$. This suggests that if a uniform nail length pattern is used, then the most critical nail will be the one at the bottom. On the other hand, for the calibrated and recalibrated CABR model cases, nails at the second and third rows have the largest lengths, whereas those at the bottom have the shortest lengths. This suggests that under the uniform nail length pattern, nails at a certain depth will be the most critical ones while nails at the bottom are the safest ones. This is a completely different conclusion from the one drawn for the default CABR model case. This finding highlights the importance of model calibration in reliability-based analysis and design of soil nail walls. It could also be true for other geotechnical structures.

For the CECS cases, overall nail lengths by the default, calibrated, and recalibrated models do not differ largely from each other. Given the same $\beta_{p}$, the three models give the same trend for nail lengths along depth, i.e., first increases and then decreases. In addition, from Fig. 12 and Table 7, it is found that nail lengths computed using the calibrated and recalibrated CABR and CECS models are comparable, regardless of nail depths.

Figure 13 shows that the total nail length, $\sum L/H$, increases with increasing target $\beta_{p}$, which is as expected. The $\sum L/H$ using the recalibrated model, regardless of CABR or CECS, is always the least. This highlights the practical benefits of model recalibration since using the recalibrated models for nail pullout design results in the most cost-effective design outcomes in terms of $\sum L/H$.

Fig. 13

Plots of total nail length $\sum L/H$ versus target design reliability $\beta_{p}$ for the pullout limit state using different CABR and CECS models

Last, from Table 7, it is found for larger $\beta_{p}$ such as 3.09 and 3.54, the computed nail lengths using the default CABR appear to be extremely large, which could be nonsensical. The excessively large $L/H$ is mainly due to the extremely high COV of $\lambda_{D}$ for the default CABR. Indeed, the $\lambda_{D}$ statistics summarized in Table 2 should be interpreted as “general” rather than project-specific. For specific projects, prior information can be extracted from engineering experience and site tests and then applied to refine the $\lambda_{D}$ statistics (e.g., using Bayesian updating technique[8, 9]). As such, the COV of $\lambda_{D}$ could be reduced, which would lead to shorter nails for design.

5.3 Nail-in-tension limit state

Similarly, the target reliability index for the nail-in-tension limit state is selected to be $\beta_{t} = 2.33$, 3.09, and 3.54. Table 8 summarizes the corresponding nail bar diameter ($d$) at different depths satisfying these target $\beta_{t}$ using the default, calibrated, and recalibrated CABR and CECS models. The case for $\beta_{t} = 2.33$ is plotted in Fig. 14. Similar trends as those for the pullout limit state (c.f. Figure 13) can be observed. For nails at the first row, the bar diameter satisfying $\beta_{t} = 2.33$ is $d = 12$ mm using both default CABR and CECS models. For nails at the bottom, $d$ has to be increased to 49 and 26 mm, respectively, to reach the same $\beta_{t}$. The bar diameter $d$ increases monotonically as $z/H$ increases. For both calibrated and recalibrated models, regardless of CABR or CECS, the peak value of $d$ is reached at the third row. Along depth, $d$ first increases and then decreases.

Table 8 Summary of nail bar diameter ($d$) at different depths satisfying target reliability of $\beta_{t}$ = 2.33, 3.09, and 3.54 using default, calibrated, and recalibrated CABR and CECS models

Fig. 14

Nail bar diameter $d$ at different depths satisfying target reliability $\beta_{t} = 2.33$ using the default, calibrated, and recalibrated CABR and CECS models for the nail tensile limit state

Using the default CABR model in this example would result in nonsensically large bar diameter for higher $\beta_{t}$. As explained earlier, the culprit is the extremely large COV of the $\lambda_{D}$. Table 8 also points out the maximum $d$ value for each design scenario. In practice, bars with the same diameter are commonly used throughout the wall height. If so, in this design example, the most critical nails for the tensile limit state would be those at the bottom row if based on the default models, and be those at the third row if based on the calibrated and recalibrated models. The influence of model selection on design outcomes and interpretations is again demonstrated.

5.4 Linking factor of safety to reliability

The current CABR [7] and CECS [10] design manuals for soil nail walls are still based on deterministic allow stress methods, where the margin of safety is characterized by factor of safety (FS). Therefore, it would be interesting to show the link between FS and reliability in this design example. Tables 9 and 10 summarize the computed $\beta_{p}$ and $\beta_{t}$ corresponding to FS = 1, 2, 3, 4, and 5 for nails at different depths using default, calibrated, and recalibrated CABR and CECS nail load models for the pullout and nail-in-tension limit states, respectively. The cases for nails at depth $z/H = 0.5$ are shown in Figs. 15 and 16.

Table 9 Linking factor of safety (FS) to reliability index for nails at different depths using default, calibrated, and recalibrated CABR and CECS nail load models for the pullout limit state

Table 10 Linking factor of safety (FS) to reliability index for nails at different depths using default, calibrated, and recalibrated CABR and CECS nail load models for the nail-in-tension limit state

Fig. 15

Plots of reliability $\beta_{p}$ versus factor of safety (FS) for nails at a depth of $z/H = 0.5$ for the pullout limit state using different CABR and CECS models

Fig. 16

Plots of reliability $\beta_{t}$ versus factor of safety (FS) for nails at a depth of $z/H = 0.5$ for the nail-in-tension limit state using different CABR and CECS models

For this design example for the pullout limit state, to reach $\beta_{p} = 2.33$, nails at depth $z/H = 0.5$ must have a FS value equal to 6.0, 4.5, and 3.8 if using the default, calibrated, and recalibrated CABR models, respectively. These FS values are 4.5, 3.8, and 3.6 if using the default, calibrated, and recalibrated CECS models, respectively. The minimum FS values dictated by the CABR and CECS manuals are 1.2 to 1.6 for nail pullout and tensile limit states. These minimum FS values correspond to $\beta_{p}$ and $\beta_{t}$ that are far less than 2.33. Hence, nail designs based on the minimum FS required in the manuals could be inadequate for this design case. Nevertheless, it should be pointed out that in practice the designed nail lengths should meet the safety requirements not only for the nail pullout limit state, but also for the wall overall stability limit state. Therefore, the final nail lengths could be longer than those determined solely based on the minimum pullout FS. Also, a factor of 1.1 to 1.2 would be applied to the design to account for the structure importance of the wall. This would increase the nail lengths in another fold. As a result, the final FSs against nail pullout failure could be much higher than the minimum values dictated by the manuals. Accordingly, the final $\beta_{p}$ would be much higher than those listed in Table 9.

For the nail-in-tension limit state, nails at $z/H = 0.5$ would need to have FS = 6.0, 4.1, and 3.4 to reach $\beta_{t} = 2.33$ with respect to the default, calibrated, and recalibrated CABR models. If the CECS models are used, then these FS values would be 4.1, 3.4, and 3.2, respectively. Again, these FS values are much higher than the minimum FS values required in the CABR and CECS soil nail wall design manuals. The discussion for the nail pullout case also applies here and thus is not repeated.

From Tables 9 and 10, several other observations can be made. By the same model, the same FS would result in different $\beta_{p}$ and $\beta_{t}$. This means that designing a nail to the same FS would not necessarily have consistent margins of safety when margin of safety is measured by reliability (or probability of failure). This is also true for the case of same FS by different models. It is also found that if nails are designed to achieve the same FS value for both pullout and tensile limit states, the $\beta_{p}$ is generally lower than the $\beta_{t}$. In this case, nails are more prone to fail due to pullout than tensile yielding.

5.5 System reliability

The system reliability index, $\beta_{sys}$, for nails in this design example can be computed using Eq. (15). Since the performance functions for nail pullout and nail-in-tension limit states share the same load terms, see Eqs. (1) and (13), $g_{p}$ and $g_{t}$ can be expected to be statistically correlated. Figure 17 shows the plots of $g_{t}$ versus $g_{p}$ for nails at $z/H = 0.5$ with $\beta_{p} = \beta_{t} = 2.33$ based on 10,000 simulations using the default CABR and CECS models. First-order polynomials are used to regress the datasets in the figures. Clearly, $g_{p}$ and $g_{t}$ are positively correlated as they tend to increase or decrease simultaneously. The Pearson’s correlation coefficients between $g_{p}$ and $g_{t}$ are $\rho_{{g_{p} ,g_{t} }} = 0.918$ and 0.892 for the default CABR and CECS models, respectively. Such strong positive correlations could have a significant influence on $\beta_{sys}$ of nail internal stability. Note that only when satisfying $g_{p} > 0$ and $g_{t} > 0$ that a nail is said to be internally stable.

Fig. 17

Plots of $g_{t}$ versus $g_{p}$ for nails at a depth $z/H = 0.5$ given $\beta_{p} = \beta_{t} = 2.33$ (based on 10,000 Monte Carlo simulations) using: a default CABR and b default CECS

The $\rho_{{g_{p} ,g_{t} }}$ values with respect to different $z/H$, $\beta_{p}$ and $\beta_{t}$, and CABR and CECS models are computed. The results are summarized in Table 11. The case for $\beta_{p} = \beta_{t} = 2.33$ is plotted in Fig. 18. Interestingly, the trends of $\rho_{{g_{p} ,g_{t} }}$ along $z/H$ are found qualitatively similar to those of $L/H$ and $d$ along $z/H$ presented in Figs. 12 and 14. For the default models, the correlations between $g_{p}$ and $g_{t}$ are strongest for nails at the bottom, whereas for the calibrated and recalibrated models, the largest $\rho_{{g_{p} ,g_{t} }}$ values are reached for the second or third rows of nails. Overall, $\rho_{{g_{p} ,g_{t} }}$ ranges roughly from 0.8 to 0.9; the variation is not very large. From Table 11, it is also observed that $\rho_{{g_{p} ,g_{t} }}$ computed using the CABR and CECS models is practically the same and independent of $\beta_{p}$ and $\beta_{t}$.

Table 11 Summary of correlation coefficient between pullout and tensile limit states and system reliability index with respect to different nail depths, $\beta_{p}$ and $\beta_{t}$, and CABR and CECS models

Fig. 18

Correlation coefficient between $g_{p}$ and $g_{t}$, $\rho_{{g_{p} ,g_{t} }}$, along nail depths using different nail load models given $\beta_{p} = \beta_{t} = 2.33$

By using Eq. (15), the system reliability indices, $\beta_{sys}$, are computed for nails with respect to different $z/H$, $\beta_{p}$ and $\beta_{t}$, and nail load models. The results are summarized in Table 11. The case of $\beta_{p} = \beta_{t} = 2.33$ is plotted in Fig. 19. The system reliability, $\beta_{sys}$, appears to be about 2.20 (probability of failure equal to 1.4%), which is smaller than $\beta_{p} = \beta_{t} = 2.33$ (probability of failure equal to 1.0%), regardless of $z/H$ and the nail load models. $\beta_{sys}$ is on the same order of magnitude as that of $\beta_{p}$ and $\beta_{t}$ in terms of probability of failure. If the correlation between $g_{p}$ and $g_{t}$ is ignored, i.e., $\rho_{{g_{p} ,g_{t} }} = 0$, then $\beta_{sys}$ will be computed as 2.06, which corresponds to a probability of failure of 2.0%. This means that ignoring $\rho_{{g_{p} ,g_{t} }}$ would result in overestimation of probability of failure or underestimation of $\beta_{sys}$. Nevertheless, since $\rho_{{g_{p} ,g_{t} }}$ is positive, ignoring it would not practically cause significant errors in estimation of $\beta_{sys}$.

Fig. 19

System reliability, $\beta_{sys}$, against nail depths given $\beta_{p} = \beta_{t} = 2.33$ using difference CABR and CECS models

5.6 Conclusions

This study presents accuracy assessments of two nail load models proposed by two nationwide soil nail wall design specifications in China and their calibrated versions reported in the literature. The nationwide specifications are Technical Specification for Retaining and Protection of Building Foundation Excavations by China Academy of Building Research (CABR) and Specifications for Soil Nailing in Foundation Excavations by China Association for Engineering Construction Standardization (CECS). The prediction accuracies of the default and calibrated CABR and CECS models are reevaluated using a total of 312 measured nail load data contained in a more general nail load database compiled by Lin et al. [28]. Model accuracy is characterized by model bias, which is defined as the ratio of measured to predicted nail load. Simple empirical terms are introduced to recalibrate the CABR and CECS models for accuracy improvement. Reliability analysis and design of soil nail walls against internal failures, including nail pullout and nail-in-tension limit states, are performed using the six nail load models. Nails are first designed to achieve target reliabilities in terms of individual limit states. Then, analyses are carried out to evaluate the system reliability of nails against internal failures. The correlation between the two limit states is explored. Its influences on the evaluation outcomes of system reliability are discussed. The main conclusions drawn from this study are as follows.

• (1) Based on the adopted database, the mean and COV of the model bias are 1.26 and 1.453 for the default CABR model, respectively. The default CABR model under-predicts nail loads by about 26% on average, and the dispersion in prediction is extremely high, while for the default CECS model, the bias mean and bias COV are 0.97 and 0.846, respectively. The default CECS model is more or less accurate on average; however, the prediction dispersion is high.

• (2) The calibrated CABR and CECS models are shown to have biases with means and COVs equal to 1.00 and 0.843, and 1.00 and 0.678, respectively, under the optimal condition. While both calibrated models are accurate on average, the dispersions in prediction are still large. In addition, the prediction accuracies of the default and calibrated CABR and CECS models are found to be correlated with their predicted magnitudes of nail loads, as well as several design parameters. Such correlations are undesirable from the perspective of reliability-based design of soil nail walls.

• (3) The recalibrated CABR and CECS models are shown to have much less dispersions in prediction, i.e., COVs of bias drop to 0.689 and 0.630, respectively. Moreover, the model biases of the recalibrated CABR and CECS models do not exhibit statistical correlations with their predicted values or any design parameters.

• (4) The model biases of the six models, i.e., the default, calibrated, and recalibrated CABR and CECS models, are demonstrated to be lognormal random variables through Kolmogorov–Smirnov tests.

• (5) Nail loads computed by the two default models exhibit monotonic trends with depth. However, for the calibrated and recalibrated model cases, nail loads exhibit a nonmonotonic trend, i.e., first increases until reaching a certain depth and then decreases thereafter. The same trends are also true for nail length and bar diameter along depth if designed to achieve the same target reliability.

• (6) When nails are designed to achieve the same factor of safety for both pullout and nail-in-tension limit states, the pullout reliability is generally lower than the tensile reliability. In that case, nails are more prone to fail due to pullout than tensile yielding.

• (7) The correlation between nail pullout and nail-in-tension limit states is positive, basically ranging from 0.8 to 0.9. The influences of depth, nail load model (CABR or CECS), target reliability for individual limit states (pullout or nail-in-tension) on the correlation are practically insignificant.

• (8) The system reliability of nail internal stability is slightly lower than the individual nail pullout and nail-in-tension reliabilities. Ignoring the positive correlation between the two limit states would lead to underestimation of system reliability; nevertheless, the underestimation is insignificant.

While the performance of the recalibrated CABR and CECS models is greatly enhanced in prediction of nail loads compared to that of the default and calibrated CABR and CECS models, the dispersions in prediction are still high, i.e., bias COVs exceeding 0.60. This suggests that more complicated modeling techniques might be needed for mapping soil nail loads, for example, response surface methods, machine learning approaches, etc. Both types of methods have been well demonstrated in geotechnical engineering applications, e.g., [3, 20, 43, 51, 53, 54]. Mapping soil nail loads using artificial neural network technique has been carried out by Lin et al. [28]. Other opportunities are not explored in this study, but left for future studies. Last, the quantified model biases can also be used in the development of reliability-based partial factor methods for soil nail walls in China. Studies on these related topics can be referenced to, e.g., [4,5,6, 13, 16, 17, 21, 23, 29, 31, 37, 38, 50].