Advantages and limitations of an α-plasticity model for sand

Abstract

The stress–strain response of sand was observed to depend on its material state, i.e., pressure and density. Successful modelling of such state-dependent response of sand relied on the correct representation of its state-dependent stress–dilatancy behaviour. In this study, an improved fractional-order $\left( \alpha \right)$ plasticity model for sands with a wide range of initial void ratios and pressures is proposed, based on a state-dependent fractional-order plastic flow rule and a modified yielding surface. Potential positive performances and negative limitations of the proposed approach in terms of the critical state of sand are discussed, based on the simulations of a series of drained and undrained triaxial tests of different sands. It can be found that unlike previous fractional models, the developed model can reasonably simulate the key features, e.g., strain softening/hardening, volumetric dilation/contraction, liquefaction, quasi-steady-state flow as well as steady-state flow, of sand for a wide range of initial states. However, due to typical forms of the critical-state lines being used, negative performances of the fractional approach could occur when simulating the undrained behaviour of very loose sand and the drained behaviour of very dense sand.

1 Introduction

The constitutive behaviour of sand, among other granular soils, is very complex and usually different from that of soft soils, e.g., clay. For clay, an associated plastic rule could provide accurate predictions of the stress–strain response [76]. However, for sand, an associated plastic flow rule would overpredict the volumetric dilation of sand samples [11, 26, 28, 37, 49,50,51]. In order to solve this problem, researchers often suggested to use an alternative stress–dilatancy equation, where the dilatancy angle was lower than the experimentally obtained friction angle [2, 65, 66, 78]. Improved performance of the model predictions was then reported. However, further researches on sands subjected to a wide range of initial void ratios and pressures revealed that the strength–deformation and stress–dilatancy behaviour of sand were highly dependent on its material state (pressure and density) [6, 7]. Constitutive models not considering such state dependence usually required different sets of model constants, in order to capture the constitutive behaviour of sand under different initial relative densities [5].

In the past decades, a substantial amount of effort had been devoted to the development of unified modelling of the stress–strain behaviour of sand [21, 36, 46, 47] and other granular soils [31, 34, 55, 68,69,70,71,72] with different initial states. It can be found that these approaches were developed by incorporating an empirical state parameter, for example, the state parameter ψ [6] and state pressure index I_p [67], into the friction angle at phase transformation state. A good agreement between the experimental results and model simulations was often reported. Nevertheless, the mathematical principles underlying the state-dependent plastic flow were missing and open for discussion. Instead of simply using ψ or I_p, Sun et al. [59, 61] developed a rigorous mathematical elaboration of the state-dependent plastic flow rule for various granular soils, including sand, by using a stress-fractional operator as suggested in Sumelka [52] and Sumelka and Nowak [53]. Further validation against a series of experimental results showed that: the proposed stress–dilatancy equation can efficiently capture the state-dependent behaviour of sand with different initial material states. A state-dependent nonassociated $\alpha$-plasticity model was then developed, based on a symmetric yielding surface [59]. However, due to the symmetry of the yielding surface, large elastic region would exist in the proposed model [14], which would result in the unrealistic prediction of the undrained behaviour of granular soils. Even though this aspect can sometimes be remedied by tuning the input model parameters, the model would be unable to capture the temporary peak or quasi-steady-state flow behaviour of sand before reaching the critical state.

This study aims to propose an improved $\alpha$-plasticity model for sand with a wide range of initial densities and pressures, by using a state-dependent fractional-order plastic flow rule and a modified yielding surface. This paper is structured as follows: Sect. 2 presents the basic definitions of the critical state, Caputo’s fractional derivative and constitutive relation for sand; Sect. 3 provides the derivations of the plastic loading, flow tensors and hardening modulus; Sect. 4 presents the detailed identification of model parameters; Sect. 5 validates the model against a series of triaxial test results of different sands with a variety of initial material states; Sect. 6 discusses the limitations of the proposed study; and Conclusions are drawn in Sect. 7. For the sake of simplicity, the study is limited to isotropic and homogeneous sands under triaxial loading, where the applied tensive stress and strain are considered as negative, while the compressive ones are positive.

2 Definitions

2.1 Critical state

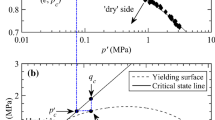
All the model derivations and discussions in this study are within the framework of the critical state soil mechanics (CSSM) [48]. Therefore, upon sufficient shearing, sand would deform and finally reach the critical state, where infinite plastic flow with no change of the stress ratio and volumetric strain took place. Such kind of critical state can be defined by using two separate equations in the $p^{{\prime }} - q$ and $e - p^{{\prime }}$ planes, respectively. According to available experimental and numerical studies [4, 12, 39], the critical-state line in the $p^{{\prime }} - q$ plane was linear and not influenced by the breakage of sand particles. Similar to that of clay, it can be defined as:

$$q = M_{\text{c}} p^{\prime }$$

(1)

where $p^{\prime } = {{(\sigma_{1}^{\prime } + 2\sigma_{3}^{\prime } )} \mathord{\left/ {\vphantom {{(\sigma_{1}^{\prime } + 2\sigma_{3}^{\prime } )} 3}} \right. \kern-0pt} 3}$ is the mean effective principal stress, while $q = \sigma_{1}^{\prime } - \sigma_{3}^{\prime }$ is the deviator stress; $\sigma_{1}^{\prime }$ and $\sigma_{3}^{\prime }$ are the first and third effective principal stresses, respectively. To obtain the effective stress ($\sigma_{i}^{{\prime }}$) from the total stress ($\sigma_{i}$), the Terzaghi’s effective stress principle is applied, where $\sigma_{i}^{\prime } = \sigma_{i} - u$; i = 1, 2, 3; u is the excess pore water pressure. Moreover, in Eq. (1), M_c is the critical-state stress ratio, which indicates the slope of the critical-state line in the $p^{{\prime }} - q$ plane, as shown in Fig. 1. Before reaching critical state, there would be possibly two relative positions of the current stress point, i.e., above or below the critical-state line, as shown in Fig. 1. If the soil was sheared from the “wet” side, it would possibly stay below the critical-state line in the $p^{{\prime }} - q$ plane, i.e., point B, until reaching the final critical state. If the soil was sheared from the “dry” side, it could be initially below the critical-state line in the $p^{{\prime }} - q$ plane and then cross the critical-state line to stay at point A, until reaching the final critical state. Inspired by this laboratory observation, Sun et al. [61] suggested a unified equation to connect the current stress state with the critical-state line, such that:

$$q_{\text{c}} = q + M_{\text{c}} \left( {p^{{\prime }} - p_{\text{c}}^{{\prime }} } \right)$$

(2)

where $q_{\text{c}}$ and $p_{\text{c}}^{\prime }$ are the critical-state stresses on the critical-state line, as shown in Fig. 1. It is easy to find that the solution of Eq. (2) depends on the determination of $p_{\text{c}}^{\prime}$, which can be obtained by using the critical-state line in the $e - p^{\prime }$ plane. Note that the critical-state line of sand in the $e - p^{\prime }$ plane was totally different from that of clay. Due to significant breakage of sand particles during loading, the critical-state line in the $e - p^{\prime }$ plane shifted with the varying void ratio (e) and pressure ($p^{{\prime }}$) [68, 69, 72, 79], as evidenced in a number of studies [24]. In order to capture such unusual behaviour, a variety of nonlinear critical-state lines in the $e - p^{\prime }$ plane had been proposed [10, 32, 33, 45]. However, the most commonly used one was suggested by Li and Wang [30] in the $e - ({{p^{\prime } } \mathord{\left/ {\vphantom {{p^{\prime } } {p_{\text{a}} }}} \right. \kern-0pt} {p_{\text{a}} }})^{\xi }$ plane, such that:

$$e = e_{\varGamma } - \lambda \left( {\frac{{p^{{\prime }} }}{{p_{\text{a}} }}} \right)^{\xi }$$

(3)

where p_a = 100 kPa is the atmospheric pressure for normalisation; $e_{\varGamma }$, $\lambda$ and $\xi$ are the material constants describing the critical-state line in the $e - ({{p^{\prime } } \mathord{\left/ {\vphantom {{p^{\prime } } {p_{\text{a}} }}} \right. \kern-0pt} {p_{\text{a}} }})^{\xi }$ plane, as shown in Fig. 2. Specifically speaking, $e_{\varGamma }$ and $\lambda$ are the intercept (at $p^{\prime } = 0$) and gradient of the critical-state line, respectively, while $\xi$ is adaptive for a better linear correlation between $e$ and ${{(p^{{\prime }} } \mathord{\left/ {\vphantom {{(p^{{\prime }} } {p_{\text{a}}^{{\prime }} )}}} \right. \kern-0pt} {p_{\text{a}}^{{\prime }} )}}^{\xi }$. Then, rearranging Eq. (3), $p_{\text{c}}^{\prime }$ can be determined as [67]:

$$p_{\text{c}}^{\prime } = p_{\text{a}} \left( {\frac{{e_{\varGamma } - e}}{\lambda }} \right)^{{{1 \mathord{\left/ {\vphantom {1 \xi }} \right. \kern-0pt} \xi }}} .$$

(4)

Fig. 1

Current stress state and critical-state line

Fig. 2

Critical-state line and current state

2.2 Caputo’s fractional derivative

In the theory of fractional calculus, fractional derivative usually has two expressions: one is the left-sided derivative, the other is the right-sided one [44]. Following Caputo [1, 8, 9], they can be defined as:

$${}_{{\mathrm{a}}}D_{{\sigma^{{\prime }} }}^{\alpha } g(\sigma^{{\prime }} ) = \frac{1}{\varGamma (n - \alpha )}\int\limits_{{\mathrm{a}}}^{{\sigma^{{\prime }} }} {\frac{{g^{(n)} (\chi ){\text{d}}\chi }}{{(\sigma^{\prime} - \chi )^{\alpha + 1 - n} }}} ,\quad {\kern 1pt} \sigma^{{\prime }} > a$$

(5)

$${}_{{\sigma^{{\prime }} }}D_{{\mathrm{a}}}^{\alpha } g(\sigma^{{\prime }} ) = \frac{{( - 1)^{n} }}{\varGamma (n - \alpha )}\int\limits_{{\sigma^{{\prime }} }}^{a} {\frac{{g^{(n)} (\chi ){\text{d}}\chi }}{{(\chi - \sigma^{{\prime }} )^{\alpha + 1 - n} }}} ,\quad {\kern 1pt} a > \sigma^{{\prime }}$$

(6)

where Eqs. (5) and (6) are the left-sided and right-sided fractional derivatives, respectively. D (= $\partial^{\alpha } /\partial \sigma^{\prime \alpha }$) denotes the partial fractional derivative of function, g; $\alpha \in (n - 1,n)$ is the fractional order [59], in which we restrict n = 1 or 2. As shown in Sun et al. [61], through strict mathematical derivation instead of empirical correlation, the state-dependent nonassociated plastic flow of granular soils can be captured by using the fractional derivatives. The fractional order, $\alpha$, determines the (geometric) non-normality of a vector with respect to a surface; it also reflects the (physical) extent of state-dependent nonassociated plastic flow of granular soils in geomechanics. Moreover, $\chi$ is the independent variable for integration; $\varGamma (\chi ) = \int_{0}^{\infty } {\exp ( - \tau )\tau^{\chi - 1} {\text{d}}\tau }$ is the gamma function; $\sigma^{\prime }$ is the current stress in this study while a is the lower or upper limit for integration. In order to capture the state dependence of sand flow, $a = \sigma_{\text{c}}^{{\prime }}$, where $\sigma^{\prime}_{{\mathrm{c}}}$ denotes the critical-state stress in this study, because the final state a soil can reach is its critical state [48]. $\sigma^{\prime}_{{\mathrm{c}}}$ should keep positive throughout the whole test. However, some previous studies [58] on fractional modelling only used the left-sided fractional derivative with a = 0, which, however, would make the model confronted with a dilemma: complex loading conditions cannot be easily captured [60], for example, (a) triaxial extension carried out by reducing $\sigma_{1}^{{\prime }}$, where the current deviator stress would be less than zero; (b) loading after anisotropic consolidation, where the initial stress (i.e., a) could be no longer equal to zero; (c) stress reversal during cyclic loading, where a would be unrealistically larger than $\sigma^{{\prime }}$ in Eq. (5).

To solve this limitation and consider the different loading states indicated by points A and B in Fig. 1, a series of constitutive approaches using both the left-sided and right-sided fractional derivatives were then developed [59, 61]. The choice of Eqs. (5) or (6) depends on the relative location between the current stress state and the critical-state line. For example, if the current stress was at point A, then $p^{{\prime }} < p_{\text{c}}^{{\prime }}$ and $q > q_{{\mathrm{c}}}$. Equation (5) would be used for calculating ${}_{{p^{{\prime }} }}D_{{p_{\text{c}}^{{}} }}^{\alpha } g(p^{{\prime }} )$, whereas Eq. (6) would be used for calculating ${}_{{q_{{\mathrm{c}}} }}D_{q}^{\alpha } g(q)$; or if the current stress was at point B where $p^{\prime} > p^{\prime}_{{\mathrm{c}}}$ and $q < q_{{\mathrm{c}}}$, Eq. (6) would be used for calculating ${}_{{p^{\prime}_{{\mathrm{c}}} }}D_{{p^{\prime}}}^{\alpha } g(p^{\prime})$, whereas Eq. (5) would be used for calculating ${}_{q}D_{{q_{{\mathrm{c}}} }}^{\alpha } g(q)$. Note that even though left or right Caputo’s fractional derivative is required due to the dependence of stress state, the final state-dependent stress–dilatancy equation is unique, as will be shown later.

2.3 Constitutive relation

The deformation of sand is considered to be consisted of two parts: elastic deformation and plastic deformation. Accordingly, the increment of the total strain ($\Delta {\varvec{\varepsilon }}$) can be decomposed as:

$$\Delta {\varvec{\upvarepsilon }} = \Delta {\varvec{\upvarepsilon }}^{e} + \Delta {\varvec{\upvarepsilon }}^{p}$$

(7)

where ${\varvec{\upvarepsilon }}^{e} = [\varepsilon_{v}^{e} ,\varepsilon_{{\mathrm{s}}}^{e} ]^{{\mathrm{T}}}$ is the elastic strain matrix, while ${\varvec{\upvarepsilon }}^{p} = [\varepsilon_{v}^{p} ,\varepsilon_{{\mathrm{s}}}^{p} ]^{{\mathrm{T}}}$ is the plastic strain matrix, respectively. The superscripts, e and p, denote the elastic and plastic components, respectively, and $\varepsilon_{v}^{{}}$ and $\varepsilon_{{\mathrm{s}}}^{{}}$ are the volumetric and generalised shear strains, respectively. Moreover, $\varepsilon_{v} = \varepsilon_{1} + 2\varepsilon_{3}$ and $\varepsilon_{{\mathrm{s}}} = {{2(\varepsilon_{1} - \varepsilon_{3} )} \mathord{\left/ {\vphantom {{2(\varepsilon_{1} - \varepsilon_{3} )} 3}} \right. \kern-0pt} 3}$, in which $\varepsilon_{1}$ and $\varepsilon_{3}$ are the first and third principal strains, respectively. $\Delta {\varvec{\upvarepsilon }}^{e}$ can be determined by using Hooke’s law, such that:

$$\Delta {\varvec{\varepsilon }}^{e} = {\mathbf{C}}^{e} \Delta {\varvec{\upsigma^{\prime}}}$$

(8)

where ${\varvec{\upsigma^{\prime}}} = [p^{\prime},q]^{{\mathrm{T}}}$ is the stress matrix. The elastic compliance C^e can be expressed as:

$${\mathbf{C}}^{e} = \left[ {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 K}} \right. \kern-0pt} K}} & {} \\ {} & {{1 \mathord{\left/ {\vphantom {1 {(3G)}}} \right. \kern-0pt} {(3G)}}} \\ \end{array} } \right]$$

(9)

in which the shear modulus (G) and bulk modulus (K) can be defined as:

$$G = G_{0} p_{{\mathrm{a}}} \frac{{(2.97 - e)^{2} }}{1 + e}\sqrt {\frac{{p^{\prime}}}{{p_{{\mathrm{a}}} }}}$$

(10)

$$K = \frac{(2 + 2\nu )}{3(1 - 2\nu )}G$$

(11)

where G₀ is the elastic constant; $\nu$ is the Poisson’s ratio. Following Pastor et al. [41], the plastic strain matrix can be determined as:

$$\Delta {\varvec{\upvarepsilon }}^{p} = \frac{1}{H}{\mathbf{n}}^{{\mathrm{T}}} {\mathbf{m}}\Delta {\varvec{\upsigma^{\prime}}}$$

(12)

where T denotes transpose, m and n are the plastic loading and flow matrices, respectively; H is the plastic modulus. Combining Eqs. (8) and (12), the elastoplastic constitutive relation for sand can be defined as:

$$\Delta {\varvec{\upvarepsilon }}^{e} = \left[ {{\mathbf{C}}^{e} + \frac{1}{H}{\mathbf{n}}^{{\mathrm{T}}} {\mathbf{m}}} \right]\Delta {\varvec{\upsigma^{\prime}}}.$$

(13)

3 Model development

3.1 Plastic loading tensor

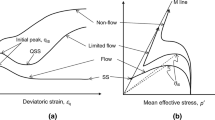
The plastic loading matrix defines the loading direction of sand. During undrained loading condition, the loading path in the $p^{\prime} - q$ plane is approximately equivalent to the yielding surface [46]. Therefore, the original MCC yielding surface used by Sun et al. [61] may not well capture the undrained behaviour of sand. For example, specimens with low initial density would experience low elastic strain, and quasi-steady-state flow with a temporary stress peak (Fig. 3) before reaching critical state. To consider such behaviour of sand, a modified yielding surface with shrunken size (reduced elastic region) should be used. Therefore, a modified yielding surface as shown in Fig. 3 is suggested in this study:

$$f = q^{2} + M_{\text{c}}^{2} p^{{{\prime }2}} - M_{\text{c}}^{2} p^{{{\prime }1 + \beta }} p_{0}^{{{\prime }1 - \beta }}$$

(14)

where $p^{\prime}_{0}$ represents the size of the yielding surface; similar to Yao et al. [74, 77], $\beta \in [0,1]$ is a material constant, which can be determined by fitting the undrained triaxial loading path of loose sand specimen. It should be noted that as $\beta$ increases from 0 to 1, the yielding surface shrinks more, where less elastic region exists. Then, the plastic loading matrix can be defined as:

$${\mathbf{m}} = \frac{1}{{\sqrt {1 + d_{{\mathrm{f}}}^{2} } }}\left[ {d_{{\mathrm{f}}} ,1} \right]^{{\mathrm{T}}}$$

(15)

where d_f can be determined by:

$$d_{{\mathrm{f}}} = \frac{{D^{1} f(p^{\prime})}}{{D^{1} f(q)}} = \frac{{(1 - \beta )M_{{\mathrm{c}}}^{2} - (1 + \beta )\eta^{2} }}{2\eta }$$

(16)

Fig. 3

Comparison between MCC and modified yielding surfaces

It can be found from Eq. (16) that: when $\beta = 0$, the proposed plastic loading matrix reduces to the classical modified Cam-clay (MCC) model. However, when $\beta = 1$, it reduces to the purely shear-induced plastic loading case with $f = q - \eta p^{\prime}$; this yielding function was often used for granular soils [13, 29].

3.2 Plastic flow tensor

According to available experimental results [6, 7, 64, 70], the plastic flow or stress–dilatancy of granular soils, including sand, exhibited highly dependence on the material state. To capture such state-dependent plastic flow of granular soil, various state-dependent stress–dilatancy equations have been developed by using empirical state parameters [10, 16, 17, 25, 31, 41, 57]. Without using predefined empirical state parameters, Sun et al. [61] theoretically developed a state-dependent stress–dilatancy equation, by conducting fractional derivatives of the MCC yielding surface. To keep consistent with the previous study, $\beta = 0$ is used when deriving the plastic flow matrix. Further substituting Eq. (14) into Eqs. (5) and (6), one has:

$$\begin{aligned} d_{{\mathrm{g}}} & = - \frac{{{}_{{p^{\prime}}}D_{{p^{\prime}_{{\mathrm{c}}} }}^{\alpha } f}}{{{}_{{q_{{\mathrm{c}}} }}D_{q}^{\alpha } f}} = - \frac{{{}_{{p^{\prime}_{{\mathrm{c}}} }}D_{{p^{\prime}}}^{\alpha } f}}{{{}_{q}D_{{q_{{\mathrm{c}}} }}^{\alpha } f}} \\ & = M_{{\mathrm{c}}}^{1 + \alpha } \frac{{(p^{\prime} - p^{\prime}_{{\mathrm{c}}} ) + (2 - \alpha )(p^{\prime}_{{\mathrm{c}}} - p^{\prime}_{0} /2)}}{{(q - q_{{\mathrm{c}}} ) + (2 - \alpha )q_{{\mathrm{c}}} }} \\ \end{aligned}$$

(17)

As can be observed, if $\alpha = 1$, Eq. (17) would reduce to the traditional MCC stress–dilatancy equation with no state dependence. However, if $\alpha$ = non-integer, a clear state dependence can be achieved via $p^{\prime} - p^{\prime}_{{\mathrm{c}}}$ and $q - q_{{\mathrm{c}}}$, which are the horizontal and vertical distances from the current stress point to the critical-state line. Thus, as $\alpha$ deviates from unit, the extent of state dependence increases [61]. Moreover, with the increase of $\alpha$, a higher volumetric dilation could be also observed. For more details of the effect on stress–dilatancy, one can refer to Sun et al. [59, 61]. In triaxial loading condition, the plastic flow matrix can be defined as:

$${\mathbf{n}} = \frac{1}{{\sqrt {1 + d_{{\mathrm{g}}}^{2} } }}\left[ {d_{{\mathrm{g}}} ,1} \right]^{{\mathrm{T}}} .$$

(18)

3.3 Hardening modulus

Sand specimens tested from the “wet” side of the critical-state line would exhibit strain hardening. In contrast, strain softening behaviour would be observed in sand specimens tested from the “dry” side of the critical-state line. The transition from hardening to softening also depends on material state [18, 19, 22]. To correctly capture such hardening/softening behaviour of sand, a reasonable state-dependent hardening modulus should be required. In this study, the hardening modulus developed by Li and Dafalias [29] is adopted, such that

$$H = h_{0} G\left\{ {\frac{{M_{{\mathrm{c}}} }}{\eta } - \exp \left[ {\vartheta (e - e_{\varGamma } + \lambda ({{p^{\prime}} \mathord{\left/ {\vphantom {{p^{\prime}} {p_{{\mathrm{a}}} }}} \right. \kern-0pt} {p_{{\mathrm{a}}} }})^{\xi } )} \right]} \right\}$$

(19)

where $h_{0} = h_{1} - h_{2} e$, in which h₁ and h₂ are the hardening parameters; and $\vartheta$ is a material constant. Note that by using Eq. (19) as hardening modulus, pure compression-induced soil hardening cannot be considered, which would result in the inability of the model in predicting pure compressive deformation. But, in engineering practice, soils are rarely subjected to pure compressive load only. For isotropic or oedometer compression of soils, specific modelling approaches, using either empirical correlation [42, 43] or theoretical derivation [38, 50], were usually reported, which, however, is not within the scope of this study.

4 Identification of model parameters

It can be found that there are eleven parameters in the developed $\alpha$-plasticity model: M_c, $e_{\varGamma }$, $\lambda$, $\xi$, $\beta$, $\alpha$, n, h₁, h₂, G₀ and $\nu$, which can be all identified from traditional triaxial test results. All the model parameters are dimensionless.

The critical-state stress ratio, M_c, can be determined by measuring the gradient of the critical-state line in the $p^{\prime} - q$ plane. The rest three critical-state parameters, $e_{\varGamma }$, $\lambda$ and $\xi$, can be identified by fitting the critical-state data points in the $e - p^{\prime}$ plane [30], through least square method.

The shape parameter, $\beta$, can be determined by fitting the undrained stress path of the soil at its loose state [25].

The fractional order, $\alpha$, can be obtained at the phase transformation state where d_g = 0, such that:

$$\alpha = \frac{{2M_{{\mathrm{c}}}^{2} p_{{\mathrm{a}}} \left[ {{{(e_{\varGamma } - e_{{\mathrm{pt}}} )} \mathord{\left/ {\vphantom {{(e_{\varGamma } - e_{{\mathrm{pt}}} )} \lambda }} \right. \kern-0pt} \lambda }} \right]^{{{1 \mathord{\left/ {\vphantom {1 \xi }} \right. \kern-0pt} \xi }}} - 2\eta_{{\mathrm{pt}}}^{2} p^{\prime}_{{\mathrm{pt}}} }}{{2M_{{\mathrm{c}}}^{2} p_{{\mathrm{a}}} \left[ {{{(e_{\varGamma } - e_{{\mathrm{pt}}} )} \mathord{\left/ {\vphantom {{(e_{\varGamma } - e_{{\mathrm{pt}}} )} \lambda }} \right. \kern-0pt} \lambda }} \right]^{{{1 \mathord{\left/ {\vphantom {1 \xi }} \right. \kern-0pt} \xi }}} - M_{{\mathrm{c}}}^{2} p^{\prime}_{{\mathrm{pt}}} - \eta_{{\mathrm{pt}}}^{2} p^{\prime}_{{\mathrm{pt}}} }}$$

(20)

where $e_{{\mathrm{pt}}}$, $p^{\prime}_{{\mathrm{pt}}}$ and $\eta_{{\mathrm{pt}}}$ are the void ratio, effective mean principal stress and stress ratio, respectively, at phase transformation state.

The peak-state parameter, $\vartheta$, defines the state dependence of the peak stress ratio during drained loading, where H = 0. Therefore, it can be obtained by:

$$\vartheta = \frac{{\ln ({{M_{{\mathrm{c}}} } \mathord{\left/ {\vphantom {{M_{{\mathrm{c}}} } {\eta_{{\mathrm{f}}} }}} \right. \kern-0pt} {\eta_{{\mathrm{f}}} }})}}{{e_{{\mathrm{f}}} - e_{\varGamma } + \lambda ({{p^{\prime}_{{\mathrm{f}}} } \mathord{\left/ {\vphantom {{p^{\prime}_{{\mathrm{f}}} } {p_{{\mathrm{a}}} }}} \right. \kern-0pt} {p_{{\mathrm{a}}} }})^{\xi } }}$$

(21)

where $e_{{\mathrm{f}}}$, $p^{\prime}_{{\mathrm{f}}}$ and $\eta_{{\mathrm{f}}}$ are the void ratio, effective mean principal stress and stress ratio, respectively, at peak failure state.

The two hardening parameters, h₁ and h₂, define the hardening behaviour of soil, which can be determined by fitting the $\varepsilon_{{\mathrm{s}}} - q$ relationship [29, 63]. It can be also determined from the drained triaxial test where $\dot{p^{\prime}} = {{\dot{q}} \mathord{\left/ {\vphantom {{\dot{q}} 3}} \right. \kern-0pt} 3}$. Assuming the elastic strain is small and substituting $\dot{p^{\prime}} = {{\dot{q}} \mathord{\left/ {\vphantom {{\dot{q}} 3}} \right. \kern-0pt} 3}$ into Eq. (13), one has:

$$h_{0} = \frac{{\eta (1 + {{d_{{\mathrm{f}}} } \mathord{\left/ {\vphantom {{d_{{\mathrm{f}}} } 3}} \right. \kern-0pt} 3}){{\dot{q}} \mathord{\left/ {\vphantom {{\dot{q}} {{{\dot{\varepsilon }_{{\mathrm{s}}} } \mathord{\left/ {\vphantom {{\dot{\varepsilon }_{{\mathrm{s}}} } {{{\sqrt {1 + d_{{\mathrm{f}}}^{2} } } \mathord{\left/ {\vphantom {{\sqrt {1 + d_{{\mathrm{f}}}^{2} } } {\sqrt {1 + d_{{\mathrm{g}}}^{2} } }}} \right. \kern-0pt} {\sqrt {1 + d_{{\mathrm{g}}}^{2} } }}}}} \right. \kern-0pt} {{{\sqrt {1 + d_{{\mathrm{f}}}^{2} } } \mathord{\left/ {\vphantom {{\sqrt {1 + d_{{\mathrm{f}}}^{2} } } {\sqrt {1 + d_{{\mathrm{g}}}^{2} } }}} \right. \kern-0pt} {\sqrt {1 + d_{{\mathrm{g}}}^{2} } }}}}}}} \right. \kern-0pt} {{{\dot{\varepsilon }_{{\mathrm{s}}} } \mathord{\left/ {\vphantom {{\dot{\varepsilon }_{{\mathrm{s}}} } {{{\sqrt {1 + d_{{\mathrm{f}}}^{2} } } \mathord{\left/ {\vphantom {{\sqrt {1 + d_{{\mathrm{f}}}^{2} } } {\sqrt {1 + d_{{\mathrm{g}}}^{2} } }}} \right. \kern-0pt} {\sqrt {1 + d_{{\mathrm{g}}}^{2} } }}}}} \right. \kern-0pt} {{{\sqrt {1 + d_{{\mathrm{f}}}^{2} } } \mathord{\left/ {\vphantom {{\sqrt {1 + d_{{\mathrm{f}}}^{2} } } {\sqrt {1 + d_{{\mathrm{g}}}^{2} } }}} \right. \kern-0pt} {\sqrt {1 + d_{{\mathrm{g}}}^{2} } }}}}}}}}{{G\left\{ {M_{{\mathrm{c}}} - \eta \exp \left[ {n(e - e_{\varGamma } + \lambda ({{p^{\prime}} \mathord{\left/ {\vphantom {{p^{\prime}} {p_{{\mathrm{a}}} }}} \right. \kern-0pt} {p_{{\mathrm{a}}} }})^{\xi } )} \right]} \right\}}}$$

(22)

Then, h₀ can be calibrated from the $\varepsilon_{{\mathrm{s}}} - q$ relationship, where h₁ and h₂ can be further identified by fitting the relationship between e and h₀, as clearly shown in Taiebat et al. [63].

The two elastic constants, G₀ and $\nu$, can be obtained from the $\varepsilon_{{\mathrm{s}}} - q$ relationship at the initial loading stage ($\varepsilon_{{\mathrm{s}}} \approx \varepsilon_{{\mathrm{s}}}^{e}$) [61], where G₀ can be obtained by rearranging Eqs. (8)–(10):

$$G_{0} \approx \frac{(1 + e)G}{{(2.97 - e)^{2} \sqrt {p^{\prime}p_{{\mathrm{a}}} } }}$$

(23)

$$\nu \approx \frac{{3\varepsilon_{{\mathrm{s}}} - 2\varepsilon_{v} }}{{6\varepsilon_{{\mathrm{s}}} + 2\varepsilon_{v} }}.$$

(24)

5 Model validation

In this section, the proposed model will be validated against a series of drained and undrained triaxial test results of six different sands, including Hostun RF sand [40] (Figs. 4, 5), Hostun III sand [15] (Fig. 6), Firoozkuh sand [3] (Fig. 7), Fuji River sand [20] (Figs. 8, 9), Toyoura sand [64] (Figs. 10, 13) and Sacramento River sand [27] (Figs. 14, 16). It is noted that test results are represented in coloured data points, while model predictions are shown by black solid lines. Detailed values of each model parameter are shown in Table 1. Note that as analytical solutions of the fractional derivative with respect to the assumed yielding function have been obtained, the subsequent numerical computation of the model would not involve any resolution of the fractional derivative. Therefore, the computational overhead of this approach should be equivalent to the traditional approaches using integer-order derivative.

Fig. 4

Drained response of Hostun RF sand: model predictions versus test results [40]

Fig. 5

Undrained response of Hostun RF sand: model predictions versus test results [40]

Fig. 6

Drained response of Hostun III sand: model predictions versus test results [15]

Fig. 7

Undrained response of Firoozkuh sand: model predictions versus test results [3]

Fig. 8

Drained response of Fuji River sand: model predictions versus test results [20]

Fig. 9

Undrained response of Fuji River sand: model predictions versus test results [20]

Fig. 10

Drained response of Toyoura sand: model predictions versus test results [64]

Table 1 Model parameters

Figures 4 and 5 show the model simulations of the drained and undrained triaxial tests of Hostun RF sand carried out by Meghachou [40]. It was found that the sand mainly consisted of angular quartz particles, with a median particle size (d₅₀) equal to 0.35–0.38 mm and a coefficient of uniformity (C_u) equal to 1.8. The maximum (e_max) and minimum (e_min) void ratios were tested to be 1 and 0.656, respectively. All the specimens were prepared by moist-tamping technique in laboratory. A wide range of the initial densities from dense state ($e_{0}$ = 0.574) to medium dense ($e_{0}$ = 0.8) and loose states ($e_{0}$ = 0.897) were used for conducting the drained triaxial tests at an initial confining pressure $\sigma^{\prime}_{3}$ of 300 kPa. As shown in Fig. 4, the developed $\alpha$-plasticity model can well capture the hardening and softening behaviour of Hostun RF sand. For dense and medium dense sands, the specimen volume initially contracted, and then continuously dilated; while for loose sand, a general volumetric contraction is observed, which can be all accurately predicted by the proposed model. Figure 5 shows the model predictions of the undrained test results of Hostun RF sand with two different $e_{0}$ (= 0.94, 0.87) and $\sigma^{\prime}_{3}$ (= 200 kPa, 397 kPa). As observed, the proposed model can also reasonably characterise the undrained behaviour of Hostun RF sand. With the increase of shear strain, the predicted deviator stress of Hostun RF sand increases and then decreases rapidly towards a state of liquefaction instability, which matches well with the corresponding test results.

Figure 6 presents the model simulations of the drained triaxial behaviour of Hostun III sand [15] under a wide range of pressures (100–1200 kPa). The sand was reported to consist of sub-angular particles with a d₅₀ of 0.307, C_u of 2.3, e_max of 0.953 and e_min of 0.612. The $e_{0}$ of 0.646, 0.646, 0.650 and 0.646 were used for tests carried out at $\sigma^{\prime}_{3}$ of 100 kPa, 400 kPa, 800 kPa and 1200 kPa, respectively. It can be found that all specimens were tested under medium to dense states, and thus exhibited volumetric dilation at the end of the test. Comparisons between the model simulations and the corresponding test results show that: the model can appropriately predict the stress–strain response of Hostun III sand, where strain hardening/softening and volumetric dilation with varying degrees can be all captured.

Figure 7 shows the model predictions of the undrained liquefaction behaviour of Firoozkuh sand [3] under different initial loading pressures. The Firoozkuh sand was a crusher-run sandy soil that consisted of sub-angular quartz particles. It had a d₅₀ of 0.26, C_u of 1.9, e_max of 0.943 and e_min of 0.568. All the specimens were prepared by using moist-tamping method. Three different $\sigma^{\prime}_{3}$ of 243 kPa, 180 kPa and 154 kPa, with the corresponding $e_{0}$ of 0.975, 0.964 and 0.972, were used, respectively, for model simulations. As the specimens were initially at loose state, it can be found that they all liquefied and become instable at the end of the tests. The proposed model can accurately capture such liquefaction instability behaviour of Firoozkuh sand.

Figures 8 and 9 show the model simulations of the drained and undrained triaxial behaviour of Fuji River sand [20]. The sand mainly consisted of sub-angular particles with a d₅₀ of 0.22 mm, C_u of 2.21, e_max of 0.99 and e_min of 0.55. All the specimens were prepared by using pluviation method. For drained tests, the $e_{0}$ of 0.750, 0.747 and 0.751 with the respective $\sigma^{\prime}_{3}$ of 98 kPa, 196 kPa and 294 kPa were used to carried out, whereas for undrained tests, the $e_{0}$ of 0.740, 0.731 and 0.718 with the respective $\sigma^{\prime}_{3}$ of 98 kPa, 196 kPa and 294 kPa were used. It can be found that both the drained and undrained behaviour of Fuji River sand can be well predicted by using the $\alpha$-plasticity model. Particularly, the model predictions exhibit an accurate match with the strain hardening data during drained loading. In addition, all the specimens underwent steady-state flow at the end of the undrained tests, which can be also reasonably captured by the model.

Figures 10, 11, 12 and 13 show the model predictions of the drained and undrained triaxial behaviour of Toyoura sand [64] with a wide range of initial void ratios and pressures. It was found that the sand mainly consisted of sub-round/sub-angular particles with a d₅₀ of 0.17 mm, C_u of 1.7, e_max of 0.977 and e_min of 0.597. The moist placement method was used for specimen preparation. For drained tests, two different confining pressures were used: $\sigma^{\prime}_{3}$ = 100 kPa for the corresponding $e_{0}$ of 0.831, 0.917 and 0.996; $\sigma^{\prime}_{3}$ = 500 kPa for the corresponding $e_{0}$ of 0.810, 0.886 and 0.960. For undrained tests, three different void ratios representing the dense ($e_{0}$ = 0.735), medium dense ($e_{0}$ = 0.833) and loose ($e_{0}$ = 0.907) states of Toyoura sand were used. As can be observed in Fig. 10, the proposed model simulates well the drained triaxial behaviour of Toyoura sand under different loading pressures. Irrespective of the applied confining pressure, specimens with low void ratios ($e_{0}$ = 0.810, 0.831) all exhibited some level of volumetric dilation, while those with relatively higher $e_{0}$ only experienced volumetric contraction throughout the entire tests. Moreover, Figs. 11, 12 and 13 show the model predictions of the undrained triaxial behaviour of Toyoura sand. For dense specimens shown in Fig. 11, the deviator stress increased continuously with the increase of shear strain, whereas the mean effective principal stress firstly decreased and then increased until reaching critical state, which can be well predicted by using the $\alpha$-plasticity model. For medium dense specimens shown in Fig. 12, test results under $\sigma^{\prime}_{3}$ of 100 kPa and 1000 kPa exhibited a continuous increase of the deviator stress with the increase of shear strain, while a temporary peak followed a slight decrease of the deviator stress can be observed in test under $\sigma^{\prime}_{3}$ = 2000 kPa. For test result obtained under $\sigma^{\prime}_{3}$ = 3000 kPa, an initial increase followed by a decrease of the deviator stress was reported. Irrespective of the loading pressures, all the tested specimens reached the critical state under sufficient triaxial shearing. These features can be all addressed appropriately by the proposed model. For loose specimens shown in Fig. 13, liquefaction instability was observed in tests under $\sigma^{\prime}_{3}$ = 1000 kPa, 2000 kPa, whereas an increase of the deviator stress was reported in test under $\sigma^{\prime}_{3}$ = 100 kPa. These characteristics can be also well captured by the developed model.

Fig. 11

Undrained response of dense Toyoura sand: model predictions versus test results [64]

Fig. 12

Undrained response of medium dense Toyoura sand: model predictions versus test results [64]

Fig. 13

Undrained response of loose Toyoura sand: model predictions versus test results [64]

Figures 14, 15 and 16 show the model simulations of the drained and undrained triaxial test results of dense and loose Sacramento River sand [27]. The sand was reported to contain fine and uniformly graded quartz particles with sub-rounded shape. It had a minimum particle size (d_m) of 0.149 mm, maximum particle size (d_M) of 0.297, e_max of 1.03 and e_min of 0.61. For drained tests, the $e_{0}$ of 0.87, 0.87, 0.87 and 0.85 are used for simulating loose specimens tested under the $\sigma^{\prime}_{3}$ of 92 kPa, 196 kPa, 442 kPa and 1241 kPa, respectively, whereas the $e_{0}$ of 0.61, 0.61 and 0.59 are used for simulating dense specimens tested under the $\sigma^{\prime}_{3}$ of 98 kPa, 294 kPa and 589 kPa, respectively. For undrained tests, the $e_{0}$ for simulating loose specimens are 0.87, 0.87, 0.86, and 0.85, corresponding to the $\sigma^{\prime}_{3}$ of 98 kPa, 294 kPa, 490 kPa and 1069 kPa, respectively; whereas the $e_{0}$ of 0.63, 0.61, 0.59 and 0.59 are used for simulating dense specimens tested under the $\sigma^{\prime}_{3}$ of 98 kPa, 1030 kPa, 1481 kPa and 1982 kPa, respectively. It is shown in Fig. 14 that the model simulates well the drained stress–strain behaviours of Sacramento River sand under both loose and dense states. Loose specimens exhibited strain hardening and volumetric contraction; however, a clear peak state followed by a decrease of the deviator stress and volumetric dilation can be observed in dense specimens. These key features of the drained response of Sacramento River sand can be appropriately captured by the $\alpha$-plasticity model. Figure 15 shows the observed and predicted undrained behaviour of loose Sacramento River sand, where a good agreement between the model predictions and test results can be observed. All the specimens are predicted to finally reach the critical-state flow, which match well with the experimental observations. Figure 16 presents the model predictions of the undrained behaviour of dense Sacramento River sand. It is found that the predicted deviator stress increased continuously with the increase of axial strain, which agrees well with the corresponding test results. Besides, with the increase of axial strain, the mean effective principal stress of specimens subjected to $\sigma^{\prime}_{3}$ of 1030 kPa, 1481 kPa and 1982 kPa initially decreased and then increased towards steady-state flow. These features can be all reasonably depicted by the proposed model. Note that the test data after 10% strain cannot be provided here, because the original data in [27] were not given.

Fig. 14

Drained response of Sacramento River sand: model predictions versus test results [27]

Fig. 15

Undrained response of loose Sacramento River sand: model predictions versus test results [27]

Fig. 16

Undrained response of dense Sacramento River sand: model predictions versus test results [27]

6 Discussions on model limitations

Even though the developed approach has positive performances when simulating the stress and strain behaviour of different sands, it could have several limitations that are associated with the type of critical-state line. Discussions will be thus made in terms of the critical-state lines that are usually used in engineering practice. It is easy to summarise the following three typical critical-state lines: (1) linear representation of the critical-state line in the $e - \ln p^{\prime}$ plane, (2) linear representation in the $e - ({{p^{\prime}} \mathord{\left/ {\vphantom {{p^{\prime}} {p_{{\mathrm{a}}} }}} \right. \kern-0pt} {p_{{\mathrm{a}}} }})^{\xi }$ plane and (3) nonlinear representation in the $e - \ln p^{\prime}$ plane.

If the first type of critical-state line was used, then the established model would not be able to characterise the constitutive behaviour of sand with wide initial material states, by only using one set of model parameters. This is due to the significant particle breakage of sand that can shift the critical-state points downwards [32, 79], which would inevitably change the critical-state parameters in the $e - \ln p^{\prime}$ plane. This type of critical-state line can be used for modelling the stress–strain response of soft soils, e.g., clay, but should be avoided in current study.

For unified modelling of the critical-state behaviour of sand with a wide range of initial material states, the linear critical-state line in the $e - ({{p^{\prime}} \mathord{\left/ {\vphantom {{p^{\prime}} {p_{{\mathrm{a}}} }}} \right. \kern-0pt} {p_{{\mathrm{a}}} }})^{\xi }$ plane can be used. However, this kind of critical-state line may also result in some limitations of the developed model. As can be observed in Fig. 2, if the material state was initially at point C, where the $e_{0}$ was quite large while $p^{\prime}$ was quite small, the calculated critical-state stress, $p^{\prime}_{{\mathrm{c}}}$, at undrained loading condition could be unreasonably negative. This could be also encountered in classical models [67, 69] using the state pressure index, $I_{{\mathrm{p}}}$ ($p^{\prime},p^{\prime}_{{\mathrm{c}}}$). In this kind of situation, $p^{\prime}_{{\mathrm{c}}} = 0$ could be probably assumed for conducting the subsequent numerical simulation. However, in practical engineering, for example, embankment and foundation engineering, this kind of density and pressure conditions should be infrequently reached. Possible ground treatment technique would be applied to compact and consolidate the soil towards initial state point D, before large-scale geotechnical construction.

In addition to points C and D, if the material was initially at point E, where the $e_{0}$ was small while $p^{\prime}$ was extremely large, the calculated critical-state void ratio, $e_{{\mathrm{c}}}$, at drained loading condition would be unreasonably negative. However, this limitation can be readily resolved by incorporating the dependence of I_p into hardening modulus, as suggested by Wang et al. [67]. It may be also remedied by using the third type of critical-state line, i.e., the nonlinear one, in the $e - \ln p^{\prime}$ plane, such as the one with three segments [45, 46] and the one with inverted S-shape [10, 31].

This model in current form is also unable to capture the true three-dimensional behaviour of sand, due to the ignorance of the dependence of Lode’s angle on the strength and dilatancy behaviour of sand. However, this limitation can be resolved by incorporating the effect of Lode’s angle on the critical-state, peak-state and dilatancy formulae, which had been well defined and applied in practice [16, 23, 34] and thus not repeated here for simplicity. It can be also extended by using some specific three-dimensional methods, for example, the transformed stress method [73,74,75] and the characteristic stress method [35, 55]. As the emphasis of current study is not put on three-dimensional modelling of sand, this aspect will not be investigated. For more details on extending the $\alpha$-plasticity approach to consider complex loading, one can refer to Sun and Sumelka [55] and Sun et al. [62]. In addition, not all the functions have analytical solution when performing fractional derivative. Therefore, only those yielding functions with power-law form, for example, the modified Cam-clay yielding function, have been adopted for model development. Nonetheless approximate solutions can be easily calculated also cf. Sumelka and Nowak [54]. Moreover, this approach did not consider the strength anisotropy and pure compressive hardening of soil; thus, it cannot simulate the stress–strain or consolidation behaviour of soils with inherent or induced anisotropy.

7 Conclusions

To capture the state-dependent stress–strain behaviour of sand with a wide range of initial densities and pressures, an improved fractional-order ($\alpha$) plasticity model was developed by using a modified yielding surface. Then, the model was validated against a series of drained and undrained triaxial test results of different sands. Discussions on several limitations of the proposed approach were also made. The main findings can be summarised as follows:

• 1. The model contained nine parameters for describing the plastic deformation and two parameters for describing the elastic deformation. All of the model parameters can be obtained from traditional triaxial test results.

• 2. The model can well capture the drained and undrained stress–strain behaviour of different sands with a wide range of initial states. The strain hardening/softening and volumetric dilation/contraction behaviour of sand under drained loading conditions can be well captured. In addition, compared with the previous fractional models, this model used a modified yielding surface, which made it capable of reasonably predicting the steady-state flow, liquefaction, quasi-steady-state flow and temporary peak behaviour of sand under undrained loading conditions.

• 3. Due to the typical forms of the critical-state line, the model may not be able to well capture the undrained behaviour of sand with initially significant large void ratio and small mean effective principal stress. It may also fail to capture the drained behaviour of sand with initially significant small void ratio and large mean effective principal stress. The effect of Lode’s angle on the critical-state, peak-state and dilatancy behaviour of sand was also ignored in this study, which would make the model unable to simulate the three-dimensional behaviour of sand.

• 4. In addition, the above study was inspired by Sumelka [52]; however, these two approaches have distinct differences. As discussed in Sun and Sumelka [56], the model in [52] was developed by accounting for the effect of neighbouring stress point on the material point of interest, where the lower and higher stress terminals adopted in defining fractional derivative were collected from neighbouring material points. On the contrary, this study is proposed by considering the stress distance from the current state to the corresponding critical state of the material point of interest. All the model parameters were proposed based on laboratory observation.

Appendix

In order to derive Eq. (17), the following analytical solutions of the power-law functions, $(\sigma^{\prime} - \sigma^{\prime}_{{\mathrm{c}}} )^{\mu }$ and $(\sigma^{\prime}_{{\mathrm{c}}} - \sigma^{\prime})^{\mu }$, are needed:

$${}_{{\sigma^{\prime}_{{\mathrm{c}}} }}D_{{\sigma^{\prime}}}^{\alpha } (\sigma^{\prime} - \sigma^{\prime}_{{\mathrm{c}}} )^{\mu } { = }\frac{\varGamma (1 + \mu )}{\varGamma (1 + \mu - \alpha )}(\sigma^{\prime} - \sigma^{\prime}_{{\mathrm{c}}} )^{\mu - \alpha }$$

(25)

$${}_{{\sigma^{\prime}}}D_{{\sigma^{\prime}_{{\mathrm{c}}} }}^{\alpha } (\sigma^{\prime}_{{\mathrm{c}}} - \sigma^{\prime})^{\mu } { = }\frac{\varGamma (1 + \mu )}{\varGamma (1 + \mu - \alpha )}(\sigma^{\prime}_{{\mathrm{c}}} - \sigma^{\prime})^{\mu - \alpha }$$

(26)

where $\mu$ is the power index. Details for deriving Eqs. (25) and (26) can be found in [44] and thus not repeated here for simplicity. Accordingly, Eq. (14) with $\beta = 0$ should be rearranged as:

$$\begin{aligned} f & = (q - q_{{\mathrm{c}}} )^{2} + 2q_{{\mathrm{c}}} (q - q_{{\mathrm{c}}} ) \\ & \quad + M_{{\mathrm{c}}}^{2} (p^{\prime} - p^{\prime}_{{\mathrm{c}}} )^{2} + 2M_{{\mathrm{c}}}^{2} p^{\prime}_{{\mathrm{c}}} (p^{\prime} - p^{\prime}_{{\mathrm{c}}} ) \\ & \quad - M_{{\mathrm{c}}}^{2} p^{\prime}_{0} (p^{\prime} - p^{\prime}_{{\mathrm{c}}} ) + q_{{\mathrm{c}}}^{2} + M_{{\mathrm{c}}}^{2} p_{{\mathrm{c}}}^{\prime2} - M_{{\mathrm{c}}}^{2} p^{\prime}_{0} p^{\prime}_{{\mathrm{c}}} \\ \end{aligned}$$

(27)

and

$$\begin{aligned} f & = (q_{{\mathrm{c}}} - q)^{2} - 2q_{{\mathrm{c}}} (q_{{\mathrm{c}}} - q) \\ {\kern 1pt} & \quad + M_{{\mathrm{c}}}^{2} (p^{\prime}_{{\mathrm{c}}} - p^{\prime})^{2} - 2M_{{\mathrm{c}}}^{2} p^{\prime}_{{\mathrm{c}}} (p^{\prime}_{{\mathrm{c}}} - p^{\prime}) \\ & \quad + M_{{\mathrm{c}}}^{2} p^{\prime}_{0} (p^{\prime}_{{\mathrm{c}}} - p^{\prime}) + q_{{\mathrm{c}}}^{2} + M_{{\mathrm{c}}}^{2} p_{{\mathrm{c}}}^{\prime2} - M_{{\mathrm{c}}}^{2} p^{\prime}_{0} p^{\prime}_{{\mathrm{c}}} \\ \end{aligned}$$

(28)

Then, substituting Eqs. (27) and (28) into Eqs. (25) and (26), respectively, one has:

$$d_{{\mathrm{g}}} = - \frac{{{}_{{p^{\prime}}}D_{{p^{\prime}_{{\mathrm{c}}} }}^{\alpha } f(p^{\prime})}}{{{}_{{q_{{\mathrm{c}}} }}D_{q}^{\alpha } f(q)}} = M_{{\mathrm{c}}}^{2} \frac{{(p^{\prime} - p^{\prime}_{{\mathrm{c}}} ) + (2 - \alpha )(p^{\prime}_{{\mathrm{c}}} - p^{\prime}_{0} /2)}}{{(q - q_{{\mathrm{c}}} ) + (2 - \alpha )q_{{\mathrm{c}}} }}\left[ {\frac{{p^{\prime}_{{\mathrm{c}}} - p^{\prime}}}{{q - q_{{\mathrm{c}}} }}} \right]^{1 - \alpha }$$

(29)

$$d_{{\mathrm{g}}} = - \frac{{{}_{{p^{\prime}_{{\mathrm{c}}} }}D_{{p^{\prime}}}^{\alpha } f(p^{\prime})}}{{{}_{q}D_{{q_{{\mathrm{c}}} }}^{\alpha } f(q)}} = M_{{\mathrm{c}}}^{2} \frac{{(p^{\prime} - p^{\prime}_{{\mathrm{c}}} ) + (2 - \alpha )(p^{\prime}_{{\mathrm{c}}} - p^{\prime}_{0} /2)}}{{(q - q_{{\mathrm{c}}} ) + (2 - \alpha )q_{{\mathrm{c}}} }}\left[ {\frac{{p^{\prime} - p^{\prime}_{{\mathrm{c}}} }}{{q_{{\mathrm{c}}} - q}}} \right]^{1 - \alpha }$$

(30)

Further substituting Eq. (2) into Eqs. (29) and (30), a unique stress–dilatancy equation is obtained:

$$d_{{\mathrm{g}}} = M_{{\mathrm{c}}}^{1 + \alpha } \frac{{(p^{\prime} - p^{\prime}_{{\mathrm{c}}} ) + (2 - \alpha )(p^{\prime}_{{\mathrm{c}}} - p^{\prime}_{0} /2)}}{{(q - q_{{\mathrm{c}}} ) + (2 - \alpha )q_{{\mathrm{c}}} }}.$$

(31)