Investigation of the effect of specific interfacial area on strength of unsaturated granular materials by X-ray tomography

Abstract

This paper studies the effect of interfacial areas (air–water interfaces and solid–water interfaces) on material strength of unsaturated granular materials. High-resolution X-ray computed tomography technique is employed to measure the interfacial areas in wet glass bead samples. The scanned 3D images are trinarized into three phases and meshed into representative volume elements (RVEs). An appropriate RVE size is selected to represent adequate local information. Due to the local heterogeneity of the material, the discretized RVEs of the scanned samples actually cover a very large range of degree of saturation and porosity. The data of RVEs present the relationship between the specific interfacial areas and degree of saturation and gives boundaries where the interfacial area of a whole sample should fall in. In parallel, suction-controlled direct shear tests have been carried out on glass beads and the material strength has been corroborated with two effective stress definitions related to the specific air–water interfacial areas and fraction of wetted solid surface, respectively. The comparisons show that the specific air–water interfacial area reaches the peak at about 25% of saturation and contributes significantly to the material strength (up to 60% of the total capillary strength). The wetted solid surface obtained from X-ray CT is also used to estimate Bishop’s coefficient χ based on the second type of effective stress definition, which shows a good agreement with the measured value. This work emphasizes the importance to include interface terms in effective stress formulations of unsaturated soils. It also suggests that the X-ray CT technique and RVE-based multiscale analysis are very valuable in the studies of multiphase geomaterials.

1 Introduction

1.1 Effective stress of unsaturated soils

Terzaghi’s principle of effective stress for soil is the cornerstone of modern soil mechanics [39]. It is valid for two-phase saturated soils and unifies the soil mechanical behavior and hydraulic conditions as:

$$\sigma_{ij}^{\prime} = \sigma_{ij} - u_{\text{w}} \delta_{ij}$$

(1)

where $\sigma_{ij}^{\prime}$ is the effective stress, $\sigma_{ij}$ is the total stress, $u_{\text{w}}$ is the pore water pressure and $\delta_{ij}$ is the Kronecker delta. However, this formulation for the effective stress is not valid for unsaturated soils. Variation in degree of saturation is the very natural situation for soils on the earth surface, and this is relevant to many engineering problems, such as the rainfall induced shallow failure of soil slopes and collapse of river or reservoir embankments due to the water level change.

The partially saturated soil is a three-phase material, and the pore air pressure should be considered in the effective stress definition. Bishop [3] proposed an effective stress definition for unsaturated soils as an extension of the classic Terzaghi’s effective stress principle as:

$$\sigma_{ij}^{\prime} = \left( {\sigma_{ij} - u_{\text{a}} \delta_{ij} } \right) + \chi \left( {u_{\text{a}} - u_{\text{w}} } \right)\delta_{ij}$$

(2)

where $u_{\text{a}}$ is the pore air pressure and $\chi$ is called the ‘Bishop’s coefficient’ which is believed to be relevant to the degree of saturation. The pressure difference between air and water, $u_{\text{a}} - u_{\text{w}}$, is named as suction which is also associated with degree of saturation.

Lu and Likos [29] proposed a suction stress characteristic curve to unify the saturated and unsaturated soil effective stress expressions:

$$\sigma_{ij}^{\prime} = \left( {\sigma_{ij} - u_{\text{a}} \delta_{ij} } \right) - \sigma_{ij}^{\rm s}$$

(3)

in which $\sigma^{\rm s}$ is the suction stress. Lu et al. [28] presented a simplified form of suction stress by approximating Bishop’s coefficient as the effective degree of saturation (by considering the free water in the pores only) as:

$$\sigma_{ij}^{\rm s} = - S_{\text{e}} \left( {u_{\text{a}} - u_{\text{w}} } \right)\delta_{ij}$$

(4)

$S_{\text{e}}$ is the effective degree of saturation, and it is expressed as $S_{\text{e}} = \frac{{S_{\text{r}} - S_{\text{r}}^{\text{r}} }}{{1 - S_{\text{r}}^{\text{r}} }}$ in which $S_{\text{r}}$ is the degree of saturation and $S_{\text{r}}^{\text{r}}$ is the residual state degree of saturation (the part of water bounded to the solid phase). This simplified form of suctions stress is more convenient for preliminary estimation of unsaturated soil strength [18, 44]. However, the more complete form of suction stress includes an extra term which accounts for the air–water interfacial area. Lu et al. [28] derives the suction stress based on the virtual work principle as:

$$\sigma_{ij}^{\rm s} = - S_{\text{e}} \left( {u_{\text{a}} - u_{\text{w}} } \right)\delta_{ij} - \sum\limits_{i} {\gamma_{i} \frac{{\partial A_{i} }}{\partial V}} \delta_{ij}$$

(5)

There may be many interfaces in a volume $V$, including air–water, air–solid and water–solid interfaces. $\gamma_{i}$ denotes the interfacial free energy of the $i$th interface, and $A_{i}$ is the interfacial surface area of the $i$th interface. Thermodynamic methods can also be employed to derive the effective stress of multiphase porous medium [4]. Recently, Nikooee et al. [34] verified Lu’s suction stress definition through a thermodynamic approach and gave a similar form of effective stress as:

$$\sigma_{ij}^{\rm s} = - S_{\text{e}} \left( {u_{\text{a}} - u_{\text{w}} } \right)\delta_{ij} - k^{\text{aw}} a_{\text{aw}} \delta_{ij}$$

(6)

where $k^{\text{aw}}$ is a material parameter related to air–water surface tension (after [27] it is approximated as the water surface tension and is taken as 0.073 N/m in this study) and $a_{\text{aw}}$ is the specific air–water interfacial area (the air–water interfacial area per total volume). Therefore, the complete form of effective stress for unsaturated soils should be formulated as:

$$\sigma_{ij}^{\prime} = \left( {\sigma_{ij} - u_{\text{a}} \delta_{ij} } \right) + S_{\text{e}} \left( {u_{\text{a}} - u_{\text{w}} } \right)\delta_{ij} + k^{\text{aw}} a_{\text{aw}} \delta_{ij}$$

(7)

and combining with Eq. 2 the Bishop’s coefficient $\chi$ can be derived as:

$$\chi = S_{\text{e}} + \frac{{k^{\text{aw}} a_{\text{aw}} }}{{u_{\text{a}} - u_{\text{w}} }}$$

(8)

Likos [27] has developed a theoretical model to consider the contribution of the interfacial area to the effective stress, and it showed that the interfacial area plays a significant role, especially at the relatively low degree of saturation range.

In addition, another form of effective stress derived from another thermodynamic approach by Gray and Schrefler [16] gives:

$$\sigma_{ij}^{\prime} = \sigma_{ij} - \left[ {x_{\text{sw}} \left( {u_{\text{w}} + \varGamma_{\text{sw}} J_{\text{sw}} } \right) + \left( {1 - x_{\text{sw}} } \right)\left( {u_{\text{a}} + \varGamma_{\text{sa}} J_{\text{sa}} } \right)} \right]\delta_{ij}$$

(9)

where $x_{\text{sw}}$ is the fraction of wetted solid surface area, ${{\Gamma }}_{\text{sw}}$ is the interfacial energy of solid–water interface, ${{\Gamma }}_{\text{sa}}$ is the interfacial energy of solid–air interface, $J_{\text{sw}}$ is the mean curvature of solid–water interface, $J_{\text{sa}}$ is the mean curvature of solid–air interface. By discounting the effect of solid surface curvatures and combining with Eq. 2, the Bishop’s coefficient can be estimated from the above expression as:

$$\chi \approx x_{\text{sw}}$$

(10)

Furthermore, Gray et al. [17] modified the expression by considering the weighted effect of the volumes of different phases as:

$$\sigma_{ij}^{\prime} = \sigma_{ij} - \left\{ {\left[ {x_{\text{sw}} - n\left( {x_{\text{sw}} - S_{\text{r}} } \right)} \right]\left( {u_{\text{w}} + \varGamma_{\text{sw}} J_{\text{sw}} } \right) + \left[ {1 - x_{\text{sw}} + n\left( {x_{\text{sw}} - S_{\text{r}} } \right)} \right]\left( {u_{\text{a}} + \varGamma_{\text{sa}} J_{\text{sa}} } \right)} \right\}\delta_{\text{ij}}$$

(11)

where $n$ is porosity. They also estimate the Bishop’s coefficient by ignoring the curvature terms as:

$$\chi \approx \left( {1 - n} \right)x_{\text{sw}} + nS_{\text{r}}$$

(12)

To investigate the specific interface area effect (effect of $a_{\text{aw}}$ and $x_{\text{sw}}$) on the effective stress of unsaturated soils, it requires a non-destructive 3D laboratory imaging technique. The high-resolution X-ray computed tomography technique is, therefore, a suitable technique to be employed.

1.2 X-ray computed tomography

X-ray computed tomography technique was originally developed by Hounsfield and Cormack for the purpose of medical examination [11, 23]. It is also more and more popular in the research of geomaterials, for the benefits of its non-invasive characterization and microscale insight into the material. Complete reviews of the high-resolution X-ray CT application in geoscience can be seen in [8, 24, 38, 48]. With the non-destructive tool of micro-CT, a large number of research applications have been done in broad scientific subjects including local porosity and pore structure characterization [9, 26, 37], 3D grain size and shape characterization [10], investigation of liquid flow or multiphase liquid flow in porous media [7, 12, 13, 47, 48] and strain localizations [1, 2, 15, 19, 21, 40].

For the study of mechanical and hydraulic behaviors of unsaturated soils, the application of micro-CT also attracted much attention in the last decade. As for a better resolution, unsaturated granular materials, such as sands, are usually studied (silt or clay have much smaller grain sizes which lead to more complicated microstructures and worse image resolution). Researchers used micro-CT to study both the mechanical response (the morphology of the liquid phase and the deformation of the microstructure [6, 22, 30, 33]) and hydraulic behavior (the water retention characteristics [25, 35]) of unsaturated granular soils. To clarify the effect of interfacial area on effective stress, the crucial point is the detection of the interface from the X-ray reconstructed image. Culligan et al. [12, 13] measured the specific air–water interface area in an unsaturated flow through glass beads by using a marching cube algorithm [14] to determine the interface from the obtained 3D digital matrix from micro-CT. Using X-ray technique to measure the specific interfacial area can also be seen in [49] by using the similar method. There are usually two limitations for the micro-CT measurement on the interfacial area: (1) the image resolution (the better the resolution, the lower measurement the error) and (2) the limited repetition of X-ray CT measurement on the same sample due to large data processing procedures and relatively long duration of one measurement.

However, the relationship between the interfacial area measurement and the material strength is still not well understood. In this paper, we measure the interfacial areas of unsaturated granular materials (glass beads) by micro-CT imaging at the Centre for X-ray Tomography in Ghent University (UGCT) [32]. Static cylindrical samples with different water contents were explored. The voxel size is about 5.85 μm. The 3D reconstructed samples were discretized into representative volume elements (RVEs) which provided local information of the porosity, the degree of saturation and also the interfacial area values. Due to the local heterogeneity of the material, the discredited RVEs of the scanned samples actually covered a very large range of degree of saturation and porosity with a limited number of X-ray CT scans. The same glass beads were sheared at different suction levels in a suction-controlled direct shear test device. The relationship between the measured interfacial area and the material strength was also discussed based on the micro-CT scans and the direct shear test results.

2 Setup of the X-ray CT investigation

2.1 Granular material and cylindrical sample

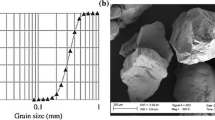
The tested granular material is a soda lime glass beads commercially supplied by Sigmund-Lindner^® with diameters ranging from 0.2 to 0.4 mm. There were five tested samples prepared in cylindrical molds made of plexiglass. The molds are 10 mm in diameter and in height. The particle size distribution of the material, and the mold can be seen in Fig. 1. For the sample preparation, the mold was first filled with glass beads under dry conditions. Because the same mass of glass beads was placed in each identical mold, the five samples have similar porosity values around 0.37. Then, a certain amount of distilled water was added with a medical dispenser. Then, a high precision balance was adopted to measure the mass difference during sample preparation which gives the degree of saturation. The measured degrees of saturation of the five samples are summarized in Table 1. After the sample was prepared, the mold was sealed by a plexiglass cover with glue and each sample was shaken heavily for about 5 min, which may help the water to be distributed in the sample. In the above preparation method, adding water into a sample initially dry will lead the sample to follow an initial hydraulic wetting path. The shaking process, however, distributes the water phase and leads the pores to drainage and wetting cycles. Consequently, due to the pore size distribution and water phase heterogeneity, after the hydraulic cycles by the shaking process, the pores in the sample cover the hydraulic behaviors from drying to wetting. The local hydraulic properties will be investigated later by discretized RVEs.

Fig. 1

Cylindrical mold and particle size distribution of the glass beads

Table 1 Comparison of the degree of saturation of the prepared cylindrical samples between values measured by high precision balance and values measured from X-ray images

2.2 X-ray CT scan setup

The samples were scanned using the custom-build device HECTOR [31], which is equipped with a microfocus directional target X-ray source, a rotation sample stage and flat panel detector. Projections were taken over 360° at 120 kV and 10 W. At this power, the focal spot is smaller than the voxel resolution which is 5.85 µm obtained with geometrical magnification. No hardware filter was applied, since the sample was contained in relative thick plexiglass molds. Image reconstruction was performed using Octopus Analysis [5, 41]. Beam hardening, which was mainly located in the mold, was corrected during reconstruction.

3 Image analysis

3.1 3D image trinarization

The 3D reconstruction process converts the series of X-ray projections into a 3D image (in form of a series of grayscale 2D image slices in the vertical direction) using Octopus Reconstruction [41, 42]. Each voxel (pixel in 2D slices) has a gray value that represents a given phase (air, water or solid). However, the gray-level probability density distributions of the three phases are three Gaussian curves with overlaps between each of them. Figure 2 presents the histogram of the gray levels for the five samples. The three phases are generally in normal distributions, but there are overlaps due to the noise and partial volume effects. Therefore, the image segmentation requires some advanced treatments of the image. In the present case, a region growing algorithm developed by Hashemi et al. [20] was employed to trinarize the grayscale images. Besides the detailed information in [20], the 3D segmentation process for the tests in this study is briefed in “Appendix 1”.

Fig. 2

Gray-level distribution of the scanned specimens

After the image segmentation process, the degree of saturation can be calculated based on the trinarized 3D image. The measured degree of saturations by the high precision balance and the calculated values by trinarized images are compared in Table 1. They have fair agreement, which confirms the efficiency of the segmentation process.

3.2 Representative volume element

Due to the heterogeneities of porosity and water distribution, the microstructure and water phase morphology varies spatially. Characterization of the local information is therefore necessary. Moreover, the macro-mechanical and hydraulic behaviors of an unsaturated granular media originate from its microbehaviors. Therefore, a local study of the material in both solid structure and liquid phase morphology will give more information even with limited scanned samples (the idea of using local information can also be found in [36] in which high-resolution local points of a shale are investigated to represent the image over a large field of view). In this work, the local information inside a sample may be investigated by a Representative Volume Element (RVE) in which the relevant micromeasurements can be extracted. To represent microcharacteristics, the RVE size should be as small as possible but without affecting the parameter measurement. By following [25], the size of the RVE is chosen based on the local measurement of porosity in this work.

Figure 3 presents how the size of the RVE is determined. We set six cubic nodes at different locations inside the 3D image. The initial size of the node is 1 voxel. Since the initial size is small, the nodes are either falling on the grains or in the pores; therefore, the porosity of the node is either equal to 1 or 0. Wet set three nodes on grains and three nodes in voids. Then, the size of the nodes is increased gradually and the porosity values are recalculated. It can be seen from Fig. 3 that with the growth of the cubic size, the porosities become stable and converge to a similar porosity value (about 0.37) when the size of the cubic element is larger than about 100 voxels. It should be noted that although a larger size of RVE could lead to a better parameter measurement, a compromise should be taken to keep the RVE size small enough to give enough RVE numbers inside a sample, which statistically present more microcharacteristics. Therefore, the RVE size is determined as 100 voxels. The image resolution is 5.85 μm per voxel, and the mean grain size of the glass beads is about 0.3 mm; thus, the appropriate RVE size is about two times of the average grain diameter.

Fig. 3

Size of cubic representative volume element (RVE)

3.3 Local mapping by RVEs

Then, the segmented 3D images can be meshed into RVEs which give local measurements of porosity and degree of saturation. Figure 4 presents the vertical cross sections of the five samples and the local porosity and degree of saturation are calculated based on the meshed RVEs. The RVEs overlapping the boundary of the sample are not included. It can be noted that the 5 min shaking does not allow obtaining a uniform distribution of water in the sample. This could be due to acceleration effect during shaking. The water distribution inhomogeneity is more obvious for samples with higher water content in which a big cluster could be easily formed in the middle region of the sample. Figure 5 plots the relationship between the degree of saturation and porosity for RVEs (the markers are colored based on the global degree of saturation). It can be seen that if the porosity is relatively high, the REV has a high probability to be at relatively low degree of saturation.

Fig. 4

The trinarized cross-sectional image (left column), map of porosity (central column) and map of degree of saturation (right column) for the scanned samples with different degree of saturation values

Fig. 5

Relationship between degree of saturation and porosity for all RVEs

3.4 Interfacial areas

By following the algorithm of [14], the interfacial areas of the segmented images can be calculated. The isosurface function in MATLAB is employed to convert the surface of a phase originally formed by cubic voxels into a smoother surface. The surface areas of the solid phase, the wetting phase (water) and the non-wetting phase (air) are firstly calculated and then the specific air–water interfacial area $a_{\text{aw}}$ can be calculated as:

$$a_{\text{aw}} = \frac{1}{2}\left( {a_{\text{n}} - a_{\text{s}} + a_{\text{w}} } \right)$$

(13)

where $a_{\text{n}}$ is the specific surface area of the non-wetting phase, $a_{\text{s}}$ is the specific surface area of the solid phase and $a_{\text{w}}$ is the specific surface area of the wetting phase (see Fig. 6). Similarly, the specific solid–water interface area is:

Fig. 6

Illustration of the interfacial area

$$a_{\text{sw}} = \frac{1}{2}\left( {a_{\text{s}} - a_{\text{n}} + a_{\text{w}} } \right)$$

(14)

Therefore, the fraction of wetted solid area, $x_{\text{sw}} = \frac{{a_{\text{sw}} }}{{a_{\text{s}} }}$, can be obtained. In this paper, the interfacial areas are not only measured globally for the whole specimens, but also measured locally based on the RVEs.

3.5 Statistical analysis of the local information

The interfacial areas of each RVE can then be analyzed statistically. Figure 7a demonstrates the probability distribution of local porosity based on the RVEs. It can be seen that the distribution looks like a Gamma distribution and the peak appears around the global mean porosity value (0.37). Figure 7b presents the relationship between the specific solid phase surface and the element porosity for each RVE in these five samples. A nearly linear relationship can be observed between these two parameters. When the porosity is smaller, there are more particles per unit volume and, consequently, the specific solid surface area is larger.

Fig. 7

a Probability distribution of local porosity based on RVEs; b relationship between local specific solid surface area and local porosity for all RVEs; c relationship between local specific air–water interfacial area and local degree of saturation for all RVEs

Figure 7c presents the relationship between the specific air–water interfacial area ($a_{\text{aw}}$ in the effective stress equation) and the local degree of saturation for all RVEs. The effect of global degree of saturation on the local specific air–water interfacial area is not obvious and the data forms a cloud. The local information on all RVEs, however, shows that the specific air–water interfacial area has a clear rise and fall trend. Under fully dry (no water in the pore) or fully saturated (no air in the pore) states, there is no meniscus and the specific air–water interfacial area is null. The $a_{\text{aw}}$ value is increased with degree of saturation within the low water moisture range (corresponding to an increase of meniscus number), and it reaches the peak at around 25% of degree of saturation followed by a decline to 0 until saturation (as the water clusters occupy more void space). The basic trend of the data cloud is divided into 50 segments along the degree of saturation axis and the average values of the highest and lowest three points are set as the upper and lower boundaries of the cloud (to reduce the effect of the scattered points). Due to the pore structure and water distribution heterogeneity, the discrete RVEs of the five samples cover the full range of porosity and degree saturation. Therefore, the two bounds of the RVE cloud data represent the two possible extreme conditions of a sample. The global specific air–water interfacial areas of samples with any degree of saturations should be within the two bounds.

4 Comparison with direct shear results

4.1 Direct shear tests at different suctions

Besides the direct measurement of the specific interfacial areas by micro-CT tomography, another way to evaluate $a_{\text{aw}}$ and $x_{\text{sw}}$ could be through a direct shear test. We will firstly evaluate the specific air–water interfacial area $a_{\text{aw}}$ by using the direct shear test. Because the X-ray scanned samples are sealed samples without measuring suction, we are not able to calculate the first form of Bishop’s coefficient in Eq. 8. Nevertheless, the air–water interfacial area can still be estimated from a direct shear test which makes the results comparable.

According to the effective stress principle, the shear strength of a cohesionless material is proportional to the normal effective stress depending on an intrinsic friction coefficient, expressed as the tangent of friction angle in soil mechanics convention. So, according to Eq. 7, the material strength is a function of the suction, the effective degree of saturation and the specific air–water interfacial area:

$$\tau = \sigma_{\text{n}}^{\prime} \tan \phi = \left[ {\left( {\sigma_{\text{n}} - u_{\text{a}} } \right) + S_{\text{e}} \left( {u_{\text{a}} - u_{\text{w}} } \right) + k^{\text{aw}} a_{\text{aw}} } \right]\tan \phi$$

(15)

The shear strength of the material, $\tau$, can be measured by a direct shear test at a certain normal stress, $\sigma_{\text{n}}$, and suction, $u_{\text{a}} - u_{\text{w}}$. In this study, since glass beads were used, water in the pores is almost all free water, therefore, $S_{\text{e}} \approx S_{\text{r}}$. The degree of saturation is associated with its suction and can be obtained from the water retention curve, while $k^{\text{aw}}$ and friction angle $\emptyset$ are material constants. Once those two material parameters are determined, the specific air–water interfacial area $a_{\text{aw}}$ can be associated with the shear strength of the material. A simple suction-controlled direct shear test device was employed to measure the shear strength and evaluate the specific interfacial area. The device and the test procedures are detailed in “Appendix 2”. An increasing horizontal force controls the direct shear. Generally, the tested samples failed suddenly at a certain applied shear force, which corresponds to the peak strength.

Before testing unsaturated samples, dry glass beads were sheared under four different normal loads to determine the friction angle $\emptyset$. Figure 8a demonstrates the linear relationship between the measured failure shear strength and the normal stress. Basically, it follows the Mohr–Coulomb failure criterion and can be fitted by a linear equation by the least squares method. It shows the cohesionless character of dry glass beads and allows to deduce the friction angle $\phi \approx 33.25^{^\circ }$.

Fig. 8

a Shear strength of dry glass beads at various normal stresses; b shear strength of wet glass beads at various suctions (with the minimum external normal load); c water retention curve

Then, the unsaturated glass beads were tested at different suction levels. As the capillarity effect is almost independent of the normal stress level, at higher stress levels, the strength of the material is mainly contributed by the mechanical contact stress. Therefore, testing the wet material under relatively low normal stress conditions could lead a more obvious observation on the suction stress. So, we applied the minimum stress without using counterweights ($N$ in Eq. 17 in “Appendix 2” is the weight of the upper cylinder and the lid). By using the burette to measure the water volume change, the degree of saturation of each sample with an applied suction can be recorded alongside the measurement of shear strength. The self-weight of the sample has a little variation with water content change, and the applied normal stress can be calculated by using Eq. 17 in “Appendix 2”.

Figure 8b, c presents the failure shear strength of the material at different suction values and the obtained water retention curve, respectively. It can be seen that the shear strength is increased with suction almost linearly until suction reaches about 1.5 kPa (which could be referred as the air entry value). In the water retention curve, it can be seen that before the air entry value the degree of saturation is not decreased obviously. Then, the material strength has a modest increase and reaches the peak strength at about 3 kPa suction. In this range, the degree of saturation starts to reduce rapidly in the water retention curve. When suction is larger than 3 kPa, further increase in suction leads to a decrease in the suction stress and therefore the shear strength becomes weaker. It can also be seen in the water retention curve that the decrease of degree of saturation becomes gentle when suction is larger than 3 kPa.

4.2 Estimated specific air–water interfacial area from shear tests

To estimate the specific interfacial area from shear strength, Eq. 15 can be rearranged as:

$$a_{\text{aw}} = \frac{1}{{k^{\text{aw}} }}\left[ {\frac{\tau }{\tan \phi } - \left( {\sigma_{\rm n} - u_{\text{a}} } \right) - S_{\text{r}} \left( {u_{\text{a}} - u_{\text{w}} } \right)} \right]$$

(16)

From the suction-controlled direct shear test introduced before, all the variables on the right side can be determined. $k^{\text{aw}}$ can be estimated as 0.073 N/m, which is the water surface tension at $20$ °C. It should be noted that the choice of the $k^{\text{aw}}$ value does not change the trend of the specific interfacial area. The estimated specific air–water interfacial area is depicted in Fig. 9a. The interfacial area has a raise and fall trend with the degree of saturation increase, and the peak is around 25% of degree of saturation. We may also relate the estimated specific air–water interfacial area to the real water morphology obtained from the scanned images. The maximum air–water interfacial area occurs at a transition stage when the water phase changes from a discontinuous phase (the pendular state [45, 46]) to a relatively continuous phase (the funicular state [43]). At this stage, the quantity of air–water interfaces decreases due to the merging of isolated meniscus into more global water clusters. Typical trinarized X-ray images of RVEs with maximum air–water interfaces can be seen in the insets in Fig. 9a. Theoretically, before the air entry, there is no air–water interface. Errors of the air–water interfacial area occur when the degree of saturation is ranging from of 0.8 to 1. This is because the suction values for these conditions are very low and the observation errors may be high.

Fig. 9

a Estimated specific air–water interfacial area from shear tests; b estimated Bishop’s coefficient from shear tests. c Contribution of specific interfacial area term to shear strength

By substituting Eqs. 16 into 8, the Bishop’s coefficient $\chi$ can also be calculated from the direct shear test (in which $a_{\text{aw}}$ and $k^{\text{aw}}$ are eliminated). Figure 9b demonstrates the measured Bishop’s coefficient from direct shear tests in which the solid line denotes the basic estimation $\chi = S_{\text{r}}$. It can be seen that $\chi = S_{\text{r}}$ underestimates the Bishop’s coefficient and the difference is largest around 25% of degree of saturation. Moreover, according to Eq. 15, the contribution of the specific interfacial area to shear strength can be presented in Fig. 9c, it can be seen that the contribution could be as large as 60% of the total strength when the specific interfacial area is around its maximum value.

The specific interfacial area calculated from the direction shear tests can then be compared with the measured values by micro-CT. Due to the sample inhomogeneity, the discretized RVEs almost cover the full range of saturation and all possible porosities. Without further micro-CT scans, it can be deduced that the specific interfacial area of the constitutive RVEs of a sample, with any degree of saturation, should fall in the bounds of the cloud in Fig. 7c. Therefore, the specific interfacial area of a whole sample, a kind of average of the values of its RVEs, should also be bounded by the cloud data boundaries obtained by micro-CT scans. Figure 10 compares the upper and lower boundaries for the cloud data and the calculated specific air–water interfacial areas from direct shear tests. The specific air–water interfacial areas obtained from the direct shear tests are almost bounded by the cloud data boundaries. Also, the peaks of the upper boundary and the lower boundary of the cloud data and the peak obtained from direct shear test results are similarly located at a degree of saturation of around 25%.

Fig. 10

Comparison of specific interfacial area between direct shear tests estimated values and X-ray tomography scan results

4.3 Bishop’s coefficient estimated from the fraction of wetted solid surface

As introduced in Sect. 1, Bishop’s coefficient ${{\chi }}$ can be either related to the air–water interfacial area or related to the fraction of wetted solid surface ($x_{\text{sw}} = a_{\text{sw}} /a_{\text{s}}$). From the trinarized 3D image obtained from X-ray CT, the value of $x_{\text{sw}}$ can be measured globally over a sample and locally on the RVEs. The discretized RVEs, which cover the full range of saturation, could be used to estimate ${{\chi }}$ based on Eqs. 10 and 12. The degree of saturation and porosity of each element can also be extracted from the images.

Figure 11 depicts a comparison of the obtained Bishop’s coefficient between the X-ray CT scanned RVEs and the direct shear test measurements. The results by using Eq. 10, in which ${{\chi }}$ is estimated as the fraction of wetted solid surface, is exhibited in Fig. 11a. The obtained values from RVEs could cover the full range of degree of saturation, all possible porosity values and a wide range of hydraulic cycles. The clouded data in Fig. 11a show that they have a similar trend with that of the measured ${{\chi }}$ from shear tests. The maximum difference between ${{\chi }}$ value and ${{\chi }} = S_{\text{r}}$ line also occurs at 25% degree of saturation, as for the analysis based on direct shear test results. Figure 11b shows the estimated ${{\chi }}$ from X-ray images based on Eq. 12. By considering the weighted effect of volumes of three phases (inclusion of porosity and degree of saturation), it can be seen that the clouded data obtained from RVEs becomes more focused. The comparison with the direct shear test measurements also indicates that it has a higher consistency. Consequently, it tends to demonstrate that Eq. (12) from Gray et al. [17] can be considered has a very good predictor of the Bishop’s coefficient ${{\chi }}$.

Fig. 11

Comparison of Bishop’s coefficient between X-ray CT results and direct shear results based on the fraction of wetted solid surface. a$\chi = x_{\rm sw}$; b$\chi = \left( {1 - n} \right)x_{\rm sw} + nS_{\rm r}$

Although the comparison in Figs. 10 and 11 cannot confirm directly that which effective definition, related to air–water interface in Eqs. 5–8 or related to solid–water surface in Eqs. 9–12, is more precise, it anyway emphasizes the importance of the interfacial area term in effective stress formulation. It also suggests that including porosity value in effective stress formulation may also be important.

5 Concluding remarks

In this paper, X-ray computed tomography is employed to study the interfacial areas of unsaturated granular materials (including air–water interfaces and solid–water interfaces), which plays an important role in the effective stress definition and material strength of unsaturated granular materials. Five glass bead samples with various water contents are scanned. After a region growing segmentation method, the 3D reconstructed images are separated into solid, air and water phases. Based on the trinarized images, the interfacial areas are therefore measured by converting the digital data into relatively continuous surfaces through a marching cubes algorithm.

Local measurements of the material properties, including porosity, degree of saturation and interfacial areas, are implemented. Cubic RVEs are introduced into the local and microanalysis. It is found that the size of the representative volume elements should be larger than 2 times of the mean grain diameter to represent enough local information. Then, the scanned samples can be meshed into RVEs to study the local properties. It gives a statistical representative set of data with a limited number of X-ray scans. Due to the nature of granular material heterogeneity and non-uniform character of the water distribution, the discretized RVEs of the tested samples cover almost the full range of degree of saturation and all possible porosities. The local measurements of interfacial area and degree of saturation, in form of a cloud data, give the basic raise and fall trend of the relationship between interfacial area and degree of saturation. The maximum specific interfacial area is at around 25% of degree of saturation.

The glass bead material is also tested in a suction-controlled direct shear device. Samples with different suctions (therefore, different degrees of saturation) are sheared, and the failure strengths are recorded. The device also measures the water retention curve. Combining with the effective stress definitions, the specific air–water interfacial area and Bishop’s coefficient can then be calculated from the material shear strength. It is observed that the peak interfacial area by back calculation is also at around 25% of degree of saturation. The air–water interfacial area could contribute up to 60% of the material strength when it reaches its maximum value. The boundary of the cloud data obtained from X-ray CT and RVE discretization bounds the specific interfacial area curve from direct shear tests.

The Bishop’s coefficient can also be estimated from the solid–water interface obtained from X-ray CT based on the second type of effective stress definition in literature. The comparison with the direct shear test results shows that they have a good agreement again. It further suggests that the importance of including porosity value in effective stress formulation. The mutual corroboration confirms both the X-ray CT results and the direct shear test results. The analysis also proof that the X-ray CT technique, together with the RVE-based multiscale analysis, could be a very valuable method in future studies of multiphase geomaterials.

Appendices

Appendix 1: 3D image segmentation

The region growing method has four steps. Firstly, as seen in Fig. 12, a partial thresholding is applied to the gray values. Half of the air phase and half of the solid phase are selected based on the first and third peak values in the histogram (voxels with a gray level smaller than the peak value of 20, noted as $P_{\text{a}}$, are air and voxels with gray level larger than the peak value of 140, noted as $P_{\text{g}}$, are solid). For the middle phase, which is water, the thresholding is taken around the middle peak to select part of the water phase. As the amount of voxels of water is varying with water content (the peak is not obvious when the degree of saturation is low), the selection is based on the sample with 46.7% degree of saturation. We take voxels with gray level larger than 49 and less than 58 (noted as $P_{\text{w1}}$ and $P_{\text{w2}}$, respectively) as the water phase, of which the probability density of the two gray level values are 80% of the middle peak at 46.7% of degree of saturation. Secondly, a procedure is taken to consider the Partial Volume Effect (PVE). Voxels on the boundary of the solid phase may have both air and water phases, but the gray level may fall in the range of the water phase thresholding. To filter the PVE, a sphere with 2 voxels radius around each voxel is selected. The voxels in the spheres on the solid–air interface have higher variance in gray-level distribution and the spheres inside the water phase have lower variance. A filtering procedure is applied to reset the voxels on the solid–air interface to undefined voxels by thresholding an appropriate variance. Thirdly, a simultaneous region growing process is applied to assign the neighboring undefined voxels into a phase. The voxels which are neighbors of only one phase with the gray-level values falling in a tolerance threshold of a phase are attributed to that phase. The tolerance range is set as: air phase < $P_{\text{w1}}$, $P_{\text{a}}$ < water phase < $P_{\text{g}}$, solid phase > $P_{\text{w2}}$. Step by step, each phase will grow up until it meets with another phase. At the interface, when the undefined voxels are neighbors of more than one phase, the voxels are set to be undefined until the final step. At the final step, the undefined voxels on the interfaces are assigned to a phase based on its most present neighboring phase. The final procedure is repeated until all voxels are attributed to the three phases. After the four steps, the 3D reconstructed images are segmented.

Fig. 12

Thresholds of the region growing method by Hashemi et al. [20]

Appendix 2: Suction-controlled direct shear test

The suction-controlled direct shear test device is depicted in Fig. 13a. The tested glass beads are placed in two superposed plexiglass cylinders. The bottom one is fixed, while the top one can be moved horizontally, driven by a weight (a cup of sand in our case) suspended to a nylon rope through a pulley. The weights of the added sand and the cup, therefore, provide the horizontal shear force. The normal stress is controlled by a top lid in which a certain number of counterweights can be added. The normal force acting on the shear plane is the total weight of the counterweights, the lid, the top cylinder and the part of the sample above the shear plane. For dry or wet samples, the normal stress on the shear plane can be calculated as:

$$\sigma_{\rm n} = \frac{N}{A} + \rho_{\text{s}} gh\left( {1 - n} \right) + S_{\text{r}} n\rho_{\text{w}} gh$$

(17)

where $N$ is the normal force on the shear plane except the sample itself, $A$ is the cross-sectional area, $\rho_{\text{s}}$ is the density of the solid grains, $g$ is gravity, $h$ is sample depth above the shear plane, $n$ is sample porosity, $S_{\text{r}}$ is the degree of saturation, and $\rho_{\text{w}}$ is the density of water.

Fig. 13

The suction-controlled direct shear test setup. a Layout of the device; b control of suction and measurement of degree of saturation

There is a small circuit at the bottom of the lower plexiglass cylinder, allowing water imbibition and drainage. A porous stone is placed at the bottom of the sample to distribute water more homogeneously over the cross section of the sample. The small circuit is connected with a burette through a plastic tube, and there is a valve at the end of the burette. Dry glass beads are poured into the cylinder to prepare a dry sample. The weight of the two cylinders is measured before and after glass beads filling, which gives the mass of the dry sample. After the two cylinders are filled with glass beads, the lid is put on the top of the sample and a certain load is applied. The procedure to apply suction is presented in Fig. 13b. Firstly, the valve is opened to allow water flow into the dry sample until some water comes out from the top. Then, the water level in the burette is adjusted to be the same as the top of the upper cylinder. This process saturates the sample. Then, the burette is lowered to a certain level. In this procedure, some water may flow out of the sample into the burette. After the stabilization of the water level, the water volume change in the burette, $z_{2}$, is the water volume drained out from the sample. Combining with the sample size and the solid phase mass, the current degree of saturation in the sample can then be calculated. The level difference between the water table in the burette and the shear plane, $z_{1}$, gives a negative pressure in the shear plane by multiplying with water density and gravity ($\rho gz_{1}$). Therefore, suction in the sample is $\rho gz_{1}$ and the pore air pressure is 0 since the top of the sample is connected with atmosphere from the edge of the lid. After the application of normal load and suction, sand is poured into the cup on the other side of the pulley gradually until failure occurred. Then, by dividing the total weight of the cup and sand with the area of the horizontal cross section, the failure shear strength can be obtained.