Full 3D investigation and characterisation of capillary collapse of a loose unsaturated sand using X-ray CT

Abstract

The aim of this paper is to characterise in 3D the capillary collapse phenomenon using X-ray Computed Tomography (X-ray CT) during water infiltration into a partially saturated soil. To understand the mechanisms leading to capillary collapse, we progressivelly saturated a specimen of sand by controlling the water pressure using the negative water column technique. During this imbibition process, we followed the granular structure using X-ray CT. The microstructure was analysed to assess the volume of water filling the pores and deformation of the granular skeleton using Volumetric Digital Image Correlation tools. Matheron’s granulometry was used in parallel to characterize the initial microstructure and its evolution during the imbibition. We show that the collapse phenomenon can occur in a clean sand and can be controlled continuously with the negative water column technique. The volume change of the specimen at local scale started at a particular water content which coincided with the coalescence of capillary bridges between grain clusters. Gravity effects leading to a non-negligible gradient of the hydrostatic pressure along the specimen’s height were observed and induced a vertical gradient of strain. Localisation of the vertical strain on conical surfaces and of the volumetric strain and water content at the bottom corner of the specimen appeared during the imbibition process. These localisations are thought to be due to an inhomogeneity of the initial density or/and an effect of cell walls facilitating the sliding of grains and the provision of water along preferential paths. However, in spite of those localisations, macroscopic measurements at the scale of the sample were representative of the local behaviour of the unsaturated sand.

1 Introduction

In unsaturated soils, capillary collapse or collapse upon wetting is usually defined as the occurrence of irreversible and sudden deformations induced by the provision of water [3, 15]. Collapse is the cause of various concerns in geotechnical engineering, like for instance the excessive settlements observed along the high-speed train railways in northern France [14, 36]. Collapse occurs in loose unsaturated soils and has been studied by many authors including in clays [3, 28], in loess [36] and in sands [34, 45], among others.

In granular soils, when capillary forces are of the same order of magnitude as other interparticle forces (i.e. skeletal forces, weight of particles, cementation [44]) and when the microstructure is loose enough, the soil can be considered as collapsible [11]. Several authors [9, 16, 17, 41, 48] wondered whether the collapse phenomenon was controllable and could occur progressively. In this work, the controllability of the collapse phenomenon in a loose clean sand was investigated for the first time.

The amount of strain that an unsaturated soil undergoes when soaked is referred to as its collapse potential. In an oedometer test, the soil specimen is loaded vertically, radial displacements are prevented and vertical displacements are monitored. Some authors also investigated collapse in the triaxial apparatus [29, 32, 47]. Collapse exhibits a maximum for some applied critical stress [1, 52]. The magnitude of collapse depends on various parameters including the initial density, water content and the microstructure, which depends on the specimen origin (natural or compacted soils) [24, 31, 34, 47].

Although thoroughly studied at macroscopic scale in fine soils, the mechanisms governing capillary collapse in granular soils have been less observed. Furthermore only few insights into small scale phenomenon leading to macroscopic capillary collapse have been published (see for instance [21]). To complement existing data, this work presents the results of an experimental program carried out using X-ray computed tomography (X-ray CT), a relevant tool to obtain 3D informations at grain scale. In combination with Volumetric Digital Image Correlation (V-DIC), X-ray CT also makes it possible to get information at a mesoscopic scale, at which the use of continuum mechanics still remains relevant. In this work, both microscopic and mesoscopic analyses have been carried out on a partially saturated Hostun sand subjected to gradual controlled imbibition in an oedometric cell.

In the first part, the material and methods are presented. The characterisation of the initial microstructure is then performed in terms of homogeneity and size of phases using respectively a statistical approach and Matheron’s granulometry. In the third part, evolution of the specimen and of its microstructure is quantified at various scales by using water content and strain measurements. Finally, results are discussed.

2 Material and methods

The experimental campaign consisted in performing a controlled imbibition of the sand specimen in an oedometric cell by infiltrating controlled quantities of water in a stepwise manner. At each level of saturation, two three-dimensional images with different voxel sizes were obtained by X-ray microtomography in order to observe the specimen at two different scales: one at the scale of the whole specimen (so-called global tomography) and another at a finer scale for a more detailed view of the grains and the pores (so-called local tomography). The oedometric cell material was in polymethyl methacrylate (PMMA) to facilitate the penetration of X-rays.

2.1 Material

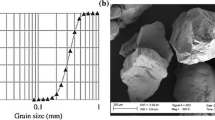
The sand used here is a Hostun sand HN31, extracted in the Drôme region in France. This sand is made of about 98 % of quartz, the remaining 2 % being mostly metallic oxides. By performing a sieve analysis (see Fig. 1), a coefficient of uniformity $C_u=2$ and a median grain size $D_{50} = 300\,\upmu$m were determined. The coefficient of uniformity—also called Hazen coefficient—was calculated using the equation $C_u=D_{60}/D_{10}$, where $D_{60}$ is the diameter at 60 % passing, and $D_{10}$ at 10 % passing. This coefficient is used in soil classification systems to evaluate the dispersion of grain sizes. The specific density of the sand was equal to 2,650 kg m$^{-3}$ [10, 19]. The Hostun sand is classified as a sub-angular to angular sand. Before specimen preparation, the sand was sieved at 250 $\upmu$m and only the retained fraction was kept. Upon sieving, the median grain size increased to 350 $\upmu$m.

Fig. 1

Cumulative grain size distribution of the natural Hostun sand HN31 and of the Hostun sand HN31 after sieving at 250 $\upmu$m

2.2 Specimen preparation

The preparation of the specimen was divided into the following steps:

• A mixture of water and sand was prepared at a gravimetric water content (the ratio of the mass of water with respect to that of dry sand) of $w=7.19 \,\%$. This water content allowed to obtain the loosest specimen.

• The oedometric cell (70 mm in diameter and 30 mm high) was then filled with the wetted sand by using a wet pluviation method as follows. A porous ceramic disk with an air entry value of 50 kPa was put at the bottom of the cell. The filling was performed by placing the wetted sand on a sieve with a 3.50 mm opening placed above a second sieve with a 2.24 mm opening. Both sieves were located above the oedometric cell to be filled and were vibrated vertically with a shaking table. Thanks to the shocks, clusters of sand particles passed sequentially through the two sieves to finally fall into the cell. The height of fall from the bottom sieve to the bottom of the cell was between 50 and 70 mm (snail cam with a fall of 20 mm). Compared with other methods such as the moist tamping method [50], this wet pluviation method minimised any manual handling of the sand.

• The specimen was then compacted to stabilise the specimen by applying a vertical strain of 19.4 %. Upon compaction, the porosity decreased from 64.5 to 55.9 %.

• Excess soil was removed.

• Finally, the cell was covered with a plastic sheet in order to minimise water evaporation during the subsequent stages.

Uncertainties of state parameters were evaluated with the international norm JCGM 100:2008 “Evaluation of measurement data—Guide to the expression” [27], by using a normal law to model balance uncertainty and a uniform law for length measurements. The standard uncertainties were 0.03 g for the balance according to the manufacturer and 0.14 mm for the length measurements. The results of the uncertainty analysis are given in Table 1: the porosity $n$ is defined as the ratio of the volume of voids to the volume of the specimen, the void ratio $e$ as the ratio of the volume of voids to the volume of grains, the degree of saturation $S_w$ as the ratio of the volume of water to the volume of voids and the air fraction $p$ as the ratio of the volume of air to the volume of the specimen. In Table 1, all intervals of confidence (not standard deviation) are expressed in absolute values: for instance, the water content is comprised between 7.15 and 7.23 % with a level of confidence of 99.73 %.

Table 1 Results of the uncertainty analysis on the initial state parameters

2.3 Imbibition experiment

The specimen in its oedometric cell was placed on the rotation table of the X-ray microtomograph and connected to a system that allowed control of the capillary pressure $p_{c}$ (see Fig. 2), which is defined as the difference between the pressure of the air and the pressure of liquid water. No stress was applied to the specimen, which was thus only subjected to its self weight.

Fig. 2

Schematic of the X-ray CT scanner and of the experimental setup to control the capillary pressure in the specimen

The capillary pressure was controlled by connecting the bottom of the cell to a graduated burette partially filled with water—a technique known as the negative water column technique [20, 51]. A valve enabled to allow or prevent any flow of water from the burette to the specimen or vice-versa. Once equilibrium is reached with the valve opened, the capillary pressure $p_c$ corresponds to the difference $\varDelta H$ in height between the top of the specimen and the meniscus in the burette through the relation: $p_c=\rho _w g \varDelta H$, where $\rho _w=1{,}000$ kg m$^{-3}$ is the mass density of liquid water and $g=9.81$ m s$^{-2}$ is the acceleration of gravity. The inner diameter of the burette was 7 mm with a graduation every 1 mm, corresponding to a resolution of 0.01 kPa in capillary pressure and a resolution of 1/26 ml in volume. A second valve connecting the burette to a water container allowed to partially fill the burette with water; this valve was only opened when the valve connecting the burette to the soil was closed. Between two consecutive steps of imbibition, the volume of water injected into the burette from the container was chosen smaller than 8 $\hbox {cm}^3$. This volume was equivalent to 12.4 % of the initial porosity and to 20.8 cm of the water column. During an imbibition step, the difference $\varDelta h$ between the initial and final heights of the meniscus (see numbers 1 and 2 in Fig. 2) defines the quantity of water exchanged with the soil specimen. The final height of the meniscus was measured at least four hours after opening the first valve. 3D images were acquired by X-ray CT once these four hours had elapsed. Those 4 hours were sufficient for the water level in the burette to reach a stabilised level, and for the specimen to remain stable during the acquisition. Since the initial capillary pressure of the prepared specimen was unknown, the first stage consisted in applying a high capillary pressure so as to drain the specimen, i.e. to extract water from the specimen between the first and the second step.

2.4 X-ray computed tomography

X-ray computed tomography is a non-destructive method that allows to obtain three dimensional images of porous materials (for more information on principles and applications, see [2, 26]). X-ray CT was performed at Laboratoire Navier with an UltraTom microtomograph (RX-Solutions, Chavanod, France), equipped with a 225 kV Microfocus Phoenix X-ray source (GE, Fairfield, USA) associated with a PaxScan 2520V flat panel detector used at full resolution (Varian, Palo Alto, USA). After each imbibition, once equilibrium was reached, two acquisitions were recorded, yielding reconstructed volumes with different sizes of voxel (volumetric pixel). The first acquisition yielded an image of the whole specimen; voxels were cubic of side 50 $\upmu \mathrm{m}$. For the second acquisition, voxels were cubic of side 25 $\upmu \mathrm{m}$ and only a region of the specimen could be reconstructed. The reconstructed volume was a cylinder of 45 mm in diameter centred in the specimen (inside of the dashed lines of Fig. 3). The second acquisition is called local or partial CT, to distinguish it from the global CT in which an image of the whole specimen is acquired. Note that partial CT yields images with a higher spatial resolution, but that are less accurate representations of the real X-ray absorption of the specimen.

Fig. 3

Vertical slice (top) and horizontal slice (bottom) of the global CT. The volume investigated by the local CT is delimited with dashed lines. The isolated-volume used to characterise the initial microstructure is delimited by solid lines. The voxel size of the global CT is 50 $\upmu$m. The Cartesian and the cylindrical systems of coordinates are represented with vectors

Source parameters were 100 kV–500 $\upmu$A for the global tomography and 90 kV–300 $\upmu$A for the local CT. For each scan, 1,440 projections on a specimen rotation of 360$^{\circ }$ were recorded and obtained by averaging 10 radiographies at each rotation angle. Each global CT required 30 min of scanning; each local CT required 1 hour of scanning. Volumes obtained, after reconstruction by the standard algorithm of Feldkamp, Davis and Kress [18] implemented by the manufacturer of the microtomograph, were 16-bit images and were rescaled into 8-bit images. Image analysis and V-DIC were performed on these 8-bit images. Note that, because of the rather high noise level of X-ray tomography with respect to other imaging techniques, the 16-bit to 8-bit conversion does not alter the signal-to-noise ratio. Therefore, the subsequent image analyses performed would have essentially yielded the same results in 16-bit as in 8-bit images [25, 38].

Slices of the global CT of the specimen in its initial state are displayed in Fig. 3. Three artefacts are visible: beam hardening, cone beam, and metal artefact. Beam hardening is due to the polychromatism of the X-ray source [12] and leads to an attenuation that apparently increases in the outer region of the specimen, so that the specimen seems to be denser near the border of the cell. Cone beam artefact is due to the fact that the X-ray source is conical and located at a finite distance from the X-ray detector. It leads to a blurring of the top and bottom parts of the specimen [53]. The metal artefact appears when materials with very different absorption properties (such as steel and unsaturated sand) are juxtaposed in the field of view of the detector. In this study, the porous ceramic disk was clamped with a stainless steel ring, which blurred the lower part of the specimen and made any quantitative analysis in this region impossible. One observes in Fig. 4 that the grey levels in the upper and lower parts of the specimen differed from those in the central part of the specimen. In this central part comprised between heights of 4 and 23 mm, grey levels averaged over a horizontal section of 1 mm thickness were comprised in the range 141.5 $\pm$ 0.4, and thus were rather homogeneous. This central part was defined as our region of interest (ROI). Note that, because of the cone beam and metal artefacts, any fine analysis of the local heterogeneity of the initial state of the specimen proved to be difficult to perform. Those artefacts are also present in the local tomographies, but details of the microstructure are finer since the voxel size is smaller than for the global tomography.

Fig. 4

Layer-averaged grey level at the initial state in the height of the specimen. Shaded areas correspond to the discrepancy of the grey level due to the cone beam hardening (bottom and top), the metal artefact (bottom) and a possible heterogeneity of the microstructure

3 Characterisation of the initial microstructure

The aim of this section is to characterize the microstructure of the specimen in its initial state, i.e. before any water transfer with the surrounding. It is in particular aimed at determining the size of the representative volume element (RVE) and the sizes of pores and aggregates. This analysis is performed on the local tomographies. The methods and algorithms employed to analyse the three-dimensional images are first described.

3.1 Image processing

To limit the effect of artefacts near the edge of the reconstructed volumes, image processing was performed only on a volume extracted from the centre of the local tomography. This volume called hereafter isolated-volume was a cube of side length 750 voxels, i.e. of side length 18.7 mm and is delimited by solid lines in Fig. 3.

Image processing was performed with the Population library (http://www.population-image.fr/) [49] that is specifically designed for three-dimensional images and gathers more than 200 algorithms. This open-source image analysis library is interfaced with Caméléon graphical language (http://www.shinoe.org/cameleon/) [46]. Labelled images are images in which each voxel is associated to one phase of the specimen. In order to obtain such images, a nonlinear anisotropic diffusion filter was first applied to decrease the noise of the image while keeping sharp boundaries between phases [39]. Then a global threshold was applied to obtain binary volumes. Threshold values were set to the local minimum values of the grey level histogram. Figure 6 shows grey level histograms of the extracted volume at each step of the procedure. Histograms of the two phases (air and aggregate) are obtained using the binarised volume to mask the initial (unfiltred) grey level volume. Figure 5 shows a slice of the volume before and after processing.

Fig. 5

Vertical slice in the local CT (left) and its associated binary image after image treatment (right). The voxel size of the local CT is 25 $\upmu$m

Fig. 6

Histograms of grey levels during the image processing sequence

Histograms exhibited only two distinguishable peaks because the volume of water was very small compared to that of air and sand and because water was trapped in smallest pores. For these reasons, the grey phase in the binary image displayed in Fig. 5 (right) encompasses both sand grains and water. In this phase, water and sand grains form saturated clusters of sand grains, called hereafter aggregates (see Fig. 5). In this same binary image, the black phase corresponds to air-filled volumes. It is worth noting that binarisation of the histogram was preferred with respect to trinarisation, because this latter would have led to high uncertainties on volume fractions and thus on liquid saturation and water content in the specimen. Therefore, precisely estimating the water content requires designing an alternative technique, which will be presented in Sect. 4.3.

3.2 Thresholding uncertainties

The specimen preparation method ensured a macroscopic air fraction of 47.6 % with an expanded uncertainty of 0.8 % (with a level of confidence of 99.7 %). Consequently, the volume fraction of air of the specimen as a whole was comprised in the interval [46.8 %;48.4 %], which defines the reference interval.

Image processing yielded an estimate of the air volume fraction of 45.3 %, a value smaller than the smallest value of the reference interval. This discrepancy could be attributed to the choice of isolated-volume, image quality and treatment sequence.

In this work, a simple approach was used to evaluate the influence of the grey-level threshold value on the resulting air volume fraction using the sensitivity coefficient defined in the norm previously cited [27]. This coefficient corresponds to the value of the normalised histogram at the threshold value of the filter image and is found equal to 0.46 % (the smallest probability between peaks in Fig. 6). In other words, an uncertainty of ten grey levels (that is, possible grey values in the interval [145;155]) leads to a minimal uncertainty of 4.6 % on the air volume fraction. As a consequence, from the image analysis point of view, the air fraction is estimated to be in the interval [43 %;47.6 %] with an uncertainty of ten grey levels. These uncertainties are relatively high compared with uncertainties coming from the specimen preparation method. In the following, the analyses made on RVE size and grain size distribution take into account these uncertainties.

3.3 Representative volume element (RVE)

The analysis of the size of the RVE is performed by choosing the air volume fraction as the parameter of interest. The standard method to evaluate the RVE size is to calculate the average air volume fraction inside randomly chosen elements of a given size and to analyse its fluctuations as a function of this size. Figure 7 shows the evolution of the air volume fraction computed in three non overlapping cubes vertically distributed along the axis of the segmented volume. For the three locations, the volume fraction is very sensitive to the cube size up to around 3 mm and becomes almost independent for larger sizes.

Fig. 7

Air fraction as a function of cube size for three sub-volumes

In order to further analyse the RVE size, an objective criterion is necessary. To this end, statistical tools can be used to evaluate the representativeness of the isolated-volume. A framework was developed by Matheron [35] from a geostatistics point of view to estimate metal content of a pit on the basis of only few drilling data. He pointed out that the variance of a content is not inversely proportional to its volume unless the macroscopic content is constant. This inverse proportionality for homogeneous images has been confirmed on real specimens [6, 30]. An image can thus be considered as homogeneous if the variance of the empirical mean (E.M.) of a parameter of interest [6] decreases asymptotically as fast as or faster than the inverse of the image size ($1/V$). In order to guarantee sampling independence, the isolated-volume (see Fig. 3) was divided into equally-sized windows called also sub-volumes. The empirical mean of air fraction was then evaluated in each window to obtain the variance of air fraction. Figure 8 shows the relationship between this variance and the sub-volume size.

Fig. 8

Effect of the size of the cube on the variance of the empirical mean of the air fraction

First, it can be observed that for small windows, when the cube size tends to one voxel, the variance of EM tends to an horizontal asymptote corresponding to the point variance $\sigma ^2$. The point variance is the variance of the image seen as a random process, i.e. $\sigma ^2=p(1-p)=0.453(1-0.453) \approx 0.25$ with $p$ the air fraction obtained from image analysis of the whole isolated-volume. Second, another asymptote is observed when the cube size increases. Equation $f(V)=a/V^b$ ($a$ and $b$ being unknown parameters) was fitted on data for cubes with a volume larger than 1 $\hbox {mm}^3$. Using the Levenberg–Marquardt algorithm to obtain the best fit, one finds $a\approx 3.9\times 10^{-3}$ and $b\approx 0.98$ with $V$ in $\hbox {mm}^3$. Scatter exaggerated by the log scale is observed for large cube sizes. Indeed, excluding cubes with a volume greater than 64 $\hbox {mm}^3$ from the fit does only slightly modify the values of the coefficients $a$ and $b$. Since $b$ is close to 1, it can be concluded based on Matheron’s criterion that the volume isolated within the initial sand specimen is homogeneous.

The obtained asymptote allows us to find a RVE size for a given confidence on the volume fraction of air or, conversely, to find an interval of confidence for a given size of the volume considered. Assuming a Gaussian distribution, the 95 %-confidence interval is $p\pm 2\sigma (V)$ with $\sigma (V)=\sqrt{a/V}$ assuming $b\,\simeq$ 1. As an illustration, if the volume fraction is estimated on a volume with a side length of 3.5 mm (i.e. approximately 10 mean diameters of the grains), the volume fraction of air is in the interval $45.3\pm 1.9\,\%$ and the relative expanded uncertainty is 2$\sigma (V)/p=4.2$ % with a 95 %-confidence. Conversely, for the relative expanded uncertainty on the quantification of the air fraction to be smaller than 1 and 5 %, the side length of the RVE must be greater than 9.4 and 3.2 mm, respectively.

Moreover, parameter $a$ introduced above is usually written $\sigma ^2 A$ where $\sigma ^2$ is the point variance and $A$ is called the integral range. This integral range is often considered as representative of the characteristic scale of the fluctuations of the investigated quantity [30]. In the present case, the integral range is equal to $15.6\times 10^{-3} \hbox {mm}^3$, thus leading to a cube size of 250 $\upmu$m that is of the same order of magnitude as the median grain diameter.

It is worth noting that thresholding uncertainties affect the horizontal asymptote since air fraction evolves with the threshold value. However, the second asymptote corresponding to large window sizes does not really change with the uncertainty of ten grey levels (see Table 2): Matheron’s criterion is verified and the integral range remains around 250 $\upmu$m.

Table 2 Parameters of the equation $f(V)=a/V^b$ fitted on the asymptotic evolution of the variance of the air fraction for the three threshold values

The previous analysis proves the homogeneity of an isolated-volume that only covers $1/17$ of the whole specimen volume. Consequently, no conclusion can be drawn on the homogeneity of the whole specimen. Extending this analysis to the entire specimen volume would certainly be useful. However, the image artefacts previously cited make any image treatment of the whole specimen untrustworthy so that the analysis has not been carried out at specimen scale.

3.4 Size of aggregates and pores

The sizes of aggregates (defined as saturated clusters of sand grains, see Sect. 3.1) and pores are estimated using Matheron’s granulometry [23]. This tool is based on a series of openings that use structuring elements with increasing sizes. This morphological operation is equivalent to applying an erosion followed by a dilatation. The opening operation permits to remove small objects while maintaining the morphology of the microstructure. The Euclidean norm was used: its associated structuring element is the discrete sphere. Each opening was applied to the initial binary image and yielded a modified image in which some voxels of the isolated phase had disappeared. This operation was repeated until an element size erasing completely the isolated phase was found. The volume fraction of the isolated phase decreased with the size of the structuring element. Finally the result of the Matheron granulometry is a cumulative volume distribution of inscribed spheres. The normalised cumulative passing (see Fig. 9) is easily deduced and is compared to the grain size distribution of the Hostun sand obtained from classical sieve analyses performed in soil mechanics (see Fig. 1). The size of aggregates obtained by image analysis is smaller than for grains by sieve analysis. The two methods of measurements are different since the sieve analysis used square meshes and Matheron’s granulometry spherical structuring elements. Moreover, this difference is accentuated by the fact that grains are angular and that aggregates are composed of just a few grains. Pore sizes are of the same order of magnitude as aggregate sizes, but more dispersed.

Fig. 9

Cumulative size distribution of air and aggregate phases by image analysis and of grains by sieve analysis. The distribution of the segmented images at grey levels of 145 and 155 is also plotted (respectively labelled $\hbox {t}=-5$ is $\hbox {t}=+5$)

The size distribution given in Fig. 10 is the difference in number of voxels between two consecutive element sizes. Granulometries are analysed using the median diameter $D_{50}$ and the coefficient of uniformity $C_{u}$ and summarised in Table 3. The differences between aggregate and grain size, evaluated by two different methods, are confirmed in this table.

Fig. 10

Size distribution of air and aggregates. Segmented images at grey levels of 145 and 155 are also added (labelled $\hbox {t}=-5$ and $\hbox {t}=+5$)

Table 3 Median diameters $D_{50}$ and coefficients of uniformity $C_{u}$ obtained by image analysis (for the air and the aggregates) and by sieve analysis (for the grains)

Threshold uncertainties affect the results of the granulometry, as shown in Figs. 9, 10 and in Table 3. The “uncertain” voxels with a grey level around the threshold value are located at interfaces between phases. Depending on the thresholding value, these voxels are attributed to the air or to the aggregates. The sensitivity of the granulometry with respect to the threshold value is higher for aggregates than for air because of the presence of uncertain voxels close to intergranular contacts. In addition, the narrower distribution of aggregates favours this higher sensitivity.

4 Evolution of the specimen during imbibition

In this section the evolution of the specimen during the imbibition process is described. First, the results are presented from a macroscopic point of view in terms of water retention behaviour (changes in water content with respect to changes in suction). Second, we present local strains (obtained from V-DIC), variations of water content (obtained from variations of grey level) and changes in the morphology of both the porous space and the aggregates.

4.1 Water retention potential

Imbibition steps are presented in Fig. 11 in terms of changes in water content due to changes in applied capillary pressure providing the water retention curve of the sand. The capillary pressure is that at the top of the specimen, and was equal to 5.8 kPa at the end of the second step. Such a value is high enough to transfer water from the specimen to the graduated burette, explaining why the water content of 3.7 % at the end of the second step is smaller than the initial water content (7.2 %). Although the capillary pressure at the third step was lower than at the second step, the water content remained equal to 3.7 %. This water content is called the residual water content and corresponds to the quantity of water in the soil that is difficult to remove by the negative column method, at least at such low values of capillary pressure. The imbibition process starts when the capillary pressure decreases below about 2 kPa. The last step of the imbibition process (step 14) corresponds to a null capillary pressure. At this step, menisci in the burette and at the top of the specimen were at the same height. The specimen had a water content of 40.8 %. This value is lower than the theoretical water content (48 %) calculated from the initial microstructure assumed water-saturated (represented by the vertical dash-dotted line on the right side of Fig. 11).

Fig. 11

Capillary pressure at the top of the specimen as a function of water content during the imbibition process. The vertical dotted line represents the initial water content (7.2 %) and the vertical dash-dotted line represents the water content (48 %) theoretically needed to fully saturate the specimen in its initial state

Figure 12 shows vertical slices of the specimen at imbibition steps 1, 10, and 14. Images in the upper row are close up views of the specimen top with the free surface. Images in the lower row come from the centre of the specimen. Arrows indicate local changes in terms of either grain displacements or pore filling by water. This figure permits qualitative description of the microstructure evolution during imbibition. The displacement of a grain located on the free surface of the specimen between steps 10 and 14 (final step) corresponds to a segment $\varDelta z$ of about 0.6 mm that results into an estimate of the macroscopic vertical strain equal to 2 %. At step 10, the smallest pores are saturated with water while largest pores remain unsaturated. Some, but not all of these larger pores become saturated at the final step. More quantitative information about these issues are investigated at the mesoscopic scale in next section.

Fig. 12

Vertical slices of partial CT scans at three imbibition steps (left to right: steps 1, 10, 14) from two regions of the specimen: close to the free surface (top) and in the centre of the specimen (bottom)

4.2 Volumetric-DIC

Volumetric digital image correlation [4] was used to quantify local strains in the whole specimen from the set of global CT scans. Details on the algorithm and procedures can be found in [7, 33]. To our knowledge, it is the first time that V-DIC is used on a specimen with evolving saturation states.

Volumetric digital image correlation exploits texture of images to find similarities between sub-volumes—named 3D correlation windows—between two distinct states (a reference and a current state). The position of the correlation windows is estimated by looking for the transformation to map the reference to the current state. Here this transformation is assumed to be a translation only (i.e. with no rotational component considered), the three translation components being unknown. A correlation coefficient is minimized to determine automatically this transformation in a search volume for each window around some a priori position. A zero-centred normalised cross-correlation coefficient was used in conjunction with a sub-voxel optimisation based on a trilinear interpolation of grey levels allowing to work with a displacement resolution smaller than the voxel size (50 $\upmu$m). The reference image was the initial state, in which the burette was not yet connected with the soil. The initial integer positions of the correlation windows were placed side by side to cover the whole specimen. Correlation windows had a volume of 1 $\hbox {mm}^3$ ($20\times 20\times 20$ voxels). In practice, after the sub-voxel optimization, the correlation coefficient of most correlation windows was lower than 0.2 (0 corresponding to a perfect match and 1 to no match [22]). For only 147 of the 118,200 initial correlation windows, the correlation coefficient was higher than 0.7 (see Table 4): the corresponding correlation windows were cancelled.

Table 4 V-DIC parameters: corners of cells are the centres of the correlation windows

From the displacement fields obtained with V-DIC, 8-node finite elements were used to calculate strains under the hypothesis of small perturbations. Element nodes were located at the centre of the correlation windows. If any node of a given cell was lost during the correlation, then strains were not evaluated for that cell. The maximum of loss was at the final step 14 with 800 cells, equivalent to 0.7 % loss of initial cells (see Table 4). The average strain tensor was computed evaluating the strains at the Gauss integration point, i.e. at the centre of the cell in the case of small perturbations. Note that strains are measured positively in extension and that the volumetric strain is the trace of the strain tensor.

Uncertainties of the output of V-DIC were estimated using the tomographies of steps 2 and 4 where displacements and variation of water content were so small in the central part of the specimen, that the transformation could be considered as a rigid body motion. Image correlation procedures were applied to compare these two steps (step 2 was the reference, and step 4 the deformed image). The uncertainties on displacement components were quantified by comparing the local DIC-evaluated displacements to the displacement associated with the best-fitting rigid body motion. The standard deviation of the displacement measurement was less than 0.1 voxel. This induces an uncertainty of 0.2 % in the strain calculation and 0.35 % for the volumetric strain. Therefore, the local fluctuations of strains in the following results (especially in Fig. 13) are likely to be induced by these correlation uncertainties. In the following results, one will also observe that V-DIC maps are somewhat noisier in a horizontal plane about a quarter of the way up the images: this noise is the consequence of a reconstruction artefact associated with an imperfect determination of the vertical position of the normal projection of the X-ray source on the detector.

Fig. 13

Maps of vertical strains (left), volumetric strains (centre) and water content (right) for imbibition steps 10, 11, 12, 13, 14 (from top to bottom). Each map is the juxtaposition of a half vertical slice in the $xz$ plan (left half of the map) and the $\theta$-average of all half vertical slices (right half of the map). Scale of color bars is percentage values. Central vertical axis of the maps coincides with central axis of the specimen

Figure 14 displays the vertical strain averaged over horizontal layers. It can be observed that strains are heterogeneous at the scale of the specimen. Figure 13 displays the vertical strain, volumetric strain, and water content for the last 5 imbibition steps. In this figure, each sub-figure results from the juxtaposition of two maps: the left map displays a vertical slice of half of the specimen, while the right map displays values averaged orthoradially on the whole specimen. This orthoradial average (noted as $\theta$-average) was obtained by averaging all cells located at a given height and at a given distance from the axis of rotation of the specimen. From Fig. 13, one observes that the heterogeneity in the specimen is in fact both radial and vertical. Also, since $\theta$-average maps are very similar to vertical slices, one concludes that strain fields and water content exhibit axial symmetry.

Fig. 14

Vertical strain averaged by horizontal layer for the drainage step 2 and for the imbibition steps 10, 11, 12, 13, 14

It is worth noting that strain localisations appear at step 13. At this step, vertical strains are localised on conical surfaces, while both the lower central part and the upper external part of the specimen deform relatively little: the upper soil mass slid on superimposed sliding surfaces, while the lower central part of the specimen remained essentially immobile. These sliding bands can be identified essentially as shear bands since they are less visible in the volumetric strain maps. In parallel, at steps 13 and 14, a localisation of contractile strains is observed at the bottom corner of the specimen.

4.3 Water content obtained by grey level analysis

Grey levels of global CT scans were exploited to deduce the local evolution of the water content. Average grey levels were computed in cubes with a side length of 2 mm and centred on Gauss points in order to cover the same volume of specimen as the one used for the calculation of strains. Cells were then averaged orthoradially ($\theta$-averages) or on horizontal layers (layer-averages). Layer-averages were performed on volumes of 7,693 $\hbox {mm}^3$, while $\theta$-averages were performed on volumes of 8 to 1,664 $\hbox {mm}^3$. According to the analysis in Sect. 3.3, the associated relative expanded uncertainties on the air fraction at the initial state are 0.3 % for layer-averages, and between 0.8 and 9.8 % for $\theta$-averages.

To describe the method used to quantify the local water content, the following notations are first introduced:

• $V_{si}, V_{wi}$,$V_{ai}$ are respectively the volumes of sand, water and air in the cell of volume $V$ at step $i$;

• $\widehat{L}_i$ is the average grey value in the cell at step $i$;

• $L_s, L_w, L_a$ are the grey levels of sand, water and air, respectively;

• $G_s=2.65$ is the specific gravity of sand;

• $\varepsilon _{vol}$ is the volumetric strain of the cell at step $i$.

In theory, the average grey level is related to the volume fractions of water, air, and sand. In a given cell, such an average is obtained by weighting the phase volumes by their grey value:

$$\begin{aligned} \widehat{L}_i=\frac{V_{si}L_s+V_{wi}L_w+V_{ai}L_a}{V} \end{aligned}$$

(1)

Calculation cells have a constant size, but evolving volumetric strains. Volumetric strain is expressed as a function of volumes of sand in the cell because sand grains are assumed incompressible:

$$\begin{aligned} \varepsilon _{vol}=\frac{V_{s1}}{V_{si}}-1 \end{aligned}$$

(2)

A variation of the absorption properties of a cell can either be due to an increase in the volume fraction occupied by sand grains (consistent with a volumetric strain), or to change of water content. Therefore, the relative variation of grey level can be split into two parts, only one of which depends on the water content variation:

$$\begin{aligned} \frac{\widehat{L}_i-\widehat{L}_1}{\widehat{L}_1}=\alpha \frac{\varepsilon _{vol}}{\varepsilon _{vol}+1}+\beta \frac{\varDelta w}{\varepsilon _{vol}+1} \end{aligned}$$

(3)

with:

$$\begin{aligned}&\alpha \!=\!-\frac{L_s\!-\!L_a\!+\!G_sw_1(L_w\!-\!L_a)}{(L_s\!-\!L_a\!+\!G_sw_1(L_w\!-\!L_a)\!+\!L_a/(1\!-\!n_1))} \end{aligned}$$

(4)

$$\begin{aligned}&\beta \!=\!\frac{G_s(L_w\!-\!L_a)}{(L_s\!-\!L_a\!+\!G_sw_1(L_w\!-\!L_a)\!+\!L_a/(1\!-\!n_1))} \end{aligned}$$

(5)

In practice, grey values are also influenced by the artefacts presented in Sect. 2, such as cone beam and metal artefacts. One observes that the upper and lower parts of the specimen are characterised by grey levels that are not consistent with those of the centre part. As a consequence, only the central part of the specimen (between 4 and 23 mm height) was analysed to obtain local water contents. In the following, this part is called region of interest (ROI).

Furthermore, the flux of the X-ray source is not constant in time and a correction is required in order to quantitatively use grey level variations. To do so, the PMMA cell and the air outside the specimen have been used as two reference regions to normalise tomographies. Each voxel of each scan was re-scaled to match the reference grey levels of the first scan using linear functions fitted to the two reference regions. The histogram of the first tomography yielded peaks of sand and air with grey levels of 170 and 100, respectively. $L_{w}$ was obtained by fitting Eq. (3) to the macroscopic water content and variation of grey level and volumetric strain in the ROI. $L_{w}$ was found equal to 147 with $\alpha =-0.2579$ and $\beta =0.4068$. The dependence of the grey level on the macroscopic water content is shown in Fig. 15. We observe that the volumetric strain only contributes to the variation of grey level at second order. Using the now calibrated Eq. (3) and presuming its integration on the ROI to be equal to the macroscopic water content, the profiles of water content are plotted in Fig. 16.

Fig. 15

Variation of grey level as a function of macroscopic water content after flux correction (normalised scans). Equation 3 is plotted for 0 and $-$2.5 % volumetric strains

Fig. 16

Evolution of water content profiles during the imbibition process, evaluated from corrected grey levels

Figure 17 shows the same profiles but with the capillary pressure as $y$-axis instead of the height in the specimen. We can notice that the slope of profiles is in good agreement with the macroscopic measurements (dots). This suggests that global measurements are representative of the local behaviour of the material evaluated from averages over layers, despite the clearly established heterogeneity of local states. Indeed, at a given stage of the experiment, water content may vary by almost 10 % throughout the specimen, which is not negligible with respect to the 35 % variation of water content throughout the test. The fluctuation of capillary pressure is less critical but still non negligible: 0.3 kPa from bottom to top of the specimen, to be compared to the 6 kPa total fluctuation during the test. The reason for which macroscopic measurements have a meaning can be explained as follows. Macroscopic capillary pressure content is the volume average $\langle p_c \rangle$ of local capillary pressure $p_c$. The global water content is also the volume average of the layer-water content as long as the fluctuations of dry density of sand are small along the vertical axis, which is true because the specimen is reasonably homogeneous in its initial state (see Sect. 3) and volumetric strains are small (a few % at most, see Fig. 14). The global capillary pressure / water content curve is thus given by $(\langle p_c\rangle , \langle w\rangle )$. If the local capillary pressure / water content curve is linear over the range of fluctuation of local water content in the specimen, then the macroscopic measurements will coincide with local curve. This seems to be the case for a water content above 10 %. Some nonlinearity in the $(p_c, w)$ behaviour is observed for lower water content. But in that range the fluctuation of $p_c$ throughout the height of the specimen is sufficiently small so that the water content is almost uniform in the specimen, and macroscopic measurements are representative of the local state.

Fig. 17

Capillary pressure as a function of water content using macroscopic (circles) and averaged by layer (continuous lines) measures. Capillary pressure corresponds here to the middle of the specimen for the macroscopic results

Maps of water content at several imbibition steps are shown in Fig. 13. Like for strains, radial and vertical distributions of water content are heterogeneous at the scale of the specimen. Heterogeneity is essentially vertical until step 11, then radial heterogeneity prevails with a more pronounced increase in water content in the bottom corner. Figure 18 shows that the relationship $\epsilon _{vol}-w$ between macroscopic volumetric strain and macroscopic water content relation is almost identical to that between volumetric strains and water contents averaged layer by layer. The behaviour of the isolated-volume (volume analysed in Sect. 3) is also plotted in this figure. Its final water content reaches 35 % and volumetric deformation $-$0.65 %, these values being significantly below the macroscopic ones. Nevertheless, the $\epsilon _{vol}-w$ relation for the segmented volume fits the ones obtained at the macroscale or from layer averages.

Fig. 18

Volumetric strain as a function of water content using macroscopic and averaged by layer results

4.4 Aggregates and air-filled pore sizes

The methodology used to characterise the initial microstructure was followed again to track the evolution of the sizes of aggregates and of the air-filled pores upon imbibition. The analysis was performed on the fixed isolated-volume shown in Fig. 3. The threshold for the grey level was again chosen as the grey level at the local minimum between the two peaks of the histogram, which yields the smallest threshold uncertainty. It is worth noting that this threshold value changes with the amount of water in the specimen, evolving from 158 at the lowest water content to 132 at the highest water content. The local water content in the volume of interest was obtained from the variation of grey level, as described previously.

The relationship between water content and air fraction is plotted in Fig. 19 for the whole specimen using the following Eq. (6) with $n_1$ the initial porosity (see macroscopic curve in Fig. 19):

$$\begin{aligned} p=1-(w G_s +1)\frac{1-n_1}{\epsilon _{vol}+1} \end{aligned}$$

(6)

The macroscopic air fraction is obtained from the macroscopic water content and the macroscopic volumetric strain. The error bars give a measurement of the sensitivity of the air fraction to the threshold value ($-$5 and $+$5 grey levels): thresholding uncertainties decrease with increasing water content. This experimental relationship can be fitted theoretically accounting for the volumetric strain in the segmented images and assuming an initial porosity of about 52 % (in Eq. 6), which is smaller than the macroscopic porosity of 56 %. This might indicate that the segmented volume is denser than the rest of the specimen and/or that the optimal thresholding value was not the valley of the histogram. For this reason, quantities are presented in the following figures with respect to local water content obtained from the relative variation of average grey level and not from the segmented volume.

Fig. 19

Air fraction as a function of water content: (i) from a macroscopic point of view (dashed line), (ii) locally, from image analysis with water content coming from grey level and air fraction from the thresholded volume (continuous line) and (iii) fit to image analysis data assuming a smaller porosity (52 %) than the macroscopic one (56 %) and accounting for the volumetric strain (dash-dotted line)

Figure 20a presents the size distributions of air-filled pores at all steps. Two modes (peaks) are observed at low water contents whereas only one remains at higher water contents. The 0.1 mm mode indeed disappears at step 6 and the 0.2 mm one moves towards larger diameters starting from step 10. Figure 20b presents the size distributions of aggregates at all steps. The whole distribution of aggregates moves towards larger diameters during the imbibition process. Figure 21a shows that the median diameters of air-filled pores and aggregates increase with water content from 240 to 370 $\upmu$m and from 250 $\upmu$m to 1.53 mm upon imbibition, respectively. The cycle of drainage-imbibition between steps 1 and 5 is reversible since $Cu$ and $D_{50}$ have the same value at the same water content (see Fig. 21a, b). The coefficient of uniformity of the air phase decreases monotonously when the water content increases, except at the last step (see Fig. 21b). The changes of the coefficient of uniformity of the aggregates is characterised by three intervals : (1) $w < 10$ %, (2) $10<w<25$ % and (3) $w>25$ %.

• 1. In the first interval ($w<10$ %), the coefficient of uniformity $C_u$ for the aggregates decreases with increasing water content with a minimum value of $C_u$ (1.75) at a water content of 10 %. This minimum appears when the smallest intra-aggregate pores become water-saturated. The corresponding median diameter of aggregates (330 $\upmu$m) is typical of the size of grain clusters. The size distribution of air-filled pores in Fig. 20a shows that the first peak (0.1 mm mode) disappears at step 6, a step with a water content of $w=10$ %.

• 2. In the second interval ($10<w<25$ %), the coefficient of uniformity $C_u$ of the aggregates increases to reach a value of 2.2. At this step, water had invaded a new class of pores leading to a wider granulometry of the aggregates characterized by a median diameter of 930 $\upmu$m and a water content of $w=25$ %. This corresponds to step 10 of the imbibition process, which matches with the step at which the second peak (0.2 mm mode) of the size distribution of air-filled voids (see Fig. 20a) started shifting towards larger values.

• 3. At the largest water contents considered ($w>25$ %), the coefficient of uniformity of the aggregates decreased again with increasing water content. During the last four imbibition steps, the largest pores are partially filled with water. At the end of imbibition, the median diameter of air-filled pores is 370 $\upmu$m.

Fig. 20

Size distribution during imbibition of (a) air-filled pores and (b) aggregates. Results are presented for each step (s1$\ldots$s14) corresponding to each equilibrium state

Fig. 21

a Median diameter of air and of aggregates and b coefficients of uniformity as functions of the local water content

5 Discussion

The experience gained from the preliminary specimen preparation tests indicated that an initial water content of around 7 % was sufficient to stabilise the loose sand microstructure before wetting. From the local analysis with a 25 $\upmu$m voxel size, the initial homogeneity within a sub-volume of the specimen was evidenced by applying the asymptotic behaviour method to the air fraction. This method, initially proposed by Matheron [35] and developed by Lantuejoul on 2D images [30], permits to link a size of RVE to the measurement accuracy. The common practical rule defining the RVE size as ten times the median grain diameter leads to a relative error (also called relative expanded uncertainty) of 4.2 % in the determination of the air fraction. For this relative error to become lower than 1 %, the RVE size must be at least equal to about 30 times the median diameter of the grains. Interested readers are referred to [8] for a detailed analysis of this method. The vertical homogeneity of a larger part of the specimen (ROI) was also observed thanks to a low variation of grey level in this region (see Fig. 4). The microstructure considered here is an arrangement of grain aggregates and is thus characterised by a double porosity [5, 13, 37, 42] with micro-pores (or intra-aggregate pores) located within aggregates and macro-pores (or inter-aggregate pores) located between aggregates. This particular microstructure was observed and analysed through Matheron’s granulometry [23]. The difference of results between the usual sieve analysis and the one obtained through Matheron’s granulometry at low water contents is thought to be due to both the angularity of grains and the fact that aggregates only contain few grains at low water contents. Indeed, on individual grains, Matheron’s granulometry yields sizes smaller than the diameter of the largest sphere inscribed in each grain, which itself is smaller than the minimum Feret diameter and thus than the opening of the mesh. Therefore, on individual grains, Matheron’s granulometry is expected to yield a finer grain size distribution than regular sieve analysis. However, this effect is slightly counterbalanced by the fact that Matheron’s granulometry is performed on binarized images composed not of individual grains, but on aggregates therefore composed of a few grains (see Fig. 5).

Until 25 % in water content, the microstructure was quasi immobile. During this first stage of imbibition, inter-aggregate pores were gradually water-filled, as confirmed in Fig. 20a in which the population of the smallest diameters of inscribed spheres in air phase decreased drastically. Figure 12 shows two slices at step 10 which corresponds to the last step just before the apparition of significant strains. We observe in this figure the complex shape of aggregates filled of water supporting the more dispersed granulometry of the aggregates seen in Figs. 20b and 21b. Despite the reduction of the capillary pressure and the coalescence of the capillary bridges, the microstructure is strong enough to support its self weight until 25 % of water content.

The microstructure began to collapse when the macroscopic water content became higher than a value of about 25 % (see Fig. 18). This particular value of water content is also observed at local scale. Indeed small strains appear in the bottom of the specimen at step 10 (see Fig. 14) which corresponds to a region in which the water content is slightly higher than 25 % (see Fig. 16). From 25 % to the final water content, water invaded the largest pores, inducing significant deformation of the microstructure and showing the importance of the coalescence of capillary bridges between grain clusters in the collapse phenomenon. This coalescence is clearly observed in the size distribution of the aggregates which is translated to higher diameters (see Fig. 20b between steps 10 and 11). One possible explanation of the collapse mechanism here is that, when the filling of macro-pores occurred, the number and the strength of intergranular capillary bridges decreased while the mechanical loading (self weight of the specimen) increased during imbibition. The limit equilibrium of the specimen was reached at this particular water content of 25 % at which the mechanical loading exceeded the strength of aggregates. At the end of imbibition, some large pores remained filled with air, while water pressure was slightly greater than atmospheric pressure everywhere in the specimen. The high initial void ratio of the specimen ($\hbox {e}=1.27\pm 0.03$ see Table 1) probably explains that here we observed a macroscopic collapse (around 2.5 %) significantly larger than the one obtained by Lins and Schanz with the same sand [34] (around 0.2 % of collapse for an initial void ratio of $\hbox {e}=0.89\pm 0.005$). The preparation of the specimen in the unsaturated state is essential to reach such low density and particular microstructure. That is why we dedicated a great care to the preparation of the specimen and designed a new method based on the pluviation of wet sand.

At larger scales, fields of strain and water content are characterised by a reasonably good axial symmetry, but by a significant heterogeneity, both vertically along the test and radially in the last three steps (see Fig. 13). More precisely, in the first part of the test, this heterogeneity essentially takes the form of a vertical gradient, with larger strains in the lower part of the specimen, associated with larger water content, and in a thin layer at its top (where water content cannot be measured accurately because of artefacts). A more pronounced heterogeneity is observed in the second part of the test (starting around stage 12, corresponding to a macroscopic water content of 34 %), with the appearance of radial gradients of both strains and water content. The vertical heterogeneity comes from the gradient of hydrostatic pressure, which itself leads to a vertical gradient of capillary pressure in the specimen. This gradient induced a heterogeneity of both water content and strain. Whereas gravity effects are usually neglected in standard geotechnical tests, it appears here that gravity led to a difference in capillary pressures of 0.3 kPa between the bottom and the top of the specimen, a difference far from being neglibible when considering the corresponding ranges of water content in the water retention curve (see Figs. 11 or 17). A volumetric (contractile) strain localisation zone appeared at the bottom corner of the specimen. We also observed a localisation of vertical strains on conical surfaces forming shear bands tilted at about 40 degrees with respect to a horizontal plane. Richefeu [40] observed a comparable shape of shear bands during the compression of an unsaturated granular material by DEM and explained his observation by the motion of the loading plate or by gravity effects. The localisation phenomenon in the bottom corner could be due to boundary conditions or heterogeneity of initial density. Indeed the central area in which the segmentation was carried out (see Fig. 3) appeared to be denser than the remaining of the specimen: the porosity of this former was estimated to 52 %, which is smaller than that of the whole specimen (the porosity of which was around 56 %). Hence, in spite of the great care devoted to the preparation of the specimen, some looser parts could exist in the bottom corners of the specimen in its initial state. Another explanation could be that the PMMA cell walls could facilitate the sliding of grains and the provision of water along preferential paths. A last explanation could be gravity effects leading to sliding and thus to a densification in the bottom corner of the specimen upon saturation: indeed, the angle of repose of sand is smaller in the saturated state than in the unsaturated one [43].

Despite the observed heterogeneity of strain and water content, a rather similar relationship between the volumetric strain and the water content was obtained at three different scales: macroscopic scale of the whole specimen, scale of the one-millimetre thick layers (Fig. 18), and the smallest scale of the $\theta$-averages displayed in Fig. 22. The fact that such similar relationships were obtained at such various scales is rather a surprising result, but can be explained with arguments similar to those explaining the similarity between the $(p_c, w)$ relationships obtained at the macroscopic and at the local scales. Indeed, the global volumetric strain is the volume average $\langle \varepsilon _v \rangle$ of the local volumetric strain $\varepsilon _v$. In case of a limited fluctuation of local strains or local water content, the macroscopic curve coincides with the local one. This is the case at the beginning of the test, up to about $w = 25\%$. A more pronounced nonlinear behaviour is observed later on, with a concave local $(\varepsilon _v, w)$ curve. In such a case, at a given water content the macroscopic strain is lower than the local one, as is indeed observed in Fig. 18. But since the fluctuation of water content (10 % at most) remains small, the discrepancy between the macroscopic curve (black dots), the mesoscopic one (triangles) and the local curve (continuous line) is limited and might be neglected in first approximation. A similar comment can be made on Fig. 22, which shows that, at a given water content, macroscopic strains tend to be smaller than local ones. One notes however that, on this figure data at the local scale are significantly scattered. This scatter has several origins, the first being experimental errors: indeed, the standard deviation of the error on local volumetric strain at a 1 $\hbox {mm}^3$ scale is of the order of 0.35 %, which is close to the observed scatter. In addition, there is a natural scatter due to the fact that $\theta$-averages are performed on volumes that are around the size of the RVE. For instance, the natural variation of local air volume fraction of 1 $\hbox {mm}^3$ cubes has a standard deviation of 10 % (see Fig. 8). Note however that local data on Fig. 22 provide additional information on the $(\varepsilon _v, w)$ curve, since values of $w$ and $\varepsilon _v$ much larger than the macroscopic ones are obtained (the largest $\theta$-averaged local volumetric strain is about twice the macroscopic one). The curve deduced from the processing of local data nicely prolongs the macroscopic one and shows the continuity of strain with the water content, thus the controllability of the collapse phenomenon. The one-to-one relationship between water content or suction and volume change observed by [48] in a silt is therefore confirmed here in a clean sand with a monotonic increase of volume change with the water content, also measured by [41] in a sandy soil, supporting again the important contribution of the coalescence of capillary bridges between aggregates in the collapse mechanism.

Fig. 22

Volumetric strain as a function of water content using macroscopic and $\theta$-averaged results

6 Conclusion

In this work, we performed an analysis of the capillary collapse phenomenon in sands using X-ray CT. An original experimental protocol allowed to initiate and to control the collapse of a loose clean sand for the first time. Images were analysed using V-DIC, calibrated variation of grey level and Matheron’s granulometry to respectively obtain strains, water content, and sizes of air-filled pores and aggregates inside the specimen, all along the test. The microstructure exhibited a double porosity which collapsed only during saturation of the macro-pores when capillary bridges between grain clusters merged.

Results showed that the gradient of hydrostatic pressure induces a vertical heterogeneity of water content and strains. The radial variability of strains and water content in the last steps of the test might be due to the heterogeneity of the initial density or/and the boundary conditions produced by the cell walls. Despite the heterogeneities, we showed that the water retention potential and the level of capillary-induced collapse are almost equivalent at both the macroscopic scale of the specimen and the mesoscopic scale of a few grains.