1 Introduction

A large number of engineering materials, in particular rock-like and cement-based materials, can be investigated in the class of cohesive granular materials. Their microstructure is mainly composed of mineral grains and voids. Unlike cohesionless granular materials such as powders and soils, the inter-granular contact interfaces in cohesive materials are bonded, generating a nonvanished macroscopic tensile strength and uniaxial compression strength. In this class of materials, the physical processes of deformation and failure are inherently related to bonds breaking or contact interfaces cracking and grain crushing. A great number of experimental, theoretical and numerical studies on various granular materials have been so far conducted. For instance and without giving an exhaustive list of reported studies, a thermomechanical constitutive model for cemented granular materials has been proposed using quantifiable internal variables by [5, 32]. Yang and Luo [34] have explored the relationship between critical state and particle shape for cohesionless granular materials. Kruyt and Rothenburg [16] have provided a micromechanical study of dilatancy in granular materials. Duriez et al. [9] have tried to identify the micromechanical nature of stresses in triphasic granular media with interfaces. La Ragione [18] has investigated the incremental response of a stressed and anisotropic granular material under loading and unloading conditions. Sibille et al. [31] have established a plastic theory for granular materials based on discrete mechanics. Borja et al. [1] have investigated shear band in sand with spatially varying density. The localization in a granular material has also been studied using a micromechanical prediction by [19]. The main issue is to capture the physical processes at microscopic scale and their impacts on macroscopic responses. For this purpose and with the fast progress of computing technology, various discrete elements methods have made a great progress during the last decades. The common feature of these methods is to replace a continuum medium by an equivalent discrete medium. Without giving an exhaustive list of different approaches, two main families of discrete media have been generally adopted, an assembly of spherical grains for granular morphology and a set of polygon blocks for polycrystal structure. For granular materials, the particle flow model is one of the widely used discrete approaches and has been extended to cohesive granular materials. Cundall and Strack [4] have first proposed a discrete numerical model and developed a particle flow code (PFC) for cohesionless granular materials. Potyondy and Cundall [27] have then developed a bonded-particle model for rock-like cohesive materials. Different extensions and improvements have been successively achieved by various authors in order to improve the quality of numerical results in terms of volumetric dilation, cracks propagation, post-peak strain softening and strain localization process [24, 39]. In particular, Jiang et al. [14] have proposed a rigid plastic element for contact interfaces and an efficient approach to capturing bonding effect in naturally microstructural sands. Jiang et al. [15] have also studied shear behavior and strain localization in cemented sand by two-dimensional distinct element method. References [7, 29] have proposed a new contact model to improve the simulated ratio of unconfined compressive strength to tensile strength in bonded-particle models. Mehranpour and Kulatilake [23] have examined and compared six major intact rock failure criteria in predicting intact rock strength under the true-triaxial stress condition using original bond models in a particle flow approach. Further, He et al. [11] have also conducted a detailed comparison of nine intact rock failure criteria using polyaxial intact coal strength data obtained through PFC simulations. Other applications of discrete element methods to rock-like materials have also been reported [3, 33]. The discrete element method has also been used to modeling fracturing process in cohesive materials [6, 20, 28]. In some studies, the discrete element method has also been applied to modeling anisotropic rocks [8, 17, 38] and jointed rock mass [10, 22, 26, 36]. Using a DEM method, Zhu et al. [40] have tried to define a common critical state for both localized and diffuse failure modes in cohesionless soil-like materials. Some similar discrete approaches have been developed for modeling cracking and fracturing in cohesion rock-like materials and compared with discrete element method [37].

In most previous studies using particle flow code, two-dimensional simulations for cohesionless materials [2, 21] as well as three-dimensional calculations for rocks [23, 25] are limited in using the same bond models, such as the contact bond model (CBM) and parallel bond model (PBM), to simulate failure behaviors of cohesive granular materials under different stress states. There is no detailed discussion so far on whether the original bond models are perfectly appropriate to describe the mechanical responses of cohesive granular materials under a large range of confining pressure and for different kinds of loading paths. In general, conventional triaxial compression tests on cylindrical samples have been considered in most studies. Further, the effect of the intermediate principal stress on deformation and failure of granular materials has not been sufficiently studied. The new contribution of the present study is then to partially complete the shortcoming of previous studies. To this end, a new failure criterion will first be proposed to describe both tensile and shear cracking of bonded contact interfaces for a large range of stress state. Fully three-dimensional simulations will then be performed on both cylindrical and cubic samples for different loading paths. Effects of confining pressure and loading path on deformation behavior and failure process of typical bonded granular materials will be clearly demonstrated. For convenience, the following stress and stress sign convention will be adopted throughout the paper: compressive stresses and strains are counted as positive quantities.

2 Failure criterion for a new bond model

In cohesive granular materials, the macroscopic strength and deformation are essentially controlled by the local behavior of inter-granular interfaces. For rock-like materials, the interfaces are generally bonded. Two types of bond models, i.e., the contact bond model (CBM) and parallel bond model (PBM), are used in standard particle flow code (PFC3D) [12, 13, 27]. There are three basic components involved in general bond model: (1) contact stiffness behavior, (2) bonding behavior and (3) slip behavior. Similarly, a brief introduction of the newly proposed bond model is provided in describing these three components as below.

2.1 Contact stiffness behavior

The deformation and failure of interfaces are closely related to local stresses. For calculation of local stresses at contacts, two main contact stiffness models (the linear and Hertz model) in PFC3D are, respectively, used to describe elastic and non-elastic behaviors of contacts, depending on the mechanical properties of the studied entities. Thus, in this work, the linear model is applied to represent the elastic behavior of cohesive materials. The relationships between force and contact stiffness are illustrated by the following equations:

$$F_{\text{n}} = k_{\text{n}} u_{\text{n}}$$
(1)
$$\Delta F_{\text{s}} = - k_{\text{s}}\Delta u_{\text{s}}$$
(2)

where the values of Fn, kn and un are, respectively, the normal force, normal stiffness and displacement at the contact; ΔFs, ks and Δus denote, respectively, the shear force, shear stiffness and relative displacements. Note that the normal stiffness, kn, is a secant modulus that relates to the total displacement and force. The shear stiffness, ks, on the other hand, is a tangent modulus that relates to the incremental displacement and force.

2.2 Failure criterion of new bonding behavior

The failure status of interfaces can be determined by comparing the calculated local stresses and bond strength at a contact. In failure analysis of interfaces, two debonding processes should be taken into account, i.e., the tensile cracking and frictional sliding. For tensile cracking, the failure condition is generally dependent on the normal tensile stress. The frictional sliding process is otherwise more complex, depending on both normal stress and tangential shear stress. The local shear strength of interfaces is strongly influenced by the normal stress. Thus, two types of bond models of interfaces, i.e., the contact bond model (CBM) and parallel bond model (PBM), are generally adopted for analyzing cohesive materials in PFC. In the CBM, the tensile and shear strength are directly regarded as a constant. Different from the PBM, the shear strength is described by a linear Mohr–Coulomb type criterion which is defined by the frictional angle and cohesion. The shortcoming of these criterions is that the effect of normal stress on the shear strength cannot be correctly described for a large range of normal stress.

Therefore, a new criterion is proposed here. The tensile failure occurs when the normal contact force Ft,f reaches the tensile strength φnt. For the shear cracking, the shear strength generally increases nonlinearly with normal pressure. The failure envelope is a convex curved surface. For the sake of simplicity, the shear strength of interfaces is here approximated by a bilinear function of normal contact force. When the normal contact force Fn is less than the transition threshold φncr, the shear strength is defined by the cohesion φs and frictional angle ϕ1. When the normal force is higher than φncr, a second frictional angle ϕ2 is introduced with ϕ2 < ϕ1 to define the shear strength. The peak shear strength envelope is presented in Fig. 1. The failure criterion for contact interface is then expressed in the following form:

$$F_{\text{n}} = \varphi_{\text{nt}} ,\quad {\text{tensile}}\,\,{\text{failure}}$$
(3)
$$F_{\text{s,f}} = \left\{ \begin{array}{ll} 0, & F_{\text{n}} <\varphi_{\text{nt}}\\ {\varphi_{\text{s}} + F_{\text{n}} \tan \phi_{1}},& \varphi_{\text{nt}} \le F_{\text{n}} \le \varphi_{\text{ncr}},\; {\text{shear}}\,\,{\text{failure}}\\ \varphi_{\text{s}} + \varphi_{\text{ncr}} (\tan \phi_{1} - \tan \phi_{2}) + F_{\text{n}} \tan \phi_{2},& F_{\text{n}} \ge \varphi_{\text{ncr}}\end{array} \right.$$
(4)

where Fs,f denotes the peak shear strength, φs the shear force applied to the interface.

Fig. 1
figure 1

Peak and residual strength envelopes of bonded contact model

Full size image

2.3 Slip behavior after bond failure

When the contact surface is broken, the tensile strength is completely vanished. However, due to the frictional force along rough interfaces, there is a residual shear strength which increases with compressive normal stress. Further, it is generally observed that the frictional angle is barely affected by interface failure, while the cohesion is drastically reduced. In the present model, it is assumed that the residual interface cohesion is reduced to zero, while the same value of frictional angles can be used for the residual shear strength. The residual strength envelope is shown in Fig. 1, and the following criterion is formulated.

$$F_{\text{s,r}} = \left\{ {\begin{array}{*{20}l} 0 \hfill \\ {F_{\text{n}} \tan \phi_{1} } \hfill \\ {\varphi_{\text{ncr}} (\tan \phi_{1} - \tan \phi_{2} ) + F_{\text{n}} \tan \phi_{2} } \hfill \\ \end{array} } \right.\begin{array}{*{20}l} { ,\quad F_{\text{n}} \le 0} \hfill \\ { ,\quad 0 < F_{\text{n}} \le \varphi_{\text{ncr}} } \hfill \\ { ,\quad \, F_{\text{n}} > \varphi_{\text{ncr}} } \hfill \\ \end{array}$$
(5)

The proposed failure criterion is implemented in the standard particle flow code. A series of numerical simulations are performed in order to investigate effects of confining pressure, loading path and the intermediate principal stress on deformation, failure process and macroscopic strength of cohesive granular materials.

3 Calibration and validation for the new bond model

The calibration and validation of the proposed new bond model as well as the effect of particle size distribution are presented hereafter in order to introduce the new nonlinear failure criterion to describe the mechanical response of cohesive materials for a large range of confining pressures.

3.1 Calibration of micromechanical parameters

As indicated in the above equations, there are seven micro mechanical parameters need to be identified in the proposed new bond model. The calibration process includes two main tasks: calibrating the elastic and strength parameters. For identifying the elastic, there is an approximating relationship between the Young’s modulus Ec and the micromechanical parameters of contact as denoted by the following equation parameters [12, 13, 23]:

$$k_{\text{n}} = 4E_{\text{c}} R,\quad k_{\text{s}} = k_{\text{r}} k_{\text{n}}$$
(6)

where R is the average radius between two adjacent particles, kr is the ratio of normal and shear stiffness, which is related to the Poisson’s ratio and generally taken as 1.0–3.0 as done in previous work [7, 15, 35]. The value of kr is set to be unit for the sake of simplicity. Then, setting the bond strength φntφs at a greater value, the calibration of Young’s modulus E can be done by adjusting Ec to match the values from laboratory experiments. Afterward, the Poisson’s ratio can be also determined by varying kr. Finally, the elastic parameters kn, ks, kr can be further obtained after an optimal process of adjustments.

In calibration of strength parameters, the normal and shear contact bond strengths φnt, φs have the following relationships with the material strengths σc, τc for pure axial and pure shear loading [30, 36]:

$$\varphi_{\text{nt}} = 4\sigma_{\text{c}} R^{2} ,\quad \varphi_{\text{s}} = 4\tau_{\text{c}} R^{2}$$
(7)

The commonly used strategy to calibrate the strength parameters φnt and φs is to specify the mean and standard deviations of the material normal strength σc as well as the shear ones τc according to Eq. (7). However, the ratio of the mean values to standard deviations of material strength can induce different failure models for the same sample. To avoid this uncertainty, the micro-parameters in this work are directly calibrated by the following method. Firstly, the frictional angle ϕ1 and ϕ2 was initially set equal as unity to reduce the number of independent parameters. Then, by reducing the normal and shear bond strengths φntφs, the peak strength between the numerical test and laboratory experiments can be approximately matched. It should be noticed that the aforementioned calibration process of strength is carried out under one confining pressure. Finally, further adjustments for frictional angle ϕ1, ϕ2 and the transition threshold φncr are needed to account for peak strengths of laboratory experiments under a large range of confining pressure.

3.2 Size effects

According to the above-mentioned calibration process, it can be found from Eq. (6) that the variation of particle average radius R will directly result in change of contact stiffness and further affect the local stress calculation. It has been reported that the size effects can have influence on the macro-mechanical strength of geomaterials in modeling. For example, Mehranpour and Kulatilake [23] have conducted a large number of uniaxial compression tests to study this effect. But for a large range of confining pressure, this effect is still needed to be verified and clarified. A series of triaxial compression tests are carried out in this paper to investigate the size effects by considering (a) constant average particle radius R to investigate the effect of particle numbers or sample size; (b) constant ratio of average particle size sample dimension to investigate the effect of particle size.

The effect of sample size is investigated by setting constant average particle radius R. Two confining pressures such as 5 and 50 MPa are considered. In the simulation, the samples are generated with ten size grades as shown in Fig. 2. The average particle radius R is 8 mm, and the diameters of sample vary from 150 to 550 mm. The micromechanical parameters for the new bond model are taken as Ec= 45 GPa, kr = 1.0, kn = 1.5 × 109 N/m, ks = 1.5 × 109 N/m, φnt= 3.5 × 104 N, φs= 7 × 104 N, φncr= 1.5 × 105 N, tanϕ1 = 0.3, tanϕ2 = 1.6, which are calibrated according to the aforementioned procedure. It is shown in Fig. 3 that both the strength and Young’s modulus of the sample seem to increase as the sample dimension increases. However, the increasing trend is negligible when the sample diameter is over 40 times of particle average radius as shown in Fig. 4a, b.

Fig. 2
figure 2

Particles size distribution used in DEM simulations

Full size image
Fig. 3
figure 3

Stress–strain curves for samples with the particle average radius of 8.0 mm and sample dimensions of 150, 250, 350, 450, and 550

Full size image
Fig. 4
figure 4

Effect of ratio of sample diameter to particle average radius on a Young’s modulus and b peak strength of sample under different confining pressures

Full size image

Thus, we further do numerical experiments at the constant ratio 1/50 between the particle radiii to the sample diameters to show the effects of particle size. These micromechanical parameters are calibrated by optimizing values according to the relationships in Eqs. (6) and (7). As shown in Fig. 5, average particle radius versus sample dimension is, respectively, as 1/50, 2/100, 4/200, 8/400 and 16/800. One can note that the Young’s moduli are similar for different samples under both confining pressures, whereas peak strength increases a little as increasing sample size. It further indicates in Fig. 6 that the size variations have a very slight effect on Young’s modulus as well as strength for samples with the same ratio of diameter to average particle radius, which indicates that size effects can be reduced when sample diameter is 50 times larger than particle radius.

Fig. 5
figure 5

Stress–strain curves for samples with the particle average radius/sample diameter of 1/50, 2/100, 4/200, 8/400, and 16/800 mm

Full size image
Fig. 6
figure 6

Effect of both changing sample dimension and particle average radius on a Young’s modulus and b peak strength of modeled sample under different confining pressures

Full size image

Therefore, size effects exist in the PFC modeling and the particle size is not an independent parameter that affects modeling results. The sample size effects can be reduced or even negligible when the ratio between sample diameter and particle radius is at a given value.

3.3 Comparison between different bond models

In order to investigate and validate the proposed new bond model, a series of triaxial compression tests using different bond models are conducted under confining pressure of 5, 20, 50 and 60 MPa. The friction coefficient is set to 0.3 and no critical normal stress is included in the PFC incorporated contact bond models. The other micromechanical parameters are taken the same as those in the proposed new bond model.

The results shown in Fig. 7 indicate that the peak stress under low confining pressure with the proposed new bond model is lower than that with the contact bond model (CBM). However, when confining pressure increases up to 60 MPa, this trend becomes different. As shown in Fig. 8, the envelope of peak strength obtained by the proposed new bond model has an obvious nonlinear characteristic, which is different from that obtained using the contact bond model (CBM).

Fig. 7
figure 7

Different stress–strain curves obtained from results, respectively, simulated using new bond model and contact bond model in PFC3D

Full size image
Fig. 8
figure 8

Comparison between new bond model and contact bond model (CBM) in describing mechanical response of sample with the same micro-parameters

Full size image

4 Three-dimensional simulation of conventional triaxial compression test

In order to further validate the new bonded model in application of labriation, three-dimensional studies of conventional triaxial compression tests are also performed. Numerical results are compared with experimental data obtained on sandstone.

4.1 Experimental tests

The experimental tests of sandstone were performed in Laboratory of Mechanics of Lille, France. A series of conventional triaxial tests were conducted on cylindrical samples of 37 mm in diameter and 75 mm in height under the confining pressures of 5, 20, 40 and 60 MPa. It can be obtained from the results that the Young’s modulus of sample increases from 15 to 18 GPa with the confining pressure changing from 5 to 60 MPa, and the envelope of strength presents an obvious nonlinear characteristic as shown in Fig. 9.

Fig. 9
figure 9

Macroscopic peak and residual strength obtained in conventional triaxial compression tests and comparison with experimental data on sandstone

Full size image

4.2 Sample generation and boundary conditions

The real microstructure of cohesive granular materials such as sandstone is complex. It is generally not possible to completely reproduce all details of the microstructure. The real material sample is replaced by a numerical sample which is an assembly of spherical grains of different diameter. In the present study, the numerical sample is constituted about 20,000 particles with ten different size grades, as shows in Figs. 2 and 10. The largest radius of particle is 13.6 mm, and the smallest one is 3.5 mm. The numerical sample is a cylinder of 370 mm wide and 740 mm high. The total porosity is about 0.2. The ratio of sample diameter to particle average radius is about 50.

Fig. 10
figure 10

Sample used in DEM modeling of triaxial compression tests

Full size image

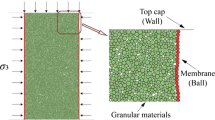
Differently with a continuum medium, the numerical specimen of granular material is composed of spherical grains. Therefore, it is not possible to directly apply a uniform stress or displacement on its boundary. In general, in order to prescribe a uniform displacement on boundary of specimen, a rigid wall is added on the top and bottom surfaces, while a soft membrane is used on the lateral surface to confine the specimen. In this way, the macroscopic axial and lateral stresses are calculated as the average reaction forces generated on the top and lateral surfaces. The axial and lateral displacements are applied in an iterative way so that the equilibrium conditions are verified with the applied confining pressure or lateral stress. Further, the axial displacement is applied symmetrically on the top and bottom walls.

4.3 Stress–strain responses and comparison with experiment

By adopting a numerical optimal procedure aforementioned, a set of model’s parameters is defined and given in Table 1. Using these parameters for the proposed bonded contact model, four conventional triaxial compression tests are calculated with different confining pressures such as 5, 20, 40 and 60 MPa. Comparisons between numerical results and experimental data are presented in Fig. 11. An overall good agreement is obtained. It is seen that with the increase in confining pressure, the peak differential stress significantly increases. This effect of confining pressure is correctly reproduced by the numerical model. Unfortunately, due to the technical limit of experimental device, the mechanical responses in the post-peak regime are not available in the laboratory tests. However, according to the numerical results obtained, one can see a clear transition from a brittle behavior under a low confining pressure to a ductile one when the confining pressure becomes higher. This kind of transition is a representative property of most rock-like materials. On the other hand, the volumetric strain exhibits a transition from compressibility and dilatancy with the increase in differential stress. The occurrence threshold of the transition also depends on confining pressure. Under a low confining pressure such as 5 MPa, the compressibility–dilatancy transition occurs clearly before the peak stress. When the confining pressure is high enough, the volumetric dilatancy occurs only when the peak stress is approached. Physically, the volumetric dilatancy in rock-like materials is generally the macroscopic consequence of deboned interfaces opening. The opening can be generated by both tensile failure and frictional sliding of contact interfaces in granular materials. When the confining pressure is low, a large number of broken contact interfaces in granular materials produce a normal opening contributing to the macroscopic dilatancy. Under a high confining pressure, most broken contact interfaces are closed and their normal opening is prevented by a high normal compressive stress. In this case, the dilatancy occurs only when there is the occurrence of localized shear strain bands around the peak stress. In the post-peak regime, the macroscopic response is mainly controlled by the deformation of localized strain bands. As most contact interfaces are broken inside the localization bands, an important volumetric dilatancy can be produced due to large relative displacements between grains.

Table 1 Geometrical, physical and mechanical parameters used in three-dimensional DEM simulations of experimental tests
Full size table
Fig. 11
figure 11

Axial (red), volume (green) and lateral (blue) strains (10−6) versus differential stress in conventional compression tests with different confining pressures: comparison between numerical results (continuous lines) experiment data

Full size image

4.4 Macroscopic strength analysis

In order to have a deep insight into the macroscopic strength of material, the macroscopic peak and residual differential stresses obtained from numerical simulations are shown in Fig. 9. The peak strength is further compared with experimental data, and a good agreement is obtained. From this figure, one can see that the peak strength envelope cannot be approached by a linear line, but it should be described a curved convex line. This nonlinear strength property is correctly reproduced by the proposed model. Further, it is interesting to observe that the distance between the peak and residual strengths decreases when the confining pressure increases. This is a direct consequence of the transition from brittle to ductile behavior with the increase in confining pressure.

5 Failure process in cohesive granular materials

The deformation and failure process of cohesive granular materials is inherently related to the breakage of bonded contact interfaces between grains. Using the proposed failure criterion, the macroscopic failure process of material is here investigated in terms of microscopic debonding.

5.1 Bond breakage analysis

At the initial state before applying differential stress, there are about 66,000 bonded inter-granular interfaces in the numerical specimen. With the increase in differential stress, bonds are progressively broken according to the proposed local failure criterion. For convenience, each broken bond is here seen as a crack. One can distinguish two families of cracks, tensile and shear cracks. The evolution of crack number can be calculated by the numerical model during the differential loading. In Fig. 12, one can see the evolution of tensile and shear cracks as a function of axial strain in four conventional triaxial compression tests with different confining pressures. The differential stress is also plotted on the same figure. In order to quantify the contact debonding process, the following bond breakage rate is defined:

$$V_{\text{n}} = \frac{{({\text{CN}}_{{\varepsilon +\Delta \varepsilon }} - {\text{CN}}_{\varepsilon } )}}{{{\text{CN}}_{ * \varepsilon } }}$$
(8)

CNɛ and CNɛ+Δɛ are, respectively, the broken contact numbers at the strain states ɛ and ɛ + Δɛ; CN*ɛ represents the total number of broken contacts in the specified strain interval *ɛ. The evolutions of debonding rate in four triaxial compression tests are presented in figure. One can see that for all confining pressures considered here, the debonding process starts before the peak strength is reached (see the points A1, B1, C1 and D1). However, only a very small number of cracks are developed in the pre-peak stage. The number of cracks increases very quickly when the peak strength is approached, and the highest debonding rate is obtained at the peak stress point (A2, B2, C2 and D2). The evolution of breakage rate in the post-peak regime is strongly influenced by confining pressure. The curve of breakage rate is clearly correlated to that of differential stress. Under low confining pressures (5 and 20 MPa), the breakage rate drops quickly after the peak stress (see the points A3 and B3) and evolves toward a stationary value when the residual strength is reached (see the points A4 and B4). Differently, under high confining pressures (40 and 60 MPa), the breakage rate decreases slowly but continuously in the post-peak regime. It is not easy to identify a clear residual phase (see the points C4 and D4). On the other hand, it is also very interesting to see that the cracking mode is also influenced by confining pressure. Under low confining pressures (5 and 20 MPa), the number of tensile cracks is clearly higher than that of shear cracks. This is the main reason of the macroscopic brittle failure obtained under a low confining pressure and of the important dilatancy obtained. When the confining pressure becomes high (40 and 60 MPa), the number of shear cracks becomes higher than that of tensile cracks. As a consequence, one obtains a ductile macroscopic failure behavior which is dominated by the frictional sliding along broken bonds (Fig. 13).

Fig. 12
figure 12

Evolution of bonds breakage number versus axial strain and differential stress in conventional triaxial compression tests with different confining pressures

Full size image
Fig. 13
figure 13

Evolution rate of bond breakage number versus axial strain and differential stress in conventional triaxial compression tests with different confining pressures

Full size image

Furthermore, in Fig. 14, one shows the distributions of displacement inside the three-dimensional specimen and in the normal section during a selected strain interval in the post-peak regime (A3–A4, B3–B4, C3–C4 and D3–D4) for four triaxial compression tests. It can be observed that the displacement distribution is also affected by confining pressure. Under low confining pressures, an inclined narrow band is obtained with an important displacement gradient on the boundary between this band and outside zones. This is in agreement with the brittle failure process of specimen. With the increase in confining pressure, the inclination angle with the axial load axis as well as the width of band increases. And finally one obtains a large and quasi-horizontal zone in the central part of specimen. This kind of displacement distribution corresponds to a ductile macroscopic failure behavior.

Fig. 14
figure 14

Illustration of displacement fields inside 3D whole specimen and in central section in conventional triaxial compression tests with different confining pressures

Full size image

5.2 Effect of loading path

The deformation and failure process is generally related to loading path. In the context of mechanics of geomaterials, two typical loading paths are particularly interesting to investigate because they could represent stress evolutions around an underground cavity. It is the lateral extension and the axial extension with a constant mean stress. In the first path, starting from a hydrostatic compression stress state, the lateral stress or confining pressure (here noted as σ2 = σ3) is reduced (Δσ2 = Δσ3 < 0), while the axial stress (noted as σ1) is increased (Δσ1 > 0) so that the mean stress is unchanged (2Δσ2 + Δσ1 = 0). In the case of axial extension, also starting from a hydrostatic compression stress state, the lateral stress or confining pressure (here noted as σ2 = σ3) is increased (Δσ2 = Δσ3 > 0), while the axial stress (noted as σ1) is decreased (Δσ1 < 0) so that the mean stress is unchanged (2Δσ2 + Δσ1 = 0). The values of Lode angle for these two loading paths are, respectively, equal to θ = π/6 and θ = − π/6. Therefore, the comparison between these two paths allows investigating the influence of Lode angle or the third stress invariant on deformation and failure process of materials. In the present study, as an example, the initial hydrostatic stress is taken as 60 MPa. The obtained stress–strain curves are presented in Fig. 15. It is shown that the peak differential stress (|σ1 − σ3|) for the lateral extension is significantly higher than that for the axial extension. The evolution of bonds breakage for the two loading paths is presented in Fig. 16. One can see that the breakage rate is quite different between the two paths. For the lateral extension, the highest rate is obtained around the peak differential stress, and the bond breakage rate decreases in the post-peak regime. However, for the axial extension, it seems that there is a quasi-stationary rate of debonding after the peak differential stress. Finally, in Fig. 17, the fields of displacement inside the specimen and in the normal section are presented. For the lateral extension, one observes an inclined localization band similarly to that in conventional triaxial compression. But for the axial extension, there is a quasi-horizontal localization band which covers all the width of specimen.

Fig. 15
figure 15

Stress–strain curves in lateral extension test (left) and axial extension test (right) with an initial hydrostatic stress of 60 MPa

Full size image
Fig. 16
figure 16

Evolutions of bond breakage number and rate in lateral extension test (left) and axial extension test (right) with an initial hydrostatic stress of 60 MPa

Full size image
Fig. 17
figure 17

Displacement fields in lateral extension test (two left figures) and axial extension test (two right figures) with an initial hydrostatic stress of 60 MPa

Full size image

5.3 Effect of intermediate principal stress

In cylinder samples considered above, two principal stresses are identical (σ2 = σ3). Based on this kind of experimental data, most failure criteria developed for geomaterials involve the major and minor principal stresses only. The role of the intermediate principal stress is generally neglected. However, in general loading conditions, three principal stresses are different and independent. Therefore, it is needed to investigate the effect of the intermediate principal stress on failure and deformation of cohesive granular materials. For this purpose, a cubic sample is considered and shown in Fig. 18. Two lateral walls are used to independently prescribe two different principal stresses. The same parameters as those given in Table 1 are used. We have performed a series of numerical tests on the cubic sample. The minor principal stress is kept to be constant and equal to 20 MPa. Different values of the intermediate principal stress ranging from 20 to 60 MPa are considered. For a selected set of two principal stresses, the axial strain is prescribed in order to generate the variation of axial stress which is the major principal stress. In Fig. 19, one compares first the numerical results obtained from both the cylinder and cubic samples when two lateral stresses are identical and equal to 20 MPa. In this particular case, the overall stresses are identical for two samples. One can see that the difference between two calculations is very small. Therefore, the effect of sample geometrical form seems to be negligible. In Fig. 20, the differential stress (σ1 − σ3) versus axial strain (ɛ1) curves are presented for five different values of the intermediate principal stress (σ2). One can see that the peak strength of granular material is significantly affected by the intermediate principal stress. The peak stress increases with the intermediate stress increase. In order to further explore the failure process in each case, the evolutions of tensile and shear cracks with axial strain are presented in Fig. 21 for each value of the intermediate stress. While the total number of cracks remains similar between five cases, the repartition between tensile and shear cracks is clearly different. With the increase in the intermediate principal stress, the shear cracking becomes the dominant process with respect to the tensile cracking. Regarding the rate of total bonds breakage shown in Fig. 22, it seems that the sharp change of breakage rate is attenuated with the increase in the intermediate principal stress. Finally, one shows the three-dimensional and two-dimensional displacement fields, respectively, inside the whole specimen and in the normal section in Fig. 23 for a strain interval in the post-peak regime. The kinetics of deformation is clearly affected by the intermediate principal stress. When the difference between two lateral stresses (σ2 − σ3) is high, the kinetics of deformation of cubic sample is progressively controlled by the sliding along an inclined direction with respect to the vertical axis (σ1). The sliding occurs on the boundary of a parallelepiped zone in the plane z − x. In contrary, for a law difference of σ2 − σ3, the deformation kinetics is rather dominated by lateral expansion of sample.

Fig. 18
figure 18

Cubic sample subjected to three independent principal stresses

Full size image
Fig. 19
figure 19

Evolutions of bonding breakage rate and accumulated number together with stress–strain curves in a triaxial compression test, respectively, on cubic sample (continuous lines) and cylinder sample (dotted lines)

Full size image
Fig. 20
figure 20

Influence of the intermediate stress on stress–strain curves of cubic specimen with 20 MPa of minor stress (strain in 10−6)

Full size image
Fig. 21
figure 21

Evolutions of accumulated bonds breakage number for different values of intermediate principal stress (σ3 = 20 MPa)

Full size image
Fig. 22
figure 22

Evolutions of differential stress and bond breakage rate for different values of intermediate principal stress (σ3 = 20 MPa)

Full size image
Fig. 23
figure 23

Distribution of displacement inside whole cubic samples and in normal sections for different values of intermediate principal stress (σ3 = 20 MPa)

Full size image

6 Conclusions

Mechanical strength and deformation of cohesive granular materials have been investigated in this paper. A new criterion for failure modeling of bonded contact interfaces between grains is proposed. Using this criterion, it is possible to describe strength and deformation of granular materials for a wide range of stresses. It is found that the overall strength of cohesive granular materials cannot be described by a linear surface but by a convex curved surface. Further, under the conventional compression condition, the tensile cracking is controlling the failure process under low confining pressure, while the shearing cracking becomes the dominating process when the confining pressure is high. There is a clear transition from a brittle to ductile behavior with the increase in confining pressure. This transition has been correctly predicted by the numerical model. The volumetric dilatancy of cohesive granular materials is directly related to opening of debonded contact interfaces. The strength and deformation of cohesive granular materials are influenced by loading path. For a given mean stress, the strength is lower in an extension loading than in a compressive one. Therefore, the influence of the third stress invariant or Lode angle should be taken into account. Finally, the influence of the intermediate principal stress on the strength and deformation has been studied. It is found that the compressive strength of cohesive granular materials significantly increases with the increase in the intermediate principal stress. Further, the shear cracking is the main failure process under high values of the intermediate stress. The kinetics of deformation and failure is also affected by the intermediate principal stress. The material failure is controlled by the lateral expansion for low values of the intermediate stress but by the sliding process for high ones. Interstitial fluid should play an important role in strength and deformation of cohesive granular materials, and this feature will be investigated in future studies.