1 Introduction

Stability analysis for fractured rock mass is challenging not only due to lack of information of the physical properties of rock materials, but also due to complicated geometry of rock discontinuities. Improvements of numerical methods such as finite element method (FEM) [1, 57, 67–69, 71], meshless method [5, 28, 30–37, 62–66, 70], discrete element method [4, 20], discontinuous deformation method (DDA) [6, 50], isogeometric analysis [13, 16, 24–26, 29], and smoothed particle hydrodynamics (SPH) [8, 21, 27], extended finite element method [6, 46] and peridynamics [7, 38, 39] have been made regarding the modeling of discontinues rock mass [12, 17, 61] and stability analysis of rock mass [59, 60]. When a large number of blocks are included, it is time-consuming to model and analyze slopes and tunnels with discontinuous rock mass using these methods. To deal with geometric aspects for failure analysis, the block theory serves as a direct and efficient method for blocky models.

At present, there are two classical methods in block theory, namely the stereographic projection method [18, 40] and the vector method [47, 49]. Based on the two methods, great improvements and application have been made in block theory and rock engineering. Young and Hoerger [51] introduced a probabilistic approach for key block analysis and applied this approach in tunnel analyses. Shi and Goodman [43] presented a practical and intuitive method for finding all unsafe areas on tunneling faces by unrolling cylindrical surface of the tunnel and joint traces onto a plane. Mauldon [22] developed a general model for the size distribution and probability of occurrence of simple 2D key blocks for arbitrary distributions of discontinuity size. Hatzor and Goodman [15] applied key block theory to saturated rock slopes of a dam using parametric addition of vectors of water pressures within the boundary joints based on enhanced stereographic projection. Wibowo [48] considered secondary blocks in key block analysis using a non-repeated and repeated rock joint system. Song et al. [44] developed a three-dimensional statistical joint modeling technique to analyze the stability of rock blocks around a tunnel. The joint diameter distribution was estimated by using the window sampling method. Bafghi and Verdel [2, 3] proposed the key-group method (KGM) grouping the rock blocks in an iterative and progressive analysis of the stability of discontinuous rock slopes. The Sarma method is implemented to generate a Sarma-based KGM. Zhang and Kulatilake [53] developed a stereo-analytical method, which is a combination of the stereographic method and analytical methods. It can be applied to both convex and concave blocks. Menendez-Diaz et al. [23] analyzed the mechanical behavior of non-pyramidal key blocks with four discontinuity planes. A modeler capable of predicting the existence of polyhedra with unlimited facets and morphologies is developed based on this study [9]. Tomas et al. [45] developed a graphical method based on the stereographic representation of the discontinuities to obtain the slope mass rating (SMR). Fu and Ma [11] proposed an extended key block method considering the force effect of key blocks in subsequent batches after the first batch exposed. Zhang and Lei [54, 56] presented an object-oriented computer model and a morphological visualization method for three-dimensional multi-block systems based on the object-oriented programming (OOP) technique. Three-dimensional block cutting analysis procedures based on optimization methods, the oriented rule and the closed rule were described by Fernandez-de Arriba [10] and Zhang [52]. Zheng et al. [58] gave a formulation using mean orientation values and mean friction angle values and developed a code to conduct probabilistic block theory analysis.

The classic KBM generates joint pyramids with all joint planes and divides a concave block using all the concave corners. An improved method using free domain (FD) and centroid sliding pyramid (CSP) is presented within the concept of two-dimensional block theory in this paper. An FD is a set of connected free surfaces of a block to simplify the geometric complexity. Based on the concept of FD, CSP calculated only from the joint planes adjoining the free planes is used to describe the possible motion region of the block centroid. The cone angle θ of CSP is the vectorial angle formed by the two candidate sliding surfaces of this CSP. Removability analysis of a block is transformed into calculating the cone angle of CSP. On the other hand, only concave corners formed by two joint planes are used for partitioning a concave block. Concave corners with free planes are excluded in the cutting process. This CSP method, fully utilizing the geometrical and topological properties of rock block, is conducted by a 2D computer program developed by the authors and validated by examples of rock slopes and tunnels.

2 Free domain

Non-convex blocks are commonly seen in practical engineering and regarded as a combination of convex blocks by extending all the cutting faces to infinite planes in KBM [41]. A non-convex block may contain one or more concave corners, and each corner has two edges in two dimensions or several faces in three dimensions. A concave block can be divided into a set of convex blocks with the infinite planes expanded by the edges or faces forming concave corners. It has been found that if all of its convex sub-blocks are removable for a finite non-convex block, the non-convex block is removable. If one unmovable convex sub-block exists, the non-convex block is also unmovable [19]. Therefore, the removability of a non-convex block can be obtained by analyzing the removability of each sub-block.

As shown in Fig. 1a, the four blocks with the same joint faces are all unmovable and the first three have concave corners formed by free surfaces. The positions and angles of these concave corners affect the shapes and removabilities of the sub-blocks in the original KBM. After the cutting process, each set of sub-blocks in Fig. 1b-1, b-2 contains an unmovable sub-block, while all the sub-blocks in Fig. 1b-3 are removable. This means the cutting method using all the concave corner planes cannot be feasible in all cases. To solve this problem, the concept of free domain is introduced to simplify the geometric and topological complexity of a block.

Fig. 1
figure 1

Decomposition of three non-convex blocks with concave corners: a four unmovable blocks, b sub-blocks of three unmovable blocks

Full size image

A free domain (FD) is defined as a set of connected free surfaces in one block. It includes one or more finite free surfaces forming a set of line segments in two dimensions. A free domain can be replaced by a single line segment named as virtual free domain (VFD) connecting the starting point and end point of this domain without changing the removability of a block. For example, each set of red solid lines is an FD for the block in Fig. 1a, respectively. The first three blocks in Fig. 1a-1, a-2, a-3 are transferred to the fourth block in Fig. 1a-4 using VFD. Thus, the removability of the three concave blocks can be computed by the simplified geometric model of Fig. 1a-4. As shown in Fig. 2, when a block has more than one free domain, all the free domains can be replaced by the corresponding line segments (VFDs). Therefore, by using free domains, the geometric and topological complexity is reduced without changing the removability of the blocky system.

Fig. 2
figure 2

Blocks with more than one free domain: a original block with two FDs, a-1 simplified block with two FDs, b original block with three FDs, b-1 simplified block with three FDs

Full size image

As shown in Fig. 3a, a complex block with two concave corners is decomposed into at least 15 convex sub-blocks according to the classic KBM. These sub-blocks are obtained by cutting the original block with four expanded concave corner planes. In CSP method, the concave corner planes in free domains are excluded in the cutting process as shown in Fig. 3b. In this case, only five sub-blocks in Fig. 3c are obtained by cutting the concave corner formed by two joint planes. Two of the sub-blocks have concave corners in their free domains, which have no effect on the removabilities of the sub-blocks and the original block. All the five sub-blocks are removable and simplified to two-dimensional pyramids, so the original concave block is also removable.

Fig. 3
figure 3

Decomposition of a non-convex block with two concave corners: a division in original KBM, b division in the CSP method, c simplified sub-blocks obtained in the CSP method

Full size image

Thus, the removability of the original block can be obtained by analyzing the combination cutting by concave corner planes expanded only from joint faces. Cutting planes are limited to edges of concave corners defined by two joint faces. For a multiply connected block in two dimensions, the cavities inside the block do not affect the removability under the assumption of rigidity.

3 Centroid sliding pyramid

3.1 Removability analysis based on CSP

An FD connects two joint faces at the start and end points, respectively. These two joint planes are defined as the candidate sliding edges (SE) in two dimensions and the candidate sliding surfaces in three dimensions. A concave corner in 2D is formed by two edges. A concave corner in 3D is formed by two faces or divided into more than one simple concave corner formed by two faces. For a rock block without any free surface, it has no FD according to the definition. Thus, this block is unmovable and excluded from stability analysis in the next stage. For a block with free domains, each domain and its corresponding candidate sliding edges can be found by sorting analysis with the right-hand screw rule.

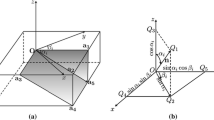
Centroid sliding pyramid (CSP) is an infinite taper area which is the possible motion region of the centroid of a block in limit equilibrium state. In other words, this infinite taper area is the set of all possible initial motion trajectory of the centroid. The infinite taper area is inside the cone angle θ formed by two sliding edges vectors as shown in Fig. 4.

Fig. 4
figure 4

Steps for generating the sliding pyramid of a free domain: a original block, b free domain identification, c candidate sliding edge vectors, d CSP generation

Full size image

The removability of a block without concave corners between joint faces is calculated using the following steps as shown in Fig. 4b, c:

  1. 1.

    Find all the free domains of this block, and record the start and end points of each sliding surface.

  2. 2.

    Calculate the two sliding edge vectors of each FD and generate the corresponding CSP.

  3. 3.

    Calculate the cone angle θ (anticlockwise vector angle) of each sliding pyramid according to the right-hand screw rule.

  4. 4.

    If at least one cone angle θ i of this block satisfies \( 0 \le \theta_{i} \le \pi \), then this block is removable; otherwise, it is unmovable.

The centroid of original block is calculated using the simplex integration [42]. However, it is unnecessary to find the centroid of block for generating CSP because CSP is essentially a relative taper area determined by relative angle of two candidate sliding vectors. The cone apex O of CSP can be arbitrary point.

According to the right-hand rule, the starting point of free domain is the terminal point of the first sliding surface vector and the end point of free domain is terminal point of the second sliding surface vector. Thus, sequence of the two vectors can be ascertained. As shown in Fig. 4d, the cone angle θ of the sliding pyramid generated by the two sliding edge vectors is calculated as follows:

The coordinates of two vectors \({\mathop{\rightharpoonup}\limits_{{A_{6} A_{1} }}}\), \({\mathop{\rightharpoonup}\limits_{{A_{5} A_{4} }}}\) are \( (x_{1} - x_{6} , \quad y_{1} - y_{6} ) \) and \( (x_{4} - x_{5} , \quad y_{4} - y_{5} ) \), respectively. The range of cone angle θ is defined between −π and π (in radians).

$$ \sin \theta^{\prime} = \frac{{(x_{1} - x_{6} )(y_{4} - y_{5} ) - (x_{4} - x_{5} )(y_{1} - y_{6} )}}{{\sqrt {(x_{1} - x_{6} )^{2} + (y_{1} - y_{6} )^{2} } \sqrt {(x_{4} - x_{5} )^{2} + (y_{4} - y_{5} )^{2} } }} $$
(1)
$$ \cos \theta^{\prime} = \frac{{(x_{1} - x_{6} )(y_{4} - y_{5} ) + (x_{4} - x_{5} )(y_{1} - y_{6} )}}{{\sqrt {(x_{1} - x_{6} )^{2} + (y_{1} - y_{6} )^{2} } \sqrt {(x_{4} - x_{5} )^{2} + (y_{4} - y_{5} )^{2} } }} $$
(2)
$$ \sin \theta^{{\prime }} \ge 0\quad 0 \le \theta \le \pi \quad \theta = { \arccos }\left( { \cos \theta^{{\prime }} } \right) $$
(3)
$$ \sin \theta^{{\prime }} < 0 \quad - \pi < \theta < 0\quad \theta = - { \arccos }\left( { \cos \theta^{{\prime }} } \right) $$
(4)

The cone angle θ i in Fig. 4d is between 0 and π. So the sliding pyramid is a positive region for motion of the centroid O and all the possible motion trail of O is inside this CSP. Therefore, the block is removable and the motion trend vector in the state of limit equilibrium is inside the CSP.

As shown in Fig. 5a, the value of cone angle θ from \({\mathop{\rightharpoonup}\limits_{{{\text{A}}_{4} {\text{A}}_{1} }}}\) to \({\mathop{\rightharpoonup}\limits_{{{\text{A}}_{1} {\text{A}}_{4} }}}\) is π. This block has no concave corner between joint faces, and thus, the CSP is a two-dimensional half space. The value of cone angle θ in Fig. 5b is 0 because vector \({\mathop{\rightharpoonup}\limits_{{{\text{B}}_{1} {\text{B}}_{2} }}}\) and \({\mathop{\rightharpoonup}\limits_{{{\text{B}}_{6} {\text{B}}_{5} }}}\) have the same starting point O and direction. The possible trajectory of block centroid is a ray having the same direction with the two vectors out from this centroid. In Fig. 5c, the value of cone angle θ is between −π and 0 according to Eqs. (1–4). In this case, \( \theta^{'} \) is a concave angle from \({\mathop{\rightharpoonup}\limits_{{{\text{C}}_{1} {\text{C}}_{2} }}}\) to \({\mathop{\rightharpoonup}\limits_{{{\text{C}}_{5} {\text{C}}_{4} }}}\) in counterclockwise direction. As the cone angle θ of the CSP is defined between −π and π (in radians), the value of θ is \( {-}\pi /6 \) (\( \theta = \theta^{'} - 2\pi \)). The sliding pyramid in Fig. 5c is a negative region for the motion of centroid O. That means there is no possible trajectory for the centroid O to move with these boundary conditions and the block is unmovable. The relations between cone angle θ and the removability of the free domain are given in Table 1.

Fig. 5
figure 5

Sliding pyramids of three types of blocks: a cone angle θ = π; b cone angle θ = 0, c cone angle −π < θ < 0

Full size image
Table 1 Relations between cone angle θ and removability of the free domain
Full size table

For the blocks in Figs. 4 and 5, each of them only has one free domain. The removability of a block with one free domain can be obtained from the cone angle of the corresponding CSP directly. However, a block without concave corners formed by joint planes may contain more than one free domain. These free domains can be simplified according to the virtual free domain (VFD) theory and transferred to a set of CSPs. If one of these free domains corresponds with a positive sliding pyramid, this block is removable. On the contrary, if all of these free domains are corresponded to negative sliding pyramid, the block is unmovable.

For a block with concave corners between joint faces, these joint planes are used to divide to a set of sub-blocks. Each sub-block k i may have j (j ≥ 0) free domains FD i1, FD i2, …, FD ij . Every free domain has a corresponding cone angle \( \theta_{ij} \). The cone angle \( \theta_{i} \) of each sub-block i is the union of all positive cone angles corresponding to the free domains belonging to this sub-block k i . However, the cone angle \( \theta_{k} \) of the original block k is the intersection of all cone angles of the sub-blocks as described in Eqs. (5, 6).

$$ \theta_{i} = {\text{union}}\left\{ { \theta_{i1} , \theta_{i2} , \ldots ,\theta_{ij} } \right\} $$
(5)
$$ \theta_{k} = {\text{intersection}}\left\{ {\theta_{1} , \theta_{2} , \ldots ,\theta_{i} } \right\} $$
(6)

3.2 Stability analysis based on CSP

After removability analysis, only removable blocks are candidates for unstable blocks. Goodman and Shi [14] introduced the computational theory for motion pattern and stability of rock blocks. The edges of CSP are possible sliding traces of centroid O in the CSP method. The sliding edge vectors and gravity projection vectors are used to compute the motion patterns and stability of blocks.

By definition of sliding pyramid, the motion patterns can be distinguished as follows (only gravity, friction force and tangential cohesive force are considered):

  1. 1.

    Lifting: The gravity vector starting at centroid O is inside the sliding pyramid region.

  2. 2.

    Sliding:

    1. (1)

      The gravity vector starting at centroid O is outside the sliding pyramid region.

    2. (2)

      The sliding edge vector and the gravity projection on the sliding edge are in the same direction.

  3. 3.

    Resting:

    1. (1)

      The gravity vector starting at centroid O is outside the sliding pyramid region.

    2. (2)

      The sliding edge vector and the gravity projection on the sliding edge are in opposite direction.

The relation of gravity vector and sliding pyramid is calculated using gravity projection on normal of sliding edge. As shown in Fig. 6, if both of the sliding edges of CSP satisfy Inequality (7), the motion pattern of this sliding pyramid is lifting. If one of the sliding edges satisfies Inequality (8) or (9), the motion pattern of this sliding pyramid is sliding and the potential sliding direction is along the sliding edge. For the cone angle θ of a sliding pyramid is between 0 and π, it is impossible for a sliding pyramid to have two edges satisfy Inequalities (8) and (9), simultaneously. Otherwise, if both of the sliding edges satisfy Inequality (10), the motion pattern of this sliding pyramid is resting and the block is stable under the gravity.

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}_{1} \ge 0\;\& \& \;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}_{2} \ge 0 $$
(7)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}_{1} < 0\;\& \& \;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} \cdot {\mathop{{SE}_{1}}\limits^{\rightharpoonup}} \ge 0 $$
(8)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {v}_{2} < 0\;\& \& \;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} \cdot {\mathop{{SE}_{2}}\limits^{\rightharpoonup}} \ge 0 $$
(9)
$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} \cdot {\mathop{{SE}_{1}}\limits^{\rightharpoonup}} < 0\;\& \& \;\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} \cdot {\mathop{{SE}_{2}}\limits^{\rightharpoonup}} < 0 $$
(10)
Fig. 6
figure 6

Motion pattern analysis using sliding pyramids: a lifting; b sliding; c resting

Full size image

Thus, the sliding force can be calculated as follows:

$$ F = g \cdot \sin \alpha - g \cdot \cos \alpha \cdot { \tan }\varphi - f_{\text{c}} $$
(11)

In original block theory [41], a block is considered as a rigid body and the contact forces between blocks are ignored. Based on the assumption of block theory, the simplified slip-resistance safety coefficient K for a movable block with one sliding surface is defined as

$$ K = \frac{{g \cdot \cos \alpha \cdot { \tan }\varphi + f_{\text{c}} }}{{g \cdot \sin \alpha }} $$
(12)

where α, φ and f c are dip angle, friction angle and tangential cohesive force of potential sliding surface, respectively. K describes the relative relation between sliding force and slip-resistance force. A block would slide if K is below 1.0 under ideal conditions. In practice, larger value of K means less risk for sliding failure.

Zheng and Tham [56] developed a method using the approximation to the total normal pressure along the slip surface to compute the factor of safety for slip surfaces of all shapes. For a group of blocks with more than one sliding surface, the rigorous limit equilibrium method [56] is adopted to calculate the slip-resistance safety coefficient of the whole slide body.

4 Validation examples

Complex rock blocks are common in practice projects. Figure 7(a) shows a complex block with eight vertices, four joint faces and four free surfaces. According to the definition of free domain, the four free surfaces are divided into two free domains. Thus, the original block can be simplified to the block shown in Fig. 7b. The simplified block only contains one concave corner \( \angle {\text{A}}_{2} A_{3} A_{4} \). Then, the concave corner edges \( A_{2} A_{3} \) and \( A_{3} A_{4} \) are expanded to the line segments \( A_{2} A_{6}^{{\prime }} \) and \( A_{4} A_{8}^{{\prime }} \), respectively. Therefore, five sub-blocks and their sliding pyramids as shown in Fig. 8 are obtained after the cutting process. The sub-blocks in Figs. 8a, b have two free domains, respectively, so each of them contains two sliding pyramids. But only one sliding pyramid is positive for each sub-block.

Fig. 7
figure 7

Free domains and combinations of a complex rock block: a original block, b block simplified by free domains, c block cutting by expanded concave corner planes

Full size image
Fig. 8
figure 8

Sub-blocks divided by expanded concave corner planes and their sliding pyramids

Full size image

The intersection of the five positive sliding pyramids of the sub-blocks is shown in Fig. 9. The two candidate sliding edges of the original block are \({\mathop{{A}_{6}{A}_{7}}\limits^{\rightharpoonup}}\) and \({\mathop{{A}_{4}{A}_{3}}\limits^{\rightharpoonup}}\). For stability analysis, \({\mathop{{A}_{4}{A}_{3}}\limits^{\rightharpoonup}}\) satisfies Eq. (8), while \({\mathop{{A}_{6}{A}_{7}}\limits^{\rightharpoonup}}\) does not. Thus, the motion pattern is sliding and sliding direction is along \({\mathop{{A}_{4}{A}_{3}}\limits^{\rightharpoonup}}\).

Fig. 9
figure 9

Sliding pyramid of the original block

Full size image

The CSP method is conducted in a computational program (CSP 2D) developed by the authors. The two-dimensional CSP code was used in stability analysis of tunnels and slopes with blocky hard rock.

Figure 10a shows an example using classic KBM. There are seven blocks in a blocky system, and the three blocks near surface are key blocks. In CSP method, the same result is computed after two iterations. In the first iteration shown in Fig. 10b, slip-resisting coefficients of the two unstable blocks are both 0.74 without friction force and tangential cohesive force. In the second iteration, the key blocks calculated in previous step are removed as shown in Fig. 10c.

Fig. 10
figure 10

Comparison with classic KBM. a A case presented by Goodman and Shi [14], b analysis result of the first iteration, c analysis result of the second iteration, d key blocks computed by CSP method

Full size image

Figure 11 shows a highway tunnel with two sets of joints in its surrounding rock. To test the code and simulate actual conditions, a set of fracture surfaces in Figs. 11 and 12 are not parallel strictly. The included angle between two fracture surfaces which are parallel approximately is 0 degree to 3.2°. The accuracy of computation is set to 0.001°. There are 58 joints and 380 blocks in this model as shown in Fig. 11a. The friction angle φ and assumptive slip-resisting safety coefficient K 0 are 25° and 1.5°, respectively. A block with value of K that is less than K 0 is considered to be unstable. A total of 105 blocks in Fig. 11b are infinite and marked in purple. After initial analysis with CSP, two key blocks are found as shown in Fig. 11c. Motion patterns of the red block on the top of tunnel and the orange block on the right side are lifting and sliding, respectively. After iterative computations using the CSP method, the possible unstable region is shown in Fig. 11d.

Fig. 11
figure 11

Stability analysis for a tunnel section with two sets of joints. a model of the tunnel and surrounding rock, b initial analysis result with CSP, c key blocks of this tunnel section, d possible unstable region

Full size image
Fig. 12
figure 12

Stability analysis for a tunnel section with three sets of joints. a Model of the tunnel and surrounding rock, b initial analysis result with CSP, c key blocks of this tunnel section, d possible unstable region

Full size image

Figure 12 shows another highway tunnel with three sets of joints in the surrounding rock mass. There are 81 joints and 1058 blocks in this model as shown in Fig. 12a. The friction angle φ and assumptive slip-resisting safety coefficient K 0 are 25° and 1.5°, respectively. A total of 132 blocks in Fig. 12b are infinite and marked in purple. After initial analysis with CSP, four key blocks as shown in Fig. 12c are found. Motion patterns of the red block on top of the tunnel and the orange blocks are lifting and sliding, respectively. After iterative computations, the possible unstable region is shown in Fig. 12d.

A rock slope is shown in Fig. 13a-1. There are 16 joints and 144 blocks in this model as shown in Fig. 13a-2. Figure 13b–i shows the analysis results in the cases with different friction angles and assumptive slip-resisting safety coefficients. Twenty-nine blocks in the model are infinite and marked in purple. Motion patterns of all key blocks are sliding. The slip-resisting coefficients K i of the orange blocks are below 1.0, and slip-resisting coefficients K i of the yellow blocks are between 1.0 and K 0. The key blocks and possible unstable region are affected by φ and K.

Fig. 13
figure 13figure 13figure 13

Stability analysis for a slope with different friction angles and slip-resisting safety coefficients. a-1 Model of a slope, a-2 model of rock blocks, b key blocks and possible unstable region (\( \varphi = 10^{\circ} \;\;K_{0} = 1.5 \)), c key blocks and possible unstable region (\( \varphi = 10^{\circ} \;\;K_{0} = 2.0 \)), d key blocks and possible unstable region (\( \varphi = 20^{\circ} \;\;K_{0} = 1.5 \)), e key blocks and possible unstable region (\( \varphi = 20^{\circ} \;\;K_{0} = 2.0 \)), f key blocks and possible unstable region (\( \varphi = 30^{\circ} \;\;K_{0} = 1.5 \)), g key blocks and possible unstable region (\( \varphi = 30^{\circ} \;\;K_{0} = 2.0 \)), h key blocks and possible unstable region (\( \varphi = 40^{\circ} \;\;K_{0} = 1.5 \)), i key blocks and possible unstable region (\( \varphi = 40^{\circ} \;\;K_{0} = 2.0 \))

Full size image

The two-dimensional CSP program was also used for stability analysis of a 7-km highway tunnel with complex geology in mountainous area of central China. Two sections of the most dangerous part in this tunnel are chosen as analysis targets.

The first section (ZK21 + 687.2) shown in Fig. 14a contains three sets of obvious joints as shown in Fig. 14b. These joints are extended in surrounding rocks for analysis of the most disadvantage distribution. There are 126 blocks in this model as shown in Fig. 14c. The friction angle φ is 20°. Figure 14d–f presents the analysis results with different assumptive slip-resisting safety coefficients K 0 (1.0, 2.0, 3.0), respectively. These results show that the key blocks are mainly distributed on the top and right (north) side of the tunnel section.

Fig. 14
figure 14

Stability analysis for the section (ZK21 + 687.2) of a highway tunnel with different safety coefficients. a Photographs of section (ZK21 + 687.2) and joint lines on the surface, b joints and tunnel profile of section (ZK21 + 687.2), c numerical model of this section, d analysis result (\( K_{0} = 1.0 \)), e analysis result (\( K_{0} = 2.0 \)), f analysis result (\( K_{0} = 3.0 \))

Full size image

The second cross section (ZK21 + 694.5) shown in Fig. 15a also contains three main sets of joints as shown in Fig. 15b. These joints are extended in surrounding rocks to analyze the most disadvantage distribution. There are 104 blocks in this model as shown in Fig. 15c. The friction angle φ is 20°. Figure 15d–f presents the analysis results with different assumptive slip-resisting safety coefficients K 0 (1.0, 2.0, 3.0), respectively. These results also show that the key blocks are mainly distributed on the top and right side of the tunnel section. Thus, for these two sections, the top and right sides are the regions with higher probability of failure.

Fig. 15
figure 15

Stability analysis for the section (ZK21 + 694.5) of a highway tunnel with different safety coefficients. a Photographs of section (ZK21 + 694.5) and joint lines on the surface, b joints and tunnel profile of section (ZK21 + 694.5), c numerical model of this section, d analysis result (\( K_{0} = 1.0 \)), e analysis result (\( K_{0} = 2.0 \)), f analysis result (\( K_{0} = 3.0 \))

Full size image

There are three measure points for stress acquisition located on the top, left and right sides of each section, respectively. The stresses on the primary lining of each section are shown in Fig. 16, respectively. For the effort of tunnel lining and cohesion of the joints, no visual failure occurred during construction near these sections. Data of field monitoring show that the stresses on the top and right parts of lining are larger than that on the left part for each section, which is in good agreement with results of CSP analysis.

Fig. 16
figure 16

Stress changing with time on the primary lining. a Stress changing with time on the primary lining of the section (ZK21 + 687.2), b stress changing with time on the primary lining of the section (ZK21 + 694.5)

Full size image

5 Conclusions

The classic KBM generates joint pyramids (JP) with all joint planes and partitions a concave block using all the concave corners. The CSP method in this paper presents two advantages over the original key KBM. Firstly, all the concave corners are considered as starting points of cutting process when a concave block is divided into a set of convex blocks in the original key KBM. But only concave corners formed by two joint planes are used for partitioning a concave block in the CSP method and concave corners with free planes are excluded in the cutting process. Secondly, JP for removability computation in the original KBM is generated using all of the joint planes, while CSP is calculated only from the joint planes adjoining the free planes. Furthermore, removability analysis of a block is transformed into calculating the cone angle of CSP. When the cone angle θ is between 0 and π, the sliding pyramid is a positive region for motion of the centroid O and all the possible motion trail of O is inside this CSP. But when the cone angle θ is between −π and 0, the sliding pyramid is a negative region for motion of the centroid O and no possible motion trail of O is inside this CSP. The gravity, friction force and tangential cohesive force are considered in stability analysis using vector projection. The slip-resistance safety coefficient K is used to evaluate the possibility of sliding failure.

The geometrical relationship is simplified, and data size for removability computation is reduced compared with the original KBM. The CSP method is implemented in a 2D computer program developed by the authors. Examples of rock slopes and tunnels have been analyzed with this code, which validate the validity of the CSP method.