1 Introduction

Bonded granular materials (e.g., cemented sands) are common in geotechnical engineering. The study of the mechanical behavior of bonded granular geomaterials is of great importance for the assessment of the safety of many types of infrastructure. Continuum mechanics, especially elasto-plastic models are traditionally adopted to model the behavior of these materials [14, 23, 30, 35, 38–40, 47, 56, 59]. However, these models were developed based on macroscopic response observed in the laboratory, and the microstructure of the materials is usually overlooked [19, 20]. Furthermore, mesh dependence has to be dealt for mesh- or grid-based solutions before successfully modeling the complex behavior of bonded granular geomaterials such as strain localization [32, 33].

Discontinuum approaches, on the other hand, have been recognized as powerful tools for investigating the mechanical behavior of bonded geomaterials. The most popular methods are the discrete (or distinct) element method (DEM) pioneered by Cundall and Strack [7]. In this approach, explicit time integration is used and sufficiently small time steps are necessary. Using the overlap of particles to calculate the contact forces is the fundamental principle of the DEM. In contrast, in the basic contact dynamics (CD) method [17, 43, 44], particles are treated as perfectly rigid. The effects of particles collisions (e.g., the non-penetration constraint and the Coulomb’s friction constraint) are adopted to calculate the contact forces [53]. The implicit time integration is adopted allowing for large time steps [2, 34, 45, 46].

However, there is relatively scarce application to the contact dynamics method because it is much more complex to implement than the classical DEM [8]. To simplify the formulation and implementation of contact dynamics, a variational formulation for contact dynamics, so-called granular contact dynamics, has recently been developed [27]. This formulation is appealing because it can be easily implemented using off-the-shelf mathematical programming solvers. Moreover, static equilibrium can be directly formulated without introducing any artificial damping or adjusting time step. However, only frictional granular materials can be formulated using mathematical programming methods until now.

To take into account the mechanical behavior of cementation in the framework of the contact dynamics method, contact models which allow for attractive contact forces have been developed in [18, 22]. Some studies using contact dynamics have been devoted to the strength and rheological properties of cemented granular materials [9–11, 50]. However, the elastic behavior of the cementation that plays an essential role in failure and the mechanical response of bonded granular geomaterials is ignored in these studies. The aim of the present investigation is to develop a bond model with elasticity in the framework of the granular contact dynamics method. To model the deformable behavior of geomaterials, the non-penetration condition is extended to allow for a penetration which is proportional to the repulse force. The proposed bond model can resist tensile force (it is taken as negative value), shear force and torque up to certain thresholds. Accordingly, three failure modes are defined for tensile strength, shear strength and torque transmission limit, respectively. After the bonds fail, the formulation degenerates to the conventional framework for uncemented granular material. This formulation for the elastic model is general because it can be degenerated to the rigid bond model or reduced to model pure static loading without introducing any artificial damping. In the present study, only two-dimensional problems are considered. The extension to three-dimensional problems is straightforward.

The paper is organized as follows. Firstly, the granular contact dynamics formulation for unbonded particles is presented in Sect. 2. In Sect. 3, the formulation for the elastic bond model is detailed and the algorithms for creating and rupturing bonds are outlined. For clarity, the formulation for the elastic bond model without shear forces is presented first and the corresponding optimality conditions are outlined in “Appendix”. In Sect. 4, uniaxial and biaxial compression tests are performed before conclusions are given in Sect. 5.

2 Granular contact dynamics for rigid unbonded materials

We first consider the case of rigid unbonded particles. The particles have both translational and rotational degree of freedoms. For the purpose of a complete presentation, the basic variational contact dynamics formulation of granular materials (i.e., unbonded materials) is reviewed in this section.

2.1 Equations of motion

The equations of motion for a single rigid particle are given by

$$\begin{aligned} m\dot{\varvec{v}} & = \varvec{f}_{\text{ext}} \\ J\dot{w} & = m_{\text{ext}} \\ \end{aligned}$$
(1)

where m is the mass, \(\varvec{v}{ = [}v_{x} ,v_{y} ]^{\text{T}}\) are the linear velocities, \(\varvec{f}_{\text{ext}} = [f_{\text{ext}}^{x} ,f_{\text{ext}}^{y} ]^{\text{T}}\) are the external forces, J is the mass moment of inertia, \(w\) is the angular velocity, and \(m_{\text{ext}}\) is the external moment, respectively.

Following [27], the equations of translational motion are discretized in time by the θ-method:

$$\begin{array}{*{20}l} {\bar{m}\Delta {\varvec{x}} = \bar{\varvec{f}}_{0},} &\quad {{\varvec{v}} = \frac{1}{\theta }\left[ {\frac{{\Delta \varvec{x}}}{\Delta t} - (1 - \theta )\varvec{v}_{0} } \right]} \hfill \\ {\bar{m} = \frac{m}{{\theta \Delta t^{2} }},} \hfill & {\bar{\varvec{f}}_{0} = \varvec{f}_{\text{ext}} + \bar{m}\varvec{v}_{0} \Delta t} \hfill \\ \end{array}$$
(2)

where 0 ≤ θ ≤ 1, Δt is the time step, \(\Delta \varvec{x} = \varvec{x} - \varvec{x}_{0}\), \(\varvec{x}\) and \(\varvec{x}_{0}\) are the positions of next and current steps and \(\varvec{v}_{0}\) is the velocity of current step.

In the same way, the angular momentum equilibrium equations are discretized as:

$$\overline{J} \Delta \alpha = \bar{m}_{0} ,\quad w = \frac{1}{\theta }\left[ {\frac{\Delta \alpha }{\Delta t} - (1 - \theta )w_{0} } \right]$$
(3)

where \(\Delta \alpha = \alpha - \alpha_{0}\) are the incremental rotation angles, and the subscript 0 again denotes known variables and

$$\bar{J} = \frac{J}{{\theta \Delta t^{2} }},\quad \overline{m}_{0} = m_{\text{ext}} + \overline{J} w_{0} \Delta t$$
(4)

The stability properties of the θ-method are well known [57]. When \(\theta = 1/2\) unconditionally stable and an energy preserving scheme is recovered, for \(\theta > 1/2\) the scheme is unconditionally stable and energy is dissipative, for \(\theta < 1/2\) its stability depends on the time step [27, 31].

2.2 Non-penetration condition

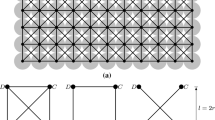
Considering two circular particles, i and j at contact I as shown in Fig. 1, the positions of the particles at time t 0 are given by \(\varvec{x}_{0}^{i}\) and \(\varvec{x}_{0}^{j}\). The non-penetration condition at time t 0 + Δt can be formulated as

Fig. 1
figure 1

Frictionless contact geometry between particles i and j at the potential contact I, where p is contact force of two particles along the initial normal

Full size image
$$\left\| {\varvec{x}^{i} - \varvec{x}^{j} } \right\| \ge (r^{i} + r^{j} )$$
(5)

As this inequality constraint is non-convex, the linear approximation is adopted as

$$\left( {\varvec{n}_{0}^{I} } \right)^{T} (\Delta \varvec{x}^{i} - \Delta \varvec{x}^{j} ) - g_{ 0} \le 0$$
(6)

where the superscript I refers to the potential contact and

$$\varvec{n}_{0}^{I} = \frac{{\varvec{x}_{0}^{j} - \varvec{x}_{0}^{i} }}{{\left\| {\varvec{x}_{0}^{j} - \varvec{x}_{0}^{i} } \right\|}}\quad {\text{and}}\quad g_{0} = \left\| {\varvec{x}_{0}^{i} - \varvec{x}_{0}^{j} } \right\| - (r^{i} + r^{j} )$$
(7)

are the initial normal vector and gap, respectively.

It is the complementary relation between the contact force p and the non-penetration equation, so-called Signorini unilateral contact condition [44], which can be stated as:

$$p\left[ {\left( {\varvec{n}_{0}^{I} } \right)^{T} (\Delta \varvec{x}^{i} - \Delta \varvec{x}^{j} ) - g_{ 0} } \right] = 0$$
(8)

2.3 Frictional contact

For frictional contact problem, the contact force between two particles i and j at contact I, as shown in Fig. 2, is resolved into tangential and normal directions i.e., \(\hat{\varvec{n}}_{0}\) and n 0. The shear force \(q^{I}\) is limited to the Coulomb friction law given by

$$\left\| {q^{I} } \right\| \le \mu p^{I}$$
(9)

where \(\mu\) is the friction coefficient, and p I is the normal contact force.

Fig. 2
figure 2

Frictional contact model between particles i and j at contact I

Full size image

The discrete linear momentum equations in time for the interacting particles at the contact I can be expressed as:

$$\begin{aligned} & \bar{m}^{i} \Delta \varvec{x}^{i} + p^{I} \varvec{n}_{0}^{I} + q^{I} \hat{\varvec{n}}_{0}^{I} = \bar{\varvec{f}}_{0}^{i} \\ & \bar{m}^{j} \Delta \varvec{x}^{j} - p^{I} \varvec{n}_{0}^{I} - q^{I} \hat{\varvec{n}}_{0}^{I} = \bar{\varvec{f}}_{0}^{j} \\ \end{aligned}$$
(10)

Similarly, the discrete angular momentum equations in time can be expressed as

$$\begin{aligned} & \overline{J}^{i} \Delta \alpha^{i} + r^{i} q^{I} = \bar{m}_{0}^{i} \\ & \overline{J}^{i} \Delta \alpha^{j} - r^{j} q^{I} = \bar{m}_{0}^{j} \\ \end{aligned}$$
(11)

Note that anticlockwise rotations are assumed positive.

2.4 Rolling resistance

Natural materials are usually composed of irregular grains so that the idealization of circular disks may result in serious errors. For instance, the macroscopic internal friction angle of a sample of bonded particle is no larger than 25º because the disks are free to rotate [54]. Accordingly, the application of the discrete methods has been considerably restricted because of ignoring of particle shapes [13]. Estrada [12] and Jiang [21] suggested that rolling resistance model could be used as a simple and effective method to account for particle shapes.

Following the approach in [15], the rolling resistance is incorporated in the time discrete angular momentum equations.

$$\begin{aligned} & \overline{J}^{i} \Delta \alpha^{i} + r^{i} q^{I} + \tau^{I} = \bar{m}_{0}^{i} \\ & \overline{J}^{i} \Delta \alpha^{j} - r^{j} q^{I} + \tau^{I} = \bar{m}_{0}^{j} \\ \end{aligned}$$
(12)

where \(\tau^{I}\) refers to the moment arisen from rolling resistance at contact I.

The rolling resistance is generated by the particle shape and the contact force. Hence, the rolling resistance can be formulated as

$$\left\| {\tau^{I} } \right\| \le \mu_{\text{r}} r^{I} p^{I}$$
(13)

where μ r is the rolling resistance coefficient. The quantity r I is the common radius between two particles, and a common choice for it is the geometric mean of the radii of the two particles. However, bearing in mind the origin of the resisting moment—the eccentric contact forces—we chose the minimum radius of interacting particles as the common radius (i.e., r I = min(r i, r j)).

2.5 Conic programming formulations

We now have the governing equations for rigid unbonded particles, i and j, at the contact I. To extend the formulations to an n-particle system, we introduce the following notations:

$$\begin{array}{llll} \bar{\varvec{M}} = {\text{diag}}(\bar{m}^{1} ,\bar{m}^{1} , \ldots ,\bar{m}^{n} ,\bar{m}^{n} ) \\ \bar{\varvec{J}} = {\text{diag}}(\bar{J}^{1} ,\bar{J}^{2} , \ldots ,\bar{J}^{n - 1} ,\bar{J}^{n} ) \\ \bar{\varvec{f}}_{0} = (\bar{\varvec{f}}_{0}^{1} , \ldots ,\bar{\varvec{f}}_{0}^{n} ),\quad \bar{\varvec{m}}_{ 0} = (\bar{m}_{ 0}^{ 1} , \ldots ,\bar{m}_{ 0}^{n} ) \\ \varvec{R}_{0} = (r^{ 1} , \ldots ,r^{n} ),\quad \varvec{R} = (r^{ 1} , \ldots ,r^{N} ) \end{array}$$
(14)

together with arrays of the state variables

$$\begin{array}{lll} \varvec{x} = (\varvec{x}^{1} , \ldots ,\varvec{x}^{n} ),\quad\varvec{\alpha}= (\alpha^{1} , \ldots ,\alpha^{n} ) \\ \varvec{p} = (p^{1} , \ldots ,p^{N} ),\quad \varvec{q} = (q^{1} , \ldots ,q^{N} ) \\ \varvec{g}_{0} = (g_{0}^{ 1} , \ldots ,g_{0}^{N} ),\quad\varvec{\tau}= (\tau^{ 1} , \ldots ,\tau^{N} ) \\ \end{array}$$
(15)

where the matrix quantities in bold refer to an n-particle assembly, the number of contacts is denoted as N, and \(\varvec{R}\) and \(\varvec{R}_{0}\) are the array with common radii of potential contacts and particle radii, respectively. Furthermore, \(\varvec{N}\) and \(\hat{\varvec{N}}\) are the matrices which collect the normal and tangential unit vectors for the potential contacts.

Following [15], the governing equations can be cast as an optimization problem

$$\begin{array}{ll}\mathop {\hbox{min} }\limits_{{\varvec{x},\varvec{\alpha}}} \mathop {\hbox{max} }\limits_{{\varvec{p},\varvec{q},\varvec{\tau}}} \left\{ {\tfrac{1}{2}\Delta \varvec{x}^{\text{T}} \bar{\varvec{M}}\Delta \varvec{x} - \Delta \varvec{x}^{\text{T}} \bar{\varvec{f}}_{0} } \right\} + \left\{ {\Delta \varvec{x}^{\text{T}} (\varvec{N}_{0} \varvec{p} + \hat{\varvec{N}}_{0} \varvec{q}) - \varvec{g}_{0}^{\text{T}} \varvec{p}} \right\} + \left\{ {\tfrac{1}{2}\Delta\varvec{\alpha}^{\text{T}} \bar{\varvec{J}}\Delta\varvec{\alpha}- \Delta\varvec{\alpha}^{\text{T}} \bar{\varvec{m}}_{0} } \right\} + \left\{ {\Delta\varvec{\alpha}^{\text{T}} (\varvec{R}_{0} \varvec{q} +\varvec{\tau})} \right\} \\ {\text{subject}}\;{\text{to}}\;\left\| \varvec{q} \right\| \le \mu \varvec{p}\\ \qquad \left\|\varvec{\tau}\right\| \le \mu_{\text{r}} \varvec{Rp} \end{array}$$
(16)

Alternatively, a force-based formulation can be constructed as

$$\begin{array}{ll} \text{minimize}&\frac{1}{2}\varvec{t}^{\text{T}} \bar{\varvec{M}}^{ - 1} \varvec{t} + \tfrac{1}{2}\varvec{r}^{\text{T}} \bar{\varvec{J}}^{ - 1} \varvec{r} + \varvec{g}_{0}^{\text{T}} \varvec{p} \\ {\text{subject}}\;{\text{to}}&\varvec{t + N}_{0} \varvec{p} + \hat{\varvec{N}}_{0} \varvec{q} = \bar{\varvec{f}}_{0} \\ & \varvec{r + R}_{0} \varvec{q} +\varvec{\tau}= \bar{\varvec{m}}_{0} \\ & \left\| \varvec{q} \right\| \le \mu \varvec{p} \\ & \left\|\varvec{\tau}\right\| \le \mu_{\text{r}} \varvec{Rp} \end{array}$$
(17)

where \(\varvec{t} = \bar{\varvec{M}}\Delta \varvec{x}\) and \(\varvec{r = \bar{J}}\Delta\varvec{\alpha}\) are dynamic forces and moments.

Similarly, a displacement based optimization problem can be obtained by solving the max part of the problem (16), which is equivalent to the above force-based one.

2.6 Implementation

Following [27], the potential contacts of the next time step are identified by the Delaunay triangulation method. An example is shown in Fig. 3.

Fig. 3
figure 3

Potential contacts by Delaunay triangulation

Full size image

A general second-order cone programming provides a convenient framework for the optimization problem discussed above. The Coulomb friction law and rolling resistance can be treated as second-order cone constraints for the mathematical programming problem [25, 29]. There are a number of efficient and robust solvers and of particular note are MOSEK [1] and SeDuMi [49].

3 The bond model

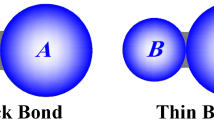
The bond model shown in Fig. 4 aims to mimic the cohesion between particles. The subscript b indicates variables related to the bond. The bond can resist tensile forces, shear forces and rolling moments up to certain thresholds. If the limit of tensile strength, the shear strength or the maximum rolling moments of the bond is reached, the bond is considered to be broken. After the bond fails, the interactions of particles turn into the pure frictional contact. In addition, the elasticity of the bond has been considered in the framework of contact dynamics, which makes the model more realistic in predicting the mechanical response of bonded granular geomaterials.

Fig. 4
figure 4

Bond model—two particles i, j bonded at contact I (a) geometry (b) intact bonds resist normal forces p b, shear forces q b and rolling moments m b, g b0 and h are the initial bond length and the width of bond, respectively. For two-dimensional plane strain, the value of h is 1

Full size image

3.1 Normal force and associated elasticity

3.1.1 Tensile strength and associated elasticity

The maximum tensile force f t that the bond can resist is controlled by the tensile strength of cementation material:

$$f_{\text{t}} = 2rh\sigma_{\text{t}}$$
(18)

where σ t is the tensile strength of the cementation material.

The linear elastic response of the bond in the normal direction can be viewed as a spring joining two particles, as shown in Fig. 5. Thus, the local constitutive law between the normal contact force and the deformation is:

$$g_{\text{b}} - g_{\text{b0}} \ge - {{p_{\text{b}}^{I} } \mathord{\left/ {\vphantom {{p_{\text{b}}^{I} } {k_{\text{N}} }}} \right. \kern-0pt} {k_{\text{N}} }}$$
(19)

where \(g_{\text{b0}}\) is the initial bond length, \(k_{\text{N}}\) is the normal stiffness, and \(g_{\text{b}}\) is the bond length in the next time step:

Fig. 5
figure 5

Linear elastic law and tensile strength of bond

Full size image
$$g_{\text{b}} = g_{0} - n_{0}^{I} \Delta \varvec{x}$$
(20)

Incorporating (19) and (20) into the non-penetration condition (8) leads to:

$$\begin{aligned} & \left( {n_{0}^{I} } \right)^{T} \Delta \varvec{x} - (g_{ 0} - g_{\text{b0}} ) \le C_{\text{N}} p_{b}^{I} \\ & (p_{\text{b}}^{I} + f_{\text{t}}^{I} )[\left( {\varvec{n}_{0}^{I} } \right)^{T} \Delta \varvec{x} - (g_{ 0} - g_{\text{b0}} ) - C_{\text{N}} p_{\text{b}}^{I} ] = 0 \\ \end{aligned}$$
(21)

where \(C_{\text{N}} = 1/k_{\text{N}}\).

3.1.2 Conic programming formulations

The governing equations for bonded particles in the normal direction are summarized as:

$$\begin{aligned} & \bar{m}^{i} \Delta \varvec{x}^{i} + p_{\text{b}}^{I} \varvec{n}_{0}^{I} = \bar{\varvec{f}}_{ 0}^{i} \\ & \bar{m}^{j} \Delta \varvec{x}^{j} - p_{\text{b}}^{I} \varvec{n}_{0}^{I} = \bar{\varvec{f}}_{ 0}^{j} \\ & \left( {\varvec{n}_{0}^{I} } \right)^{T} \Delta \varvec{x} - (g_{ 0} - g_{\text{b0}} ) \le C_{\text{N}} p_{\text{b}}^{I} \\ & (p_{\text{b}}^{I} + f_{\text{t}}^{I} )\left[ {\left( {\varvec{n}_{0}^{I} } \right)^{T} \Delta \varvec{x} - (g_{ 0} - g_{\text{b0}} ) - C_{\text{N}} p_{\text{b}}^{I} } \right] = 0 \\ & p_{\text{b}}^{I} + f_{\text{t}}^{I} \ge 0 \\ \end{aligned}$$
(22)

For an n-particle system, the governing equations are extended to

$$\begin{aligned} & \bar{\varvec{M}}\Delta \varvec{x} + \varvec{N}_{0} \varvec{p}_{{\mathbf{b}}} = \bar{\varvec{f}}_{0} \\ & \varvec{N}_{0}^{\text{T}} \Delta \varvec{x} - (\varvec{g}_{ 0} - \varvec{g}_{\text{b0}} ) \le C_{\text{N}} \varvec{p}_{\text{b}} \\ & (\varvec{p}_{\text{b}} + \varvec{f}_{\text{t}} )[\varvec{N}_{0}^{\text{T}} \Delta \varvec{x} - (\varvec{g}_{ 0} - \varvec{g}_{\text{b0}} ) - C_{\text{N}} \varvec{p}_{\text{b}} ] = {\mathbf{0}} \\ & \varvec{p}_{\text{b}} + \varvec{f}_{\text{t}} \ge {\mathbf{0}} \\ \end{aligned}$$
(23)

where \(\varvec{p}_{\text{b}} + \varvec{f}_{\text{t}} = {\text{diag}}(p_{\text{b}}^{1} + f_{\text{t}}^{1} , \ldots ,p_{\text{b}}^{N} + f_{\text{t}}^{N} )\), \(\varvec{p}_{b} = (p_{b}^{1} , \ldots ,p_{b}^{N} )\).

These equations constitute the first-order Karush–Kuhn–Tucker (KKT) optimality conditions associated with the following optimization problem (see the “Appendix” for details):

$$\begin{aligned} & \mathop {\hbox{min} }\limits_{{\Delta \varvec{x}}} \mathop {\hbox{max} }\limits_{{\varvec{p}_{\text{b}} }} \left\{ {\tfrac{1}{2}\Delta \varvec{x}^{\text{T}} \bar{\varvec{M}}\Delta \varvec{x} - \Delta \varvec{x}^{\text{T}} \bar{\varvec{f}}_{0} } \right\} \\ & \quad + \left\{ {\Delta \varvec{x}^{\text{T}} \varvec{N}_{0} \varvec{p}_{\text{b}} - (\varvec{g}_{ 0} - \varvec{g}_{\text{b0}} )^{T} \varvec{p}_{\text{b}} - \frac{1}{2}\varvec{p}_{\text{b}}^{\text{T}} C_{\text{N}} \varvec{p}_{\text{b}} } \right\} \\ & {\text{subject}}\;{\text{to}}\;\varvec{p}_{\text{b}} + \varvec{f}_{\text{t}} \ge {\mathbf{0}} \\ \end{aligned}$$
(24)

Solving the min part of problem (24) gives the following force-based problem:

$$\begin{aligned} & \mathop {\text{maximize} }\limits_{{\varvec{p}_{\text{b}} }} - \tfrac{1}{2}\Delta \varvec{x}^{\text{T}} \bar{\varvec{M}}\Delta \varvec{x} - (\varvec{g}_{ 0} - \varvec{g}_{\text{b0}} )^{T} \varvec{p}_{\text{b}} - \frac{1}{2}\varvec{p}_{\text{b}}^{\text{T}} C_{\text{N}} \varvec{p}_{\text{b}} \\ & {\text{subject}}\;{\text{to}}\;\varvec{p}_{\text{b}} + \varvec{f}_{\text{t}} \ge {\mathbf{0}} \\ & \quad \bar{\varvec{M}}\Delta \varvec{x} + \varvec{N}_{0} \varvec{p}_{\text{b}} = \bar{\varvec{f}}_{0} \\ \end{aligned}$$
(25)

Similarly, solving the max part of problem (24), the equivalent displacement based problem can be obtained.

3.2 Shear force and associated elasticity

The shear strength of the bond is defined by a modified Mohr–Coulomb model as indicated in Fig. 6. The shear force threshold f s that the bond can resist is

$$f_{\text{s}} = cA_{\text{b}}^{I} + \mu_{\text{b}} p_{\text{b}}^{I}$$
(26)

where \(c\) is the cohesion, \(A_{\text{b}}^{I}\) is the contact area \(A_{\text{b}}^{I} {=} 2r^{I} h\), \(\mu_{\text{b}}\) is the internal friction coefficient of the bond, \(\mu_{\text{b}} = \tan \varphi_{\text{b}}\) and \(\varphi_{\text{b}}\) is the microscopic friction angle.

Fig. 6
figure 6

Shear rupture criterion

Full size image

Adopting the same principle in the DEM, the shear forces and tangential deformation are updated in every time step [48, 54, 58]. Therefore, the term accounting for the shear forces and the associated moments needs to be added to the objective function [28]. Moreover, the constraints related to the shear strength have to be modified. Finally, the following problem is derived:

$$\begin{aligned} & \mathop {\hbox{min} }\limits_{{\Delta \varvec{x},\Delta\varvec{\alpha}}} \mathop {\hbox{max} }\limits_{{\varvec{p}_{\text{b}} ,\varvec{q}_{\text{b}} }} \left\{ {\tfrac{1}{2}\Delta \varvec{x}^{\text{T}} \bar{\varvec{M}}\Delta \varvec{x} - \Delta \varvec{x}^{\text{T}} \bar{\varvec{f}}_{0} } \right\} \\ & \quad + \left\{ {\Delta \varvec{x}^{\text{T}} \left( {\varvec{N}_{0} \varvec{p}_{b} + \hat{\varvec{N}}_{0} \varvec{q}_{\text{b}} } \right) - (\varvec{g}_{ 0} - \varvec{g}_{\text{b0}} )^{T} \varvec{p}_{b} - \frac{1}{2}\varvec{p}_{\text{b}}^{\text{T}} C_{\text{N}} \varvec{p}_{\text{b}} - \frac{1}{2}\Delta \varvec{q}_{\text{b}}^{T} C_{\text{T}} \Delta \varvec{q}_{{\mathbf{b}}} } \right\} \\ & \quad + \left\{ {\tfrac{1}{2}\Delta\varvec{\alpha}^{\text{T}} \bar{\varvec{J}}\Delta\varvec{\alpha}- \Delta\varvec{\alpha}^{\text{T}} \bar{\varvec{m}}_{ 0} } \right\} \\ & \quad + \left\{ {\Delta\varvec{\alpha}^{\text{T}} \varvec{R}_{0} \varvec{q}_{\text{b}} } \right\} \\ & {\text{subject}}\;{\text{to}}\;\varvec{p}_{\text{b}} + \varvec{f}_{\text{t}} \ge {\mathbf{0}} \\ & \quad \left\| {\varvec{q}_{{\mathbf{b}}} } \right\| \le c\varvec{A}_{\text{b}} + \mu_{\text{b}} \varvec{p}_{\text{b}} \\ \end{aligned}$$
(27)

where \(\varvec{q}_{\text{b}}\) are the shear forces, and \(\varvec{\alpha}\) are the angles of rotation.

In the above problem, both the normal deformation C N = 1/k N and the tangential deformation C T = 1/k T are considered.

3.3 Rolling resistance

The rolling resistance is defined as the maximum torque that the bond can transmit. Following the cohesive bond in [9, 22, 51], the rolling friction law is given by

$$\left\| {\tau_{\text{b}} } \right\| \le \mu_{\text{r}} r\left( {p_{\text{b}} + f_{\text{t}} } \right)$$
(28)

where τ b is the maximum torque that the bond can resist.

The bond model that includes elasticity and rolling resistance is

$$\begin{aligned} \mathop {\hbox{min} }\limits_{{\Delta \varvec{x},\Delta\varvec{\alpha}}} \mathop {\hbox{max} }\limits_{{\varvec{p}_{\text{b}} ,\varvec{q}_{\text{b}} ,\varvec{\tau}}} \left\{ {\tfrac{1}{2}\Delta \varvec{x}^{\text{T}} \bar{\varvec{M}}\Delta \varvec{x} - \Delta \varvec{x}^{\text{T}} \bar{\varvec{f}}_{0} } \right\} \\ & \quad + \left\{ {\Delta \varvec{x}^{\text{T}} \left( {\varvec{N}_{0} \varvec{p}_{\text{b}} + \hat{\varvec{N}}_{0} \varvec{q}_{\text{b}} } \right) - (\varvec{g}_{ 0} - \varvec{g}_{\text{b0}} )^{T} \varvec{p}_{\text{b}} - \frac{1}{2}\varvec{p}_{\text{b}}^{\text{T}} C_{\text{N}} \varvec{p}_{\text{b}} - \frac{1}{2}\Delta \varvec{q}_{\text{b}}^{T} C_{\text{T}} \Delta \varvec{q}_{{\mathbf{b}}} } \right\} \\ & \quad + \left\{ {\tfrac{1}{2}\Delta\varvec{\alpha}^{\text{T}} \bar{\varvec{J}}\Delta\varvec{\alpha}- \Delta\varvec{\alpha}^{\text{T}} \bar{\varvec{m}}_{ 0} } \right\} \\ & \quad + \left\{ {\Delta\varvec{\alpha}^{\text{T}} \left( {\varvec{R}_{0} \varvec{q}_{\text{b}} +\varvec{\tau}_{\text{b}} } \right)} \right\} \\ {\text{subject}}\;{\text{to}}\;\varvec{p}_{\text{b}} + \varvec{f}_{\text{t}} \ge {\mathbf{0}} \\ & \quad \left\| {\varvec{q}_{{\mathbf{b}}} } \right\| \le c\varvec{A}_{\text{b}} + \mu_{\text{b}} \varvec{p}_{\text{b}} \\ & \quad \left\| {\varvec{\tau}_{\text{b}} } \right\| \le \mu_{\text{r}} \varvec{R}\left( {\varvec{p}_{\text{b}} + \varvec{f}_{\text{t}} } \right) \\ \end{aligned}$$
(29)

3.3.1 Optimality conditions

Following the procedure in the “Appendix”, the KKT conditions associated with (29) can be shown to comprise the following sets of governing equations relating to translational momentum balance:

$$\bar{\varvec{M}}\Delta \varvec{x} + \varvec{N}_{0} \varvec{p}_{\text{b}} + \hat{\varvec{N}}_{0} \varvec{q}_{\text{b}} = \bar{\varvec{f}}_{0}$$
(30)

rotational momentum balance:

$$\bar{\varvec{J}}\Delta\varvec{\alpha}+ \varvec{R}_{0} \varvec{q}_{\text{b}} +\varvec{\tau}_{\text{b}} = \bar{\varvec{m}}_{ 0}$$
(31)

shear strength conditions:

$$\begin{array}{*{20}l} {c\varvec{A}_{\text{b}} + \mu_{\text{b}} \varvec{p}_{\text{b}} - \left\| {\varvec{q}_{b} } \right\| - \varvec{s}_{1} = {\mathbf{0}},} \hfill & {\varvec{s}_{1} \ge {\mathbf{0}}} \hfill \\ {{\text{diag(}}\varvec{s}_{{\mathbf{1}}} )\varvec{\lambda}_{{\mathbf{1}}} { = }{\mathbf{0}},} \hfill & {\varvec{\lambda}_{{\mathbf{1}}} \ge {\mathbf{0}}} \hfill \\ \end{array}$$
(32)

torque transmission conditions:

$$\begin{aligned} & \mu_{\text{r}} \varvec{R}\left( {\varvec{p}_{\text{b}} + \varvec{f}_{\text{t}} } \right) - \left\| {\varvec{\tau}_{\text{b}} } \right\| - \varvec{s}_{2} = {\mathbf{0}} \\ & {\text{diag(}}\varvec{s}_{2} )\varvec{\lambda}_{{\mathbf{2}}} = {\mathbf{0}},\quad\varvec{\lambda}_{{\mathbf{2}}} \ge {\mathbf{0}} \\ \end{aligned}$$
(33)

and kinematics incorporating the elastic deformation characteristics:

$$\begin{aligned} & \varvec{N}_{0}^{\text{T}} \Delta \varvec{x}+\mu_{\text{b}} {\varvec{\uplambda}}_{1} + \mu_{\text{r}} \varvec{R}{\varvec{\uplambda}}_{2} = (\varvec{g}_{ 0} - \varvec{g}_{\text{b0}} ) + C_{N} \varvec{p}_{b} \\ & \hat{\varvec{N}}_{0}^{\text{T}} \Delta \varvec{x + R}_{0} \Delta\varvec{\alpha}= C_{\text{T}} \Delta \varvec{q}_{{\mathbf{b}}} + {\text{Sgn}}(\varvec{q}_{\text{b}} ){\varvec{\uplambda}}_{1} \\ & \Delta\varvec{\alpha}= {\text{Sgn}}(\varvec{\tau}_{\text{b}} ){\varvec{\uplambda}}_{2} \\ \end{aligned}$$
(34)

where Sgn, and λ 1 and λ 2 are the sign function and Lagrange multipliers, respectively. When the failure criteria are not met, the value of \(\uplambda_{1}^{I}\) and \(\uplambda_{2}^{I}\) are zero according to Eqs. (32) and (33). Regrading the kinematics, the obvious dilation described in [27] can be found in Eq. (34) because of the associated sliding rule. However, this may be viewed as an artifact of the time discretization [27, 28, 41].

3.3.2 Force-based problem

Alternatively, it is possible to cast the problem into the following force-based problem:

$$\begin{array}{ll} \text{maximize}& - \tfrac{1}{2}\varvec{t}^{\text{T}} \bar{\varvec{M}}^{ - 1} \varvec{t} - \tfrac{1}{2}\varvec{r}^{\text{T}} \bar{\varvec{J}}^{ - 1} \varvec{r} - (\varvec{g}_{ 0} - \varvec{g}_{\text{b0}} )^{T} \varvec{p}_{\text{b}} \\ & - \frac{1}{2}\varvec{p}_{\text{b}}^{\text{T}} C_{\text{N}} \varvec{p}_{\text{b}} - \frac{1}{2}\Delta \varvec{q}_{\text{b}}^{T} C_{\text{T}} \Delta \varvec{q}_{{\mathbf{b}}} \\ {\text{subject}}\;{\text{to}}&\varvec{t + N}_{0} \varvec{p}_{\text{b}} + \hat{\varvec{N}}_{0} \varvec{q}_{{\mathbf{b}}} = \bar{\varvec{f}}_{0} \\ & \varvec{r + R}_{0} \varvec{q}_{{\mathbf{b}}} +\varvec{\tau}_{\text{b}} = \bar{\varvec{m}}_{0} \\ & \left\| {\varvec{q}_{{\mathbf{b}}} } \right\| \le c\varvec{A}_{\text{b}} + \mu_{\text{b}} \varvec{p}_{\text{b}} \\ & \left\| {\varvec{\tau}_{\text{b}} } \right\| \le \mu_{\text{r}} \varvec{R}\left( {\varvec{p}_{\text{b}} + \varvec{f}_{\text{t}} } \right) \end{array}$$
(35)

where t and r are the dynamic forces and moments, \(\bar{\varvec{M}}\Delta \varvec{x}\) and \(\bar{\varvec{J}}\Delta\varvec{\alpha}\), respectively.

This mathematical programming problem is solved by the second-order cone programming solver- MOSEK [1]. The rotation cone is adopted to formulate elastic elements in the objective function. The displacements are obtained from the Lagrange multipliers associated with the equality constraints.

3.3.3 Static problem

Omitting the dynamic forces and moments (i.e., r and t) in the problem (35) gives the following static formulation:

$$\begin{aligned} & \text{maximize} - (\varvec{g}_{ 0} - \varvec{g}_{\text{b0}} )^{T} \varvec{p}_{\text{b}} - \frac{1}{2}\varvec{p}_{\text{b}}^{T} C_{\text{N}} \varvec{p}_{\text{b}} - \frac{1}{2}\Delta \varvec{q}_{\text{b}}^{T} C_{\text{T}} \Delta \varvec{q}_{{\mathbf{b}}} \\ & {\text{subject}}\;{\text{to}}\;\varvec{N}_{0} \varvec{p}_{\text{b}} + \hat{\varvec{N}}_{0} \varvec{q}_{{\mathbf{b}}} = \bar{\varvec{f}}_{0} \\ & \quad \varvec{R}_{0} \varvec{q}_{{\mathbf{b}}} +\varvec{\tau}_{\text{b}} = \bar{\varvec{m}}_{0} \\ & \quad \left\| {\varvec{q}_{{\mathbf{b}}} } \right\| \le c\varvec{A}_{\text{b}} + \mu_{\text{b}} \varvec{p}_{\text{b}} \\ & \quad \left\| {\varvec{\tau}_{\text{b}} } \right\| \le \mu_{\text{r}} \varvec{R}\left( {\varvec{p}_{\text{b}} + \varvec{f}_{\text{t}} } \right) \\ \end{aligned}$$
(36)

In explicit DEM, the quasi-static state is simulated using artificial damping and specified boundary conditions, which requires additional calibration for the global and/or local damping parameters. This may make the numerical model complex and inaccurate [52]. In contrast, the static problem can be directly formulated with implicit time integration scheme [37]. This feature is a significant advantage of the proposed method. The principle is governed by the internal pseudo time rather than physical time.

3.4 Criteria of bond creation and rupture

3.4.1 Creation of bonds

The particles assembly is first generated before creating the bonds. If the initial gap g 0 between two particles is less than a certain length g int, a bond is created. This parameter is of great importance in determining the microstructure of the bonded material. For example, when g int is relatively small, more bonds are created and so particle interlocking is increased. Accordingly, the overall strength of the simulated medium is therefore increased [48].

3.4.2 Rupture of bonds

There are three criteria for a bond to break: tensile strength, shear strength and rolling resistance. Once one of these local criteria is reached, the bond breaks. In other words, a crack forms. The loss of the bond turns the contact of bonded particles into a purely frictional one. Accordingly, the local bond properties are set to zero. The corresponding force-based problem is given by:

$$\begin{array}{ll} \text{maximize} &- \tfrac{1}{2}\varvec{t}^{\text{T}} \bar{\varvec{M}}^{ - 1} \varvec{t} - \tfrac{1}{2}\varvec{r}^{\text{T}} \bar{\varvec{J}}^{ - 1} \varvec{r} - \varvec{g}_{ 0}^{T} \varvec{p} \\ & - \frac{1}{2}\varvec{p}^{\text{T}} \varvec{C}_{{\mathbf{N}}} \varvec{p} - \frac{1}{2}\Delta \varvec{q}^{\text{T}} \varvec{C}_{{\mathbf{T}}} \Delta \varvec{q} \\ {\text{subject}}\,{\text{to}}&\varvec{t + N}_{0} \varvec{p} + \hat{\varvec{N}}_{0} \varvec{q} = \bar{\varvec{f}}_{0} \\ & \varvec{r + R}_{0} \varvec{q} +\varvec{\tau}= \bar{\varvec{m}}_{0} \\ & \left\| \varvec{q} \right\| \le \mu \varvec{p} \\ & \left\|\varvec{\tau}\right\| \le \mu_{\text{r}} \varvec{Rp} \end{array}$$
(37)

It is apparent that this formulation, without the torque transmission, is identical to the problem (27) in [28].

4 Examples

In the following, the force-based static formulation was implemented. The program for the bond model was first verified using three simple examples in which the numerical results were compared to analytic solutions. The uniaxial and biaxial compression tests were then used to examine the ability of the proposed bond model in simulating the bonded geomaterials. The effects of bonding on the mechanical behavior of the particles assembly were investigated. We note that the following numerical tests are distinct from the common DEM models because the pure static formulations were employed.

The initial configurations of first three examples are presented in Fig. 7. The radius of two particles is 6 mm with a bond thickness of 1 mm. The local parameters listed in Table 1 are used in the numerical test.

Fig. 7
figure 7

Initial configurations of numerical models

Full size image
Table 1 Local parameters used in the test
Full size table

4.1 Tension test

Figure 8 shows the force–displacement response obtained from tension test. The bond is subjected to pure tension, and the tensile force is increased stepwise until bond breakage occurs. The analytical solution of normal deformation for the bond is obtained from Eq. (21). According to Fig. 8, the normal elasticity of the bond model is completely reproduced.

Fig. 8
figure 8

Relationship between the tensile force and normal deformation

Full size image

4.2 Direct shear test

Figure 9 shows the results from direct shear test under varied normal bond forces P b = −10, 0 and 10 N. For the sake of simplicity, rotational degrees of freedom was not considered. The linear elastic law in the tangential direction has been successfully reproduced as shown in Fig. 9. The shear strengths of the bond under varied normal forces P b = −10, 0 and 10 N are computed as 42, 48 and 54 N, respectively, which are exactly the same value as analytical solution.

Fig. 9
figure 9

Relationship between the shear force and shear displacement

Full size image

4.3 Combined rolling compression test

This example is used to test the rolling resistance of the bond. In the test, there are two types of rolling resistance: the bond between particles and particle-to-wall. When the normal compressive force is less than 24 N, the maximum torque under the static equilibrium is limited to the particle-to-wall type rolling resistance. In contrast for the larger compressive force, the maximum torque that the bond can resist is limited to rolling resistance of the bond model. The analytical solution for this problem can be obtained from Eqs. (13) and (28). In Fig. 10, the maximum torque predicted from analytical solutions has been successfully reproduced by numerical simulations.

Fig. 10
figure 10

Relationship between the compressive force and rolling resistance

Full size image

4.4 Uniaxial compression test

The previous three examples are used to validate the bond model. In the following, the potential of the bond model for the modeling of cemented geomaterials is investigated.

4.4.1 Sample construction

During sample construction, a static formulation for rigid particles with frictionless contact was adopted. After omitting the dynamic forces, the elasticity and shear forces, problem (37) reduces to

$$\begin{array}{ll} \text{maximize} & - \varvec{g}_{ 0}^{T} \varvec{p} \\ {\text{subject}}\;{\text{to}}&\varvec{N}_{0} \varvec{p} = \bar{\varvec{f}}_{0} \\ & \varvec{p} \ge {\mathbf{0}} \end{array}$$
(38)

The sample construction includes three procedures: particle generation, compression and cementation. In the particle generation phase, 7380 particles with radii uniformly distributed within the range 0.3–0.6 mm were randomly placed at the nodes of a square grid. As shown in Fig. 11a, the length of the grid is 1.2 mm so that the particles do not overlap. 

Fig. 11
figure 11

Sample construction a particle generation, b bonded particles

Full size image

In the compression phase, the upper horizontal wall was moved downwards and the other walls were fixed. This procedure was repeated until the required height of 12 cm was reached. The initial porosity of the sample was 0.19.

In the cementation phase, the initial gaps g 0 of all the potential contacts were calculated. If g 0 was less than a length g int, a bond was employed for the contact. Figure 11b shows the obtained sample. The local parameters used for the sample are listed in Table 2.

Table 2 Local parameters used in the simulations
Full size table

4.4.2 Rigid bond model

The bond model without elasticity was considered first, i.e., k N = k T = ∞. This formulation can be easily derived by setting \(C_{\text{N}}\) = \(C_{\text{T}}\) = 0 in the objective function in problem (36). For the uniaxial compression test, the lower boundary was fixed while the upper boundary was moved downward.

The sample immediately broke down in one step with an axial compressive stress of 1.14 GPa. In the next step, the sample cannot support any further loading and its failure is shown in Fig. 12. This result is peculiar to the nature of the physical test, but reasonable in this numerical static test. The sample was first densely compacted with rigid particles, while in the cementation phase, the pores of the sample were filled with rigid cement. Finally, the sample cannot bear any deformation, and the immediate failure would be expected. Furthermore, because the analysis is purely static and rigid particles are used, the external work cannot be absorbed as kinetic or strain energy. As a consequence, the sample collapsed in merely one step.

Fig. 12
figure 12

Failure of rigid bond sample after. The red lines between particles indicate a bond breakage (color figure online)

Full size image

Although bonded granular materials with the rigid cementation model can be created in the contact dynamics framework proposed by [3, 9], the tree-like structure cannot represent the real microstructure of the material and the loading process on the sample may not be simulated in the right way. It is well known that failure of a material is generally a progressive process, accompanied by elastic–plastic deformation. Thus, elasticity should be included as in the following static numerical tests.

4.4.3 Elastic bond model

This example concerns uniaxial compression test on a rock sample. The rock core sample was obtained from the tunnel Äspö, and the uniaxial compression test was carried out in the Hard Rock Laboratory (HRL) [24]. The sample is intact without macroscopic fractures. The local properties of rock were calibrated with the proposed method and listed in Table 2. The numerical predictions of our model together with the results from the Particle Flow Code (PFC; [16, 42]) are shown in Fig. 13. In the static test, a stepwise displacement increment is imposed on the specimen by the top wall, while the bottom wall is fixed. The mean number of iterations per time step is 66 using MOSEK programming solver. The overall computation time of the uniaxial compression test is 24.7 min using a personal computer with the Intel Core-Dual 3.00 GHz CPU.

Fig. 13
figure 13

Results of uniaxial compression tests a complete stress–strain curves and the accumulated number of microcracks, b fracture evolutions (I) before peak (0.33 % strain), (II) peak, (III) after peak (0.46 % strain), (IV) after peak (0.6 % strain)

Full size image

As we conducted the numerical simulation for the same Äspö diorite sample, the peak strength and Young’s modulus are in good agreement with the observed values given in [24]. But for the post-peak behavior, the stress–strain curve of the granular contact dynamics sample tends to be more brittle than the PFC sample. The accumulated number of microcracks from the two methods is compared in Fig. 13a. The progressive failure process of the sample is shown in Fig. 13b. The cracks are randomly distributed in the sample and their interaction is not clear (Fig. 13b-I). According to [5, 36], at an axial stress 88.5 % of the short-term peak strength, the state I (Fig. 13b-I) is in an unstable cracking phase. A macro-failure plane can be seen at the peak axial load where most of microcracks were localized, as shown in Fig. 13b-II. With increasing axial strain, the microcracks progressively coalesce until a persistent shear band is formed (Fig. 13b-IV). Once the macro-failure plane formed, the sample failed.

4.5 Biaxial compression test

The second example involves a biaxial compression test on cemented sands. The sample has 6160 particles with an initial porosity of 0.17. Figure 14 shows the initial sample where the particles are colored in purple and gray to show global deformation. Four movable rigid walls were placed as the boundaries. The local properties used for the cemented sand are shown in Table 3.

Fig. 14
figure 14

Setup of the biaxial compression test

Full size image
Table 3 Local properties used for the biaxial compression test
Full size table

To achieve the specified confining stress in DEM, servomechanism algorithms for the moving walls have to be developed. Even with this algorithm, the appropriate velocities of the walls are still not easy to determine [6]. In contrast, the force-based constraint for the specified confining stress can be directly imposed on the sample in our method.

If the confining force is applied to the sample in a single step, the large force increment may cause large deformation and thus damage the specimen. In this study, the force employed by the walls was gradually increased in five steps to the specified confining stress.

Figure 15a shows the stress–strain relationship of the cemented sand with a bond strength R of 10, 50 and 100 kPa, respectively. As expected, the peak shear strength of the sample increases with increasing bond strength. The strain softening behavior of the cemented sands is apparent compared to the uncemented sample. As for the volumetric response, the samples experienced volumetric dilation after an initial contraction (Fig. 15b). The initial contraction is greatest when the strength of the bond is high. Since the boundary condition with rigid walls can inhibit the free deformation of the specimen, the post-peak behavior may not be realistic until the problem is studied with a flexible boundary to model a soft rubber membrane.

Fig. 15
figure 15

Mechanical responses of the sample: a stress versus axial strain, b volumetric strain versus axial strain

Full size image

The bond breakage was recorded with red line segments in the specimen as shown in Fig. 16. Significant deformation and bond breakage are concentrated in two major shear bands. It can be seen that several potential shear bands formed at the peak deviatoric stress. As the shear strain further increases, significant deformation and bond breakage are mostly in one conjugate shear band. The intense particle rotate, deformation and bond breakage are consistently observed in the localization region, as shown in Fig. 16.

Fig. 16
figure 16

Numerical results obtained from biaxial compression results with R = 10 kPa. a distribution of bond breakage at peak deviatoric stress, b distribution of bond breakage: strain = 12 %, c distribution of particles indicating the specimen deformation: strain = 12 %, d contour plot indicating the relative magnitude of the rotation rate: strain = 12 %

Full size image

In this numerical test, stepwise displacement, γ = 0.3 mm/step is applied to top and bottom walls. For a series of biaxial compression test, the mean computation time is 3.7 h using a server with 256 GB RAM and Intel(R) Xeon(R) CPU E5-4617 0 @ 2.90 GHz. The number of iterations per time step is around 56 using MOSEK programming solver.

The sensitivity of displacement increment γ on the mechanical behavior of samples is studied with four different values of 0.2, 0.3, 0.4 0.5 and 1.0 mm/step. The above configuration for the biaxial compression test is employed for the cemented sand with a bond strength R of 10 kPa. The numerical results of biaxial compression test are shown in Fig. 17. The results show that the influence of displacement increment to the mechanics behaviors is insignificant. Further studies on the effect of displacement increment involving the crack development, material shear strength and strain and stress fields may need to be carried out.

Fig. 17
figure 17

Effect of displacement increment on the mechanical behavior: a stress versus axial strain, b volumetric strain versus axial strain

Full size image

5 Conclusion

In contrast to traditional DEM, implicit time discretization is adopted in developed granular contact dynamics, so large time step can be adopted in the model. Moreover, a static formulation can be directly formulated by omitting dynamic forces and moments, which is valuable for modeling common laboratory tests such as triaxial compression test. In the current paper, a bond model based on the granular contact dynamics framework is proposed for cemented geomaterials. The elastic behavior, tensile strength, shear strength and torque transmission are considered in the model. Both uniaxial compression and biaxial compression tests are conducted to demonstrate its potential. The conclusions are summarized as:

  1. 1.

    The traditional rigid granular contact dynamics formulation is extended to include the elastic bond. The formulation is more general than the common DEM because it recovers the rigid bond model and pure static problem.

  2. 2.

    Three failure criteria are employed in the proposed bond model, respectively, defining the tensile, shear and torsional strength. The tensile and shear strength criteria are formulated based on the modified Mohr–Coulomb failure criterion. The torsional strength criterion is introduced based on the rolling resistance model. The bond failure leads to irreversible loss of bond strength. Unlike the explicit DEM, quasi-static problems can be simulated directly.

  3. 3.

    Rigidly bonded samples break down in merely one step in the static test because the external work cannot be absorbed as kinetic or strain energy in the sample. An elastic bond is essential for the simulation of dense, bonded granular geomaterials.