1 Introduction

The need for mechanized excavation of tunnels in cities has continuously increased in recent years. One important subject for tunneling by the shield machine (i.e., EPB shield or slurry shield) is to control the face stability, especially in cohesionless soils (e.g., sandy soils). That means, in the practical tunnel engineering, sufficient support pressure must be required in the machine’s chamber to balance the external earth and water pressure in front of the tunnel face to prevent the face collapse. Thus, how to properly calculate the minimum support pressure (i.e., limit support pressure) for tunnel face stability is very crucial.

Traditionally, there are two kinds of theoretical methods to calculate the limit support pressure for tunnel face stability. One is the limit analysis method [9, 20, 21, 23] and the other is the limit equilibrium method [1, 2, 5, 11, 13, 17]. Generally, the limit analysis method is much more complicated for the engineering use. Besides that, the accuracy of the results mainly depends on the proper choice of the statically admissible stress field or the kinematically admissible deformation field. Comparing to the limit analysis method, the limit equilibrium method is more widely used in the practical engineering due to its simplicity. Although many kinds of limit equilibrium models have been established, the most popular one is the wedge model. Horn [11] firstly introduced a 3D wedge-silo model, which assumed a sliding wedge loaded by a soil silo. On the basis of Horn’s model [11], Anagnostou and Kovari [2] proposed the classical wedge-prism model to calculate the limit support pressure in the homogeneous stratum. The classical wedge-prism model assumes that the failure zone is a wedge in front of the tunnel face and a vertical prism above the wedge. By considering the mechanical equilibrium of the wedge, the limit support pressure of the tunnel face can be easily obtained. Theses years, the classical wedge-prism model has been used and extended in many subsequent works [1, 5, 17].

Although many researchers have modified the classical wedge-prism model, there are still considerable potentials for improving this model in order to predict the limit support pressure more accurately. One aspect is the improvement of the failure mechanism. In the classical model, the height of the prism in the limit state was thought to be the whole cover above the tunnel crown. Actually, according to the results of the centrifuge model tests conducted by Chambon and Corte [6], it is found that the cover-to-diameter ratio C/D (i.e., relative depth; C is the cover depth and D is the diameter of the tunnel) has significant effect on the failure mechanism. That means, when relative depth C/D is low (e.g., C/D = 0.5), the failure zone in the limit state has extended to the ground surface. When C/D is high (e.g., C/D = 1 or 2), the failure zone in the limit state will be still in the interior of the ground. These conclusions were also confirmed by Oblozinsky and Kuwano [24] according to the photographs taken during their centrifuge model tests, Chen et al. [7] and Karim [16] via DEM (i.e., discrete element method) simulations, Takano et al. [25] through X-ray CT, Ahmed and Iskander [3], Idinger et al. [12], and Kirsch [18] by means of the technology of particle image velocimetry (i.e., PIV). Therefore, the influence of the relative depth on the failure mechanism cannot be ignored, which should be considered in an improved wedge-prism model. The other aspect of the improvement is properly considering soil arching effects (Broere [5]) to calculate the vertical force applied on the wedge’s upper surface more accurately, as it has significant influence on the limit support pressure. Soil arching effects can be mainly embodied in the lateral stress ratio K s between the prism and the adjoining soils. In the classical wedge-prism model, the K s value was thought to be 0.8 based on experience. Strictly speaking, the friction angle of soil has significant influence on the arching effect. That is to say, K s should be a function of the friction angle of soil. Lots of formulas have been adopted for calculating K s, such as the formula of the Rankine’s active earth pressure coefficient (Marston [22]), the formula of the earth pressure coefficient at rest (Jaky [14], Kirsch and Kolymbas [17]), the formula of the Rankine’s passive earth pressure coefficient (Aubertin et al. [4]), and some other formulas (Krynine [19], Handy [10]). Although many different analytical methods mentioned above for calculating K s were suggested, the calculated results via these methods are quite different. Therefore, a feasible method for calculating K s which is based on the actual distribution of stress in the stratum in the limit state should be established in an improved wedge-prism model. Only in this way, the vertical force applied on the wedge’s upper surface can be accurately obtained for properly calculating the limit support pressure.

In this paper, an improved 3D prism-wedge model for calculating the limit support pressure for tunnel face stability in cohesionless soils was firstly proposed. In this model, the height of the prism was put forward on the basis of the previous researchers’ results. Considering the effects of soil arching on the limit support pressure, an appropriate analytical expression of the lateral stress ratio K s between the prism and the part adjoining the prism was proposed. Then, in order to evaluate the quality of this proposed model, comparisons of the limit support pressures via the theoretical models (including the theoretical models proposed in this paper and in the literatures) with those of the typical reported model tests were performed. Finally, a design chart using this proposed method for the proper calculation of the limit support pressure of the tunnel face in cohesionless soils was given for the convenience of industrial application.

2 The improved 3D wedge-prism model

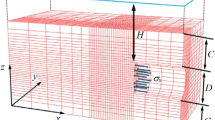
As mentioned above, in order to calculate the limit support pressure on the tunnel face much more accurately in the homogeneous cohesionless ground, an improved 3D wedge-prism model (see Fig. 1) was proposed in this paper. In this improved model, the failure zone is assumed to be a sliding wedge ade-bcf loaded by a prism cdef-ghij (see Fig. 1). The material of the ground conforms to the Mohr–Coulomb failure criterion. The limit support pressure is thought to be the maximum value of the necessary support pressures corresponding to the wedges with different inclination angles β. Compared to the classical wedge-prism model (Anagnostou and Kovari [2]), two aspects are mainly modified in the improved model. One is height of the prism which is closely related to relative depth C/D, the other is the lateral stress ratio K s between the prism and the soils adjoining the prism which is significantly influenced by the friction angle of soil. In this part, we firstly briefly discussed the height of the prism for the improved model. Then, based on the actual distribution of stress in the stratum in the limit state, an analytical expression of the lateral stress ratio K s was established. Finally, a theoretical formula for calculating the limit support pressure was derived by the mechanical equilibrium of the wedge.

Fig. 1
figure 1

The improved 3D wedge-prism model proposed in this paper

Full size image

2.1 Height of the prism

In the process of tunnel face failure, stratum settlement decreases gradually from the tunnel crown to the ground surface. Chen et al. [8] performed 1 g large-scale model tests to investigate the relations between the support pressure and the ground surface settlement. It is found that, if C/D is relatively low (e.g., C/D = 0.5), significant surface settlement is observed when the limit support pressure is imposed on the tunnel face. That means the failure zone has extended to the ground surface in the limit state for the shallow buried tunnel. If C/D is relatively high (e.g., C/D = 1 or 2), no significant surface settlement (only little elastic settlement) is observed when the limit support pressure is imposed on the tunnel face. That is to say, the failure zone is still in the interior of the ground in the limit state for the deep buried tunnel. Therefore, the height of the prism is significantly affected by the relative depth C/D, which is not revealed in the classical wedge-prism model since the height of the prism equals the whole cover above the tunnel crown. In order to suggest the proper height of the prism in the improved 3D wedge-prism model, some typical research results were summarized in Table 1. It should be mentioned that in the centrifuge model tests, the height of the prism H was identified by excavating the ground with the pre-buried colored sand layers after the test (e.g., Chambon and Corte [6]) or by analyzing the photographs taken during the tests as half of the tunnel was investigated (e.g., Oblozinsky and Kuwano [24]). While in the 1 g model tests, H was identified by the variations of earth pressures above the tunnel crown (e.g., Chen et al. [8]) or by analyzing the X-ray CT images (e.g., Takano et al. [25]). As shown in Table. 1, for the relatively deep buried tunnel (e.g., C/D = 1 or 2), the height-to-width ratio H/L of the failure prism (L is width of the prism) is in the range of 1.52–2.36. While for the relatively shallow buried tunnel (e.g., C/D = 0.5), the H/L value is much smaller than that for the relatively deep buried tunnel and H is very close to C. Thus, for the relatively deep buried tunnel, H can be approximately thought to be 2L (i.e., 2D cot β; β is the inclination angle of the wedge). It is about the mean value of the H/L values presented in Table 1 for this condition, and it also induces relatively small deviation of the real H/L value. As for the relatively shallow buried tunnel, the height of the prism H equals the cover depth C. To sum up, the height of prism H is equal to min{C, 2L} in the improved 3D wedge-prism model.

Table 1 Summaries of the height-to-width ratio H/L of the failure prism for different relative depths C/D
Full size table

2.2 Lateral stress ratio K s between the prism and the adjoining soils

For the improved 3D wedge-prism model, properly determining the vertical force on the wedge’s upper surface is very crucial as it is directly related to the calculation of the limit support pressure. The vertical force on the wedge’s upper surface is not equal to the total soil weight above the tunnel crown, which can be attributed to the soil arching effect. In order to properly calculate the vertical force on the wedge’s upper surface, the suitable lateral stress ratio K s between the prism and the adjoining soils due to soil arching effect should be proposed. As mentioned in the introduction part, although many suggestions or formulas for calculating the K s have been proposed, it is found that the results (i.e., K s) are quite different. The main reasons can be attributed to insufficient understanding of the stress in the stratum in the limit state. Chen et al. [8] investigated the variation of soil stress via lots of pre-embedded earth pressure cells in the 1 g large-scale model tests on tunnel face failure. It is found that a significant rotation of principal stress occurs in the upper part of the failure zone (i.e., the prism). This phenomenon was also found by Vermeer et al. [27] with FEM analysis. Besides that, according to the numerical results (Vermeer et al. [27]), the trajectory of the maximum principal stress in the prism in the limit state seems to be an upper convex circular arc.

Based on the results of model experiments (Chen et al. [8]) and numerical analysis (Vermeer et al. [27]), a new method for calculating K s with the consideration of soil arching effect were proposed in this paper. In this new method, the following assumptions were made for the derivation of K s.

  1. 1.

    The cohesionless soil conforms to the Mohr–Coulomb failure criterion and moves vertically downward in the failure prism.

  2. 2.

    The shape of the arch is thought to be an upward circular arc. This arc is also the trajectory of major principal stresses in the limit state. Herein, the arch is defined as “maximum principal stress arch” (see Fig. 2) which is different from “minor principal stress arch” in Handy’s method [10].

    Fig. 2
    figure 2

    Maximum principal stresses arch

    Full size image
  3. 3.

    The principle stresses are constant throughout the arch, and the principle stress ratio is equal to the Rankine’s active earth pressure coefficient (i.e., \( \frac{{\sigma_{3} }}{{\sigma_{1} }} = K_{\text{a}} \)).

In the following part, we will propose the detailed derivation process of K s. Considering the equilibrium condition of any element in the arch, the vertical stress σ v and horizontal stress σ v can be expressed as follows (see Fig. 2).

$$ \sigma_{v} = \sigma_{1} \sin^{2} \theta + \sigma_{3} \cos^{2} \theta $$
(1)
$$ \sigma_{\text{h}} = \sigma_{1} \cos^{2} \theta + \sigma_{3} \sin^{2} \theta $$
(2)

Where σ 1 and σ 3 are the maximum and minimum principal stress of the element in the arch, respectively. θ is the angle between the direction of the maximum principal stress and the horizontal plane.

Since \( \frac{{\sigma_{3} }}{{\sigma_{1} }} = K_{\text{a}} \), Eq. 1 and Eq. 2 are rewritten as

$$ \frac{{\sigma_{\text{v}} }}{{\sigma_{ 1} }} = \sin^{2} \theta + K_{\text{a}} \cos^{2} \theta $$
(3)
$$ \frac{{\sigma_{\text{h}} }}{{\sigma_{1} }} = \cos^{2} \theta + K_{\text{a}} \sin^{2} \theta $$
(4)

Dividing Eq. 3 by Eq. 4 gives

$$ K = \frac{{\sigma_{\text{h}} }}{{\sigma_{\text{v}} }} = \frac{{\cos^{2} \theta + K_{\text{a}} \sin^{2} \theta }}{{\sin^{2} \theta + K_{\text{a}} \cos^{2} \theta }} $$
(5)

For the slip planes (as at points A and C in Fig. 2), \( \theta = \theta_{0} = \frac{\pi }{4} + \frac{\phi }{2} \), \( K = \frac{{1 - \sin^{2} \phi }}{{1 + \sin^{2} \phi }} \). For the centre line (as at point B in Fig. 2), θ = 0, \( K = K_{\text{p}} = \tan^{2} \left( {\frac{\pi }{4} + \frac{\phi }{2}} \right) \).

As shown in Fig. 2, the circular arc can be described with

$$ x^{2} + y^{2} = \frac{{d^{2} }}{{\sin^{2} \theta_{0} }} $$
(6)

The average vertical stress on the “trapdoor” can be obtained by

$$ \sigma_{\text{av}} = \frac{1}{2d}\int\limits_{ - d}^{d} {(\sigma_{1} \sin^{2} \theta + \sigma_{3} \cos^{2} \theta )dx} $$
(7)

In which d is the half width of the trapdoor. Considering the assumption (3) (i.e., σ 1 = Const throughout the arch), the solution of Eq. 7 is

$$ \sigma_{\text{av}} = \left[ {\frac{1}{3}(1 - K_{\text{a}} )\sin^{2} \theta_{0} + K_{\text{a}} } \right]\sigma_{1} $$
(8)

Defining the distribution factor of vertical stress m as

$$ m = \frac{{\sigma_{\text{v}} }}{{\sigma_{\text{av}} }} = \frac{{\sin^{2} \theta + K_{\text{a}} \cos^{2} \theta }}{{\left[ {\frac{1}{3}(1 - K_{\text{a}} )\sin^{2} \theta_{0} + K_{\text{a}} } \right]}} $$
(9)

As shown in Fig. 3, the upward shear stress τ acting on the side of a differential element between the two slip planes (point A in Fig. 3) can be expressed as

Fig. 3
figure 3

A differential element between the two slip planes

Full size image
$$ \tau = K^{\text{A}} \sigma_{\text{v}}^{\text{A}} \tan \phi $$
(10)

Where K A is the ratio of horizontal stress to vertical stress at the slip plane; \( \sigma_{\text{v}}^{\text{A}} \) is the vertical stress at the slip plane. Since \( \sigma_{\text{v}}^{\text{A}} = m^{\text{A}} \sigma_{\text{av}} \) (see Eq. 9), the shear stress on the slip plane can be rewritten as

$$ \tau = K^{\text{A}} m^{\text{A}} \sigma_{\text{av}} \tan \phi $$
(11)

Therefore K s = K A m A

$$ K^{\text{s}} = \frac{{\cos^{2} \theta_{0} + K_{\text{a}} \sin^{2} \theta_{0} }}{{\frac{1}{3}(1 - K_{\text{a}} )\sin^{2} \theta_{0} + K_{\text{a}} }} $$
(12)

Where \( \theta_{0} = \frac{\pi }{4} + \frac{\phi }{2} \), \( K_{\text{a}} = \tan^{2} \left( {\frac{\pi }{4} - \frac{\phi }{2}} \right) \).

Figure 4 shows the value of lateral stress ratio K s for different friction angles ϕ by using various methods. As shown in Fig. 4, according to the method proposed in this paper (Eq. 12), the K s decreases with the increase in ϕ, and this tendency is also revealed by Handy [10], Kirsch and Kolymbas [17], and Marston [22] with other methods. While in the classical wedge-prism model (Anagnostou and Kovari [2]) or in the Terzaghi’s work [26], K s is thought to be a constant which is independent of ϕ. As also shown in Fig. 4, the value of K s from this paper’s method is larger than the at-rest earth pressure coefficient K 0 (Kirsch and Kolymbas [17]) for the same ϕ, which is mainly due to the larger decreasing amplitude of the vertical stress comparing to that of the horizontal stress in the prism (Chen et al. [8] ). It seems that the average value of K s via this paper’s method is much closer to the Terzaghi’s result [26] (i.e., K s = 1.0), which is a little more than the value suggested in the classical wedge-prism model (Anagnostou and Kovari [2]).

Fig. 4
figure 4

Lateral stress ratio K s for different friction angles ϕ by using various methods

Full size image

2.3 Formula for calculating the limit support pressure

Similar to the classical wedge-prism model, the limit support pressure via the improved 3D prism-wedge model is also obtained by the mechanical equilibrium of the wedge (see Fig. 5). In this improved model, the circle-shaped tunnel face is approximated by a rectangle abcd with the same area (see Fig. 5), whose height and length is D (i.e., tunnel diameter) and B (i.e., \( \frac{D}{4} \)), respectively. The inclination angle of the wedge surface abfe is assumed to be β.

Fig. 5
figure 5

Mechanical equilibrium of the wedge

Full size image

The forces acting on the sliding wedge (see Fig. 5) include the following: (1) the self-weight G of the wedge abcdef; (2) the vertical force σ av acting on the upper surface of the wedge (i.e., cdef); (3) the reaction force Q 1 acting on the inclined slip surface abfe; (4) two horizontal normal forces 2Q 2N and two frictional forces 2Q 2T acting on the vertical slip surfaces (i.e., adeand bcf); and (5) the support force S acting on the tunnel face.

It should be noted that the friction force acting on the upper surface of the wedge (i.e., cdef) is ignored in the improved model, which is also not considered in the classical wedge-prism model (Anagnostou and Kovari [2]).

The self-weight G of the wedge is

$$ G = \frac{\pi }{8}\gamma D^{3} \cot \beta $$
(13)

Where γ is the unit weight of the material.

The vertical force σ av is obtained on the basis of the silo theory (Janseen [15]), and the mechanical equilibrium of a series of the thin horizontal slices in the prism is adopted for the detailed derivation of σ av (Broere [5], Kirsch and Kolymbas [17]). Eq. 14 shows the formula ofσ av.

$$ \sigma_{\text{av}} = \frac{\gamma A}{{UK^{s} \tan \phi }}\left( {1 - e^{{ - K^{s} \frac{U}{A}\tan \phi H}} } \right) + q_{0} e^{{ - K^{s} \frac{U}{A}\tan \phi H}} $$
(14)

with

$$ A = B \times L = \frac{\pi D}{4} \times \frac{D}{\tan \beta } $$
(14-1)
$$ U = 2 \times (B + L) = 2 \times \left( {\frac{\pi D}{4}{ + }\frac{D}{\tan \beta }} \right) $$
(14-2)
$$ H = \hbox{min} \left\{ {C,\frac{2D}{\tan \beta }} \right\} $$
(14-3)
$$ q_{0} = \gamma \times \left\{ {C - \hbox{min} \left\{ {C,\frac{2D}{\tan \beta }} \right\}} \right\} $$
(14-4)

Note that A is the area of the cross section of the prism, Uis the circumference of the cross section of the prism, K s is the lateral stress ratio between the prism and the adjoining soils (see Eq. 12), ϕ is the friction angle of the material, H is the height of the prism, and q 0 is the surcharge acting on the upper surface of the prism.

In order to obtain two frictional forces Q 2T acting on the vertical slip surfaces (i.e., ade and bcf), a linear distribution of the vertical stress σ z along the slip surfaces (i.e., ade and bcf) will be assumed (see Fig. 6). As shown in Fig. 6, the gradient of σ z is thought to be γ.

Fig. 6
figure 6

Distribution of the vertical stress σz along the two side slip surfaces of the wedge

Full size image
$$ Q_{{2{\text{T}}}} = \frac{\lambda }{2}\sigma_{\text{av}} D^{2} \cot \beta + \frac{\lambda }{6}\gamma D^{3} \cot \beta $$
(15)

With

$$ \lambda = 1 - \sin \phi $$
(15-1)

Where λ is the ratio of horizontal to vertical stress in the wedge.

Therefore, the support force S can be determined by the equilibrium of the sliding wedge in horizontal and vertical directions.

$$ S = \sigma_{\text{av}} A\tan (\beta - \phi ) + G\tan (\beta - \phi ) - 2Q_{2t} \left[ {\tan (\beta - \phi )\tan \beta + 1} \right]\cos \beta $$
(16)

Thus, the limit support pressure s lim can be expressed as:

$$ s_{\lim } = \hbox{max} \left\{ {\frac{4S}{{\pi D^{2} }}} \right\} = \hbox{max} \{ f_{1} \sigma_{av} + f_{2} \gamma D\} $$
(17)

Where

$$ f_{1} = \frac{\tan (\beta - \phi )}{\tan \beta } - \lambda \varepsilon \tan \phi $$
(17-1)
$$ f_{2} = \frac{\tan (\beta - \phi )}{2\tan \beta } - \frac{1}{3}\lambda \varepsilon \tan \phi $$
(17-2)
$$ \varepsilon = \frac{4}{\pi }\left[ {\cot \beta + \tan (\beta - \phi )} \right]\cos \beta $$
(17-3)
$$ \beta \in [\frac{\pi }{4},\frac{\pi }{2}) $$
(17-4)

3 Results and discussions

3.1 Verification of the improved wedge-prism model

Two typical model tests were selected to verify the accuracy of the improved wedge-prism model. One is the centrifuge model tests conducted by Chambon and Corte [6], the other is the 1 g large-scale model tests performed by Chen et al. [8]. The material used in the centrifuge model tests [6] is the Fontainebleau sand (ϕ = 38°–42°), while the material adopted in the 1 g large-scale model tests [8] is the Yangtze River sand (ϕ = 37∘). Moreover, other theoretical methods were also added for the comparisons, including the classical wedge-prism model (Anagnostou and Kovari [2]), the empirical equation by fitting the FEM results (Vermeer et al. [27]), the wedge-prism model considering horizontal arching (Anagnostou [1] ), the upper-bound solution propose by Leca and Dormieux [20], and the upper-bound solution suggested by Mollon et al. [23].

Figures 7 and 8 compare the normalized limit support pressures s lim/γD for different relative depths C/D obtained from the above-mentioned theoretical methods with those from the centrifuge model tests [6] and 1 g large-scale model tests [8], respectively. Due to a slight uncertainty of the friction angle ϕ of the Fontainebleau sand in the centrifuge model tests [6], two extreme values of ϕ (i.e., ϕ = 38° or ϕ = 42°) were adopted for the calculations (see Fig. 7a, b), respectively. In Figs. 7 and 8, when C/D is less than 1.0, s lim/γD obtained from the improved wedge-prism model (i.e., this study) increases obviously with the increase in C/D, which are also revealed by Anagnostou and Kovari [2]. When C/D is more than 1.0, the s lim/γD via this study seems to increase slowly with the increase in C/D as the results of the centrifuge model tests (Chambon and Corte [6]) shows, which is slightly different from the results of Anagnostou and Kovari [2], Anagnostou [1], Leca and Dormieux [20], Vermeer et al. [27], and Mollon et al. [23].

Fig. 7
figure 7

Comparison of normalized support pressures s lim/γD obtained from the theoretical methods using different fiction angles ϕ with those from centrifuge model tests (Chambon and Corte [6]): a ϕ = 38°, b ϕ = 42°

Full size image
Fig. 8
figure 8

Comparison of normalized support pressures s lim/γD obtained from the theoretical methods with those from 1 g model tests (Chen et al. [8])

Full size image

As shown in Figs. 7 and 8, it should be noted that the normalized limit support pressures s lim/γD obtained from the experiments (i.e., centrifuge model tests (Chambon and Corte [8]) and 1 g model tests (Chen et al. [8])) are less than the results predicted by the above-mentioned theoretical methods in cohesionless soils (i.e., cohesion c = 0). Theoretically, the upper-bound solutions (Mollon et al. [23], Leca and Dormieux [20] ) are the unsafe estimations of the actual limit support pressure for face stability (i.e., smaller or equal to that actually required). Herein, conflicts exist between the results obtained from the experiments and the upper-bound solutions in cohesionless soils. The reasons for the conflicts can be attributed to not fully dried sand adopted in the experiments (Chambon and Corte [6], Chen et al. [8]), which means the soils of the experiments have a little cohesion (i.e., c = 0–5 kPa for the Fontainebleau sand (Chambon and Corte [6]) and c = 0–0.5 kPa for the Yangtze River sand (Chen et al. [8])). As shown in Figs. 7a and 8, if little cohesions are considered in the upper-bound solutions (Mollon et al. [23], Leca and Dormieux [20] ), no conflicts exist between the results of the model tests (Chambon and Corte [6], Chen et al. [8]) and those of the upper-bound solutions (Mollon et al. [23], Leca and Dormieux [20]). Moreover, the cohesion of the material will induce the measured limit support pressure in the model tests less than the actual one without cohesion. More details about the model tests and the upper-bound solutions can refer to the related literatures (e.g., Chambon and Corte [6], Chen et al. [8], Mollon et al. [23]).

As also shown in Figs. 7 and 8, the improved wedge-prism model (i.e., this study), the classical wedge-prism model (Anagnostou and Kovari [2]), and the empirical equation (Vermeer et al. [27]) are reasonable on theory as the s lim/γD obtained from these methods are greater than the s lim/γD predicted by the upper-bound solutions (Leca and Dormieux [20], Mollon et al. [23]). It can be seen that comparing to the improved wedge-prism model (this study) and Vermeer et al.’s empirical equation [27], the classical wedge-prism model (Anagnostou and Kovari [2]) is relatively conservative for predicting the s lim/γD especially for the cohesionless soil with the relatively low friction angle ϕ (e.g., ϕ = 38°). The s lim/γD obtained from the improved wedge-prism model (i.e., this study) agree very well with that from the Vermeer et al.’s empirical equation [27] on the condition that C/D > 1. Note that the Vermeer et al.’s empirical equation [27] was proposed on the basis of a series of rigorous FEM calculations; thus, it means the improved wedge-prism model (i.e., this study) has sufficient accuracy for predicting the limit support pressure. Moreover, the wedge-prism model considering horizontal arching (Anagnostou [1] ) seems to slightly underestimate the actual limit support pressure as the s lim/γD obtained from this method are smaller than the s lim/γD predicted by the upper-bound solution proposed by Mollon et al. [23]. In addition, the upper-bound solution proposed by Mollon et al. [23] can predict s lim/γD more accurately than the upper-bound solution suggested by Leca and Dormieux [20] due to the optimization of the failure mechanism.

Furthermore, the effects of H (i.e., the height of the prism) on s lim (i.e., the limit support pressure) should also be investigated for the relatively deep buried tunnel (e.g., C/D = 1 or 2). As pointed in Sect. 2.1, for the relatively deep buried tunnel, the recommended value of H/L in the improved wedge-prism model is 2, while the range of H/L in Table 1 is 1.5–2.5. Thus, consider H/L of 1.5 and 2.5, respectively, as the lower limit and upper limit of H/L in the improved wedge-prism model. As shown in Eq. 17, s lim increases with the increase in σ av (i.e., the vertical force acting on the upper surface of the wedge). Take the derivative of Eq. 14 with respect to H, the following equation (i.e., Eq. 18) can be obtained.

$$ \sigma_{\text{av}}^{'} = - \gamma \left( {C - H} \right)K^{\text{s}} \frac{U}{A}\tan \phi e^{{ - K^{\text{s}} \frac{U}{A}\tan \phi H}} $$
(18)

Obviously, \( \sigma_{\text{av}}^{'} \) is less than zero. That means σ av decreases with the increase in H. Then, we can get a conclusion that s lim decreases with the increase in H for the relatively deep buried tunnel. Thus, \( s_{{_{\lim } }}^{{{\text{H/L = }}2.5}} > s_{{_{\lim } }}^{{{\text{H/L = }}2}} > s_{{_{\lim } }}^{{{\text{H/L = 1}} . 5}} \) (\( s_{{_{\lim } }}^{{{\text{H/L = }}2.5}} \), \( s_{{_{\lim } }}^{{{\text{H/L = }}2}} \), and\( s_{{_{\lim } }}^{{{\text{H/L = 1}} . 5}} \)corresponding to the limit support pressure via H/L = 2.5, 2, and 1.5, respectively). As \( s_{{_{\lim } }}^{{{\text{H/L = }}2}} \)has good accuracy (see Figs. 7 and 8), \( s_{{_{\lim } }}^{{{\text{H/L = }}2.5}} \)is relatively conservative, while the safety degree of \( s_{{_{\lim } }}^{{{\text{H/L = 1}} . 5}} \)for the engineering application will decrease. In general, H/L = 2 is suitable for the improved wedge-prism model for calculating the limit support pressure of the tunnel face in the relatively deep buried tunnel.

To sum up, the improved wedge-prism model has sufficient accuracy as the limit support pressure obtained via this model agrees well with that obtained via Vermeer et al.’s method [27] which was proposed based on a series of rigorous FEM calculations. In addition, the improved wedge-prism model is also a relatively safe estimation of the limit support pressure for the practical application.

3.2 A design chart of the limit support pressure

Considering the convenience of industrial application, a design chart of the limit support pressure for cohesionless soils via the improved wedge-prism model was given in this paper (see Fig. 9). Fig. 9 shows the calculated normalized support pressure s lim/γD with different friction angle ϕ for a series of relative depth C/D. As shown in Fig. 9, for the same C/D, the s lim/γD decreases with the increase in ϕ, and the rate of reduction for s lim/γD also decrease as the increase in ϕ. As also shown in Fig. 9, for the same ϕ, the s lim/γD increases with the increase in C/D, while the rate of increase for s lim/γD decreases with the increase in ϕ. For the situations that the s lim/γD may not be directly obtained from the design chart (e.g., C/D = 0.8 and ϕ = 34.5∘), the linear interpolation method can be adopted for the approximate determination of s lim/γD.

Fig. 9
figure 9

Design chart of the limit support pressure for cohesionless soils

Full size image

4 Conclusions

In order to properly calculate the limit support pressure for tunnel face stability in cohesionless soils, an improved 3D wedge-prism model which optimizes the failure mechanism and considers soil arching effects was proposed in this paper. The height of the prism H is thought to be min {C,2L} (where C is the cover depth and L is the width of the prism). An analytical formula for the lateral stress ratio K s between the prism and the adjoining soils which reflects soil arching effects was also proposed. Comparing the results (i.e., limit support pressure) from the theoretical models and type model tests (i.e., centrifuge model test (Chambon and Corte [6]) and 1 g model tests (Chen et al. [8])), it is found that limit support pressure obtained by the improved wedge-prism model is sufficiently accurate as it is very close to the result obtained by Vermeer et al.’s method [27] which was put forward based on a series of rigorous FEM calculations. For the convenience of industrial application, a design chart on the basis of the improved wedge-prism model was proposed finally for calculating the limit support pressure in cohesionless soils. The main conclusions on the limit support pressure are presented as follows:

  1. 1.

    When the relative depth C/D ≤ 1, the normalized support pressure s lim/γD increase obviously as the increase in C/D. When C/D > 1, the normalized support pressure s lim/γD seems to increase slowly with the increase in C/D.

  2. 2.

    For the same relative depth C/D, the normalized support pressure s lim/γD decreases with the increase in ϕ, and the rate of reduction for s lim/γD also decrease as the increase in ϕ.

  3. 3.

    For the same friction angle ϕ, the s lim/γD increases with the increase in C/D, while the rate of increase for s lim/γD decreases with the increase in ϕ.