Viscoelastic damage model for asphalt concrete

Abstract

The strain rate-dependent mechanical behavior of asphalt concrete was characterized using unconfined compression tests carried out at different loading rates. It was shown that at high strain rates, the elastic deformation and peak axial stress are highly sensitive to strain rate. Both increase as the strain rate increases. At very low strain rates, elastic response and unconfined compressive strength are relatively independent of the loading rate. Based on the experimental observations, a simple viscoelastic damage model is proposed for the strain rate-dependent unconfined compression behavior of asphalt concrete. In the model, strain rate response is modeled by a two-component viscoelastic model consisting of a constant elastic modulus and a viscous modulus that is related by a power-law function to the axial strain rate. Failure and strain softening are modeled via a damage formulation where damage evolution in the asphalt concrete is given by a simple form of the Weibull distribution function. The model was shown to be capable of describing the strain rate-dependent deformation, compressive strength, strain-softening and creep behavior of asphalt concrete. The model is relatively simple and requires only five material parameters.

1 Introduction

Pavement materials are expected to perform well in terms of bearing capacity, rutting resistance, cracking resistance, drainage, tolerance of using lower grades aggregates, ease of maintenance, and long service life. Satisfying these demands simultaneously at high levels is not easy, because a change in mix design of an asphalt concrete aimed at improving some aspects of performance may degrade other aspects as a trade-off. In addition, the mechanical behavior of asphalt concrete is generally complex due to rate dependency, damage and fracture evolution, and the interaction of aggregates and binder. The mechanistic-empirical design procedure is acknowledged as the most advanced approach for the current practical design of asphalt concrete mixes and pavement (e.g., [2, 10]). Empirical methods are generally not suitable for complex design conditions and for newly developed materials, pavement structures, and construction methods. The success of mechanics-based design depends heavily on the development of appropriate constitutive models of pavement materials capable of accounting for complex material behavior.

Studies relating macroscopic mechanical response to microstructural properties and microstructural evolution are necessary to develop reliable constitutive models appropriate for wide-ranging asphalt concrete materials subjected to complex design conditions. Damage evolution and crack growth during deformation have been one of the main concerns in studies on the mechanical response of viscoelastic/viscoplastic materials [1, 3, 4, 6, 9, 12, 15, 16, 19, 20]. Experimental investigations that relate microstructural observations to macroscopic behavior and micromechanical models based on particulate composites indicate that viscoelastic behavior and crack growth are the main mechanisms accounting for the macroscopic behavior of asphalt concrete [15, 16]. Aggregate re-orientation in hot mix asphalt, de-bonding between aggregates and binder, fracture/damage growth, and interlocking of aggregates have been visually observed in asphalt concrete subjected to uniaxial and triaxial loading [18, 19]. Theoretical framework of constitutive models developed for elastic and viscoelastic behavior and damage growth of composite materials [15–17] have been applied to asphalt concrete materials [7, 14]. Constitutive models for the mechanical behavior of asphalt concrete should account for behavior of aggregates such as dilatancy, anisotropy, stress level dependency, and microstructural changes [5, 8, 18].

In order to be applicable to various asphalt concrete mixes including newly developed materials, a constitutive model should be described by intrinsic mechanical properties and behavior of the constituent materials. Constitutive modeling techniques are becoming sophisticated, and they generally provide good agreement with experimental data on the behavior of asphalt concrete. However, most of these models are relatively complicated and need several mostly curve-fitting model parameters. Extensive laboratory tests are often required to determine the model parameters (e.g., [2, 4, 7, 11]).

This paper aims to present a relatively simple constitutive model for asphalt concrete that requires only five easy to determine model parameters. The model accounts for the rate-dependent response of asphalt concrete using viscoelasticity, and for failure and strain-softening behavior using damage mechanics. The model is based on the results of unconfined compression tests on specimens of different mixtures of asphalt binder and aggregate, including pure asphalt binder, loaded at different strain rates. Tests on pure asphalt binder were conducted to determine whether the strain rate behavior of asphalt concrete is controlled mainly by that of the binding material. A procedure is proposed to statistically quantify the damage evolution of asphalt concrete. A damage evolution function in the proposed model is based on a statistical distribution model originally proposed to describe the probability of failure of engineering materials. The proposed model is validated against experimental data.

2 Test materials and procedures

2.1 Test material

Two types of materials were used for the unconfined compression tests: (1) asphalt concrete mix consisting of asphalt binder and aggregates, and (2) pure asphalt binder. The specimens of the former material were prepared by compacting a mixture of straight asphalt, filler, and silica aggregate equally divided in five layers. The mass mix proportions of asphalt, filler, and aggregate are 0.12, 0.43, and 1.0, respectively. The pure binder specimens are a mixture of the straight asphalt and the filler. The mix proportion of asphalt–filler is the same as that of the asphalt concrete specimen. The silica aggregate used has the grain size distribution curve shown in Fig. 1, and the grain density is 2.65 g/cm³.

Fig. 1

Grain size distribution of silica aggregate

The preparation procedures of the asphalt concrete specimens are as follows: the straight asphalt (PG58-28) is mixed with the filler (a heavy calcium carbonate powder) at the prescribed mix proportion. Then, the asphalt–filler mixture is mixed with the aggregate. The mixtures of the individual layers are prepared separately, and each layer is tamped in a cylindrical aluminum mold to remove air bubbles as much as possible. The internal diameter and the length of the aluminum mold are 50.8 and 101.6 mm, respectively. The entire sample mixing and preparation were done at a temperature of approximately 160°C. The hot mixture is then statically compacted by applying 5.0 MPa of axial stress. After the temperature of mold is decreased to room temperature, the specimen is extruded from the mold by applying axial stresses not exceeding 1.0 MPa. Both ends of the specimen are polished with wet silicon carbide sandpapers graded as 120 and 220 grits to ensure good contact between the aggregate grains embedded in the specimen ends and loading platens of unconfined compression apparatus. The bulk density of the specimen is about 2.35 g/cm³. The specimens are cured for 4 days before testing. The averages of the diameter and length of the specimens are 50.9 and 102 mm, respectively.

The asphalt binder specimens are prepared by pouring the asphalt–filler mixture in the mold at 160°C. Air bubbles trapped in the mixture are vented by sufficiently heating the mixture in the mold and pouring the mixture at a slow rate. The asphalt binder specimens have been prepared without compaction. The axial stresses applied when the specimens are extruded from the mold are lower than 0.5 MPa. Both ends of the specimens are polished using sandpaper to make those flat and parallel. The curing period is 4 days. The bulk density of the specimens is 2.00 g/cm³. The average dimensions of the asphalt binder specimens are 50.7 mm in diameter and 100 mm in height.

2.2 Unconfined compression tests

The unconfined compression tests were carried out on both the asphalt binder and asphalt concrete specimens. The loading frame used to load the sample is equipped with a DC motor capable of providing a range of loading speeds from 0.2 to 50.8 mm/min. A load cell of 50-kN capacity was used to measure the axial load. The maximum non-linearity of the load cell is 0.03% of full scale. The axial displacement was measured by using a linear strain conversion transducer having 10 mm of capacity and non-linearity better than ±0.1% of full-scale deflection. Both ends of the specimens used for the test were lubricated by using a silicon grease to reduce the friction and adhesion between the specimen and the loading platens. The loading platens are short aluminum cylinders having 102 mm of diameter and 25 mm of thickness. The top loading platen is not allowed to tilt during loading. The testing temperature is 22 ± 1°C. The values of axial strain rate $\dot{\varepsilon }$ in constant rate-unconfined compression test are 4.2 × 10⁻⁶, 1.7 × 10⁻⁵, 1.7 × 10⁻⁴, and 1.7 × 10⁻³ s⁻¹.

3 Strain rate-dependent compression behavior

Figure 2 shows the unconfined compression stress–strain curves of the asphalt binder specimens at different strain rates. Following the initial linear response, each stress–strain curve reached the peak point followed by strain-softening behavior at axial strains ranging from 0.10 to 0.14. The repeatability of the unconfined compression test results can be confirmed from a good agreement between two test results observed at $\dot{\varepsilon }$ = 1.7 × 10⁻³ s⁻¹. The peak stress increased with increasing strain rate when $\dot{\varepsilon }$ ≥ 1.7 × 10⁻⁵ s⁻¹. The values of peak stress are 0.64, 0.66, 1.03, and 1.69 MPa at axial strain rates of 4.2 × 10⁻⁶, 1.7 × 10⁻⁵, 1.7 × 10⁻⁴, and 1.7 × 10⁻³ s⁻¹, respectively. The elastic modulus is also sensitive to the strain rate and increases with the strain rate when $\dot{\varepsilon }$ ≥ 1.7 × 10⁻⁵ s⁻¹. The values of elastic modulus (Young’s modulus) are 7.5, 7.2, 10, and 14 MPa at strain rates of 4.2 × 10⁻⁶, 1.7 × 10⁻⁵, 1.7 × 10⁻⁴, and 1.7 × 10⁻³ s⁻¹, respectively. The elastic Young’s moduli were determined as the tangent modulus of the linear portions of axial stress versus axial strain curves observed at axial strains less than 6.0 × 10⁻². The unconfined compression response of asphalt binder specimens appears to be independent of strain rates when $\dot{\varepsilon }$ ≤ 1.7 × 10⁻⁵ s⁻¹.

Fig. 2

Unconfined compression stress–strain curves of asphalt binder at different strain rates

Similar rate-dependent stress–strain results were obtained for the asphalt concrete specimens as shown in Fig. 3. Both the elastic modulus taken from the initially linear part of the stress–strain curve and the peak stress increase with increasing strain rate. The peak axial stress values are 0.946, 1.45, 2.78, and 5.75 MPa at strain rates of 4.2 × 10⁻⁶, 1.7 × 10⁻⁵, 1.7 × 10⁻⁴, and 1.7 × 10⁻³ s⁻¹, respectively. The corresponding elastic modulus determined as the tangential modulus of the linear parts of axial stress-axial strain curves observed when the axial strain is lower than 1.0 × 10⁻² are 55, 80, 140, and 370 MPa, respectively. On the other hand, the axial strain values corresponding to the peak axial stress appear to be similar and independent of the strain rate. The range of axial strain at peak is from 2.5 × 10⁻² to 3.0 × 10⁻².

Fig. 3

Unconfined compression response of asphalt concrete at different strain rates

The strain rate dependencies of the stress–strain response of the asphalt concrete and asphalt specimens are shown in Fig. 4 in terms of the elastic Young’s moduli E as function of the axial strain rate $\dot{\varepsilon }$ in the log–log plot. The effects of the viscous behavior of the asphalt binder clearly appear on the strain rate-dependent Young’s modulus. The asphalt concrete specimens have consistently higher Young’s modulus than the asphalt binder in the tested range of strain rates. The Young’s modulus of asphalt concrete can be adequately given by a power-law function with a power exponent of 0.31. Similarly, the Young’s modulus of asphalt binder is adequately represented by a power-law function of strain rate; however, the Young’s modulus becomes less sensitive to loading rate when $\dot{\varepsilon }$ ≤ 1.7 × 10⁻⁵ s⁻¹. The slope of the linear part of log(E) − log($\dot{\varepsilon }$) plot is 0.13. The asphalt concrete is more sensitive to strain rate in the Young’s modulus compared to the asphalt binder.

Fig. 4

Strain rate sensitivity of elastic modulus of asphalt concrete and asphalt binder

The unconfined compression strengths $\sigma_{\max }$ of the asphalt binder and the aggregate-mixed specimens are compared in Fig. 5. Similar to the Young’s modulus, a linear log–log relationship exists between $\sigma_{\max }$ and $\dot{\varepsilon }$ for the asphalt concrete specimens. For the asphalt binder specimens, a similar linear log–log relationship is valid only when $\dot{\varepsilon }$ ≥ 1.7 × 10⁻⁵ s⁻¹. Below this strain rate, $\sigma_{\max }$ of asphalt binder is almost unaffected by strain rate. The slope of the linear log–log plot is equal to 0.20 for the asphalt binder and 0.30 for the asphalt concrete. The strain rate sensitivities of the elastic modulus and $\sigma_{\max }$ as expressed by their respective slopes in the log–log plot appear to be comparable. The $\sigma_{\max }$ of the asphalt concrete specimens were 1.5–3.4 times higher than that of the asphalt binder specimens.

Fig. 5

Strain rate sensitivity of unconfined compression strength of asphalt concrete and asphalt binder

4 Observations of deformation and failure processes

It can be concluded from the above results that the presence of aggregates in the asphalt matrix increases the compressive strength and stiffness of asphalt concrete. The bonding stiffness between aggregate grains, intergranular friction, and constrained dilatancy of aggregate grains are considered as the main mechanisms responsible for the increased elastic modulus and compressive strength of asphalt concrete. However, it can be seen from Figs. 4 and 5 that the reinforcement provided by aggregates decreases as the strain rate decreases.

The initially linear unconfined compression responses of the asphalt concrete specimens shown in Fig. 3 are likely to arise from the linear response of asphalt concrete observed in Fig. 2 and the interaction of aggregate grains bearing the axial loading. The aggregates resist the axial loading by mobilizing contact stiffness and intergranular friction. The asphalt binder should behave like an elastic wall against the dislocation of aggregate grains induced by local contact sliding, contact force chain rearrangement, and dilatancy.

The fractures that appeared in the asphalt concrete specimens were visually different from those of the asphalt binder specimens. The asphalt concrete specimens have bulged in radial direction due to axial loading. As shown in Fig. 6, which is a photograph of the asphalt concrete specimen at the end of an unconfined compression test, shear bands have formed in the bulged zone. It can be seen that a number of crack openings are distributed in a diamond pattern on the lateral surface of sheared zone. The sheared zone being obviously less dense than the undamaged zone indicates that the sheared zone has developed as a result of strong dilatancy.

Fig. 6

Picture of a asphalt concrete specimen after failure

To determine the role of fracturing in the response of the asphalt binder and asphalt concrete, the total energy inputs required for fracturing (total energy input at the peak of stress) at the different strain rates are plotted in Fig. 7. The energy input is calculated as:

Fig. 7

Comparison of total energy inputs required for fracture between asphalt concrete and asphalt binder

$$ W_{\text{p}} = \int\limits_{0}^{{\varepsilon_{\text{p}} }} {\sigma d\varepsilon } $$

(1)

where ε_p is the axial strain at peak stress point. The required energy for both specimens increases as the strain rate increases in a power-law relation with the axial strain rate. The asphalt concrete and the asphalt binder specimens macroscopically require similar levels of energy input to be fractured when $\dot{\varepsilon }$ ≥ 1.7 × 10⁻⁵ s⁻¹, although the fracture of reinforcement provided by aggregates seems to need higher energy. This may be attributed to the fact that the interface between aggregate grains and asphalt binder exists and contributes to a different pattern of fracturing. The interface is in general more susceptible to damage and fracture than the binding material. In addition, the highly localized deformation observed in the asphalt concrete requires smaller fracture energy. It was observed that the deformations of the asphalt binder specimens are more homogeneous compared to the asphalt concrete specimens that have fractured. The asphalt binder specimens uniformly expanded in the radial direction without development of visible shear bands.

The strain rate sensitivity of the required energy is unlikely to depend on the presence of aggregates when $\dot{\varepsilon }$ ≥ 1.7 × 10⁻⁵ s⁻¹. This may suggest that the crack growth process in the asphalt concrete specimens is not dependent on the strain rate. In the fracture growth process, dilatancy, rolling, and sliding of aggregate grains should occur. If, for example, the degree of dilatancy changes depending on the strain rate, the strain rate sensitivity of the required energy may be different from the asphalt binder specimen. The axial strain at which the maximum stress is mobilized is almost independent on the strain rate for asphalt concrete as shown in Fig. 3. This experimental evidence indicates that the initial geometrical arrangement of aggregate grains in asphalt concrete controls the macroscopic failure of asphalt concrete irrespective of strain rate.

5 Model for strain rate-dependent behavior of asphalt concrete

Strain rate dependency of the Young’s modulus of the asphalt concrete specimens was represented by a linear log–log function as shown in Fig. 4. However, the Young’s modulus of the asphalt binder is insensitive to the strain rate when $\dot{\varepsilon } \le 1.7\times10^{-5}\,\hbox{s}^{-1}$. It is reasonable to assume that the Young’s modulus of asphalt concrete should also become constant at lower strain rates. In other words, elastic response is rate independent at very low strain rates and rate dependent above a threshold strain rate, for both asphalt binder and asphalt concrete. Based on this observation, the model for the linear stress–strain response of asphalt concrete is assumed to consist of a static spring E _s and a strain rate-dependent spring E _v connected in parallel as shown schematically in Fig. 8. The constitutive relationship of this model can be expressed as

Fig. 8

Schematic diagram of the constitutive model for the viscoelastic response of asphalt concrete

$$ \sigma = \left( {E_{\text{s}} + E_{\text{v}} } \right)\,\varepsilon . $$

(2)

From Fig. 4, the strain rate-dependent component of Young’s modulus can be defined as a power-law function of strain rate:

$$ E_{\text{v}} = E_{\text{vr}} \dot{\varepsilon }^{{r}} $$

(3)

where E _vr and r are the material parameters. The parameter r characterizes the strain rate sensitivity of the Young’s modulus.

Linkage between microstructural change caused by damage growth and macroscopic behavior can be described in the framework of continuum damage mechanics [13]. The mechanical response of a material with damage growth is described through an imaginary undamaged material having the equivalent load-carrying area to the damaged material [6, 13]. A parameter representing the degree of damage is given by the ratio of the total area of the damaged portions A _D, and the total sample cross-sectional area A:

$$ D = \frac{{A_{D} }}{A} $$

(4)

The range of the damage parameter is 0 ≤ D ≤ 1, where D = 0 for an intact material and D = 1 for a fully damaged material. The corresponding effective stress applied to the imaginary undamaged material is given by:

$$ \sigma_{\text{e}} = \frac{\sigma }{1 - D} $$

(5)

where σ_e is the effective stress and σ is the stress of the damaged material.

Assuming the effective stress σ_e governs the mechanical behavior of the damaged material, the complete stress–strain relationship of the aggregate-mixed specimen can be written as:

$$ \sigma = \left( {1 - D} \right)\left( {E_{\text{s}} + E_{\text{vr}} \dot{\varepsilon }^{{r}} } \right)\varepsilon $$

(6)

The unconfined compression behavior (Fig. 3) indicates that the damage evolution in the asphalt concrete should be a function of strain. Weibull [21] proposed a statistical distribution functions applicable to problems concerning material failure. A general form of the Weibull cumulative distribution function of the probability of an event x can be written as:

$$ F\left( x \right) = 1 - \exp \left[ { - \left( {\frac{x}{\lambda }} \right)^{m} } \right] . $$

(7)

for $x \ge 0$ and $F(x) = 0$ for $x < 0$. In the above equation, m is a shape parameter and λ > 0 is a scaling parameter.

It is expected that the damage will increase with increasing axial strain ε, and thus the damage or probability of failure may be related to the axial strain ε. Substituting ε for the event parameter x in Eq. (7) yields the following damage evolution law for asphalt concrete:

$$ 1 - D = \exp \left[ { - \left( {\frac{\varepsilon }{{\varepsilon_{0} }}} \right)^{m} } \right] $$

(8)

where ε₀ and m are treated as material parameters. The parameter (1–D) corresponds to the probability of survival of asphalt binder. The parameter ε₀ represents the strain value at which the probability of survival decreases to 0.37. The shape parameter m is also termed the Weibull modulus. More generalized forms are proposed in previous studies (e.g., [11]). Compared to the generalized functions, Eq. (8) is very simple and characterized by only two material parameters.

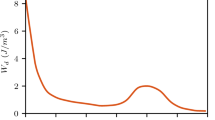
To provide a micromechanical basis for the proposed damage model, Fig. 9 compares the proposed damage evolution function calculated using best-fit values of ε₀ and m against visual observation data of void content growth in a hot mix asphalt material from the study of Tashman et al. [18]. The experimental data in the literature were obtained from X-ray CT images of unconfined compression specimen. In the Tashman et al. investigation, the void content increased from 7 to 13.5% as the axial strain increases from 0 to 8 × 10⁻². The experimental data are normalized by using the value of void content growth at 8 × 10⁻² of axial strain to indicate the evolution of damage. They mentioned that this void content change is considerably lower than that estimated from the damage to which the asphalt concrete is subjected. It is reported that the small change in void content is due to the effect of localized fracture of asphalt concrete observed. This point is the same with the asphalt concrete tested here as shown in Fig. 6. On the other hand, models developed based on the continuum damage mechanics assume a uniform distribution of cracks and voids advancing in material.

Fig. 9

Comparison of the proposed damage evolution function with the literature data on normalized void content change during unconfined compression carried out on different asphalt concretes [18]

Nevertheless, it can be seen that the shape of the damage evolution function agrees well with that of the experimental relationship between the change of void content normalized and axial strain. This agreement provides a micromechanical basis for the validity of the proposed evolution function form. However, the void content should not be sufficient to quantify the damage accumulated in the asphalt concrete. The local dislocation of aggregate grains can degrade the adhesion at asphalt-aggregate interface and the asphalt binder itself without visible crack advance as long as the local strain is not so significant. To develop a model reflecting more realistic damage evolution, the approach to quantify the degradation in the absence of crack advance as well as the localized damage growth needs to be clarified in detail. Note that the proposed model assumes no damage in the material at the initial state.

Combining Eqs. (6) and (8) yields the following model for the rate-dependent stress–strain behavior of asphalt concrete:

$$ \sigma = \exp \left[ { - \left( {\frac{\varepsilon }{{\varepsilon_{0} }}} \right)^{m} } \right]\,\left[ {E_{\text{s}} + E_{\text{vr}} \left( {\frac{d\varepsilon }{dt}} \right)^{r} } \right]\varepsilon $$

(9)

The maximum axial stress predicted by Eq. (9) can be obtained by differentiating the above equation with respect to axial strain that yields:

$$ \frac{d\sigma }{d\varepsilon } = \left[ {1 - m\left( {\frac{\varepsilon }{{\varepsilon_{0} }}} \right)^{m} } \right]\,\left[ {E_{\text{s}} + E_{\text{vr}} \left( {\frac{d\varepsilon }{dt}} \right)^{r} } \right]\exp \left[ { - \left( {\frac{\varepsilon }{{\varepsilon_{0} }}} \right)^{m} } \right] $$

(10)

The maximum stress state should be observed when dσ/dε = 0. Setting Eq. (10) equal to zero and solving for ε gives the following axial strain at which the maximum stress state occurs:

$$ \varepsilon = \varepsilon_{0} m^{{ - {1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-\nulldelimiterspace} m}}} \text{ at }\sigma = \sigma_{\max } $$

(11)

The above equation indicates that the axial strain at which the maximum axial stress occurs is constant and independent of strain rate. This prediction is approximately in accord with the experimental results shown in Figs. 2 and 3. Substituting Eq. (11) in Eq. (9) yields the analytical expression for unconfined compressive strength of asphalt concrete:

$$ \sigma_{\max } = C_{1} \left[ {E_{\text{s}} + E_{\text{vr}} \left( {\frac{d\varepsilon }{dt}} \right)^{r} } \right] $$

(12)

where

$$ C_{1} = \exp \left( { - \frac{1}{m}} \right)\,\varepsilon_{0} m^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} m}} \right. \kern-\nulldelimiterspace} m}}} $$

(13)

Eqs. (12) and (13) predict that the maximum axial stress increases as a power function of the strain rate and is a direct function of the material parameters E _s , E _vr, ε₀, m, and r. Finally, Eq. (9) can also be inverted to yield an equation for the strain rate:

$$ \frac{d\varepsilon }{dt} = \left\{ {\left( {\frac{\sigma }{{E_{\text{vr}} \varepsilon }}} \right)\exp \left[ {\left( {\frac{\varepsilon }{{\varepsilon_{0} }}} \right)^{m} } \right] - \frac{{E_{\text{s}} }}{{E_{\text{vr}} }}} \right\}^{{{1 \mathord{\left/ {\vphantom {1 r}} \right. \kern-\nulldelimiterspace} r}}} $$

(14)

This equation can be numerically integrated with respect to time to simulate the deformation of asphalt concrete during creep under a constant stress level σ.

6 Model performance and validation

The performance of the proposed model is compared with the results of the previously presented uniaxial compression tests on specimens of asphalt concrete. To characterize the Young’s modulus of asphalt concrete, it is assumed that the static component E _s is the same with that of the asphalt binder. The values of E _s, E _vr, and r for the asphalt binder specimen are determined to be 5.70 × 10⁻³ GPa, 4.46 × 10⁻² GPa·s^r, and 0.278 by fitting Eqs. (2) and (3) to the experimental data. For the asphalt concrete, the other parameters, E _vr and r, are determined to be 3.15 GPa and 0.339, respectively, by fitting Eqs. (2) and (3) and substituting 5.70 × 10⁻³ GPa in E _s to the experimental data. Figure 10 compares the model curves for Young’s modulus determined with the experimental data. The model adequately represents both experimental data in the range of strain rate examined. The model curves coincide when the strain rate is lower than 1.0 × 10⁻¹² s⁻¹.

Fig. 10

Modeling of strain rate dependency of Young’s modulus of asphalt concrete and asphalt binder specimens

The material parameters for the damage evolution function were determined as shown in Fig. 11 in which a relationship between the probability of survival of the asphalt binder in the asphalt concrete specimens and the axial strain is presented. Note that the degradation model applies to the asphalt binder as mixed with aggregate and not the pure binder. The probability of survival can be experimentally given by the ratio of axial stress to the product of elastic modulus and axial strain, which are derived from Eq. (6), that is:

$$ \left( {1 - D} \right) \approx \frac{\sigma }{E\varepsilon } $$

(15)

The experimental relationships between the probability of survival and axial strain shown by using the plots are almost the identical irrespective of the strain rate. The damage growth becomes significant, i.e., becomes significantly less than 1.0, when the axial strain exceeds 2 × 10⁻².

Fig. 11

Fitting of damage evolution function to the experimental data. Damage evolution function curves are obtained by using ε₀ = 4.06 × 10⁻²

The material parameters ε₀ and m characterizing the damage evolution process were determined by minimizing the following weighted residual:

$$ S = \sum\limits_{i = 1}^{n} {W_{i} r_{i}^{2} } $$

(16)

where W _i is the weight and r _i is the residual between the experimental data points given by Eq. (15) and the function values of Eq. (8). The effect of damage on mechanical behavior becomes more significant at larger strain levels. As for the weighting function, a monotone increasing function of axial strain should be appropriate, e.g.,

$$ W_{i} = \beta \varepsilon^{\alpha } $$

(17)

where α and β are constants. In this study, 2 and 1,000 were used for the values of the respective constants. A best-fit curve was obtained with ε₀ = 4.06 × 10⁻² and m = 1.73. Note that these values are very similar to the values of ε₀ = 4.9 × 10⁻² and m = 2.72 obtained in the curve fitting of the damage parameter D through the void content change measurements made in [18]. Better agreement can be seen between the experimental data and the model curve when ε ≥ 3.0 × 10⁻².

The sensitivity of the probability function to the Weibull modulus m can be seen in Figs. 11 and 12. The axial strain at which a significant decrease in the probability of survival occurs increases with increasing m. On the other hand, the probability of survival becomes lower as m increases when ε > ε₀. The higher Weibull modulus gives the more sudden and rapid degradation of asphalt binder for ε > ε₀. The values of the model parameters for the aggregate-mixed asphalt material are shown in Table 1.

Fig. 12

Sensitivity of model stress–strain curve to the Weibull modulus at 1.7 × 10⁻⁵ s⁻¹ of strain rate

Table 1 Model parameters used to simulate the strain rate sensitive compression behavior of asphalt concrete

Figure 12 indicates the sensitivity of the stress–strain curve to the Weibull modulus at a strain rate of 1.7 × 10⁻⁵ s⁻¹. The values of the other material parameters are the same with those shown in Table 1. The stress–strain curves deviate from the elastic relationship at different strain levels and subsequently reach individual peak points. The axial strain values at which the deviation occurs are approximately 4 × 10⁻³, 8 × 10⁻³, and 2.5 × 10⁻² for m = 1.0, 1.73, and 10, respectively. The peak stress values are 1.21, 1.35, and 2.37 MPa for m = 1.0, 1.73, and 10, respectively. The peak stress becomes higher and the strain softening becomes strong as the Weibull modulus increases.

A comparison result of the model generated stress–strain curves with the experimental data is shown in Fig. 13. The model stress–strain curves are generally in good agreement with the experimental data. Transition from linear to nonlinear stress–strain behavior and the strain rate sensitivity of the peak stress are appropriately described in the model behavior. In addition, the strain-softening behavior given by the model satisfactorily agrees with the experimental data within 7 × 10⁻² of axial strain.

Fig. 13

Comparison of simulated and experimental unconfined compression behavior of asphalt concrete at different strain rates

Figure 14 shows a comparison of the strain rate-dependent unconfined compressive strength of the asphalt concrete from Eq. (12) and the experimental data. As can be seen, the model fits the experimental data well. Note that the constant $C_{1}$ used to plot Eq. (12) in Fig. 14 was determined from the material parameters listed in Table 1.

Fig. 14

Comparison of simulated and experimental strain rate-dependent unconfined compressive strength of asphalt concrete

The final comparison of the model predictions with experimental data is shown in Fig. 15 in terms of uniaxial creep deformation. Creep tests were conducted on two asphalt concrete specimens at constant axial stresses σ₀ of 0.2 and 3 MPa by using the unconfined compression test equipment. The testing temperature is 22 ± 1°C. The prescribed axial stresses 0.2 and 3 MPa were generated at 1.7 × 10⁻³ and 9.4 × 10⁻⁴ s⁻¹ of strain rates, respectively, in the begging of the tests.

Fig. 15

Comparison of simulated and experimental creep deformation of asphalt concrete at two constant stress levels. The lower and upper x-axes indicate the time scales for data obtained at σ₀ = 0.2 and 3 MPa, respectively

To simulate the experimental results, Eq. (14) was integrated numerically in time using the same set of parameters given in Table 1. As can be seen in Fig. 15, the model predictions agree satisfactorily with experimental results. An interesting observation is that the model is able to predict the three stages of creep for the tested materials: primary, secondary, and tertiary. The three stages are particularly visible in the simulation of the creep test at 3.0 MPa. In the initial or primary creep stage, the creep rate is relatively high but slows with increasing time. At secondary or steady-state creep, the creep rate eventually reaches near constant value. In the tertiary stage, creep exponentially increases with time because of accelerated fracturing and failure of the tested material. In the observed creep behavior, the boundary between the primary and the secondary phases is likely at 20 s. The tertiary creep is observed after 90 s from the start of creep test. The times predicted by using the model as the starting points of secondary and tertiary phases are 30 and 100 s. At σ₀ = 0.2 MPa, the secondary phase of creep seems to have started at 22 h, but the tertiary creep is not observed in the tested range of time. The boundary between the primary and the secondary phases predicted by the model is approximately 36 h.

The strain rates experimentally observed and predicted in the uniaxial creep test at σ₀ = 0.2 MPa are compared in Fig. 16. The $\dot{\varepsilon }$ experimentally observed varies from 1 × 10⁻⁴ to 1 × 10⁻⁸ s⁻¹. The predicted $\dot{\varepsilon }$ becomes smaller than 4.2 × 10⁻⁶ s⁻¹ at t > 6 × 10⁻² h. The strain rate dependency of Young’s modulus at $\dot{\varepsilon }$ < 4.2 × 10⁻⁶ s⁻¹ has been characterized without experimental data as shown in Fig. 10. Nevertheless, it can be seen that the predicted creep behavior is in good agreement with the observed behavior even in such low range of strain rate. The predicted probability of survival of the asphalt binder, 1–D, is also shown in the figure and indicates that the effect of damage evolution on the predicted behavior is small. The value of D increases to 0.12 at t = 10 h. Even at t = 80 h, D is not greater than 0.27.

Fig. 16

Strain rate and calculated area ratio of undamaged to initial during uniaxial creep test at σ₀ = 0.2 MPa

The above results show that the proposed model can predict unconfined compression response of asphalt concrete at strain rates ranging from 4.2 × 10⁻⁶ to 1.7 × 10⁻³ s⁻¹. In addition, the model is capable of predicting uniaxial creep responses observed at different stress levels by using the material parameters determined from constant rate-unconfined compression tests. The response at strain rate varying by four orders of magnitude observed at the lower stress level was predicted with sufficient accuracy. The model is capable of predicting also the tertiary creep behavior observed at the higher stress level.

7 Conclusions

The strain rate-dependent mechanical behavior of asphalt concrete was characterized using unconfined compression tests carried out at different loading rates and modeled using a combined viscoelastic and damage formulation. The experimental results showed that higher strain rates lead to the higher unconfined compressive strength and elastic modulus and that the asphalt concrete specimens showed higher unconfined compressive strength and elastic modulus than the asphalt binder. Evidently, the aggregate contributed to the higher strength and stiffness of the asphalt concrete, and several mechanisms for the reinforcing effects of the aggregate were proposed. There were, however, no significant differences between the strain rate sensitivity of the elastic modulus and that of the unconfined compressive strength as shown by the similarity of the slopes of the log–log plots of these parameters against axial strain rate. The similarity in the strain rate sensitivity of both types of materials was also shown through the resemblance in the total energy input required for fracture of the asphalt concrete and asphalt binder specimens.

Based on the experimental observations, a relatively simple viscoelastic damage model, which requires only five model parameters, was proposed for the strain rate-dependent unconfined compression behavior of asphalt concrete. The strain rate response was modeled by an elastic modulus that is related by a power-law function to the axial strain rate. Viscoelastic response is only observed at high strain rates, while at low loading rates, elastic response become rate independent. Failure and strain softening were modeled via a damage formulation where damage evolution in the asphalt concrete is given by a simple form of the Weibull distribution function. Analytical expressions were derived from the model for both stress- and strain-controlled loading, and for the rate-dependent unconfined compressive strength. The model predictions were compared with experimental data. It was shown that the model is capable of describing the strain rate-dependent deformation, compressive strength, strain-softening and creep behavior of asphalt concrete.