Simple substitution distance and metamorphic detection

Abstract

To evade signature-based detection, metamorphic viruses transform their code before each new infection. Software similarity measures are a potentially useful means of detecting such malware. We can compare a given file to a known sample of metamorphic malware and compute their similarity—if they are sufficiently similar, we classify the file as malware of the same family. In this paper, we analyze an opcode-based software similarity measure inspired by simple substitution cipher cryptanalysis. We show that the technique provides a useful means of classifying metamorphic malware.

1 Introduction

Viruses and worms are types of malware that can replicate and spread from one computer to another [2]. Although the terminology is not consistent, viruses are generally considered to be parasitic, in the sense that they embed themselves in other executable files, while worms generally do not [25]. In this paper, we use the terms virus and malware interchangeably.

The most widely used anti-virus methodology is signature detection [25]. In its simplest form, a signature consists of a sequence of bytes (possibly, including wildcards) extracted from a known virus. Various string matching techniques are used to efficiently scan files for multiple signatures [2].

Since signature detection is the most commonly-used detection strategy, virus writers have developed many techniques to evade such detection. Arguably, metamorphic malware represents the most sophisticated strategy yet developed for evading signature-based detection. A metamorphic virus morphs its code at each infection. That is, the internal structure of the code is altered, but the primary functionality remains unchanged [27].

Previous research has focused on software similarity measures as a means of detecting metamorphic malware [4, 23, 30]. A variety of other techniques, including machine learning [1, 30], statistical analysis [28], and opcode-graph analysis [20], have also been applied to the metamorphic detection problem. In addition, improved metamorphic techniques for evading these detection schemes have been considered [16, 24].

Similarity-based techniques classify an executable file as containing a virus belonging to a given metamorphic family, provided the viral code is sufficiently similar to a known member (or members) of the virus family [18, 30]. The goal of this research is to analyze an opcode-based similarity measure inspired by simple substitution cipher cryptanalysis [15]. This similarity measure shares some characteristics with an edit distance [14].

In a simple substitution cipher, each plaintext letter is mapped to one ciphertext letter, that is, the mapping between plaintext and ciphertext is one-to-one and fixed. This is in contrast to a homophonic substitution, where multiple ciphertext symbols can map to a single plaintext symbol, or polyalphabetic substitutions, where the plaintext-to-ciphertext mapping changes. The infamous “Zodiac 408” cipher is an example of a homophonic substitution [11], while the World War II-era Enigma cipher machine provides a well-known example of a polyalphabetic substitution [26]. The so-called Caesar’s Cipher—where each plaintext letter is mapped to the letter three positions ahead in the alphabet—is a trivial example of a simple substitution. In general, any permutation of the alphabet can serve as the key in a simple substitution.

Suppose that we have a simple substitution ciphertext that was generated from English. By using English language statistics, we can expect to algorithmically recover at least 80 % of the plaintext, provided the message is of sufficient length [11]. However, if we apply the same procedure to a simple substitution ciphertext that was generated from, say, French, the results will likely be poor.

Here, we develop a score based on how well we can “decrypt” an opcode sequence, based on opcode statistics derived from a specific metamorphic family. If this “decryption” yields a good fit with the family statistics, we classify the virus as a member of the metamorphic family; otherwise, we classify it as not belonging to the metamorphic family. Of course, we do not actually decrypt opcode sequences, since the sequences are not encrypted. However, when we apply our score to a family virus, we are attempting to de-obfuscate the opcode sequence in a process analogous to uncovering English plaintext based on English statistics. On the other hand, when we score code that is not a family virus, our attempt at de-obfuscation is analogous to trying to decrypt French ciphertext based on English statistics. In the former case, we might reasonably expect good results, while in the latter case, we expect relatively weak results.

This paper is organized as follows. Section 2 provides background information, including an overview of malware, and a discussion of an efficient attack on simple substitution ciphers that forms the basis of our scoring technique. Section 3 discusses our proposed opcode-based similarity score, while Sect. 4 contains experimental results, including justification of our choice of parameters. Section 5 concludes the paper.

2 Background

In this section, we provide an overview of relevant background information. First, we briefly discuss metamorphic malware. Then be give a fairly detailed discussion of an efficient attack on simple substitution ciphers. This attack forms the basis for the similarity score that we apply to the metamorphic detection problem in this paper.

2.1 Metamorphic malware

Malware is a software that is designed with malicious intent. In this section, we briefly discuss metamorphic malware, with the emphasis on various strategies used to generate such code. We also outline previous work on the metamorphic detection problem.

A metamorphic virus morphs its code before each new infection. We assume that the mutated virus has the same functionality as the original, but the internal structure differs. Metamorphic virus use a variety of code morphing strategies. Next, we outline a few elementary morphing techniques.

2.1.1 Register swapping

Register swapping is a simple obfuscation technique employed by one of the first metamorphic viruses, namely, Win95/Regs wap virus [27]. As the name implies, register swapping consists of simply using different registers. For example, POP EBX could be replaced with POP EAX, if the EAX register is not in use. Note that register swapping does not alter the opcode sequence.

2.1.2 Subroutine permutation

Metamorphic viruses such as Win32/Ghost employ subroutine permutation. If a program has $n$ subroutines, then $n!$ different copies can be generated by simply reordering the subroutines.

2.1.3 Garbage instruction insertion

Metamorphic viruses such as Win95/ZPerm [27] insert (and remove) garbage code, i.e., “do-nothing” instructions, to create morphed copies. Examples of garbage instructions include NOP and ADD EAX,0, as well as series of instructions such as INC EAX followed by DEC EAX. Such instructions do not change the function of the program, but care must be taken so that addresses and alignments remain valid.

2.1.4 Instruction substitution

Morphed copies can be generated by replacing an instruction (or group of instructions) with another equivalent instruction (or group of instructions). For example, SUB EAX,EAX can be replaced by XOR EAX,EAX.

2.1.5 Transposition

Reordering instructions is a powerful metamorphic technique [6]. Subroutine permutation, as discussed above, is a special case of code transposition. More generally, we can reorder any instructions that have no dependency. For example,

$$\begin{aligned}&\mathtt MOV R1,R2 \\&\mathtt ADD R3,R4 \end{aligned}$$

can be reordered to obtain

$$\begin{aligned}&\mathtt ADD R3,R4 \\&\mathtt MOV R1,R2 \end{aligned}$$

2.1.6 Formal grammar mutation

Formal grammars have been proposed as a means of formalizing many existing morphing techniques [12, 31]. A morphing engine can be viewed as a non-deterministic automata, where transitions are possible from every symbol to every other symbol, with the symbol set consisting of all possible instructions. In this setting, we can apply formal grammar rules to create viral copies with great variation; see [31] for examples.

2.2 Metamorphic detection

It is easily proved that well-designed metamorphic code cannot be detected using elementary signatures [6, 29]. While metamorphic detection remains a challenging research problem, various strategies have met with some success, particularly with respect to hacker-produced metamorphic malware.

In [30], hidden Markov models (HMM) are trained on opcode sequences extracted from family viruses. The trained models are shown to be effective at detecting some examples of highly metamorphic code. Profile hidden Markov models (PHMM) are considered in [1], but the results are not as promising as those obtained using HMMs in [30].

Among other techniques, a graph-based approach is analyzed in [20], while statistical analysis is considered in [28]. A score based on “structural entropy,” i.e., changes in entropy within an executable, is applied to the metamorphic detection problem in [23] and further analyzed in [4]. Eigenvalue analysis is considered in [10]. While many of these detection strategies are effective against certain classes of metamorphic malware, practical strategies for defeating these detection techniques are discussed in [16, 24].

2.3 Jackobsen’s Algorithm

In this paper, we employ techniques from simple substitution cipher cryptanalysis as a means of measuring the distance between executables. An efficient, general technique for simple substitution cryptanalysis is given by Jackobsen [15]. In this paper, an analog of Jackobsen’s algorithm is used to compute our simple substitution distance between executable files.

Substitution ciphers are one of the earliest methods of encryption [25]. In such a cipher, every plaintext symbol has a ciphertext symbol substituted for it, and the original position of the plaintext symbol is retained in the ciphertext [11, 17].

As the name suggests, simple substitution ciphers are the simplest of the substitution ciphers [25]. In a simple substitution, each plaintext symbol corresponds to one ciphertext symbol, that is, the mapping between the plaintext and the ciphertext symbol is fixed and one-to-one.

An example of a simple substitution—the well-known Caesar’s cipher—is given in Table 1. In this example, each plaintext letter is replaced with the letter that is three positions ahead in the alphabet [25].

Table 1 Example of a simple substitution key

The simple substitution is known to be a very weak cipher. Attacks on the simple substitution generally rely on elementary statistical properties of the plaintext language [11].

An efficient general algorithm to cryptanalyze simple substitution ciphers is given by Jackobsen in [15]. The algorithm starts by making an initial guess for the key which is then refined through a number of iterations. At each step, a scoring function is used to determine whether the putative key is an improvement over the current key; if so the putative key is retained; otherwise it is not. This algorithm is a hill climbing attack, since it ignores any modification to the key that does not improve the score.

Jackobsen’s algorithm relies on the digraph distribution of the plaintext language. The attack is extremely efficient because the ciphertext is parsed only once to construct an initial digraph distribution matrix. All subsequent scoring is done by manipulating this matrix directly, and hence there is no need to re-decrypt the ciphertext.

For this discussion of Jackobsen’s algorithm [15], we assume that the plaintext language is English and the ciphertext symbols consist of the 26 letters of the alphabet. We choose an initial key that best matches English monograph statistics. That is, we assume that the most frequent ciphertext letter maps to the most frequent letter in English, which is E, the second most frequent ciphertext letter maps to T, and so on.

The algorithm modifies the current key by swapping elements. We then compute a score to determine whether the resulting putative plaintext is closer to English language statistics. The swap is retained provided that the score improves.

Let $K = k_{1}, k_{2},\ldots , k_{26}$ be the putative key. Then $K$ is a permutation of the 26 letters. The basic letter swapping procedure is as follows. First, all adjacent elements are swapped, that is, $k_{1}$ is swapped with $k_{2}$, then $k_{2}$ is swapped with $k_{3}$ and so on. Then the elements at distance two are swapped, that is, $k_{1}$ is swapped with $k_{3}$, and so on. Then elements at distance three are swapped, and so on. Finally, at the $n^{th}$ step, $k_{1}$ is swapped with $k_{n+1}$. This basic procedure is illustrated in (1), where “$|$” represents the swapping operation.

(1)

In Jackobsen’s algorithm, we restart from the beginning of the swapping schedule in (1) each time the score improves. Consequently, the minimum number of score computations is ${25\atopwithdelims ()2}$, or, more generally, ${n\atopwithdelims ()2}$ if there are $n$ symbols. The average-case performance will depend on the statistics and the length of the ciphertext. In [11], empirical results are given for the average number of score computations. As expected, as the length of the ciphertext increases, the average number of score computations decreases; for example, for a ciphertext of length 500, an average of 1,050 score computations are needed, while for ciphertext of length 8,000, on average only 630 score computations are used. In Sect. 4, we consider variations on this swapping schedule in the context of metamorphic detection.

Next, we present the scoring function that is used in Jackobsen’s algorithm. Let $D = \{d_{ij}\}$ be the digraph distribution matrix for the putative plaintext corresponding to the putative key $K$ and let $E = \{e_{ij}\}$ be the expected digraph distribution matrix for English. Then the score is given by the sum of absolute differences, that is,

$$\begin{aligned} {score}(K) = d(D,E) = \sum _{i,j} |d_{ij} - e_{ij}|. \end{aligned}$$

(2)

Note that ${score}(K)\ge 0$, with equality obtained for a perfect match. In Sect. 4, we evaluate variations on this scoring function in the context of metamorphic detection.

To illustrate the process used to update the $D$ matrix, we consider a simple substitution example on a restricted 10-letter alphabet. For this example, the plaintext symbols are

$$\begin{aligned} \mathtt{E },\ \mathtt{T },\ \mathtt{A },\ \mathtt{O },\ \mathtt{I },\ \mathtt{N },\ \mathtt{S },\ \mathtt{R },\ \mathtt{H },\ \mathtt{D } \end{aligned}$$

where we have listed the letters in descending order of their expected frequency in English. Based on this limited alphabet, suppose we are given the simple substitution ciphertext

$$\begin{aligned}&\mathtt{TNDEODRHISOADDRTEDOAHENSINEOARDTTDT }\nonumber \\&\quad \mathtt{INDDRNEDNTTTDDISRETEEEEEAA }. \end{aligned}$$

(3)

For the ciphertext in (3), the frequency counts are

$$\begin{aligned} \begin{array}{|r|cccccccccc|}\hline \mathrm{{ciphertext}} &{} \mathtt{E } &{} \mathtt{T } &{} \mathtt{A } &{} \mathtt{O } &{} \mathtt{I } &{} \mathtt{N } &{} \mathtt{S } &{} \mathtt{R } &{} \mathtt{H } &{} \mathtt{D } \\ \hline \mathrm{{frequency}} &{} 11 &{} 9 &{} 5 &{} 4 &{} 4 &{} 6 &{} 3 &{} 5 &{} 2 &{} 12 \\ \hline \end{array} \end{aligned}$$

Consequently, our initial guess for the key is

$$\begin{aligned} \begin{array}{|r|cccccccccc|}\hline \mathrm{{plaintext}} &{} \mathtt{E } &{} \mathtt{T } &{} \mathtt{A } &{} \mathtt{O } &{} \mathtt{I } &{} \mathtt{N } &{} \mathtt{S } &{} \mathtt{R } &{} \mathtt{H } &{} \mathtt{D } \\ \hline \mathrm{{ciphertext}} &{} \mathtt{D } &{} \mathtt{E } &{} \mathtt{T } &{} \mathtt{N } &{} \mathtt{A } &{} \mathtt{R } &{} \mathtt{I } &{} \mathtt{O } &{} \mathtt{S } &{} \mathtt{H } \\ \hline \end{array} \end{aligned}$$

(4)

Using the initial putative key in (4), we find the initial putative plaintext corresponding to the ciphertext in (3) is given by

$$\begin{aligned}&\mathtt{AOETRENDSHRIEENATERIDTOHSOTRINEAAEASO }\nonumber \\&\quad \mathtt{EENOTEOAAAEESHNTATTTTTII }. \end{aligned}$$

(5)

Therefore, the digraph distribution matrix corresponding to the initial key is

(6)

The first step in the hill climb is to swap the first two elements of the key. Swapping the first two elements in (4) yields the putative key

(7)

Applying the key in (7) to the ciphertext in (3), we obtain the putative plaintext

$$\begin{aligned}&\mathtt{AOTERTNDSHRITTNAETRIDEOHSOERINTAATASO }\nonumber \\&\quad \mathtt{TTNOETOAAATTSHNEAEEEEEII }. \end{aligned}$$

(8)

The digraph distribution matrix corresponding to the key in (7) is

(9)

It is evident from the matrices in (6) and (9) that swapping the elements in the key and recomputing the putative plaintext is equivalent to simply swapping the corresponding rows and columns of the digraph distribution matrix (6). Consequently, there is no need to decrypt the ciphertext for each putative key; instead we can simply swap the appropriate row and column of the $D$ matrix.

Table 2 Jackobsen’s Algorithm [11, 15]

Note that the algorithm is nearly independent of the length of the ciphertext, since we only decrypt once. Pseudocode for Jackobsen’s algorithm appears in Table 2.

3 Proposed similarity score

In this section, we develop a technique analogous to Jackobsen’s algorithm [15] for measuring the similarity of executables based on extracted opcode sequences. The purpose is to obtain a similarity score that is applicable to the metamorphic detection problem.

In Jackobsen’s algorithm, the score measures the degree to which the putative plaintext matches the plaintext language statistics. The score we give here can be viewed as a measure of the distance between the opcode sequence of a given executable, and the opcode statistics of a metamorphic family. In the remainder of this section, we discuss the application of Jackobsen’s algorithm in this context.

First, we extract opcode sequences from a large number of viruses, all of which were produced by the same metamorphic generator. We use these opcodes to construct the analog of the $E$ matrix in Jackobsen’s algorithm, that is, we construct the digraph distribution matrix. Then, given an executable that we want to classify, we extract its opcode sequence and generate the analog of the $D$ matrix, as discussed below.

We limit these matrices to the most frequent $n$ opcodes, with symbol $n+1$ used to denote any opcodes that is not among the $n$ most common. We discuss the choice of $n$ in Sect. 4. Then $E = \{e_{ij}\}$ and $D = \{d_{ij}\}$ are both of dimension $(n+1)\times (n+1)$. For additional information on the relative frequencies of opcodes in malware, see [3, 5, 9]

We choose an initial “key” $K$ that best matches the monograph opcode statistics of the family viruses. That is, we assume that the most frequent opcode in the family viruses maps to the most frequent opcode in the suspect code, the second most frequent opcode in the family maps to the second most frequent opcode in the suspect code, and so on. We determine the matrix $D$ based on “decrypting” with this initial key $K$. That is, we follow the same procedure as used to construct the $D$ matrix in Jackobsen’s algorithm.

We normalize both the $E$ and $D$ matrices so that our scores are independent of the length of the opcode sequence.¹ We experimented with different normalization strategies; this topic is discussed in Sect. 4.

As in Jackobsen’s algorithm, the score is computed as the Manhattan distance between $D$ and $E$, as in (2). We experimented with variations on this standard scoring function. These experiments are discussed in Sect. 4.

The swapping schedule for Jackobsen’s algorithm appears in (1) and is discussed in Sect. 2.3. For our scoring algorithm, we experimented with variations on the standard swapping strategy. Again, these experimental results are presented in Sect. 4.

Next, we consider an example to illustrate the process used to choose the initial “key” and to update the $D$ matrix. This example parallels the example used to illustrate Jakobsen’s algorithm in Sect. 2.3.

For simplicity, suppose that only five distinct opcodes appear in the family viruses. Then the $D$ and $E$ matrices will be $5 \times 5$. Further, suppose that these five opcodes are

$$\begin{aligned} \mathtt{MOV },\ \mathtt{CALL },\ \mathtt{ADD },\ \mathtt{XOR },\ \mathtt{CMP } \end{aligned}$$

(10)

where the opcodes are arranged in descending order of frequency.

Assume that the extracted opcode sequence that we want to score is

$$\begin{aligned} \mathtt{JMP }, \mathtt{MOV }, \mathtt{MOV }, \mathtt{ADD }, \mathtt{INC }, \mathtt{INC }, \mathtt{INC } \end{aligned}$$

(11)

For the opcode sequence in (11), the frequency counts are

(12)

Consequently, our initial guess for $K$ is

(13)

Note that the first row in (13) comes from the metamorphic family statistics in (10) and the second row is from the statistics of the sequence to be scored, as summarized in (12). The putative “key” in (13) implies that we “decrypt” the sequence (11) by substituting MOV for each occurrence of INC in (11), and substituting CALL for each MOV in (11), and so on. The resulting “decrypted” sequence is

$$\begin{aligned} \mathtt{XOR },\ \mathtt{CALL },\ \mathtt{CALL },\ \mathtt{ADD },\ \mathtt{MOV },\ \mathtt{MOV },\ \mathtt{MOV } \end{aligned}$$

(14)

which gives us the initial $D$ matrix, i.e., the digraph distribution matrix

(15)

After scoring this $D$ matrix versus the $E$ matrix, the next step is to swap the first two opcodes in the putative key, that is, we swap MOV and CALL in the first row of (13). This is accomplished by simply swapping the first two rows and columns of (15). This modified matrix is given by

(16)

From this point, the algorithm proceeds exactly as in Jackobsen’s algorithm. That is, we score the matrix in (16) using the $E$ matrix obtained from the metamorphic family, swap elements, and so on. The score for the opcode sequence is given by the score for the final $D$ matrix. Table 3 gives pseudocode for our scoring and classification technique.

Table 3 Metamorphic malware scoring and detection

4 Experimental results

This section contains our experimental results. First, we provide results to justify our choice of parameters and scoring function. Then we give results for our scoring technique when applied to metamorphic malware. Finally, we compare our results to previous work.

4.1 Parameter selection

There are several parameters in our algorithm. Here, we consider variations on the scoring function, the size of the opcode matrix, the matrix normalization, and the swapping schedule. Some of these are shown to have a significant effect on performance.

When comparing parameters, we measure effectiveness by computing the area under the curve (AUC) of receiver operating characteristic (ROC) curves [7]. For an ROC curve, the AUC gives the probability that a randomly chosen positive instance will score higher than a randomly chosen negative one. Consequently, an AUC of 1 implies perfect classification, while an AUC of 0.5 implies that classification is no better than flipping a coin.

For all of the experiments in this section, we used the same set of malware files, namely, MWOR metamorphic worms with a padding ratio of 4.0 [24]. The benign files and our experimental design are discussed below in Sect. 4.2. Also, for the sake of brevity, we omit the ROC curves in this section and just give the AUC statistics. The ROC curves for all of the cases considered here can be found in [21].

4.1.1 Opcode matrix size

An important parameter is the number of opcodes we use in the $E$ and $D$ matrices. Recall that we distinguish the $n$ most frequent opcodes, with all remaining opcodes combined into category $n+1$. We conducted experiments for values for $n$ in the range of 15–100. The results are summarized in Table 4 where we see that $n=25$ gives the best results from the values tested. Hence, for all experiments discussed below, the $D$ and $E$ matrices are $26\times 26$.

Table 4 Comparison of matrix sizes

It is not surprising that a relatively small number of opcodes provides better results than a larger number. Previous research has shown that the 14 most frequent opcodes account for more than 92 % of all opcodes in malware samples [5, 9]. Consequently, for the scoring technique considered in this paper, uncommon opcodes will tend to act as noise, as opposed to providing useful information. However, the mere presence of rare opcodes can serve as a useful heuristic for malware detection [5]. For example, certain opcodes do not occur in compiled code [3]. Since malware is much more likely to be written in assembly than benign code, the presence of any such opcodes would indicate suspect code.

4.1.2 Scoring function

Among others, we experimented with the following three scoring functions:

$$\begin{aligned} \text{ score}_1(K)&= \sum _{i,j} |d_{ij} - e_{ij}| \\ \text{ score}_2(K)&= \sum _{i,j} |d_{ij} - e_{ij}|^2 \\ \text{ score}_3(K)&= \sum _{i,j} |d_{ij}^2 - e_{ij}^2| \\ \end{aligned}$$

Note that $\text{ score}_1$ is the Manhattan distance between $D$ and $E$, which is the standard scoring function used in Jackobsen’s algorithm [15], while $\text{ score}_2$ differs by a constant factor from the square of the Euclidean distance, and $\text{ score}_3$ computes the sum-of-squares error.

Table 5 Comparison of scoring functions

Our experimental results are given in Table 5. From these results, we see that $\text{ score}_1$ outperforms the other two scores, so we have used this score in all experiments discussed below, where we drop the subscript and simply refer to it as $\text{ score}$.

4.1.3 Normalization

Since multiple family viruses contribute to the matrix $E$, we experimented with two different normalization techniques. In the first method, we accumulate totals from all files that contribute to $E$, and then we simply divide each cell by the sum of all of the cells. For the second method, we create a matrix for each file, normalizing each by dividing the count in each cell by the total for that matrix. Then we average these individual matrices to obtain the $E$ matrix. Note that this second approach weights each file equally, while the first approach weights each opcode equally.

Table 6 Comparison of normalization techniques

The AUC and standard error for both normalization methods is shown in Table 6. These results indicate that there is little difference between the tested normalization methods, but the second technique performs marginally better, so we use the second method to construct the $E$ matrix in our experiments.

4.1.4 Swapping strategies

We experimented with the following six swapping strategies:

Swapping strategy 1: Swap all adjacent pairs of opcodes, then all pairs at distance 2, then all pairs at distance 3 and so on until we have done exactly ${n\atopwithdelims ()2}$ swaps.

Swapping strategy 2: Swap as in strategy 1, but any time the score improves, start again from the beginning. Note that this is the strategy employed in Jackobsen algorithm [15].

Swapping strategy 3: Swap all adjacent pairs of opcodes, then all pairs at distance $2$, then all pairs at distance 3, and so on. Once we complete these ${n\atopwithdelims ()2}$ steps, we iterate the entire process, repeating until we complete one entire iteration without any swap improving the score.

Swapping strategy 4: Only swap adjacent pairs of opcodes, that is, we make only $n$ swaps.

Swapping strategy 5: This is similar to strategy 4, except that whenever a swap improves the score, we continue swapping that element until the score no longer improves, at which point we revert to the position where the series of swaps began.

Swapping strategy 6: As in strategy 4, we do $n$ swaps of adjacent pairs. We then repeat, until we go through one entire iteration without any swap improving the score.

Table 7 Comparison of swapping strategies

The results in Table 7 show that swapping strategy $2$ yields the best results, so we employ strategy 2 in our experiments. It is interesting to note that the fast swapping strategy 1, and the even faster strategy 4, are surprisingly competitive. Hence, for the sake of efficiency, it might be worth considering sacrificing a small degree of accuracy for this improved performance, at least in some applications.

4.2 Test data

The metamorphic families considered here are the Next Generation Virus Generation Kit (NGVCK) [22], Second Generation Virus Generator (G2) [30], and the metamorphic worm developed and analyzed in [24], which we refer to as MWOR.

The corresponding ROC curves appear in Fig. 4, with the AUC and standard error for each tabulated in the “Simple Substitution Score” columns of Table 8.

Table 8 Simple substitution scoring vs HMM scoring (MWOR worms)

The MWOR worms [24] use various “padding ratios,” where the padding ratio is given by the ratio of dead code instructions to the number of instructions that constitute the core functionality of the worm. So, for example, a padding ratio of 0.5 indicates that the virus has half as much dead code as worm instructions.

Our test set of metamorphic viruses consists of 50 NGVCK files, 50 G2 files. In addition, for the MWOR worm, we test 100 files for each of the padding ratios of 0.5, 1.0, 1.5, 2.0, 2.5, 3.0, 3.5 and 4.0. The various padding ratios for MWOR files are denoted

$$\begin{aligned} \mathrm{MWOR\_0\_5}, \mathrm{MWOR\_1\_0},\ldots , \mathrm{MWOR\_4\_0}. \end{aligned}$$

So that our results are comparable to previous research [16, 20, 28, 30], for NGVCK and G2, we use Cygwin utility files [8] as representative examples of benign files. For testing MWOR, which is a Linux worm, we use Linux library files. Since the MWOR metamorphic generator [24] uses Linux library files as its source of dead code, these library files should provide a more challenging test case, as compared to randomly selected files.

For each experiment, we employed five-fold cross-validation. In this approach, the data is partitioned into five sets and five separate experiments are performed. In each experiment, 80 % of the data is used for training, with the remaining 20 % reserved for testing, and in each of the five “folds” a different subset is reserved for testing. Advantages of this approach include a reduction in data bias, as well as an increase in the number of data points generated from a given dataset [28].

4.3 Test results

We present our classification results in this section. We use ROC curves to evaluate the effectiveness of the scores as a detection system [7]. Each ROC curve is represented as a two-dimensional plot, in which the $x$-axis represents the false positive rate and the $y$-axis represents the corresponding true positive rate. The overall accuracy is quantified by computing the area under the curve (AUC). As discussed above, an AUC of 1 represents perfect scoring, while an area of 0.5 represents random scoring.

4.3.1 NGVCK and G2 viruses

The graphs in Fig. 1a and b show the results obtained for NGVCK and G2 family viruses, respectively. These results indicate that NGVCK and G2 family of viruses are easily distinguishable from benign files using our scoring technique. While these results are strong, comparably good results for these metamorphic families can be found in [20, 28, 30], for example.

Fig. 1

NGVCK and G2 Scores

4.3.2 MWOR worms

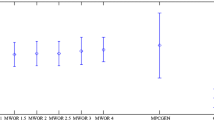
The similarity scores obtained by applying our detection system to MWOR files with various padding ratios are shown in Figs. 2 and 3. The corresponding ROC curves appear in Fig. 4, with the AUC and standard error for each tabulated in the “Simple Substitution Score” columns of Table 8.

Fig. 2

MWOR Scores for padding ratios from 0.5 to 2.0

Fig. 3

MWOR Scores for padding ratios from 2.5 to 4.0

Fig. 4

ROC Curves for MWOR worms

As expected, detection success for the MWOR worms declines at higher padding ratios. However, the decline is surprisingly modest. In [24] a scoring system based on hidden Markov models (HMM) is tested against the MWOR metamorphic families. The results from [24] are reproduced here in “HMM Score” columns of Table 8. For the MWOR worms, our results offer a significant improvement over this HMM-based detection strategy. Note that the HMM-based approach has proven difficult to surpass in previous metamorphic detection research [16, 20, 28, 30].

4.4 Efficiency

In this section, we present results on the efficiency of our simple substitution scoring technique. Note that the results here only apply to the scoring phase, that is, we ignore the (costly) step of extracting opcodes.

In Table 9 we give results for number of score computations and number of swaps, along with timings, for various test cases when scoring family viruses. Analogous results for benign files appear in Table 10.

In these tables, the “comparisons” columns refer to the number of steps of the key schedule algorithm (1) that are executed. Equivalently, “comparisons” is the number of times that we compute $\text{ score}(K)$. The “swaps” columns refer to the number of the score computations for which the score improves, in which case the elements of $K$ are actually swapped. Note that the number of “swaps” is also the number of times that we restart from the beginning of the swapping schedule in (1).

Table 9 Scoring family viruses

Table 10 Scoring benign files

The results in Tables 9 and 10 indicate that our simple substitution score is reasonably efficient, with an average processing time between 0.02 and 0.04 s, neglecting the cost of extracting opcode sequences. Of course, improved efficiency is always desirable for virus scanning, and the results in Sect. 4.1.4 indicate that faster swapping strategies may yield comparable results.

5 Conclusions and future work

We designed and implemented an opcode-based software similarity technique and applied it to the metamorphic malware detection problem. The algorithm utilizes a scoring approach based on an efficient attack on simple substitution ciphers [15].

Our algorithm was implemented and extensively tested. The technique achieves a high degree of accuracy when tested on some challenging cases. In particular, this technique outperformed a previously developed approach based on hidden Markov models [30], which has served as a benchmark in several recent studies [16, 20, 24, 28].

Future work could include efforts to improve on the digraph frequency analysis that forms the basis of our simple substitution score. Efforts to improve scoring efficiency might also be worth considering. For example, experiments using faster or randomized swapping strategies might decrease score computation times without diminishing the results. Ideally, we would like to avoid the costly disassembly step and instead generate scores directly from binary files. A comparison of our simple substitution score—both in terms of performance and efficiency—to an analogous score based on Levenshtein distance [14] could also be considered. Finally, it would be interesting to analyze the relative strengths and weaknesses of the simple substitution score in comparison to other scoring techniques.