Behavioral portfolio selection and optimization: an application to international stocks

Abstract

The behavioral approach of decision making has emerged as a diversified solution in the presence of risk and uncertainty. Using the popular cumulative prospect theory as an objective function for portfolio selection, this study implements the classical mean–variance model to compare the portfolio performance of high behavioral stocks with that of stocks with lower behavioral values. Based on a sample of 37 international stocks over the period from October 1998 to November 2017, empirical results from D-vine pair copula GARCH-GEV indicate that the portfolio of high behavioral prospect stocks outperforms the portfolio of stocks with low behavioral scores. This finding may suggest that portfolios with high behavioral values coincide with rational efficiency sets.

1 Introduction

Portfolio selection and management remain crucial problems for investors and continue to attract the attention of academics and practitioners. Under the assumption that investors seek maximum profit and minimum risk in their investment decisions, the mean–variance model has become the conventional solution to these problems. Since its creation (Markowitz 1952), this framework has been subject to ongoing theoretical and empirical developments and/or extensions, resulting in alternative optimization modeling procedures. One such development relates to the use of an appropriate measure of risk. For example, Low et al. (2016) emphasize the role of asymmetry in risk measurement, while the finance literature advocates the mean-CVaR models instead of mean-VaR models given the superiority of the conditional value at risk (CVaR) over the traditional value at risk (VaR) known as an incoherent risk measure which does not satisfy the sub-additivity and convexity axioms (see, e.g., Banihashemi and Navidi 2017).

Another development involves the nature of the optimal solution. Rather than providing a solution area in the form of an efficient frontier as in the standard mean-risk models, alternative optimization approaches allow assessing the relative efficiency of decision-making units. An illustration is the mean–variance model based on data envelopment analysis (DEA) suggested by Morey and Morey (1999) in which the portfolio variance and expected return are used, respectively, as input and output to DEA models. Some behavioral models incorporate irrationality in the decision-making process, cumulative prospect theory (CPT) being one of the most popular objective functions used for portfolio selection models (Coelho 2014). Considering the ability of CPT in assessing decision makers’ behavior in the context of risk and uncertainty (Coelho 2014) and given the investors’ tradition to strive for minimum risk and maximum return, one important question arises: How does a portfolio of high behavioral stocks compare with one comprised of low behavioral ones?

Although the field of finance and particularly portfolio selection offers an adequate framework for application of behavioral theories, most related studies focus on estimating and comparing the parameters of the value function and probability weighting function with the outcome from laboratory experiments. These include Quiggin (1982), De Giorgi and Hens (2006), Gurevich et al. (2009), Kliger and Levy (2009), Bernard and Ghossoub (2010) and Pirvu and Schulze (2012) among others. Only a few studies consider modeling decision maker preferences by behavioral theories within the conventional optimization framework for portfolio selection. For instance, Coelho et al. (2012) make use of a CPT objective function for optimization to analyze the behavior of farmers in regard to the Common Agricultural Policy in Portugal. In the field of finance, Coelho (2014) studies the behavior of CPT parameters within a discrete optimization framework for portfolio selection. Contrary to Coelho (2014), whose conclusion is not based on real-world data, and following the traditional optimization strategy, the goal of this paper is to assess the performance of behavioral portfolio selection of international stocks with decision maker preferences defined by CPT.

We study a sample of 37 international stocks using a two-step procedure. The first step consists of selecting the top and bottom stock portfolio based on behavioral values as described by CPT. In the second step, a performance analysis is carried out to compare the high and low behavioral portfolios using the copula approach. Modeling portfolio performance requires the use of an adequate modeling strategy for statistical dependence (also known as co-movement) between return or loss components of the portfolio and, in this regard, copula approaches have advantages over correlation-based strategies.

The increasing integration of stock markets has contributed to the global dependence of international financial markets as a result of volatility spillovers as well as contagion effects. Moreover, in the presence of extreme events such as global financial crises that result in permanent changes in joint dynamics and network relationships (Brunnermeier 2009; Moshirian 2011; Florackis et al. 2014; Bekiros et al. 2015), correlation tools are unlikely to accurately model the statistical dependence between components of a portfolio. Unlike correlation, a copula is thought to be universally valid due to its ability to accommodate both elliptical and non-elliptical distributions. Moreover, its two modeling levels (marginal distributions in the first level and dependence structure fitted on the marginal distributions in the second level) makes it possible to fit different marginal distributions depending on the risk factor, therefore allowing a wide range of dependence structures to be fitted to the data (Dowd 2005). There are two major copula approaches: the bivariate and the pair copula. The marginal distribution provided by the bivariate copula is appropriate only when all the pair variables have the same dependence structure. The pair copula design is thus not restricted and has greater flexibility in capturing distributional features of different forms, hence outperforming pair copula alternatives¹ (Low et al. 2013; Bekiros et al. 2015). According to Bekiros et al. (2015), the pair regular vine copulas rely on the dissections and decompositions of graphical theory to capture different forms of distributions in a more localized and specialized way. Since the decomposition is not unique, the R-vine offers different tree structures, including, but not limited to, canonical vines and drawable vines, each of which provides a specific way of decomposing the density in order to construct marginal distributions. However, given the multiplicity of possible decompositions offered by each vine copula, the inference in the C-vine seems to be more driven by the pairs’ selection than is the case for the D-vine where one can freely select which pairs to model (Aas et al. 2009). Following recent copula applications in investment strategies (Humphrey et al. 2015; Rad et al. 2016; Low 2017), this study implements both multivariate t-Student copula GARCH-GEV and D-vine pair copula GARCH-GEV models for the portfolio optimization; the choice of the generalized extreme value (GEV) distribution being motivated by its ability to accurately model tail risk associated with extreme events.

The rest of the study is organized as follows. Section 2 describes the methodology, and Sect. 3 discusses the empirical findings. The paper ends with some concluding remarks.

2 Methodology

As indicated earlier, the empirical strategy starts with computing the behavioral values of each stock based on CPT, which are further used to construct top CPT and bottom CPT portfolios. Then, the study proceeds with a comparative analysis of the performance of these portfolios using the multivariate t-Student copula GARCH-GEV model.

2.1 Portfolio selection under CPT

Introduced by Tversky and Kahneman (1992), CPT is presented as the generalization of the expected utility theory (EUT), which is the pioneer decision theory under risk and uncertainty. Its major attraction lies not only in its exclusive properties to capture loss aversion, risk seeking, nonlinear preferences, and source dependence, but also in its consistency with the stochastic dominance axiom, thus allowing prospects with a large number of outcomes. In its parametric form, CPT preferences are jointly determined by the value function, V(x), and the probability weighting function, W(p). The value function captures four risk profiles of investors: (1) risk seeking for gains, (2) risk aversion for loss, (3) low probability of risk aversion for gains, and (4) high probability associated with risk seeking for losses. In addition, the value function exhibits the following properties: reference dependent, diminishing sensitivity, and loss aversion. Therefore, V(x) is both concave (above the reference point) and convex (below the reference point) so as to ensure a decreasing impact of changes in gains and losses as the distance from the reference point increases (diminishing sensitivity). There is a lack of consensus on the exact reference point, but the current value of the investment (stock prices in our case) is deemed an acceptable reference (De Palma et al. 2008). Furthermore, given that losses are considered to loom longer than gains, V(X) is steeper for losses than for gains. Formally, V(x) is represented by the classical power function as follows:

$$ V\left( {x_{i} } \right)\left\{ {\begin{array}{*{20}c} {x^{\alpha } } &\quad {{\text{if}}\;x \ge 0} \\ { - \lambda \left( { - x} \right)^{\beta } } & \quad{{\text{if}}\;x < 0} \\ \end{array} } \right. $$

(1)

where $\lambda \ge 1$ represents the loss aversion parameter; $\alpha , \beta (0 < \alpha , \beta \le 1$) are parameters of risk aversion in gains and risk preference in losses, respectively. The following estimates have been provided for these parameters: $\lambda = 2.225$ and $\alpha = \beta = 0.88$ (Tversky and Kahneman 1992). On the other hand, the decision weight takes the form of a cumulative probability weighted in a nonlinear way. Thus, it incorporates nonlinear preferences and the four risk profiles outlined above. Similar to V(x), the diminishing sensitivity property also applies to the weighting function, with a different reference. The response to changes in probability decreases as probability deviates from the frontiers of impossibility and certainty. The decision weighting functions for gains and losses are both S-shaped with reference to the identity line (45-degree line). In addition to diminishing sensitivity, the weighting function also captures the attractiveness property. So, the higher the curve, the greater the attractiveness of the prospect for the investor.

The parametric form proposed by Tversky and Kahneman (1992) is the following:

$$ \left\{ {\begin{array}{*{20}c} {W^{ + } \left( p \right) = \frac{{p^{\gamma } }}{{\left( {p^{\gamma } + \left( {1 - p} \right)^{\gamma } } \right)^{{\frac{1}{\gamma }}} }} \quad {\text{for}}\,{\text{gains}}} \\ {W^{ - } \left( p \right) = \frac{{p^{\delta } }}{{\left( {p^{\delta } + \left( {1 - p} \right)^{\delta } } \right)^{{\frac{1}{\delta }}} }}\quad {\text{for}}\,{\text{losses}}} \\ \end{array} } \right. $$

(2)

where $\gamma$ and $\delta$ are the respective curvature of $W^{ + } \left( p \right)$ and $W^{ - } \left( p \right)$ and the point at which they cross the 45-degree line. Tversky and Kahneman (1992) estimated these parameters to be $\gamma = 0.61$ and $\delta = 0.69$, implying that $W^{ - } \left( p \right)$ is higher and less curved.

Finally, the prospect value, CPT, is obtained from combining V(x) and decision weights π(p) as follows:

$$ {\text{CPT}}\left( {x, p} \right) = \pi ^{ - } \left( p \right)V\left( {x^{ - } } \right) + \pi ^{ + } \left( p \right)V\left( {x^{ + } } \right) $$

(3)

where

$$ \left\{ {\begin{array}{*{20}c} {\pi ^{ - } \left( p \right) = W^{ - } \left( {\mathop \sum \nolimits_{ - m}^{i} p_{i} } \right) - W^{ - } \left( {\mathop \sum \nolimits_{ - m}^{i - 1} p_{i} } \right) \quad {\text{for}}\, 1 - m \le i \le 0 } \\ {\pi ^{ + } \left( p \right) = W^{ + } \left( {\mathop \sum \nolimits_{i}^{n} p_{i} } \right) - W^{ + } \left( {\mathop \sum \nolimits_{i + 1}^{n} p_{i} } \right) \quad {\text{for}}\,0 \le i \le n - 1} \\ \end{array} } \right. $$

(4)

This paper uses Tversky and Kahneman’s (1992) estimates to compute the behavioral prospects of investors with regard to the selected stocks. This allows us to construct extreme behavioral stock portfolios in the sense of CPT, namely a portfolio of the top CPT prospect stocks and a portfolio of the bottom CPT prospect stocks. This choice is rational given that, under CPT, only extreme outcomes are overweighed.

The next section describes the approach used to model the dependence structure, which is one of the milestones of portfolio risk modeling.

2.2 Copula approaches

There are various families of bivariate copula, but the t family has the advantage of capturing both lower and upper tails, whereas its alternatives focus on either tail. Because of the importance of the tail dependence property in financial applications, the n-dimensional t-Student copula is widely used to model financial returns. In a portfolio of stock returns, if the tail dependence of different pairs of risk factors in the portfolio is very divergent, as indicated earlier, the marginal distribution provided by the multivariate t-Student copula is no longer appropriate. Using the pair copula can mitigate such issues given its aptitude to handle different marginal distributions within the same setup.

2.2.1 Multivariate t-Student copula

The so-called copula function introduced by Sklar (1959) consists of simulating multivariate distributions in order to provide an idiosyncratic description of the dependence structure between random variables, irrespective of the marginal distribution of the random variables.

A $d$-dimensional copula $C$ is a $d$-dimensional distribution function on $\left[ {0,1} \right]^{d}$, with uniformly distributed marginal $U\left( {0,1} \right)$ on [0, 1]. Sklar’s (1959) theorem states that every multivariate distribution $F$ with marginals $F_{1} , \ldots ,F_{d}$ for some copula $C$ can be written as:

$$ F(x_{1} ,x_{2} , \ldots ,x_{d} ) = C\left( {F_{1} (x_{1} } \right),F_{2} \left( {x_{2} } \right), \ldots ,F_{d} \left( {x_{d} } \right)), $$

(5)

Conversely, any copula $C$ may be used to join any collection of univariate distributions to create a multivariate distribution. Given a $d$-dimensional random vector $X = (X_{1} ,X_{2} , \ldots ,X_{d} )$, the copula of their joint distribution function may be extracted from Eq. (5) by evaluating:

$$ C(u_{1} ,u_{2} , \ldots ,u_{d} ) = F\left( {F_{1}^{ - 1} (u_{1} } ),F_{2}^{ - 1} (u_{2} ), \ldots ,F_{d}^{ - 1} (u_{d} )\right), $$

(6)

where $F_{i}^{ - 1}$’s are the quantile functions of the marginal univariate distribution. Given that marginal distributions of asset returns are not necessarily normally distributed, one can use Sklar’s (1959) theorem to link these distributions with a copula. Recent developments generated several types of copulas from two families: elliptical and archimedean copulas. In our document, we present the functional forms of t-(Student’s) copula (i.e., t copula) that are derived from multivariate elliptical distributions.

A random vector $X = (X_{1} ,X_{2} , \ldots ,X_{d} )$ is t distributed with degrees of freedom $v$, mean µ, and correlation matrix Ʃ, (i.e., $X \sim t_{d} \left( {v,\mu ,\varSigma } \right)$) when its density function is defined as follows:

$$ f\left( x \right) = \frac{{\varGamma \left. {\left( { \frac{v + d}{2}} \right.} \right)}}{{\varGamma \left. {\left( { \frac{v}{2}} \right.} \right)\sqrt {\rho (\pi v)^{d} } }}\left. {\left( {1 + \frac{{\left( {x + \mu } \right)^{'} \varSigma^{ - 1} \left( {x - \mu } \right)}}{v}} \right.} \right)^{{ - \frac{v + d}{2}}} $$

(7)

where $\varGamma$ is the Gamma function defined by $\varGamma \left( x \right) = \mathop \smallint \limits_{0}^{\infty } t^{x - 1} e^{ - t} {\text{d}}t.$ Demarta and McNeil (2004) highlight the ability of the t copula to capture the dependency of fat tails and suggest that the elliptical multivariate t distribution $X$ have the following representation:

$$ X = \mu + \frac{\sqrt v }{S}Z, $$

(8)

where $S\sim\chi^{2} \left( v \right)$ and $Z \sim N\left( {0,\varSigma } \right)$ are independent distributions. Next, marginal distributions are transformed into their inverses, creating a uniform distribution $U$ over [0,1]. From the maximum likelihood, a multivariate t distribution fit is generated to obtain a t copula identified with its parameter ρ (correlation matrix) and $v$ (degrees of freedom).

The t copula with $d$-dimensional distribution can be written as:

$$ C_{v,\rho }^{t} = \mathop \smallint \limits_{ - \infty }^{{F_{1}^{ - 1} (u_{1} )}} \mathop \smallint \limits_{ - \infty }^{{F_{2}^{ - 1} (u_{2} )}} \ldots \mathop \smallint \limits_{ - \infty }^{{F_{d}^{ - 1} (u_{d} )}} f\left( x \right){\text{d}}x $$

(9)

with the $d$-dimensional copula density function defined by:

$$ C_{v,\rho }^{t} {\left( {F_{1} (x_{1} } \right),F_{2} \left( {x_{2} } \right), \ldots ,F_{d} \left( {x_{d} } \right)}) = \frac{{\varGamma \left. {\left( { \frac{v + d}{2}} \right.} \right)}}{{\varGamma \left. {\left( { \frac{v}{2}} \right.} \right)\sqrt \rho }}\left. {\left( {\frac{{\varGamma \left. {\left( { \frac{v}{2}} \right.} \right)}}{{\varGamma \left. {\left( { \frac{v + 1}{2}} \right.} \right)}}} \right.} \right)^{d} \frac{{\mathop \prod \nolimits_{k = 1}^{d} \left. {\left( {1 + \frac{{\varOmega^{\prime}\varSigma^{ - 1} \varOmega }}{v}} \right.} \right)^{{ - \frac{v + d}{2}}} }}{{\mathop \prod \nolimits_{i = 1}^{d} \left. {\left( {1 + \frac{{\varOmega_{i}^{2} }}{2}} \right.} \right)^{{ - \frac{v + 1}{2}}} }} $$

(10)

where $\varOmega = \left( {F_{1}^{ - 1} (u_{1} } ),F_{2}^{ - 1} (u_{2} ), \ldots ,F_{d}^{ - 1} (u_{d} )\right)$ is the t-Student univariate vector inverse distribution function.

The empirical analysis is carried out in a stepwise fashion. First, the returns series obtained from the log-differenced prices are filtered for both autocorrelation and heteroscedasticity. Subject to the validity of the arch effect, this step involves fitting a mean equation (an autoregressive moving average model (ARMA)) and a variance equation (a generalized autoregressive conditional heteroskedastic model (GARCH)) from which residuals are derived and standardized to make the filtered returns.² Second, the generalized extreme value (GEV) distribution is used to fit the filtered returns series in order to account for the fat tails due to extreme events as usually evidenced by financial time series. The use of GEV restricts the analysis to the negative residuals (lower tail), hence emphasizing losses rather than gains. This step is crucial as it provides the shape parameters conditioned upon which the presence of the fat tail in the empirical distribution is determined. Besides the shape parameters, the Student’s distribution parameters (rho and the degree of freedom) obtained from the t copula fit eventually are used to form the multivariate marginal distribution required to simulate the new data for the portfolio’s selection and risk evaluation.

2.2.2 D-vine copula

Consider a set of variables ($X_{1} , \ldots ,X_{p}$) with joint distribution $F$ and density $f.$ By definition, a bivariate copula is a distribution function $C:\left[ {0,1} \right]^{2} \to IR$ with uniform marginal. Let $F$ be a bivariate distribution with marginal distributions $F_{1}$ and $F_{2}$. The following theorem gives the existence and unicity conditions for $C$(Sklar 1959): There exists two-dimensional copula $C\left( {.,.} \right)$ such that

$$ \forall \left( {x_{1} ,x_{2} } \right) \in IR^{2} :F\left( {x_{1} ,x_{2} } \right) = C\left( {F_{1} \left( {x_{1} } \right), F_{2} \left( {x_{2} } \right)} \right) $$

(11)

If $F_{1}$ and $F_{2}$ are continuous, then $C$ is unique.

The joint density is then given by

$$ f\left( {x_{1} ,x_{2} } \right) = c_{12} \left( {F_{1} \left( {x_{1} } \right), F_{2} \left( {x_{2} } \right)} \right).f_{1} \left( {x_{1} } \right).f_{2} \left( {x_{2} } \right) $$

(12)

where $c_{12} \left( { \cdot , \cdot } \right)$ is a bivariate density given by

$$ c_{12} \left( {u_{1} ,u_{2} } \right) = \frac{{\partial^{2} C_{12} \left( {u_{1} ,u_{2} } \right)}}{{\partial u_{1} \partial u_{2} }} $$

(13)

Using Eq. (12), we can express the conditional density of $x_{1}$ given $x_{2}$ as

$$ f\left( {x_{2} |x_{1} } \right) = c_{12} \left( {F_{1} \left( {x_{1} } \right), F_{2} \left( {x_{2} } \right)} \right).f_{2} \left( {x_{2} } \right) $$

(14)

To start the construction, we use the recursive decomposition of a multivariate density into products of conditional densities:

$$ f\left( {x_{1} , \ldots ,x_{p} } \right) = \mathop \prod \limits_{i = 2}^{p} f(x_{i} |x_{1} , \ldots ,x_{i - 2} ) \cdot f\left( {x_{1} } \right) $$

(15)

For distinct indices $k,l,k_{1} , \ldots ,k_{d}$ with $k < l$ and $k_{1} < \cdots < k_{d}$, we let

$$ c_{{k,l|k_{1} , \ldots ,k_{d} :\,=\,}} c_{{k,l|k_{1} , \ldots ,k_{d} }} \left( {F\left( {x_{k} |x_{{k_{1} }} , \ldots ,x_{{k_{d} }} } \right), F\left( {x_{l} |x_{{k_{1} }} , \ldots ,x_{{k_{d} }} } \right)} \right) $$

(16)

Using Eq. (16), we have

$$ f\left( {x_{i} |x_{1} , \ldots ,x_{i - 1} } \right) = \left[ {\mathop \prod \limits_{j = 1}^{i - 2} c_{j,i|j + 1, \ldots ,i - 1} } \right] \cdot c_{{\left( {i - 1} \right),i}} \cdot f_{i} \left( {x_{i} } \right) $$

(17)

Using Eq. (17) in  (1) with $j = k, i = k + l$, it follows that

$$ f\left( {x_{1} , \ldots ,x_{p} } \right) = \left[ {\mathop \prod \limits_{l = 1}^{p} \mathop \prod \limits_{k = 1}^{p - l} c_{{k,\left( {k + l} \right)|\left( {k + 1} \right), \ldots ,\left( {k + l - 1} \right)}} } \right] \cdot \left[ {\mathop \prod \limits_{s = 1}^{p} f_{s} \left( {x_{s} } \right)} \right] $$

(18)

The decomposition given by Eq. (18) is called a pair copula decomposition. According to Bedford and Cooke, this PCC is called a D-vine distribution.

In the present case, d = 4, corresponding to the four stock returns under investigation for each of the two portfolios considered. The simulation of the marginal distribution involves three sequential steps, T1, T2, and T3, corresponding to the six pair copula following the graphical decomposition below. T1 allows constructing three marginal distributions by combining: (i) assets 1 and 2 to obtain 12; (ii) assets 2 and 3 to obtain 23; and (iii) assets 3 and 4 to obtain 34. In the second step (T2), only two pairs can now be formed from the previous 12, 23, and 34, leading to 13 given 2 (13/2) and 24 given 3 (24/3), which will be combined in the last step (T3) to obtain 14 given 23 (14/23).

With the D-vine tree as represented in Fig. 1, the corresponding vine distribution has the joint density given by

$$ f\left( {x_{1} , \ldots ,x_{4} } \right) = \left[ {\mathop \prod \limits_{s = 1}^{4} f_{s} \left( {x_{s} } \right)} \right] \cdot c_{12} \cdot c_{23} \cdot c_{34} \cdot c_{13|2} \cdot c_{24|3} \cdot c_{14|23} $$

(19)

Fig. 1

(Source: Brechmann and Schepsmeier 2013)

Four-dimensional D-vine structure.

This construction of multivariate distributions and copulas is very general and flexible, since any bivariate copula can be used as a building block in the PCC model. The pair copulas family mostly used in finance are the Gaussian copula, the t copula, the Clayton copula, and the Gumbel copula. As indicated in Table 3, the building blocks for the PCC involve different copula families selected using the R package CD vine. These families comprise the t copula for all the building blocks.

2.3 Portfolio optimization and evaluation

In the portfolio optimization exercise, the main challenge consists of designing a proper model that empirically best fits the data while remaining feasible and robust enough to generate simulation-based inference for risk evaluation. In the optimization algorithm, investors’ preferences are expressed through a quadratic utility function that needs to be maximized subject to the minimization of a specified risk measure. This is referred to as the mean–variance model (MVM).

Formally, the basic optimization problem with the variance risk is:

$$ \mathop {\hbox{min} }\limits_{w} \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\sum\nolimits_{j = 1}^{m} {w_{j} \left( {r_{i,j} - \mu_{j} } \right)} } \right)}^{2} $$

(20)

Subject to:

$$ \sum\limits_{j = 1}^{m} {w_{j} } \mu_{j} = \mu_{p} $$

(21)

$$ \sum\limits_{j = 1}^{m} {w_{j} } = 1 $$

(22)

$$ w_{j} \ge 0,j = 1, \ldots ,m $$

(23)

where $\mu_{p}$ is the return of the portfolio.

Equations (21–23) represent the target return of the portfolio, the unity constraint on the sum of the portfolio weights $w_{j}$, and the semi-definite positivity constraint on every weight (short sales are not considered). As a symmetric risk measure, the variance-based optimization algorithm relies on the normality assumption, which is not, however, suitable for the tail risk characteristics of asset returns.

Alternatively, the optimization problem can be recast into a loss-function-based minimax algorithm. Equations (21)–(23) are common to all portfolio optimization problems; however, the minimax risk measure for portfolio optimization in the linear programming problem is more conservative due to the constraint that the difference between the maximum loss of portfolio $M_{p}$ and the forecast target return of the portfolio be less than or equal to zero (Bekiros et al. 2015). Hence, unlike the variance risk measure, the minimax optimization problem is modified as follows:

$$ \mathop {\hbox{min} }\limits_{{M_{p} ,w}} M_{p} $$

(24)

Subject to:

$$ M_{p} - \sum\limits_{j = 1}^{m} {w_{j} r_{ij} \le 0,\;\forall_{i} } \in \left\{ {1, \ldots ,n} \right\} $$

(25)

and the three common constraints indicated above (Eqs. 21–23).

Considering a coherent risk measure such as CVaR, which is more appropriate to the loss function of the tail distribution, the optimization problem becomes:

$$ \mathop {\hbox{min} }\limits_{w,d,\upsilon } \frac{1}{na}\sum\limits_{i = 1}^{n} {d_{i} } + \upsilon $$

(26)

Subject to:

$$ \sum\limits_{j = 1}^{m} {w_{j} r_{i,j} + \upsilon \ge - d_{i} } ,\forall_{i} \in \left\{ {1, \ldots ,n} \right\} $$

(27)

$$ d_{i} \ge 0,\forall_{j} \in \left\{ {1, \ldots ,n} \right\} $$

(28)

in addition to the standard constraints (Eqs. 21–23),where $\mu_{p}$ is the portfolio target return as explained above, $\upsilon$ is the CVaR at the a-coverage risk, and $d_{i}$ accounts for the deviation values below the CVaR.

Practically, the optimization is implemented using the R package with fPortfolio developed by Ghalanos and Pfaf (2015). However, the optimal solution obtained from the multivariate GARCH models are based on both linear and nonlinear programming algorithms embedded in the parma function by Wuertz et al. (2009). The R package used in the optimization exercise characterizes the portfolio in terms of expected return and CVaR, which further determine our performance assessment criteria.

3 Data and portfolio selection

The dataset drawn from Bloomberg is comprised of daily returns (100 times the difference in logarithms of stock prices) of 37 international stocks from October 1998 to November 2017 selected based on data availability. These stocks are listed in Table 1 along with their CPT prospects, based on which the high prospect and the low prospect stock portfolios are constructed. Table 1 shows that the four top stocks in terms of behavioral prospect are Dow Jones Shangai, Brazil Bovespa-TOT Return IND, Russian Micex Index, and Russian RTS Index. The four bottom stocks by CPT behavioral prospect are Taiwan SE Weighted Taiex, TEL AVIV SE TA-35, FTSE/JSE top 40, and S&P/ASX 300. Note that these stocks with extreme behavioral values are virtually from emerging financial markets. Their summary statistics (Table 2) show that all the selected stocks have skewness very close to the normal value of 0, which tolerates a symmetric measure of risk. However, the kurtosis values are very high, suggesting that our sample stocks are leptokurtic, which is consistent with rejection of the null hypothesis of normal distribution, as displayed by the small probability of the Jarque–Berra test of normality.

Table 1 List of stock indices and their behavioral prospects

Table 2 Descriptive statistics of selected indices based on CPT

In addition, not only does high kurtosis confirm the existence of heavy tails in the stock distributions, it also implies that large fluctuations are more likely to occur in the fat tail, therefore confirming our decision to use the generalized extreme distribution.

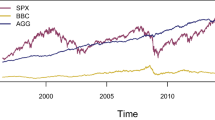
Interestingly, the irrational behavioral can be derived from the descriptive statistics. Contrary to the conventional wisdom that a high return stock is associated with high risk, stock D3 has the highest standard deviation while its returns are among the lowest. Similarly, stock R3 has the highest return, although the associated standard deviation is far from being the highest. While both D3 and R3 are characterized by a high prospect score, in general, low behavioral prospect stocks have lower standard deviations than stocks in the high behavioral prospect portfolio. The historical evolution of returns depicted in Fig. 2 shows that stock returns from the high prospect portfolio exhibit greater fluctuation than those from the low prospect portfolio. Could it be that the portfolio with high behavioral prospect stocks performs poorly? The answer is provided by the performance evaluation, which requires modeling the dependence structure between stocks in a portfolio.

Fig. 2

a Historical returns of top CPT indices. b Historical returns of bottom CPT indices

4 Portfolio optimization and evaluation

Starting from the dependence structure on which the efficient optimization is built, Tables 3 and 4 display the association between stocks using Kendal tau.

Table 3 Dependence structure results from the multivariate t-Student copula-GARCH

Table 4 Dependence structure results from the D-vine pair-copula-GARCH

The t-Student-type family selected for the multivariate copula appears to also be selected by the pair copula in the D-vine pair construction (see Table 3). This possibly suggests that the returns of the selected stocks are less likely to fluctuate in normal market conditions (which does indeed characterize the Frank-type copula) and are more exposed to tail events. It can thus be inferred that international stocks are more volatile and riskier in crisis periods when the level of market confidence is low.

However, as is common in the empirical literature on pair copulas, the dependence structure tends to decrease with the number of construction blocks, leading in most cases to independence between stocks (see Table 4), hence the decision to limit portfolio size. This highlights the existence of a trade-off in the pair copula approach between the advantage of accommodating marginal distributions of different forms and the cost of relying only on the initial pairs’ dependence, as the final pairs are almost always likely to lead zero dependence, which amounts to independence.

Optimization results are summarized in Table 5. Both behavioral portfolios appear to be efficient (EP). In terms of expected return, the high behavioral prospect stock portfolio outperforms the low behavioral prospect stock portfolio with 2.6016 against 2.0178 under multivariate Student’s GARCH-copula. However, the opposite conclusion holds when portfolio performance is measured by CVaR. This contrast might be driven by the assumption made on the marginal distribution as the multivariate framework imposes a similar marginal distribution when fitting the dependence structure.

Table 5 Behavioral portfolio optimization results

The pair copula results, on the other hand, are relatively consistent across performance metrics. The expected returns are comparable between stock portfolios with a high behavioral profile, while the CVaR points to the greater expected loss from the stock portfolio with a low behavioral score. Contrary to the multivariate t-Student copula, the portfolio of stocks with high CPT values outperforms that with a low CPT score. Given the superiority of the pair copula over the multivariate alternative, it can be inferred that a high behavioral profile a la CPT coincides with rational efficiency. This finding is consistent with Levy and Levy (2004), who concluded that CPT and MVM efficient sets almost match.

5 Conclusion

In contrast to the standard approach of using the same framework for both portfolio selection and optimization, this paper combines the behavioral theory of decision making with the classical MVM to analyze a portfolio of 37 international stocks from the period from October 1998 to November 2017. Specifically, CPT is used to construct extreme behavioral prospect stock portfolios, namely a portfolio of high prospect value stocks and a portfolio of stocks with low CPT values. Using copula approaches to modeling portfolio risk following the mean-CVaR model, we find that a portfolio of stocks with low behavioral scores outperforms the high CPT stocks portfolio. The inference is derived from the pair copula framework, whereas the multivariate outcome appears divergent across performance metrics, possibly due to the assumption of similar marginal distributions for all pairs of stocks in a portfolio.

This finding is in line with Levy and Levy (2004), who document the similarity between CPT and MVM efficient sets, but alternative performance measures (see, e.g., Cherny and Madan 2009; Madan 2009) may shed further light on this topic. Moreover, different analytical approaches that can accommodate relatively large portfolios sizes are likely to provide further insight. From a practical point of view, the pair copula better handles relatively small portfolio sizes due to the trade-off between the number of pair construction blocks and the high prevalence of zero dependence.