1 Introduction

Research in the field of autonomous micro-aerial vehicles (MAVs) is currently divided into several different approaches: One part of the community focuses on improving the accuracy of quadrocopter control and has led to notable advances such as aggressive flight maneuvers [1, 2], ping pong [3] and even collaborative construction tasks [4]. While these developments are certainly impressive, such systems nonetheless require external motion capture systems to perform these demanding tasks properly. Another part of the community focuses on outdoor flights where GPS-based pose estimation is possible. Although complete solutions in this field are already available [5], researchers continue to work on improvements in stabilization, [6], photogrammetry, obstacle detection and avoidance.

However, by far the largest part of the community is interested in the most popular topic in the field of MAV’s—autonomous flying in indoor GPS-restricted environments.

A wide variety of different approaches to this task have already been investigated. These range from methods which enable the quadrotor to learn a map offline from previously recorded manual flight [7], to approaches utilizing wireless network sensors [8] and hybrid ultrasound systems [9]. However, the most popular and challenging approach relies entirely on MAV onboard sensors with the use of Simultaneous Localization and Mapping (SLAM) algorithms.

Recent research has improved the accuracy of SLAM methods by combining data from laser scanners, stereo-cameras and inertial measurement units (IMU) [10], but such a complex sensing system requires high initial investment and significant computer power. In order to overcome this problem and to enable even low-cost platforms to fly autonomously, SLAM techniques using monocular sensor systems have been explored. Parallel Tracking And Mapping (PTAM) algorithm has been used successfully [11], but this method requires the MAV to remain in more or less constant visual contact with the initial starting scene, a restriction which ultimately limits the actual operating area of the MAV. Stabilizing controllers based on optical flow have also been investigated [12], but these systems tend to drift over time and are therefore not considered suitable for reliable long-term navigation.

A much easier and more intuitive method of low-cost MAV indoor localization and navigation may lie in the technique of distributing augmented reality (AR) markers in the environment, and a number of studies have already investigated this possibility. Among the earliest research in this field was that published by Eberli et al. [13] in which the camera pose was estimated from the elliptic appearance of a circle in perspective projection. By estimating 5DoF and assuming that yaw is controlled independently, this approach enables the quadrotor to take off, hover over the marker and land autonomously.

An alternative monocular pose estimation technique was proposed by Lamberti et al. [14]. A marker-less visual odometry algorithm exploiting SIFT descriptors was combined with a marker-based tracking method relying on AR markers. Markers were distributed at precise locations in the environment and served as reference points for the quadrotor. When flying from one marker to another, the position of the quadrotor was estimated entirely from the visual odometry algorithm and corrected once the next marker had been detected. One major drawback of this method, however, was the fact that the positions of the reference markers had to be hardcoded to the MAV prior to flight.

AR markers were also used in a 2014 study published by Hartmann et al. [15] which focused on improving the precision of vertical landings of quadrotors. The landing platform was tagged by several markers mounted on exact positions which thereby enabled the MAV to localize the landing area from different angles and to perform precision landings.

The research presented in our study was inspired by recent work from Munoz-Salinas et al. [16] from the University of Cordoba. In their latest paper, a novel mapping and localization approach using planar markers was presented and compared with state-of-the-art Structure from Motion and Simultaneous Localization and Mapping Techniques. The “Marker Mapper” method which they introduced is capable of obtaining better maps and localization results under a wider range of viewpoints than up-to-date SLAM techniques such as LSD-SLAM or ORB-SLAM2.

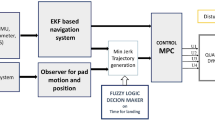
Inspired by these results, we decided to experiment with the Marker Mapper approach and to use it for real-time MAV localization and mapping. Since the original Marker Mapper method is intended to be used offline to process previously recorded video footage, our implementation simplified the existing pipeline to allow near real-time performance (Fig. 1). In order to prove its effectiveness for MAVs, we developed our work further and achieved fully autonomous flight with an off-the-shelf quadrotor relying solely on our mapping method and fuzzy control. The overall accuracy of the proposed system was tested under different lighting conditions and measured by a laser tracker station during flight. This paper is also accompanied by a video which demonstrates the robustness of our approach and the ability to follow a predefined trajectory accurately. It is available online at: http://youtu.be/3mCu_7Ek2fs.

2 Hardware platform

The Parrot AR Drone, a commercially available quadrocopter, was used as the platform for our experiments. The low unit cost of the Parrot in comparison with other MAVs is not the only advantage which it offers; the AR Drone is also robust and can safely operate in close proximity to people. Its main drawback, however, is the lack of flexibility; neither the MAV’s onboard software nor the hardware itself can be easily modified.

Fig. 1
figure 1

Our approach enables low-cost quadrocopter to follow trajectories defined by artificial landmarks

Full size image

The AR Drone is equipped with two cameras, an ultrasound, pressure altimeter, a 3-axis gyroscope, an accelerometer and a magnetometer. The frontal 720p HD camera has a \(92^{\circ }\) diagonal field of view at a streaming rate of 30 fps. The bottom camera covers a \(64^{\circ }\) field at 60 fps with a resolution of \(320 \times 240\) pixels. Communication with the Parrot is effected through wireless LAN from the ground station (Fig. 2).

The onboard software running a 1 GHz 32 bit ARM Cortex A8 processor uses sensor data to control the roll \(\Phi \), pitch \(\Theta \) heading \(\Psi \) and vertical velocity \({\dot{z}}\) according to external set points received from control system every 10 ms. The AR Drone weighs 420 g and measures \(53 \times 52\) cm.

Fig. 2
figure 2

Intel miniITX-based ground station for off-board processing and control

Full size image

3 ArUco pose estimation and mapping

ArUco library was originally developed by Rafael Muñoz and Sergio Garrido [17] to generate a set of AR fiducials and to simplify the estimation of 6DoF marker poses. It is based on OpenCV and enables the detection of various tag dictionaries. Its detection pipeline is much more effective and faster than the pipeline of the similar AprilTag library.

In general, ArUco markers are synthetic square markers comprising a wide black border with an inner binary matrix. The black border facilitates the fast detection of the image and the binary codification allows marker identification, the application of error detection and correction techniques.

The marker detection process is performed in two main steps—the detection of marker candidates and codification analysis.

In the detection process, adaptive thresholding and contour extraction in combination with additional extra filtering is used in order to detect square shapes which are candidates to be markers.

The goal of the second step is to analyze inner codification. Perspective transformation is used initially in order to obtain the marker in canonical form; Otsu thresholding method is then applied to separate white and black sections, and bit by bit analysis is finally performed in order to determine whether the marker belongs to a specific tag dictionary. The position of the four marker corners in the image and the real size of the marker are sufficient to allow the system to estimate its full pose in absolute scale.

In this standard use, the camera is identified with world origin, while the marker position is calculated in respect to the camera frame. If C denotes camera frame and M-marker frame, then the pose of the marker with respect to the camera is expressed as:

$$\begin{aligned} \left[ {{\begin{array}{l} X \\ Y \\ Z \\ 1 \\ \end{array} }}\right] _{\mathrm{C}} =T_{\mathrm {MC}} \left[ {{\begin{array}{l} X \\ Y \\ Z \\ 1 \\ \end{array} }} \right] _{\mathrm{M}} \end{aligned}$$
(1)

where \(T_{\mathrm {MC}}\) is a transformation matrix calculated as:

$$\begin{aligned} T_{\mathrm {MC}} =\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {\left( {e_0^2 +e_1^2 -e_2^2 -e_3^2 } \right) }&{} {2\left( {e_1 e_2 +e_0 e_3 } \right) }&{} {2\left( {e_1 e_3 -e_0 e_2 } \right) }&{} {t_{\mathrm{X}} } \\ {2\left( {e_1 e_2 -e_0 e_3 } \right) }&{} {\left( {e_0^2 -e_1^2 +e_2^2 -e_3^2 } \right) }&{}{2\left( {e_2 e_3 +e_0 e_1 } \right) }&{} {t_{\mathrm{Y}} } \\ {2\left( {e_1 e_3 +e_0 e_2 } \right) }&{} {2\left( {e_2 e_3 -e_0 e_1 } \right) }&{} {\left( {e_0^2 -e_1^2 -e_2^2 +e_3^2 } \right) }&{} {t_{\mathrm{Z}} }\\ 0&{} 0 &{} 0&{} 1\\ \end{array}}} \right] \end{aligned}$$
(2)

with \(e_{0}\), \(e_{1}\), \(e_{2}\), \(e_{3}\) expressing quaternion components, and \(t_{x}\), \(t_{y}\), \(t_{z}\) translational components of marker positions.

This approach allows us to estimate marker pose whether the camera is identified as world origin, but for mapping purposes an inverted approach in which the camera position is estimated with respect to the static markers is more convenient.

The same principle is also used in the AprilSLAM technique originally developed by Chao Qu and Gareth Cross from Kumar Robotics. But while AprilSLAM recalculates the position of each visible marker continuously, our approach is slightly different. In our implementation, the world’s origin is defined by the first detected marker while each consecutive marker is fixed to these world’s coordinates firmly immediately after the detection. While AprilSLAM is only aware of the locations of currently visible markers (and even these are continuously being re-calculated), our algorithm stores the positions of all of the previously detected markers. This pipeline may not be precise at the sub-milimeter level, but in combination with the more effective detection pipeline of ArUco library in general, results in the robust and smooth localization system viable even for real indoor MAV flights. For a fuller understanding of the proposed algorithm, see the original video available at the ArUco_mapping ROS Web site: https://youtu.be/MlOy9qt_K4Y.

So, in case of inverted principle, the transformation between camera frame and marker is:

$$\begin{aligned} \left[ {{\begin{array}{l} X \\ Y \\ Z \\ 1 \\ \end{array} }} \right] _{\mathrm{M}} =T_{\mathrm {MC}}^{-1} \left[ {{\begin{array}{l} X \\ Y \\ Z \\ 1 \\ \end{array} }} \right] _{\mathrm{C}} \end{aligned}$$
(3)

Creating a chain of marker pose estimations, or calculating the position of the second marker with respect to the first, and the third marker to the second, etc., is the key to successful mapping (Fig. 3). In general, the nth marker position can be computed as:

$$\begin{aligned} T_{\mathrm {MnWo}} =T_{\mathrm{M1 M0}} T_{\mathrm{M2 M1}} T_{\mathrm{M3 M2}} \ldots T_{\mathrm{MnMn-1}} \end{aligned}$$
(4)

The only prerequisite of serialized mapping is the simultaneous occurrence of the \(n-1\)th marker within a camera image at the moment when the nth marker is detected for the first time. By calculating the pose of the newly detected marker in respect to the previous one, it is possible to keep track of the whole trajectory and to locate the absolute camera position in respect to the world origin during the whole flight. In a real-world scenario, this limits the mutual distances of following landmarks when creating a trajectory, since at least two landmarks must be visible at the same time. If two or more markers are visible, camera pose is estimated with respect to all of them, but in order to maximize the accuracy of the system, the value used as the actual camera pose is calculated from the closest marker.

Fig. 3
figure 3

Localization and mapping approach—serialization as a main principle

Full size image

4 Fuzzy control

Robust and reliable localization is not the only requirement for autonomous flying—a precise and accurate control mechanism is also vital. PID controllers are commonly used for MAV, but recent years have seen an increased interest in the field of fuzzy control [18]. Fuzzy logic is a proven control method for nonlinear systems in situations in which exact parameter identification is difficult or even impossible. Its inference mechanism also allows simpler transition of human experience into the control algorithm and this is of considerable benefit in the development of autonomous MAV flight. Several interesting studies have been proposed in recent years describing dynamical models, simulations, identification and the development of fuzzy controllers for quadrotors [19,20,21,22, 24].

Our approach is very similar to the work recently published by Indrawati et al. [25]. This study also deals with the fuzzy control of a Parrot AR Drone, and the authors define a set of linguistic rules and membership functions according to the experience of a human pilot in an approach very similar to that outlined in our study. However, the main difference when compared to our approach is the fact that our controller is capable of controlling not only movement in X-, Y-, Z-axis, but also the heading of the MAV, thereby allowing circular motions in real flight as shown in Fig. 4.

Fig. 4
figure 4

Additional fuzzy control of heading enables circular motions

Full size image

A simplified mathematical model of the quadrocopter is shown in Fig. 5. The sum of forces \(F_{i}\) and momentum \(M_{i}\) serves as the input for the Newton–Euler motion equation, a formula which is typically used to derive mathematical models of systems with 6DoF.

Fig. 5
figure 5

Simplified mathematical model of quadrocopter

Full size image
Fig. 6
figure 6

Control diagram—the quadrocopter is a nonlinear system with four inputs and position feedback

Full size image

Newton–Euler motion equations describe the movement of the center of gravity of the body caused by the actuation of external forces and momentum. The first Eq. (5) expresses the change in quadrocopter rotation \({\omega '}_\mathrm{b}\) due to the effect of momentum on individual axes. Changes of rotation are dependent on the magnitude of momentum and mass distribution within the drone, which is represented by the momentum of inertia. Angular rates \(\omega _{x}\), \(\omega _{y}\), \(\omega _{z}\) together with input forces are used to calculate changes in linear velocities \({V'}_\mathrm{b}\) (Eq. 6). Changes of angular rates are transformed to the change of attitude quaternion \({q'}_\mathrm{E}\) (Eq. 7), and the last equation transforms the linear velocities \(V_{x}\), \(V_{y}\), \(V_{z}\) expressed in the body frame to changes in pose \({P'}_\mathrm{E}\) in Earth frame (Eq. 8).

$$\begin{aligned} {\omega '}_{\mathrm{b}}= & {} \left[ {{\begin{array}{lll} {I_{{x}} }&{} 0&{} 0 \\ 0&{} {I_{{y}} }&{} 0 \\ 0&{} 0&{} {I_{\mathrm{z}} } \\ \end{array} }} \right] ^{-1}\left[ \left[ \begin{array}{l} {\hbox {Ltg}\left( {{\pi }/2} \right) k\left( {{\omega }_1^2 -{\omega }_2^2 -{\omega }_3^2 +{\omega }_4^2 } \right) } \\ \begin{array}{l} {\hbox {Ltg}\left( {{\pi }/2} \right) k\left( {-{\omega }_1^2 -{\omega }_2^2 +{\omega }_3^2 +{\omega }_4^2 } \right) } \\ \sum \nolimits _{{i=1}}^4 b\omega _{{i}}^2 \\ \end{array} \\ \end{array} \right] \right. \nonumber \\&\left. -\left[ {{\begin{array}{l} {I_{{z}} {\omega }_{{y}} {\omega }_{{z}} -I_{{y}} {\omega }_{{y}} {\omega }_{{z}} }\\ {I_{{x}} {\omega }_{{x}} {\omega }_{{z}} -I_{{z}} {\omega }_{{x}} {\omega }_{{z}} }\\ {I_{{y}} {\omega }_{{x}} {\omega }_{{y}} -I_{{x}} {\omega }_{{x}} {\omega }_{{y}} }\\ \end{array} }} \right] \right] \end{aligned}$$
(5)
$$\begin{aligned} V'_{\mathrm{b}}= & {} \left[ {{\begin{array}{lll} m&{} 0&{} 0 \\ 0&{} m&{} 0 \\ 0&{} 0&{} m \\ \end{array} }} \right] ^{-1}\left[ \left[ {{\begin{array}{l} 0 \\ 0 \\ {\mathop \sum \nolimits _{i=1}^4 k\omega _{{i}}^2 } \\ \end{array} }} \right] -\frac{1}{m}\left[ {{\begin{array}{l} {c_{{x}} V_{{x}} } \\ {{\begin{array}{l} {c_{{y}} V_{{y}} } \\ {c_{{z}} {V}_{{z}} } \\ \end{array} }} \\ \end{array} }} \right] \right. \nonumber \\&\left. -{m}\left[ {{\begin{array}{l} {{g}_{{x}} } \\ {{\begin{array}{l} {{g}_{{y}} } \\ {{g}_{{z}} } \\ \end{array} }} \\ \end{array} }} \right] -\left[ {{\begin{array}{l} {{V}_{{z}} {m}\omega _{{y}} -\hbox {V}_{{y}} {m}\omega _{{z}} } \\ {\hbox {V}_{{x}} {m}\omega _{{z}} -\hbox {V}_{{z}} {m}\omega _{{x}} } \\ {\hbox {V}_{{y}} {m}\omega _{{x}} -\hbox {V}_{{x}} {m}\omega _{{y}} } \\ \end{array} }} \right] \right] \end{aligned}$$
(6)
$$\begin{aligned} {q'}_{\mathrm{E}}= & {} \left[ {{\begin{array}{lll} 0&{} {{\omega }_{{z}} }&{} {-{\omega }_{{y}} } \\ {-{\omega }_{{z}} }&{} 0 &{} {{\omega }_{{x}} } \\ {{\omega }_{{y}} }&{} {-\omega }_{{x}} &{} 0 \\ \end{array} }} \right] \left[ {{\begin{array}{lll} {{q}_{11} }&{} {{q}_{12} } &{}{{q}_{13} } \\ {{q}_{21} }&{} {{q}_{22} } &{} {{q}_{23} } \\ {{q}_{33} }&{} {{q}_{32} } &{} {{q}_{33} } \\ \end{array} }} \right] \end{aligned}$$
(7)
$$\begin{aligned} {P'}_{\mathrm{E}}= & {} \left[ {{\begin{array}{lll} {2{q}_0^2 -1+2{q}_1^2 }&{}\quad {2{q}_1 {q}_2 +2{q}_0 {q}_3 } &{}\quad {2{q}_1 {q}_3 -2{q}_0 {q}_2 } \\ {2{q}_1 {q}_2 -2{q}_0 {q}_3 }&{}\quad {2{q}_0^2 -1+2{q}_2^2 } &{}\quad {2{q}_2 {q}_3 +2{q}_0 {q}_1 } \\ {2{q}_1 {q}_3 +2{q}_0 {q}_2 }&{}\quad {2{q}_2 {q}_3 -2{q}_0 {q}_1 } &{}\quad {2{q}_0^2 -1+2{q}_3^2 } \\ \end{array}}} \right] ^{-1}\nonumber \\&\left[ {{\begin{array}{l} {{V}_{{x}} } \\ {{V}_{{y}} } \\ {{V}_{{z}} } \\ \end{array} }} \right] \end{aligned}$$
(8)

In contrast to systems which use direct thrust control for each motor, the Parrot AR Drone uses built-in controllers to stabilize each axis. The system therefore expects steering commands in the form of total thrust, roll, pitch and heading set points.

The built-in stabilization system of the Parrot permitted the use of a fuzzy controller to control the quadrocopter positionand heading directly through four system outputs (See Fig. 6). For the purposes of this study, a discrete fuzzy controller with a standard PI structure—input variables e, and \(\Delta e\), with output \(\Delta u\) for all four control variables—was chosen.

In the case of our controller, regulation deviation e describes the difference between the desired and current speeds. Changes in regulation deviation \(\Delta e\) provide information about the actual dynamics of the system for each axis—if the system accelerates or decelerates. The control effort \(\Delta u\) is the output value—speed set point in particular axis.

In theory, a Mamdani fuzzy controller is comprised of four main blocks [23]—fuzzifier, knowledge base, inference mechanism, defuzzifier. If a normalized signal is required, two additional blocks normalization and denormalization are added to the controller. The most important element is the base of rules which implements the relationship between the input and the output of the system. The rule-base houses a collection of IF–THEN rules summarizing the knowledge base that underpins the decisions made by the fuzzy controller.

Fig. 7
figure 7

Fuzzy control diagram with Mamdani’s interference method and standard PI structure

Full size image

In our study, a set of linguistic rules illustrated in Fig. 7 was obtained from previously conducted experiments and the experience of human pilots.

The following value range is used in the tables:

  • N2—Large Negative

  • N1—Small Negative

  • Z—Zero

  • P1—Small Positive

  • P2—Large Positive

Table 1 shows the set of rules for the X, Y axes plus heading control, while the second table provide rules for altitude control—Z-axis.

Table 1 Set of linguistic rules for X, Y and heading controller with standard symmetric distribution
Full size table
Table 2 Set of linguistic rules for Z controller with non-symmetric distribution
Full size table

The main problem in quadrocopter control is the fact that the propellers are unable to generate negative thrust, and this places significant limits on altitude control. In a real flight, it means that in order to stop the quadrocopter at a specific height during takeoff, it is necessary to reduce actual thrust just before the desired altitude is reached. This limitation affects the set of rules for the altitude—Z-axis controller as shown in Table 2.

In order to convert the linguistic rules to real output values, standard triangular membership functions were used and these are listed in Fig. 8. Membership functions are defined for each input (e, \(\Delta e\)) and output (\(\Delta u\)) values by five clusters.

Fig. 8
figure 8

Triangular membership functions of linguistic variables—e, \(\Delta e\), \(\Delta u\) are defined by five clusters

Full size image
Table 3 Measurement of pose estimation accuracy—real vs. estimated pose
Full size table

The variables of the inference system were represented as membership functions with each input normalized to the range of \(\langle -1, 1\rangle \). Defuzification was based on the singleton weight centers method due to the short processing time required.

As is shown in the experiments section, our fuzzy controller was capable of controlling the quadrocopter in fully autonomous mode.

5 Experiments and results

In order to analyze properties of the proposed system, three different experiments were conducted.

The goal of the first measurement was to estimate the overall accuracy of the mapping algorithm. In order to guarantee the precision of our measurements, we printed our testing track in real-world scale on a 4 m long roll of paper. The seven markers printed on the sheet, each of which are 135 mm wide, were placed 585mm apart. Three different cameras (industrial BlueFox MLC200, Parrot AR Drone front HD camera and wide-lens Genius F100, each properly calibrated) were used to collect data. During this measurement, the cameras were manually guided along the trajectory while estimating the position of each new marker with respect to the previous one. This difference between real and estimated positions was essential for evaluating the accuracy of the system. The results obtained with all three devices are shown in Table 3.

The most accurate device according to the results listed in Table 2 was the industrial Bluefox MLC200W camera which demonstrated an error of only 1.80 cm in the x-axis. This low level of absolute error is a result of the small distortion of the high-quality 2.4 mm lens in combination with proper calibration using a large scale calibration grid. The lower accuracy of the results obtained from the AR Parrot HD camera (6.14 cm) and the wide-lens Genius F100 Parrot (9.45 cm) shown in Fig. 9 can likely be attributed to the low-cost nature of the optics used in these cameras, however this combination would still be acceptable for various robotics navigation applications.

The goal of the second experiment was to measure the accuracy of the overall localization. For the purposes of this experiment, 32 markers were distributed over the floor in random positions. A Parrot AR drone was equipped with an additional \(360^{\circ }\) reflector and its front camera was tilted down by \(45^{\circ }\). The measurement was performed in an underground parking lot in order to simulate real-world conditions. During this experiment, the quadrocopter was manually controlled to fly over the area of markers while two different sources were used to estimate its position.

The first source was the camera stream in conjunction with the proposed algorithm. The algorithm was run on the ground station and generated a map of markers according to the incoming images while simultaneously localizing the Parrot in space and capturing the trajectory of the Parrot’s actual flight. When several markers were visible within a frame, the current location was calculated with respect to the position of the marker closest to it. The second source used to determine the ground truth position of the quadrocopter was a Leica laser station (Fig. 10). The laser station provided ground truth data since it was able to pinpoint the location of the \(360^{\circ }\) reflector attached to Parrot chassis approximately 10 times per second with an error margin of less than 1mm.

Fig. 9
figure 9

Absolute error of marker pose estimation for three different cameras

Full size image
Fig. 10
figure 10

Measurement of localization accuracy

Full size image

In order to compare the precision of the proposed method, the trajectories acquired during real flight were aligned using standard ROS tools. As is shown in the axis decomposition in Fig. 11, even though several measurement disturbances were detected, the precision of our localization system was still convincingly accurate—the average overall error within this experiment was less than 7 cm. Additional filtering of estimated values might improve the overall precision even further by removing the noise and measurement disturbances causing plot spikes. We assume that their occurrence and size is closely related to the camera chip size and lens distortion. When using a standard 4:3 camera format, the measurement error of the marker detected at the very right edge of the frame was greater than the error of the marker detected at the very top of the frame. The reason for this is the level of distortion which is closely coupled with the absolute distance from the optical center axis.

Figure 12 combines data from previous plots and provides a comparison of estimated and ground truth trajectory in 3D space.

Fig. 11
figure 11

Laser Station data compared with ArUco estimation, an error was within 5–7 cm range

Full size image
Fig. 12
figure 12

Aligned data from laser tracker station (red color) and ArUco-based localization (green color) (color figure online)

Full size image

Our final experiment (Fig. 13) combined both ArUco-based localization and fuzzy control into the operation of a fully autonomous flying quadrocopter. In order to test this system, two different trajectories, rectangular and triangular, were created in an empty warehouse. Markers were arranged in ascending order with the exactly determined orientation the x-axis of every nth marker pointed to the center of the \(n+1\)th marker in order to provide direction for the off-board processing system.

Fig. 13
figure 13

Final experiment—Parrot autonomously following triangle trajectory defined by ArUco markers

Full size image

As in the previous experiment, the front Parrot HD camera was tilted down by \(45^{\circ }\) and the video stream was transferred to the ground station, where marker positions as well as Parrot’s actual position were determined in near real time. In addition to the pure localization performed in the previous experiment, the system was in fully autonomous operation in this situation. The fuzzy controller calculated steering commands in accordance with the feedback from the ArUco-based localization. The Parrot was guided by controlling program to approach currently visible marker with the highest ID. However, due to a combination of mutual marker distances, height of flight and camera field of view, the next marker with higher ID was detected before the closer one was actually approached—a new goal was set before the previous was reached, resulting in the continuous forward movement seen in the final video.

6 Conclusion

In this study, a marker-based system for the autonomous flying of quadrocopter is presented. It was inspired by recent progress in the field of marker-based localization and mapping and enables simultaneous localization and navigation of the MAV in unstructured, GPS-denied environments using only a single onboard camera and augmented reality markers. Our implementation which also available as a standard ROS package called ArUco_mapping is capable of creating both 2D and 3D maps of detected markers in a real-time, while simultaneously estimating the position of the MAV with respect to a coordinate system defined by the first detected marker. In order to demonstrate the practicality and robustness of marker-based navigation even for low-cost hardware platforms, we developed our system further using fuzzy control and achieved a fully autonomous flight. The average localization error in optimal conditions was less than 2 cm with the manually guided camera and less than 7 cm for the onboard camera during a real flight.

By adding fuzzy logic for MAV control and utilizing a mapping approach, we achieved a fully autonomous flight in which the quadrocopter was able to navigate visually and to follow a predefined trajectory while estimating its own absolute position in a world reference frame.

As a suggestion for further study, the precision of the mapping approach could be improved even further by integrating closing-loop detection algorithms which have been recently developed for keypoint-based SLAM methods. The stability of the quadrotor in flight could also be refined by examining the flight data using Lyapunov function. In order to reach faster system response and more accurate control in flight, a nonlinear estimation based on the mathematical model described in the fuzzy control section could also be added to the existing system.