1 Introduction

Increased environmental awareness has led to increased interest in the transport of water and the redistribution of solutes in soils and aquifers. Water transport has important effects on soil erosion (Ehigiator and Anyata 2011), flooding (Yang and Zhang 2011), redistribution of soil nutrients (Armstrong et al. 2011), vegetation patterns (Ruiz-Sinoga et al. 2010), and animal activity (Lima et al. 2011). Soil saturated hydraulic conductivity (K S) plays a key role in these processes since it determines the maximum capacity of saturated soil to transport water, and it is commonly used in models to make unsaturated conductivity predictions (Mualem 1992). However, the determination of K S is challenging because it can change by many orders of magnitude over short distances (Sobieraj et al. 2004) unlike other indexes of soil properties such as soil moisture, soil bulk density, and most of the nutrient indexes. It sometimes varies so widely that it is difficult to find representative values to use in drain spacing calculations or other aspects of soil management (Van Schilfgaarde 1970; Topp et al. 1980; Puckett et al. 1985; Gupta et al. 1993; Mohanty et al. 1994). According to classic statistics, when the variability is higher and other conditions are constant, more samples are required. Hence, more samples are required to achieve a reliable estimate of K S than for the other soil parameters mentioned above. Knowledge of geostatistics gained from more intensive or extensive sampling could give a clearer picture of the spatial variability of a given regionalized variable, whereas less intensive sampling, although cheaper, could miss important spatial features (Van Groenigen et al. 1999). Moustafa (2000) has shown that neglecting the spatial variability of K S can lead to error rates of between −27 % and +3 % in the design of drain spacing, and overestimates of the required sample size by about 76 %. However, making intensive or extensive measurements is costly, time-consuming and cumbersome. It is therefore important to know how K S varies with sampling scales in order to understand and predict hydrological processes at a range of scales.

Although the parameters used to describe the spatial variability of K S are scaling-dependent, most studies have been carried out at different scales, or the scales at which K S has been measured were inappropriate for the scales at which K S predictions were needed. Three factors, which were defined as a scale triplet, characterize patterns of sampling: spacing, extent and support (Blöschl and Sivapalan 1995). “Spacing” refers to the distance between samples; “extent” refers to the overall coverage; and “support” refers to the area integrated by each sample. Lin et al. (2005) noted that there can be substantial variation in soil properties, such as the depth of the A-horizon and pH, over even relatively short distances (in meters). Franklin and Mills (2003) indicated that such spatial heterogeneity in soil properties can cause variation in the structure of soil microbial communities over similar scales (centimeters to meters). Zimmermann and Elsenbeer (2008) found regionally important disturbances significantly affected K S within a research area of 2 km2 from which 30–150 samples per soil depth were collected; cattle grazing significantly affected the spatial mean K S whereas landslides of different ages did not, but both processes affected the spatial structure of the topsoil K S. Hu et al. (2008) collected 106 samples from slope with an area of 9,600 m2 and found that the heterogeneity and spatial dependence of hydraulic properties were greater for the shaded than for the sunny aspects. Buttle and House (1997) collected 35 samples from a 3.22 ha forested basin to investigate the spatial variability of K S and concluded that the spatial scale of the soil profile’s bulk K S was most relevant to the characterization of the spatial variability in hydraulic conductivity as an input for distributed hydrological models. Sobieraj et al. (2002) investigated the spatial variability of K S, collecting 18 samples along a tropical rainforest catena, and found that the spatial correlation for K S was very low or non-existent at distances greater than 25 m for all soil depths (0–1 m). Moustafa (2000), however, found that the correlation range for K S varied from 1,600 to 2,700 m when the study was conducted in more extensive areas, ranging from 941 to 1,848 ha.

To compare the results obtained by sampling at different spatial scales, it is important to understand how K S changes as a function of scaling. Although the issue of spatial scaling is important, few studies have investigated the problem in the field. For example, Western and Blöschl (1999) examined scale-dependency in the Australian Tarrawarra catchment (10.5 ha) for 1,536 soil moisture content samples and found that sampling scales had different effects on the statistical properties, the variance and the correlation length. Garten et al. (2007) tested the hypothesis that variability of certain parameters would increase with sampling scale, which ranged from small (1 m) to large (1 km) in a temperate, mixed-hardwood forest ecosystem in Tennessee, but obtained different results for 11 soil properties that did not include K S. However, their study was limited by two factors: (a) the small number of samples (24) limited the application of semivariogram analysis and reduced the reliability of the results; and (b) the sampling scales used were not further divided into spacing, extent and support. Gao and Shao (2012) analyzed the changes in interpolation accuracy with changing sampling scales for seven soil properties, including K S and they noted that the interpolation accuracy of K S increased with decreasing sampling spacing and increasing sampling extent. The limited area (900 m2), however, limited the further application of their findings. This paucity of systematic studies, and the complexity of the scaling issue, means that many problems still exist and no consistent conclusions have yet been reported. In particular, there have been very few reports concerning the scaling dependency of K S, especially in the region of the Loess Plateau, China. One of the main reasons is that measuring K S in the field is costly and time-consuming (Moustafa 2000).

Thus, a comprehensive, systematic investigation into how the statistical properties for K S vary as a function of spatial scale is relevant. The main aims of the present study were: (1) to analyze how the apparent statistical properties of K S (variance, correlation length, and nugget–sill ratio) change with the changes in sampling scale, in terms of spacing, extent and support in a small watershed; and (2) to provide a reference for decision-making when planning sampling strategies for K S.

2 Materials and methods

2.1 Field site description

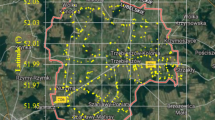
The study was conducted in the Daye watershed within the larger Liudaogou watershed (110°21′–110°23′ E, 38°46′–38°51′ N) located in Shenmu County, Shaanxi Province, China (Fig. 1). The area has been susceptible to ongoing severe water and wind erosion since ancient times (Tang et al. 1993) that affects the environmental conditions and has resulted in a fragmented landform, characterized by a large number of deep gullies and undulating slopes. The Daye watershed extends over an area of 50 ha at altitudes ranging from 1,130 to 1,233 m (a. s. l.). The climate is classified among the moderate-temperate and semi-arid zones: the mean annual precipitation is 437.4 mm, nearly half of which falls from July to September; the potential evapotranspiration is 785 mm; the mean aridity index is 1.8; and the mean annual daily temperature is 8.4 °C. A deep (up to 100 m) loess layer, which originated during the Quaternary period, covers the area. The dominant soil (a cultivated loessial soil), is an Ust-Sandic Entisol. Sandy loam and silty loam textures (mean particle size fractions: clay: 5 %; silt 43 %; sand 52 %, USDA) dominate the upper 10 cm soil layer and the mean soil bulk density of the 0–5 cm layer is 1.35 g/cm3 (Wang et al. 2010). Soil organic contents are low (Fu et al. 2010) and the soil structure is poor. Land uses include scrubland of predominantly bunge needle grass and caragana and also some cultivated farmland and arboriculture.

Fig. 1
figure 1

Spatial distribution of 4,865 samples collected from the small Daye watershed on the Loess Plateau

Full size image

2.2 Sampling and measurements

Detailed measurements of the spatial patterns of K S were made in the Daye watershed from August 03 to September 28 in 2009. During this time, the volumetric soil water contents of the 0–5 cm soil layer ranged approximately from 10 to 15 %, under which conditions the samples were easier to remove without disturbance enabling intact soil cores to be obtained. In addition, K S was almost constant over time during the experimental period (Hu et al. 2009), ensuring that most of the observed variations in K S were spatial in nature. In the present study, a total of 4,865 soil samples were collected to a depth of 5 cm from which K S values were later determined. The large number of samples made it possible for a series of inherent scales to be investigated. In the present study, the scale factors of spacing and support could be changed over a range of two orders of magnitude, and eight different spatial scales could be applied by changing the extent. A regular grid sampling system has been proven to be more accurate in predicting spatial distributions than randomized sampling (Hirzel and Guisan 2002). Therefore, this method was employed in the present study, collecting samples from locations set out in a regular grid comprising of square cells with 10 m between rows and columns (see Fig. 1). However, due to the highly complex topography of the study area, some of the grid-point locations were omitted due to inaccessibility.

Data were collected from the field as follows: first, the position of the sampling point was located using a Trimble 5700 GPS and the geographic coordinate was recorded. A sample of undisturbed soil was taken using a soil-corer, 5 cm long and 5 cm in diameter. The K S was measured using the constant head method (Klute and Dirksen 1986). The ambient temperature of the laboratory was constant at 20 °C. To make our results comparable with others, we transformed the K S value measured at 20 °C to their equivalents at 10 °C using the equation (Liu 1982):

$$ {K_{{10}}} = \frac{{{K_t}}}{{0.7 + 0.03 \times t}} $$
(1)

where K 10 is the K S at 10 °C, K t is the K S at t°C, and t is the temperature at which K S was measured. The values of K S referred to in this paper all refer to K 10.

2.3 Data analysis methodology

Data were analyzed in two main steps. The first step was an analysis of the full dataset, to generate the “true” values of the parameters. The second step analyzed sub-sets of data extracted from the full dataset to generate “apparent” parameters values obtained by “re-sampling”. We then analyzed the differences between the “true” values and the “apparent” values to determine scale-dependency. The parameters examined in this study were the variance, the correlation length, and the nugget–sill ratio.

The variance was obtained by classical statistics and geostatistical analysis produced the correlation length and the nugget–sill ratio. Semivariograms were used to evaluate the spatial dependence of the K S data. Romano (1993) and Logsdon (2002) had reported positively skewed and log-normal distributions of K S data due to preferential flow phenomenon, which was applicable to the present datasets. In this study, all the raw datasets that were not normally distributed were logarithmically (Log10) transformed. In both steps, an exponential model with a nugget was used in the geostatistical analysis using GS+ (Gamma Design Software 2004), since most of the integral scale data were also best fitted by the exponential variograms having the highest determination coefficient and the lowest residual sum of squares. Based on the regionalized variable theory and intrinsic hypotheses (Krige 1994), a semivariogram can be expressed as:

$$ \gamma (h) = \frac{1}{{2N(h)}}\sum\limits_{{i = 1}}^N {{{\left[ {Z\left( {{x_i}} \right) - Z\left( {{x_i} + h} \right)} \right]}^2}} $$
(2)

where γ(h) is the semivariance, h is the lag distance, N(h) is the number of sampling couples in the interval h, Z(x i ), and Z(x i + h) are values of variable Z at positions x i and (x i + h).

Note: in the present study, no single model was the best-fitted model for all the K S datasets of the various sampling scales but most of the empirical semivariograms were better fitted by the exponential model while the next best-fit was obtained using the spherical model. Therefore, in this study, in order to compare the results, we chose to use the exponential semivariogram, which was expressed as:

$$ \gamma (h) = {C_0} + {C_1}\left[ {1 - \exp \left( { - \frac{h}{\lambda }} \right)} \right] $$
(3)

where C 0 is nugget variance, C 1 is structural variance, and λ is distance parameter called correlation length.

2.3.1 Analysis of the full dataset

The spatial map of predicted K S obtained by ordinary kriging based on all 4,865 samples from the study area is shown in Fig. 2. The exponential model was used to describe the semivariograms of K S (Fig. 3). The summary statistics of the full K S dataset (Table 1) could be defined as the “true” values since they were derived from the full dataset, rather than from part of the dataset.

Fig. 2
figure 2

Spatial interpolation map (ordinary kriging) of K S based on the full dataset

Full size image
Fig. 3
figure 3

Semivariograms with fitted models for K S based on the full dataset for the small Daye watershed

Full size image
Table 1 Summary statistics for the K S of soils in the Daye watershed based on the full dataset (n = 4,865)
Full size table

Two notable features can be seen in Table 1. First, K S was moderately spatially dependent in the study area (nugget–sill ratio 25–75 %; Chien et al. 1997), and had strong variability (coefficient of variation = 98.3 %); the maximum value was more than 8,000 times that of the minimum value (8.3 and 0.001 mm/min, respectively), which was similar to the findings of Sobieraj et al. (2004). The highest high values of K S data in this small watershed were generally found in sandier soils, which were located at the middle or top of the steeper slopes where weathered soil parent material from underlying rocks was exposed. Lower values occurred in clayier soils in the valleys under grassland. However, the range of K S in the present study differed from those of other studies (Zimmermann and Elsenbeer 2008; Mohanty and Mousli 2000), due mainly to the differences in scale. Second, the data was not normally distributed but was strongly and positively skewed (4.13) and was more strongly leptokurtic (32.2) than normal. However, the data were approximately log-normal, with a skewness value of 0.2 and a kurtosis value of 1.5. The relatively high kurtosis value was likely due to “outliers”, which we retained after confirming that they were not a result of experimental error in the measurements and that they were likely to be representative of certain locations in the watershed. Transforming non-normally distributed data by using logarithms (log10) is a common method (Journel 1980; Saito and Goovaerts 2000) and is especially applicable to K S studies (Romano 1993).

2.3.2 Re-sampling analyses

The aim of the re-sampling analysis was to emulate hypothetical sampling scenarios (or model scenarios) for which only a fraction of the full dataset might be available (Western and Blöschl 1999). The hypothetical sampling scenarios differed in terms of the scale of the samples. In the framework used here, we considered three aspects of scale—spacing, extent, and support—each of which could be re-sampled at a range of different spatial scales for the re-sampling analyses. For each re-sampled dataset the “apparent” variance, “apparent” correlation length and “apparent” nugget–sill ratio were calculated for each of the respective scales. In most cases, the “apparent” values, derived from the re-sampled data, and the “true” values, derived from the full dataset, differed in a manner that reflected the bias introduced by the differences in the measurement scales.

In the case of spacing, in order for the data to be representative, sets of samples were re-sampled from the same regular grid by increasing the spacing between samples in 10 m increments from 10 to 160 m for each dataset. Using classical statistics and geostatistical analysis, the variance, correlation length, and nugget–sill ratio were calculated for each sampling scale. As the spacing was increased from 10 to 160 m, the number of samples decreased from 4,865 to 22. The summary statistics of the data sampled at these different scales of spacing are given in Table 2. The scale, in terms of the spacing, a Spc (in meters), was defined as the average spacing of the samples:

$$ {a_{\rm{Spc}}} = {\left( {\frac{A}{n}} \right)^{{1/2}}} $$
(4)

where a Spc (in meters) is the spacing of samples; A (in square meters) is the area of the domain; and n is the number of samples.

Table 2 Summary statistics for K S under different sampling scales, in terms of spacing, extent and support
Full size table

In the case of extent, the first scenario used all of the grid-points. In the next scenario, the domain was subdivided into two contiguous regions and the data from each region were each considered to be one realization to give two realizations comprising 2,432 and 2,433 samples, respectively. For each of the two realizations, the “apparent” values of variance, correlation length, and nugget–sill ratio were estimated. The mean values of the parameters of the two realizations were then used as the “apparent” parameters at this scale. In the next scenario, the domain was subdivided into four contiguous regions and treated as above to derive the means of the parameters of the four realizations to give the “apparent” parameter values. We continued to divide the domain in this way up to a maximum of 128 contiguous regions, at which level each region contained only 38 samples. The summary statistics for the full list of all eight levels of subdivision of the sampling grid for the case of extent are given in Table 2. The scale, in terms of the extent, a Ext (in meters), was defined as the square root of the area of the region:

$$ {a_{\rm{Ext}}} = {\left( {{A_{\rm{region}}}} \right)^{{1/2}}} $$
(5)

where a Ext (in meters) is the extent of the samples; and A region (in square meters) is the ratio of the total area to the number of regions, or realizations, that was given by:

$$ {A_{\rm{region}}} = \frac{A}{{{n_{{{\rm{real}}{\rm{.Ext}}}}}}} $$
(6)

where n real.Ext is the number of contiguous regions.

In the case of support, the first scenario used data from each individual grid-point. In the next scenario, four adjacent points (20 × 20 m) in contiguous sub-plots were averaged to give one mean value of K S and its corresponding mean geographic coordinate. Thus, at this scale of support (20 m), 1,216 aggregated values and their corresponding geographic coordinates were obtained. Classical statistics and geostatistical analyses were then used to estimate the variance, correlation length, and nugget–sill ratio at this scale. In the next scenario, nine adjacent points (30 × 30 m) were aggregated, and so on, until the scenario where 196 adjacent points (140 × 140 m) were aggregated. The summary statistics of the re-sampling analyses for support are summarized in Table 2. The scale, in terms of the support, was defined as the square root of the area over which the samples were aggregated:

$$ {a_{\rm{Supp}}} = {A_{\rm{aggreg}}}^{{1/2}} $$
(7)

where a Supp (in meters) is the support of the samples; and A aggreg (in square meters) is the area over which the samples were aggregated.

3 Results and discussion

Figure 4 shows the results of the re-sampling analysis. The apparent parameters of K S depended to different degrees on the sampling scale in terms of spacing, extent and support.

Fig. 4
figure 4

Results of the re-sampling analyses: apparent variance (top), apparent correlation length (center), and the apparent nugget–sill ratio (N/S; bottom) as a function of a spacing; b extent, and c support

Full size image

With an increase of spacing, the apparent variance decreased slightly (see Fig. 4a, top). Although the regression equation was not significant (p = 0.137), it differed from the results reported by Western and Blöschl (1999) who found that sampling spacing did not affect the apparent variance of soil moisture. The different methods used to re-sample might partly explain the difference: in their study, variance was the mean value of all the variances of their sub-datasets; in our study, however, because we collected 4,865 samples in a regular 10 × 10 m grid, we were able to select each re-sampled point only once for each specific spacing scale, and sampling from a regular grid probably reflects reality more accurately. In addition, the variability of K S is much greater than that of soil moisture. Both K S and soil moisture are variable in space due to differences in soil texture (Biswas and Si 2011; Rawls et al. 1998), soil structure (Dörner et al. 2010), climate (Wang et al. 2011), and land use (Hu et al. 2009; Wang et al. 2011). However, soil moisture can move between locations along soil water potential gradients as well as by “hydraulic lift” (Richards and Caldwell 1987), which inherently reduces the spatial variability of soil moisture contents. Garten et al. (2007) also found whether measurement variability increased with increasing spatial scales (1 m to 1 km) depended on the soil properties when the variability in 11 soil properties was tested in a temperate, mixed-hardwood forest ecosystem, in Tennessee, USA.

Spacing had a significant effect on apparent correlation length (p < 0.01; see Fig. 4a, center). The true correlation length in the present study was 70 m (see Fig. 3). Below 1.1 times this length (i.e., 80 m), as spacing increased the apparent correlation length decreased from 70 m for a spacing of 10 m to its lowest value of about 30 m for a spacing of 50 m. At this point of inflection, further increases in sampling space generally resulted in increases in correlation length, and the rate of increase also increased with sampling spacing. Generally, when sampling spacing increased, the internal variability could be ignored and the apparent correlation length increased with increased spacing. However, when spacing was small enough, the internal variability was also small and sampling was intensive enough for any increase in spacing not to cause a corresponding increase, or even to actually cause the observed decrease, in the apparent correlation length. For example, Kerry and Oliver (2007) reported that the apparent range of clay content also decreased as spacing increased from 20 to 80 m. Our results were similar to those reported by Western and Blöschl (1999), but the point of inflection occurred at 1.5 times the correlation length in their study. However, for a larger spacing, the internal variability was not well-represented by the sparser sampling, and the apparent correlation length increased significantly with further increases in spacing. This can best be understood in terms of the frequency domain. Large spacing causes an overestimation of apparent correlation length because, at these larger scales, sampling only resolves the low frequencies while neglecting the smaller scale, high frequencies. However, the high frequencies were partly “folded back” from the lower frequencies. This effect is termed “aliasing” in sampling theory (Vanmarcke 1983; Jenkins and Watts 1968) and has been examined by Matalas (1967). When the spacing is small, the effect of the “folded back” phenomenon is obvious, and with increasing spacing, the effect decreases. Hence, the apparent correlation length does not increase when the spacing increases from 10 to 80 m, but increased significantly for spacing larger than 80 m in the present study. A similar effect has been discussed in detail in relation to studies on groundwater (Gelhar 1993) and soils (Russo and Jury 1987).

The difference in the positions of the inflection points observed in the present study and in the study by Western and Blöschl (1999) might be a result of inherent differences in the natural levels of variability generally observed for K S and soil moisture. Thus, the lower natural variability of soil moisture allows for a larger spacing of sampling than is necessary for K S. Based on this, the sampling spacing for K S required for reliable estimates of the correlation length in this study was 1.1 times the true correlation length (i.e. 80 m, see Fig. 3), with a sample size of 76 (see Table 2).

However, the apparent nugget–sill ratio decreased with increased spacing indicating that spatial dependency was overestimated at larger scales (see Fig. 4a, bottom). This might be due to the scale of internal variability being neglected: only samples collected at the largest scales did not reflect the true variability. With increasing sampling spacing, the nugget variance and structure variance changed. However, the decrease of the apparent nugget–sill ratio was mainly caused by the decreasing nugget variance at spacing smaller than the true correlation length, and by the increasing structure variance at sampling spacing exceeding the true correlation length.

Apparent variance, apparent correlation length and apparent nugget–sill ratio increased with increasing extent (see Fig. 4b). Similar results were reported by Western and Blöschl (1999) when the variance and correlation length of soil moisture data were investigated. The variability in the parameters of K S mainly derived from the processes controlled by the sampling extent; because the parameters were the mean values of all the sub-areas. This observation could also be interpreted in terms of the frequency domain. When keeping the spacing and the support of samples uniform, the small extent resulted in a natural variability that was only sampled at high frequencies, while the low frequencies were not sampled. Consequently, the total variance was lower and the integral scale was biased towards high frequencies (small scales). Unlike spacing, no obvious “aliasing” phenomenon was observed for extent.

Another interesting phenomenon was that the ratio between extent and the apparent range or correlation length was nearly constant. Gelhar (1993) reported the apparent correlation length to be about 10 % of the extent in the case of hydraulic conductivity in aquifers. Blöschl (1998) found similar results with patterns of snow cover in an Alpine catchment in Austria, as did Western and Blöschl (1999) for soil moisture in the Australian Tarrawarra catchment. In the present study, we found the ratio between the apparent correlation length and extent for K S (from 8 to 12 %; see Fig. 4b, center) to be reasonably consistent with the results mentioned above. A further point of interest regarding the extent data of Fig. 4b is that, although the three fitted curves indicated positive correlations, the shape and slope gradients of each curve differed. With increasing extent, from the minimum value of 63 m to a moderate value of 177 m and to the maximum value of 701 m, the slope gradients of the curves for apparent nugget–sill ratio increased from −1.1E−05 to 1.5E−04 to 8.8E−04, for apparent correlation length they were relatively constant changing from 0.06 to 0.07 to 0.13, while for apparent variance they decreased from 6.2E−04 to 2.7E−04 to 8.6E−05. This meant that with increasing sampling extent the heterogeneity of K S tended to increase at a decreasing rate. However, the spatial dependency expressed by the nugget–sill ratio, increased at an increasing rate. Generally, both nugget variance and structure variance increased with increasing sampling extent. Nugget variance was a more sensitive parameter than the latter one, which resulted in an increasing nugget–sill ratio with increasing extent.

Increasing support decreased apparent variance, increased apparent correlation length, and decreased the apparent nugget–sill ratio (see Fig. 4c). It was evident that variability was reduced when data were sampled at increasing levels of support. Several studies have examined the relationships between apparent variance and support. For example, Lauren et al. (1988) found that the variability for K S decreased with increases in sampling volume in a clayey soil with macropores. Furthermore, Rodríguez-Iturbe et al. (1995) analyzed soil moisture data derived from ESTAR measurements of the sub-humid Little Washita watershed in south-west Oklahoma. They examined a reduction in variance that occurred when a grid of 200 × 200 m pixels was aggregated to create a 1 × 1 km grid cell and concluded that soil moisture exhibited power law behavior with the exponent α having values between −0.21 and −0.28 in the relationship:

$$ \delta_{{{\rm{app}}{,_{\rm{Suoo}}}}}^2 = A_{\rm{aggreg}}^a $$
(8)

According to Eq. (7), Eq. (8) is equivalent to the exponent having a value between −0.42 and −0.56 in the relationship between apparent variance and support. Western and Blöschl (1999) also estimated the change of apparent variance with changing support. They collected 1,536 samples in the Australian Tarrawarra catchment and found that the section of the plot from a support of about 0.3 × λ true to about 3 × λ true, could be approximated by a straight line with a slope in the range of −0.42 and −0.56. In the present study, the relationship between apparent variance and support, when support changed from 0.29 × λ true (20 m) to 2 × λ true (140 m), was similar to the results of these other studies. When fitted by a power function, the exponent was −0.456, and the coefficient of determination (R 2) was 0.855. However, we found that a logarithmic, rather than a power function, to be a better function since it gave a higher R 2 of 0.934. Differences in the experimental design and the subsequent re-sampling procedures as well as the difference in the investigated soil parameter likely account for these slight differences between the studies.

For a constant extent, the apparent correlation length and apparent nugget–sill ratio had opposite trends (see Fig. 4a and c). For example, if apparent correlation lengths increased with changing scales, in terms of sampling spacing (see Fig. 4a) and sampling support (see Fig. 4c), then the apparent nugget–sill ratio decreased. This is explained by the fact that the nugget–sill ratio reflects the proportion of random variability within the total variability; hence the smaller the value of the nugget–sill ratio, the stronger is its spatial dependency, which in turn results in a greater correlation length. However, if the extent increased or decreased, then both the apparent correlation length and the apparent nugget–sill ratio will correspondingly increase or decrease (see Fig. 4b). The differences were in the rate of change of the apparent correlation length and the nugget–sill ratio, which has been discussed above. This demonstrated that the effect caused by extent was more important than the interaction of the apparent correlation length and the apparent nugget–sill ratio.

In order to compare apparent and true values quantitatively, the information in Fig. 4 was re-plotted in a non-dimensional form (Fig. 5). The apparent variance, correlation length, and nugget–sill ratio were all normalized by their true counterparts. Similarly, the sampling scales at which spacing, extent, and support had been conducted were normalized by the true correlation length. The overall trend of the effect of measurement scale on the apparent variance and the apparent correlation length is consistent with that in Fig. 4 but now, the effects can be discussed more quantitatively and are more comparable with the results from other studies, regardless of the differences in the true correlation length.

Fig. 5
figure 5

Results of the re-sampling analyses: normalized apparent variance (top), normalized apparent correlation length (center), and the normalized apparent nugget–sill ratio (N/S; bottom) as a function of a spacing; b extent, and c support

Full size image

Spacing had no significant effect on the apparent normalized variance but did affect the apparent normalized correlation length and the nugget–sill ratio (see Fig. 5a). The biases for variance were all lower than 26 % (except for 39.6 % at the spacing of 50 m) when the spacing changed within 1.6 × λ true (i.e. 110 m). However, when the spacing exceeded 1.6 × λ true, the biases were more than 50 % for most spacings. Hence, sampling at a greater density than 1.6 × λ true, with a sample number of 40 was suitable when designing a sampling strategy for variance in the present study. Once spacing exceeded about two times the true correlation length, the apparent correlation length was biased by up to a factor of two. The nugget–sill ratio was more affected by spacing than by correlation length. If the spacing was large enough, the value of the nugget–sill ratio might be as small as 5 % of its true value. Extent had a significant effect on both the apparent correlation length and the apparent nugget–sill ratio, but its effect on the apparent variance was relatively small (see Fig. 5b). The mean biases were −15.4 % (ranging from 0 to −37.4 %), −50.5 % (ranging from 0 to −71.4 %) and −61.3 % (ranging from 0 to −88.5 %) for variance, nugget–sill ratio, and correlation length, respectively, when the sampling extent decreased from 500 to 62.5 m. One-way ANOVA proved that the differences were all significant (p < 0.01) except for the difference between the nugget–sill ratio and the correlation length. Compared with spacing or support, extent was more closely related to the three variables having mean coefficient of determination values of 0.53, 0.88 and 0.96 for spacing, support and extent, respectively. As long as the extent was greater than about seven times the true correlation length, the bias in variance, correlation length, and nugget–sill ratio was small, each being more than 75 % of their true values. However, when the extent was as small as the true correlation length, which was close to the smallest investigated scale, the apparent variance, correlation length, and nugget–sill ratio also reached their lowest values at 60, 10, and 35 % of their true values, respectively. Support significantly affected all the statistical parameters. If it was smaller than about 15 % of the true correlation length, the biases in variance, correlation length, and nugget–sill ratio were small. However, if support increased, the apparent variance could be as small as 20 % of the true value, the correlation length could be as large as six times the true value and the nugget–sill ratio could be as small as 1 % of its true value (see Fig. 5c). All of these effects, except for that of spacing on variance, were significant (p < 0.01) and most of the results corroborated the findings of Western and Blöschl (1999) who investigated the variance and correlation length of soil moisture data.

Figure 5 clearly shows that the ideal case for a sampling scale is one with a very small spacing, a very large extent and a very small support, which all lead to the apparent variance, correlation length, and nugget–sill ratio being closer to their true values. As spacing increased, or extent decreased, or support increased, bias is introduced. However, since the taking of more samples implies higher costs, it is important to identify an optimal sampling scale. Since the nugget–sill ratio is a non-dimensional parameter without physical significance, we will discuss only the sampling scales of variance and correlation length. In practice, support is usually determined by the measurement technique and is chosen by default when the measurement technique is chosen. In addition, since support is usually very small in field studies, it is generally not the limiting factor. Table 3 showed the required scales for apparent variance and correlation length, in terms of sampling spacing and extent, under different bias levels. As discussed above, sampling spacing had no significant effect on variance, so spacing was not an effective index by which to predict variance. With the decrease of acceptable bias, the sampling spacing should decrease and sampling extent should increase. Furthermore, the correlation length required sampling at a lower sampling spacing and at a greater extent than variance. For example, the sampling extent for variance should be >0.2 × λ ture, >1.1 × λ ture, >4.5 × λ ture, and >6.0 × λ ture if the admissible bias is 50, 30, 10, and 5 %, respectively. However, the critical extent is 5.6 × λ ture, 7.5 × λ ture, 9.2 × λ ture, and 9.6 × λ ture, respectively, for the same bias for correlation length (see Table 3).

Table 3 Sampling scales required for apparent variance (δ 2app ) and apparent correlation length (λ app) under the allowable biases
Full size table

Sampling extent was more closely related to all three parameters when compared with spacing and support, which resulted in upscaling or downscaling being more accurate for extent than for the other scale indexes based on the results of this study. For an area with uniform soil and vegetation properties, it would be more reasonable to distribute sampling locations in a smaller sub-area at a higher density than to distribute them across the whole study area at a lower density. However, if the study area demonstrated greater spatial heterogeneity, the choice of a sub-area, which could accurately represent the mean condition of the whole area, needs to be made more carefully. For the sub-area, we could obtain the extent using Eq. (5) and apparent variance, correlation length, and nugget–sill ratio using classical statistics and geostatistical analysis. Through the polynomial equation presented in Fig. 5b (center), we could calculate the true correlation length. Then true variance and true nugget–sill ratio values could be obtained from the equations also presented in Fig. 5b (top and bottom). If the sampling spacing and sampling support were inconsistent with the case of Fig. 5b, we could convert them by the equations presented in Fig. 5a or in Fig. 5c. However, the disadvantage of doing this is that bias would be introduced during the conversion.

4 Conclusions

In the presented study, we examined the effect of using re-sampling analyses on the apparent spatial statistical properties of K S (variance, correlation length, and nugget–sill ratio) as the scale of three aspects of sampling—spacing, extent and support—changes. We concluded that:

  1. (1)

    The statistical properties for K S were scale-dependent. Apparent variance tended to decrease with increase in sampling spacing but increased with increase in extent and decreased with increase in support. Apparent correlation length always increased with increases in spacing, extent or support. Apparent nugget–sill ratios decreased with increase in spacing and support, and increased with increase in extent. All the fitted relations were significant (p < 0.01) except for that between variance and spacing.

  2. (2)

    Upscaling or downscaling for the parameters of K S were more reliable when based on sampling extent than on spacing or support in this study. Consequently, distributing limited sample locations in a sub-area of the main study area at a higher sampling density is an alternative sampling method, especially in a more homogeneous study area.

  3. (3)

    The investigated statistical properties behaved differently according to sampling scales. For example, correlation length required more samples than variance for the same bias.

Our results could increase the understanding of the effects of scaling on K S determinations for an area, and aid decision-making when planning sampling strategies. However, the present study was conducted in a small area (50 ha) for K S alone. Hence, additional studies are needed for larger study areas and for other soil properties to examine whether the results were site and/or variable specific.