1 Introduction

Life cycle inventory (LCI) datasets available to practitioners can be separated in two types: unterminated datasets and terminated datasets. What distinguishes them is the presence of links to other activities. Unterminated datasets, also referred to as unit process datasets, contain information on the links between the activity modelled by the dataset and other activities. Terminated datasets, also referred to as (vertically) aggregated datasets or system process datasets, represent cradle-to-gate product systems that have been traversed. Aggregated datasets contain information on the cradle-to-gate LCI of a given product and contain no information on the links between the activities that make up this cradle-to-gate product system.

Mathematically, unit process datasets are individual columns in the A and B matrices, respectively, representing direct technosphere and elementary inputs and outputs of activities. Life cycle calculations for a given functional unit f require that all activities be traversed or, otherwise stated, that the system of (often thousands of) linear equations As = f be solved (Heijungs and Suh 2002). The result of this solution (the scaling vector s) quantifies how much each activity must be produced. It can then be used to calculate the life cycle inventory g as g = Bs or the life cycle impact score h for a given impact category as h = cBs, where c is a vector of characterisation factors.

Aggregated datasets are based on the solution to the system of linear equations. Aggregated datasets can be LCI datasets, i.e. the inventory calculated by g = BA−1 f for a given output f, or life cycle impact assessment (LCIA) scores, calculated by h = cBA−1f. In either case, an LCA carried out with aggregated datasets linearly combines multiple aggregated datasets: for a metric x of interest (an inventory vector or an impact score), the metric on a life cycle basis is given as:

$$ x=\sum \limits_i{\alpha}_i{x}_i $$
(1)

where αi is a scaling factor (how much of an input i is required) and xi is the metric per unit of product i (e.g. CO2 emissions per unit product i).

The relative advantages of using both types of datasets are well documented in a chapter dedicated to this issue in the “Shonan Guidance Principles” for LCI database (Broadbent et al. 2011). Aggregated datasets have the disadvantage of masking information, which prevents analysts from gaining an understanding of the structure of the product systems they model and of adapting unit process datasets to better represent the activities they wish to model. Despite these disadvantages, there are many reasons why a database provider or a user may wish to use aggregated LCI data, such as to ensure confidentiality, to preserve data integrity, and for efficiency of calculations (see Table 3.1 of the Shonan Guidance Principles for a full list).

Of specific interest in this paper is the use of aggregated datasets in eco-design tools that analyse the relative environmental performance of design options and that do not need to do in-depth analyses of product systems, for which unit process data would be needed. Key characteristics of this type of eco-design tool are ease of use, given that the users are not LCA experts, and calculation speed, as the need to solve a large system of linear equations is avoided.

The use of aggregated datasets makes uncertainty analyses more difficult. While it is possible to represent the inventory flows or LCIA scores of aggregated datasets as probability distributions that account for the uncertainty of underlying parameters in the A and B matrices, using these distributions to calculate the uncertainty of an LCA result implies that the distributions of the aggregated datasets are independent. They are usually not—when aggregated datasets are built on the same underlying A and B matrices, each Monte Carlo iteration should be based on the same sampled values of the parameters of the A and B matrices. Having one Monte Carlo iteration using aggregated datasets where the cradle-to-gate CO2 emissions for electricity production would represent the value of the 99th percentile (i.e. a very high value) but that the cradle-to-gate CO2 emissions for a product dominated by electricity consumption would represent the first percentile (i.e. very low value) would not make any sense and yet would be completely possible if the values for both datasets were independently sampled.

Recent publications have shown that there is still some disagreement concerning the effect of dependent sampling on the uncertainty of LCA results. Notably, Qin and Suh (2017) argue that aggregated datasets with probability distributions can be used for fast uncertainty analysis and extend this conclusion to comparative LCA in Suh and Qin (2017). Heijungs et al. (2017) disagree, stating that this approach “cannot” be used for comparative LCA and that the uncertainty values generated using independent sampling from aggregated datasets would be largely overestimated.

That uncertainty analysis in comparative LCA should account for the correlation in input data used across compared options has often been explained, demonstrated and dealt with using dependent sampling (e.g. Huijbregts et al. 2003; De Koning et al. 2010; Mattila et al. 2011; Henriksson et al. 2015). To our knowledge, however, no author, before the discussion initiated by Qin and Suh (2017), specifically deal with the correlation that may occur between aggregated datasets.

The premise of this paper is that eco-design tools should indeed simply linearly combine aggregated datasets rather than attempt to solve large systems of linear equations but that the users of these tools should have access to rapid and valid information on the uncertainty of the LCA scores they are obtaining. The objectives of this paper are (1) to show the link between the correlation of aggregated datasets and the error introduced in uncertainty analysis using independent sampling of aggregated datasets in single-product LCA; (2) show that independent sampling of aggregated datasets is simply incorrect in comparative LCA; and (3) propose two methods to overcome the limits imposed by the use of aggregated datasets: the inclusion of covariance terms in the approximate analytical approach based on a limited Taylor series expansion and the use of dependent, precalculated samples.

The paper is structured as follows. First, a simple addition of two standard lognormal probability distributions is presented to exemplify the difference in uncertainty when independent and dependent sampling methods are used. Second, an example LCA of an aluminium water bottle is used to show the link between the correlation of aggregated datasets and the influence of independent sampling in single-product LCA and to show the importance of independent sampling in comparative LCA. Third, having shown the role of correlation in determining whether or not independent sampling of aggregated datasets yields inaccurate uncertainty results with the water bottle example, the correlation between all pairs of aggregated datasets in ecoinvent 2.2 and 3.3 is calculated, helping determine whether high correlation between datasets is frequent. Fourth, two approaches that allow the use of correlated aggregated datasets are presented: an approach based on the use of stored precalculated Monte Carlo simulation results (rather than the use of distributions based on these Monte Carlo simulation results) and the inclusion of the covariance term in the analytical approach to uncertainty propagation. Then, the proposed approaches are used for a case study comparing beef, vegetarian and vegan burger patties. Finally, other uses of the approach based on the use of presampled Monte Carlo results in LCA are also discussed.

2 Illustrative examples

2.1 Illustrating the problem with the simplest possible case

To illustrate that dependent and independent sampling in a Monte Carlo simulation can indeed change results, one can take the simplest possible case: the sum of two identical distributions. Let us take two standard lognormal distributions (i.e. lognormal distributions whose underlying normal distributions have a mean μ = 0 and a standard deviation σ = 1), ln1 and ln2. The two distributions are assumed to represent the same object (e.g. CO2 emissions for a given aggregated dataset), which means that the same value should be sampled for each iteration. Notebooks detailing calculations used in this paper are provided in the Electronic Supplementary Material (ESM); the sampling and analysis of results are detailed in SI1.

In dependent sampling, the same value is sampled for each Monte Carlo iteration. To simulate this, 1,000,000 random samples of a standard lognormal distribution were generated and multiplied by two to simulate two inputs. The large number of samples was used to eliminate the possibility of any observed results being due to sampling artefacts.

In independent sampling, different values of ln1 and ln2 are sampled for each iteration. To simulate independent sampling, two arrays of 1,000,000 random samples for ln1 and ln2 were generated and added together.

While the resulting means of the two distributions (presented in Fig. 1) are the same (2 × e(0 + 1 / 2) = 3.29), their median and dispersion are not. The dispersion of the sum of dependently sampled lognormal distributions is appreciably higher than that of the independently sampled lognormal distributions: the variance is twice as high (18.6 vs. 9.3), and the square of the geometric standard deviation (GSD2) is 1.64 times as high (7.4 vs. 4.5). This is to be expected, as the probability of sampling two very low or two very high values in the same iteration is lower than that of sampling just one such value. Following Qin and Suh (2017), the similarity of the two resulting distributions is represented using Overlap Ratio (OVL), which measures the area the distributions’ density curves share and is given by OVL(f, g) =  ∫ min {f(x), g(x)}dx. The OVL of the two distributions in Fig. 1 is 0.84, meaning the histograms share 84% of their surface.

Fig. 1
figure 1

Distribution of the sum of samples from two standard lognormal distributions, based on a 1,000,000 iteration Monte Carlo simulation

Full size image

2.2 Illustrating the problem with a simple product system (water bottle)

2.2.1 Presentation of the product system

To illustrate that independent sampling in Monte Carlo can indeed lead to a faulty estimation of the dispersion of LCA results, a simple example of an LCA of a fictive reusable water bottle is analysed. The production of the water bottle has two inputs: 0.15 kg of recycled aluminium from new scrap and 0.15 kg of one-stroke cold impact extrusion, both modelled using ecoinvent version 2.2. Since they are modelled using the same database, the product systems for recycled aluminium and impact extrusion will contain many unit processes in common. Notably, both products rely directly on medium voltage electricity from the UCTE grid, and this electricity contributes substantially to the scores of both inputs for most impact categories (see SI2 for code and SI3 for detailed results).

2.2.2 Sampling in single-product LCA

Because they share unit processes in their background, the inventory and LCIA scores for recycled aluminium and impact extrusion will be correlated. To calculate this correlation, a 10,000 iteration Monte Carlo simulation was carried out where the cradle-to-gate inventory of each product was calculated using the same sampled values for the A and B matrices (dependent sampling), and the Pearson product-moment correlation coefficients was calculated between the resulting LCIA scores for all 17 ReCiPe 1.08 hierarchist midpoint categories (Table 1). Two other 10,000 iteration Monte Carlo simulations were carried out where the scores for aluminium and impact extrusion were calculated independently.

Table 1 Pearson product-moment correlation coefficients between secondary aluminium and impact extrusion at LCIA score level (ReCiPe hierarchist midpoint categories), based on 10,000 iteration Monte Carlo simulations
Full size table

Finally, lognormal distributions were fitted to the independent samples, and new samples were generated from these fitted distributions, to simulate the use of fitted distributions for LCA (see SI2 for the shape parameters of these distributions). While the overlap ratio between (1) the samples generated from the fitted lognormal distributions and (2) the original samples on which the fitted distributions were based are higher than 0.90 for two-thirds of the samples, they are sometimes as low as 0.26 (Table 2), indicating a very poor fit.

Table 2 Overlap ratio between (1) the distribution of LCIA scores resulting from a 10,000 iteration Monte Carlo simulation and (2) 10,000 samples drawn from a lognormal distribution fitted over the Monte Carlo results
Full size table

The actual correlation coefficients for dependent sampling vary from close to zero (urban land occupation) to very low (metal depletion = 0.05) to very high (Ionising radiation = 0.98), with the average being 0.35. The scores of recycled aluminium and impact extrusion are of course uncorrelated when based on independent sampling or sampling of the fitted distributions.

In this paper, three measures of dispersion are used: the mean absolute deviation (MAD) (Eq. (2)), the interquartile range (Q3–Q1) and the mid-99% interpercentile range (percentile 99.5% to percentile 0.5%).

$$ \mathrm{MAD}=\frac{1}{n}{\sum}_{i=1}^n\left|{x}_i-x=\right| $$
(2)

Figure 2 shows the ratio of these measures of dispersion for LCIA scores calculated using independent and dependent sampling. As expected, independent sampling results in smaller dispersion (values are smaller than 1 on the y-axis). Also, there is a general tendency for the difference in dispersion between sampling approaches to be greater when the scores of the two inputs are more correlated, i.e. the higher the correlation of inputs, the greater the risk that independent sampling will underestimate the dispersion of the score. In the most extreme case, for ozone depletion, the independent sampling simulation does not cover 30% of the 99% confidence interval covered by the dependent sampling simulation.

Fig. 2
figure 2

Ratios of dispersion of the LCIA scores of bottle production as calculated for 10,000 iteration Monte Carlo simulations using independent (numerator) and dependent (denominator) sampling, as a function of the Pearson product-moment correlation coefficient of the two inputs to bottle production as presented in Table 1. For a given measure of dispersion, each point represents a ReCiPe Midpoint (hierarchist) impact category. Three categories are singled out as examples

Full size image

To show these differences in dispersion, distributions are graphed for two impact categories: climate change that presents an average correlation of inputs (0.40) and ozone depletion which presents a high correlation of inputs (0.79) (Fig. 3). Visually, the climate change probability distributions are quite similar, and those for ozone depletion are less so. The overlap ratio for climate change is 0.96 and that of ozone depletion is 0.86.

Fig. 3
figure 3

Probability distribution functions for two ReCiPe Midpoint impact categories (climate change and ozone depletion impact categories) resulting from dependent and independent sampling, based on a 10,000 iteration Monte Carlo simulation for the water bottle example

Full size image

The difference between independent and dependent sampling of aggregated datasets is not constant—the difference increases when the aggregated datasets are heavily correlated. Correlation between datasets depends on the metric of interest (i.e. on the specific impact category or inventory item). It is therefore probably inappropriate to use a one-size-fits-all correction factor when carrying our uncertainty analyses with aggregated datasets, as was suggested by Suh and Qin (2017).

2.2.3 Sampling in comparative LCA

To show that a correction factor is especially inappropriate in comparative LCA, a second bottle was modelled. It also has recycled aluminium and impact extrusion as inputs but is heavier than the original bottle. Its static LCIA scores are greater than the lighter bottle in exactly the same proportions as the increase in mass, and our physical intuition tells us the same conclusion should apply under uncertainty assessment. The comparison of products under uncertainty is often done by simply counting the share of Monte Carlo iterations where one alternative has a lower LCIA score than that of another product it is compared to, i.e. n(A < B) (Heijungs and Kleijn 2001; Huijbregts et al. 2003; Mattila et al. 2011). In a Monte Carlo simulation using dependent sampling, all iterations result in the heavier bottle having a higher LCIA score, regardless of the magnitude of the increase in mass. Independent sampling, however, gives more ambiguous results. Figure 4 shows the calculated probability the heavier bottle has a smaller LCIA score that the lighter bottle for a given independently sampled Monte Carlo iteration. At very small differences in mass, there is no clear preference between the two bottles, and even when the mass is doubled, there is some ambiguity: for ionisation radiation, the Monte Carlo simulation indicates that there is a 23% chance that the lighter bottle has a higher LCIA score. The use of correction factors would not fix this discernibility problem.

Fig. 4
figure 4

Probability under independent sampling that a heavier bottle is environmentally preferable to a lighter but otherwise equivalent bottle. The intuitively correct probability, confirmed by dependent sampling, is 0% for any increase in mass

Full size image

3 Method and data

3.1 Measuring correlation of activities in an LCI database

The importance of dependent sampling is more pronounced for higher correlation among inputs used in an LCA. It therefore behoves us to determine the level of correlation of datasets (or, more precisely, cradle-to-gate product systems) in LCI databases.

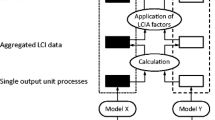
To do so, a suite of Python routines was built on top of the Brightway2 LCA framework (Mutel 2017). Given a database for which elements of the A and B matrices are described by probability density functions (PDF), the routines calculate n LCA results for a set of m final demands and p LCIA methods. The steps to do so, represented in a simplified fashion in Fig. 5, are as follows:

  • 1) Select m products for which aggregated datasets are required and convert into as many final demand vectors f.

  • For n iterations:

    • 2) Sample new values for the elements of the A and B matrices based on their PDF.

    • 3a) Calculate the cradle-to-gate LCI for each m final demands. Inventories for a final demand j and a Monte Carlo iteration i are given by \( {\mathbf{g}}_{ij}={\mathbf{B}}_i{\mathbf{A}}_i^{-1}{\mathbf{f}}_j \), although the actual algorithm used does not actually invert the technosphere matrix.

  • 3b) The resulting LCI vectors for each iteration are stacked, per final demand, resulting in m LCI arrays of dimensions equal to the number of elementary flows in the database x n iterations. The stacking order is always the same, ensuring that the ith column in the LCI arrays of two different final demands refers to the same underlying (ith) Monte Carlo iteration and hence to the same underlying sampled values for the elements of the A and B matrices.

  • 4, 5) The resulting LCI arrays can be converted to LCIA score arrays for p selected impact categories. The result is a set of m × p one-dimensional arrays containing n results. Again, the ith results in any of the LCIA score arrays are based on the same underlying ith Monte Carlo iteration. Note that this characterisation step is not necessary: one could very well simply use LCI results directly in subsequent calculations.

Fig. 5
figure 5

Graphical representation of the database-wide Monte Carlo algorithm. For each iteration, new samples are drawn from probability distributions in the A and B matrices. These are then used to calculate the LCIA scores for a set of unit demands. The result is a set m (number of final demands) × p (number of LCIA methods) one-dimensional arrays containing n (number of Monte Carlo iterations) results. The ith element of any of these arrays stems from the same Monte Carlo iteration

Full size image

The sampling process is parallelizable, meaning iterations can be calculated on multiple CPUs on a given computer or even on multiple computers.

This procedure was applied to the ecoinvent 2.2 database (m = 4087, i.e. the set of final demands covered all products in the database) and the ecoinvent v3.3 database (m = 3545, i.e. the set of final demands covered all products supplied by market activity datasets). For both databases, the procedure was carried out for n = 10,000 iterations. LCIA scores were carried out for ReCiPe midpoint impact categories (p = 17). For each database and each impact assessment method, Pearson product-moment correlation coefficients were calculated for each pairs of final demands (over 8.3 million unique pairs for ecoinvent 2.2, and about 6.3 million unique pairs for ecoinvent 3.3). The code is given in SI4.

The results from this analysis can be used to determine whether the use of aggregated datasets in a particular LCA has the potential of leading to an important underestimation of the dispersion of the results. If all inputs to a product system are largely uncorrelated for the impact categories of interest, the risk of introducing large discrepancies in the measure of dispersion when carrying out a Monte Carlo simulation using aggregated datasets is limited.

3.2 Uncertainty analysis and aggregated datasets using presampled results

The database-wide Monte Carlo simulation presented in Section 3.1 results in a set of ordered arrays of cradle-to-gate LCIA scores where the ith element of any array corresponds to the same ith Monte Carlo iteration. It is proposed in this paper that these precalculated results can be stored and reused directly to conduct Monte Carlo simulations for LCA using aggregated datasets.

Take an LCA defined as a linear combination of datasets: \( \mathrm{result}=\sum \limits_1^m{\alpha}_j{x}_j \) where m is the number of aggregated datasets used in the system and α and x are, respectively, the scaling factor and the aggregated result for dataset j. If one has arrays with n dependently sampled aggregated dataset results, one can simulate a Monte Carlo simulation by constructing a result array of dimension n where each of its elements i is based on the elements i of the aggregated dataset LCIA score arrays, i.e. \( \mathrm{result}\ \mathrm{array}=\left[{\left({\sum}_{j=1}^m{\alpha}_j{x}_j\right)}_1,{\left({\sum}_{j=1}^m{\alpha}_j{x}_j\right)}_2,\dots, {\left({\sum}_{j=1}^m{\alpha}_j{x}_j\right)}_i,\dots, {\left({\sum}_{j=1}^m{\alpha}_j{x}_j\right)}_n\ \right] \).

Note that the same approach could be used with precalculated arrays of LCI results rather than LCIA scores.

3.3 Uncertainty analysis and aggregated datasets using the analytical approach

Another method for propagating the uncertainty of input terms in an LCA is the approximate analytical approach based on a limited Taylor series expansion. This approach has been used in various LCA studies (Hong et al. 2010; Imbeault-Tétreault et al. 2013) and compared to sampling approaches like Monte Carlo simulations in Heijungs and Lenzen (2014). The approximate analytical approach is always presented or used in the context of LCA conducted with unit process datasets. In those cases, the sensitivity and variance of all elements of the A and B matrices are considered. The covariance terms, which would describe the covariance of values in the A and B matrices, are usually assumed to be zero. Note that this covariance is different than that discussed previously, which was the covariance between values in the calculated inventory results (aggregated datasets).

In the simple water bottle example, the analytical approach with disaggregated datasets would need to account for the sensitivity and variance of the over 90,000 uncertain parameters in ecoinvent version 2.2. The equations for calculating the sensitivity of these terms are presented in Heijungs (2010).

The use of aggregated datasets, by transforming the set of linear equations to a simple linear combination of terms (Eq. (3)), simplifies the analytical approach drastically:

(3)

Where,

y :

is some metric of interest (e.g. an inventory item, an LCIA score) for the LCA

n :

is the number of aggregated datasets i in the LCA

i :

(or j) is an aggregated dataset

x i :

is the corresponding metric (an inventory item, an LCIA score) for a given aggregated dataset i

α i :

is the scaling factor for aggregated dataset i

var:

refers to the variance of a term

cov:

refers to the covariance of a term

Looking in detail at each term of the equation:

  • \( \sum \limits_i^N{\alpha}_i^2\operatorname{var}\left({x}_i\right) \) accounts for the uncertainty of the aggregated datasets. Note that the sensitivity term is simply the associated scaling factor. The variance of the aggregated datasets can be computed ad hoc from a separate Monte Carlo iteration or precalculated using the database-wide Monte Carlo approach presented above.

  • \( 2{\sum}_{i=1}^{N-1}{\sum}_{j=i+1}^N{\alpha}_i{\alpha}_j\operatorname{cov}\left({x}_i{x}_j\right) \) accounts for the covariance of the aggregated datasets. As was shown above, this covariance is sometimes far from being negligible and hence should not be discarded without a prior verification of its importance. However, it can easily be computed ad hoc from a separate Monte Carlo simulation or precalculated using the database-wide Monte Carlo approach presented above.

  • \( {\sum}_{i=1}^N{x}_i^2\operatorname{var}\left({\alpha}_i\right) \) accounts for the uncertainty of the scaling factors, if relevant. This uncertainty is contextual (i.e. specific to an LCA study) and cannot be precalculated. Note that the sensitivity term is simply the value of the associated aggregated dataset.

  • \( 2{\sum}_{i=1}^{N-1}{\sum}_{j=i+1}^N{x}_i{x}_j\operatorname{cov}\left({\alpha}_i{\alpha}_j\right) \) accounts for the covariance of the scaling factors, if relevant. Again, this covariance is contextual.

  • \( 2{\sum}_{i=1}^N{\sum}_{j=i}^N{\alpha}_i{x}_j\operatorname{cov}\left({\alpha}_i{x}_j\right) \) accounts for the covariance between aggregated datasets and scaling factors. In most circumstances, these should be equal to zero given that scaling factors refer to the foreground and aggregated datasets refer to the (normally independent) background.

Except the terms associated with the uncertainty of scaling factors, all the terms can be precalculated (for a given background database) using the procedure outlined above.

Despite the simplicity of the analytical approach, it suffers from two notable disadvantages: the distribution of the result cannot be known (only its variance), and, in comparative LCA, it cannot be used to determine whether the difference between two product systems is significant (Heijungs and Lenzen 2014). Some authors have proposed comparison indicators whereby the significance can be calculated (Hong et al. 2010; Imbeault-Tétreault et al. 2013), but these are based on two assumptions: the parameters are lognormally distributed and, more problematic, that the two systems are independent.

3.4 Case study

One eco-design tool that uses aggregated datasets is the EcodEX software, produced by Selerant (2017). EcodEX is specifically focused on the LCA of food products. It is simple enough to be used by non-LCA experts and is meant to be used early in the design process, while design freedom is still high. It provides estimates of the environmental hotspots in a product’s value chain and can compare the environmental performance of different design alternatives. The software is notably used by Nestlé R&D community to gain insights into the environmental performance of food products early in the design phase (Schenker et al. 2014).

Calculations in EcodEX use three types of information: Nestlé-specific recipe data, modeller-supplied information such as distances and electricity consumptions, and background LCI data, principally on ingredients, energy vectors, transport and packaging. The majority of background LCI data are taken from public sources: ecoinvent 2.2 (Frischknecht et al. 2005), World Food LCA Database (Quantis 2017) and Agribalyse (ADEME 2017; Quantis 2017). The background data is stored as aggregated datasets, and the calculations are simply linear combination of these aggregated datasets expressed as LCIA scores for five impact categories.

Uncertainty analysis in LCA using precalculated aggregated datasets is presented for an LCA of three fictional but nonetheless reasonable burger patty recipes (Table 3). This type of study is representative of what would be done with the EcodEX tool, though it omits transport and packaging. First, the procedure for approximating the variance of the scores of individual burgers using the Taylor series expansion analytical approach is presented. It is also shown how considering the covariance between aggregated datasets influences the total variance. The uncertainty of both single-product and comparative LCA results is then calculated with Monte Carlo sampling using four sampling approaches: dependent sampling using unit process datasets, independent sampling, sampling of fitted distributions and reuse of stored samples.

Table 3 Burger patty recipes
Full size table

4 Results and discussion

4.1 Correlation between all pairs of aggregated datasets in ecoinvent databases

Pearson product-moment correlation coefficients were calculated for each pair of aggregated datasets from ecoinvent version 2.2 and for all market datasets from version 3.3. These are based on dependent samples and are calculated for 17 ReCiPe midpoint categories. The several million correlation coefficients are presented in electronic SI5 (ecoinvent v2.2) and SI6 (ecoinvent v3.3) and are plotted in histograms (Fig. 6) to provide an overview of their values, per database and per impact category. Three types of results can be discerned.

Fig. 6
figure 6

Histograms of (1) Pearson product-moment correlation coefficients for all pairs of datasets, in grey, and (2) the concentration ratio of all product systems, in blue, for all products in ecoinvent v2.2 (a) and ecoinvent 3.3 (b) for 17 ReCiPe midpoint impact categories

Full size image

First, several impact categories such as climate change show a majority of low correlations across pairs of aggregated datasets. Correlation coefficients will be lower if the main contributors in the supply chain to the LCIA scores and, more precisely, to the contribution to variance in the LCIA scores are different for the two compared datasets. These low correlations are consistent with impacts distributed among many unit processes and emissions.

Second, two impact categories (human toxicity and ionising radiation) show a majority of high correlation factors across pairs of aggregated datasets. High correlation over most pairs of aggregated datasets indicates that there are relatively few datasets which contribute to the variance of these impact categories in the databases and that these datasets are in the background of most aggregated datasets.

Finally, a few impact categories fall somewhere in between these two extremes, with correlation coefficients distributed across the spectrum.

Figure 6 also contains a histogram of the one exchange concentration ratio of all product systems in the databases. The concentration ratio is a concept borrowed from economics, where it is used to measure the relative weight of the largest companies in a sector (Besanko et al. 2004). The concentration ratio represents the share of the LCIA score that is attributable to the single elementary flow from a single activity that contributes the most to the LCIA score: a concentration ratio of 1 would represent a product system where 100% of the score is attributable to a single elementary flow. Generally, impact categories where many product systems have a high concentration ratio (e.g. ionisation radiation) also have many pairs of aggregated datasets with high correlation coefficients. Conversely, impact categories where many product systems have a low concentration ratio (e.g. climate change) also have many pairs of aggregated datasets with low correlation coefficients.

It was shown above (Section 2.2.2) that the risk of underrepresenting the dispersion of single-product LCA results in independent sampling of aggregated datasets increases as the correlation among inputs increases. The results in Fig. 6 indicate that correlation among inputs can be high, and even in impact categories where the average correlation is low, there can be highly correlated datasets. For example, for the climate change category, there are over 7000 ecoinvent 2.2 dataset pairs for which the correlation coefficient is greater than 0.8 and over 1200 for which it is higher than 0.99. Having access to a precalculated list of correlation coefficients can help determine whether there is a risk of mischaracterizing the uncertainty of an LCA result calculated with aggregated datasets.

Note that this type of calculation is exactly what would provide the required input for use of the analytical approximation method, provided that the covariance between pairs of datasets is calculated rather than the correlation.

4.2 Case study

4.2.1 Deterministic results and contribution analyses

The deterministic results for all three burgers, as well as the relative contribution of the different ingredients, are presented in SI7. The beef burger is unsurprisingly associated with much higher scores per patty than the veggie or vegan alternatives, from over 6.5 times more (natural land occupation) to over 60 times more (ionisation radiation). The results are much closer for the comparison between the veggie and vegan options, with more than half the impact categories being different by less than 10%. The contributions of the various ingredients are also very different: for the beef burger, impacts are dominated by the meat, while for the veggie and vegan burgers, the impacts come from a more diversified list of ingredients, such as soybean, wheat and, for the vegetarian option, chicken egg.

4.2.2 Uncertainty of individual products—approximate analytical approach

To estimate the variance using the analytical approach based on a limited Taylor series expansion (Eq. (2)), 10,000 dependent samples for each ingredient used in the various burgers were generated. These were used to calculate both the variance of the unit scores of each ingredient (the var(xi) terms) as well as the covariance across ingredients (the cov(xixj) terms). It was assumed that the uncertainty in the amount of each ingredient used in the making of the burgers was null, i.e. var(αi) = 0, and by extension that any covariance term that include scaling factors α is also null, i.e. cov(αixj) = cov(αiαj) = 0.

The code implementation of Eq. 2 is presented in SI8. The importance of including the covariance of aggregated datasets in this evaluation was estimated by comparing the total variance (calculated with Eq. 2) to the total variance calculated without the cov(xixj) terms. Detailed results for the Fossil depletion category are presented in Table 4. For the beef burger, the total variance is dominated by a single ingredient (beef), and the covariance terms are relatively unimportant (1% of total variance in total). For the veggie and vegan burgers, however, the covariance terms collectively contribute more to the total variance than the variance of the individual ingredients. This indicates that ignoring the covariance across ingredients would largely underestimate the total variance. This is not true of all impact categories assessed. The relative differences between variance calculated with and without covariance terms for all ReCiPe midpoint impact categories are presented in Table 5. Note that 0.5% of all calculated covariance terms were negative, meaning that their inclusion actually reduced the total estimated variance. However, in all these cases, the actual contribution of the covariance term to the total variance was small, and in only one case was the total variance actually higher when covariance terms were left out (vegan burger, marine eutrophication, − 1% difference). In general, the analytical method to estimate variance of LCA using precalculated results while ignoring the covariance across aggregated datasets leads to an underestimation of the total variance, and in some cases, this underestimation is very substantial.

Table 4 Variance and covariance terms for the fossil depletion score as estimated using the approximate analytical approach
Full size table
Table 5 Percent difference between variance estimated with and without covariance terms for ReCiPe midpoint scores of individual burgers, as calculated by the analytical approach
Full size table

4.2.3 Uncertainty of individual products—sampling approaches

The uncertainty of scores for individual burgers was calculated using a 10,000 iteration Monte Carlo simulation with four sampling approaches: (1) dependent sampling (default, to which other sampling approaches are compared); (2) independent sampling of individual ingredients followed by linear combination of sampled values; (3) linear combination of values sampled from lognormals that were fitted on the samples for each individual ingredient; and (4) linear combination of dependently presampled values for ingredients, which constitutes the core of the proposed approach in this paper (see SI8). The resulting dispersion for each burger and each of the ReCiPe midpoint impact categories are compared using three metrics: MAD, interquartile range (IQ) and mid-99% interpercentile range. The dispersion results using the independent sampling, fitted lognormals and dependently presampled values are normalised by dividing by the corresponding dispersion results for the dependent sampling approach (Fig. 7). Normalisation allows us to more easily see the relative changes in dispersion. The code used for this analysis is available as Electronic Supplementary Material (SI8).

Fig. 7
figure 7

Comparison of dispersion for ReCiPe midpoint scores of individual burgers using different sampling approaches. Values lower than 1 indicate that the sampling method (independent sampling, sampling of fitted lognormal distribution and using dependently presampled results) yield dispersion indicators lower than dependent sampling

Full size image

The independent sampling approach results in lower dispersion than dependent sampling for all measures of dispersion, all burgers and most impact categories. This was expected, since dependent sampling accounts for the correlation across aggregated datasets, and independent sampling does not. The difference in dispersion between dependent and independent sampling is much less pronounced for the beef burger: this is because the uncertainty of the beef burger scores is dominated by the beef ingredient.

The use of fitted lognormals, as proposed in Qin and Suh (2017), yields dispersions that are very often very different from those from dependent sampling. Lognormal distributions were chosen for the fitting because all exchanges in the product system that are from the WFLDB are either lognormally distributed or have no uncertainty, and all the others are from ecoinvent 2.2, whose exchanges are mostly also lognormally distributed. The process used for fitting the lognormals and the resulting shape parameters are presented in SI8. It follows from this that the assumption in Qin and Suh (2017) that lognormal distributions can be used with relative confidence is not robust.

Finally, the use of dependently presampled arrays of values yields, for all cases, ratios that are very close to one. Since a linear combination of dependently sampled aggregated data is mathematically equivalent to the dependent sampling of the whole system, the small differences are attributed to the random nature of Monte Carlo simulations.

4.2.4 Comparison between the analytical approximation and sampling approaches

The two previous sections showed that the dispersion of LCIA results for individual burgers changes when correlation across aggregated datasets is ignored, and that it is usually underestimated. Figure 8 shows the relation between results obtained by the analytical and sampling approaches: the x-axis presents the fraction of total variance that is captured when covariance terms are excluded from Eq. (2), and the y-axis represents the ratio of dispersion indicator calculated using independent sampling over that calculated by dependent sampling. Although no simple relationship can be obtained from this comparison, and even though the actual measure of dispersion is different, a rough agreement is observed: for most burger-impact category combinations, when the analytical approximation approach identifies that a fraction of the variance is unaccounted for, the sampling method finds the same.

Fig. 8
figure 8

Comparison of fraction of dispersion that is unaccounted for when ignoring correlation across aggregated datasets when using the analytical approximation and sampling approaches. The x-axis values are derived from Table 5 and the y-axis values correspond to the results presented in the first column of Fig. 7

Full size image

4.2.5 Uncertainty in comparative results

Dependent sampling is especially important in comparative LCA, as is well known (Henriksson et al. 2015) and as was shown with the simple water bottle LCA above. In this case study, the veggie burger is taken as the default product to which the beef and vegan burgers are compared. The distribution of the difference between burgers for the climate change and ozone depletion impact categories are presented in Fig. 9. The rest of the results are presented in SI8. For the comparison with beef, the sampling approach does not make much difference. This can be readily explained: the beef burger scores are much larger than those of the veggie burger, and the sampling approach for the beef burger does not make much of a difference as it is dominated by one ingredient (beef). For the comparison with vegan patties, however, the sampling approach does make a marked difference. Indeed, the uncertainty of the comparison is overestimated by independent sampling. Suh and Qin’s conclusion (2017) that uncertainty is underestimated when independently sampling aggregated datasets therefore may be true for individual product systems but is not the case for comparative LCA.

Fig. 9
figure 9

Distribution of the difference between the scores for two burgers under different sampling strategies

Full size image

Comparative LCA can also look at other metrics, such as the results of hypothesis testing to determine whether product systems A and B are significantly different (Henriksson et al. 2015) or the frequency at which an option A is preferable to option B (e.g. Heijungs and Kleijn 2001; Huijbregts et al. 2003; Mattila et al. 2011). For the beef-veggie comparison, the results are unambiguous: the burger scores are higher for all iterations of all Monte Carlo simulations, regardless of the sampling strategy used. In this circumstance, then, the sampling approach is irrelevant. For the vegan-veggie comparison, though, the sampling strategy does change the number of iterations for which one option is better than the other (Table 6). Marked differences can occur between dependent sampling and independent sampling or sampling of fitted lognormal distributions, considerably lowering the confidence in results. However, the results obtained using presampled dependent scores for ingredients are almost exactly those yielded from dependent sampling. Again, this indicates that Suh and Qin’s conclusion (2017) that uncertainty is underestimated when using aggregated datasets does not hold for comparative LCA. Note that the difference in veggie and vegan burgers is very small. Even if the confidence that one option is better than the other is high, it does not mean that the magnitude of this difference will be important enough to sway decisions.

Table 6 Percentage of 10,000 Monte Carlo iterations where the vegan burger had a score lower than that of the veggie burger under different sampling strategies
Full size table

5 Discussion

5.1 Using fitted distributions as proposed by Suh and Qin (2017)

An interesting discussion between Suh and Qin (2017) and Heijungs et al. (2017) was recently published on the issue of dependent vs. independent sampling and the use of aggregated datasets in uncertainty analysis. Qin and Suh (2017) argue that aggregated datasets with probability distributions can be used for fast uncertainty analysis. Heijungs et al. (2017) responded by stating that this approach “cannot” be used for comparative LCA and that the uncertainty values generated using independent sampling from aggregated datasets would be largely overestimated.

Suh and Qin (2017) provided a useful rebuttal where they make two very important observations: dependent sampling is relevant not only in comparative LCA, but for any LCA that combines aggregated datasets, and calculating the uncertainty for a given product system using precalculated distributions underestimates rather than overestimates uncertainties. The results presented above corroborate both points. However, Suh and Qin make three additional points that are not supported with the findings of this paper.

First, they extend their conclusion regarding the uncertainty of a product system (i.e. that independent sampling underestimates the uncertainty of a given product system, and that this underestimation is usually small) to comparative LCA. As the bottle case study demonstrated (Section 2.2.3), this is not true. For bottles identical in all aspects except their total weight, the heavier bottle is guaranteed to have larger impact scores than the lighter bottle even for very small differences in weight. While dependent sampling yields this expected conclusion, independent sampling cannot distinguish between both bottles for very small mass differences and, for some impact categories, still does not yield unequivocal results when the mass of the heavier bottle is double that of the lighter bottle.

Second, they state that if two aggregated datasets were generated using the same Monte Carlo simulation (i.e. that dependent sampling was used), then there is no independent sampling problem. While this is true for each Monte Carlo iteration result that was used to construct the aggregated LCIs, it is certainly not true of Monte Carlo simulations that will be carried out with the resulting fitted probability distributions. Indeed, in subsequent Monte Carlo simulations, sampling from the probability distributions that were fitted on the originally sampled values will be independent.

Finally, they state that the uncertainty associated with the linear combination of aggregated datasets can be adjusted by a rule-of-thumb factor to account for the inability to do a dependent sampling. While this proposal is attractive, and indeed seems to fit the data for the LCI of the 100 ecoinvent unit processes that they analysed, it does not account for the great variability of the influence of independent sampling. Indeed, as was shown in this paper, the influence of independent sampling depends on the correlation between datasets used in an LCA, and this correlation varies widely and depends on the specific datasets used and on the metric compared (e.g. on the impact categories of interest). The table with correlation factors for each pair of products in ecoinvent v2.2 and v3.3, published as SI with this paper, could allow one to speculate whether independent sampling will result in marked underestimation of the scores.

5.2 Feasibility of the presampling approach

This paper suggested an alternative to the two approaches being debated by Suh and Qin (2017) and Heijungs et al. (2017): precalculating arrays of dependent results (LCI or LCIA) that can then be linearly combined in LCA work. The difficulty of this approach is the time required for the initial calculation of presampled arrays. Calculating, cleaning and concatenating 1000 dependent LCI results for all datasets from ecoinvent version 3.3 take about 24 h on a modern eight-core desktop. Each such LCI array takes about 100 MB. Converting them to LCIA arrays reduces their size to approximately 60 MB per 1000 iterations. Once this work is done, subsequent uncertainty analyses of LCA results using the arrays can be carried out in real-time. For example, identifying, loading, scaling and adding the ingredients in a beef burger in order to generate a 10,000 iteration score array for one method take 0.014 s with the computer described above. This speed makes it relevant for use in eco-design software tools.

5.3 Use of the correlation factors

The approach based on the generation of dependent precalculated results also yielded two useful coproducts: a table with correlation factors for pairs of products in ecoinvent databases (provided in Supporting Information) and a related covariance matrix (not provided). With the former, the risk of underestimating the uncertainty when using aggregated datasets can be crudely evaluated, since it was shown that high correlation between aggregated datasets leads to larger underestimations of uncertainty when independently sampling aggregated datasets. The data in the covariance matrix makes it possible to use the analytical approach to estimate the total variance as well as to determine the contribution of different aggregated datasets (variance) and pairs of datasets (covariance) to the total variance.

5.4 Other applications

The approach of precalculating dependent samples can be used in other spheres of the LCA calculation chain where there is uncertainty and where dependent sampling is important. Three examples are given below.

5.4.1 Presampling characterisation factors

Characterisation factors are calculated models using a variety of uncertain parameters, and some LCIA methods present characterisation factors as probability distributions (e.g. Roy et al. 2014). If characterisation uncertainty has been used at all, it has been approached in the same fashion as inventory uncertainty, where parameters were assumed to be independent. However, this assumption is invalid in LCIA and especially for regionalized LCIA. No LCIA method developer would use different values for common model parameters (e.g. different mean H+ concentration in a water body, different runoff rates) used in the calculation of characterisation factors for two different elementary flows, and yet this is exactly what is simulated when characterisation factors are sampled from independent distributions. Presampling and then applying characterisation factors generated using dependent sampling of common model parameters would be a substantial advancement for LCIA.

5.4.2 Dependent technological parameters—case of mass balances

Unit process datasets are often associated with inputs and outputs of flows that should be physically balanced, such as carbon or water (water directly input, water in moisture content of inputs, evaporation, water discharges, etc.). While unit processes are normally water balanced, any Monte Carlo iteration will break this balance if any of the water flows are uncertain. Presampling balanced sets of water flow amounts would allow water balances to be conserved across all Monte Carlo iterations.

5.4.3 Dependent technological parameters—case of market mixes

Similarly, independently sampling the quantity of different inputs into a market mix where the inputs should sum to one, such as electricity inputs into a grid mix unit process, invariably results in market mixes that do not balance. It is already known that standard functions, such as the normal or lognormal, are poor fits for real electricity generation data, which is often multi-modal or highly biased. Independent sampling, which ignores why certain generators would be positively or negatively correlated with other generators, only adds insult to injury. A far superior approach would be to sample from a time series of relative production volumes and to associate each Monte Carlo iteration with one of these presampled values.

5.5 Outlook

Given that the most time and resource-consuming step is the calculation of dependent arrays for a database, centralising their generation for the whole of the LCA community would be relevant and useful. For example, a database provider like the ecoinvent Center could sell arrays of Monte Carlo results in quite the same way it now sells unit process datasets and aggregated datasets. Centralised generation would also allow many Monte Carlo iterations to be generated, as well as allowing for investment in sampling strategies like space-filling curves or Latin hypercubic sampling that would ensure consistent coverage of the entire probability distribution of each parameter. Covariance matrices could also be made available, facilitating the use of the analytical approximation approach. A whole ecosystem of software tools able to use these directly could then be developed. The same can be true for other parameters used in LCA, such as characterisation factors and dependent technological parameters that are useful for carrying our LCA.

6 Conclusions

Streamlined LCA tools have a strong incentive to continue using aggregated LCA data. This traditionally posed a problem for uncertainty analysis: the data in aggregated datasets were normally only point values instead of uncertainty distributions, and the proposed techniques to account for uncertainty in LCA using aggregated datasets either did not consider correlation across datasets (Qin and Suh 2017), or proposed correction factors that are not generally applicable or relevant for comparative LCA (Suh and Qin 2017). The findings in this paper confirmed Suh and Qin’s statement (2017) that the uncertainty of LCA results for individual products is underestimated when calculated by independently sampling the distributions of aggregated datasets and showed that the magnitude of this underestimation can vary widely. It also corroborated the findings of Henriksson et al. (2015) that independent sampling in comparative LCA can lead to a severe overestimation of the uncertainty in comparative metrics.

Two techniques were proposed to more correctly carry out uncertainty analysis in LCA using aggregated datasets. The first is based on the approximate analytical approach based on a limited Taylor series expansion, which is useful to estimate the variance of single-product LCA results and to estimate the importance of the covariance of aggregated datasets to this variance. However, it was not shown to be useful for comparative LCA. The second is based on the linear combination of dependently presampled Monte Carlo results. This approach is shown to yield results similar to those obtained by Monte Carlo analysis using unit process datasets with a negligible computation time, making it acceptable for streamlined or even mainstream LCA tools. Indeed, this approach has already been implemented by an existing tool, EcodEX. Both solutions require a one-time calculation of dependent samples for all aggregated datasets. This step is time-consuming, and could be done centrally by database providers.

The dependent presampling strategy can also be applied to improve other aspects of the LCA calculation chain, such as market mixes, characterisation factors and flows that need to balance or are otherwise correlated at the unit process level. The implementation of such strategies would require modifications to the structure of LCA software, as was shown with the adaptation of the EcodEX tool, but would bring a significant increase in realism.