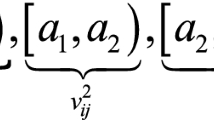A multiobjective model for the green capacitated location-routing problem considering drivers’ satisfaction and time window with uncertain demand

Abstract

Location-routing problem is a combination of facility location problem and vehicle routing problem. Numerous logistics problems have been extended to investigate greenhouse issues and costs related to the environmental impact of transportation activities. The green capacitated locating-routing problem (LRP) seeks to find the best places to establish facilities and simultaneously design routes to satisfy customers’ stochastic demand with minimum total operating costs and total emitted carbon dioxide. In this paper, features that make the problem more practical are: considering time windows for customers and drivers, assuming city traffic congestion to calculate travel time along the edges, and dealing with capacitated warehouses and vehicles. The main novelty of this study is to combine the mentioned features and consider the problem closer to the real-world case uses. A mixed-integer programming model has been developed and scenario production method is used to solve this stochastic model. Since the problem belongs to the class of NP-hard problems, a combination of the progressive hedging algorithm (PHA) and genetic algorithm (GA) is considered to solve large-scale problems. It is the first time, as per our knowledge, that this combination is implemented on a green capacitated location routing problem (G-CLPR) and resulted in satisfactory solutions. Nondominating sorting genetic algorithm II (NSGA-II) and epsilon constraints methods are used to face with the bi-objective problem. Finally, sensitivity analysis is performed on the problem’s input parameters and the efficiency of the proposed method is measured. Comparing the results of the proposed solution approach with those of the exact method indicates that the solution approach is computationally efficient in finding promising solutions.

Introduction

While logistics costs are one of the major costs of distribution companies, managing a distribution network has always been one of the most important issues in the supply chain management. Supply chain activities include around 10% of the gross domestic product (Simchi-Levi et al. 2008). In today’s competitive marketing environment, industry efficiency is the key to success. As a result, businesses must improve their efficiency in all areas, particularly in their logistical operations (Nekooghadirli et al. 2014).

Moreover, businesses and governments understand the necessity to assess impacts of their logistics activities on the environment (Nujoom et al. 2018). The importance of the green location-routing problems is reflected in reducing fuel consumption, time loss, traffic volume, and air pollution. Nowadays, most corporations recognize and accept the need to evaluate and decrease the environmental impact of their products’ manufacturing and handling. Thus, this study’s main motivation is to decrease such logistics costs and total CO₂ emission by considering both location and routing problems in an integrated multiobjective model to come up with better results.

On the other hand, one of the main challenges of location routing problems (LRP) is to strike a balance between strategic and operational goals. Also, since the LRP should simultaneously deal with location and routing problems simultaneously, many different aspects, features, and parameters must be considered in this study. As a result, we would consider time windows for customers and drivers, assume city traffic jams to calculate travel time along the edges, and deal with the capacitated warehouses and vehicles. The key contributions of this work are given below that set it apart from other studies in the related literature:

• Studying a bi-objective integrated G-CLRP

• Investigating the problem in multiproduct mode

• Considering city traffic depending on vehicles’ departure time

• Considering the social factor by focusing on managing the working time of drivers

• Eliminating the assumption that the slope of roads is constant at each edge

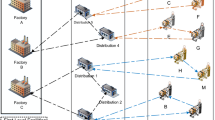
In general, the problem discussed in this paper seeks to satisfy the stochastic demand of customers by finding the best places for establishing the warehouses and routing vehicles with the lowest cost as well as by emitting the lowest carbon dioxide. Urban traffic, which has a notable impact on the travel times of product shipments and CO₂ emission is also considered in the problem. Moreover, shortage is allowed and it is assumed to be lost sales. To increase drivers’ satisfaction and reduce the risk and destructive effects of overworking, their working hours during the day will be managed. Meanwhile, soft time windows (TW) are considered for each customer. Fig. 1 demonstrates an example solution of the current problem schematically.

Fig. 1

Example of a solution to the problem

The rest of the paper is organized as follows. In the “Literature review” section, we give a summary of discussions about the previous related studies in LRP. The problem will be stated and mathematical formulations will be given in the “Problem description and mathematical formulation” section. The “Solution approach” section provides an overview of the solution approach for the underlying problem. In the “Numerical results” section, numerical and computational results are reported. The proposed framework is implemented on a real case study in the “Isfahan case study” section. The “Sensitivity analysis” section presents the sensitivity analysis and managerial insights and finally, “Conclusion and future works” section provides concluding remarks and enlightens the future research directions.

Literature review

The first location-routing models were studied in the late 1970s and early 1980s; however, Weber (1929) first introduced the concept of location-routing in the 1960s. Over the past few years, researchers have added other features to the location-routing problem. The emergence of location-routing problem with more accurate assumptions is related to the late 1990s (Min et al. 1998). In LRP, the capacity limit is usually related to the facility or the vehicle, and several researchers have examined this problem with the capacity limit, both for facilities and vehicles. This is known as capacitated location routing problem (CLRP). It means that the amount of cargo that each truck travels in its tour should not exceed the maximum fixed volume of that truck (Prins et al. 2006).

Many studies have examined the environmental aspects of product delivery. Govindan et al. (2014) considered a multiobjective location-routing problem applied to perishable food delivery. The two objective functions were to minimize the total costs and to reduce the total carbon dioxide emissions. Toro et al. (2017) raised a two-objective problem, G-CLRP, intending to minimize operating costs as well as total greenhouse gas emissions. They proposed a new approach for calculating the vehicles’ total fuel consumption and subsequently the total greenhouse gas emissions. Finally, they employed the epsilon constraint method to solve the model. Tang et al. (2016) tried to minimize the total costs and the amount of carbon emissions for an inventory-location-routing problem. One of the latest studies on the green location-routing problem is the combination of fuzzy decision-making trial and evaluation (FDEMATEL) and fuzzy analysis network process (FANP). The associated multiobjective mixed-integer programming model aims to minimize total costs while reducing the shortage of uncertain fuzzy demands (Govindan et al. 2020).

The time window constraint is less focused on capacitated location-routing problems, despite its several real-world applications. Jabal-Ameli et al. (2011) presented a mathematical model for the CLRP with soft and hard time windows constraint. The objective function of the problem was to minimize the total costs. Their solution approach was based on a variable neighborhood descent and they validated their method by solving small examples. Nikbakhsh and ZEGORDI (2010) presented a two-level location-routing problem considering soft time windows for customers. They expanded a mathematical modeling and used a heuristic method to tackle the problem. Hu et al. (2019) addressed a multiobjective model for the LRP with city traffic congestion constraints. It aims to minimize total costs and total risks and to maximize customer satisfaction simultaneously. They applied genetic algorithm to tackle the problem and considered a case study to demonstrate the proposed solution approach. Zhong et al. (2020) addressed a multiobjective mixed-integer nonlinear programming model for LRP with stochastic demand to manage and control operational and strategic issues in disaster recovery. The solution approach to solve the problem was based on a genetic algorithm. To encounter the bi-objective model, NSGA-II method has been adopted to produce the Pareto front.

From the social issues point of view, Zhalechian et al. (2016) extended a sustainable mixed-integer model for the inventory-location-routing problem, which involved a variety of uncertainties in demand. The feature of their proposed model is the study of potential new job opportunities. Minimizing costs and maximizing the job opportunities were the two objectives of this model, which were solved by a metaheuristic hybrid algorithm. Reducing costs and increasing public satisfaction were the two objective functions that Caballero et al. (2005) considered in their multiobjective model. They used metaheuristic methods to solve the problem. Ghaderi and Burdett (2019) studied a two-stage stochastic programming model for a bi-modal transportation network. It simultaneously minimizes the total costs and risks. Abdi et al. (2021) studied a supply chain network problem under uncertainty and suggested a new two-stage stochastic optimization approach. Also, GA was used as one of the solution methods to solve the problem. In another study, Fathollahi-Fard et al. (2020a) investigated a two-stage stochastic programming formulated on a scenario-based approach for a multiobjective problem for a closed-loop supply chain network. Biuki et al. (2020) discussed sustainability in their location-routing-inventory problem of supply chain for perishable products in a four-echelon network. The proposed multiproduct problem assumes that the type of demand is fuzzy. In addition to the particle swarm optimization method, GA has been used as a solution approach to solve this problem. Shen et al. (2019) studied emergency logistics conditions using a two-phase solution algorithm with fuzzy demand. The proposed mixed-integer programming model aims to reduce the total costs and delivery time while minimizing the total amount of CO₂ emissions. Thus, the model considers both economic and social factors.

Since location-routing is one of the NP-hard problems, researchers mostly have focused on heuristic and metaheuristic solutions. Quintero‐Araujo et al. (2017) considered the LRP with limited vehicle capacity and proposed a metaheuristic algorithm to solve it. Reducing operating costs and minimizing service time were the two objective functions of Nekooghadirli et al. (2014). In their problem, travel time and customer demands were uncertain. Stochastic travel time was considered in (Fathollahi-Fard et al. 2020b), too. Four metaheuristic methods had been utilized to solve this problem, including multiobjective parallel simulated annealing (MOPSA), nondominated sorting genetic algorithm (NSGA-II), multiobjective imperialist competitive algorithm (MOICA), and Pareto archived evolution strategy (PAES). Zarandi et al. (2013) considered a fuzzy constraint programming and simulated annealing solution approach to solve the CLRP with time windows. Minimizing the total costs and travel distance were the two objective functions of their presented mathematical model.

Assuming lost-sales for unmet demand during the delivery process for LRP could be seen in (Chan et al. 2001), (Caballero et al. 2005), and Bozorgi-Amiri and Khorsi (2016). Bozorgi-Amiri and Khorsi (2016) investigated a multiobjective location-routing model. The objective functions were minimizing the maximum amount of unsatisfied demand, reducing costs, and decreasing travel times. The proposed model was solved by the epsilon constraint method and implemented on a case study. They assumed shortage allowance in both lost-sale and backorder. Rabbani et al. (2019) studied a stochastic location-routing problem for waste disposals recycling centers of hazardous wastes. Their multiobjective model takes into account the inventory decisions, too. The model aims to minimize the total operating costs, site risks, and transportation risks. They used a scenario-based solution approach to solve their mixed-integer linear programming model and combined NSGA-II and Monte Carlo simulation to face with the multiobjective problem.

Table 1 presents the comparison between previous studies and the current research. As shown, the current paper is covering all of the mentioned features for the green capacitated location routing problem. This paper’s distinctive feature is to consider the combination of attributes such as capacitated trucks, shortage allowance, closed loops, social concerns, time window, and traffic. The combination of such features, which make the problem closer to real-life situations, is the paper’s main contribution.

Table 1 Comparing previous researches with the current study

Problem description and mathematical formulation

In the proposed model, we have a set of nodes called V, which is the collection of facilities (warehouses) I and customers’ nodes J. The problem aims to connect the customers to the facilities to minimize the total costs and CO₂ emissions. Each warehouse has a specific establishing cost, O_i, and a specific capacity, W_i. Each edge (i, j) has the cost of c_ij and distance of d_ij. Each truck has a fixed cost of F and a fixed capacity of Q_i. Each customer can be served in a specific time interval [LB_i, UB_i]. Also, each customer has a certain soft time window [e_i, r_i]. Delivery outside of this range leads to earliness and tardiness penalty costs. Drivers, like customers, have a hard [LK, UK] and a soft time window [ek_i, rk_i]. The travel time, which affects the arrival time to customers and drivers’ working hours, depends on the time that trucks leave each node, LT_i.

In soft time window, delivery of products outside the specified time window is also allowed. More precisely, for each customer, in addition to a time window, a time interval is defined. The services performed outside the time window interval are penalized. If the fine is considered infinite, then the soft time window becomes a hard time window. For each driver, a soft time window is considered, and for the amount of working hours beyond the soft time windows, additional fees should be paid to the drivers. Thus, the amount of working hours is controlled by the amount of penalty costs paid. Customers’ demands are uncertain, and every customer requires a set of products; in other words, the problem is considered in a multiproduct mode.

This study seeks to minimize the total operational costs and total emission of carbon dioxide by calculating the amount of energy consumed by vehicles. This paper aims to simultaneously select a set of customers to meet their demands, find a set of locations for establishing the distribution centers and design the delivery routes to the customers. City traffic (traffic congestion), which affects delivery time of products and the emission of polluting gasses, is considered in the problem to approach the real world situations. Moreover, the real travel times are obtained as follows. The minimum travel time between all pairs of nodes when the streets are solitary will be calculated. Then incremental coefficients were added to estimate the travel time in different periods of the day. Other features of the problem include closed-loop, homogenous fleet and soft time window.

The following list of assumptions are taken from (Toro et al. 2017):

• Each customer is served only once and only by one truck.

• Each customer’s demand can be satisfied only by one warehouse with limited capacity.

• Each tour starts from a warehouse and ends at the same warehouse.

• The cost of establishing warehouses is fixed.

• The cost of using vehicles is fixed.

• The size of the vehicles’ fleet is fixed and homogeneous and has limited capacities.

And the second list of assumptions are contributed to the problem as follows:

• Demand shortage assumed as lost in sales.

• Customers must be visited within a specified time window; otherwise, either earliness or tardiness penalty costs are applied.

• Drivers have a specific time for service i.e. if the driver's working time is outside a specific range, earliness and tardiness penalty costs will be added to the total costs.

• The cost of establishing warehouses is fixed.

• The cost of using vehicles is fixed.

• The size of the vehicles’ fleet is fixed and homogeneous and has limited capacities.

The following sets, parameters and decision variables are used for the mathematical description of the problem:

Sets
I	Set of warehouses	i = {1, 2, …, I}
J	Set of costumers	j = {1, 2, …, J}
V	Set of nodes	v = {1, 2, …, V}
L	Set of time interval	l = {1, 2, …, L}
P	Set of products	p = {1, 2, …, P}
Ω	Set of scenarios θ ∈ Ω	Ω = {1, 2, …, | Ω| }
Parameters
βij	The gradient of the road from node i to j
v	Fixed vehicles speed
[ei, ri]	Soft time window of costumer i
Pe	Customers earliness penalty cost
Pl	Customers tardiness penalty cost
LBi	Lower bound of hard time window of customer i
UBi	Upper bound of hard time window of customer i
LK	Lower bound of hard time window for each driver
UK	Upper bound of hard time window for each driver
PKe	Earliness penalty cost per unit of drivers’ workload time
PKl	Tardiness penalty cost per unit of drivers’ workload time
[eki, rki]	Soft time window of driver i
Oi	Cost of activating of warehouse i
Wip	Capacity of warehouse i of product p
M	A big number
F	Fixed cost of using trucks
Q	Capacity of each truck
Djpθ	Demand of customer j of product p in scenario θ
sc	Penalty cost of each product shortage
cij	Travel cost between nodes i and j
dij	Distance between nodes i and j
g	Gravity constant
b	Constant depending on the terrain
m0	Mass of each truck
E	Total CO2 emissions per unit of energy (kg of CO2/J)
σl	Coefficients for travel time between two nodes regarding trucks leaving time
timeij	Travel time between nodes i and j when the streets are solitary
EPM	Amount of CO2 emissions while the vehicle is in place (working but not moving)
Decision variables
xijθ	1, if the path between nodes i and j ∈ V in scenario θ is used; 0 otherwise
yi	1, if facility i ∈ I is used; 0 otherwise
fijθ	1, if the customer at node j ∈ J is served by a route that starts at the warehouse i ∈ I in scenario θ; 0 otherwise
aijθ	1, if a vehicle uses node j to return from the end of its route (at node j) to a warehouse (at node i) in scenario θ; 0 otherwise
tijθ	The volume of load transported between nodes i and j in scenario θ
zjθ	1, if the customer j is the last customer served in a route in scenario θ
shipθ	The amount of shortage of product p of customer i in scenario θ
ybilθ	Binary auxiliary variable indicating if the leaving time of customer i is in the time interval l in scenario θ
LTLilθ	Continuous auxiliary variable for linearization of the constraint regarding city traffic
LTiθ	Departure time of truck from node i in scenario θ
gijlθ	Binary auxiliary variable to linearize the second objective function in scenario θ
Tiθ	Arriving time of truck in node i in scenario θ
yeiθ	Amount of earliness of delivering for customer i in scenario θ
yliθ	Amount of tardiness of delivering for customer i in scenario θ
ykeiθ	Amount of earliness of driver i service time in scenario θ
ykliθ	Amount of tardiness of driver i service time in scenario θ

In this section, a scenario-based modeling method is presented. Our model’s goals are to minimize the total costs, (fixed costs, expected travel costs, and expected penalty costs, in all scenarios) and to minimize the total amount of CO₂ emissions. We consider a two-stage stochastic programming approach to deal with the stochastic demands. Location decisions are made in the first stage, and decisions regarding routing and scheduling customers’ visits are made in the second stage.

$$ FS=\sum \limits_{i\in I}{O}_i{y}_j $$

(1)

FS indicates decision variables and their values in the first stage. The formula selected for the second stage of the i_th objective function, SS_i, are as follows: (For more details regarding the calculation of total CO₂ emission, see (Toro et al. 2017))

$$ {SS}_1=\sum \limits_{\mathrm{i}\in I,j\in J}F{a}_{i j\theta}+\sum \limits_{i,j\in V}{c}_{i j}{x}_{i j\theta}+\sum \limits_{i\in I,j\in J}{c}_{i j}{a}_{i j\theta}+\sum \limits_{i\in I}\left({P}_e\times {ye}_{i\theta}+{P}_l\times {yl}_{i\theta}\right)+\sum \limits_{i\in I}\left({PK}_e\times {yke}_{i\theta}+{PK}_l\times {ykl}_{i\theta}\right)+\sum \limits_{j\in J,p\in P} sc\times {sh}_{jp\theta} $$

(2)

$$ {SS}_2=E\left[\sum \limits_{i,j\in V}{m}_0g\left( bcos{\beta}_{ij}+\mathit{\sin}{\beta}_{ij}\frac{v^2}{2g{d}_{ij}}\right){d}_{ij}{x}_{ij}+{\sum}_{i\in I,\kern0.5em j\in J}{d}_{ij}{a}_{ij}\right]+E\left[\sum \limits_{i,j\in V}g\left( bcos{\beta}_{ij}+\mathit{\sin}{\beta}_{ij}\frac{v^2}{2g{d}_{ij}}\right){t}_{ij}{d}_{ij}\right]+ EPM\sum \limits_{i,j\in V,l\in L}{\sigma}_l\left({LT}_i\right)\ast {time}_{ij}{x}_{ij} $$

(3)

where Ψ₁ is the sum of first stage value and the expected value of second stage variables of the first stage variables and Ψ₂ denotes the expected value of second stage variables of the second objective function. More details have been provided in the appendix (section (a)) regarding the two objective functions. The complete model is presented below:

$$ {\varPsi}_1= FS+E\left({SS}_{\varPsi_1}\right) $$

(4)

$$ {\varPsi}_2=E\left({SS}_{\varPsi_2}\right) $$

(5)

$$ \mathit{\operatorname{Min}}\ {\varPsi}_1,{\varPsi}_2 $$

(6)

$$ \sum \limits_{i\in v}{x}_{ij\theta}\le 1\kern0.5em \forall j\in J,\forall \theta \in \Omega \kern0.75em $$

(7)

$$ \sum \limits_{k\in J}{x}_{jk\theta}+\sum \limits_{i\in I}{a}_{ij\theta}=\sum \limits_{i\in v}{x}_{ij\theta}\kern0.5em \forall j\in J,\forall \theta \in \Omega $$

(8)

$$ \sum \limits_{j\in J}{x}_{ij\theta}=\sum \limits_{j\in J}{a}_{ij\theta}\kern0.5em \forall i\in I,\forall \theta \in \Omega \kern0.75em $$

(9)

$$ {x}_{ij\theta}+{x}_{ji\theta}\le 1\kern0.5em \forall I,j\in V,\forall \theta \in \Omega $$

(10)

$$ \sum \limits_{i\in V,i\ne j}{t}_{ij\theta}=\sum \limits_{k\in V,k\ne j}{t}_{jk\theta}+\sum \limits_{p\in P}{D}_{jp\theta}-\sum \limits_{p\in P}{sh}_{ip\theta}\kern1em \forall j\in J,\forall \theta \in \Omega $$

(11)

$$ \sum \limits_{i,j\in V}{x}_{ij\theta}\le \left|J\right|\kern0.75em \forall \theta \in \Omega $$

(12)

$$ \sum \limits_{i\in I}{f}_{ij\theta}\le 1\kern0.5em \forall j\in J,\forall \theta \in \Omega $$

(13)

$$ {t}_{ij\theta}\le Q{x}_{ij\theta}\kern0.5em \forall I,j\in V\kern0.5em ,\forall \theta \in \Omega \kern0.5em $$

(14)

$$ \sum \limits_{j\in J}{t}_{ij\theta}\le \sum \limits_{i\in I}{W}_{ip}{y}_i\kern0.5em \forall i\in I\kern0.5em ,\forall \theta \in \Omega, p\in P $$

(15)

$$ \sum \limits_{k\in I}{x}_{j k\theta}=1-{z}_{j\theta}\kern0.5em \forall j\in J\kern0.5em ,\forall \theta \in \Omega $$

(16)

$$ \kern0.5em 1+{a}_{ij\theta}\ge {f}_{ij\theta}+{z}_{j\theta}\kern0.5em \forall i\in I,\forall j\in J\kern0.5em ,\kern0.5em \forall \theta \in \Omega $$

(17)

$$ -\left(1-{x}_{ju\theta}-{x}_{uj\theta}\right)\le {f}_{ij\theta}-{f}_{iu\theta}\kern0.5em \forall i\in I,\kern0.5em \forall j,u\in V\kern0.5em ,\kern0.5em \forall \theta \in \Omega $$

(18)

$$ {f}_{ij\theta}-{f}_{iu\theta}\le \left(1-{x}_{ju\theta}-{x}_{uj\theta}\right)\kern1.00em \forall i\in I,\kern0.5em \forall j,u\in V\kern0.5em ,\kern0.5em \forall \theta \in \Omega $$

(19)

$$ {f}_{ij\theta}\ge {x}_{ij\theta}\kern0.5em \forall i\in I,j\in J,\forall \theta \in \Omega \kern0.5em $$

(20)

$$ \kern0.75em \sum \limits_i{y}_i\ge \frac{\sum_j{\sum}_p\left({D}_{jp\theta}-{sh}_{ip\theta}\right)}{\sum_i{\sum}_p{W}_{ip}}\kern0.5em \forall i\in I,\forall \theta \in \Omega $$

(21)

$$ {\sum}_{j\in J}{x}_{ij\theta}\le \kern0.75em \frac{\sum_p{W}_{ip}}{Q}\kern1.25em \forall i\in V,\forall \theta \in \Omega $$

(22)

$$ \sum \limits_{i\in I,j\in J}{x}_{ij\theta}\ge \sum \limits_{j\in J}\frac{\sum_p\left({D}_{jp\theta}-{sh}_{ip\theta}\right)}{Q}\kern0.75em \forall \theta \in \Omega\ \kern1em $$

(23)

$$ {T}_{i\theta}+\sum \limits_{l\in L}{g}_{i j l\theta}\times {time}_{i j}\times \left(1+{\sigma}_l\right)\le {T}_{j\theta}+M\left(1-{x}_{i j\theta}\right)\kern0.5em \forall i,j\in V,\forall \theta \in \Omega $$

(24)

$$ {T}_{i\theta}+\sum \limits_{l\in L}{g}_{i j l\theta}\times {time}_{i j}\times \left(1+{\sigma}_l\right)\le {T}_{j\theta}+M\left(1-{a}_{i j\theta}\right)\kern0.75em \forall i,j\in V,\forall \theta \in \Omega \kern0.5em $$

(25)

$$ {T}_{i\theta}\ge {LB}_i\kern0.75em \forall i\in V,\forall \theta \in \Omega $$

(26)

$$ \kern0.5em {T}_{i\theta}\le {UB}_i\kern0.5em \forall i\in V,\forall \theta \in \Omega $$

(27)

$$ {ye}_{i\theta}\ge {e}_i-{T}_{i\theta}\kern0.5em \forall i\in V,\forall \theta \in \Omega $$

(28)

$$ {yl}_{i\theta}\ge {T}_i-{r}_i\kern0.5em \forall i\in V,\forall \theta \in \Omega \kern0.50em $$

(29)

$$ {T}_{i\theta}\ge LK\kern0.75em \forall i\in V,\forall \theta \in \Omega $$

(30)

$$ {T}_{i\theta}\le UK\kern0.75em \forall i\in V,\forall \theta \in \Omega $$

(31)

$$ {yke}_{i\theta}\ge {ek}_i-{T}_{i\theta}\kern0.5em \forall i\in V,\forall \theta \in \Omega $$

(32)

$$ {ykl}_{i\theta}\ge {T}_{i\theta}-{rk}_i\kern0.5em \forall i\in V,\forall \theta \in \Omega $$

(33)

$$ {\sigma}_l\left({LT}_{i\theta}\right)=\sum \limits_{l\in L\backslash {L}_{end}}{\sigma}_l\times {yb}_{i l\theta}\kern3.00em \forall i\in V,\forall \theta \in \Omega $$

(34)

$$ \kern0.5em {L}_l\le {LT}_i\le {L}_{l+1}\kern0.5em \forall i\in V,\forall l\in L\backslash {L}_{end}\kern0.75em $$

(35)

$$ {T}_{0\theta}\ge 6\kern0.5em \forall \theta \in \Omega $$

(36)

$$ {T}_{i\theta}\le 24\kern0.5em \forall \theta \in \Omega $$

(37)

$$ {x}_{i j\theta},{y}_i,{f}_{i j\theta},{z}_{i\theta},{a}_{i j\theta},{yb}_{i j\theta},{g}_{i j l\theta}\in \left\{0,1\right\}\kern0.75em \forall i,j\in V,\forall \theta \in \Omega, \forall \theta \in \Omega $$

(38)

$$ {t}_{ij\theta},{LTL}_{il\theta}\in \mathbb{R}\kern0.5em \forall i,j\in V,\forall \theta \in \Omega $$

(39)

$$ {sh}_{i p\theta},{LT}_{i\theta},{T}_{i\theta},{ye}_{i\theta},{yl}_{i\theta},{yke}_i,{ykl}_i\in {\mathbb{R}}^{+}\kern0.5em \forall i\in I,\forall p\in P,\forall \theta \in \Omega $$

(40)

Constraint (7) ensures that a maximum of one edge is connected to each customer, meaning that any customer is visited by only one truck. Constraint (8) states that the input and output edges of a node must be balanced, i.e., the number of input paths to the node must be equal to the node’s output paths. Constraint (9) balances the number of output paths from each facility with the number of edges entering the facility. Constraint (10) is applied to prevent duplication of the arcs at the same time. Constraint (11) sets the balance of the truck's load and demand of each customer and the amount of its shortage. The minimum number of edges needed to connect customers is expressed in constraint (12). This eliminates subtours in the problem. Constraint (13) guarantees that customers’ demand on each route must be connected to a warehouse. Constraint (14) prevents cargo overload from truck capacity. Constraint (15) limits the amount of cargo associated with each warehouse according to its capacity. Constraint (16) ensures the last visited customer on each route to return to the warehouse. Constraint (17) ensures that an edge exists which connects the last customer to a warehouse. Constraints (18) and (19) ensure that all the active edges are connected to warehouses. If an edge connects warehouse i to customer j, it is guaranteed by constraint (20) that customer j is connected to warehouse i. Constraint (21) indicates a lower bound for the number of warehouses used based on total demand and warehouse capacity. By constraint (22), the number of routes started from a warehouse is limited. Constraint (23) ensures the number of routes is sufficient to meet all customers’ demands. Constraints (24) and (25) guarantee that if a truck travels from node i to node j, the time to reach node j is greater than the time spent to reach node i, according to the time spent along the edge ij. Constraints (26) and (27) state that trucks must deliver products to each customer within their hard time windows. Constraints (28) and (29) calculate the earliness and tardiness of product deliveries to each customer regarding each customer’s soft time window. Constraints (30) and (31) ensure that drivers’ working time should be in the required range, from 6 a.m. to 12 p.m. Constraints (32) and (33) calculate the earliness and tardiness of each driver’s working hours. The arrival time of the customer j is considered as the arrival time of the previous customer plus the travel time between customers i and j, which is a function of traffic congestion at the time of leaving the customer i, σ_l(LT_iθ). This is satisfied by constraint (34). In this constraint, L_end is referred to as the last range of time interval. Constraints (35) guarantee that the departure time of each truck be in range of time intervals. Constraints (36) and (37) ensure the daily planning interval. Constraints (38) to (40) determine the variables of the problem.

Model linearization

The second objective function of the proposed model and the constraints of urban traffic are nonlinear. The term ${\sum}_{i,j\in V,l\in L}{\sigma}_l\left({LT}_i\right)\times {time}_{ij}{x}_{ij}$ is nonlinear in the second objective function. Consider σ_l as a function of LT_i is a linear expression. By adding an auxiliary binary variable, yb_il, assume that ${\sigma}_l\left({LT}_i\right)={\sum}_l{\sigma}_l\times {yb}_{il}$. Since x_ij and yb_il are two binary variables; thus, according to the technique used in (Liberti 2007), g_ijl, which is equal to x_ij × yb_il would a binary variable. As a result, Ψ₂ would be linearized as follows:

$$ {\varPsi}_2=E\left[\sum \limits_{i,j\in V}{m}_0g\left( bcos{\beta}_{ij}{d}_{ij}{x}_{ij}+\mathit{\sin}{\beta}_{ij}\frac{v}{2g}\right)+{\sum}_{i\in I,\kern0.5em j\in J}{d}_{ij}{a}_{ij}\right]+E\left[\sum \limits_{i,j\in V}g\left(b{t}_{ij}{d}_{ij}\mathit{\cos}{\beta}_{ij}+\mathit{\sin}{\beta}_{ij}\frac{v}{2g}\right)\right]+ EPM\sum \limits_{i,j\in V,l\in L}{g}_{ij l}{\sigma}_l\times {time}_{ij} $$

(41)

Assume we have 9 time intervals from 06:00 AM to 12:00 AM. Then, the nonlinear format of their constraints would be as follow:

$$ 6\le {LT}_i\le 8\to {\sigma}_1=1.24\kern0.5em \forall i\in V\kern0.50em $$

(42)

$$ 8\le {LT}_i\le 10\to {\sigma}_2=0.52\kern0.5em \forall i\in V $$

(43)

$$ 10\le {LT}_i\le 12\to {\sigma}_3=0.64\kern0.5em \forall i\in V $$

(44)

$$ 12\le {LT}_i\le 14\to {\sigma}_4=0.60\kern0.5em \forall i\in V $$

(45)

$$ 14\le {LT}_i\le 16\to {\sigma}_5=0.71\kern0.5em \forall i\in V\kern0.5em $$

(46)

$$ 16\le {LT}_i\le 18\to {\sigma}_6=1.25\kern0.5em \forall i\in V $$

(47)

$$ 18\le {LT}_i\le 20\to {\sigma}_7=1.23\kern0.5em \forall i\in V $$

(48)

$$ 20\le {LT}_i\le 22\to {\sigma}_8=0.55\kern0.5em \forall i\in V $$

(49)

$$ 22\le {LT}_i\le 24\to {\sigma}_9=0.17\kern0.5em \forall i\in V $$

(50)

As it was mentioned before, σ_l is a function of LT_i and based on (Sherali and Adams 1998) the best way to linearize such constraints with the minimum number of added constraints is to add the auxiliary binary variable yb_il and a new binary variable LTL_ilθ. Moreover, yb_il indicates whether the leaving time of truck i is in the range of time interval of l, and LTL_ilθ represents the leaving time of trucks with respect to the time intervals. Thus, to linearize the constraints related to taking urban traffic at different hours of the day, the following constraints will be considered:

$$ {\sigma}_l\left({LT}_i\right)=\sum \limits_l{\sigma}_l\times {yb}_{il} $$

(51)

$$ {\displaystyle \begin{array}{l}\mathrm{S}.\mathrm{t}\\ {}{L}_l\times {yb}_{il\theta}\le {LTL}_{il\theta}\le {L}_{l+1}\times {yb}_{il\theta}\kern0.5em \forall i\in V,\forall \theta \in \Omega, \forall l\in L\backslash {L}_{end}\end{array}} $$

(52)

$$ {LT}_{i\theta}=\sum \limits_{l=1}^{L\backslash {L}_{end}}{ LT L}_{i l\theta}\kern0.5em \forall i\in V,\forall \theta \in \Omega $$

(53)

$$ \sum \limits_{l=1}^{L\backslash {L}_{end}}{yb}_{il\theta}=1\kern0.75em \forall i\in V,\forall \theta \in \Omega $$

(54)

Constraint (51) represents the linear expression of coefficients for travel time between two nodes as a function of trucks leaving time. Constraint (52) ensures that the leaving time of each truck should be in the range of time intervals associated with the auxiliary variables for the linearization and constraint (53) indicates the increase in travel time ratio according to different hours of the day. Constraint (54) ensures that each truck could leave only one node in each time interval.

Solution approach

The method that has been chosen in this paper to encounter the uncertainty of demand is the combination of progressive hedging algorithm (PHA) method and genetic algorithm (GA), called PHA-GA. In the following subsections, individually, PHA and GA methods, are briefly described, then combination of them is illustrated.

Progressive hedging algorithm

One way to solve stochastic problems based on problem division is the PHA method, introduced by Rockafellar and Wets (1991). The problems that are less solvable due to memory limitation and computational time are made smaller and solvable by PHA. This method analyzes uncertainties based on scenarios. The important feature of this method is that when the stochastic problem space is convex, the PHA converges to the optimal solution (Løkketangen and Woodruff 1996), (Fan and Liu 2010), and (Watson and Woodruff 2011).

The PHA method repeatedly solves the scenarios separately and tries to gradually approach to a viable solution by adding a penalty cost to the objective function(s). Table 2 provides a general overview of the PHA algorithm. Assume that τ > 0 is a penalty factor and ϵ is a convergence threshold.

Table 2 PHA algorithm

The index k indicates the number of iterations, and the Euclidean distance is expressed in the k_th iteration as π^k. The vectors ${y}_s^k$, ${\overline{y}}^k$, and ${wt}_s^k$, respectively, represent the decision variables for scenario θ in iteration k, the weighted decision variable in iteration k, and penalty cost for scenario θ at iteration k.

Genetic Algorithm (GA)

Genetic algorithm is one of the most popular metaheuristic solution approaches for solving NP-hard problems. In the proposed genetic algorithm, first, the problem parameters are determined, including the number of customers, the number of potential locations for warehouses, the number of the initial population, and customers' demands. Then, we produce the initial population given by pop.

Chromosome representation

We define the individual chromosomes for the location and routing variables by illustrating an example presented in Fig. 2. Let’s suppose we have ten customers and ten potential locations for locating warehouses. Numbers greater than the number of customers (10 in this case) determine which vehicle is assigned to which customers. Then for location variables, three locations from the set of available locations are randomly selected, and the customers of each section of the first array (chromosome) are allocated to the warehouses in the specified locations. Table 3 shows the allocation of customers to warehouses with different vehicles.

Fig. 2.

An example of chromosome representation for decision variables

Table 3 Solution set of the represented chromosome

Population size and content

We use a random method to produce the initial population for location and routing variables. It is assumed that n is the number of potential locations for establishing warehouses, pop denotes the number of primary population, r is the total number of customers, and veh indicates the number of vehicles and d is the number of selected facilities.

To generate the initial population for location and routing variables, we first generate a matrix by dimension pop × (r + veh) as a random displacement of customers. Moreover, veh is randomly selected in the range of $\left[0,\raisebox{1ex}{$r$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right]$ and is numbered in greater order than the customer index in the routing variables. This random setup determines the sequence of customers’ visits and trucks’ tour. In the next step, we randomly divide each chromosome by a random number in the range of [1, n − 1]. Then, according to the number of sections separated from each chromosome, the selected locations will be generated randomly for construction. Binary arrays will be created for each chromosome; 1 for the location where a warehouse is located and 0 for locations without located warehouse. (To find details about parent selection procedure, crossover, and mutation, see Appendix section (b))

Fitness function

Two fitness functions are examined to compare the populations produced in different generations. Total operating costs and total CO₂ emissions are the two objective functions that should be considered as fitness functions for the genetic algorithm.

$$ {\varPsi}_1= FS+E\left({SS}_{\varPsi_1}\right) $$

(55)

$$ {\varPsi}_2=E\left({SS}_{\varPsi_2}\right) $$

(56)

PHA-GA approach

It is the first time, in our best knowledge, that combination of progressive hedging algorithm and genetic algorithm is used and implemented for a green location routing problem. The “Experimental results” section presents the promising solutions of the proposed approach which demonstrates that PHA-GA approach is computationally efficient and produces satisfactory results. The flowchart of the proposed solution approach is demonstrated in Fig. 3.

Fig. 3.

The flowchart of the PHA-GA method

The problem consists of |Ω| scenarios that their probabilities are given by pr_θ. We start solving the problem in order from the first scenario. We store the optimal solution for the location variables and obtain their mean based on each scenario’s probability. According to Table 2, a penalty function is multiplied by the difference in the solution of the location variables from the obtained average and is added to the cost function. This algorithm iterates until the convergence of the solutions.

In the PHA-GA method, if a solution is found in which the decision variables are equal after several iterations, the method has converged. After reaching the maximum number of generations, MaxNumGen, the algorithm terminates and the results are obtained.

NSGA-II

Nondominated sorting genetic algorithm II (NSGA-II) is among the most popular evolutionary algorithms for dealing with multiobjective problems. As the name implies, the genetic algorithm has an important role in this algorithm. The difference between this algorithm and single-objective genetic algorithms is in the process of sorting solutions.

The nondominating sorting algorithm quickly offers a wide range of solutions and its good performance is evident in many two-objective problems (Rabbani et al. 2017), (Rabbani et al. 2019), (Karampour et al. 2020). The NSGA-II uses a Pareto front range and adopts the nondominating sorting mechanism to maintain the best solutions. To get acquainted with this algorithm, the concept of rank and crowding distance should be defined. See Appendix section (c) to find more information regarding NSGA-II and the concepts of rank and crowding distance, see Appendix.

Numerical results

To analyze the performance of the proposed solution method, several numerical examples in different scales are examined. These examples are solved once with CPLEX software to provide a basis for comparing the proposed algorithm solutions with the exact solutions. All instances run on the Intel Core ™ i7-8750 CPU 2.20 GHz processor with 16GB of RAM.

Examples are shown in the format of R–F, where R returns the number of customers and F returns the number of candidate spots for placing warehouses. For example, format 4–3 indicates that the number of customers and potential warehouse locations are 4 and 3, respectively. Customers and facility coordinates are also randomly assigned in the range of [1,100]. The distance between nodes in the problem network is calculated based on the Euclidean distance. Other parameters are illustrated in Table 4.

Table 4 Ranges from which the parameters were randomly generated

Parameter tuning

The optimization design method was first used by Ronald Fisher (Yang and Tarng 1998) in 1920 and Taguchi presented the Taguchi method as an effective and systematic approach to obtain optimal parameters (Davidson et al. 2008). In this paper, for parameter tuning of the proposed genetic algorithm, the Taguchi method was implemented in Minitab 19.2. This method dramatically reduces the number of necessary tests using orthogonal arrays. To use the proposed GA, we set 3 factors as the input parameters of this algorithm. Candidate values for the parameters are determined and are given in Table 5:

Table 5 Candidate amount of parameters for the proposed GA

Four comparison criteria are considered to validate the proposed GA: Quality metric (QM), Mean ideal distance (MID), Diversification metric (DM), and Spacing metric (SM) (Nekooghadirli et al. 2014). QM and MID are two quantitative criteria and DM and SM are two qualitative criteria. The weights of qualitative and quantitative criteria are 1 and 2, respectively (Asefi et al. 2014). The utility function will be as follows.

$$ UF=\sqrt{(QM)^2+{(MID)}^2+{(DM)}^1+{(SM)}^1} $$

(57)

The results of the implementation of the GA to investigate the direct effect of factors using the Taguchi method can be seen in Fig. 4:

Fig. 4.

Main effects plot of factors for GA

Based on Fig. 4, it is recommended that MaxIteration, PopSize, PMutation, and PCrossover be rated at their third level so that the genetics algorithm can provide the best possible result.

Scenario reduction

In this paper, we use a scenario-based approach to deal with the stochastic problem. The number of scenarios is determined regarding the best solution’s accuracy and can be calculated by the value of the expected objective function, given by,

$$ S(sn)=\sqrt{\frac{\sum_{s=1}^{sn}{\left(E\left[ Cost\right]-{Cost}_s\right)}^2}{sc-1}} $$

(58)

where sn shows the number of scenarios, Cost_s is the total value of the objective function for the scenario s and E[Cost] indicates the value of the expected objective function.

The 1 − α confidence interval is given below,

$$ \left[E\left[ Cost\right]-\frac{z_{\alpha /2}S(sn)}{\sqrt{sn}},\kern0.5em E\left[ Cost\right]+\frac{z_{\alpha /2}S(sn)}{\sqrt{sn}}\right] $$

(59)

where z_α/2 is the standard deviation so that 1 − α/2 is the standard normal distribution in z~N(0, 1), Pr (z ≤ z_α/2) = 1 − α/2 covers. If the sample estimator S(sn) and the optimal confidence interval H are given, we can obtain the minimum number of required scenarios by,

$$ N={\left[\frac{z_{\alpha /2}S(sn)}{H}\right]}^2 $$

(60)

Thus, to specify the number of scenarios N, we will consider a small stochastic model with sn number of scenarios. We may obtain the number of scenarios regarding the desired confidence interval in order to determine the number of samples S(sn).

To estimate the required number of scenarios, we first consider 30 scenarios in which the demand from the first to the last scenarios are 5, 10, 15, ..., 150, respectively. Then, we obtain the required number of scenarios, which is 8. We divide the customer demand values in the range of 5 to 150 for each product in eight intervals to get the demand for eight scenarios.

Experimental results

This section examines the results of the proposed NSGA-II method and epsilon-constraint method on the problem. The proposed PHA-GA and the exact method are coded, respectively, in MATLAB and CPLEX. The calculation time of obtaining the Pareto front of ten Pareto optimal solutions is given by Run time. According to Table 6, for medium and large problems, the run time of the NSGA-II is significantly shorter than that of the epsilon-constraint method. The maximum execution time for each step in the epsilon-constraint method is set to 1080 seconds. Hence, the obtained Pareto front solutions of medium and large problems are not optimum. As it was mentioned before, instances are presented in the format of R–F, where R returns the number of customers and F returns the number of candidate locations for placing warehouses. According to Table 6, the execution time for instances more than R–F ≈15 – 4 would drastically increase due to the large scale complexity of the problem.

Table 6 Computational results

The hyperarea is a criterion used to compare the proposed solution approach’s results with the exact solution’s results regarding each Pareto front polygons area. The value of this criterion for each algorithm is calculated as follows (Van Veldhuizen 1999),

$$ {HA}^A=\left({obj}_1^1\times {obj}_1^2\right)+\sum \limits_{num=2}\left(\left({obj}_{num}^2-{obj}_{num-1}^2\right)\times {obj}_{num}^1\right) $$

(61)

where ${obj}_{num}^1$ and ${obj}_{num}^2$ are the values corresponding to the first and second objective functions in the num ^th nondominated solution. The hyperarea ratio is shown by:

$$ HR=\frac{HA^{NSGA- II}}{HA^{epsilon- constraint}} $$

(62)

The corresponding value of this metric for instances in Table 6 are shown in Table 7. If HR be greater than 1, it shows that the performance of the proposed solution method is better than the epsilon-constraint method and vice versa. According to Table 7, the epsilon-constraint method performs better for small-scale problems. However, the proposed solution method generates superior Pareto fronts for medium and large problems in a shorter time.

Table 7 Comparing the performance of NSGA-II and ε-constraint method

As depicted in Fig. 5, the total operating costs and total CO₂ emissions are in conflict. By reducing the total costs, the amount of emitted carbon dioxide increases. Such Pareto front helps managers make the right decision regarding corporations' current priorities. Subsequently, the optimal Pareto front is presented in Fig. 6.

Fig. 5.

Inverse relationship between two objective functions

Fig. 6.

Pareto front of a sample instance

Isfahan case study

The case study is to locate the drug depots of a small local drug distribution company (in Isfahan) and to schedule its trucks to meet the demand of a number of pharmacies and health centers, in a way that operating costs and emitted carbon dioxide will be minimized. In this case study, the drug distribution company has provided a dataset related to the demand of 30 pharmacies and 6 health centers in Isfahan. Also, the number of potential places to establish warehouses is 8. The number of health centers and pharmacies that the drug distribution company should serve is 36, drawn in Fig. 7.

Fig. 7.

Location of pharmacies and health centers in Isfahan

The distance between customers and the distance between customers and depots are given. The slope between nodes in the city network is obtained by an approximation of Google Erath and ArcGIS software, and the travel times between nodes in the best and most secluded states are also provided. Google Map software was used to estimate the travel time between nodes.

Figure 8 shows the Pareto front of the case study. This chart helps managers make decisions and enables them to select a point in the chart according to the company’s needs and priorities.

Fig. 8.

Pareto front of the case study

Sensitivity analysis

We evaluate the performance of the model and its accuracy by applying changes to the problem parameters in this section. We have produced several small-scale problems in 4–3 format and in each of them, we change a specific parameter and examine its effect on the solution set and the objective functions.

We consider the effect of fixed cost changes in this problem. First, we consider the effect of fluctuations on the fixed costs of using each truck. Then, we examine the effects of fixed cost changes on establishing warehouses on the objective functions. We change the fixed cost of using each truck and keep the other parameters of the problem constant. Table 8 presents the comparative results of the objective function’s values.

Table 8 Computational results of trucks' fixed cost changes

According to Fig. 9, operating costs increase as fixed vehicle cost increases, but CO₂ emissions do not have a significant relationship with the fixed costs. The noteworthy point is the sudden increase in the fixed cost of vehicles. Instead of optimizing the cost of shortages by increasing the customers’ demand, the model seeks to reduce the use of high-cost fixed vehicles. In other words, the amount of added costs caused by the demand shortage is less than the use of vehicles with such fixed cost.

Fig. 9.

Objective Functions trends vs. fixed truck costs

To study the effects of the fixed cost for establishing facilities, several problems are generated with different fixed costs, which are illustrated in Table 9:

Table 9 Computational results of changing O_i

As seen in Fig. 10, when fixed warehouse costs increase, the total operating costs increase. The important point is an increase in the shortage due to the fixed cost of establishing warehouses and satisfying customer demand. In other words, in the trade-off between the demand shortage and establishing the warehouses, the first one is chosen.

Fig. 10

Trend of total costs towards the changes in O_i

Managerial insights

The points of view and approaches that help the distribution company managers regarding the issue studied in this paper are as follows:

• Negotiate with customers (pharmacies and health centers) to increase the time window of product delivery to reduce early and late fines for exceeding the time window.

• Negotiate with customers to share sales information to reduce costs associated with shortages and fluctuations in demand for various products.

• Operate the delivery processes on weekends due to light traffic congestion.

Conclusion and future works

Since the LRP consists of a combination of location and routing problems, and each of them is NP-hard, we encountered the problem with extraordinarily high solution time to solve, especially for large-scale problems. That is why we used genetic algorithm to solve the problem. To address the uncertainty in the problem, we also considered using the progressive hedging algorithm. We investigated the problem by separating the main variables of the problem: location and routing decisions. As a result, we considered the problem as a two-stage problem. By using the progressive hedging algorithm, we identified the variables of the first step, which were the location variables, and then solved the routing problem. The implementation of the PHA method was performed using the genetic algorithm.

In general, the proposed problem is related to the integrated decision-making of location and routing in a wide range of areas. Researchers have done a lot of research and development over the years, but this topic is still attractive for future research because of the applicability of this problem. The following remarks are a number of aspects for developing the model:

• Considering service time for each customer according to the customer’s demands

• Considering the probability of disruption occurrences such as vehicle crashes and breakdowns

• Development of problem based on heterogeneous transport fleet

• Allowance of backorders for demand shortage.

Appendix

Section a) CO₂ emission formula

In Toro et al. (2017), all the forces toward the truck are discussed. Below the schematic of such forces on the truck is depicted. Using mathematical relations and static mechanics, the total amount of energy consumed, and the total amount of fuel consumed, followed by the total amount of carbon dioxide emissions, are calculated (Fig. 11).

Fig. 11.

Forces act on the truck

$\overrightarrow{F_R}$ represents the forces that are opposed to the movement of the vehicle, $\overrightarrow{F_M}$ represents the forces created by the engine and transmitted to the tire of the vehicle, mg is the weight of the vehicle, and $\overrightarrow{N}$ is the surface force on the vehicle.

$$ \sum {F}_x=m{a}_x\kern2.25em {a}_x=0\kern0.5em {F}_M-{F}_R- mgsin{\beta}_{ij}=0 $$

(63)

$$ \sum {F}_y=m{a}_y\kern2.25em {a}_y=0\kern0.5em N- mgcos{\beta}_{ij}=0 $$

(64)

$\overrightarrow{F_{R, tires}}$ represents the force created between the wheels without traction and the ground, which is opposite to the movement of the vehicle. $\overrightarrow{F_{R, wind}}$ is the force exerted by the wind against the motion of the vehicle. $\overrightarrow{F_{R, internal}}$ represents the equivalent force of internal forces opposing the motion of the vehicle, and $\frac{m\ {v}^2}{2{d}_{ij}}$is the force required by the vehicle to achieve steady state dynamic energy. The mass of the loaded vehicle is the sum of the unloaded vehicle's mass (the mass of the vehicle itself) m₀ and the load carried between nodes i and j.

$$ \overrightarrow{F_R}=\overrightarrow{F_{R, tires}}+\overrightarrow{F_{R, wind}}+\overrightarrow{F_{R, internal}}+\frac{m\ {v}^2}{2{d}_{ij}} $$

(65)

$$ m={m}_0+{t}_{ij} $$

(66)

$$ {F}_{R, tires}= Nb $$

(67)

$$ \overrightarrow{F_M}=\left( mgcos{\beta}_{ij}\right)b+\overrightarrow{F_{R, wind}}+\overrightarrow{F_{R, internal}}+\frac{m\ {v}^2}{2{d}_{ij}}+ mgsin{\beta}_{ij} $$

(68)

In this step, we calculate the work function (U_ij) done by the truck, which is the same force in the displacement amount. Next, the total amount of gas emissions will be obtained.

$$ {U}_{ij}=\left[\left({m}_0+{t}_{ij}\right) gbcos{\beta}_{ij}+\overrightarrow{F_{R, wind}}+\overrightarrow{F_{R, internal}}+\frac{\left({m}_0+{t}_{ij}\right){v}^2}{2{d}_{ij}}+\left({m}_0+{t}_{ij}\right)g\ \mathit{\sin}\ {\beta}_{ij}\Big]\right]{d}_{ij} $$

(69)

$$ {U}_{ij}=\left[{m}_0g\ \left( bcos{\beta}_{ij}+\mathit{\sin}{\beta}_{ij}\frac{v_{ij}^2}{2g{d}_{ij}}\right)+{F}_{R, wind}+{F}_{R, internal}\right]{d}_{ij}+\left[g\left( bcos{\beta}_{ij}+\mathit{\sin}{\beta}_{ij}\frac{v_{ij}^2}{2g{d}_{ij}}\right)\right]{t}_{ij}{d}_{ij} $$

(70)

The amount of fuel (diesel) required to do the whole work function, i.e., ∑_{i, j ∈ V}U_ij, is obtained by the conversion factor E₁ (gallon diesel/joule). Another conversion factor obtains each fuel unit’s emission rate, E₂ (grams of CO₂/gallon diesel). Therefore, the amount of carbon dioxide emissions is calculated as follows:

$$ {E}_1\times {E}_2\times {\sum}_{i,j\in V}{U}_{ij}=E\times {\sum}_{i,j\in V}{U}_{ij} $$

(71)

Another part of the second objective function that needs to be addressed is the amount of carbon dioxide emitted in terms of the amount of time the vehicle is in traffic congestion. We can calculate this by the following equation of carbon dioxide emissions.

$$ {E}_2\times {E}_3\times \sum \limits_{i,j\in V,l\in L}{\sigma}_l\left({LT}_i\right)\ast {time}_{ij}{x}_{ij}= EPM\sum \limits_{i,j\in V,l\in L}{\sigma}_l\left({LT}_i\right)\ast {time}_{ij}{x}_{ij} $$

(72)

In this regard, the EPM, which is the conversion factor of the idle hours of truck operation to the amount of carbon dioxide produced, is obtained using two conversion factors. The first conversion factor, E₃, is for gallons of diesel and the second conversion factor is equal to the same factor E₂.

Section b) GA parent selection and operators

• 1. Parent selection

In the proposed GA, two types of parent selection procedures, including random selection and roulette wheel selection, are involved in the model. However, based on the results of the genetic algorithm’s implementation in several identical examples, the roulette wheel selection method has performed better than another method (Yu et al. 2019). According to (Amal and Chabchoub 2018), half of the chromosomes with the highest fitness function will be selected for the next generation.

• 2. Crossover

Two different types of crossover are used randomly with the same probability to produce offspring from two selected parents: single-point crossover and two-point crossover (See (Asefi et al. 2014) for more details). The two types of crossover are depicted in Figs. 12 and 13.

Fig. 12

An example of single-point crossover on location variable

Fig. 13

An example of two-point crossover on location variable

• 3. Mutation

Three mutation operators will be used for location variables, and two mutation operators will be used for routing variables in the proposed GA. Mutation operators for location variables are change, swap, and insertion, and routing variables are swap and insertion.

In the change mutation operator, two random points are selected from each chromosome. Two points are chosen randomly along the chromosome. Then, as depicted in Fig. 14, if the chosen point is 0, it will be converted to 1, and vice versa. Other mutation operators are illustrated in (Asefi et al. 2014). Figs. 15 and 16 clearly show how such operators perform.

Fig. 14.

An example of change mutation for location variables

Fig. 15.

An example of swap mutation for location variable

Fig. 16.

An example of insertion mutation

Section c) NSGA-II

Ranking means that we want to rank the solutions according to the concept of quality. To rank the initial population solutions, we put the solutions that never dominated in the first place. Then, we remove non-dominated solutions from the solution set and again compare the rest of the solutions. Once again, we put non-dominated solutions on the second frontier. In this way, all the solutions will be categorized into different boundaries.

If the solutions are ranked only by the rank criterion, there is no need for the crowding distance defined by the neighbors of a solution and the first (best) and last (worst) chromosome of the population (Van Veldhuizen and Lamont 1999).