Mathematical modeling for green supply chain considering product recovery capacity and uncertainty for demand

Abstract

Competition in today’s market is the most important concern of companies and producers in free markets. Buyers are also looking for higher quality and lower prices. Manufacturers should, therefore, reduce production costs and increase budgets for research and product development. On the other hand, the limitation of mineral resources in each country and in the world in general is a very important factor for increasing the price of raw materials which increases the cost of production of a product. In this study, a green aspect of decision-making, concurrent modeling for inventory-routing, and application of maximum entropy (ME) method for overcoming uncertainties of demands are applied to optimize the usage of raw materials and returning of defective products to the production cycle in a closed-looped supply chain under multi-period planning horizon. Also, dynamic modeling is used to balance the inventory level in all stages of the network that leads to optimum usage of the raw materials. For this purpose, the first objective function reduces production, transportation-routing, and inventory costs, and the second objective reduces greenhouse gas emissions through all levels of the network. Finally, this model is solved by using the exact solution method with the help of Gams software as well as the non-dominated sorting genetic algorithm II (NSGAII) and multi-objective particle swarm optimization (MOPSO) algorithm. Sensitivity analysis has been performed on failure rates, greenhouse gas emissions during recycling and production, and the optimistic-pessimistic coefficient of the ME solution method. Solution methods have been compared using several criteria, and the NSGAII method has finally obtained the best result. The results show that the manager should pay more costs in order to prevent backorder demands. Also, collecting the more defective products leads to increasing production amount since the collective products can return to the production line. Finally, it is required for the managers to control products’ failure rate to optimize capacity usage in the model.

Introduction

In today’s business environment, competitiveness is one of the keys to the success of any manufacturing system. In this way, the lower price competition, along with other components, leads to customer attraction. Therefore, manufacturers need to use cost-cutting strategies. By a quick look at the manufacturers’ financial reports in the manufacturing systems, we can find that between 15 and 30% of the production cost is associated with the raw material purchased and between 20 and 25% of the production costs is for the raw material processing (Resat and Unsal 2019; Ilyas et al. 2020). Also, the limited mineral resources are a very important factor in increasing the price of raw materials which increases the cost of production of a product. According to these descriptions, it can be seen that the special consideration of the provision of inexpensive raw materials can be a very influential factor in the competitiveness of a manufacturing company. Recycling products in the closed-loop supply chain is one of the new ways to reduce the cost of purchasing raw materials and ultimately reduce production costs (Zhou et al. 2019; Martinez et al. 2019).

Literature review

In this section, we aim to categorize the main four groups of related works to the current study and discuss each of them in details.

Recycling in supply chains

The recycling of products in the closed-loop supply chain network begins at the factory return stage. Therefore, in order to reduce costs, a system should be set up to bring the minimum wasted products to the beginning of the production line and minimize the return costs by applying processes to maximize the savings. On the other hand, it is expected that product recovery can have a significant impact on reducing the environmental pollution. This will reduce the amount of mineral waste and the extraction of new minerals, as well as the reduction of greenhouse gas emissions during the production process (Torkabadi et al. 2018; Liu et al. 2020).

Distributing new products and collecting recyclables from scattered geographical locations require an efficient transportation network. One of the efficient features of a transport network is the minimum travel time and distance traveled, which is possible if we choose the best route for moving vehicles, and this is precisely the purpose of vehicle routing issues (Kara and Onut 2010). Bettac et al. (1999) studied several freight return projects. Projects included the printer cartridge recycling project in the UK, the power tool recycling project in Germany, the project of collecting and reusing disposable cameras from around the world, and the project of collecting and refurbishing IT equipment around the world. In these cases, the transportation of old products and the delivery of new products were conducted at the same time. Returns can be collected during subsequent delivery, but the collection may be delayed until a certain amount of return goods is available.

Closed-loop supply chains

The complete closed-loop supply chain includes forward logistics and reverse logistics as well as repair, processing, troubleshooting, and disposal of recyclables. One of the important factors for designing a reverse logistics network is the uncertainty in demand as well as the type and quality of return products (Torkabadi et al. 2018). Listes and Dekker (2005) considered this issue in a rock recycling network and proposed a stochastic mixed-integer programming model with the goal of maximizing profits and developed this model with different scenarios. Cruz-Rivera and Ertel (2009) focused on all aspects of reverse logistics, including networking and inventory analysis, collecting consumables, determining prices, reselling, and revitalizing.

Govindan et al. (2015) tested the use of equipment and industrial unit design models in reverse supply chain management. In one of the considered categories, they divided the subject literature from reverse logistics to closed-loop logistics. Most authors use equipment design models to formulate logistic networks. Rogers and Tibben-Lembke (1999) presented a different integer programming model. This model can identify the locations of distribution and resuscitation units, dispatching, production, and an optimal amount of remanufactured products, and consumed parts. Azar et al. (2011) presented a complex nonlinear programming model with integer variables in which a multi-period, two-echelon, and multi-product model of reverse supply chain network design were discussed. They considered forward and reverse states simultaneously. De Figueiredo and Mayerle (2008) provided a framework for network analyzing. This model determines the deployment decision for different classes of different products along with the allocation of locations and capacity decisions for the equipment. One of the processes of a closed-loop supply chain that is very popular in today’s world is recycling. The most important goal of this process is to reduce the volume of dry waste produced (due to the end-of-life or end-of-use or defective products). Currently, according to environmental protection laws, manufacturers need to produce products that are convenient and convenient to disassemble, reuse, and rebuild. On the other hand, the number of customers who support the environment by sending their consumed products to collection centers is increasing (Lee and Dong 2008; Zhou et al. 2019).

Vehicle routing in supply chains

Liu et al. (2011) proposed a clustering algorithm to solve the vehicle routing problem in a closed-loop supply chain with the aim of reducing path length and overlap between different two-lane routes. This algorithm has a set of new strategies for constructing solutions, including clustering strategies, improved global pheromone update roles, and crossover factor. The results show that the optimal path length and compactness presented by the algorithm are calculated with a clustering-based strategy which is better than the optimal paths calculated by the ant colony algorithm. Wy et al. (2013) are among the latest investigations into the issue of vehicle waste collection routing. This research introduces a roll-on and roll-off waste collection vehicle routing problem involving large containers that accumulate large amounts of waste at construction sites and shopping areas. Complex limitations discussed in this study include multiple disposal facilities, multiple container storage yards, seven types of customer demand services, different time windows for customer demand and facilities, different container types and sizes, and lunch time for the tractor driver. For this problem, an iterative heuristic approach based on neighborhood search that includes several algorithms is presented.

Green supply chains

Kannan and Devika (2010) presented a mixed-integer linear programming model that encompasses multi-class, multi-period, multi-product closed-loop reverse chain networking for product returns and optimization of raw materials and production levels. Distribution and inventory, disposal levels, and recycling levels in different facilities were defined in the model to minimize total supply chain costs. Here, the daily demand of the customer is definitely considered. Recently, a new concept of green supply chain management (GSCM) has emerged for new product developments, incorporating steps in the product life cycle from designing to recycling. One of the issues in this area is the reduction of greenhouse gas emissions. Therefore, some articles in the design of the green supply chain network have focused on reducing carbon emissions, such as Abdallah et al. (2012). In their paper, a complex integer programming model considering green purchasing based on the pollution reduction perspective was presented. The amount of carbon dioxide pollution was considered as the decision variable.

Hsu et al. (2013) have presented a research on the green supply chain at the strategic level. In this paper, the authors intended to improve suppliers’ performance, in the long time, using the decision-making and evaluation of laboratory techniques. Their case study was an electric company. They sought to find the most important quantitative and qualitative criteria for supplier selection and used the network analysis process technique. The result of their efforts was that, with regard to environmental factors, the carbon element had the most influence on this selection. Sahebi et al. (2014) proposed another nonlinear mixed-integer model for the green supply chain at strategic and tactical levels ranging from wells to crude oil terminals. The decisions of this model included location, allocation, project planning, and transportation.

Li et al. (2008) proposed a multi-objective mathematical model (maximizing profit and minimizing greenhouse gas emissions) for locating distribution centers. In this model, greenhouse gas emissions from vehicles as well as greenhouse gases in the process of crop production were investigated. In another study, the amount of carbon released into the grid had been investigated using the static (production and storage) and non-static (vehicles) approach. The authors had also incorporated reverse logistics into their model by placing the goods’ recovery facilities (Sundarakani et al. 2010).

Overall, according to the studies surveyed in this section, it seems that most researches in the field of production planning and supply chain have taken place simultaneously over a period of time, while the real-world considerations need to be studied such as planning for multi-periods as well as multiple products concurrently (Yan et al. 2019). In order to further adapt the research to today’s world conditions, recycling and reconditioning of products are considered simultaneously, so that recycled materials as raw materials as well as recycled products as the end products are returned to the supply chain. Warehousing is also discussed in a three-tiered supply chain. Alongside the issues mentioned, the problem of transporting ended products and returned products are discussed by selecting the number of vehicles and the route between the nodes. Also, the demand for realization of uncertainty conditions has been considered. In this model, not only the material costs of production are taken into account but also the reuse of raw materials and defective products for less environmental damage are considered. Finally, the effects of change in failure rate and greenhouse gas emission rate on the type of transport network are studied.

The rest sections of the paper are organized as follows. The “Literature review” section presents the notations and mathematical modeling. The “Mathematical modelling” section indicates the solution approaches and their framework. Computational experiments are conducted in the “Solution methods” section. Finally, conclusion, managerial insights, and future directions are discussed in the “Computational results” section.

Mathematical modeling

In this section, we aim to develop a new model for optimizing production costs and greenhouse gas emissions in a three-level supply chain including suppliers, manufactures, and demand zones. In this model, the amount of demand is assumed uncertain and the routing decisions from manufactures to demand zones are considered to collect defective products. In addition, inventory planning and control and finished products are optimized in the model. Defective products returned to the production cycle in both recovery and recycling situations. The type of model is defined as a multi-product and multi-period. At first, the assumptions of the model are explained, and then sets, parameters, and variables are introduced. Finally, the mathematical model is constructed using two objective functions and a number of constraints.

Assumptions

• The problem will be formulated as a multi-period model.

• Demand in each node is uncertain.

• The amount of returned products in the reverse system is a percentage of the demand for the previous period.

• Closed-loop supply chain will be considered as a three-level problem including suppliers, manufacturers, and demand centers.

• Returned products are collected periodically.

Notations

Sets

Index	Definition
i	Index of different types of raw material using in final products
j	Index of different types of final products
t	Index of time periods
s	Index of suppliers
n	index of demand nodes
v	Index of vehicles

Parameters

Parameters	Definition
${\overset{\sim }{Dem}}_{jnt}$	Amount of demand node n for product j in period t
α ij	A matrix denoting the ratio of using raw material i in final product j
capm	Capacity of production for factory
Capv v	Capacity for vehicle v
Capi	Capacity for storage in the factory
h 1	The cost of storage raw material in the factory
h 2	The cost of storage final product in the factory
θ	The rate of failure for products
γ	The percentage of returned products that are repairable
λ	The percentage of returned products that are recyclable
Voli i	The volume of raw material i
Volj j	The volume of final product j
CCost j	The cost of producing final product i
${C}_s^1$	The transportation cost of raw material from supplier s to the factory
${C}_{n{n}^{\prime}}^2$	The transportation cost of final product from node n to node n’
Payoff	The amount of discount per each reversed product
BCost j	The recycling cost per each product j
TCost j	The repairing cost per each product j
Co2RateB	The amount of greenhouse gas emissions when recycling a unit of product
Co2RateT	The amount of greenhouse gas emissions when repairing a unit of product
Co2RateP	The amount of greenhouse gas emissions when producing a unit of product
$Co2{Rate}_s^1$	The amount of greenhouse gas emissions during transporting a unit of raw material from supplier s to the factory
$Co2{Rate}_v^2$	The amount of greenhouse gas emissions during transporting a unit of final product by vehicle v
${dis}_{n{n}^{\prime}}^2$	The distance between node n and node n’
${dis}_s^1$	The distance between supplier s and the factory

Decision variables

Binary variables

Variables	Definition
${W}_{n{n}^{\prime } vt}$	= 1, if vehicle v goes from node n to node n’ in period t, 0, otherwise
Gnvt	= 1, if vehicle v visits node n in period t, 0, otherwise

Positive variables

Variables	Definition
Xsit	Amount of raw material i sent from supplier s to the factory in period t
${In}_{it}^1$	Amount of inventory of raw material i in period t in the factory
${In}_{jt}^2$	Amount of inventory of final product j in period t in the factory
Yjt	Amount of production for product j in period t
${Q}_{jnvt}^1$	Amount of transported final product from factory to node n using vehicle v in period t
${Q}_{jnvt}^2$	Amount of reversed final product from node n to the factory using vehicle v in period t

Mathematical model

$$ \min {Z}_1=\sum \limits_s^S\sum \limits_i^I\sum \limits_t^T\left({X}_{sit}^1\ast {C}_s^1\right)+\sum \limits_n^N\sum \limits_{n^{\prime}}^N\sum \limits_v^V\sum \limits_t^T\left({W}_{n{n}^{\prime } vt}\ast {C}_{n{n}^{\prime}}^2\right)+\sum \limits_i^I\sum \limits_t^T\left({In}_{it}^1\ast {h}_1\right)+\sum \limits_j^J\sum \limits_t^T\left({In}_{jt}^2\ast {h}_2\right)+\sum \limits_j^J\sum \limits_t^T\left({Y}_{jt}\ast {CCost}_j\right)+\sum \limits_j^J\sum \limits_n^N\sum \limits_v^V\sum \limits_t^T\left({Q}_{jnvt}^2\ast \gamma \ast {TCost}_j\right)+\sum \limits_j^J\sum \limits_n^N\sum \limits_v^V\sum \limits_t^T\left({Q}_{jnvt}^2\ast \left(1-\gamma \right)\ast \lambda \ast {BCost}_j\right)+\sum \limits_j^J\sum \limits_n^N\sum \limits_v^V\sum \limits_t^T\left( Payoff\ast {Q}_{jnvt}^2\ast \gamma \right) $$

(1)

$$ \min {Z}_2=\sum \limits_j^J\sum \limits_t^T\left({Y}_{jt}\ast Co2{Rate P}_j\right)+\sum \limits_j^J\sum \limits_n^N\sum \limits_v^V\sum \limits_t^T\left({Q}_{jnvt}^2\ast \left(1-\gamma \right)\ast \lambda \ast Co2{Rate B}_j\right)+\sum \limits_j^J\sum \limits_n^N\sum \limits_v^V\sum \limits_t^T\left({Q}_{jnvt}^2\ast \gamma \ast Co2{Rate T}_j\right)\kern1.5em +\sum \limits_n^N\sum \limits_{n^{\prime}}^N\sum \limits_v^V\sum \limits_t^T\left({W}_{n{n}^{\prime } vt}\ast Co2{Rate}_v^2\ast {dis}_{n{n}^{\prime}}^2\right)+\sum \limits_s^S\sum \limits_i^I\sum \limits_t^T\left({X}_{sit}\ast Co2{Rate}_s^1\ast {dis}_s^1\right) $$

(2)

S.T:

$$ \sum \limits_v^V\sum \limits_n^N{W}_{0 nvt}\ge 1\kern0.5em \forall t $$

(3)

$$ \sum \limits_v^V\sum \limits_n^N{W}_{n{n}^{\prime } vt}=1\kern0.5em \forall t,{n}^{\prime } $$

(4)

$$ \sum \limits_n^N{W}_{n{n}^{\prime } vt}-\sum \limits_{n^{"}}^N{W}_{n^{\prime }{n}^{"} vt}=0\kern0.5em \forall {n}^{\prime },t,v $$

(5)

$$ {W}_{0 nvt}={G}_{nvvt}\kern0.5em \forall n,t,v $$

(6)

$$ {W}_{n{n}^{\prime } vt}\le {G}_{nvvt}\kern0.5em \forall n,{n}^{\prime },v,t $$

(7)

$$ \sum \limits_n^N{W}_{n{n}^{\prime } vt}={G}_{n^{\prime } vt}\kern0.5em \forall {n}^{\prime },t,v $$

(8)

$$ \sum \limits_j^J{Q}_{jnvt}^1+\sum \limits_j^J{Q}_{jnvt}^2\le bigM\ast \sum \limits_{n^{\prime}}^N{W}_{n^{\prime } nvt}\kern0.5em \forall n,t,v $$

(9)

$$ {W}_{nnvt}=0\kern0.5em \forall n,t,v $$

(10)

$$ \sum \limits_v^V{Q}_{jnvt}^1\ge {\overset{\sim }{Dem}}_{jnt}\kern0.5em \forall j,n,t $$

(11)

$$ {Q}_{jnvt}^2=0\kern0.5em \forall t=1,j,n,v $$

(12)

$$ \sum \limits_v^V{Q}_{jnv t}^2=\theta \ast \sum \limits_v^V{Q}_{jnv\left(t-1\right)}^1\kern0.5em \forall t\ge 2,j,n $$

(13)

$$ {Y}_{jt}=\sum \limits_n^N\sum \limits_v^V{Q}_{jnvt}^1+{In}_{jt}^2\kern0.5em \forall t=1,j $$

(14)

$$ {Y}_{jt}+{In}_{j\left(t-1\right)}^2+\sum \limits_n^N\sum \limits_v^V{Q}_{jnvt}^2\ast \gamma =\sum \limits_n^N\sum \limits_v^V{Q}_{jnvt}^1+{In}_{jt}^2\kern0.5em \forall t\ge 2,j $$

(15)

$$ \sum \limits_s^S{X}_{sit}=\sum \limits_j^J\left({Y}_{jt}\ast {\alpha}_{ij}\right)+{In}_{it}^1\kern0.5em \forall t=1,i $$

(16)

$$ \sum \limits_s^S{X}_{sit}+\sum \limits_j^J\sum \limits_n^N\sum \limits_v^V\left({Q}_{jnvt}^2\ast \left(1-\gamma \right)\ast \lambda \ast {\alpha}_{ij}\right)+{In}_{i\left(t-1\right)}^1=\sum \limits_j^J\left({Y}_{jt}\ast {\alpha}_{ij}\right)+{In}_{it}^1\kern0.5em \forall t\ge 2,i $$

(17)

$$ \sum \limits_j^J{\mathrm{Y}}_{jt}\le Capm\kern0.5em \forall t $$

(18)

$$ \sum \limits_j^J\sum \limits_n^N{Q}_{jnvt}^1\ast {Vol}_j\le Capv\kern0.5em \forall v,t $$

(19)

$$ \sum \limits_i^I{In}_{it}^1\ast {Voli}_i+\sum \limits_j^J{In}_{jt}^2\ast {Volj}_j\le Capi\kern0.5em \forall t $$

(20)

${W}_{n{n}^{\prime } vt}\ \mathrm{and}\kern0.5em {G}_{nvt}$ are binary. ${X}_{sit},{In}_{it}^1,{In}_{jt}^2,{Y}_{jt},{Q}_{jnvt}^1,\mathrm{and}\ {Q}_{jnvt}^2$ are positive.

Equation (1) expresses the first objective function, which minimizes the cost of transporting raw materials and distributing and retrieving products between demand points, maintenance costs, production costs, recycling, and repair of defective products. There are also discounts for sending defective goods to the system. Equation (2) expresses the second objective function. The first part of this function calculates the amount of greenhouse gas emissions during production, the second part calculates the amount of greenhouse gas emissions during recycling, and the third part calculates the amount of greenhouse gas emissions when repairing defective products. In the fourth and fifth terms, the amount of greenhouse gas emissions in the transportation of raw materials and finished products is investigated.

Constraint (3) guarantees that at each period, at least one vehicle will exit the distribution center and move to the demand points. Constraint (4) ensures that each node is only visited by one vehicle. Constraint (5) is also the equilibrium equation for each node. Constraints (6), (7), and (8) have been used to eliminate the sub-tours in the routing problem. Constraint (9) ensures that if a vehicle visits a node, it can move the product to that node and pick-up from that node. Equation (10) guarantees that a vehicle will not go from any node to the same node. Constraint (11) guarantees that all available demand is met. Constraints (12) and (13) are equilibrium equations for the return of defective goods. Constraints (14) to (17) are the equations for the equilibrium of the initial inventory and the final products. Constraints (18) to (20) are also equations related to production capacity, transportation capacity of each vehicle, and warehouse capacity at the factory.

Uncertainty modeling in the proposed model

In the context of the problem under study in this paper, one of the effective parameters is uncertain due to its unpredictable nature and the impossibility of definitive numerical assignment to this parameter. The above parameter is related to the demand of each node that is considered nonlinear. The maximum entropy (ME) method was used to include the uncertainty in the parameter mentioned in the current study (He et al. 2019; Xu and Dang 2019).

ME uncertainty method

The use of possibility theory is one of the most widely used and well-known methods in this field. This method determines the uncertainty of an event by two numbers of possible size (Pos) and necessity size (Nec). In constraint (21), Pos represents the probability level in the most optimistic case in the event of an uncertain event, and Nec indicates the least probability level in the worst case. These baseline indicators often face limitations in dealing with the real issues of uncertain decision-making because, in uncertain decision-making processes, decision-makers usually have different optimistic-pessimistic attitudes. But the size of the ME allows the decision-maker to choose between these two attitudes:

$$ Me\left\{A\right\}= Nec\left\{A\right\}+\lambda \left( Pos\left\{A\right\}- Nec\left\{A\right\}\right) $$

(21)

where λ(0 ≤ λ ≤ 1) is a pessimistic-optimistic parameters in order to determine the decision-maker’s combined attitude.

With this size, we can develop a new way to convert possibility models into deterministic models with the help of the expected value model and the chance constraint. It is noteworthy that in the proposed method, two approximate lower-limit (LAM) and upper-limit (UAM) models are presented in order to gain the best possible fit to the expected value model and the chance constraints’ indefinite state. Consider the following multi-objective fuzzy model (22):

$$ {\displaystyle \begin{array}{l}\max \left[{f}_1\left(x,\varsigma \right),{f}_2\left(x,\varsigma \right),\dots, {f}_m\left(x,\varsigma \right)\right]\\ {}s.t.\left\{\begin{array}{l}{g}_n\left(x,\zeta \right)\le 0\ n=1,2,\dots, \mathrm{N}\\ {}x\in X\end{array}\right.\end{array}} $$

(22)

Where ς is a vector including fuzzy variable. The expected model for the objectives and chance constraints (ECM) for above model is as follows:

$$ {\displaystyle \begin{array}{l} ECM:\max \left[E\left[{f}_1\left(x,\varsigma \right)\right],\mathrm{E}\left[{f}_2\left(x,\varsigma \right)\right],\dots, \mathrm{E}\left[{f}_m\left(x,\varsigma \right)\right]\right]\\ {}\kern4.25em s.t.\left\{\begin{array}{l} ch\left\{{g}_n\left(x,\zeta \right)\le 0\right\}\ge {\tau}_n\ n=1,2,\dots, \mathrm{N}\\ {}x\in X\end{array}\right.\end{array}} $$

(23)

In above formulation (23), E and Ch are operators for expected value and chance constraint.

This method is used to define the expected value operator of the size of ME, which has a better moderation than the definition of the probability value and the necessary value. The expected value operator is defined using the ME measure (24):

$$ \mathrm{E}\left[\varsigma \right]={\int}_0^{+\infty } Me\left\{\varsigma \ge n\right\} dn-{\int}_{-\infty}^0 Me\left\{\varsigma \le n\right\} dn $$

(24)

We also have the chance limit operator (Ch) using the size of ME (25):

$$ ch\left\{{g}_n\left(x,\varsigma \right)\le 0\right\}\ge {\tau}_n\iff Me\left\{{g}_n\left(x,\varsigma \right)\le 0\right\}\ge {\tau}_n $$

(25)

In above model, τ_n is a confidence level by the decision-maker for satisfying constraint n. Therefore, the mentioned expected value model can be stated as follows (26):

$$ ECM:\left\{\begin{array}{l}\max \left[E\left[{f}_1\left(x,\varsigma \right)\right],E\left[{f}_2\left(x,\varsigma \right)\right],\dots, E\left[{f}_m\left(x,\varsigma \right)\right]\right]\;\\ {}s.t.\\ {} Me\left\{{g}_n\left(x,\varsigma \right)\le 0\right\}\ge {\tau}_n,\kern1em n=1,2,\dots, N\\ {}x\in X\ \end{array}\right. $$

(26)

It can be shown that for each x₀ ∈ X, the following formulation is satisfied (27):

$$ Pos\left\{{g}_n\left({x}_0,\varsigma \right)\le 0\right\}\ge Me\left\{{g}_n\left({x}_0,\varsigma \right)\le 0\right\}\ge Nec\left\{{g}_n\left({x}_0,\varsigma \right)\le 0\right\}\ge {\tau}_n $$

(27)

Finally, using the above relation, two approximate lower-level (LAM) and upper-level (UAM) models for the expected value model and chance constraints are presented as follows (28) and (29):

$$ LAM:\left\{\begin{array}{l}\max\ \left[E\left[{f}_1\left(x,\varsigma \right)\right],E\left[{f}_2\left(x,\varsigma \right)\right],\dots, E\left[{f}_m\left(x,\varsigma \right)\right]\right]\;\\ {}s.t.\\ {} Nec\left\{{g}_n\left(x,\varsigma \right)\le 0\right\}\ge {\tau}_n\kern1.5em n=1,2,..N\\ {}x\in X\end{array}\right. $$

(28)

$$ UAM:\left\{\begin{array}{l}\max\ \left[E\left[{f}_1\left(x,\xi \right)\right],E\left[{f}_2\left(x,\xi \right)\right],\dots, E\left[{f}_m\left(x,\xi \right)\right]\right]\\ {}s.t.\\ {} Pos\left\{{g}_j\left(x,\xi \right)\le 0\right\}\ge {\delta}_j\kern1.5em j=1,2,\dots, m\\ {}x\in X\end{array}\right. $$

(29)

Now, it is possible to approximate a solution space of a possibilistic model using two deterministic models UAM and LAM. Since the parameters used in our research are fuzzy, the summary for computing expected value, necessary value, and possible value for rectangular numbers is presented below. It should be noted that the applied rectangular numbers in the following formulations such as $\tilde{c_{ij}}$ are as (c_{i, j}, α_{i, j}^c, β_{i, j}^c).

$$ E\left[\sum \limits_{j\in J}{\tilde{c}}_{ij}^T{x}_j\right]=\sum \limits_{j\in J}\left(\frac{\left(1-\lambda \right)}{2}\left({c}_{ij}-{\alpha}_{ij}^c\right)+\frac{c_{ij}}{2}+\frac{\lambda }{2}\left({c}_{ij}+{\beta}_{ij}^c\right)\right){x}_j $$

(30)

$$ Nec\left\{{\tilde{a}}_n^Tx\le {\tilde{b}}_n\right\}\ge {\tau}_n\iff {a}_n^Tx+\left(1-{\tau}_n\right){\beta}_n^{aT}x\le {b}_n-{\tau}_n{\alpha}_n^b\kern1.5em \mathrm{n}=1,2,\dots, N $$

(31)

$$ Nec\left\{{\tilde{a}}_n^Tx\ge {\tilde{b}}_n\right\}\ge {\tau}_n\iff {a}_n^Tx-{\tau}_n{\alpha}_n^{aT}x\ge {b}_n+\left(1-{\tau}_n\right){\beta}_n^b\kern1.5em \mathrm{n}=1,2,\dots, N $$

(32)

$$ Pos\left\{{\tilde{a}}_n^Tx\le {\tilde{b}}_n\right\}\ge {\tau}_n\iff {a}_n^Tx-\left(1-{\tau}_n\right){\alpha}_n^{aT}x\le {b}_n+\left(1-{\tau}_n\right){\beta}_n^b\kern1.75em \mathrm{n}=1,2,\dots, N $$

(33)

$$ Pos\left\{{\tilde{a}}_n^Tx\ge {\tilde{b}}_n\right\}\ge {\tau}_n\iff {a}_n^Tx+\left(1-{\delta}_n\right){\beta}_n^{aT}x\ge {b}_n-\left(1-{\delta}_n\right){\alpha}_n^b\kern1.75em \mathrm{n}=1,2,\dots, N $$

(34)

Defined model according to the ME method

Based on the explanation given in the preceding section, the uncertain model of the green closed-loop supply chain problem presented in this paper will be changed as follows. Since the only parameter of uncertainty is in constraint (11), the new version of the constraint is as follows (35).

$$ \sum \limits_v^V{Q}_{jnvt}^1\ge \frac{\left(1-\lambda \right)}{2}\left({c}_{jnt}-{a}_{jnt}\right)+\frac{c_{jnt}}{2}+\frac{\lambda }{2}\left({c}_{jnt}+{b}_{jnt}\right)\kern0.5em \forall j,n,t $$

(35)

In this study, λ is considered as the optimistic-pessimistic parameter in the ME method, according to previous studies, 0.7. This number is mostly toward the pessimistic approach.

Solution methods

In this section, we introduce and define the proposed solution methods for the model. We first define the Epsilon constraint method, which is used to solve multi-objective problems such as the model of this study in small dimensions. Then, considering that the research model are NP-Hard, we consider two proposed meta-algorithms non-dominated sorting genetic algorithm II (NSGAII) and MOPSO that will be used to solve the model in medium and large dimensions. We choose NSGAII and MOPSO for solving the proposed model because our mathematical model is a type of network modeling including both binary and positive variables. The previous studies proved that these algorithms are efficient to solve such models, and therefore, we selected them (Jafarian et al. 2020; Govindan et al. 2014).

Epsilon constraint method

The Epsilon constraint method is one of the common methods used to solve multi-objective problems. In this method, at each stage, one of the objective functions is considered as the optimal objective function and the other objective functions as the constraint.

$$ {\displaystyle \begin{array}{c}\begin{array}{c}\mathit{\operatorname{Max}}\kern0.5em {f}_1(x)\kern1.50em \\ {}\begin{array}{cccc} St& & & \end{array}\\ {}\begin{array}{cccc}{f}_2(x)\ge {e}_2& & & \end{array}\end{array}\\ {}\begin{array}{cccc}& & & \dots \end{array}\\ {}\begin{array}{cccc}{f}_2(x)\ge {e}_p& & & \end{array}\\ {}\begin{array}{cccc}x\upepsilon s& & & \end{array}\end{array}} $$

(36)

To produce optimal Pareto solutions, it is necessary to systematically change the Epsilon value between two boundary points and to solve the model for each change. For this purpose, the interval between the two boundary points (best and worst for the objective function added to the constraints) is usually divided into equal intervals, and the endpoints of each of these equal parts are used as the Epsilon value.

Non-dominated sorting genetic algorithm II

The NSGAII method is used to find Pareto solutions to large-scale multi-objective problems (Yang et al. 2019). The following steps must be followed to apply this method: In the first step, a random population set is generated as usual, based on the scale and constraints of the problem. Next, the population generated is evaluated based on the objective functions of the problem. To calculate the rank of the population, it is assumed that the individuals with ni = 0 are the first front Pareto front or F1. Now, for each member of Fi, the dominated set of si is assumed, and nj corresponding to its jth member. The population with nj = 0 will belong to the set H. After completing H, for all F1 members, it can be said that H is the second Pareto front. To continue, F1 is removed and H is considered the first Pareto front. Then, the same process is repeated for other members. The crowding distance is then calculated for each member in each group and represents a measure of how close the sample is to other members of the population in that group. The large amount of this parameter will lead to divergence as well as a better range in the population. To calculate the congestion distance for solutions on the front of F, first, calculate the number of solutions on the front of i and we call it 1 (1=|F|).

For each i in this set, the initial value of the congestion distance is assumed to be zero (di). Then, for each objective function m, the boundary solutions (starting points and endpoints) are assigned a large congestion distance, and finally, the following relation is used to calculate this index for the rest of the solutions:

$$ {{\mathrm{d}}_1}_{\mathrm{j}}^{\mathrm{m}}={{\mathrm{d}}_1}_{\mathrm{j}}^{\mathrm{m}}+\frac{{\mathrm{f}}_{\mathrm{m}}^{1_{\mathrm{j}+1}^{\mathrm{m}}}-{\mathrm{f}}_{\mathrm{m}}^{1_{\mathrm{j}-1}^{\mathrm{m}}}}{{\mathrm{f}}_{\mathrm{m}}^{\mathrm{m}\mathrm{ax}}-{\mathrm{f}}_{\mathrm{m}}^{\mathrm{m}\mathrm{in}}} $$

(37)

In the above equation, ${1}_{\mathrm{j}}^{\mathrm{m}}$ represents the solution j in the ordered list of solutions based on the objective function m. The fractional form on the right of the Eq. (37) represents the difference of the value of the objective function m for the two adjacent solutions j and j + 1. The denominator of the fraction represents the difference between the minimum and maximum values of the objective function m in the population. Next, some populations are selected as parents to generate new populations. In this research, the selection process is performed using binary tournament operator based on two parameters of poor ranking and congestion distance.

Then, there is a certain amount of probability for the crossover operator to be applied and then a mutation operation on the parent to create children. Eventually, new offspring (based on the selection process) is replaced in the population and a new population is created. This cycle will continue until termination occurs.

Multi-objective particle swarm optimization

The particle swarm optimization algorithm was first introduced in 1995 (Ehyaei et al. 2019). It is inspired by the social behavior of organisms. In particular, it is inspired by the group of flying birds and the group of swimming fish and their social life, formulated using a series of simple relationships. Like all evolutionary algorithms, the particle optimization algorithm starts by creating a random population of people, here referred to as a group of particles. The properties of each particle in the group are determined by a set of parameters whose optimal values must be determined. In this way, each particle represents a point in the solution space of the problem. Each of the particles has a memory, which means that they remember the best position they can reach in the search space.

In fact, the PSO method is an optimization method that deals with problems whose solution is a point or a surface in the next n space. In such an environment, assumptions are made and elementary velocities are assigned to the particles, as well as the channels of communication between the particles. These particles then move through the response space, and the results are calculated on a “merit criterion” after each time interval. As time goes, the movement toward particles of higher qualification and in the same communication group is accelerated.

Each particle strives to improve its position using current position information, current velocity, distance between current position and personal optimum, and ultimately the distance between current position and the optimum.

Each particle has its own position X = (X1, X2,…, Xdi) and its own velocity in the space of response, v = (v1, v2,… vDI). In the t + 1 generation, the velocity of each particle changes using the relation (38) and consequently its new position as the relation (4).

$$ {v}_{id}^{t+1}={w}_{t+1}{v}_{id}^t+{c}_1{r}_1\left({p}_{id}^t-{x}_{id}^t\right)+{c}_2{r}_2\left({p}_{gd}^t-{x}_{id}^2\right) $$

(38)

$$ {x}_{id}^{t+1}={x}_{id}^t+{v}_{id}^{t+1} $$

(39)

In the above equations, i = 1, ..., NP, and NP are the population sizes, d = 1, ..., di, and di are the dimensions of the solution space, and c1 and c2 are two constant values greater than zero. r1 and r2 are also random values in the range of [0,1], ${p}_{id}^t$ is the best particle characteristic of the tth generation, and ${p}_{gd}^t$ is also the best population characteristic in the tth generation. The performance of each particle is also evaluated on the basis of the predefined objective function considered for the problem. It is worth noting that the inertia coefficient in Eq. (38) is dynamically adjusted as well as using Eq. (40).

$$ {\mathrm{w}}_{\mathrm{t}+1}={\mathrm{w}}_{\mathrm{t}}\cdot {\mathrm{f}}_{\mathrm{w}} $$

(40)

In the MOPSO algorithm, a concept called Archive 2 or Repository is added to the PSO algorithm, also known as Hall of Fame. The members of the reservoir represent the Pareto front and contain undesirable particles. So instead of Gbest, a member of the repository is selected. For this reason, there is no repository in PSO because there is only one target and only one particle has the best value. But in MOPSO, there are several undesirable particles in the solution set.

Solution representation

The model representation of this research consists of three distinct parts, each of which represents an independent variable. The first part is a j × 2 t matrix, all of which are filled with numbers between zero and one. This section is related to Y_jt. The first column is used to decide on production and the remaining columns show the amount of productions. The method of extracting the corresponding variable is that if the number in the t cell was less than 0.5, we would not have that product in that time period, and if it was over 0.5, we will produce that product. The production rate is also obtained after normalizing the second half of the matrix by multiplying the normalized number by the factory production capacity.

The second part of the solution is related to the variable ${Q}_{jnvt}^1$. A 4-dimensional matrix with dimensions of v, n, j + 1, and t, respectively, and a number between zero and one in a cell represent the second part of the solution. The following steps must be performed to extract the corresponding variable.

• Step 1. On the surface v and n on each column (n), we use the maximization operator, and the row corresponding to the maximum cell in each column represents the vehicle used to send the product to the demand node corresponding to that column.

• Step 2. We convert cells that do not correspond to n and v to zero.

• Step 3. Sum up all the cells corresponding to each time period of each vehicle.

• Step 4. Divide the number in each cell by the number obtained for the corresponding vehicle and over the corresponding time period.

• Step 5. Multiply the number obtained for each cell in the respective vehicle capacity. Then, replace the exact demand number if the number obtained was greater than the demand value of that point.

The third part of the answer also corresponds to the variable ${Q}_{jnvt}^2$, which is quite similar to the second part considered, except that in step 5, the quantity of defective products will be available for return instead of its demand value.

Solution generation

Point-to-point crossover operators have been used to produce children. That is, the corresponding binary matrix with the same dimensions of the binary matrix is randomly generated. If the cell number is 1, the corresponding cell is used to represent the first child’s response to the first parent, and if the cell is zero, the corresponding cell in the first child is used by the second parent. For the mutation operator, the reverse mutation is also considered for all chromosomes.

Computational results

In this section, we first solve a small numerical example using GAMS software and Epsilon constraint method and illustrate the response network. Then, in order to determine the accuracy and performance of each of the meta-heuristic algorithms used in this study, twelve problems with Gams software as well as the two meta-heuristic algorithms are solved and compared with the most desirable criteria.

Solving a sample problem by GAMS software

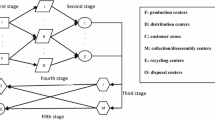
To verify the validity of the proposed model, a small problem with random data is created and solved using the GAMS 22.6 software. Given the small sample size problem, it takes about an hour to solve, and this illustrates that meta-heuristic methods should be used for large-scale problems. This problem is solved using Epsilon constraint method with alpha coefficient of 0.1 in GAMS software. The following schematic shows a solution.

The example above is solved with two suppliers, seven demand nodes, three vehicles, two raw materials, and two types of end products, and the transportation network is in Table 1. All the data required in the numerical example are randomly generated according to Akbari-Jafarabadi et al. (2017) and the distribution functions considered for each parameter in Table 2.

Table 1 The size of example

Table 2 The distribution of the input parameters for the example

In this example, 61.5% of defective products are recovered from the system and returned to the production chain through recycling and repairing. In this example, two vehicles were used and only one supplier (supplier # 1) was used to supply the raw materials. One hundred percent of defective products are returned at points 2, 5, and 6; no product is returned at point 1. In this example, there are nine Pareto optimal solutions that one of them is shown in Fig. 1. No vehicle was used to load defective products from demand points in all of the responses reviewed.

Fig. 1

The formed network and material flows for the example

Validating the solution methods

Pareto front analysis

In Fig. 2, we present a set of Pareto front solution for an example which is solved by three methods. The example is designed in small dimensions. In this example, there are 20 demand centers, 4 suppliers, 7 vehicles, 3 types of raw materials, 4 types of finished products, and finally 6 consecutive time periods. The graphical representation of the values of the objective functions using the methods described for this sample problem is shown.

Fig. 2

Analyzing the Pareto front for the different solution approaches

The trend of graphs in analyzing the Pareto front of different methods well-illustrates a min-min model. As can be seen in the graph, GAMS presents better Pareto solutions than the two meta-heuristic algorithms. Among the two heuristic algorithms, the NSGAII algorithm provided a better Pareto set.

Analysis based on optimality gap criterion

Because of the use of the iterative process to insert values in Table 3, the average percentage relative gap (APRG) for both meta-heuristic methods was used to solve 12 sample problems. This metric shows the percentage of gap between the average of solutions per each objective function and the best solution found for each solution method. For example, the number 0.7 indicates that the average of value for the first objective function by NSGAII method has 0.7% difference from the best solution while MOPSO has 2.2% difference from the best solution.

Table 3 Comparison of the solution methods based on the optimality gap

As shown in Table 3, the APRG1 values for the first objective function and the APRG2 for the second objective function for the small size of the problem indicate the utility of the NSGAII method over the other one.

Pareto optimal analysis of the number of optimal solutions

Figure 3 is a graphical representation of the number of Pareto solutions obtained by different methods. The results show that for both objective functions, the NSGAII algorithm performs better than GAMS when the criterion is the number of optimal Pareto solutions. Also, MOPSO is in third place.

Fig. 3

Comparison of the solution approaches based on the number of Pareto solutions

Time-based analysis

Figure 4 shows the time of solving each of the sample problems by the methods used. The observations indicate that the NSGAII algorithm, with the shortest solution time, outperforms the MOPSO algorithm as well as the Gams software.

Fig. 4

Comparison of the solution approaches based on the run time

Distance-based criterion analysis

The uniformity of the spread of the non-dominated set solutions is calculated by this metric. To compute this metric, the Euclidean distance between consecutive solutions in the obtained non-dominated set of solutions and the average of these distances is calculated. As the value of this metric reduces, the algorithm shows a better performance.

Figure 5 shows the distance criterion for each sample problem solved by the algorithms. The observations indicate that the MOPSO algorithm is less desirable than the other two methods. The other two methods also have very close results. Therefore, in order to increase the accuracy of the analysis of the results, pairwise comparison experiments were used, and the result shows that the Gams software is in the first place and the NSGAII algorithm is in the second place with very little difference.

Fig. 5

Comparison of the solution approaches based on the distance

Analysis based on dispersion criterion

For this metric, the spread of a Pareto solution set for each algorithm is calculated. A higher value in this metric represents a better performance of the algorithm by the following equation.

$$ \sqrt{{\left(\frac{\max {f}_{1i}-\min {f}_{1i}}{f_{1, total}^{\mathrm{max}}-{f}_{1, total}^{\mathrm{min}}}\right)}^2+{\left(\frac{\max {f}_{2i}-\min {f}_{2i}}{f_{2, total}^{\mathrm{max}}-{f}_{2, total}^{\mathrm{min}}}\right)}^2} $$

(41)

where n is the number of non-dominated solutions, fmax i;total is the maximum value of ith objective function among all non-dominated solutions obtained by the algorithms, fmin i;total is the minimum value of ith objective functions among all non-dominated solutions obtained by the algorithms, and f best i is the ideal solution of ith fitness function.

Figure 6 shows the dispersion criterion for each of the sample problems solved by the algorithms. It is obvious that the MOPSO algorithm is less desirable than the other two methods. The other two methods also work very closely together. Therefore, in order to increase the accuracy of the results analysis, paired comparison experiments have been used and the result shows that the Gams software is in the first place and the NSGAII algorithm is in the second place with very little difference.

Fig. 6

Comparison of the solution approaches based on the dispersion criterion

Sensitivity analysis

In the sensitivity analysis, the effectiveness of the solution to the problem will be examined by modifying one or more parameters to evaluate the effect of the parameters. In this study, by changing the three optimistic-pessimistic coefficients of the ME method, the ratio of greenhouse gas emissions to new product recycling with new product production as well as the percentage of defective products will be separately investigated.

Optimistic-pessimistic coefficient of ME method

In this section, we attempt to investigate the pattern of changes in the solution by modifying the Landa parameter (optimistic-pessimistic coefficient) in the ME method. In fact, we want to know what will change in the optimistic and pessimistic state of affairs. The results are shown in Table 4 and Figs. 7, 8, and 9.

Table 4 Sensitivity analysis on the coefficient of optimistic-pessimistic in ME method

Fig. 7

Illustrating how to change the return percentage of defective products

Fig. 8

Show how changes to the first objective function (cost)

Fig. 9

Show how changes to the second objective function (greenhouse gases)

As clearly shown in Table 4 and Fig. 7, there was no significant trend following the change in the optimistic-pessimistic coefficient of the ME method in product return rates. As the corresponding coefficient changes, the amount of demand sent to the nodes changes, too. Thus, once the coefficient moves more to the optimistic way, the lower amount of products sent to the nodes. As shown in Figs. 8 and 9, the first and second objective functions have decreased simultaneously. Given the pessimistic coefficient, the demand considered in the model is closer to the upper bound of the triangular fuzzy number, and as the demand increases, the first and second objective functions have grown again. But the important point is that the rate of return products has not changed significantly and this indicates that with the change in demand nodes, there will not be a fundamental change in the distribution network, and the solutions provided are reasonably robust.

The proportion of greenhouse gas emissions for recycling to new production

As expected, the higher the denominator of this fraction or the smaller its numerator (the ratio decreases), the results tend to gather more defective products from demand centers. Following the changes, the first objective function (cost) does not follow a uniform incremental or decreasing trend. Careful examination of the distribution and routing network revealed that at the breakpoints of the figure, additional vehicles were used to return defective products, which not only resulted in lower greenhouse gas emissions but also transportation costs. Table 5 and Figs. 10, 11, and 12 show the results.

Table 5 Sensitivity analysis of the ratio of greenhouse gas emissions to old crop recycling and new production

Fig. 10

Presenting how the percentage of defective product returns changes

Fig. 11

Presenting the trend of changes for the first objective

Fig. 12

Presenting the trend of changes for the second objective

As shown in Fig. 10, all defective products have been recovered once the rate of generation greenhouse gases is 15%. Since the number of vehicles used in this case is higher than the others, the cost of transportation and consequently the amount of the second objective function also increased dramatically, which is illustrated in Fig. 11. Also, Fig. 12 which relates to the second objective function shows that with increasing the percentages of defective products, greenhouse gas emissions will increase, because new vehicles will need to be used at break-even points (where the graph is growing).

Percentage of defective products to total products (θ)

By changing the percentage of defective products, the results cannot show a meaningful change once the rate is more than 50%. The reason is also clear from the results and because of the fact that the defective products are returned up to the maximum capacity of the vehicle. Also, since using a new vehicle is more than the difference between product cost and recovery/reuse cost, so this action is not cost-saving. Table 6 and Figs. 13, 14, and 15 will display the results.

Table 6 A sensitivity analysis on the proportion of greenhouse gas emissions in new crop production and old crop recycling

Fig. 13

Presenting the trend of changes for product return rate

Fig. 14

Presenting the trend of changes for the first objective

Fig. 15

Presenting the trend of changes for the second objective

As shown in Fig. 15, as the percentage of defective products increases, the system is not willing to use a new vehicle or change its routing. So, it only carries the maximum capacity with defective products in the visiting nodes. Therefore, as the percentage of failures increases, there is no change in product loading further. Thus, the first and second objective functions remain constant. However, as the product’s failure rate decreases and as the system is reluctant to change the routings, the number of returned products decreases while the percentage of the total defective product increases against to the total number of returned products. In other words, the system tends to fill the maximum capacity of each vehicle with defective products, and at the 10% chance of failure, nearly 100% of the defective products will be returned. Now, as the rate of product’s failure decreases, the number of returned products decreases, and the number of products recovered or reused reduces. Finally, the costs of producing new products and the cost of producing greenhouse gases, as shown in Figs. 14 and 15, slightly increased.

Managerial insights

One of the important parameters in the model is the optimistic-pessimistic coefficient. In this way, once this parameter is more pessimistic, the more products are needed for satisfying the demands. So, the more costs and more greenhouse gases are generated. Actually, the manager pays more costs in order to prevent backorder demands. On the other hand, if the manager is more optimistic, the lower amount of products will be transported while the probability of backorder demands is more.

The other important parameter is the ratio of greenhouse gas emission for recycling to the new product. The higher the value for this ratio, the results tend to gather more defective products from demand centers. So, collecting the more defective products leads to increasing production amount since the collective products can return to the production line. By this way, the total cost is reduced as indirect result. On the other hand, the number of used vehicles may increase and total transportation cost will increase, too. Therefore, it is necessary for the manager to balance between these two types of cost.

The last important parameter is the product’s failure rate. Once this parameter decreases and since the system is reluctant to change the routing patterns in the model, the number of returned products decreases while the percentage of the total defective product increases against to the total number of returned products. Therefore, it is required for the managers to control this parameter in order to optimize capacity usage in the model.

Conclusion

In this study, a mathematical model of the green closed-loop supply chain was developed in which the impact of product recovery on reducing production costs as well as reducing environmental pollution was studied. The uncertainties for the product demand parameter per each node were taken into account in the constraints and solved by the maximum entropy (ME) method. Then, the developed model was solved using the Epsilon constraint method and also NSGAII and MOPSO meta-heuristic methods. As a result of the comparisons, it was found that the NSGAII method is capable of solving large-scale models. Then, sensitivity analysis of the main parameters of the model results and behavior was investigated.

The results show that the manager should pay more costs in order to prevent backorder demands. Also, collecting the more defective products leads to increasing production amount since the collective products can return to the production line. Finally, it is required for the managers to control products’ failure rate to optimize capacity usage in the model.

The following are some guidelines for developing current research.

• Incorporating pick-up delivery routing decision in the reverse section of supply chain.

• Considering fuzzy and random failure rate in the reverse section and undesirable products.

• Considering other reverse facilities such as disposal centers, minor corrections centers, and remanufacturing centers for designing the closed-loop supply chain.

• Considering other environmental issues for design closed-looped supply chain such as recovery gas emissions and disposal factors.