Introduction

Sediment transport, which is among the most important aspects of river flow, is significantly influenced by the flow condition and the size of the particles (Ehteram et al. 2019c). The characteristics of sedimentation in fluvial systems can be better understood, through a process known as suspended sediment load (SSL) estimation. Sedimentation stems from erosion and weathering (Misset et al. 2019). Suspended sediment load and sediment transportation are affected by geological and geomorphological issues (Chang et al. 2019). The SSL prediction represents a major issue in the fields of hydraulic engineering and river basin development. The influence of different meteorological parameters (rainfall, temperature and discharge), on sediment transport, renders the modelling of SSL a complicated undertaking (Samantaray and Ghose 2018). In order to overcome the issues of complexity and nonlinearity that come with SSL prediction, data-driven models are often brought into the picture. The selection of an appropriate model for SSL prediction has proven to be an exceedingly difficult task (Talebi et al. 2016). According to the literature, empirical models fall short when it comes to comparison with accurate SSL predictions (Khan et al. 2018; Khosravi et al. 2018; Samantaray and Ghose 2018; Chang et al. 2019; Misset et al. 2019). As such, the prediction of the SSL based on local data is deemed the way forward for an accurate SSL prediction (Jothiprakash and Garg 2009). Jothiprakash and Garg (2009) used artificial neural network (ANN) to predict the volume of sediment in a reservoir. They opined that the accuracy level of ANN is above that of a regression model. The major benefit that comes with ANN usage is its capacity to model mathematical relationships, between input and output data, through a learning process, without prior knowledge of the problems (Melesse et al. 2011; Nourani and Andalib 2015; Ethteram et al. 2018; Ehteram et al. 2019c). To prepare an adequate architecture of ANN, several trial and error procedures need to be carried out. Also required is extensive input data for the training process (Ehteram et al. 2019c). Melesse et al. (2011) used ANN, multiple linear regression (MLR) and multiple nonlinear regression (MNLR) to estimate SSL. According to the results attained, the ANN estimations for most simulations were better than those realized through the MLR and MNLR. Kisi et al. (2012) employed genetic programming (GP), ANN and adaptive neuro-fuzzy inference system (ANFIS) to estimate SSL. They concluded that GP is superior to the ANFIS and ANN models. Kakaei Lafdani et al. (2013) investigated the estimation of daily SSL with a support vector machine (SVM) and ANN. Streamflows and rainfall were employed as the input data. They reported that the ANN model is significantly more accurate than other SSL estimation models. Vafakhah (2012) used the ANFIS and ANN models for the modelling of SSL. They forwarded that the ANFIS model provides a better estimation than the ANN model. Tayfur et al. (2013) investigated the potential of ANN-genetic algorithm (GA) for predicting SSL. They found the performance of ANN-GA to be superior to that of ANN. Afan et al. (2014) used radial basis function neural network (RBFNN), and multilayer perceptron (MLP) neural network, for SSL modelling. They claimed that the MLP model delivers better accuracy than the RBFNN model. Nourani and Andalib (2015) examined the capabilities of least square support vector machine (LSSVM) and ANN models in estimating SSL. The results indicate that the LLSVM model provides better accuracy than the ANN model. Talebi et al. (2016) utilized regression trees and model trees for estimating SSL. They reported that the performance of regression trees and model trees is superior to that of the ANN model. Emamgholizadeh and Demneh (2018) examined the proficiency of GP, ANN and ANFIS for SSL modelling. The results give credence to the fact that the accuracy level of the GEP model is above that of the ANN and ANFIS models.

While data-driven models are highly regarded for predicting hydrological variables, these models require tuning through training algorithms (Banadkooki et al. 2020). In order to complete the final network training, it is essential that the entire data-driven model be fine-tuned. Of late, optimization algorithms such as bat algorithm (BA), GA, particle swarm optimization (PSO), shark algorithm (SA) and firefly algorithm (FFA) have been used to train data-driven models, in order to determine their optimal parameter values (Allawi et al. 2018; Ehteram et al. 2018a, b, 2019a, b; Farzin et al. 2018; Abobakr Yahya et al. 2019; Yousif et al. 2019; Valikhan-Anaraki et al. 2019; Najah Ahmed et al. 2019; Afan et al. 2020). According to the relevant literature, optimization algorithms increase the convergence speed of traditional training algorithms, such as the gradient descent method and the backpropagation algorithm (Allawi et al. 2018; Ehteram et al. 2018b; Farzin et al. 2018). To the best of our knowledge, no previous attempt has been made to employ an ANN model–based ant lion optimization (ALO) for predicting SSL, thus the aim of this study.

ALO was initially introduced by Mirjalili (2015). Scholars frequently used the ALO for a variety of optimization issues. These optimization issues include those related to energy consumption forecasting (Wang et al. 2018), parameter optimization of SVM (Tian et al. 2018), optimal power flow (Ali et al. 2017) and hydraulic turbines (Tharwat and Hassanien 2017). The forte of the ANN model lies in its capacity to optimize ANN parameters such as weight connections and bias values. In this paper, a novel ALO algorithm was used to train the ANN model. An innovative hybrid ANN model was introduced for the forecasting of daily SSL. The two main goals of this undertaking are (a) to evaluate the capacity of hybrid ANN models for SSL estimation and (b) to evaluate the uncertainty of the ALO, BA and PSO algorithms for the training of ANN models. The following sections provide information on the applied models, the study location and the data involved. We close with an output analysis and an explanation on the conclusions derived.

Materials and methods

Artificial neural network

The inspiration of ANN model came from the desire to provide intelligent calculations that mimics the routine structure of brain. The ANN models are composed of computational units, namely neurons (Allawi et al. 2018; Ehteram et al. 2018b; Farzin et al. 2018). Each neuron is linked to other neurons by means of weight connections. The ANN model is mostly made up of three layers: an input layer, the hidden layers and an output layer. An illustration of the most frequently employed ANN model is presented in Fig. 1.

Fig. 1
figure 1

Schematic structure of ANN (three-layer MLP)

Full size image

For this study, only one hidden layer network was used, as it was deemed sufficiently dynamic for the prediction of any hydrological variable. Many investigations have been conducted to determine the optimal number of hidden neurons in the ANN model. These investigations led to the introduction of several empirical equations. The following equation (Karkalos et al. 2019) was employed for this study:

$$ n=\sqrt{N_{\mathrm{inp}}+{N}_{\mathrm{out}}}+a $$
(1)

where Ninp is the number of input neurons, Nout is the number of output neurons, a is the number between zero and 10 and n is the number of hidden neurons.

A variety of transfer functions exist which can be used to construct an artificial neural network neuron. Transfer functions are needed to describe the input-output relationship at each neuron layer. Nonlinear transfer functions are usually employed to introduce nonlinearity into the network. In order to minimize the network error, it is essential that the components of weights and biases be fine-tuned. The ANN models use training algorithms to find the optimal value of weight connection and biases (Ethteram et al. 2018; Tikhamarine et al. 2020). The most commonly used algorithm for ANN training is the backpropagation algorithm (BPA). The BPA is a traditional method for tuning the weight and bias values. Currently, optimization algorithms are frequently applied for the training of ANN hyperparameters. It is noteworthy that the BPA may experience slow convergence and may also be trapped in local minima. The BPA executes an iterative gradient descent procedure to decrease the network error.

Ant lion optimization

The ALO is capable of mimicking the hunting behaviour of ant lions in nature. An ant lion (ANL) moves along a circular path to dig a hole in sand (Mirjalili 2015). The ant lion larvae hide at the bottom of the pit (trap) and wait for ants (prey). With the arrival of the prey (ant), the ant lions pull it into the pit by throwing sand towards the edge of the hole. The performance of the algorithm is based on the following assumptions (Wang et al. 2018):

  1. 1-

    Ants (the prey) move randomly in the search space, and the traps of the ANLs affect the movement of the ants.

  2. 2-

    The best fitness ANL makes a large hole.

  3. 3-

    The ability to hunt an ant, by an elite ANL, is proportional to the fitness of that ANL.

  4. 4-

    Each ant (AN) may be hunted by each ANL in each iteration (Fig. 2).

Fig. 2
figure 2

Hunting behaviour of ANLs

Full size image

Random walk of ants

The ALO has two groups of search agents: ant (prey) and ant lion. The best search agents (ant lions) never change their locations, except during the substitution of a special ant. Ant agents can perform random walks in the search space (Mirjalili 2015). The ants trapped in a hole may be hunted by the ant lions. Through random walks, ants update their position around the search space (Mirjalili 2015).

$$ {X}_t=\left[0,\mathrm{cumsum}\left(2{r}_t\left({t}_1\right)-1\right),\mathrm{cumsum}\left(2{r}_t\left({t}_2\right)-1\right),\dots, \mathrm{cumsum}\left(2{r}_t\left({t}_n\right)-1\right)\right] $$
(2)

where t is the step of random walk, cumsum is the cumulative sum, n is the maximum number of iterations, n is the population size and r is the stochastic function which is computed through the following equation (Mirjalili 2015):

$$ r(t)=\left[\begin{array}{l}1\leftarrow \mathrm{if}\left(\operatorname{rand}>0.5\right)\\ {}0\leftarrow \mathrm{if}\left(\operatorname{rand}\le 0.5\right)\end{array}\right] $$
(3)

Equation (3) ensures that the ants move within the boundaries of the search space

$$ {R}_t^j=\frac{\left({X}_i-{a^t}_i\right)\times \left({d^t}_i-{c}_i^t\right)}{\left({b}_i^t-{a}_i\right)}+{c}_i^t $$
(4)

where ati is the minimum step of random walk (RW), \( {X}_i^t \) is the position of ith anti at tth iteration, bi is the maximum step of random walk, \( {R}_t^j \) is the position of anti i after performing the random walk to nearby ant lion j, \( {c}_i^t \) is the minimum ith variable at tth iteration and dti is the maximum ith variable at tth iteration (Fig. 2).

Trapping hole of the ANL

As mentioned above, the traps of the ANLs affect the random walks of the ANs. The following equation is used to mathematically model this hypothesis (Wang et al. 2018):

$$ {d}_i^t=\mathrm{Ant}\ {\mathrm{lion}}_j^t+{d}^t $$
(5)
$$ {c}_i^t=\mathrm{Ant}\ {\mathrm{lion}}_j^t+{c}^t $$
(6)

where ct is the minimum of all variables at tth iteration, \( {c}_i^t \) is the minimum of all variables for ith ant, dt is the maximum of all variables at tth iteration and \( {d}_i^t \) is the maximum of all variables for ith ant. Figure 3 shows the random walk of an ant.

Fig. 3
figure 3

Random walk of an ant

Full size image

Building the trap

A roulette wheel mechanism is used to simulate the ANL’s hunting ability. As shown in Fig. 3, the ANs are hypothesized to be trapped in only one chosen ANL pit. The ALO algorithm uses the roulette wheel mechanism to select ANLs based on their fitness during optimization. The fitter ANLs are more likely to be successful in hunting an ant (Mirjalili 2015).

Sliding ants towards the ant lion

When the ANL realizes that there is an AN in the trap, it throws sand towards the edge of the hole to pull the prey (ant) in. This behaviour is simulated through the following equation:

$$ {\displaystyle \begin{array}{l}{c}^t=\frac{c^t}{I}\\ {}{d}^t=\frac{d^t}{I}\end{array}} $$
(7)

where ct is the minimum of all variables at tth iteration, dt is the maximum of all variables at tth iteration and I is the ratio. The computation of the I parameter is portrayed in Fig. 4.

Fig. 4
figure 4

Flowchart of ant lion optimization

Full size image

Catching prey and rebuilding the trap

In order to increase its chances of catching new AN, the ANL has to alter its position to the position of the hunted ant. This behaviour is simulated in Eq. (10)

$$ \mathrm{Ant}\ {\mathrm{lion}}_j^t=\left[\begin{array}{l}{\mathrm{Ant}}_i^t\leftarrow \mathrm{if}\left(f\left({\mathrm{Ant}}_i^t\right)\right)<\left(f\left(\mathrm{Ant}\ {\mathrm{lion}}_i^t\right)\right)\\ {}\mathrm{Ant}\ {\mathrm{lion}}_j^t\leftarrow \mathrm{otherwise}\end{array}\right] $$
(8)

where \( {\mathrm{Ant}}_i^t \) is the location of jth ANL, \( {\mathrm{Ant}}_i^t \) is the position of ith ANL and t is the current iteration.

Elitism

The ALO has two groups of search agents: ant (prey) and ant lions. The best search agents (ant lions) only alter their locations during the substitution of a special ant. Ant agents can perform random walks in the search space (Mirjalili 2015). The ant lions hunt ants trapped in a hole. The ant lion with a superior fitness level in each iteration is regarded an elite ant lion. The following equation is used to attain the position of the ants (Mirjalili 2015):

$$ {\mathrm{A}\mathrm{nt}}_i^t=\frac{R_{\mathrm{A}}^t+{R}_{\mathrm{e}}^t}{2} $$
(9)

where \( {R}_{\mathrm{A}}^t \) is the random walk around the ant lion (ANL) chosen by way of the roulette mechanism (RM), \( {R}_{\mathrm{e}}^t \) is the random walk around the elite ant lion at tth iteration and \( {\mathrm{Ant}}_i^t \) is the location of ith ant lion at tth iteration (Fig. 4).

Bat algorithm

BA is an optimization algorithm for global optimization. This algorithm mimics the behaviour of bats. Each bat flies randomly with a velocity (vi) at location (solution) xi with a changing frequency or loudness (Ai). When the bat seeks and finds its prey, its frequency, pulsation rate (r) and loudness are altered. The position, velocity and frequency of bats are updated as follows (Cui et al. 2019):

$$ {f}_l={f}_{\mathrm{min}}+\left({f}_{\mathrm{max}}-{f}_{\mathrm{min}}\right)\times \beta $$
(10)
$$ {y}_l(t)={y}_l\left(t-1\right)+{v}_l(t),t=1,\dots, T $$
(11)
$$ {v}_l(t)=\left[{y}_l\left(t-1\right)-{Y}_{\ast}\right]\times {f}_l,t=1,\dots, T $$
(12)

where fmin is the minimum frequency, fmax is the maximum frequency, β is the random value, yl(t) is the position at time step (t), Y∗ is the best solution, fl is the frequency and T is the total period of assessment.

Subsequent to the selection of a solution from among the best current solutions, a new solution for each bat is derived locally through Eq. (13) (random walk)

$$ y(t)=y\left(t-1\right)+\varepsilon A(t),t=1,\dots, T $$
(13)

where A(t) is the average loudness and ε is the random number. Figure 5 shows the flowchart of the BA. The pulsation rate increases when a bat finds its prey, while the loudness decreases. The loudness and pulsation rate values are updated as follows:

$$ {r}_l^{t+1}={r}_l^0\left[1-\exp \left(-\gamma t\right)\right]{A}_l^{t+1}=\alpha {A}_l^t $$
(14)

where γ and α are the constant values.

Fig. 5
figure 5

Flowchart of bat algorithm

Full size image

Particle swarm optimization

The PSO is applied in a wide variety of areas. This includes rock strength estimation, energy demand forecasting, coefficient discharge estimation, water resource management and classifier selection (Wang et al. 2018). PSO’s group of particles seeks out the best global (gbest) and personal (pbest) positions. The updating of the position, and velocity of particles in this algorithm, is based on the following equation:

$$ {V}_{\mathrm{new}}=\omega \times V+{C}_1\times {r}_1\left({p}_{\mathrm{best}}-X\right)+{C}_2\times {r}_2\left({g}_{\mathrm{best}}-X\right) $$
(15)
$$ {X}_{\mathrm{new}}=X+{V}_{\mathrm{new}} $$
(16)

where X is the current position of the particles, C1 and C2 are the acceleration coefficients, r1 and r2 are the random values and ω is the inertia weight.

Hybrid ANN and optimization models

As mentioned previously, the output of ANN is affected by the bias and weight values. The aim of any optimizer is to determine the optimal values of the ANN parameters. To achieve this goal in the hybrid ANN and optimization models, optimization algorithms are employed to optimize the weight and bias values. These weight and bias values are then used as inputs to the optimization algorithms. Put plainly, each agent in each optimization algorithm is a representative of a bias or weight value. The optimization-simulation process usually begins with the initialization of a collection of random agents. The hybrid ANN optimization models are trained with the initial position of the agents (i.e. with their original weights and bias parameters). At the next level, the fitness of the agents is computed. An objective function (i.e. the root-mean-square error) is defined to decrease the hybrid model error. The calculated error is decreased through alterations in the position of the agents. This process continues until a stopping criterion is met.

Case study

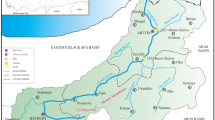
An agricultural basin located in the north of Iran was selected for this case study. The Goorganrood basin is positioned at longitude 10′ 54° to 26′ 56° N and latitude 35′ 36° to 38′ 15° E, as shown in Fig. 6. Except for the period between May and July, a wet climate with moderate temperatures prevails in this area. The average annual rainfall is 515 mm, while the average annual temperature is 17.8 °C. The lowest and highest rainfall levels occur in August and March, respectively. August is the hottest month and January the coldest.

Fig. 6
figure 6

Location of the case study

Full size image

The construction of accurate SSL prediction models involves the generation of input data for all the soft computing models, by means of statistically significant lagged combinations of historical SSL. These inputs were used for a 1-day-ahead forecast of SSL. In this study, first, the soft computing models were evaluated using the data at Narmab station in the Goorganrood basin. Three hundred eighty daily data were used from the Narmab station. Then, climate data of the Salian station, Narmab station, Tamar station and Basir Abad station were used to validate the models. Three thousand six hundred daily data of these stations were used as the inputs to the models; 70% and 30% of data were used for the training and testing levels, respectively, as shown in Figs. 7 and 8. Different data splitting ratios have been examined to achieve the best data splitting ratio. However, the best results were obtained for 70% of data and 30% of data for the training and testing levels, respectively. Figure 9 shows the best objective function value obtained for different sizes of data through the ANN model. The results indicated that the best results are obtained by the 70% and 30% of data for the training and testing levels, respectively.

Fig. 7
figure 7

Time series of SSL for the training stage

Full size image
Fig. 8
figure 8

Time series of SLL for the testing stage

Full size image
Fig. 9
figure 9

a, b Sensitivity analysis for the data splitting ratios

Full size image

Table 1 shows the statistical characteristics of data. The mean, maximum and minimum values at the Narmab station is 41,000, 65,000 and 2800, respectively. In this study, the SSL was estimated with and without meteorological data. First, Eq. (18) was used to estimate SSL without meteorological data. Then, the SSL was estimated using meteorological data.

Table 1 Statistical indices of the collected data for SSL and meteorological inputs
Full size table

Statistical analysis generated a unique set of inputs, with a total of five different input combinations derived by way of the periodicity (day) and historical SSL. In this study, first, the soft computing models are evaluated using

$$ {\displaystyle \begin{array}{l}\mathrm{SSL}(t)=f\left[\mathrm{SSL}\left(t-1\right)\right],\left(1:\mathrm{Number}\ \mathrm{of}\ \mathrm{scenarios}\right)\\ {}\mathrm{SSL}(t)=f\left[\mathrm{SSL}\left(t-1\right),\mathrm{SSL}\left(t-2\right)\right],\left(2:\mathrm{Number}\ \mathrm{of}\ \mathrm{scenarios}\right)\\ {}\begin{array}{l}\mathrm{SSL}(t)=f\left[\mathrm{SSL}\left(t-1\right),\mathrm{SSL}\left(t-2\right),\mathrm{SSL}\left(t-3\right)\right],\left(3:\mathrm{Number}\ \mathrm{of}\ \mathrm{scenarios}\right)\\ {}\mathrm{SSL}(t)=f\left[\mathrm{SSL}\left(t-1\right),\mathrm{SSL}\left(t-2\right),\mathrm{SSL}\left(t-3\right),\mathrm{SSL}\left(t-4\right)\right],\left(4:\mathrm{Number}\ \mathrm{of}\ \mathrm{scenarios}\right)\\ {}\mathrm{SSL}(t)=f\left[\mathrm{SSL}\left(t-1\right),\mathrm{SSL}\left(t-2\right),\mathrm{SSL}\left(t-3\right),\mathrm{SSL}\left(t-4\right),\mathrm{SSL}\left(t-5\right)\right],\left(5:\mathrm{Number}\ \mathrm{of}\ \mathrm{scenarios}\right)\end{array}\end{array}} $$
(17)

where t − 1 is the pervious-day SSL, t − 2 is the previous 2-day SSL, t − 3 is the previous 3-day SLL, t − 4 is the previous 4-day SLL and t − 5 is the previous 5-day SSL.

The principal component analysis

In this study, the principal component analysis (PCA) is used to reduce the dimensionality of input data. The PCA is used to select the appropriate climate data for predicting SSL at the Salian station, Narmab station, Tamar station and Basir Abad station. The PCA converts the given input data into a smaller number of independent variables (Noori et al. 2011). The new set of variables is named principal components (PCs). A set of principals has a number of features, including the following: (1) all PCs are uncorrelated, (2) each PC is a linear integration of input variables and (3) the first PC explains most of the variability in the data (Noori et al. 2011).

$$ Z={a}_{i1}{X}_1+{a}_{i2}{x}_2+\dots +{a}_{ip}{X}_p $$
(18)

where Zi represents PCs, X is the input variable and a is the eigenvector. The dimension of new future space is determined by the eigenvalues. The variance of data along the new feature space is described by the eigenvalues (Noori et al. 2011).

$$ \left|R-\lambda I\right|=0 $$
(19)

where I is the unit matrix, R is the variance-covariance matrix and λ is the eigenvalues.

The sample size of data should be investigated before modellers use the PCA. Kaiser-Meyer-Olkin (KMO) coefficient is computed to investigate the adequacy of sample sizes. The minimum value for KMO should be 0.5. In this study, the value of KMO was 0.85, 0.84, 0.79 and 0.65 for the Salian station, Tamar station, Basir Abad station and Narmab station, respectively (Tayfur et al. 2013).

$$ \mathrm{KMO}=\frac{\sum {\left(\mathrm{correlation}\right)}^2}{\sum {\left(\mathrm{correlation}\right)}^2+\sum {\left(\mathrm{partial}\ \mathrm{correlation}\right)}^2} $$
(20)

The lagged meteorological data of temperature, discharge and rainfall were used for a 1-day-ahead forecast of SSL.

  1. 1.

    Q (t − 1), Q(t − 2) and Q(t − 3) are the previous-day discharge, two-previous-day discharge and three-previous-day discharge, respectively.

  2. 2.

    R(t − 1), R(t − 2) and R(t − 3) are the previous-day rainfall, two-previous-day rainfall and three-previous-day rainfall, respectively.

  3. 3.

    T(t − 1), T(t − 2) and T(t − 3) are the previous-day temperature, two-previous-day temperature and three-previous-day temperature, respectively.

Tables 2, 3, 4 and 5 show the descriptive statistics of the PCs and eigenvectors obtained through the PCA application.

Table 2 Outputs of the PCA model for the selection of the appropriate metrological inputs for the Narmab River station
Full size table
Table 3 Outputs of the PCA model for the selection of the appropriate metrological inputs for the Basir Abad station
Full size table
Table 4 Outputs of the PCA model for the selection of the appropriate metrological inputs for the Salian station
Full size table
Table 5 Outputs of the PCA model for the selection of the appropriate metrological inputs for the Tamar station
Full size table

Narmab station

The cumulative variance proportion (CVP) shows the contribution rate of PCs. The CVP of 0.90 or more than 0.90 is significant (Zhao and Huang 2017). As observed in Table 2, the analysis of first four principal components summed up a contribution rate of 93%. The eigenvectors evaluate the coefficients for the formation of PCs. The coefficients of 0.75 or more than 0.75 have the most effects on the PCs (Zhao and Huang 2017). The results indicated that Q(t − 1), R(t − 1) and T(t − 1) had the most effect on the first four PCs in the Narmab station.

Basir Abad station

As observed in Table 3, the first four principal components summed up a contribution rate of 91%. The results indicated that the Q(t − 1), R(t − 1) and T(t − 1) had the most effect on the first four PCs. Thus, the first four principal components were used as the inputs to the models.

Salian station

As observed in Table 4, the first two PCs summed up a contribution rate of 90%. Thus, they were used as the inputs to the models. The results indicated that the Q(t − 1), R(t − 1) and T(t − 1) had the most effect on the first two PCs.

Tamar station

As observed in Table 5, the first two PCs summed up a contribution rate of 90%. Thus, they were used as inputs to the models. The results indicated that the Q(t − 1), R(t − 1) and T(t − 1) had the most effect on the first two PCs.

Simultaneous parameter and input uncertainty estimation

In this study, an integrated framework was used to quantify the parameter and input uncertainty of the used soft computing models. The parameters of ANN models (bias values and weight connections) can be considered as the source of uncertainty. The input data (temperature, rainfall and discharge) can be considered as another source of uncertainty. Thus, it is necessary to quantify the input and parameter uncertainty simultaneously. A soft computing model can be defined as follows (Mustafa et al. 2018):

$$ \mathrm{SSL}=M\left(I\overline{N},\theta \right)+e $$
(21)

where SSL is the SSL (output) matrix of the model (M), \( I\overline{N} \) is the input matrix of the model, e is the residual error and θ is the model parameter. The error input model is used to quantify the uncertainty of input data (Mustafa et al. 2018)

$$ {IN}_i=\overline{I}{N}_i\times {m}_i $$
(22)

where \( \overline{I}{N}_{ij} \) is the observed input data for the ith day and mi is the respective input multiplier. The multipliers are assumed as additional latent variables (ALVs). The ALVs are computed along with model parameters. In this study, a uniform prior probability distribution was used for each input parameter and model parameter.

The inability of the standalone and hybrid ANN structures is considered as another source of uncertainty. The Bayesian model is widely used to account for the model structural uncertainty. Traditionally, the residual errors in SSL modelling are normally distributed with mean zero and constant standard deviation. Thus, the likelihood equation can be defined as follows (Mustafa et al. 2018):

$$ {\displaystyle \begin{array}{l}L\left(\theta | IN, SS\hat{L}\right)={\prod}_{t=1}^N\frac{1}{\sqrt{2\pi }.\sigma}\exp \left(-\frac{1}{2{\sigma}^2}{\left( ss{\hat{l}}_t-{ssl}_t\right)}^2\right)=\\ {}{\left(\frac{1}{\sqrt{2{\pi \sigma}^2}}\right)}^N\exp \left(-\frac{1}{2{\sigma}^2}\sum \limits_{t=1}^N{\left( ss{\hat{l}}_t-{ssl}_t\right)}^2\right)\end{array}} $$
(23)

where \( SS\hat{L} \) is the measured suspended sediment load, sslt is the estimated suspended sediment load at time t, \( ss{\hat{l}}_t \) is the measured SSL at time t, σ is the standard deviation and N is the total number of time steps. In this article, the differential evolution adaptive metropolis (DREAM) algorithm was used as a sampler to sample the posterior distribution using likelihood function. The DREAM algorithm is known as a multichain Markov Chain Monte Carlo method (Vrugt 2016). The DREAM algorithm is widely used to estimate the uncertainty arising from the input parameter and model parameter (Vrugt 2016; Vrugt et al. 2009). A Markov chain is generated by the DREAM algorithm. This chain is ergodic with the unique stationary distribution. More explanations about the methods are observed in Vrugt (2016).

Bayesian model averaging

To combine predictions from multiple predictive models, the Bayesian model averaging (BMA) should be used (Mustafa et al. 2020).

The uncertainty of each model’s prediction can be considered by the BMA. An average prediction along with an associated prediction distribution is provided by the BMA (Mustafa et al. 2018). The posterior distribution of the BMA predictions can be computed as follows:

$$ {\displaystyle \begin{array}{l}{\mathrm{SSL}}_j=\sum \limits_{k=1}^K{\mu}_k{F}_{jk}+{e}_j\\ {}p\left({\mathrm{SSL}}_j|{F}_{jk}\right)=\sum \limits_{k=1}^kp\left({\mathrm{SSL}}_j|{F}_{jk},{N}_k\right)p\left({N}_k|{F}_{jk}\right)\end{array}} $$
(24)

where SSLj is the weighted average prediction of SSL, Fjk is the point prediction of each model for j (1, 2,…, n observations) and k (1, 2,…), K is the number of models, μk is the weight vector of each model, p(SSLj| Fjk, Nk) is the posterior predictive distortion of SSLj on Fjk under the regarded model Nk and p(Nk| Fjk) is the posterior probability of the respective model Nk. The BMA predictive mean and variance of SSL are conditional to the discrete ensemble of the suggested models.

$$ E\left[{\mathrm{SSL}}_j|{F}_{jk}\right]={E}_N\left[E\left({\mathrm{SSL}}_j\right)|{F}_{jk},N\right]=\sum \limits_{k=1}^KE\left[{\mathrm{SSL}}_j|{F}_{jk},{N}_K\right],p\left({N}_k|{F}_{jk}\right) $$
(25)
$$ {\displaystyle \begin{array}{l}\mathrm{Var}\left[{\mathrm{SSL}}_j|{F}_{jk}\right]={E}_N\left[\mathrm{Var}\left({y}_j|{F}_{j,k},N\right)\right]+\mathrm{Var}\left[E\left({y}_j\right)|{F}_{j,k},N\right]\\ {}=\sum \limits_{k=1}^k\mathrm{Var}\left[{\mathrm{SSL}}_j|{F}_{jk},{N}_k\right]p\left({N}_K|{F}_{jk}\right)+\sum \limits_{k=1}^k{\left(E\left[{\mathrm{SSL}}_j|{F}_{j,k},{N}_k\right]-E\left({\mathrm{SSL}}_j|{F}_{jk}\right)\right)}^2p\left({N}_K|{F}_{jk}\right)\end{array}} $$
(26)

where E(SSLj) ∣ Fjk, N is the expected value of SSL and Var(yj| Fj, k, N) is the variance of SSLj on Fjk under the regarded model Nk.

The BMA can provide the accurate estimations if the widths and standard deviation are accurately estimated. The log-likelihood function is used to estimate the weights and standard deviations.

$$ L\left({\mu}_{\mathrm{BMA}},{\sigma}_{\mathrm{BMA}}|F,\mathrm{SSL}\right)=\sum \limits_{j=1}^n\log \left[\sum \limits_{k=1}^k{\mu}_k\frac{1}{\sqrt{2{\pi \sigma}_k^2}}\exp \left[\frac{-1}{2}\right]{\sigma}_k^{-2}{\left({\mathrm{SSL}}_j-{F}_{kj}\right)}^2\right] $$
(27)

In this study, the fully Bayesian approach using input uncertainty multipliers is integrated with the Bayesian model averaging as follows:

  1. 1-

    A number of predictive models (ANN-ALO, ANN-BA and ANN-PSO) are suggested to estimate the SSL.

  2. 2-

    The uncertainty is computed using model parameters and input data (Mustafa et al. 2020).

  3. 3-

    An error input model is defined using Eq. (6).

  4. 4-

    The hydrologically rational pristine domains are chosen for the input data (Temperature, rainfall, and discharge) and model parameters (weight values and bias connections) (Mustafa et al. 2018).

  5. 5-

    A likelihood function is considered such as section ‘Simultaneous parameter and input uncertainty estimation’ (Eq. (23)).

  6. 6-

    The DREAM algorithm is used to compute input multipliers and model parameters.

  7. 7-

    A pre-determined number of outputs are provided for each model, using the parameter values found from level 2 to 6 (Mustafa et al. 2020).

  8. 8-

    The DREAM algorithm is used to compute the model weights and variances of each ensemble member of as described in section ‘Bayesian model averaging’.

  9. 9-

    The weights for all chosen ensemble members of each predictive model are summed to calculate the model weights.

  10. 10-

    Finally, multimodal forecasts are found by evaluating predictive mean and variance using Eqs. (25) and (26), respectively.

The following indices are used to evaluate the performance of the soft computing models:

$$ \mathrm{MAE}=\frac{1}{N}\sum \limits_{i=1}^N\left|{S}_{i0}-{S}_{ic}\right| $$
(28)
$$ \mathrm{RMSE}=\sqrt{\frac{1}{N}\sum \limits_{i=1}^N{\left(\left({S}_{i0}\right)-\left({S}_{ic}\right)\right)}^2} $$
(29)
$$ \mathrm{NSE}=1-\frac{\sum \limits_{t=1}^N{\left({S}_{i0}-{S}_{ic}\right)}^2}{\sum \limits_{t=1}^N{\left({S}_{ic}-{\overline{S}}_{ic}\right)}^2} $$
(30)
$$ p=\frac{1}{N}\mathrm{count}\left(\mathrm{SSL}|{\mathrm{SSL}}_{\mathrm{L}}\le \mathrm{SSL}\le {\mathrm{SSL}}_{\mathrm{U}}\right)\times 100 $$
(31)
$$ {\displaystyle \begin{array}{l}d=\frac{{\overline{d}}_x}{\sigma_x}\\ {}{\overline{d}}_x=\frac{1}{N}\sum \limits_{l=1}^N\left({\mathrm{SSL}}_{\mathrm{U}}-{\mathrm{SSL}}_{\mathrm{L}}\right)\end{array}} $$
(32)

where RMSE is the root-mean-square error, NSE is the Nash-Sutcliff efficiency, MAE is the mean absolute error, N is the data count, SSLL is the lower value of SSL, SSLU is the upper value of SLL, p is the percentage of observed data bracketed by the 95% prediction uncertainty (95PPU), σx is the standard deviation and d is the average width of confidence interval.

Results and discussion

Sensitivity analysis

The application of the optimization algorithms, into the ANN model, requires the prior adjustment of a suitable set of parameters. As in any optimization algorithm, the BA, ALO and PSO are relatively sensitive to setup parameters. Hence, to get the most out of optimization algorithms, it is necessary to fine-tune the parameters, before applying them to the ANN model. While the objective function value is varied for a parameter of interest, by changing the value of that parameter, the values of other parameters in each algorithm are fixed. For this undertaking, we used RMSE as the objective function. However, depending on problem complexity, the value of the parameter of interest is altered for the running of the algorithm. Table 6 shows the results of sensitivity analysis for the optimization algorithms. It should be noted that the best result of the BA algorithm, i.e. minimum objective function value, occurs at a population size of 100, minimum frequency of 3, maximum frequency of 7, maximum loudness of 0.7 and minimum loudness of 0.3. The outputs of other algorithms are illustrated in Table 6.

Table 6 Sensitivity analysis of the different algorithms
Full size table

Statistical results for soft computing models for the Narmab station

The outputs of the statistical parameters, for studied models in the training level, are provided in Table 7. As portrayed in this table, the periodicity significantly increased the accuracy of each model. For the ANN-ALO model, the NSE increased from 0.86 (for the first input combination) to 0.97 (for the fifth input combination). The RMSE and MAE decreased from 1.62 to 0.812 and from 1.24 to 0.732, respectively. A comparison of the ANN-ALO, ANN-BA and ANN-PSO models revealed the superiority of the ANN-ALO (5) model over the ANN-BA and ANN-PSO models. The ANN-PSO model was also outperformed by the ANN-BA model. According to the results attained, the ANN-ALO (5) model improved the accuracy of the ANN-BA (5) and ANN-PSO (5) models by approximately 18% and 26% for the RMSE, respectively. The results also indicate that the ANN-BA (5) model increased the accuracy of the ANN-PSO (5) model by 9.4% and 8.01% for RMSE and MAE, respectively.

Table 7 Evaluation parameters of studied models in the training and testing levels (Narmab River)
Full size table

The results from investigations on the statistical parameters for models studied in the testing level are provided in Table 7. These results revealed that (a) the periodicity enhanced the accuracy of the hybrid ANN models and (b) the highest RMSE and MAE values were achieved by the ANN-PSO (1) model. From Table 6, it can be surmised that generally, the ANN-ALO (5) models are the most favourable and the ANN-PSO (1) models the least favourable. Figure 10 shows the bar chart for the soft computing models. In terms of the R2 index, the ANN-ALO (5) model, with the values of 0.95 (training level) and 0.92 (testing level), performed better than the other models. It was also observed that the accuracy of the ANN-BA model is superior to that of the ANN-PSO model. It is noteworthy that the highest and lowest values of R2 were attained by the ANN-ALO (5) and ANN-PSO (1) models, respectively.

Fig. 10
figure 10

Coefficient of determination (R2) for all used models for the training and testing stages

Full size image

As mentioned earlier, one of the main aims of this undertaking is to investigate the uncertainty of the different hybrid ANN models, by way of the p and d factors. The lagged input data (lagged SSL values) have the uncertainties due to the error measurements. Thus, it is necessary to perform the uncertainty analysis. The reduction in d parameter and the increase in p parameter resulted in a more favourable uncertainty for all the models. In the case of the ANN-ALO model, p increased from 0.66 (the first input combination) to 0.94 (the fifth input combination). The results indicate that the periodicity significantly improved the accuracy of each model. As can be observed in Fig. 11, the minimum and maximum values of p are 0.66 and 0.94 for ANN-ALO (5) and ANN-PSO (1), respectively, while the maximum and minimum values of d are 0.39 and 0.14 for ANN-ALO (5) and ANN-PSO (1), respectively. A comparison between the ANN-BA and ANN-PSO models revealed that the ANN-BA model has a higher value of p and a lower value of d.

Fig. 11
figure 11

Uncertainty analysis for the proposed SSL models in the Narmab River

Full size image

Evaluation of ANN models using meteorological inputs

Table 8 (training) shows the training results of statistical models using meteorological input data. Comparison of ANN-ALO, ANN-BA and ANN-PSO indicated that the ANN-ALO model was better than the ANN-BA and ANN-PSO models. The ANN-ALO increased the accuracy of ANN-BA and ANN-PSO by approximately 2.4% and 5.4% for RMSE in the Narmab River, respectively. From the MAE point of view, ANN-ALO with the values of 1.14 ton, 1.10 ton, 1.10 ton and 1.06 ton had better accuracy in comparison with the ANN-BA and ANN-PSO in the Narmab River, Tamar, Basir Abad and Salian stations. Table 8 (testing) indicates the testing results using meteorological input data. The results revealed that the ANN-ALO was the optimum model, as verified by a RMSE value of 1.25, MAE of 1.16 ton and NSE of 1.93 in the Narmab River. Among the hybrid ANN models, the hybrid ANN-ALO was seen to have the highest value of NSE in the Narmab River, Tamar, Basir Abad and Salian stations. The results also indicated that the ANN-ALO and ANN-BA had the lowest MAE values in the Narmab River, Tamar, Basir Abad and Salian stations. According to Table 8, the accuracy of the ANN-PSO model with the higher values of RMSE and MAE and lower values of NSE is worse than that of the other models. Figure 12 shows the boxplot of ANN models in different stations. The results indicated that the maximum and minimum shapes of boxplots provided by the ANN-ALO followed the observed values compared to those provided by the ANN-BA and ANN-PSO models. It can be concluded that there is a significant difference between the ANN-PSO with the observed data. Figure 13 indicates the uncertainty results using meteorological inputs. In the case of the ANN-ALO model, the d value decreased from 0.16 (ANN-PSO) to 0.12 (ANN-ALO), from 0.19 (ANN-PSO) to 0.12 (ANN-ALO), from 0.25 (ANN-PSO) to 0.21 (ANN-ALO) and from 0.26 (ANN-PSO) to 0.22 (ANN-ALO) in the Narmab River, Tamar, Basir Abad and Salian stations, respectively. As observed in Fig. 12, the maximum and minimum values of p are 0.91 and 0.89 in the Narmab River. A comparison between the ANN-BA and ANN-PSO models revealed that the ANN-PSO model has a lower value of p and a higher value of d in different stations.

Table 8 Results of models with meteorological data
Full size table
Fig. 12
figure 12figure 12

The boxplots for the a Narmab River, b Basir Abad, c Salian and d Tamar stations

Full size image
Fig. 13
figure 13

The uncertainty results using meteorological inputs

Full size image

Conclusions

The modelling of different SSL input scenarios (including previous sediment values) was performed to investigate the effectiveness of the ANN-ALO model. The outputs were compared with the ANN-PSO and ANN-BA models. The meteorological inputs and lagged SSLs were used as the inputs to the models. First, lagged SSLs were used to estimate the SSL in the Narmab River station. Five input combinations were used to estimate the lagged SSLs in the Narmab River station. The results indicated that the ANN-ALO (5) model improved the accuracy of the ANN-BA (5) and ANN-PSO (5) models by approximately 18% and 26% for the RMSE, respectively. Then, the meteorological inputs were used to estimate SSL in different stations. The principal component analysis was used to select the best input combinations. The ANN-ALO model was the optimum model as verified by a RMSE value of 1.22, 1.12, 1.14 and 1.10 for the training data set in the Narmab River, Tamar, Basir Abad and Salian stations. The results reflected that the ANN-PSO model was the worst model, as verified by the RMSE value of 1.29 (Narmab River), 1.18 (Tamar), 1.19 (Basir Abad) and 1.15 (Salian) for the training data set. The uncertainty results indicated that the ANN-ALO model had the highest p value and the lowest d value in different stations. The findings of the current study indicate that the hybrid ANN models have a high ability for predicting SSL. The next papers can integrate the climate models with the hybrid soft computing models to predict SSL for the future periods under climate change condition. Additionally, the ALO can be used to develop the other soft computing models such as ANFIS and SVM model for predicting SSL.