Introduction

Digital Image Correlation (DIC) and Digital Volume Correlation (DVC) [6, 11, 24] are now widely used in experimental mechanics. These families of methods are intended to measure 2D or 3D displacement fields from digital planar or volume images, respectively. In their initial version, the idea was to search for the best parameters of a given transformation to register small independent subsets of pixels. In the context of experimental mechanics, the use of Finite Elements in the framework of DIC/DVC (FE-DIC/DVC [2, 23]) has been extensively developed during the last decade. Among the many advantages of this technique, the main interest for the present work lies in the fact that it provides a very simple bridge between experiments and simulations, which is very convenient for validation [16] and identification purposes [9, 14, 19] and for performing mechanically regularized measurements.

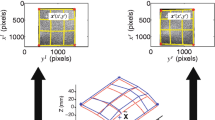
Even in situations where 2D-DIC could be used, Stereo-DIC is preferred for both its accuracy and its simplicity [5, 25]. Classically, the idea of Stereo-DIC is to use one stereoscopic image pair, f 1 and f 2, in a reference configuration at t 0 and a second pair, g 1 and g 2, at t 0 + d t in a deformed configuration, see Fig. 1.

Fig. 1
figure 1

Main steps of a 3D displacement field measurement of a surface with classical Stereo-Digital Image Correlation. Pairings are in green and triangulations in blue

Full size image

The classical Stereo-DIC procedure involves a chain of optimization problems:

Calibration:

1) find ex/in-trinsic parameters from a

 

set of images of calibration grids

Shape

2) find matching field d between

Measurement:

reference images f 1 and f 2

 

3) triangulation: find X at t 0 from x 1 and

 

x 2 = x 1 + d(x 1)

Displacement

4) find matching t between images f 1

Measurement:

and g 1

 

5) find matching t ′ between images f 1

 

and g 2

 

6) triangulation: find X at t 0 + d t from

 

\(\mathbf x_{1}^{\prime }=\mathbf x_{1}+\mathbf t(\mathbf x_{1})\) and \(\mathbf x_{2}^{\prime }=\mathbf x_{1}+\mathbf t^{\prime }(\mathbf x_{1})\)

Eventually, the 3D displacement is estimated by comparing measured shapes: U = X ′−X. The drawback of this classical Stereo-DIC formulation is that the displacement is not the unknown of a single optimization problem as it is the case with 2D-DIC and DVC. In this situation, the bridge between measurement and simulation is less direct. In particular, it is not possible to apply mechanical regularization in this framework.

In contrast to that on DIC and DVC, the literature on FE-Stereo-DIC (or FE-SDIC) is much less prolific - certainly because the extension is not straightforward. The first attempt was proposed in [22], where a theoretical FE mesh was used to provide the displacement measurement solution to one single problem defined in the world coordinate system. In [22], this formulation is not fully exploited since it is not used for calibration and shape measurement. A very similar global stereo formulation based on IsoGeometric Analysis (IGA) was proposed in [1, 3]. It is used not only for the displacement measurement but also for the calibration of a linear camera model and shape measurement.

In the present paper, we develop and give a detailed description of a general framework covering all the aspects of FE-Stereo-DIC. It consists of a formulation in the world coordinate system that makes it possible to calibrate a stereo rig (with possibly non-linear camera models), to measure the actual shape of the specimen and to measure the displacement field, using an FE interpolation. A technique is proposed for building the minimal number of integration points in this context. In addition, it becomes possible to add a regularization based on an FE mechanical model. For instance, the method is illustrated with a measurement of the kinematic fields of a bending plate; in this case, the meaning of kinematic field includes not only displacements but also rotations.

In “Rewriting the Stereo-DIC Problem in the World Coordinate System with Finite Elements” the three problems of calibration, shape measurement and displacement measurement will be rewritten as three optimization problems where the unknowns are the intrinsic/extrinsic parameters, the shape, and the 3D displacement. Then, in “Stereo-DIC and Plate Regularization (R-FE-SDIC)”, it will be shown that, with the proposed framework, it is possible to directly add a constraint of regularity such as a mechanical regularization term. It will also be shown that the use of a plate model in the regularization is likely to provide accurate rotation fields. Finally in Section “Application”, both a synthetic and a real test case will be presented in order to illustrate the efficiency of the method, the effects of the parameters, and the method’s robustness with respect to noise.

Rewriting the Stereo-DIC Problem in the World Coordinate System with Finite Elements

This section contains the three parts of the measurement of a 3D displacement in the reference system R W described by the mesh. With an FE mesh, the theoretical shape does not necessarily correspond to the real one. Therefore, a displacement measurement needs two preliminary steps (Fig. 2).

Fig. 2
figure 2

Steps of the new Stereo-DIC formulation with a Finite-Element mesh (FE-SDIC): (a) first guess of the theoretical CAD mesh plate (black) on the real (a priori unknown) plate (green) before any calibration or shape measurement. (b) Calibration of the extrinsic parameters by DIC (with fixed 3D points X). (c) Shape measurement (with fixed parameters p c ). (d) Temporal measurement of the 3D displacement U (from the black position of the mesh to the red one)

Full size image

Firstly, cameras have to be located in the world coordinate system. This is called the extrinsic parameters calibration but intrinsic parameters can also be optimized according to the mesh used (“Calibration of Extrinsic and Intrinsic Parameters”). Then, the mesh shape has to be corrected: the projections of each point of the mesh in the two cameras (with their projectors P c ) have to be stereo-matched (the corresponding grey-levels must be equal). This is the shape measurement step (Section “Shape measurement with an FE mesh”). A very similar approach has already been published in [1] for a CAD-based shape measurement with NURBS. Finally, the 3D displacement between two steps can be measured (Section “3D displacement measurement”).

Calibration of Extrinsic and Intrinsic Parameters

In this study, since the method is based on a Gauss-Newton algorithm, the calibration has to be initialized with the Stereo Software Vic-3DTM. The calibration consists of finding all parameters p c of each camera’s projector P c :

  • Six extrinsic parameters in order to find the position of the camera’s reference system in R W : three translations and three rotations.

  • Four linear intrinsic parameters in order to project a point from the camera to its image : two focal lengths (f u ,f v ) and two centres of image (c u ,c v ) along the horizontal, u, and vertical, v, directions.

  • At least two non-linear intrinsic parameters : the first order of radial distortion κ and the skew angle.

More details on the non-linear models of cameras can be found in [5, 17]. In this paper, the intrinsic parameters are initialized with Vic-3DTM. The first problem is to find the extrinsic parameters in order to locate the 3D Finite Element mesh (considered rigid) as close as possible to the real surface, which is unknown. In the following, p c denotes the extrinsic parameters of the projector P c associated with the image f c (the intrinsic parameters are fixed). For the sake of simplicity, we first consider a standard stereo bench, i.e. c={1;2}. The parameters p c are assessed by minimizing the following objective functional based on the grey-level conservation assumption:

$$ \mathbf p_{1}^{\star},\mathbf p_{2}^{\star} = \underset{\mathbf p_{1},\mathbf p_{2}}{\arg\min} \; {\int}_{\Omega} \Big[ f_{1}\left( \mathbf P_{1}(\mathbf X,\mathbf p_{1})\right) - f_{2}\left( \mathbf P_{2}(\mathbf X,\mathbf p_{2})\right) \Big]^{2} d\mathbf X $$
(1)

where X stands for a 3D point located on the visible surface, Ω, of the specimen.

As mentioned previously, the quadrature is performed in the 3D domain and one image is not preferred over another (there is no concept of master-slave), each camera being treated symmetrically. This non-linear problem is solved with a Newton algorithm. At iteration k, parameters p=[p 1,p 2]T are sought in the form p k+1 = p k + δ p. After linearization and differentiation, the problem reads:

$$\mathbf M_{ext}^{k} \;\delta\mathbf p = \mathbf b_{ext}^{k} $$
$$\left\{ \begin{array}{ll} M_{ext,ij}^{k} &= {\int}_{\Omega} \left( \frac{\partial \mathbf P_{1}}{\partial p_{i}} \nabla f_{1} - \frac{\partial \mathbf P_{2}}{\partial p_{i}} \nabla f_{2} \right) \left( \frac{\partial \mathbf P_{1}}{\partial p_{j}} \nabla f_{1} - \frac{\partial \mathbf{P}_{2}}{\partial p_{j}} \nabla f_{2} \right)^{T} d\mathbf{X}\\ \mathbf b_{ext,i}^{k} &= - {\int}_{\Omega} \left( \frac{\partial \mathbf P_{1}}{\partial p_{i}} \nabla f_{1} - \frac{\partial \mathbf{P}_{2}}{\partial p_{i}} \nabla f_{2} \right) \left( f_{1}\left( \mathbf{P}_{1}(\mathbf{X},{\mathbf{p}_{1}^{k}})\right) - f_{2}\left( \mathbf{P}_{2}(\mathbf{X},{\mathbf{p}_{2}^{k}})\right) \right) d\mathbf{X} \end{array}\right. $$

where \(\frac {\partial \mathbf P_{c}}{\partial p_{i}}\) are the projectors P c gradient with respect to the extrinsic parameters (even with a non-linear model, an analytical expression is known). ∇f c is image f c gradient at \(\mathbf {P}_{c}(\mathbf {X},{\mathbf {p}_{c}^{k}})\) which depends on p c . This means that the operator \(\mathbf {M}_{ext}^{k}\) has to be re-assembled at each iteration.

For a gradient algorithm, the initial guess should be close to the solution. The first guess can be obtained “by hand” by selecting some points in each image and on the mesh. (It would also be possible to detect at least three particular points with a pattern recognition algorithm.) Then, a small non-linear problem has to be solved. This problem has the same expression as the bundle adjustment (2) [28] but, here, X, x 1, x 2 = x 1 + d(x 1) are fixed and only the extrinsic parameters are sought:

$$ \mathbf p_{1}^{\star},\mathbf p_{2}^{\star} = \underset{\mathbf p_{1},\mathbf p_{2}}{\arg\min} \; \|\mathbf P_{1}(\mathbf X,\mathbf p_{1}) - \mathbf x_{1}\|_{2}^{2} + \|\mathbf{P}_{2}(\mathbf{X},\mathbf{p}_{2}) - \mathbf{x}_{1} - \mathbf d(\mathbf{x}_{1})\|_{2}^{2} $$
(2)

In order to illustrate these steps, Fig. 2(a) shows the first guess of the position of the mesh on the real surface. Figure 2(b) is the situation after the extrinsic calibration (equation (1)). In these two steps, the mesh X is considered fixed in its reference system and the goal is to position this system as close as possible to the unknown surface by finding the rigid translations and rotations.

In ref. [1], some intrinsic parameters of linear camera models are estimated using the same framework (using the speckle pattern of the specimen only). However, the measurement of a least one distance is needed to obtain an absolute estimate of, for instance, the focal length. Here, the model of the camera is more complex (non-linear with distortions) and the initial mesh is flat. Thus, intrinsic parameters cannot be optimized at the same time as the extrinsic ones. The idea would be to release all intrinsic parameters once the extrinsic are optimized. The functional is the same (equation (1)) but with p c containing only intrinsic parameters (c u ,c v ,f u ,f v ,κ,s k e w) (the extrinsic parameters are now fixed). It is possible to iterate these optimizations alternately.

In practice, and in order to be more generic, we decided to calibrate the intrinsic parameters using classic planar calibration targets. This step was achieved using Vic-3DTM. It was verified that these parameters were very close to the local minimum of the above grey-level-based functional.

Shape measurement with an FE mesh

Once all the cameras’ parameters p c are known (and optimized), the shape has to be corrected. Measuring the shape means finding the position X that verifies grey-level conservation. Here, it is verified between the reference images of the two cameras . The method used is the same as for the camera parameters but the unknowns are the 3D positions X:

$$ \mathbf X^{\star} = \underset{\mathbf X}{\arg\min} \, {\int}_{\Omega} \Big[ f_{1}\left( \mathbf P_{1}(\mathbf X,\mathbf p_{1})\right) - f_{2}\left( \mathbf P_{2}(\mathbf X,\mathbf p_{2})\right) \Big]^{2} d\mathbf X $$
(3)

At iteration k, the estimate of the position is written X k+1 = X k + δ X, where the displacement correction δ X is sought in the finite element subspace with \(\delta \mathbf {X} = {\sum }_{i} \mathbf {N}_{i}(\mathbf {X}) q_{i}\):

$$\mathbf M_{shape}^{k} \mathbf{q} = \mathbf b_{shape}^{k} $$
$$\left\{ \begin{array}{ll} \mathbf M_{shape,ij}^{k} &= {\int}_{\Omega} {\mathbf N_{i}^{T}} \left( \nabla \mathbf P_{1} \nabla f_{1} - \nabla \mathbf P_{2} \nabla f_{2} \right) \left( \nabla \mathbf{P}_{1} \nabla f_{1} - \nabla \mathbf{P}_{2} \nabla f_{2} \right)^{T} \mathbf{N}_{j} d\mathbf{X} \\ \mathbf b_{shape,i}^{k} &= {-}{\int}_{\Omega} {\mathbf N_{i}^{T}} \left( \nabla \mathbf P_{1} \nabla f_{1} - \nabla \mathbf P_{2} \nabla f_{2} \right) \left( f_{1}\left( \mathbf P_{1}(\mathbf{X}^{k},\mathbf{p}_{1})\right) - f_{2}\left( \mathbf{P}_{2}(\mathbf{X}^{k},\mathbf{p}_{2})\right) \right) d\mathbf{X} \end{array}\right. $$

where ∇P c are the projectors’ spatial gradients which have an analytical form. As for the calibration, the operator \(\mathbf {M}_{shape}^{k}\) has to be re-assembled at each iteration. After convergence, an estimate of the real shape is obtained (see Fig. 2(c)).

Remarks:

  • Since this is based on a Gauss-Newton algorithm, the algorithm requires an initialization step. Usually, a multigrid initialization with pixel aggregation (coarse graining) is used [18]. However, unlike what is usually done in 2D-DIC, where this step is carried out with a coarse mesh, here the same mesh is used with a decreasing Tikhonov regularization in order to avoid 3D projection of fields from one mesh to another.

  • As noted previously, \(\mathbf M_{shape}^{k}\) has to be re-assembled at each iteration. This induces a significant cost because, here, the reference images of all cameras are compared by pairs. For n cameras, there are \(\frac {n(n-1)}{2}\) pairs of cameras. On the other hand, in [4], a reference object ̂f with an intrinsic texture is created, and all images are compared to ̂f, which is faster when the number of cameras is four or more because only n pairs are considered.

Regularization

As always in DIC, this problem is ill-posed. With the classical approach, there are two unknowns (the components of the left-right disparity field, d, on the image) for only one scalar equation (grey-level conservation). Here, a 3D field is sought, which means that, for the same number of equations, there is one more unknown. In problem (3), the mesh can slide along the surface of the object. There can be global sliding (see Fig. 3(b)) which implies that the dimension of the operator’s kernel is at least 3 (sliding along two surface directions and one rotation). But in the formulation, the problem is even harder because each node can move relatively to another (see Fig. 3(c)) without changing the value of the functional. Thus, a higher degree of regularization has to be added to the functional.

Fig. 3
figure 3

Illustration of the ill-posed problem of shape measurement. (a) Theoretical position of the mesh after calibration and shape measurement. (b) Global or (c) Local sliding during the shape measurement

Full size image

For the local sliding, an isometric constraint can be imposed, like a Tikhonov regularization term:

$$\begin{array}{@{}rcl@{}} \delta\mathbf X^{\star} &=& \underset{\delta\mathbf X}{\arg\min} \; {\int}_{\Omega} \Big[ f_{1}(\mathbf P_{1}(\mathbf X + \delta\mathbf X,\mathbf p_{1}))\\ &&- f_{2}(\mathbf P_{2}(\mathbf X + \delta\mathbf X,\mathbf p_{2})) \Big]^{2} d\mathbf X + \lambda\; \| \delta\mathbf X\|_{\mathbf K}^{2} \end{array} $$

where the norm ∥⋅∥ K can be associated with a mechanical operator K (truss, stiffness or Laplace). One advantage of using SDIC with NURBS [1] is that only a few control points are necessary to describe a surface that indirectly regularizes the problem. So the shape interpolation can be uncoupled from the displacement interpolation, which can be refined without modifying the shape. In FE, this uncoupling is not possible and the same mesh is used for both shape and displacement measurement. Thus, it must be regularized externally.

However, both NURBS and FE approaches are subject to global sliding. The previous regularization does not prevent that problem. These shifts are particularly visible when iterating alternately between the optimization of the camera parameters and the shape measurement.

To avoid these shifts and restore the uniqueness of the problem, it was decided to seek the correction of the nodal displacement along the normal to the surface [13]. The problem then has only one degree of freedom (dof) per node. In practice, the surface normal is estimated at each node (average of the neighbouring element normals) in the initial shape of the mesh.

3D displacement measurement

Once the real shape (thus, the real mesh) is known, it is possible to measure the 3D displacement U between two steps (t 0 and t 0 + d t). Unlike classical Stereo-DIC, the three optimisation problems are turned into a single problem where U is the only unknown. The main idea for this reformulation is to work only in the 3D mesh, chosen to be the world coordinate system R W . All problems are written in this 3D coordinate system and weak-form integrals of the grey-level conservation are also in R W .

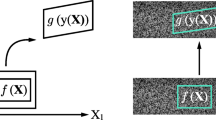
For each 3D point X, the projector P c gives a point x in the image. Obviously, it is also possible to have the projection of the displaced point X ′ = X + U(X) (at t 0 + d t) in the images of the deformed configuration g c (see Fig. 4).

Fig. 4
figure 4

3D displacement measurement in Stereo-DIC with a finite element based method (FE-SDIC)

Full size image

The point X is projected on the reference image f c and X ′ is projected on the image g c . Their grey-levels should be equal for each camera c. Thus, the functional reads:

$$\begin{array}{@{}rcl@{}} \mathbf U^{\star} = \underset{\mathbf U}{\arg\min} \, \sum\limits_{c} {\int}_{\Omega} \Big[ f_{c}\left( \mathbf P_{c}(\mathbf X,\mathbf p_{c})\right)\\ - g_{c}\left( \mathbf P_{c}(\mathbf X + \mathbf U(\mathbf X),\mathbf p_{c})\right) \Big]^{2} d\mathbf X \end{array} $$
(4)

which is just the grey-level conservation equation for each camera. This corresponds to the vertical pairing in Fig. 4. Each term of each camera being independent, it is possible to consider more than two cameras [4]. Such a formulation in the world coordinate system was first introduced in [22]. The benefit is that each camera is used symmetrically. At iteration k, a correction of the 3D displacement field is introduced: \(\mathbf {U}^{k+1} = \mathbf {U}^{k} + {\sum }_{i} \mathbf {N}_{i}(\mathbf {X}) q_{i}\) and the problem reads:

$$\underbrace{\left( \sum\limits_{c} \mathbf{M}_{dic}^{c,k} \right)}_{\mathbf{M}_{stereo}^{k}} \mathbf{q} = \underbrace{\left( \sum\limits_{c} \mathbf{b}_{dic}^{c,k} \right)}_{\mathbf{b}_{stereo}^{k}} $$
$$\begin{array}{@{}rcl@{}} \left\{\begin{array}{lll} \mathbf{M}_{dic,ij}^{c,k} &=& {\int}_{\Omega} \mathbf{N}_{i}^{T} (\nabla \mathbf{P}_{c} \nabla f_{c}) (\nabla \mathbf{P}_{c} \nabla f_{c})^{T} \mathbf{N}_{j} d\mathbf{X}\\ \mathbf{b}_{dic,i}^{c,k} &=& {\int}_{\Omega} \mathbf{N}_{i}^{T} (\nabla \mathbf{P}_{c} \nabla f_{c}) \left( f_{c}(\mathbf{P}_{c}(\mathbf{X},\mathbf{p}_{c}))- g_{c}(\mathbf{P}_{c}(\mathbf{X}+\mathbf{U}^{k},\mathbf{p}_{c})) \right) d\mathbf{X} \end{array}\right. \end{array} $$

Remarks:

  • Both the left and right hand sides are sums of the independent operators on each camera. This implies that this problem can be parallelized as in the domain decomposition method in 2D-DIC [15].

  • Like shape measurement, this algorithm needs an initialization step, such as a multigrid initialization based on pixel aggregation (coarse graining), and a Tikhonov regularization with a Laplacian operator.

  • The correlation operator \(\mathbf M_{stereo}^{k}\) depends on the displacement (because of the gradient of the projectors ∇P c (X + U k)), which means once again that it should be re-assembled at each iteration. In practice, this is not done because the multigrid initialization is close to the actual displacement. Thus, no significant difference is found between the situations with or without re-assembling (except that the former is far more time consuming).

To avoid a time drift of the pairing, it is also possible to introduce an additional term that minimizes the difference of grey-level between the images of the deformed configuration g c at t 0 + d t taken in pairs (this corresponds to a horizontal pairing in Fig. 4):

$$\begin{array}{@{}rcl@{}} \mathbf{U}^{\star} &=& \underset{\mathbf U}{\arg\min} \; \sum\limits_{c} {\int}_{\Omega} \Big[ f_{c}\left( \mathbf P_{c}(\mathbf X),\mathbf p_{c}\right) - g_{c}\left( \mathbf P_{c}(\mathbf X +\! \mathbf U(\mathbf X),\mathbf p_{c})\right) \Big]^{2} d\mathbf X\\ &&+ \sum\limits_{c} \sum\limits_{e< c} {\int}_{\Omega} \Big[ g_{c}\left( \mathbf P_{c}(\mathbf X \,+\, \mathbf U(\mathbf X),\mathbf p_{c})\right) \,-\, g_{e}\left( \mathbf P_{e}(\mathbf X\! \,+\, \mathbf U(\mathbf X),\mathbf p_{e})\right) \Big]^{2} d\mathbf X\\ \end{array} $$
(5)

The pairing at t 0 is already verified with the calibration and the shape measurement. Of course, with this last term, a non-negligible cost is added when more than two cameras are used.

Quadrature

In all the previous equations, quadrature was performed in the 3D world coordinate system and not on the images as with classical DIC. So a dedicated quadrature method had to be set up. In contrast to simulation where a Gauss method is efficient, here, the integrand involves the greyscale gradient, which has a very short variation length. A Riemann integral method was therefore chosen by splitting each finite element homogeneously and homothetically. This choice has been proven to be more accurate [17]. In practice, a smaller number of points can be built with equivalent accuracy. This method considers an inhomogeneous partition of quadrangles and triangles in the isoparametric coordinate system, built by homogeneous partition of the two smallest edges. In Fig. 5, we show that such a technique significantly reduces the number of integration points. According to our tests, with this method, there is rarely more than one integration point per pixel.

Fig. 5
figure 5

Example of a different quadrature rule in the isoparametric coordinate system in order to find as few integration points as possible

Full size image

Remark

In this work, this formulation in the 3D coordinate system is needed in order to add a mechanical regularization term to the Stereo-DIC measurement. However, this is also interesting in 2D-DIC [17] for two reasons:

  • The pixel based quadrature does not integrate a constant function accurately. The area of an element is approximated by an integer number of pixels and depends on the point of view of the camera. Even the shapes of the elements are not accurate because of the linear approximation of the element edges: with distortions the projection of a segment is not necessarily linear. This has little impact on the standard uncertainty of the measurement but can improve the systematic bias by an order of magnitude, even with a simple linear model of the camera.

  • A more complex model of the camera with distortions can be used which drastically decreases measurement uncertainties. This is useful when identifying parameters with a FEMU method based on displacement (FEMU-U). It is also an essential method for crack propagation based on Williams series if it is not possible to use a telecentric lens.

Stereo-DIC and Plate Regularization (R-FE-SDIC)

Once the 3D displacement is the only unknown, it is easier to add a regularization term. The idea is not only to make a measurement, but also to filter it with a mechanical model. This is very important when trying to measure rotation fields accurately.

Furthermore, for a plate or shell model, not only displacements but also rotations at the mid-surface are considered (see Fig. 6). The 3D displacement, U, measured with Stereo-DIC is the displacement of the observed surface, i.e. the top one. Here, we propose a method for measuring the mid-plane unknowns directly.

Fig. 6
figure 6

Representation of a 3D plate or shell of thickness h. The 3D displacement U measured with an optical bench is on the observed surface whereas the plate or shell model considers displacements V and rotations 𝜃 at the mid-surface

Full size image

Plate kinematic regularization

With a plate theory (such as the Mindlin-Reissner theory of plates), a simple linear projector π can be used to determine the displacement of the upper skin depending upon the displacements V and rotations 𝜃 of the mid-surface. By extension and for the sake of simplicity, the vector of unknowns containing displacements and rotations of the mid-surface is denoted by V.

$$\mathbf U = {\Pi} \mathbf V \Leftrightarrow \left[\begin{array}{c} U_{x}\\ U_{y}\\ U_{z} \end{array}\right] = {\Pi} \left[\begin{array}{c} V_{x}\\ V_{y}\\ V_{z}\\ \theta_{x}\\ \theta_{y} \end{array}\right] $$

Then the Stereo-DIC problem can be written:

$$\begin{array}{@{}rcl@{}} \mathbf{V}^{\star} = \underset{\mathbf{V}}{\arg\min} \, &&\frac{1-\lambda_{m}}{\alpha_{v}}{\sum}_{c} {\int}_{\Omega} \Big[ f_{c}\left( \mathbf{P}_{c}(\mathbf{X},\mathbf{p}_{c})\right)\\ &&- g_{c}\left( \mathbf{P}_{c}(\mathbf{X} + {\Pi} \mathbf{V}(\mathbf{X}),\mathbf{p}_{c})\right) \Big]^{2} d\mathbf{X}\\ &&+ \frac{\lambda_{m}}{\alpha_{m}} \|\overline{\mathbf{K}} \mathbf{V}\|^{2}_{2} \end{array} $$
(6)

where the unknowns are not only the displacement of the upper skin, U, but also the five degrees of freedom, V, of the mid-surface. α v and α m are weighting coefficients for vision and stiffness terms. Thus, λ m is a dimensionless coefficient for the mechanical regularization term, set between 0 and 1 (see Section “Regularization coefficients”). Finally, \(\overline {\mathbf {K}}\) is a regularization matrix since, when two unknowns are added per node, a regularization term is needed. Due to the formulation in the world coordinate system, the real 3D displacement is the unknown of the problem. Thus, it is easy to add a mechanical operator (such as K V = F for an elastic deformation) in order to regularize the functional. However, for the present study, it is not possible to obtain the external forces. Thus, the stiffness matrix K is replaced by \(\overline {\mathbf {K}}\), a regularization matrix defined by \(\overline {\mathbf {K}}=P_{k}\mathbf {K}\) with P k a diagonal matrix (7). The latter could be Boolean but, in this study, P k is used to weight some dofs (e.g. to weigh the influence of rotations with respect to the membrane behaviour):

$$ \left\{\begin{array}{lll} P_{k}^{ij}&=& 0 \hspace{20pt} \forall j\neq i\\ P_{k}^{ii}&=& 0 \hspace{20pt} \text{for all \textit{dofs} on the non-free edges}\\ P_{k}^{ii}&=& 0 \hspace{20pt} \text{for the membrane \textit{dofs} related to \(V_{x}\) and \(V_{y}\)}\\ P_{k}^{ii}&=& 1 \hspace{20pt} \text{for the \textit{dofs} related to \(V_{z}\)}\\ P_{k}^{ii}&=& \frac{1}{h^{2}} \hspace{20pt} \text{for the \textit{dofs} related to \(\theta_{x}\) and \(\theta_{y}\) (\textit{h} being the element size)} \end{array}\right. $$
(7)

Thus, \(\overline {\mathbf K}\) is a matrix containing all dofs except those supported by the nodes that are concerned with Dirichlet boundary conditions [20].

At iteration k, the problem reads:

$$\underbrace{\left[\frac{1-\lambda_{m}}{\alpha_{v}}{\Pi}^{T}\mathbf M_{stereo}^{k}\;{\Pi} \,+\, \frac{\lambda_{m}}{\alpha_{m}} \overline{\mathbf K}^{T}\overline{\mathbf K}\right]}_{\mathbf M_{\overline{\mathbf K}}} \delta \mathbf{q} = \frac{1-\lambda_{m}}{\alpha_{v}}{\Pi}^{T}\mathbf b_{stereo}^{k} - \frac{\lambda_{m}}{\alpha_{m}} \overline{\mathbf K}^{T}\overline{\mathbf K}\; \mathbf{q}_{0} $$

Remark

Replacing K by \(\overline {\mathbf K}\) means no regularization on the degrees of freedom of the non-free edges. Thus the behaviour of the nodes of these edges is only towed by the vision term. However, in this study, a plate model is used, which means that the unknowns are 3 displacements and 2 rotations at the mid-plate surface. An additional difficulty arises due to the fact that each dof on the non-free edges implies a singularity in \(\mathbf {M}_{\overline {\mathbf {K}}}\). On the one hand, if these dofs are not taken into account, the problem cannot be solved. On the other hand, if they are removed from \(\mathbf {M}_{\overline {\mathbf {K}}}\) the associated nodes are clamped. Thus, there is a difficulty, which will be solved in “Mechanical and Tikhonov regularization”, especially for the rotations, as the displacement dofs can be considered in \(\mathbf {M}_{stereo}^{k}\) but the rotation dofs cannot.

Mechanical and Tikhonov regularization

To overcome the absence of mechanical regularization on the non-free edges (particularly for rotations of these nodes in question), it is possible to add a Tikhonov regularization term (minimization of a Laplacian term):

$$\begin{array}{@{}rcl@{}} \mathbf V^{\star} = \underset{\mathbf V}{\arg\min}\, &&\frac{1-\lambda_{m}-\lambda_{t}}{\alpha_{v}}{\sum}_{c} {\int}_{\Omega} \Big[ f_{c}\left( \mathbf{P}_{c}(\mathbf{X},\mathbf{p}_{c})\right)\\ &&- g_{c}\left( \mathbf{P}_{c}(\mathbf{X} + {\Pi} \mathbf V(\mathbf{X}),\mathbf{p}_{c})\right) \Big]^{2} d\mathbf{X}\\ &&+ \frac{\lambda_{m}}{\alpha_{m}} \|\overline{\mathbf{K}} \mathbf V\|^{2}_{2} + \frac{\lambda_{t}}{\alpha_{t}} \|{\Delta} \mathbf V\|^{2}_{2} \end{array} $$
(8)

which gives:

$$\begin{array}{@{}rcl@{}} &\left[\frac{1-\lambda_{m}-\lambda_{t}}{\alpha_{v}}{\Pi}^{T}\mathbf M_{stereo}^{k}\;{\Pi} + \frac{\lambda_{m}}{\alpha_{m}} \overline{\mathbf K}^{T}\overline{\mathbf K} + \frac{\lambda_{t}}{\alpha_{t}} \mathbf{T}^{T} \mathbf{T}\right] \delta \mathbf{q}\\ &= \frac{1-\lambda_{m}-\lambda_{t}}{\alpha_{v}}{\Pi}^{T}\mathbf{b}_{stereo}^{k} - \frac{\lambda_{m}}{\alpha_{m}} \overline{\mathbf{K}}^{T}\overline{\mathbf{K}}\; \mathbf{q}_{0} - \frac{\lambda_{t}}{\alpha_{t}} \mathbf{T}^{T} \mathbf{T}\; \mathbf{q}_{0} \end{array} $$

where T is the Tikhonov matrix corresponding to the Laplacian term, α t is a weighting coefficient and λ t is a second dimensionless coefficient for this regularization term, set between 0 and 1 with respect to λ m (see “Regularization coefficients”). In concrete terms, each node excluded from K will be associated with a zero eigenvalue. Adding the Laplacian term amounts to imposing the condition that these nodes adopt a behaviour similar to that of their neighbours.

Remark

The normalization coefficients α v and α m are computed with the initial guess of the displacement U 0. For α t , since any non-zero value would be appropriate, it is set to 1. The coefficients are defined by:

$$\left\{\begin{array}{lll} \alpha_{v} &=& \mathbf{U}^{0^{T}}\mathbf{M}_{stereo}^{k}\mathbf{U}^{0} \\ \alpha_{m} &=& \mathbf{U}^{0^{T}}\overline{\mathbf{K}}^{T}\overline{\mathbf{K}}\mathbf{U}^{0} \\ \alpha_{t} &=& 1 \end{array}\right. $$

Application

Synthetic test case

In order to quantify the measurement error with the regularization method described, the goal here is to create some synthetic images for a plate test case. A pair of real images taken during a test is used (Fig. 8). The plate size is 26.5×26.5 c m 2. Both cameras being calibrated, the two projectors P c are known. On the initial plate, for each camera c, the 3D reference points of the plate X r =(X,Y,0)T are also known. It therefore suffices to determine the displaced points (according to a plate model) corresponding to each reference point to create a new image. According to the small strain and small displacement assumption, each point originally located at position X r =(X,Y,0)T will be moved to the point X d =(X,Y,p(X,Y))T with p a function giving the out-of-plane position of a point according to a chosen plate model. Thus, for all pixel positions x of the new image, two unknowns (X,Y) are sought as the solution to a system of two equations that can be solved with a Newton algorithm (Fig. 7(a)):

$$\mathbf{P}_{c}((X, Y, \mathit{p}(X,Y))^{T})-\mathbf{x}=0 $$
Fig. 7
figure 7

Creation of a synthetic image of a deformed configuration g c with a plate model p. (a) search for the 3D displaced point X d that corresponds to the pixel x according to a plate model p. (b) projection of this displaced point onto the initial shape in order to find the reference 3D point X r . (c) interpolation of the reference image to associate a grey-level with the pixel x of the new image g c

Full size image
Fig. 8
figure 8

Real images of a plate in bending. Reference images of left (a) and right (b) camera used to create synthetic images with a plate model p. The plate size is 26.5×26.5 c m 2

Full size image

Then, it is known that this displaced point was originally located at position X r =(X,Y,0)T (Fig. 7(b)). It is thus possible to create a synthetic image of a deformed configuration by interpolating the grey-level of the reference image f c at the pixel x by projecting the reference 3D point P c (X r ) (Fig. 7(c)).

With this method, a pair of synthetic images is created for a bending plate study (Fig. 8). It is then possible to compute the measurement error by comparing the measure to the prescribed model p.

Influence of the mesh size

The idea here is to calculate the measurement error according to the mean size of the elements of an FE mesh. Both FE-SDIC and R-FE-SDIC (regularized, here with a plate model) are used. Figure 9 presents the standard deviation of the error with both methods when measuring the out-of-plane displacement V z and the rotation 𝜃 y . For the latter, with an FE-SDIC method, only the 3D displacement of the upper skin U is measured and the rotations are calculated using the derivative of the out-of-plane displacement U z = V z .

Fig. 9
figure 9

Standard deviation of the error on the out-of-plane displacement V z (a) and the rotation 𝜃 y (b) for different sizes of mesh. This is computed with both methods: FE-SDIC (red) and R-FE-SDIC regularized measurement using a plate model (blue)

Full size image

It can be seen in Fig. 9(a) that, when the mesh size decreases, the measurement error also decreases due to the “FE error” until a mean element size of approximately 10 m m is reached. Then, because of a lack of pixels in the projected elements, the error increases, which corresponds to the “DIC error”. In contrast, it can be noted, in blue, that thanks to the mechanical regularization, the error does not increase. Figure 9(b) shows that it is possible to measure the rotations directly, regardless of the mean element size. Also, as expected, the derivative of the measured field (in red) is noisier than the measured rotation field (in blue).

Noise robustness

It is also possible to study the behaviour of measurement uncertainties if a different level of noise is added when creating the synthetic images, cf. Fig. 10. For that purpose, we added zero-mean white Gaussian noise with an increasing standard deviation ranging from 1 to 8 grey-levels. The measurement with mechanical regularization is much more robust relative to noise.

Fig. 10
figure 10

Standard deviation of the error on the out-of-plane displacement V z (a) and the rotation 𝜃 y (b) versus the standard deviation of the noise. This was computed with both methods: FE-SDIC (red) and R-FE-SDIC regularized measurement using a plate model (blue)

Full size image

Remarks:

  • In this study, the image noise was estimated to be less than 3 grey-levels (Allied Vision Pike FireWire 5 Megapixels).

  • No filtering algorithm was used in this work. The only regularisation was based on the use of a mechanical operator.

Regularization coefficients

Obviously, the result of such a measurement depends on the parameters λ m and λ t used. They are the cut-off wavelength of low-pass filters [8, 10, 21]. Usually, parameters of this kind are set between 0 and 1 (equation (9)). Thus, the three terms of (8) are normalized with α v , α m and α t .

$$ \left\{ \begin{array}{ccc} 0 \leq & \underbrace{1-\lambda_{m}-\lambda_{t}}_{\lambda_{vision}} & \leq 1\\ 0 \leq & \lambda_{m} & \leq 1\\ 0 \leq & \lambda_{t} & \leq 1 \end{array} \right. $$
(9)

Thus, different values of λ m can be used in order to study the measurement error. Without mechanical regularization, a displacement can be observed but a rotation cannot. Thus, the rotation measurement with a low value of λ m , corresponding to a low mechanical regularization, should not be less accurate than with a larger regularization coefficient. But, as can be seen in Figs. 11(a) and (c), it is hard to find the optimal parameter, especially when looking at the rotation. The simplest way to find it, for such an approach, is to draw an L-curve [7, 12] that represents both DIC and Mechanical residual. The optimal parameter will naturally be at the corner of the L-curve (cf. Fig. 11(e)).

Fig. 11
figure 11

Schemes for studying the influence of λ m (left) and λ t (right). Standard deviation of the error when measuring the out-of-plane displacement V z (a, b) and the rotation 𝜃 y (c, d) for different values of λ m and λ t . This is computed with the R-FE-SDIC measurement regularized with a plate model (blue) and the value corresponding to the FE-SDIC method is plotted (red) for comparison. L-curve (e, f) of both parameters in order to minimize both DIC and Mechanical residual

Full size image

On the other hand, the parameter λ t aims to take account of the degrees of freedom with a Dirichlet condition. At first view, it might seem that setting this parameter to any non-zero value would suffice: λ t ≠ 0. Yet it can be seen in Fig. 11(b), (d) and (f) that this parameter does have an impact on the measurement. In fact, the weight of this coefficient has an influence on the boundary. And since boundary displacement uncertainty has a tendency to spread in the mechanically regularized region, it has an effect on the solution [8].

Real test case

The same measurement is now carried out with real images. As expected, the measurement of the rotation by R-FE-SDIC (FE-Stereo-DIC mechanically regularized with a plate theory) is more accurate than without mechanical regularization, because the latter (FE-Stereo-DIC) is the numerical derivative of a measured field (cf. Fig. 12).

Fig. 12
figure 12

Comparison of the measurement of the displacement V z (a) or the rotation 𝜃 y (b) with different approaches : FE-SDIC (red) or R-FE-SDIC (black)

Full size image

The main advantage of a Stereo method based on the world coordinate system is that it is possible to use a real mesh. In a classical FE-SDIC method, the mesh has to be adapted to the measurement. Here, the goal is to adapt the measurement in order to set up a real dialogue between experiment and simulation. The mesh chosen for a simulation can also be used for a measurement. For example, the mesh can be refined in the centre for a potential defect (cf. Fig. 13). In this figure, the shape measurement is compared to the shape computed by Vic-3DTM. It can be seen that the point cloud resulting from Vic-3DTM is close to the mesh except at the boundary, where the Vic-3DTM shape is not available.

Fig. 13
figure 13

Shape of a large plate measured by SDIC during an actual experiment. A suitable mesh was devised to provide a better resolved FE-SDIC measurement around a potential defect located in the centre of the plate. The FE-SDIC shape measurement (mesh) is compared to a classical SDIC shape measurement (Vic-3DTM: point cloud)

Full size image

With this kind of mesh, even the displacement field computed without regularization would not be correct because of the mesh refinement at the centre (cf. Fig. 14).

Fig. 14
figure 14

Comparison of the out-of-plane displacement fields V z measured by FE-SDIC without regularization (a), or R-FE-SDIC with regularization (b)

Full size image

The quality of these results is verified, by looking at Vic-3DTM measurements of the same images sets. For example, in Fig. 15, the out-of-plane displacement fields V z were measured by Stereo-DIC (Vic-3DTM) with two subset sizes (and associated steps) in order to compare the results with small or large subsets equivalent to the small and large elements of the mesh of Fig. 13.

Fig. 15
figure 15

Comparison of the out-of-plane displacement fields V z measured by Stereo-DIC (Vic-3D) with two subset sizes: (left) a small subset size comparable to the small elements of the mesh of Fig. 13; (right) a large subset size comparable to the large elements of the mesh of Fig. 13

Full size image

It can be noticed that the noise level in the out-of-plane displacement measured by standard DIC code is comparable to the one measured by FE-SDIC without mechanical regularisation. In the center of the mesh where the elements are smaller, the level of noise is comparable to the one when using small subsets size. The same conclusion holds for larger elements and subset size. Thanks to FE-SDIC, it is possible to further regularize the measurement when using mechanical regularisation as shown in Fig. 14.

Conclusion

A full stereovision framework for measuring the 3D shape and displacements using a Finite Element mesh has been developed. The formulation incorporates a grey-level-based calibration step extended to non-linear camera models. It has been shown that, unlike stereovision using NURBS functions [1], the shape measurement is very ill-posed and requires additional regularization. For that purpose we used a type of isometric constraint. Thanks to this formulation in the world coordinate system, the same FE mesh can be shared between both numerical simulation and measurement. It is thus a good tool for performing quantitative comparisons between non-planar experiments and corresponding simulations, which are most often based on Finite Elements [26, 27]. In addition, a technique has been proposed to build the minimal number of integration points in such a context.

As an application, the method was used for the measurement of the displacement and rotation fields of a plate in bending, using a mechanical regularization based on the elastic stiffness operator associated with the FE mesh. In addition, stereo synthetic test cases were developed and analysed in order to exemplify the efficiency of the proposed method.