Introduction

Rapid advances in three-dimensional (3D) imaging and data acquisition have increased the need for accurate full-field displacement measurement techniques of internal deformation fields ranging from inclusion problems to analyzing the 3D motion of mammalian cells interacting with soft biomaterials [1]. Digital volume correlation (DVC), the volumetric extension of the popular surface displacement mapping technique of digital image correlation (DIC) has successfully addressed this need in large parts [2]. Although the mathematical formulation of DVC can be derived using the same fundamental minimization equations used in DIC, direct application of this approach to DVC has suffered from high computational cost and time.

The processing speed of DVC is worsened when higher order terms such as the deformation gradient are considered in the overall motion estimate. Yet ignoring these higher-order terms can have a significant effect on the accuracy of the calculated displacements fields especially when large rotations and stretches are present [3, 4]. In 2011 Gates et al. address these shortcomings by presenting a complete, 12 degree of freedom DVC algorithm derived from the same mathematical principles as DIC. To handle the issue of computational cost the authors utilize high performance parallel computing, producing average run times just under 6 h for 393 voxel correlation grid points with interrogation window sizes of 413 voxels [5].

While these improvements in accuracy and computation times have significantly advanced the maturity and practicality of DVC, there are still key challenges remaining before DVC will be as versatile and robust as DIC. Perhaps one of the most important aspects of a potential wide-spread and user-friendly DVC methodology is close to real-time computation times allowing the analysis of tens to hundreds of time-lapse video frames. This will allow DVC algorithms to produce motion estimates of dynamically evolving 3D displacements within practical time frames similar to DIC [6–8].

Another yet equally important parameter is the maximization of DVC spatial resolution without adversely affecting the computational cost. Generally, DVC measurements are highly dependent on the choice of interrogation window size, which determines the spatial resolution and displacement uncertainty of the generated results [9, 10]. Both of these parameters, namely computational tractability and spatial resolution, are particularly important for applications focused on quantifying cell-material interactions, which typically require analysis of long 3D time-lapse series featuring locally applied non-linear deformation fields [11–15].

We address these two critical technical hurdles by developing a new DVC algorithm capable of capturing any general non-linear finite deformation that is performed on a graphic processing unit (GPU). This new algorithm termed fast iterative DVC, or FIDVC, maximizes the spatial resolution per given deformation field and speckle pattern while providing almost real-time computation times even for large 3D volumes. The main principle behind the proposed algorithm lies in an iterative mapping approach similar to schemes widely used in the particle image velocimetry (PIV) community [16–18]. Similar to our previous DVC algorithm the proposed method is based on the standard cross-correlation formulation with the addition of an iterative image deformation method (IDM). This deformation method is applied to both deformed and undeformed volumetric images, which improves the analysis accuracy. One main advantage of the method is the multi-step interrogation window refinement during the iteration process allowing for the accurate capture of higher spatial frequencies including localized large displacement gradients.

The paper is organized as follows: “Fast Iterative Digital Volume Correlation (FIDVC)” presents the mathematical background and implementation details of the FIDVC technique. “Validation of the FIDVC Algorithm” presents numerical and experimental validation of our FIDVC algorithm based on experimentally generated 3D laser scanning confocal microscopy images. Specifically, the accuracy and computational performance of our FIDVC technique is quantified and compared against our previously published DVC algorithm [4] since both are 3D, FFT-based, and local deformation tracking techniques. “Conclusion” concludes and provides an outlook for potential uses of our algorithm.

Fast Iterative Digital Volume Correlation (FIDVC)

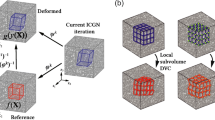
The fast iterative digital volume correlation (FIDVC) method is a fast, non-invasive, 3D full-field measurement technique for determining large-deformation internal displacement fields in soft materials. By utilizing a fast Fourier transform (FFT) based cross-correlation formulation in conjunction with the iterative deformation method (IDM), the FIDVC efficiently computes finite deformation fields generally non-resolvable by our previous DVC algorithm. The flowchart in Fig. 1 illustrates the basic procedure of how the FIDVC calculates the 3D displacement field, u=(u 1,u 2,u 3), between two volumetric images, I(x) and \(\hat {I}(\boldsymbol {x})\), where x=(x 1,x 2,x 3) is the image coordinate system. The first step involves the acquisition of volumetric images of the undeformed, I 0(x) and deformed configuration, \(\hat {I}^{0}(\boldsymbol {x})\) using 3D imaging modalities such as computed tomography (CT), magnetic resonance imaging (MRI) or, for the purpose of this study, laser scanning confocal microscopy (LSCM) [2, 4, 19]. Each image should contain unique intensity variations, or speckle patterns, in order to allow for accurate motion estimation [20]. In LSCM, these intensity distributions are in the form of micron-sized fluorescent particles that are randomly dispersed throughout the imaging medium [4]. The precision and resolution ultimately depends on this intensity information, including the particle density, size, and distribution.

Fig. 1
figure 1

Flowchart showing the FIDVC method. The final displacement, u is equal to the last iteration of the calculated displacement field, u k

Full size image

Calculating Displacements ( u k)

Once the set of volumetric images I 0(x) and \(\hat {I}^{0}(\boldsymbol {x})\) are obtained, each volume is subdivided into interrogation windows of specified overlap ratios, i.e., subset spacing. These two factors determine the final resolution of the DVC displacement field, and can be adjusted during each iteration to provide resolution refinement to increase the overall displacement field resolution. During each iteration the incremental displacements, du=(d u 1,d u 2,d u 3), of corresponding windows in the undeformed and deformed images are estimated using the general cross-correlation relation

$$ I^{k-1}(\boldsymbol{x})\otimes\hat{I}^{k-1}(\boldsymbol{x})\rightarrow\boldsymbol{du}, $$
(1)

with k being the integer iteration counter starting at one until convergence. Equation (1) can be rewritten in terms of the cross-correlation coefficient, C, as

$$ C(\boldsymbol{du})=\sum_{\boldsymbol{x}=-L/2}^{L/2}f(\boldsymbol{x}){\cdot}\hat{f}(\boldsymbol{x} + \boldsymbol{du}). $$
(2)

Here, f(x) and \(\hat {f}(\boldsymbol {x})\) are the gray level intensity values of the undeformed and deformed interrogation windows.

Sub-voxel resolution can be achieved by fitting the 33 voxel cross-correlation peak to a Gaussian polynomial to yield a more accurate estimate of the true sub-voxel peak location. While the literature has produced a wealth of various sub-voxel algorithms [21–23], we have previously demonstrated that a 3rd order polynomial Gaussian peak fitting scheme provides both good accuracy and time efficiency [4].

Due to the intrinsic averaging process in the cross-correlation formulation some of its high-frequency content is inevitably lost, which can be related to the Nyquist criterion [13, 24]. Consequently the minimum wavelength that can be resolved is only greater than twice the mean distance between markers within an interrogation window [25]. Therefore, the modular transfer function (MTF) of the classical cross-correlation approach shown in equation (2) is approximated by the frequency response of a moving average filter [26]. In the case of a 3D moving average filter, the MTF is given by:

$$ \textit{MTF}(\boldsymbol{\lambda}) = \prod\limits_{i=1}^{3} \frac{\sin(\pi L/ \lambda_{i})}{\pi L/ \lambda_{i}} $$
(3)

where L is the side length of the interrogation window, and λ = (λ 1,λ 2,λ 3) are the wavelengths under study along the x = (x 1, x 2, x 3) directions, respectively. It is evident that when λ=L/n, n being a positive integer, the MTF = 0 and thus the frequency response is unstable; the moving average produces irreversible loss of information. Motivated by this, an appropriate choice of a window weighting function can be used to flatten the frequency response of a moving average. While there are many choices of weighting functions that stabilize the frequency information, we choose to adopt the robust and straightforward formulation by Nogueira et al. [27] given by

$$\begin{array}{@{}rcl@{}} w(\boldsymbol{x})& = &\prod\limits_{i=1}^{3} \Bigg(12\left|\frac{x_{i}}{L}\right|^{2}-12\left|\frac{x_{i}}{L}\right|+3 \notag\\ && +0.15\cos(4\pi x_{i}/L) + 0.2\cos(6\pi x_{i}/L)\notag\\ && +0.1\cos(8\pi x_{i}/L) + 0.05\cos(10\pi x_{i}/L)\Bigg)^{1/2} . \end{array} $$
(4)

By incorporating this particular weighting function into the FIDVC process, the cross-correlation coefficient shown in equation (2) becomes

$$ C(\boldsymbol{du}) = \sum_{\boldsymbol{x}=-L/2}^{L/2} w(\boldsymbol{x})f(\boldsymbol{x}) \cdot w(\boldsymbol{x}+\boldsymbol{du})\hat{f}(\boldsymbol{x}+\boldsymbol{du}) $$
(5)

in which f(x) and \(\hat {f}(\boldsymbol {x})\) are gray level intensity values of the undeformed and deformed interrogation windows respectively, and w(x) is the window weighting function given by equation (4). In the case for our FIDVC, equation (5) is implemented in Fourier space as

$$ C(\boldsymbol{du}) = \mathcal{F}^{-1}\{\mathcal{F}\{w(\boldsymbol{x})f(\boldsymbol{x})\}^{*} \cdot \mathcal{F}\{w(\boldsymbol{x}+\boldsymbol{du})\hat{f}(\boldsymbol{x}+\boldsymbol{du})\}\}. $$
(6)

As before, the integer-voxel displacements are obtained by finding the location of the global maximum of C. Although the use of the weighting function does not completely eliminate the low-pass behavior of the cross correlation process it significantly improves the reconstruction of the high frequency displacement information per interrogation window.

The Iterative Digital Volume Correlation Method

In order to account for large material deformations but yet remain computationally efficient, the deformation field between images I(x) and \(\hat {I}(\boldsymbol {x})\) is linearized into k-increments for which the cross-correlation algorithm is well suited. As previously mentioned, such an experimental approach has been well documented for particle image velocimetry (PIV) measurements, and is known as the image deformation method (IDM) [28, 29]. Here we extend the IDM method to measure material displacements in three dimensions. Figure 2 illustrates the working principle of the IDM of our FIDVC algorithm.

Fig. 2
figure 2

Schematic showing the IDM. The undeformed and deformed images are symmetrically warped by the linearized, incremental displacement field until they reach the same final configuration

Full size image

In Fig. 2, it shows that the original images I 0(x) and \(\hat {I}^{0}(\boldsymbol {x})\) are symmetrically warped by the displacement field of the current iteration, u k, which is equal to the sum of all the previous displacement increments, i.e.,

$$ \boldsymbol{u}^{k} =\sum_{k} \boldsymbol{u}^{k-1} +\boldsymbol{du}. $$
(7)

The warping of the two images, i.e.,

$$ \begin{array}{l} I^{k}(\boldsymbol{x})=I^{0}(\boldsymbol{x} - \boldsymbol{u}^{k}/2) \\ \hat{I}^{k}(\boldsymbol{x})=\hat{I}^{0}(\boldsymbol{x} + \boldsymbol{u}^{k}/2) \end{array} $$
(8)

is implemented using a trilinear interpolation scheme. We purposefully choose a symmetric image warping and trilinear interpolation to achieve the second order accuracy at reasonable computational costs [30, 31]. It should be noted that for the iterative algorithms, higher order interpolation schemes can be implemented at the expense of increased computational cost [5, 32]. Although not presented in this work, GPU based interpolation can help to decrease computation times [33].

The iterative process in the IDM is intrinsically unstable and unless proper steps are taken, the results may diverge [26, 32, 34]. Furthermore, in multi-frequency displacement fields, the larger spatial wavelengths ( λ>L) tend to diverge later in the iterative process while the smaller spatial wavelengths are still converging. For this reason employing a spatial filter during the iterative process serves as a suitable option to deal with these undesired results. A class of linear low-pass convolution filters have been introduced by Schrijer et al. that are computationally efficient and have the ability to change strength depending on a single input parameter [34]. The one-dimensional formulation of the filter is described by the following equation:

$$ p(\xi)=\left(\frac{L}{2}\right)^{z} - \left|\xi\right|^{z} $$
(9)

where the kernel window length given by L is equal to the interrogation window side length. The parameter z controls the strength of the low-pass filter. No filtering occurs when z → 0 since the filter approximates a Dirac delta function and as z → ∞ the filter becomes a top-hat filter. The filter strength therefore increases with z and provides higher instability damping at the expense of lower spatial resolution. Performing numerical and experimental assessments of different filter strengths show optimal dampening and modulation characteristics over the range of 10−3 ≤ z ≤ 10−2 [34].

However, the results vary depending on when the filter is applied during the iterative process. For example, the filter can have an indirect influence on the displacement field if it acts on the incremental displacement field, i.e., p∗du. It is chosen that the filter acts on the current displacement field, u k given by

$$ \boldsymbol{u}^{k} = p\ast(\boldsymbol{u}^{k-1} + \boldsymbol{du}), $$
(10)

thus affecting the FIDVC results directly.

In addition to implementing a displacement damping filter prior application of the IDM, any non-physical displacements are also removed by means of a universal median test. This assists in producing smoother gradient fields by ensuring that spurious displacement values are removed. In general, DVC measurements are sensitive to noise in the recorded volumetric images and to the choice of interrogation window size. There is an optimal trade-off between the interrogation window size, the number of spurious displacements and spatial resolution present in the DVC results. For this reason, the results for every iteration are analyzed by the universal median test [35]. In this test, the median value u m of a 33 voxel neighborhood surrounding a displacement value u 0 is calculated. Using the median value, a residual defined by r=|u 0−u m | is determined for each displacement value of the surrounding neighborhood, [u 1,...,u 26]. The median residual, r m of [r 1,...,r 26] is then used to normalize the residual,

$$ \boldsymbol{r}'=\frac{|\boldsymbol{u}_{0}-\boldsymbol{u}_{m}|}{\boldsymbol{r}_{m}+\epsilon} $$
(11)

where 𝜖 represent the typical fluctuation level of the cross-correlation. This procedure is repeated for every displacement vector and any residual greater than a chosen level is removed.

The final step in the FIDVC process is to check whether the displacement values, u k have converged. Having a well defined stopping criterion is important to provide proper balance between accuracy and computation times in the FIDVC algorithm. For example, stopping the algorithm prematurely will produce under-predicted displacement fields, while over iterating will be time consuming without a significant gain in displacement accuracy. Hence the most natural stopping criterion is at a point in which the images have fully-matching intensity profiles. The image similarity metric of choice is the normalized sum of squared error at the current iteration, e k, given by

$$ e^{k} = \frac{1}{\overline{\sigma}}\sqrt{ \frac{1}{N} \sum\limits_{\boldsymbol{x}=1}^{N} \left(I^{k}(\boldsymbol{x}) - \hat{I}^{k}(\boldsymbol{x})\right)^{2} }. $$
(12)

Here N is the number of voxels, and \(\overline {\sigma }\) is the mean standard deviation of the undeformed and deformed images, I k(x) and \(\hat {I}^{k}(\boldsymbol {x})\).

After each iteration, the difference in the error between the current and previous iteration is calculated and used as an interrogation window size refinement or stopping criterion. To illustrate how the convergence of the FIDVC works, consider the following example run flowchart in Fig. 3. In the first step, the displacement field of the current iteration, k is calculated from equation (5) and the images are warped according to equation (8). The normalized sum of squared error is calculated for the current iteration, e k and is used to calculate the error difference between the current and previous iteration, i.e., Δe=e k−e k−1. If Δe k/Δe 0 is less than or equal to the user defined stopping threshold 𝜖 0 than the FIDVC is stopped and said to have converged. If this condition is not met, we test against the interrogation window refinement criterion; if Δe k/Δe j is less than or equal to 𝜖 1 the interrogation window length, L is reduced by half and the loop continues. The subscript j is a simple counter denoting the last time point at which the interrogation window size is changed.

Fig. 3
figure 3

Run flow chart showing the convergence scheme of the FIDVC

Full size image

3D Displacement Gradient Calculations

In addition to displacement measurements, correlation techniques in 2D or 3D serve as a powerful tool to measure strains in many research fields; e.g. investigations of cell traction force microscopy [1, 15, 36], biological tissues characterization [37], material fracture [38, 39], and full-field soft matter characterization [40]. All of these examples rely on accurate measurements of the 3D internal material strains. Care must be exercised when differentiating the displacement field in the presence of noise and large displacement gradients. Based on the work of Farid et al. [41], we implement several suitable filters that mitigate sampling aliasing errors. Specifically, we formulate the optimal differentiation and interpolation kernel solution as a minimization problem with the constraints that the filters are linear, separable, and rotationally-invariant. In Fourier space, this set of constraints allows reformulating the problem as a 1D minimization procedure making it fast to calculate large filters with kernel lengths of nine or more points. The matching pair of filters that make up the gradient operator are called optimal n-tap, where n denotes the length of the filter kernel. Precaution has to be taken when choosing an appropriate filter length: while larger n values reduce errors due to noise, they provide excessive smoothening of the recorded displacements resulting in a poorer gradient estimate. More sophisticated noise mitigation models can be implemented, which are beyond the scope of this work [42].

Validation of the FIDVC Algorithm

This section presents the quantitative validation of our FIDVC methodology detailing the spatial resolution limits and average processing times. The validation examples presented here are primarily based on simulated deformation fields. To mimic experimental conditions, all of our simulated images are corrupted with experimental noise determined from actual laser scanning confocal microscopy (LSCM) images. The choice in numerical rather than experimental validation allows us to generate analytically exact, non-linear localized material deformations to assess the FIDVC spatial resolution limits quantitatively.

Generation of Simulated Volumetric Images and Displacement Fields

Figure 4 shows three representative volumetric images that were used in the validation of the FIDVC algorithm.

Fig. 4
figure 4

Slices of three volumetric images used for FIDVC validation. (a) The first image displays an actual experimental image of a transparent polyacrylamide gel embedded with 0.5 micron-sized fluorescent spheres recorded via LSCM. (b) The second image shows a numerically simulated image based on the image properties of (a) without noise. (c) The third image is the numerically simulated image (b) with added Gaussian noise

Full size image

The optical system’s point spread function (PSF) is determined by least-squares fitting of a 3D Gaussian profile to the intensity values of 1000 randomly sampled micron-sized fluorescent particles within the image [43]. The PSF with amplitude A and standard deviation, σ = (σ 1,σ 2,σ 3) is expressed as

$$ \textit{PSF}(\boldsymbol{x}) = A \exp \left( -\sum\limits_{i=1}^{3}\frac{{x_{i}^{2}}}{2 {\sigma_{i}^{2}}} \right). $$
(13)

The following fitting parameters σ = (5, 5, 10), and ρ = 0.004 markers per voxel are determined from the experimental data and used for the generation of all subsequent synthetic images. Next, a 12-bit grayscale undeformed image I 0(x) is digitally generated by superimposing the intensities of multiple PSFs at random integer locations throughout the image shown in Fig. 4(b). This superposition of intensities is given by

$$ I(\boldsymbol{x}) = \sum\limits_{n=1}^{N} \textit{PSF}(\boldsymbol{x}-\boldsymbol{x}^{n}) $$
(14)

where \(\boldsymbol {x}^{n}=\left ({x_{1}^{n}},{x_{2}^{n}},{x_{3}^{n}}\right )\) is the center location of the nth micron-sized fluorescent sphere. The total number of beads, N, is calculated by multiplying the marker seeding density, ρ, with the number of voxels in the image, V, i.e., N = ρV. Any image intensity greater than the maximum 12-bit gray scale level, is saturated to simulate true LSCM images. The same procedure is utilized to digitally generate the deformed image, \(\hat {I}(\boldsymbol {x})\), except each marker location, x n is translated to its new location, \(\boldsymbol {X^{n}}=\left ({X_{1}^{n}},{X_{2}^{n}},{X_{3}^{n}}\right )\) by the prescribed displacement field, u n, i.e.,

$$ \boldsymbol{X}^{n} = \boldsymbol{x}^{n} + \boldsymbol{u}^{n}. $$
(15)

Following our typical experimental approach [4], all simulated volumetric images are deconvolved using the Lucy-Richardson deconvolution algorithm prior to calculating the displacement field using FIDVC [44].

To rigorously characterize and quantify the spatial resolution of our new FIDVC technique a superposition of Gaussian displacement functions is applied to a set of volumetric images given by

$$ g(\boldsymbol{x}) = \sum\limits_{j} A^{j} \exp \left( -\sum\limits_{i=1}^{3}\frac{(x_{i} - c^{j})^{2}}{2 \left({\sigma^{j}_{i}}\right)^{2}} \right) $$
(16)

where

  1. 1.

    The number of Gaussian functions, j is chosen by the user.

  2. 2.

    The Gaussian width is defined as two times the full width at half maximum (FWHM) of the standard deviation, i.e. \(w = 4\sqrt {2\ln {2}}\ \sigma \), and is equal in all directions.

  3. 3.

    The amplitude, A, is chosen such that the applied material deformation field falls into the finite deformation regime. The analytical Lagrangian strain is computed from the deformation field given in equation (16). The amplitude, A, is adjusted such that the maximum value of any strain component equals 15 %, thus ensuring finite deformations.

  4. 4.

    The center position of the peak, c for each Gaussian displacement field is chosen not to overlap with any neighboring functions.

First, this approach allows simultaneous application of several well defined spatial deformation wavelengths to assess the FIDVC resolution limits. Second, it provides an analytical benchmark for a quantitative assessment of various finite difference schemes in estimating the Lagrangian strains. Physical examples of such displacement fields can be found in many cell-induced material deformations [11–14].

The FIDVC algorithm is written in MATLAB (MathWorks, Natick, MA) and executed on a custom built PC with an Intel i7-3820 CPU at 3.6 GHz, 8GB RAM memory, and Nvidia GTX 690 GPU. To significantly reduce computation times, equation (6) is executed on the PC’s GPU using the commercially available AccelerEyes Jacket library (AccelerEyes, Atlanta, GA).

FIDVC Convergence

Since the FIDVC algorithm is an iterative technique, the convergence behavior of the algorithm needs to be carefully characterized. A simulated image of size 512 × 512 × 256 voxels is deformed according to a displacement field given by a superposition of four Gaussian functions of widths 32, 64, 96, and 128 voxels (Fig. 5(a)). The total error, e between the undeformed and deformed images given by equation (12) is used as the convergence metric detailed in “The Iterative Digital Volume Correlation Method”. Figure 5(b) shows the error per iteration along with the corresponding x 1−x 2 contour maps of the calculated displacement field magnitude |u| in iterations 2, 4, and 6. The corresponding interrogation window lengths for the iterations shown in Fig. 5 are 64, 32, and 32 voxels with a window overlap of 50 %, 50 %, and 75 % respectively. The displacement contours inset at iteration 2 depicts the typically recovered displacement field using our previous DVC method [4]. Qualitative comparison with the prescribed solution clearly shows that most of the higher frequency content is not properly captured. By utilizing more iterations and smaller interrogation window sizes, the FIDVC successfully captures the higher spatial frequencies and converges towards the prescribed displacement field.

Fig. 5
figure 5

(a) Prescribed displacement field, |u|. (b) Normalized residual error, e calculated according to equation (12). The contour maps represent an x 1−x 2 cross-section of the displacement field magnitude, \(\boldsymbol {\left |u\right |}\) for iterations 2, 4, and 6

Full size image

Spatial Resolution of the FIDVC Technique

To quantify the spatial improvements of the FIDVC over our previous DVC technique and to investigate the spatial limitations of both algorithms we apply the following deformation field: an image of size of 384 × 256 × 256 voxels is deformed by a superposition of three Gaussian displacement functions of widths 32, 64, and 128 voxels. Figure 6(a) shows a contour map of the prescribed displacement magnitude, |u| along the x 1−x 2 plane.

Fig. 6
figure 6

(a) Analytical Gaussian displacement field used to compare the FIDVC and DVC algorithm’s spatial resolution. The widths of the Gaussian functions are, from left-to-right, 32, 64, and 128 voxels. (b) A line plot across the dotted line in (a) compares the results of the DVC and FIDVC algorithm to the prescribed analytical displacement field

Full size image

The undeformed and deformed images are processed using the FIDVC algorithm with an initial interrogation window size of 64 voxels and window overlap of 50 %. The universal outlier removal filter is performed with a threshold of 2 and a fluctuation level of 0.1 based on the previously published displacement standard deviation values [4, 35, 40]. The polynomial degree of the predictor filter, z is chosen to be 7.5 × 10−3 and the convergence threshold for the interrogation window refinement is 𝜖 1 = 0.25. The stopping threshold is set to 𝜖 0 = 0.0625 based on empirical evidence of the various validation cases.

For all numerical experiments performed using our previous DVC algorithm, the interrogation window size and window overlap is fixed at its value of 643 voxels with a 87.5 % window overlap. The final spatial resolution for both the FIDVC and previous DVC algorithms results in an equal grid spacing of 8 voxels, and 49 × 49 × 33 correlation points. The corresponding line-profiles comparing the DVC, FIDVC, and prescribed analytical displacements are shown in Fig. 6(b).

For low spatial frequencies both algorithms capture the extent of the applied deformations accurately. However, the DVC algorithm underpredicts the amplitude of the imposed displacements. For high spatial frequencies the original DVC algorithm is unable to accurately predict the correct peak amplitude, and shows an approximately 80 % difference compared to the prescribed solution at the spatial frequency of 32 voxels. This effect stems from the intrinsic low-pass smoothing behavior of the cross-correlation formulation, in which case the DVC algorithm can be regarded as a moving-average operation [18, 26, 45]. In contrast, the FIDVC algorithm successfully captures most of the applied deformations even at subsets of 32 voxels.

To quantify the resolution limits and errors associated with each algorithm more rigorously, we vary the width of a single applied displacement function incrementally from 16 to 160 voxels. An undeformed image of size 2563 voxels is numerically deformed and processed through both FIDVC and DVC algorithms. To quantify the error between the numerically calculated and analytically prescribed displacements, the normalized residual error for the displacement magnitude, e calculated by equation (12) for each width is shown in Fig. 7. The corresponding normalized error values and DVC/FIDVC error ratios are summarized in Table 1. For both algorithms, the normalized residual error between the prescribed and numerically calculated displacement fields is worst for small signal widths and best for large signal widths as expected. The error from the DVC algorithm is a factor of 3 to 21 larger when compared to the FIDVC, resulting in a poorer overall displacement estimate. This result is not surprising since the regular DVC algorithm does not account for the higher order terms in its estimate of the displacement field.

Fig. 7
figure 7

Comparison of the spatial resolution between the FIDVC and DVC algorithms. Plot of the normalized residual error associated with the prescribed Gaussian displacement fields. (Inset) Contour plot of the prescribed Gaussian displacement field with a signal width of 128 voxels

Full size image
Table 1 Normalized residual error corresponding to the prescribed Gaussian displacement field of different signal widths for the FIDVC and DVC algorithms
Full size table

It is also noted that the FIDVC is capable of detecting spatial widths below the smallest interrogation window size of 32 voxels. This is possible due to the use of the MTF weighting function given by equation (4) as well as the refinement of interrogation windows. With an increase in fiducial marker seeding density, it is possible to decrease the smallest interrogation window size to 16 voxels thereby further improving the spatial detection capability of the FIDVC algorithm (see Supplemental Information).

Determination of the FIDVC Measurement Precision and Accuracy

To determine the measurement precision of the FIDVC algorithm, a zero-strain deformation is experimentally acquired using LSCM. In this experiment, a polyacrylamide hydrogel embedded with 0.5 micron-sized flourescent particles is rigidly translated by 4.4 voxels along the x 1 direction. Images before and after translation are processed through the FIDVC to calculate the displacement field. The distribution along with the mean and standard deviation values are summarized in the histogram shown in Fig. 8. The mean and standard deviation of the corresponding Lagrangian strain field is computed using an optimal-11 tap gradient kernel and is summarized in Table 2.

Fig. 8
figure 8

Histograms of the displacement field corresponding to an experimentally applied rigid translation of 4.4 voxels along the x 1 direction. (a) u 1, (b) u 2, (c) u 3

Full size image
Table 2 Mean and standard deviation values corresponding to the experimental zero-strain deformation
Full size table

The values of the standard deviation of the displacements are an order of magnitude smaller than those previously reported [4, 40]. This large increase in precision is likely due to the universal outlier removal process that is performed during each iteration. The axial precision of the displacements and strains in the x 3 direction is approximately 3–4 times lower than the transverse precision in the x 1, x 2 directions, caused by an axially elongated PSF seen in Fig. 4. The values of all strain components are close to zero and smaller than their corresponding standard deviation values confirming a zero-strain deformation.

Calculating Displacement Gradients

It is important to assess the performance of different differentiation schemes used to calculate the displacement field gradient in the presence of noise. In this numerical experiment, the previous four-pole Gaussian displacement field with widths 32, 64, 96, and 128 voxels is corrupted with Gaussian white noise corresponding to varying signal-to-noise ratios (SNR). The choice of adding Gaussian white noise is motivated by the normal distributions in the displacement noise shown in Fig. 8. This allows quantification of the performance of various finite difference schemes as a function of SNR. For each displacement field, the gradient is calculated with a Prewitt [46], Sobel [47], optimal-5 tap, and optimal-11 differentiation kernel and compared to the analytically calculated displacement field gradient. Figure 9 shows the root-mean-square error, e r m s value calculated between the finite difference schemes and the prescribed analytical displacement gradient magnitude, |∇u| for SNR levels ranging from 1 to 100.

Fig. 9
figure 9

Root-mean-square error, e r m s between the FD kernels (a)–(d) and the prescribed analytical displacement gradient magnitude, \(\left |\nabla \boldsymbol {u}\right |\) for SNR levels ranging from 1 to 100. The inset shows the (a) Prewitt, (b) Sobel, (c) Optimal-5 tap, (d) Optimal-11 tap FD kernels

Full size image

Out of the four kernels, the optimal-11 tap shows the best performance in handling noise and recovering the correct displacement gradient. To visualize how the RMS error affects the displacement gradient, Fig. 10 shows a contour map of the displacement gradient magnitude, |∇u| along the x 1−x 2 plane for the four differentiation kernels with a SNR of 5.

Fig. 10
figure 10

Comparison of various finite difference schemes applied to a prescribed four-pole Gaussian displacement field with SNR of five. (a) The corresponding analytical gradient magnitude and comparison with the (b) Prewitt, (c) Sobel, (d) optimal-5 tap, (e) optimal-11 tap differentiation kernels

Full size image

The Prewitt and Sobel kernels show the most fluctuations in the calculated displacement gradient and thus are the most unreliable predictors of the correct strain field at low SNRs. On the other hand, the optimal-11 tap kernel shows the best performance in recovering the displacement gradient while retaining higher spatial frequencies.

Spherical Inclusion Problem

We demonstrate the full capability of the FIDVC algorithm by measuring a ubiquitous non-uniform 3D deformation, the classical solution of a spherical inclusion in an infinite linear elastic solid subjected to a remote stress along the x 3 direction [48]. In the presence of the inclusion under stress, the material both deforms non-uniformly around the cavity perimeter and homogeneously due to compression. To perform the numerical experiment, the analytical displacement field of an inclusion of radius a = 48 pixels under a remote stress of \(\hat {\sigma }_{\infty }=\frac {\sigma _{\infty }}{E} = 0.04\) is applied to a 2563 voxel undeformed image. The generated undeformed and deformed images are processed through the FIDVC algorithm, and the calculated full-field deformation fields are compared against the prescribed analytical solution. Figure 11(a)–(b) compares the displacement magnitudes, |u| of the calculated FIDVC results to the prescribed inclusion solution along the x 2−x 3 inclusion center plane. The corresponding contour map of the deformation gradient’s first invariant, t r(F) is shown in Fig. 11(c)–(d). For visualization purposes, the spherical inclusion is shown in black and the region around the cavity is cropped to 1283 voxels to better visualize the high gradients close to the inclusion. Qualitative comparison of the contour maps of the displacement fields between the FIDVC computed results and the prescribed solution show excellent agreement in both the spatial distribution and magnitude of the color contour levels. When examining the first invariant, there is some deviation between the analytical solution and the FIDVC results due to slight numerical error associated with the FIDVC method.

Fig. 11
figure 11

x 2−x 3 slice comparing the (a) prescribed displacement field magnitude, \(\left |\boldsymbol {u}\right |\) near a spherical inclusion under uniaxial compression with the (b) FIDVC results. The corresponding (c) analytical and (d) FIDVC calculation of the deformation gradient’s first invariant, t r(F)

Full size image

Efficiency

The computational cost of DVC computations is expected to be significantly higher than that of regular 2D DIC due to the cubic interrogation window size. Consider two similar calculations, one with a DIC displacement grid of m 2 points with a square interrogation window size of L 2 pixels, and one with a DVC displacement grid of m 3 points with a cubic interrogation window size of L 3 voxels. The computational cost of the DVC calculations will be m × L times greater than that for the DIC. The computational cost will be even higher at the usual DVC grid sizes of m equals 50 to 100 points with an interrogation window size of 643 voxels. For DVC applications to be competitive and widely applicable, fast computation speeds without compromising high-accuracy measurements are imperative.

The computational efficiency of our FIDVC algorithm is investigated and compared against our previous DVC algorithm by processing a series of images using the CPU and GPU. Each image of size 512 × 512 × M voxels where, M is varied from 32 to 256 voxels in increments of 32 voxels, is deformed by the prescribed displacement field in “FIDVC Convergence”. Due to the refinement of the interrogation window size in FIDVC, the final grid spacing is set to 8 voxels for a window size of 323 voxels, producing a 75 % overlap. To accomplish an equal grid size or number of computation points for the DVC execution, we set an 8 voxel grid spacing, or 87.5 % overlap for the set window size of 643 voxels. It is possible to use smaller window sizes that would yield lower computation times; however there is a trade-off between spatial resolution and capturing large displacements [9].

Figure 12 summarizes the average computation speed up factors for the different combinations of processors and algorithms. As a baseline comparison without GPU acceleration, the FIDVC is ≈ 2.9 × faster than our previous DVC because of the optimized interrogation window and overlap sizes. When executing each algorithm separately on the GPU, substantial speed improvements of ≈ 22× and ≈ 5.5× are found, resulting in 1–2 min processing times (Fig. 12(b)). As a final comparison, execution of the FIDVC on a GPU offers computational speed up times of up to ≈16× when compared to our previous DVC method run on a CPU. These computational benefits are especially important since the purchasing cost of GPUs are far less than both supercomputing time and high end CPUs. The same GPU processing times can be maintained within a low to medium range personal computer. We hope that this will allow many end-users to take advantage of the FIDVC formulation for their studies.

Fig. 12
figure 12

(a) Speed-up comparison of (1) DVC processed on the CPU against FIDVC processed on the CPU, (2) DVC processed on the CPU against DVC processed on the GPU, (3) FIDVC processed on the CPU against FIDVC processed on the GPU, and (4) DVC processed on the CPU against FIDVC processed on the GPU. (b) Processing times for an image of size 512×512×256 voxels with 65×65×33 computation points. The image is processed using both our previous DVC and FIDVC technique and executed on the CPU and GPU. The FIDVC converged after 7 iteration

Full size image

Conclusion

This paper presents a new FIDVC technique capable of capturing large 3D non-linear deformation fields. The technique utilizes the well-known iterative deformation method in conjunction with a window weighting function allowing it to maximize the final resolution of the displacement field while maintaining low computational cost. A finite difference scheme that addresses the typical sampling issues of discrete signal differentiation is presented and validated for calculating 3D deformation gradients. This approach has shown to drastically improve strain measurement accuracy by up to 50 % in low signal-to-noise displacement fields. The FIDVC results are validated using a combination of experimental, and numerically simulated volumetric images that are compared against our previous DVC technique [4].

The results show that the FIDVC can successfully capture displacements information with a subset size resolution as small as 16 voxels, which is an approximate four-fold increase in resolution compared to previous DVC techniques [4, 40]. Execution of the FIDVC on a GPU offers computational speed up times of up to 16× when compared to traditional DVC methods run on a CPU. Replacing expensive implementations on high performance computers by GPU implementation on average personal computers will open new doors in allowing DVC to be run by a wide-spread user base similar to DIC. To further support end users in utilizing the FIDVC technique, our algorithm will be freely accessible via download from our website ( http://franck.engin.brown.edu). Having the capability to compute any non-linear finite deformation field quickly and accurately should provide powerful means for investigating new areas in experimental mechanics that can benefit from non-invasive 3D measurement techniques.