CT and DVC in Experimental Mechanics

Computed Tomography (CT) has been a revolution in materials science [1]. Accessing the intimate microstructure of solids in a non destructive way has opened new horizons [2–4]. Progress toward higher performances is still extremely active, and concerns about all frontiers [5], namely, smaller length [6] and time [7] scales can be resolved nowadays, small absorption imaging thanks to phase contrast [8], combined use of tomography and diffraction to extract crystal orientations [9], energy resolved tomography to get chemical information [10], and more generally multi-modalities are a promising field of development.

At the same time X-ray Computed Tomography (XCT) becomes accessible as a lab-scale equipment and not only at synchrotron facilities. Moreover, their state-of-the-art performances may in some cases compare well with synchrotron tomography. Last, the recent development of extremely powerful Graphical Processing Units (GPUs), and the ability to make use of their potential for 3D-image reconstruction makes real-time reconstruction accessible. All these arguments explain the amazing developments of tomography in the recent years [4].

All the previous developments are making in situ testing not only possible [11, 12] but will allow for significant progress to be achieved [3, 13]. 3D imaging in a nondestructive manner of mechanical tests allows different mechanisms to be observed and quantified, even though they remain invisible to the bare eyes of experimentalists. One additional step consists of evaluating the in situ 3D kinematics of the tested material. This can be achieved by tracking individual features (e.g., secondary particles) or digital volume correlation for full field-measurements.

Digital Volume Correlation, or DVC, aims at capturing the way a solid is being deformed under a specific external load [14–16]. It is the three dimensional counterpart of digital image correlation [17, 18]. Based on the registration of two volumes (i.e., 3D-images), a space resolved displacement field can be estimated very accurately. The exploited property is that the microstructure responsible for the image contrast is preserved in time, and hence gray level patterns can be traced from the reference to the deformed configuration. DVC can be seen as a way to image 3D-motion (i.e., the so-called optical flow). As such, it is a natural complement to CT and in situ tests giving access to its time evolution if the microstructure is preserved.

One potential limitation of DVC is that the estimate of the three dimensional displacement field has to be based on two reconstructed volumes, each being acquired independently. Although recent progress has been achieved in ultra-fast tomography [7], for very high brightness synchrotron beamlines, standard tomography requires several tens of minutes, and hence, it is to be assumed that the sample remains motionless during one entire scan, an assumption that may be extremely limiting.

The present paper aims at introducing a new methodology to save acquisition time to measure displacement fields in a solid (i.e., akin to DVC at a much faster pace). First, a very brief overview of DVC and image reconstruction is given to introduce the notations. It also presents the rationale behind the proposed projection-saving strategy. Second, the proposed approach is presented and some details about the GPU implementation are provided. Third, an experimental synchrotron-based case issued from a mechanical tensile test performed on a nodular graphite cast iron specimen [19, 20] is used to assess the performance of the approach. The displacement resolution as a function of the number of projections is evaluated. Fourth, a discussion on possible ways to improve the proposed methodology is developed.

Overview of DVC and Image Reconstruction

Digital Volume Correlation

Two scans are acquired at two stages of loading of a specimen. The volumes are subsequently reconstructed from these raw data. The first one is considered as the reference, f 1(x), and the second one f 2(x) is acquired after a mechanical loading has been applied to the specimen (i.e., the 3D image in the deformed configuration). These 3D images encode the details of the microstructure through the gray level f 1 or f 2 at discrete points (or voxels) x (Fig. 1(a)). This microstructure is assumed not to vary during load, and hence the two images are related by the so-called texture (or gray level) conservation

$$ f_{2}(\boldsymbol{X})=f_{1}(\boldsymbol x) $$
(1)
Fig. 1
figure 1

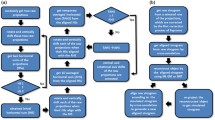
Schematic representation of the data flow for the measurement of the displacement field via DVC. The classical procedure is shown in (a) where DVC consists of measuring the displacement field U so that the reference reconstructed volume advected by the displacement, \(\tilde f_{\boldsymbol U}\), matches the deformed one. The proposed Projection-based DVC (P-DVC) is shown in (b), where the displacement field is determined so that the projection of \(\tilde f_{\boldsymbol U}\) can be registered onto the measured radiographs, s 2. The benefit of the proposed procedure is a drastic reduction in the number of needed projections n ϕ

Full size image

where the reference, x, and deformed, X, coordinates are related either by a Lagrangian displacement field u(x)

$$ \boldsymbol X(\boldsymbol x)=\boldsymbol x +\boldsymbol u(\boldsymbol x) $$
(2)

or its Eulerian counterpart U(X)

$$ \boldsymbol x(\boldsymbol X)=\boldsymbol X +\boldsymbol U(\boldsymbol X) $$
(3)

DVC aims at estimating u, or U, from f 1 and f 2. Let us stress that although it is traditional to consider the Lagrangian displacement field in solid mechanics [21], for reasons that will become clearer later on, we opt here for the Eulerian version. DVC in the same way as its two dimensional variant Digital Image Correlation, or DIC [17, 18] consists of repeated resolution and correction steps. Corrections update the trial displacement field V to compute an artificially deformed image from the reference one \(\tilde f_{\boldsymbol V}\) such that

$$ \tilde f_{\boldsymbol V}(\boldsymbol X)=f_{1}(\boldsymbol X +\boldsymbol V(\boldsymbol X)) $$
(4)

The objective of the resolution steps is reaching full 3D coincidence of f 2 and \(\tilde f_{\boldsymbol V}\). It is achieved through the global minimization of

$$ \mathcal{T}(\boldsymbol V)=\Vert f_{2}-\tilde f_{\boldsymbol V} \Vert^{2}_{\text{ROI}} $$
(5)

where ∥…∥ROI is usually the L 2 norm computed here with a uniform measure over the region of interest (ROI) in the deformed configuration, X. Assuming a small incremental correction on V, a linearization of the argument of the norm is performed. Let us emphasize that the above Euclidian L 2 norm is the best suited one for white Gaussian noise. When noise correlations are known, or when the noise probability density function is not Gaussian, a different adjusted norm may be proposed. In the case of CT images, the reconstruction step introduces correlations from the approximately white noise that is present in the radiographs, but their form is too complicated (e.g., not spatially invariant) to be correctly accounted for. Therefore, although convenient, the chosen Euclidean norm is not the best choice. It will be seen that the proposed approach allows for a more suited treatment of noise.

To make the problem well-posed, regularization is needed. The simplest choice is to restrict V to belong to a vector space of low enough dimensionality. One natural and convenient choice is to search V through the decomposition on a set of well chosen basis fields, Ψ i , for instance finite element shape functions [22]

$$ {\boldsymbol V}=\sum a_{i} \boldsymbol{\Psi}_{i}(\boldsymbol X) $$
(6)

where a i are the amplitudes to be determined. Minimization \(\cal T\) of (for the L 2 norm) leads to linear systems in the unknown corrections Δa i gathered in vector {Δa}

$$ [\mathbf{M}] \{\boldsymbol{\Delta a}\}=\{\mathbf{m}\} $$
(7)

with

$$ M_{ij}=\iiint_{\text{ROI}} (\boldsymbol\nabla \tilde f_{\boldsymbol V}\cdot\boldsymbol{\Psi}_{i})(\boldsymbol\nabla \tilde f_{\boldsymbol V}\cdot\boldsymbol{\Psi}_{j})~\mathrm{d} \boldsymbol X $$
(8)

and

$$ m_{i}=\iiint_{\text{ROI}} (\boldsymbol\nabla \tilde f_{\boldsymbol V}\cdot\boldsymbol{\Psi}_{i})(\tilde f_{\boldsymbol V}-f_{2})~\mathrm{d} \boldsymbol X $$
(9)

X-Ray Computed Tomography

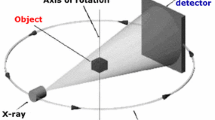
The two considered images are three-dimensional and assumed to be obtained from X-Ray CT, that is they are computed from sinograms, i.e., s 1(r, 𝜃) and s 2(r, 𝜃). The latter ones are computed from 2D radiographs, I(r, 𝜃), recorded at position r of a detector, for a sample rotated by an angle 𝜃. The sinogram is defined as

$$ s(\boldsymbol r,\theta)=-\log\left(\frac{I(\boldsymbol r,\theta)}{I_{0}(\boldsymbol r)}\right) $$
(10)

where I 0(r) is the bare incident beam intensity, which would be received by the detector if no sample were present.Footnote 1 In the simplest geometry, which is appropriate for synchrotron facilities, the source is located far away from the detector so that the beam can be considered as parallel. Radiographs are acquired for different orientations 𝜃 of the specimen as it is rotated along an axis perpendicular to the beam axis. The sinograms are related to the local absorption coefficient, f(x), by

$$ s(\boldsymbol r,\theta)=\iiint f(\boldsymbol x) \delta(\Pi(\boldsymbol R_{\theta} \cdot \boldsymbol x)-\boldsymbol r))~\mathrm{d} \boldsymbol x $$
(11)

where R 𝜃 describes the rotation transformation of the specimen on the rotation stage, and Π the projection operator on the detector plane generally set normal to the beam axis. The number of projection angles that usually spans a π-radian interval, has to be high enough to correctly reconstruct the volume image f from the sinograms s. The rule is that the maximum displacement of a physical point imaged at two consecutive angles should not exceed one pixel on the detector. If the maximum distance of a point from the rotation axis is Δ x /2 when expressed in detector pixels, the number of projections should thus be of the order of n 𝜃 = (π/2)Δ x . The linear operator allowing for the reconstruction of f is the inverse Radon transform, and is denoted here \(\mathfrak {T}\)

$$ f=\mathfrak{T}[s] $$
(12)

while the direct projection (Radon transform) is denoted \(s=\mathfrak {P}[f]\). For a divergent beam (relevant for lab tomographs) a similar algorithm for reconstructing the volume can be devised [23].

Projection-Saving Potential

In the following, 3D finite element meshes are chosen over which the displacement is projected. More precisely, the sum of squared differences between the corrected reference volume and the deformed volume are minimized over all displacement fields that can be decomposed as a sum of finite element shape functions for structured or unstructured meshes.

The uncertainty of measured displacements σ u is dictated by the ratio α of the number of available information (i.e., voxels) per kinematic degree of freedom [22, 24]. Noise sensitivity scales as σ u ∝α −1/2. Hence, a fine spatial resolution implies a small mesh size (i.e., many kinematic DOFs) and thus large uncertainties. Conversely, a small uncertainty on the displacement value implies a poor spatial resolution. Thus a compromise is to be chosen. In any case, the minimum cube element size that is usually considered is of the order of a = 10 voxels. This involves α = a 3/3 ≈ 333 voxel per scalar kinematic degree of freedom.

When α < 1 the number of unknowns would be greater than the number of equations, and hence the problem is under-determined. When α > 1, there are more equations than unknowns, so that there is generally no solution compatible with all constraints, but a solution for instance in the least squares sense exploits redundancy to reduce the impact of noise. For DVC, α ≫1 or in other words there is much less information to be measured in the displacement field than available in the entire image. Consequently, much less radiographs are needed to evaluate displacements U than to reconstruct the 3D image f 2. The expected gain is a reduction in the number of voxels by (at most) a factor α, and a little less if some redundancy is preserved to limit noise sensitivity. With the above cited numbers a gain by more than 2 orders of magnitude may be anticipated.

Projection-based Digital Volume Correlation (P–DVC) Procedure

Displacement Evaluation

The first step of the proposed analysis is to completely reconstruct the 3D image \(f_{1}=\mathfrak {T}[s_{1}]\) in the reference configuration. It is proposed to save on the number of projections (i.e., radiographs) of the volume in the deformed configuration. Therefore the sinograms are assumed to be available only for a reduced set of angles, denoted s 2(r, ϕ). This set is defined for the same detector pixels, r, but a subset of angular values ϕ of cardinality n ϕ much smaller than the number n 𝜃 required to reconstruct f 2. Hence, it would not be possible to compute f 2 entirely from the sole sinograms s 2. However, most of the microstructural details are known from f 1, and it is assumed that its evolution due to mechanical load requires much less information to be accurately captured. It is proposed, see Fig. 1(b), to determine the displacement field U through the registration of radiographs

$$ \boldsymbol{U} = \mathop{\mathrm{arg\; min}}\limits_{\boldsymbol{V}}\left(\sum_{\phi} \left\Vert s_{2}(\boldsymbol{r},\phi)-\mathfrak{P}_{\phi}[\tilde f_{\boldsymbol{V}}]\right\Vert^{2}\right)$$
(13)

The procedure used to solve the above problem (13) proceeds along the same lines as earlier presented for DVC, namely, starting from an approximate displacement field \(\boldsymbol V=\sum a_{i}\boldsymbol {\Psi }_{i}(\boldsymbol X)\), a correction to the degrees of freedom Δa i is looked for in the form of small perturbations. Based on the chosen kinematic basis (6), the incremental change of image f 1 is computed

$$ g_{i}(\boldsymbol X)= \boldsymbol\nabla \tilde f_{\boldsymbol V}(\boldsymbol X)\cdot \boldsymbol{\Psi}_{i}(\boldsymbol X) $$
(14)

Note that g i has the same support as the basis function Ψ i and hence for a finite-element basis, it is sparse. The projection of the incremental corrections are denoted by

$$ z_{i}(\boldsymbol r,\phi)=\mathfrak{P}_{\phi}[g_{i}] $$
(15)

The linearized problem is thus expressed as

$$\begin{array}{ll}\{\boldsymbol{\Delta a}\}&=\mathop{\mathrm{arg\;min}}\limits_{\{\mathbf{b}\}}\left(\sum_{\phi} \left\Vert s_{2}(\boldsymbol{r},\phi)-\mathfrak{P}_{\phi}[\tilde f_{\boldsymbol{V}}+\sum_{i} b_{i} g_{i}(\boldsymbol{r},\phi)]\right\Vert^{2}\right)\\&\approx\mathop{\mathrm{arg\;min}}\limits_{\{\mathbf{b}\}}\left(\sum_{\phi} \left\Vert s_{2}(\boldsymbol{r},\phi)-\mathfrak{P}_{\phi}[\tilde f_{\boldsymbol{V}}]-\sum_{i} b_{i} z_{i}(\boldsymbol{r},\phi)\right\Vert^{2}\right)\end{array} $$
(16)

so that {Δ a} is the solution to the following linear system

$$ [\mathbf{N}] \{\boldsymbol{\Delta a}\}=\{\mathbf{n}\} $$
(17)

with

$$ N_{ij}= \sum\limits_{\phi} \iint z_{i}(\boldsymbol r,\phi)z_{j}(\boldsymbol r,\phi)~\mathrm{d} \boldsymbol r $$
(18)
$$ n_{i}= \sum\limits_{\phi} \iint (s_{2}(\boldsymbol r,\phi)-\mathfrak{P}_{\phi}[\tilde f_{\boldsymbol V}])z_{i}(\boldsymbol r,\phi)~\mathrm{d} \boldsymbol r $$
(19)

The photon noise on the detector can be considered as Poissonian whose variance increases with the intensity I. Assuming that this variance is a small perturbation with respect to the incident beam intensity and that the typical absorption is not extreme, the noise on the sinogram s is white of variance proportional to η 2 = σ 2(1 + I 0/I) = σ 2(1 + e s). To account for this noise, the least squares registration is performed on the sinogram s using a weight inversely proportional to the variance on each detector pixel, e.g., proportional to (1− tanh(s/2)). Let us underline that this treatment of noise is now performed in a satisfactory way, in contrast to DVC performed on reconstructed images, where the actual image noise correlation induced by the reconstruction step are always ignored. Thus although this is not the main motivation of the present study, noise is more appropriately accounted for.

If multiple loading steps are considered, all acquired radiographs have to be related to the reference state. This may appear as increasingly difficult because of the larger displacement amplitudes involved. However, as for standard DVC, the difficulty may not be the ill-posedness of the problem, but rather having an appropriate initial displacement guess allowing for convergence of the DVC algorithm. To overcome this limitation, a classical procedure of DVC (and DIC) is to initialize the displacement of step n by that of step n−1. This is usually quite efficient and involves no extra cost [25]. Otherwise a multiscale procedure will be discussed in Section “Multiscale Approach” as a possible extension (not yet tested). For classical DVC/DIC, such a procedure is a very powerful tool to reach convergence. Hence the true limitation may come from a change in the microstructure that forbids a good match between the deformed and reference cases. In such a case, every N steps, one may “refresh” the reference image by performing a complete tomography.

GPU Implementation

The above algorithm has been implemented on a GPU, which is well-suited to such treatments, and allowing one to benefit from its very high computing power. The implementation is mainly based on the CUDA language to take full advantage of the power of Nvidia GPUs. Most of the execution time is utilized for the construction of matrix N and vector {n}. In terms of distribution, each CUDA group computes z i (r, ϕ) for all r crossing non-zero Ψ i , for a given node i and projection angle ϕ. CUDA threads have then to compute the partial contribution for a given r. In a second phase, contributions for a given angle ϕ are obtained by simple scalar products between the images z i (r, ϕ), which may have different supports. To get the best of the dedicated hardware and cache memory, \(\tilde f_{\boldsymbol V}\) is stored as a texture.

For a 200 × 340 × 400-voxel reconstruction, it takes approximately 0.5 sec on an Nvidia GTX 680 board to get the contributions to [N] and {n} for each projection for a mesh comparable to that shown in the following example. The proposed algorithm is observed to converge exponentially fast with the (very favorable) material microstructure and (rather coarse) mesh presented hereafter, giving a stationary solution after a number of iterations ranging from 10 to 30 (due to the need for relaxation in some cases). The chosen stopping criterion is defined as ∥ ΔV∥ < 10−2 voxel.

For the studied example, a reconstruction based on a classical filtered back-projection, implemented on the same GPU, requires 3.2 s. A CPU (not GPU) version of the global DVC computed over the same volume and mesh, requires 37 s to compute the displacement field. The proposed analysis depends very much on the number of radiographs, n ϕ , used. The larger n ϕ , the longer the computation. Some operations (loading of data into memory, correction of the reference volume) are independent of the number of projections n ϕ , while others are simply proportional to n ϕ so that the total computation time is expected to be an affine function of n ϕ . For n ϕ = 600, the computation time is 53 min (for 12 iterations), while for n ϕ = 2 (11 iterations) the displacement field is obtained in 31 s. It is worth emphasizing that for n ϕ = 2, the computation time is actually smaller than that of a classical DVC analysis (although it is fair to stress that the latter is not GPU optimized).

Analysis of Cast Iron Specimen Tested In-Situ

P-DVC is tested when based on a nodular graphite cast iron specimen whose tomography has been acquired at the European Synchrotron Radiation Facility (ESRF) in Grenoble (France) [19, 20]. This material has a high volume fraction of graphite (14 vol. %) with nodule size of the order of 50 μm, and an equivalent distance between nodules. The sample shape is parallelipedic, 1.6 ×0.8 mm 2 in cross-sectional area and 10 mm in length, with a rough surface. It is loaded in situ with a specially designed tensile testing machine [12]. Two scans are acquired, one in the reference state (for an applied tensile load of 22 N), and one under a 151 N tensile load.

Tomography is performed with a monochromatic beam (energy 60 keV). A very good contrast in absorption between carbon and iron is observed with such a wave length. The detector is a 2048 × 2048-pixel CCD camera imaging a scintillator. The voxel size is equal to 5.1 μm. 600 radiographs are acquired to reconstruct each volume. One dark-field (without beam), and 7 flat-fields (images of the incident beam without specimen) have been acquired. The flat fields are evenly distributed along the rotation from the start to the end of the 180° scan. The sinograms are obtained from the natural logarithm of the ratio of the radiographs (after subtracting the dark-field), over a linear interpolation of the flat-fields (themselves corrected by the dark-field) at the corresponding angle. This treatment is the standard procedure [23] and hence for short we will refer to these processed radiographs as projections or sinograms.

Figure 2(a) shows the reconstructed volume in the Region Of Interest (ROI) of 180 × 330 × 400 voxels (along the x, y and z directions respectively). The graphite nodules are very clearly apparent in the shown section.

Fig. 2
figure 2

(a) Region of interest of the reference reconstructed volume and (b) mesh composed of 303 tetrahedra (T4 elements) used in the analysis

Full size image

An unstructured mesh is used to describe the kinematics. It is composed of 303 tetrahedra, with linear interpolations of the displacement field. Based on the number of voxels per element, the average element would be equivalent to a 423 voxel cube. It is important to note that the sample is strictly contained within the mesh so that the residual, i.e., difference between actual and computed projections, could be decreased as much as possible.

On this precise example, redundancy can be estimated, namely, the number of voxels is n vox ≈ 2.4 × 107. The number of scalar degrees of freedom is n dof ≈ 300. In each projection, the number of useful pixels is at most of the order of n pro ≈ 1.5 × 105 (note that this estimate is based on the widest possible projection). Therefore, using a standard DVC approach based on the above mesh, the redundancy parameter would be α DVC = n vox /n dof ≈ 80,000. Using the P-DVC approach, redundancy is α P = n pro n ϕ /n dof ≈ 500n ϕ . Hence for n ϕ = 2, the gain with respect to standard DVC is very significant (a factor of 80), yet redundancy remains large ( 103) and hence noise sensitivity is not expected to be a drastic limitation.Footnote 2

Resolution Analysis

To estimate the displacement resolution of the proposed procedure, the analysis is first applied using the reference state as the deformed one without any additional noise or motion. Hence, the expected real displacement field is U = 0. In spite of the fact that this case appears as trivial since the sinogram s 2 is extracted from the original sinogram used to compute the reference volume, the projection and the reconstruction are not exactly inverse operators. Hence the re-projection of the reconstructed volume \(s'(\boldsymbol r,\phi ) = \mathfrak {P}_{\phi }[\mathfrak {T}[s]]\) differs from s(r, ϕ). Different reasons contribute to this discrepancy. Some correspond to experimental imperfections (e.g., global beam intensity modulation, detector noise or nonlinear response, inadequate flat-field, dead detector pixels). Others may be due to discretization errors at voxel scale, or to approximations used in the reconstruction procedure that do not account for multi-spectral beams, scattering or phase contrast effects. The fact that only a few projection directions are considered may further amplify the weight of some of these factors such as noise that is already present in the considered radiographs (note that no additional noise is considered).

Figure 3 shows the x-component of the displacement field for three sets of used projections, n ϕ = 48, 6 and 2. The average displacement is very close to 0 as expected. The standard deviation of the nodal displacement, σ U , provides a more interesting information concerning the resolution. It constitutes a lower bound to the actual uncertainty that incorporates in particular the imperfection of the reconstruction procedure. The systematic change of this resolution as a function of the number of projections is shown in Fig. 4. As expected, the resolution decreases with the number of projections n ϕ . These fluctuations have been characterized for each space direction independently. It is observed that the (x, y) components are larger than the z one, which is consistent with the fact that the reconstruction/projection steps are responsible for a significant part of the remaining residual. In both reconstruction and projection operations, sub-pixel interpolations are to be used in the x and y directions. Ideally, that should not be the case along the rotation axis z in the absence of noise.

Fig. 3
figure 3

x-component of the displacement field as estimated by P-DVC with different numbers of projections, n ϕ when the “deformed” state is identical to the “reference” one . (a) n ϕ = 48, (b) n ϕ = 6, (c) n ϕ = 2

Full size image
Fig. 4
figure 4

Resolution analysis. (a) Standard deviation of the nodal displacement σ U vs. the number, n ϕ , of used projections. (b) σ U as a function of the number of different faces the node belongs to. Different symbols refer to different numbers of used projections n ϕ

Full size image

As soon as noise comes into play, a non-zero displacement along z will be estimated calling for an interpolation procedure but this effect is less pronounced along z than in the (x, y) plane where the inverse Radon transform cannot be avoided. It is of interest to stress that from n ϕ = 12 to 48, the uncertainty is almost constant (in particular in the directions perpendicular to the rotation axis) and of the order of 0.1 voxel.

As earlier mentioned, the mesh contains the entire sample. This implies that the elements that reach the bounding box have much less microstructural features within their volume (part of it being outside the actual sample). To quantitatively evaluate this effect, a label is assigned to each node, n face , that counts the number of external faces the node belongs to. Hence for an internal node n face = 0, and for a face, edge or corner node respectively, n face = 1, 2 or 3. The standard deviation of the displacement when sorted according to n face is shown in Fig. 4(b). It is observed that the higher n face , the larger the standard resolution. This effect is classical for digital image or volume correlation [26], but the fact that the region of interest is larger than the actual sample further amplifies this effect. It is observed that the resolution can be reduced by close to a decade, when moving from the corner to an internal node. For internal nodes and a number of projections equal to n ϕ = 2, the bulk uncertainty is of the order of 0.1 voxel. When n ϕ = 96, the uncertainty would amount to 0.04 voxel. For classical DVC, the level of uncertainty estimated for such an element size amounts to 0.02 voxel [20].

Hence, as information used to measure the displacement field is reduced the resolution degrades. However, it is fair to note that the amount of exploited data is in that case reduced from 600 to 2 projections, that is a 300-fold reduction. In comparison, the increase in uncertainty is modest.

Evaluation of Artificial Rigid Body Motion

Before studying the actual deformed image, a second test case is analyzed where a known rigid body motion is artificially applied to the sample. First it is to be noted that translations would not be discriminating as it would simply translate the projections (sinograms) in their plane, hence mainly testing 2D image correlation. For similar reasons, a rotation along the z-axis would simply amount to selecting different ϕ projection angles. Only rotations along an axis in the (x, y) plane are of interest. A rotation by 0.2° along the y-axis has been selected.

The difference, δU, between the measured displacement and the known field, δU = U measured −U imposed is characterized by its fluctuations (or standard deviation). Figure 5 displays the change of standard deviations of the three components of displacement with the number of projections used. The fluctuations are the lowest along the rotation axis, which is consistent with the fact that the prescribed displacement itself vanishes along that direction. For the other components, the fluctuations are somewhat larger but they remain essentially at a few hundredths of the voxel size or below. The fluctuation is larger along the axes where the second moment of the displacement is the largest. It is also worth emphasizing that the uncertainty increases (modestly) with n ϕ in contrast to what could have been anticipated. One possible origin of this observation is round-off errors, but this question remains to be clarified.

The difference, δU, between the measured displacement and the known field, δU = U measured −U imposed is characterized by its fluctuations (or standard deviation). Figure 5 displays the change of standard deviations of the three components of displacement with the number of projections used. The fluctuations are the lowest along the rotation axis, which is consistent with the fact that the prescribed displacement itself vanishes along that direction. For the other components, the fluctuations are somewhat larger but they remain essentially at a few hundredths of the voxel size or below. The fluctuation is larger along the axes where the second moment of the displacement is the largest. It is also worth emphasizing that the uncertainty increases (modestly) with n ϕ in contrast to what could have been anticipated. One possible origin of this observation is round-off errors, but this question remains to bes clarified.

Fig. 5
figure 5

Standard deviation σ U of the difference of nodal displacement between measured and prescribed displacement field, for a rigid body rotation along the y-axis, vs. the number, n ϕ , of used projections

Full size image

Evaluation of Actual Displacement Field due to Loading

The deformed state is now considered as that for which the applied load was 151 N. The quality of the registration on the sinograms is first evaluated. Figures 6(a) and (b) show the two projections when n ϕ = 2. It is to be stressed that sinograms are usually shown with one axis along the angular direction. However, since only two angles are considered here, it was chosen to show the two sinograms s 2(r 1, r 2, ϕ), (i.e., the radiographs scaled by the bright-field, and using a log scale for the gray level) for the two ϕ angles. Figures 6(c) and (d) show the corresponding residual images, i.e., the differences of projections \(s_{2}(\boldsymbol r,\phi ) -\mathfrak {P}_{\phi }[\tilde f_{\boldsymbol U}]\) for the two angles. Ideally, these differences should be 0 if the registration were perfect. It is observed that most of the two residual fields are very close to 0. A small border (outside the region of interest) shows roughly the raw sinogram difference for the corresponding angles. The ratio \(\left \Vert s_{2}(\boldsymbol r,\phi )-\mathfrak {P}_{\phi }[\tilde f_{\boldsymbol U}]\right \Vert ^{2} / \left \Vert s_{2}(\boldsymbol r,\phi )\right \Vert ^{2} \), is of the order of 2.2 % over the region of interest. Note that when no displacement occurs, \(\left \Vert s_{1}(\boldsymbol r,\phi )-\mathfrak {P}_{\phi }[ \mathfrak {T}[s_{1}]\right \Vert ^{2} / \left \Vert s_{1}(\boldsymbol r,\phi )\right \Vert ^{2} \) amounts to 1.6 %. The latter value gives the absolute limit that could be achieved if the displacement field were ideally measured and if no noise were present in the projections. Hence, the registration of the sinograms can be considered as very good.

Fig. 6
figure 6

(a), (b) Two sinograms s 1(r, ϕ) obtained for the two angles used for the registration. (c), (d) Corresponding residuals \(s_{2}(\boldsymbol r,\phi )-\mathfrak {P}_{\phi }[\tilde f_{\boldsymbol U}]\) for the same angles. Note that the Region of Interest extends from 60 ≤ r 2 < 460, so that the top of these images shows roughly the raw difference of sinograms s 2(r, ϕ)−s 1(r, ϕ)

Full size image

In contrast with the previous case, the exact displacement field is not known. Two references can be considered, namely, the first one is that obtained from a classical DVC procedure, U DVC, based on the two reconstructed 3D images. The second one is obtained with the present algorithm but taking into account the whole set of projections, i.e., n ϕ = 600. The latter displacement field is denoted U 600. These two fields are used as references for other evaluations of the displacement field based on a variable number n ϕ of projections ranging from 96 to 2. Figure 7 shows the measured displacement field with the same range for different values of n ϕ . Only the component of the displacement along the tensile axis, z, is shown, but the overall good agreement is general, even when the number of projections is reduced to its absolute minimum, 2. Note that the displacement is shown on three faces where the uncertainty is expected to be larger than in the bulk.

Fig. 7
figure 7

Displacement field along the tensile axis U z in voxels as estimated by the proposed methodology with two reconstructions and with different numbers of projections. (a) Classical DVC, (b) n ϕ = 600, (c) n ϕ = 48, (d) n ϕ = 2

Full size image

For a more quantitative judgement, Fig. 8, shows for the same parameters, contours of the same displacement component in the mid-thickness (y, z)-plane. The overall agreement is generally quite good, but edges and corners are significantly more perturbed.

Fig. 8
figure 8

Contours of the component of the displacement field along the tensile axis U z in voxels in the mid-thickness (y, z)-plane as estimated with different numbers of projections. (a) Classical DVC, (b) n ϕ = 600, (c) n ϕ = 48, (d) n ϕ = 2

Full size image

To estimate the systematic error and standard uncertainty of a given evaluation, U as compared to the reference field U ref , the difference, δ U = U−U ref , is considered. Its space-average 〈δ U〉 and RMS level \({\sigma _{U}^{2}}=\langle (\boldsymbol \delta \boldsymbol U)^{2}\rangle -\langle \boldsymbol \delta \boldsymbol U\rangle ^{2}\) are computed. Figure 9 shows these quantities as a function of n ϕ when U ref = U DVC. The systematic error is generally in the few hundredths of voxel range, about 0.05 voxel (apart from one case, n ϕ = 3 where one corner node had a clearly wrong estimate), see Fig. 9(a). Thus it may be concluded that the proposed estimation is essentially unbiased. The actual limitation for the displacement measurement is the standard uncertainty. Figure 9(b) shows that σ U decreases from n ϕ = 2 to reach very quickly a plateau regime at σ≈0.25 voxel where apparently the number of projections does not seem to play any role.

Fig. 9
figure 9

(a) Systematic error and (b) fluctuation of displacement fields estimated using n ϕ projections based on U DVC as a reference

Full size image

Figure 10 shows the same quantities for U ref = U 600. The overall shape is quite comparable (including the odd corner node for n ϕ = 3). However, it may be noted that the systematic error is slightly reduced down to a level of about 0.02 voxel. More strikingly, the fluctuations now approximately display a power-law decay up to the largest number of projections (excluding the reference), where roughly \(\sigma _{U}\sim n_{\phi }^{-1/2}\). Hence the saturation of σ U based on U DVC is due to systematic differences between classical DVC and the procedure used herein. Although these methodologies are comparable in spirit, the detailed way of handling imperfections of data acquisition, approximations used in the reconstruction, and discretization errors in the reconstruction are the most severe sources of uncertainty. Ironically, the motion of the specimen itself has a more limited influence. Let us also stress that the noise present in the radiographs is treated in a proper way within P-DVC, whereas the correlations induced by the reconstruction are ignored in classical DVC.

Fig. 10
figure 10

(a) Systematic error and (b) fluctuation of displacement fields estimated using n ϕ projections based on U 600 as a reference

Full size image

To further analyze the standard displacement uncertainty Fig. 11 shows the average of σ U for both reference fields U ref , after having sorted nodes according to the number of faces they belong to. As in the previous subsection, it is observed that inner nodes n face = 0 are much more accurately determined than corner nodes. For two projections, inner nodes show only about 0.2-voxel uncertainty. It is observed again that n ϕ essentially controls the distance to U 600, but only mildly affects the difference with U DVC.

Fig. 11
figure 11

Standard deviation of U−U ref based on (a) U ref = U DVC and (b) U ref = U 600. The standard deviations are estimated for subsets of mesh nodes belonging to a given number of faces n face

Full size image

It worth noting that a large part of the displacement in this experimental case is a rigid body rotation. It is therefore interesting (but demanding) to study the estimated overall tensile strain, 〈ε zz 〉. Figure 12 shows the tensile strain ε zz estimated from the displacement of the inner nodes (such that n face = 0). The strain is plotted as a function of the number of projections n ϕ , together with the estimate based on the full DVC analysis considered as a reference, and indicated as a dotted line. Based on the uncertainty reported for U z , and the sample length (i.e., 400 voxels), the strain uncertainty ranges from 5 ×10−4 for n ϕ = 2 to 2 ×10−4 for n ϕ = 600. Considering those levels of uncertainty, all estimates are consistent.

Fig. 12
figure 12

Estimated tensile strain based on inner nodes ( n face = 0) as a function of n ϕ . The dotted line corresponds to the result obtained with classical DVC

Full size image

Possible Improvements

Reconstruction Strategies

In the present study, the reconstruction algorithm is chosen to be the standard Filtered Back-Projection (FBP) [23]. It is the most commonly used algorithm as it combines simplicity and speed of execution. However, the quality of the reconstruction is not the best that can be achieved and alternative techniques designated under the name of Algebraic Reconstruction Technique (ART) are available as more accurate but more costly procedures [23]. Although different variants exist, they typically aim at iteratively reducing the reconstruction residual \(s-\mathfrak {P}_{\phi }[\mathfrak {T}[s]]\). As it was observed that this difference was one of the major limitations of the proposed procedure, resorting to such an algorithm is presumably a good way of enhancing the quality of the displacement measurement. Such a progress is also expected to come together with an extra cost, due to the iterative nature of these algorithms. However, if a series of images is to be analyzed, the investment made to achieve the best quality out of the reference image is performed once for all and the subsequent use of this reference volume for the entire series will distribute the extra cost to numerous images.

Moreover, the present cost of an FBP reconstruction is negligible as compared to the cost of the correlation procedure (mainly due to the cost of gradient projections). That of an ART iteration should be comparable to the cost of one projection as used in the displacement analysis but has to be repeated over the complete set of projections (i.e., 600 angles in the present example), and often about 10 ART iterations are to be performed before reaching a stationary solution. Hence, this direction is worth being investigated especially when the FBP reconstruction is facing difficulties for the reconstruction (e.g., because of nonuniform angular sampling, or high level of noise). In other cases, resorting to an ART strategy may induce an extra cost that may not be compensated by the extra quality of the reconstruction.

Last, it may also be a way to identify biases in the acquisition of the raw radiographs by considering the irreducible residuals. Such an identification may provide a much better way of handling further comparisons. However, this implies to revisit the details of the reconstruction procedure including phase contrast, nonlinearities of the detector, which may be demanding in terms of resources.

Multiscale Approach

One of the most limiting difficulty in DVC is that convergence requires a good initial guess for the sought displacement. Otherwise, the risk of being trapped in secondary minima increases fast with the distance of the initial displacement field to the actual solution. One effective strategy to avoid or limit such local trappings is to first solve the DVC problem based on smoothed images as obtained from a low pass filter. After convergence, the obtained displacement is used as a starting point for a new DVC problem where more details are restored in the images. This procedure is iterated down to the full image. This pyramidal approach has been shown to be very useful for a wide category of problems in DIC and DVC analyses [18, 22, 27].

For the present algorithm, the same procedure could be applied as obtaining a coarse reconstruction can easily be achieved using FBP (or ART) algorithms. It may also decrease the number of iterations needed to reach a steady state solution, and is therefore an appealing strategy. However for the test case studied herein the strain level was small enough not to require such a multiscale approach.

Regularization Strategy

In the field of DIC and DVC, the benefit of using an elasticity-based regularization has been demonstrated as giving rise to significantly better results in terms of stability, and larger basin of attraction for the actual solution, and in terms of regularity of the obtained displacement field [19, 24, 28, 29]. It allows ill-conditioned modes to be efficiently dealt with, i.e., those that correspond to the lower eigenvalues of matrix M (equation (8)). Those modes are expected to be encountered especially for face, edge and corner nodes, those that have been seen to be responsible for the worst uncertainty in the previous analysis. In the present case, four faces are free surfaces, and thus the use of vanishing tractions may be a very appropriate way of handling the poor conditioning of these modes, if some approximate elastic properties are available. In the present case one could consider to penalize a non-zero traction vector on the free surfaces, the latter traction being computed from the finite element discretization and an estimate of the Poisson’s ratio of the material. A very large weight given to this constraint would enforce the appropriate boundary condition on those elements where information is lacking. Such an attempt has not been explored further in the present study so that reported results are representative of the sole P-DVC procedure.

It is also to be noted that regularization can be understood through the temporal axis [30, 31]. When a series of states are to be characterized, prescribing a specific regularity in the time evolution of all degrees of freedom (be they of kinematic type or others) is a natural way of reducing the uncertainty and promote robustness.

Conclusion

It has been shown that global DVC applied to CT volumes could be performed based on a drastically reduced number of projections (here by more than 2 orders of magnitude) yet preserving subvoxel resolutions. The new formulation, which is written in terms of the raw data of CT (i.e., the sinograms), is based upon the complete reconstruction of one volume in the reference configuration and the volume in the deformed configuration only needs a limited number of projections. The lower the latter the poorer the displacement resolution. However, very reasonable results have been obtained even with only two projections. With the proposed algorithm, only one complete scan is needed to assess the displacement resolution.

The present approach, which is referred to as projection-based DVC (or P-DVC), has been applied to analyze one step of a tensile test on nodular graphite cast iron. Meshes based upon 4-noded tetrahedra encompass the considered sample. The measured displacement fields obtained with P-DVC are very close to those measured with standard T4-DVC in which two full CT scans are considered. This result validates the P-DVC algorithm.

The proposed methodology has been implemented on a GPU board allowing displacement fields to be measured on several mega-voxel regions of interest within about 30 s computation time. The computation time is proportional to the number of projections, n ϕ , and hence the smaller the number of projections, the smaller the computation cost. The P-DVC technique opens new possibilities to characterize the time evolution of systems that have been imaged in their reference state, and this without requiring any upgrading of existing equipment.