Introduction

Composite materials, because of their remarkable compromise between weight and mechanical properties become more and more present in the aeronautic industry, even for demanding applications. During the past decade, a major step has been achieved through the development of 3D woven composites as their (especially through-thickness) resistance were considerably increased [1–3]. Indeed, in contrast with laminated composites where delamination is a major failure mode, 3D woven composites are strengthened by weaving the different layers together.

The design of components made out of those composites is based on a homogenized equivalent material. The homogenization technique has been intensively studied, and reviewed in [4–6]. Its predictive ability has been demonstrated in particular for elastic properties [7–9]. However, these approaches call for assumptions on the periodicity and the regularity of the fabric that the process can not reach. Consequently, the homogenized equivalent material behavior does not account for the scattered results observed in experimental tests [10, 11]. Alternatively, assumptions on the contact forces between weft and warp fibres, may lead to models whose parameters are to be finally determined from experimental tests [12].

In all those cases, either to identify parameters, or to validate a model, confrontations between modeling and experiment are required.

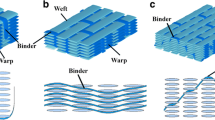
The present study is based on a layer-to-layer interlock woven composite developed by SNECMA (SAFRAN group) made out of carbon fiber tows and an epoxy matrix. The fibre volume fraction is 58 %. The composite is periodic along the three directions (x,y,z), containing respectively one period on the warp direction, two on the weft direction, and two on the out-of-plane direction. The unit cell is shown schematically in Fig. 1. Homogenization methods predict that the homogenized elastic properties are orthotropic. However, the quantitative comparison between a homogenized material description and the actual material reveals a number of shortcomings, which call for a specific methodology explored in the present article. The major difficulty comes from the coarse microstructure of the material. Indeed, field measurement technique used in this study reveal very clearly the architecture of the material, and hence the spatial resolution of this experimental technique is potentially finer than the scale at which a homogenized material is expected to be a valid description. Adjusting the experimental technique, not at its best performance, but at the level where it can match the proposed modeling framework, constitutes a novel challenge addressed in the present work.

Fig. 1
figure 1

Example of a unit cell of an interlock woven composite used for the test

Full size image

An additional focus of the proposed approach is to account faithfully for the actual experiment, modeling the test as it is and not as it should ideally be. Tolerance to deviation from ideality, reveals to be a major strength of the proposed methodology which nevertheless does not demand numerous or sophisticated additional sensors. Our analysis is indeed performed on a standard three point bending test, and a digital camera is the only required additional device as compared to a standard test.

Finally, as our objective is the quantitative evaluation of an elastic property, a special attention is devoted to the evaluation of uncertainties throughout the entire procedure.

Section “Three-Point Bending Test” presents the mechanical three-point bending test to be exploited and that will be used to evaluate the performance of the different steps of the identification procedure. The proposed methodology is based on Digital Image Correlation (DIC) on the one hand, and the Finite Element Model Updating (FEMU) on the other hand, that are detailed in Sections “Global Digital Image Correlation” and “Finite Element Model Updating” respectively. The former section introduces the software platform that hosts the entire procedure, presents the global DIC technique, and reports on the uncertainties attached to DIC per se. Section “Finite Element Model Updating” recalls the principle of the FEMU method, and its connection to DIC through the specific metric used. This section also provides an estimate of the uncertainty in the identified elastic modulus that results from the entire chain of analysis. It is shown that the uncertainties are very small, and that the main limitation of the methodology is the very concept of an equivalent homogenized medium. Indeed, DIC is sufficiently accurate to reveal strain modulations which are due to the weaving. Thus the issue of having a consistent identification with the sought simplified description brings to light an original issue of choosing a mesh which is adapted to the weaving periodicity, a point which is discussed in Section “Suited Mesh for Identification”. Finally, Section “Conclusion and Perspectives” proposes some conclusions and perspectives.

Three-Point Bending Test

In order to characterize the InterLaminar Shear Strength (ILSS) and the out-of-plane shear modulus, the sample is subjected to a standard three point bending test (referenced as ASTM D2344) and shown schematically in Fig. 2. The specimen is placed onto two cylinder shaped supports parallel to the y-axis and referred to in the following as supports 1 and 2 for the left and right ones respectively. The load is applied on top with a third cylinder shaped contact element, called 3. The warp fiber direction of the specimen is along the horizontal x-axis whereas the weft fiber direction is along the y-axis. The sample geometry and size was determined based on the test standards and also considering the Representative Volume Element dimensions [13]. If the height (along the z-axis) is denoted by h, the length along the x-axis is 5h and the depth (along the y-direction) is 3h. The test is displacement controlled, with a velocity of 8.33×10 − 3   mm.s − 1. During the test, the loading is registered and digital images are acquired at imposed time intervals in order to measure a two dimension full-field displacement on the surface sample by DIC. For this purpose a fine-grained black and white speckle pattern is applied on the side face of the specimen. The choice was made to observe only the left half of the sample in order to increase the image resolution. An actual image showing the field of view (ROI) and surface pattern has been superimposed on the scheme shown in Fig. 2. Images (1376×1040 pix.) are acquired by a digital 12-bit CCD camera system, SensicamTM, providing a high signal-to-noise ratio.

Fig. 2
figure 2

Schematic view of the 3 point bending test. The specimen is placed on two cylinder shaped supports (labeled 1 and 2), and the load is applied through a third contact element (labeled 3). The field of view of the camera is shown as the inserted image. Note that only the left part of the specimen is seen

Full size image

As the aim of this test is to identify elastic properties, the absence of fibre breaking or debonding in the loading range considered in the present study was validated using acoustic emission technique. The loading rate was chosen as low to avoid significant viscosity effect. This is essential to secure the considered loading in the elastic regime.

Global Digital Image Correlation

A Specific Software Environment : The LMTpp Platform

Identification involves a dialog between measurements and modeling. Usually, simulation and measurements are done with different softwares. The present study has been performed within a unique environment in order to provide an identification procedure of macroscopic elastic parameters with minimal sources of uncertainty and benefit from the entire field of view. The specific environment is a C+ + environment, “LMTpp”, developed in house [14, 15]. Moreover, a global DIC algorithm is used [16] so that the displacement field is, from its basic formulation, expressed in a finite-element formalism. Note that DIC only uses the mesh and the finite-element shape functions as a convenient way to decompose the displacement field from the registration of images. However, no mechanical modeling is involved at this stage. The constitutive law and balance equations are not exploited in global DIC.

Mechanical modeling will be used later for the FEMU analysis. Based on parametrized boundary conditions, and constitutive parameters, the displacement field will be computed exploiting the mechanical equations. The boundary conditions and elastic constants will then be optimized so that the DIC measured and the computed displacement fields coincide. This procedure is shown schematically through a flow diagram in Fig. 3. We will come back in details on both DIC and FEMU procedures in the following, but we stress here that the homogeneity of the kinematic description, and of the LMTpp environment involves no loss in the dialog between the different parts of the entire identification procedure.

Fig. 3
figure 3

Flow diagram of the identification procedure where DIC stands for Digital Image Correlation and FEA for Finite Element Analysis. DIC is used to measure the experimental displacement field. FEA is used to compute the displacement field from boundary conditions and material parameters which are determined so as to minimize the difference with the measured displacement Field

Full size image

Global DIC

DIC [17] aims at measuring a full-field displacement from images taken during the test on the side surface of the sample. These images are analyzed to calculate the displacement in each point of the observed area called Region Of Interest (ROI). In this study, a global DIC formulation was adopted [16]. A reference image is chosen, usually taken before any loading is applied. The user selects a ROI on this image, and meshes it with quadrilateral or triangle elements for which shape functions are bilinear. The grid can be structured or unstructured [18]. Global DIC consists in estimating the projection of the displacement field onto a suited basis, here given by finite-element shape functions, so that it matches the one used in the modeling.

The basic assumption of DIC is to assume that the image texture (i.e. surface patterns) is simply advected by the displacement, so that we can assume

$$ \label{eq:dic1} g(\underline x+\underline u(\underline x)) = f(\underline x)+\eta(\underline x) $$
(1)

where \(f(\underline x)\), respectively \(g(\underline x)\), is the gray level at each point \(\underline x\) of reference image, respectively of the deformed image, and \(\eta(\underline x)\) is the CCD sensor noise.

Introducing a decomposition of u(x) on the classical FE basis function, it is possible to estimate the solution u by minimizing over the entire domain Ω the following functional suited to a gaussian white noise:

$$ \label{eq:dic2} {\cal T}(\underline u)= \int_\Omega \left[g\left(\underline x +\sum\limits_{\alpha=1}^2\sum\limits_{i=1} ^{n} a_{\alpha i}N_i(\underline x)\underline e_\alpha\right) -f(\underline x)\right]^2~d\underline x $$
(2)

where N i are the finite element functions relative to node i, and \(\underline e_\alpha\) are unit vectors along the axes. The amplitudes a αi are the unknown degrees of freedom used to describe the kinematic field.

The above functional is strongly non-linear, because of the rapidly varying texture f and g. Hence, an iterative procedure is used, based on successive corrections of the deformed image, g (n), such that \(g^{(n)}(\underline x+\underline u^{(n)}(\underline x))=f(\underline x)\) where \(\underline u^{(n)}\) is the displacement field determined at step n until g (n) matches f. Incremental corrections of the displacement field \(\delta \underline u^{(n+1)}\) are computed from the minimization of the linearized form of the objective functional, \({\cal T}_{\mathrm{lin}}\)

$$ \label{eq:dic21} {\cal T}_{\mathrm{lin}}(\delta \underline u^{(n+1)})= \int_\Omega \left[g^{(n)}(\underline x)-f(\underline x) -\delta \underline u^{(n+1)}\nabla f(\underline x) \right]^2 ~d\underline x $$
(3)

where a Taylor expansion of f has been used as well as a small strain assumption. Updating of the displacement field is simply \(\underline u^{(n+1)}=\underline u^{(n)}+\delta \underline u^{(n+1)}\). It should be noted that the above linearized form is only useful for determining the correction, however, convergence is established based on the full (non-linear) functional \(\cal T\). Thus, an approximate fulfillment of the small strain assumption does not endanger the quality of the final solution.

The main interest of the above writing is that the determination of the displacement increment \(\delta\underline u^{(n)}=\delta a^{(n)}N\underline e\) resumes to the solution of linear system

$$ \label{eq:dic3} M.\delta a^{(n+1)}=b^{(n)} $$
(4)

where M is the matrix

$$ \label{eq:dic4} M_{\alpha i;\beta j}= \int_\Omega [N_i(\underline x) N_j(\underline x)\partial_\alpha f(\underline x) \partial_\beta f(\underline x)] ~d\underline x $$
(5)

and b is the vector

$$ \label{eq:dic5} b_{\alpha i}^{(n)}= \int_\Omega [(g^{(n)}(\underline x)-f(\underline x))N_i(\underline x) \partial_\alpha f(\underline x)]~d\underline x $$
(6)

Note that M is the same at all steps of the iteration, so that only b has to be updated.

Finally, the last difficulty is related to the use of a Taylor expansion to first order in order to estimate the displacement. This may cause trapping in secondary minima of the non-linear functional \(\cal T\). To deal with this problem a multiscale approach is developed: a crude determination of the displacement is first performed based on strongly low-pass filtered images. Large displacements are captured by these first steps. Then, based on this first determination, finer and finer details are re-introduced in the images in order to progressively obtain a more accurate determination of the displacements. This procedure is carried down to unfiltered images in the final pass. The convergence criterion is based on the infinity norm of \(\delta\underline u^{(n)}\) displacement increment between two consecutive steps and is taken as \(\Vert\delta\underline u^{(n)}\Vert_{\infty}<10^{-4}\).

Several options and parameters are to be set in the DIC procedure: possible accounting of a brightness correction (relaxing the texture conservation equation (1)), the type of image interpolation for computing g (n) or the computation of the gray level gradient \(\nabla f\). Whereas brightness correction increases the number of degrees of freedom, the choice is made to use it in order to correct the brightness disparity between images. Following the literature [19, 20], the spline interpolation for subpixel displacements of g is chosen to obtain better results in terms of systematic error and uncertainty. Gray level gradients are computed as centered finite differences.

Uncertainty Due to DIC

The above presented global DIC is an ill-posed problem, the measured displacement field computed as such is limited by uncertainty, especially concerning subpixel displacement. Using the global DIC explained above with the chosen options, an uncertainty study is performed to quantify the uncertainty on the measured displacement field. As maximum uncertainty occurs for subpixel displacement of 0.5 pixel, an artificial deformed image is obtained by adding a half-pixel displacement to the reference image in both x and y direction. This is done by a Fast Fourier Transform (FFT) where the ROI size is reduced to the maximum power of 2 available as s = 2n < ROI size. A new image, \(\tilde{f}\) of twice the size s, is created from the initial image, f, by symmetrizing the reduced ROI in order to satisfy the periodicity needed by the FFT. Then, in the Fourier space, the translated image \(\tilde{f_t}\) is obtained by:

$$ \label{eq:uncer1} \tilde{f_t}(\underline{x})= \Re(\overline{\mathcal{F}}(\hat{f}(\underline{\lambda})e^{-i(\underline{\lambda}.\underline{u})})) $$
(7)

where \(\hat{f}(\underline{\lambda})\) is the Fourier Transform of image \(f(\underline{x})\), \(\overline{\mathcal{F}}\) is the inverse Fourier Transform and \(\underline{u}\) is the needed translation displacement. \(\tilde{f_t}(\underline{x})\) is finally rescaled to the initial size of the reduced ROI (Fig. 4).

Fig. 4
figure 4

Procedure used to create a translated image f t of half a pixel on each direction from an original image f. An image twice as large as the reference one is built from mirror symmetric copies. The result is now a periodic image suitable for FFT. Half a pixel translation is performed through a phase shift in Fourier space. Finally, the upper left quarter of the image is cropped, and saved as f t

Full size image

Then, from the global DIC led on these two images, f and f t , for different element size, from 16 to 64 pixels, the mean error and the uncertainty plotted on Fig. 5 show a decreasing uncertainty and mean error as the element size increases. Hence, the uncertainty is much higher than the mean error. It is worth noting that if the kinematic field is not described by the basis function on which the displacement is sought, the error on the displacement field increases. Indeed, a complex kinematic field cannot be described accurately with a large element size.

Fig. 5
figure 5

Uncertainty (a) and mean error (b) of the DIC analysis as a function of the element size are shown in a log-log plot. These data are obtained for the worst case of half a pixel displacement in both x and y directions. Dotted lines show a power- law going through the first data points

Full size image

Finite Element Model Updating

Principles

Several techniques have been proposed to identify material parameters from kinematic field measurements [21, 22]. The FEMU is the most generic and intuitive method [23]. It is based on over-determined data, a full-field displacement measurement in this case, and allows for dealing with a complex geometry. The principle consists in finding iteratively parameter values introduced in a Finite Element (FE) simulation to minimize the cost function, \(\cal R\), measuring the gap between measured displacement fields by DIC, \(\underline U_{\mathrm{mes}}\), and calculated ones i.e.,  \(\underline U_{\mathrm{cal}}\) (Fig. 3).

$$ \label{eq:femu} {\cal R}^2 = (\underline U_{\mathrm{mes}}-\underline U_{\mathrm{cal}}) {\bf C}^{-1}(\underline U_{\mathrm{mes}}-\underline U_{\mathrm{cal}}) $$
(8)

Contrary to the classical approaches based on the comparison of strain fields [24], one notes that this objective functional is based on the displacement field itself. This specific character is important as it relaxes the sensitivity to spurious high frequency modes inevitably present in the measured displacement and very much amplified in strain evaluations (the alternative being to smooth out the strain field based on arbitrary a priori assumptions).

In the equation (8), C  − 1 is the covariance matrix of the displacement measured by DIC, when noise is the dominant source of variability which can be evaluated exactly as proportional to the matrix M [25]. It provides a positive-definite weighting of the kinematic degrees of freedom based on the measurement.

The FE simulation, as the measured field, is performed in 2D, in the plane defined by the x-axis and z-axis, with a plane strain hypothesis. The latter is justified by the large thickness of the sample compared to the two other dimensions and the fact that it is the weft fibers orientation.

The boundary conditions chosen for the FE simulation are shown in Fig. 6: At the contact point with the left support (called “support 1”), a displacement \((U_x^1,U_z^1)\) is imposed. At the contact point with the right support (“support 2”), only a vertical displacement is imposed \(U_z^2\). The load being applied onto the central upper cylinder (“contact element 3”) is modeled through a distributed vertical force. Finally, as can be seen on Fig. 7, the displacement field shows that the test does not obey the expected left-right symmetry. To account for this effect, and additional tangential (horizontal) force is applied on the contact element 3.

Fig. 6
figure 6

Mesh used for FEA on which the boundary conditions are schematically represented. Note that a horizontal load has to be included at the upper contact element 3 to account for the observed dissymmetry of the test. The ROI on which DIC is performed is delimited as a dot-dashed rectangle

Full size image
Fig. 7
figure 7

Magnitude of the measured displacement field represented on the deformed mesh (amplified 50 times). Note that the expected left-right symmetry of the test is violated as can be clearly seen from the displacement underneath the central load bearing contact element 3

Full size image

Besides, the strain in the vicinity of the contacts is quite large so that the linear elastic behavior assumed in the simulation is dubious. As a consequence, these areas will be omitted in the identification procedure.

The shear modulus G 13, as well as the displacements of the two outer cylinders and the tangential force applied on the central one are sought based on the FEMU method. The normal force is set to the experimentally measured value, and the contact surfaces are determined from the image.

Those elastic parameters are issued from a modeling of the composite structure using the software TexComp [28]. The latter is based on a geometrical description of the fabric, and a homogenization procedure for the elastic properties of the textile composite based on the Eshelby inclusion method [26, 27]. Although this approach involves a number of simplifications and approximations, many studies have proved its efficiency. The major source of uncertainty comes from the difficulty of accounting for the transverse compression of fibres. As a result, in-plane constitutive parameters, and in particular E 1, agree quite well with their computed estimates [27]. Out-of-plane parameters are much more uncertain. One way to probe the effect of the uncertainty resulting from approximate estimates of the elastic constant is to compute the sensitivity fields, \(\partial U_{\mathrm{cal}}/\partial p\) where p is either ln (E 1), ln (E 3) or ν 13. The spatial mean of the modulus of the three sensitivity fields is reported in Table 1. The overall sensitivity of those parameters is quite modest (this could have been expected from the very choice of our test which is chosen to maximize the sensitivity with respect to G 13 : a few percent variation of ln (E 3) or ν 13 cannot be resolved as the mean change in displacement is in the centi-pixel range. E 1 is the most sensitive parameter, and indeed its value affect our estimate of G 13 since it directly influences the deflected shape of the calculated sample. However, it is to be stressed that E 1 is the constitutive parameter which is the most securely estimated either with the modeling code, or experimentally. Thus, the three elastic constants (E 1, E 3 and ν 13) are considered as trustful in the present study.

Table 1 Mean, m, over the entire domain of the magnitude of the sensitivity map calculated analytically as \(\partial U_{\mathrm{cal}} / \partial p\)
Full size table

Uncertainty in The Identification Process

One major source of uncertainty lies in the CCD sensor noise that induces an uncertainty on the measured displacement field. As the measured full-field displacement is taken as a reference for the identification step, it is necessary to know the propagation of this noise along the identification chain. For that purpose, the introduction of the camera noise on a synthetic image is characterized and propagated through the complete identification process to isolate the effect of the CCD sensor noise from other possible artifacts. The results are made dimensionless for confidentiality reasons. The reference value for the elastic shear modulus, \(G_{13_0}\), is obtained from the mean value from Iosipescu tests led by SNECMA, with a scatter of ± 4 % around this mean value.

Evaluation of the CCD sensor uncertainty

Besides the uncertainty due to DIC evaluated in Section “Uncertainty Due to DIC”, an other major source of uncertainty on the measured displacement field using the global DIC, is the CCD sensor noise. It is possible from N images of the same state considered as reference to characterize the noise due to the acquisition (essentially the intrinsic noise of the CCD sensor). Once this noise characterized, the attention would be devoted to the propagation of the gray level noise along the identification process in Section “Propagation of uncertainty along the identification chain”.

A first DIC analysis is performed to evaluate a possible displacement between images. Choosing one image as a reference, the N − 1 other images are chosen as deformed pictures. Typical translation evaluations reveal an unanticipated displacement of order 0.1 pixel at most. These small amplitude translations nevertheless contribute significantly to image differences.

An attempt was made to determine, in addition to noise, a gray level offset and rescaling, so that introducing the (unknown) noiseless reference image, \(f_0(\underline x)\), image number i is written

$$ f_{i}(\underline x)=(1+b_i)(a_i+f_{0}(\underline x)+\eta_i(\underline x)) $$
(9)

where a i is the gray level offset, and (1 + b i ) the gray level rescaling which may come from fluctuation in the exposure time (or lighting). \(\eta_i(\underline x)\) is the noise whose spatial average is 0.

$$ \langle f_{i}(\underline x)\rangle =(1+b_i)(a_i+\langle f_{0}(\underline x)\rangle) $$
(10)

and, for i ≠ j,

$$\begin{array}{lll} \langle f_{i}(\underline x)f_{j}(\underline x)\rangle -\langle f_{i}(\underline x)\rangle\langle f_{j}(\underline x)\rangle\nonumber\\ \quad = (1+b_i)(1+b_j)(\langle f_{0}^2\rangle-\langle f_{0}\rangle^2) \end{array}$$
(11)

This last set of N(N − 1)/2 equations allows for the determination of the N unknowns b i if one assumes \(\langle \log(1+b_i)\rangle_i=0\). Similarly, assuming \(\langle a_i\rangle_i=0\), the first equation allows for estimating a i . The above assumptions on a and b are needed because f 0 is unknown. From the gray level corrected images, \(f'_i(\underline x)=f_i(\underline x)/(1+b_i)-a_i\), the noise η i can be characterized

$$ \langle f_{i}(\underline x)^2\rangle -\langle f_{i}(\underline x)\rangle^2 =(1+b_i)^2((\langle f_{0}^2\rangle-\langle f_{0}\rangle^2)+\langle \eta_i(\underline x)^2\rangle) $$
(12)

hence

$$ \langle f'_{i}(\underline x)^2\rangle -\langle f'_{i}(\underline x)\rangle^2 =(\langle f_{0}^2\rangle-\langle f_{0}\rangle^2)+\langle \eta_i(\underline x)^2\rangle $$
(13)

The variance of each image noise \(\langle \eta_i(\underline x)^2\rangle\) can thus be estimated.

Images are encoded with a 16-bit deep gray level (thus ranging from 0 to 65535). The determined rescaling corrections b are of order of 10 − 4, and a of order 10 gray levels. Thus these corrections are very modest.

It is observed that the noise level is very similar in each image. Finally, the histogram of corrected image differences f′ i  − f′ j can be computed, showing that it could be very well approximated by a Gaussian of zero mean and variance v 2 as shown in Fig. 8. The standard deviation is estimated to be v ≈ 310 gray levels, much larger than the above gray scale corrections.

Fig. 8
figure 8

Histogram obtained from the pixel-to-pixel difference between images. Data points are shown as ∘ symbols, and a Gaussian fit (bold curve) is drawn as a guide to the eye

Full size image

Propagation of uncertainty along the identification chain

A reference image is artificially deformed with a displacement field issued from a finite element calculation for which the material properties are known. Thus, the material properties that have to be identified are known. However, the gray level value of a pixel for which the displacement assumes a non-integer value has to be interpolated from the reference image.

Once noise is added to the deformed image by specifying the mean and the standard deviation of a Gaussian distribution, as determined in the previous subsection, the FEMU identification is performed for two hundred random samples. The results are shown in Table 2. Both the mean difference between known and estimated parameters (termed “systematic error”) and the standard deviation of the estimates (termed “uncertainty”) are reported. This characterizes the uncertainty on the identified parameters due to the CCD sensor noise using the FEMU identification.

Table 2 Uncertainty on the identified shear modulus and boundary condition parameters obtained from applying the proposed procedure to synthetic data and added noise
Full size table

The uncertainty on the displacement at support 1 (left) is much less than that of support 2 (right). The reason is that only the left part of the specimen was in the field of view of the camera and the displacement at support 2 has to be extrapolated at a far distance, inducing thereby a limited accuracy on this identified parameter. However, the uncertainties on the identified parameters are still rather small. The FEMU identification performances can thus be considered as reliable.

Suited Mesh for Identification

Taking into account a real material and experiment to feed the identification chain reveals yet another obstacle to overcome. The homogenized model used in the finite element method provides a smooth displacement field with slow variations. In the real case, the presence of the underneath textile architecture in the studied composite material induces large local modulations of the displacement field as shown in the Fig. 9. These local variations have to be filtered out in order to compare both measured and calculated displacement fields. Let us stress that the challenge here is not to obtain the best accuracy from DIC, but rather to resort to a coarse analysis in order to match the chosen homogenized material description.

Fig. 9
figure 9

Horizontal component of the displacement field as measured by DIC with a regular square mesh of 16 pixel element size. A clear modulation can be seen which reflects the underlying microstructure

Full size image

The main difficulty with filtering the displacement field as a post-processing step after DIC is that correspondence with the experimental data is lost and hence all the effort invested in securing identification with experimental data would be ruined. Although such smoothing processes of DIC displacement field are often performed when strain are to be used, a clear appreciation of actual uncertainties would not recommend such a practice.

The proposed procedure is to filter the displacement field while preserving the connection to experimental images. Would the microstructure be ideally periodic, a DIC analysis performed with a mesh size equal to the period would indeed directly filter the periodic component as required, yet preserving the DIC strategy to determine the long wavelength components of the displacement field.

In order to test the applicability of this idea, the systematic influence of the mesh size is studied.

Mesh sizes ranging from 115 ×130 pixel to 47 ×22 pixel are systematically explored without changing any other parameters in the identification chain. Figure 10 shows the impact of the mesh size on the estimated dimensionless shear modulus G 13 normalized by the mean value obtained through Iosipescu tests, \(G_{13_0}\).

Fig. 10
figure 10

Map of the identified dimensionless shear modulus \(G_ {13}/G_{13_0}\) as a function of the mesh size along x and z directions

Full size image

One notes that the mesh size along the x-direction has no or little systematic influence, whereas the z-direction has a very systematic influence.

To understand this sensitivity, it is of interest to consider the microstructure of the specimen surface prior to the application of the speckle pattern as shown in Fig. 11. The microstructure appears as periodic along the z-axis but not along the x-axis (the period along this direction is about 200 pixels, and would require too coarse meshes to be seen).

Fig. 11
figure 11

Microstructure of the specimen surface layer. The periodicity of the weaving along the z-axis is clearly seen

Full size image

The power spectrum of the microstructure image in the Fourier domain along the z-axis shown in Fig. 12 presents a well defined peak at a period of 62 pixels. In the same figure, the FEMU residual is also plotted showing a minimum for twice this size.

Fig. 12
figure 12

FEMU residuals obtained for a regular square mesh whose size is L z along the z-axis are shown with ∙ symbols. The power spectrum of the microstructure (shown in Fig. 11) along the z direction and averaged over x is shown on the same graph as a dotted curve, it is plotted as a function of L z  = 2π/k. A first peak is observed for the spatial period of the weaving, and a second one at twice the period

Full size image

The absolute lowest FEMU residual is reached for a mesh size equal to 84×122 pixels.

For this mesh size, the residual maps of \(\underline U_{\mathrm{mes}}-\underline U_{\mathrm{cal}}\) along both space direction are shown in Fig. 13(a) and (b). The computation of the difference is carried out on the nodes of the FEMU analysis, and the DIC displacement is interpolated at those nodes using a bi-linear interpolation. On this plot, the masked region underneath the central cylinder is clearly visible. The range of displacement difference is about 0.12 pixel along the x axis and 0.25 pixel along the z axis.

Fig. 13
figure 13

  Horizontal x component (a) (respectively (c)) and vertical z component (b) (respectively (d)) of the difference between measured and computed displacement fields. The data is shown for a correlation mesh of 84×122 pixels. The minimization of \(\cal R\) (equation (8)) is made on the FE mesh (respectively on the correlation mesh) without (respectively with) making use of a weight matrix. Difference between measured and computed displacement fields decreases when using a weighting matrix

Full size image

The identification can also be led with this optimal correlation mesh and the difference of \(\underline U_{\mathrm{mes}}-\underline U_{\mathrm{cal}}\) along both space direction can be evaluated on the nodes of the DIC mesh, in order to benefit from the weight matrix estimated from DIC. The residual maps, shown in Fig. 13(c) and (d), have a range of displacement difference slightly smaller than previously, about 0.12 pixel along the x axis and 0.18 pixel along the z axis. It shows the improvement in the identification coming from the use of the DIC correlation matrix. The values of the identified parameters, for this last identification, are shown in Table 3.

Table 3 Identified values for the best correlation mesh, the element size of which is 84×122 pixels
Full size table

Let us stress that the best boundary conditions (displacement and forces at the contact points) applied to the finite element analysis are identified by the FEMU in order to be consistent with the measurement extracted from the experiment. It is observed that the horizontal force F X taken into account in the modeling is far from being negligible. Indeed it is the order of 8.6 % of the applied vertical load. This horizontal force—which would typically be ignored in modeling—is due to the asymmetry of the test, found consistently in the identified values of the two outer applied vertical displacements.

The final estimate of the out-of-plane shear modulus is finally determined with an accuracy of about 1.5 %. It is to be observed that the main source of uncertainty results from the required modeling assumption which ignores the material microstructure. The camera noise contributes to about 0.5 %, a rather small amount as compared to the homogeneity assumption.

However, the results differs from other experiments led by SNECMA on Iosipescu tests by a significant amount (much larger than the uncertainty level). One possible explanation of this discrepancy is the fact that the stress state is very heterogeneous for the latter tests, and for a composite material having a coarse microstructure, the relevance of an equivalent homogeneous material becomes questionable. The required scale separation between the microstructure and the spatial variability of the stress field is poorly satisfied. To clarify this issue, it would be extremely informative to apply a strategy similar to the one proposed herein, based on a combination of DIC and FEMU, to the Iosipescu test.

Conclusion and Perspectives

This study was conducted on a model specimen with a coarse periodic weaving, although an homogenized elastic property was sought. The applicability of an identification procedure based on DIC and FEMU on such a material has been demonstrated. A continuous pathway has been paved from test images to the identified property allowing for a tracking of all sources of errors and uncertainties. One major source of uncertainty was shown to be due to the camera noise. However, the most limiting one is the constraint to ignore the influence of the microstructure although it could be clearly revealed by the DIC analysis.

The simplicity of the present methodology opens new horizons to identify elastic properties (or more generally stiffness) of complex materials and structures under arbitrary loadings (preserving however a two-dimensional kinematics). The detailed tracking of uncertainties, including camera noise, down to the final identification result not only provides an answer to the sough properties, but also a way to evaluate in an objective fashion the value of the determined information. Extension of the present approach to inelastic behaviors will be investigated in the future.