Measurement of Orthogonal Stress Gradients Due to Impact Load on a Transparent Sheet using Digital Gradient Sensing Method

Abstract

A full-field optical method called Digital Gradient Sensing (DGS) for measuring stress gradients due to an impact load on a planar transparent sheet is presented. The technique is based on the elasto-optic effect exhibited by transparent solids due to an imposed stress field causing angular deflections of light rays quantified using 2D digital image correlation method. The measured angular deflections are proportional to the in-plane gradients of stresses under plane stress conditions. The method is relatively simple to implement and is capable of measuring stress gradients in two orthogonal directions simultaneously. The feasibility of this method to study material failure/damage is demonstrated on transparent planar sheets of PMMA subjected to both quasi-static and dynamic line load acting on an edge. In the latter case, ultra high-speed digital photography is used to perform time-resolved measurements. The quasi-static measurements are successfully compared with those based on the Flamant solution for a line-load acting on a half-space in regions where plane stress conditions prevail. The dynamic measurements, prior to material failure, are also successfully compared with finite element computations. The measured stress gradients near the impact point after damage initiation are also presented and failure behavior is discussed.

Introduction

The optical transparency requirement is an essential characteristic of solids used in many engineering applications such as automotive windshields, electronic displays, aircraft windows and canopies, hurricane resistant windows, bullet resistant enclosures, personnel helmet visors, and transparent armor materials used by the military [1, 2]. In applications involving military armor, helmet visors and personnel enclosures, the ability of a material to continue to remain transparent and bear load after impact is critical for personnel safety. Over the years, there has also been a great deal of interest in developing novel transparent composites for a variety of other engineering applications [3–6] as well. In all these situations, understanding the mechanical failure characteristics of transparent materials in general and under stress wave loading conditions in particular is critical.

Performing full-field, non-contacting, real-time measurement of deformations, strains, and stresses during stress wave dominant events in solids, transparent or otherwise, is rather challenging due to stringent spatio-temporal resolution requirements. Over the years, a few optical methods have been successfully used for understanding failure mechanisms involved and for quantifying the associated engineering parameters. For example, de Graaf [7] used photoelasticity to witness stress waves around a dynamically growing crack in steel. Photoelasticity continues to be popular in the study of fast fracture/failure events [8–10]. The method of caustics was popular for studying dynamic fracture mechanics and contact mechanics problems in the 1980s [11, 12] in view of a relatively simple optical setup and stress intensity factor extraction procedure. The presence of triaxial stress zone near a crack tip and the associated difficulty to position the initial curve (that produces the optical caustic) outside the zone of triaxiality during stress-wave loading event led to a shift away from this method [13]. In its wake, a full-field lateral shearing interferometer called Coherent Gradient Sensing (CGS) attained popularity. Its applicability to transparent and opaque solids and insensitivity to rigid body motions/vibrations [14–17] contributed to its viability to experimental fracture mechanics. Moiré interferometry has also been used in dynamic fracture studies to measure in-plane displacement fields with sub-micron sensitivity [18]. The need for coherent optics and an elaborate specimen preparation involving high-frequency diffraction gratings on engineering substrates to implement the method has limited its usage to a few dynamic studies. There are also a few early reports of laser speckle photography and holographic interferometry to study dynamic problems [19, 20] as well.

The above mentioned techniques are generally based on optical interference principles and require special material (optical) characteristics (e.g., optical birefringence for photoelasticity), coherent optics and/or special surface preparation (e.g., moiré interferometry and CGS) to be implemented successfully. In recent years, however, due to advances in digital high-speed photography and image processing, and ubiquitous computational power, digital image correlation (DIC) method [21] has become popular for studying transient problems. The work of Chao, et al., [22] to study deformations around a propagating crack with the aid of a Cranz-Schardin film camera is an early attempt in this direction. They digitized analog film recordings using a scanner to correlate successive images and estimate displacements. With the advent of modern digital high-speed cameras offering recording rates from a few thousand to a few million frames per second, there has been a significant interest in this method for studying highly transient problems [23–26]. The fact that this method (i) needs little or no surface preparation, (ii) uses white light illumination, and (iii) can be fashioned to measure 2D (planar) or 3D displacement components are indeed very attractive. In this context, it is worth noting that the state-of-the-art digital image correlation method can measure macro- and micro-scale displacements very accurately [27]. The measured strains from DIC, however, tend to be of a lower accuracy due to reasons such as first order representation of displacement gradients or numerical differentiation of noisy displacement data [28]. This is an issue of significance particularly for investigating mechanical failures caused by stress risers producing steep deformation gradients. From this perspective, it is attractive to have a method that offers all the advantages of DIC yet capable of directly measuring stress gradients in the whole field near stress concentrators during dynamic events. Accordingly, a full-field optical method called Digital Gradient Sensing (DGS) based on stress-optic effect and 2D DIC principles has been proposed recently by the authors for measuring small angular deflections of light rays caused by stresses in transparent planar solids [29]. In mechanically loaded planar objects, the angular deflections can be related to spatial gradients of stresses when plane stress conditions hold. In this paper, the feasibility of this new method to study evolution of transient stress gradients in the vicinity of an impact loaded edge of an elastic sheet is examined.

In the following, first the experimental method of DGS, its working principle and the governing equations are presented. After discussing issues related to material homogeneity and measurement accuracy of DGS method, stress gradients in the load point vicinity of a statically applied edge load on a transparent PMMA sheet are presented and discussed. Subsequently, the extension of the method to transient impact loading experiments using digital high-speed photography is described. The time-resolved stress gradients and the estimated load histories in the impact point vicinity are presented. These results are compared to those from a complementary finite element analysis of the problem. Stress gradient data pertaining to post-failure initiation are also presented and discussed. Lastly, the results are summarized and conclusions are drawn.

Experimental Procedure

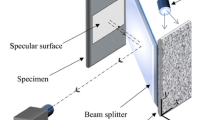
Figure 1 shows the experimental schematic for the DGS method. A transparent planar specimen to be investigated is placed between a digital camera and a target plane coated with random speckles. Ordinary white light sources are used for illuminating the speckle/target plane uniformly. The recording camera fitted with a long focal length lens is used to image speckles from a relatively large distance from the specimen (L) and target (L + Δ) [28] planes. (The distance between the mid-plane of the specimen and the target is Δ.) By using a relatively small lens aperture (or a high F^#) a good depth of focus is achieved. This is also helpful in recognizing the specimen features (e.g., specimen edges) in the recorded image. An image of the speckle pattern on the target plane is captured under no-load condition and is used as the reference or ‘undeformed’ image. The ‘deformed’ image of the speckle target is captured during loading. The speckles in the deformed image are displaced relative to the undeformed ones due to local changes in thickness and refractive index of the specimen [29]. If a point in the reference image is displaced by δ _x and δ _y in the x- and y-directions, respectively, due to deformation the angular deflection fields, ϕ _x and ϕ _y can be obtained since Δ is known. These angular deflections can be related to in-plane stress gradients, as discussed in the following section.

Fig. 1

Schematic of the experimental set up for Digital Gradient Sensing (DGS) method to determine planar stress gradients in phase objects

Working Principle

In Fig. 1, let the in-plane Cartesian coordinates of the specimen and target planes be (x, y) and (x ₀ , y ₀ ), respectively, and the optical axis of the setup coincide with the z-axis. Let the speckles on the target plate be photographed normally through the transparent specimen of nominal thickness B and refractive index n in its reference (undeformed) state. That is, a generic point P on the target plane, corresponding to point O on the specimen (object) plane, is recorded by the camera in the reference state. Upon imposing the load (say, force F acting on the edge of the specimen in Fig. 1), both refractive index and thickness changes occur throughout the specimen. A combination of these changes causes light rays to deflect. That is, the light ray OP in the reference/undeformed state now corresponds to OQ after the specimen deforms. By quantifying the vector PQ and knowing the separation distance Δ between the mid-plane of the specimen and the target, the angular deflection of the light ray relative to the optical axis can be determined.

Let $\widehat{i},\,\widehat{j}$ and $\widehat{k}$ denote unit vectors in the Cartesian coordinates defined with point O as the origin. When the specimen is undeformed, the unit vector $\widehat{k}$ is collinear with OP bringing point P(x ₀ , y ₀ ) to focus when imaged by the camera via point O(x, y). Upon deformation, the optical path is locally perturbed, thereby bringing a neighboring point ${\text{Q}}\left( {{x_0} + {\delta_x},\,{y_0} + {\delta_y}} \right)$ to focus. Here δ _x and δ _y denote components of the vector PQ in the x- and y-directions. Let the unit vector corresponding to the perturbed optical path OQ be,

$$ \widehat{d} = \alpha \widehat{i} + \beta \widehat{j} + \gamma \widehat{k}, $$

(1)

where α, β and γ are the direction cosines of $\widehat{d}$, and ϕ _x and ϕ _y are the components of angular deflection ϕ in the x-z and y-z planes, respectively, as shown in Fig. 2.

Fig. 2

Schematic of the working principle of DGS

If the initial thickness and refractive index of the specimen are B and n, respectively, the optical path change, δS _, for symmetric deformation of the specimen about the mid-plane in the z-direction, is given by the elasto-optical equation [30],

$$ \delta S\left( {x,y} \right) = 2B\left( {n - 1} \right)\int_0^{{{{1} \left/ {2} \right.}}} {{\varepsilon_{{zz}}}d\left( {{{z} \left/ {B} \right.}} \right)} + 2B\int_0^{{{{1} \left/ {2} \right.}}} {\delta n\,d} \left( {{{z} \left/ {B} \right.}} \right) $$

(2)

The two terms on the right hand side of the above equation represent the contribution of thickness-wise normal strain, ε _zz , and the change in refractive index, δn, to the overall optical path change, respectively. The refractive index change in an optically isotropic medium caused by the local normal stresses is given by the well known Maxwell-Neumann relation [31],

$$ \delta n\,x,y = {{D}_{1}}\left( {{{\sigma }_{{xx}}} + {{\sigma }_{{yy}}} + {{\sigma }_{{zz}}}} \right), $$

(3)

where D ₁ is the stress-optic constant and σ _xx , σ _yy , and σ _zz are normal stresses in the x-, y- and z-directions, respectively. Using the generalized Hooke’s laws for an isotropic, linear elastic solids, the normal strain component ε _zz can be related to normal stresses $\left( {{\varepsilon_{{zz}}} = \frac{1}{E}\left[ {{\sigma_{{zz}}} - \upsilon \left( {{\sigma_{{xx}}} + {\sigma_{{yy}}}} \right)} \right]} \right).$ That is, equation (2) can be written as,

$$ \delta S = 2B({{D}_{1}} - \frac{\upsilon }{E}\left( {n - 1} \right))\,\int_{0}^{{1/2}} {\left\{ {\left( {{{\sigma }_{{xx}}} + {{\sigma }_{{yy}}}} \right)\left[ {1 + {{D}_{2}}\left( {\frac{{{{\sigma }_{{zz}}}}}{{\upsilon ({{\sigma }_{{xx}}} + {{\sigma }_{{yy}}})}}} \right)} \right]} \right\}} \,d(z/B), $$

(4)

where, ${D_2} = {{{\left[ {\upsilon {D_1} + {{{\upsilon \left( {n - 1} \right)}} \left/ {E} \right.}} \right]}} \left/ {{\left[ {{D_1} - {{{\upsilon \left( {n - 1} \right)}} \left/ {E} \right.}} \right]}} \right.}$, E is the elastic modulus and υ is the Poisson’s ratio of the specimen. In equation (4), the term ${D_2}\left( {\frac{{{\sigma_{{zz}}}}}{{\upsilon \left( {{\sigma_{{xx}}} + {\sigma_{{yy}}}} \right)}}} \right)$ represents the degree of plane strain, which can be neglected for applications where plane stress assumptions (in-plane dimensions >> thickness of the specimen and σ _zz  = 0) are reasonable. Thus, for plane stress conditions, equation (4) reduces to,

$$ \delta S\left( {x,y} \right) \approx {{C}_{\sigma }}B\left( {{{\sigma }_{{xx}}} + {{\sigma }_{{yy}}}} \right), $$

(5)

where ${C_{\sigma }} = {D_1} - \left( {{{\upsilon } \left/ {E} \right.}} \right)\left( {n - 1} \right)$ is the elasto-optic constant of the transparent material. In equation (5), stresses σ _xx and σ _yy denote the average values over the specimen thickness.

The angular deflection of a generic light ray is caused by the change in the optical path due to elasto-optic effects. Hence, the propagation vector can be related to the optical path change. That is, using eikonal equations of optics [11, 12, 31], the propagation vector can be expressed as,

$$ \widehat{d} \approx \frac{{\partial (\delta S)}}{{\partial x}}\widehat{i} + \frac{{\partial (\delta S)}}{{\partial y}}\widehat{j} + \widehat{k}. $$

(6)

From equations (1), (5) and (6), for small angular deflections, the direction cosines α and β are proportional to in-plane stress gradients as,

$$ \begin{array}{*{20}{c}} {\alpha = \frac{{\partial (\delta S)}}{{\partial x}} = {{C}_{\sigma }}B\frac{{\partial \left( {{{\sigma }_{{xx}}} + {{\sigma }_{{yy}}}} \right)}}{{\partial x}},\quad {\text{and}}} \hfill \\ {\beta = \frac{{\partial (\delta S)}}{{\partial y}} = {{C}_{\sigma }}B\frac{{\partial ({{\sigma }_{{xx}}} + {{\sigma }_{{yy}}})}}{{\partial y}}.} \hfill \\ \end{array} $$

(7)

By performing a geometric analysis for the perturbed ray OQ, the relationship between the direction cosines α, β and angular deflection components ϕ _x , ϕ _y , respectively, can be established. Referring to Fig. 2, the perturbed ray subtends solid angles θ _x and θ _y with the x- and y-axes. The angular deflections ϕ _x and ϕ _y as defined earlier are also shown in Fig. 2. With reference to the planes defined by OQC, OQA, OPE and OPD,

$$ \cos {\theta_x} = \frac{{{\delta_x}}}{R},\,\cos {\theta_y} = \frac{{{\delta_y}}}{R},\,\tan {\phi_x} = \frac{{{\delta_x}}}{\Delta }\,{\text{and}}\,\tan {\phi_y} = \frac{{{\delta_y}}}{\Delta }, $$

(8)

where R $\left( { = \sqrt {{{\Delta^2} + \delta_x^2 + \delta_y^2}} } \right)$ is the distance between O and Q. From the above, expressions for the angular deflection components can be obtained as,

$$ \tan {\phi_x} = \frac{R}{\Delta }\cos {\theta_x}\,{\text{and}}\,\tan {\phi_y} = \frac{R}{\Delta }\cos {\theta_y}. $$

(9)

After recognizing that $\frac{R}{\Delta } = \sqrt {{1 + \frac{{\delta_x^2 + \delta_y^2}}{{{\Delta^2}}}}}$ in equation (9), for δ _x , δ _y <<Δ, ${\phi_x} \approx \cos {\theta_x} = \alpha$ and ${\phi_y} \approx \cos {\theta_y} = \beta$. Thus, for the case of small angular deflections (tanϕ _x,y  ≈ ϕ _x,y ) of light rays, equation (7) reduce to

$$ \begin{array}{*{20}{c}} {{{\phi }_{x}} \approx \alpha = {{C}_{\sigma }}B\frac{{\partial ({{\sigma }_{{xx}}} + {{\sigma }_{{yy}}})}}{{\partial x}},} \hfill \\ {{{\phi }_{y}} \approx \beta = {{C}_{\sigma }}B\frac{{\partial ({{\sigma }_{{xx}}} + {{\sigma }_{{yy}}})}}{{\partial y}},} \hfill \\ \end{array} $$

(10)

which serve as the governing equations for the method and can be used to obtain stress gradients when specimen parameters C _σ and B are known.

The above governing equations reveal that the angular deflections ϕ _x and ϕ _y , and hence the stress gradients in the x- and y-directions can be obtained by quantifying local displacements δ _x , δ _y when the separation distance Δ is known. The displacements can be evaluated by carrying out a standard 2D digital image correlation of speckle images recorded in the reference and deformed states of the specimen. A subtle but important point to note here is that displacements δ _x , δ _y are evaluated on the target plane whose coordinates are (x ₀ , y ₀ ), but can be replaced with the specimen plane coordinates (x, y) for Δ<<L [29]. Alternatively, a mapping function can be used to rectify the coordinates using paraxial approximation. It is also interesting to note that equation (10) shows that DGS method measures quantities identical to the ones measured by the Coherent Gradient Sensing (CGS) method [14, 23, 32]. However, unlike CGS, DGS can be used to measure two orthogonal stress gradients simultaneously and does not require any coherent optics. Furthermore, from equation (8) it can be noted that the measurement sensitivity depends on Δ and it can be chosen suitably during an experiment. Further, the measurement sensitivity for δ _x and δ _y is dictated by a number of parameters that affect 2D digital image correlation methods including speckle characteristics/size, parameters of the recording device (pixel size, sensor resolution, optical magnification) and image processing algorithm employed. For the sake of brevity, discussion of those issues is avoided here and can be readily found in the literature [27]. For the speckle and camera parameters used in this study, the in-plane displacement resolution is approximately 3 μm as demonstrated in the previous works [23, 24].

Optical Homogeneity and Measurement Accuracy

The DGS method assumes optical homogeneity of refractive index and specimen thickness in the unloaded/reference state. Mass produced materials such as PMMA sheets used in this work could have spatial variations of these parameters or an initial residual stress state when machined from a larger sheet stock. To examine this aspect and the resulting measurement errors, an experiment was carried out on a PMMA specimen using a setup shown schematically in Fig. 3 but without applying any mechanical load.

Fig. 3

Schematic of the experimental set up used to check for residual stresses in transparent planar specimens

A target plane decorated with a speckle pattern was placed at a relatively large distance of ~1575 mm from a recording camera (Nikon D3000 digital camera fitted with a 70–300 mm lens; aperture setting #11) and an extension tube. Then, the specimen, a clear, 9.3 mm thick PMMA plate, was mounted on a multi-axis translation stage with micrometer adjustments and introduced between the camera and the speckle plane. A 40 mm square window/aperture, placed in front of the specimen, was used to fix the region of observation during the test. The distance from the mid-plane of the specimen to the speckle plane, Δ, was 30 mm. The camera was focused on the speckle plane through the specimen and a reference image of the speckle pattern was recorded. Then, while the target plate was held stationary, the specimen alone was translated horizontally in steps of 1 mm and speckles were recorded at each step. (The choice of these translational steps was based on the maximum anticipated total displacement due to mechanically imposed loads, expected not to exceed a couple of mm.) The same was repeated in the vertical direction as well. A pixel resolution of 1936 × 1296 pixels (1 pixel = 38 μm on the target plane) was used for recording the speckles. In these translated positions, the speckles were recorded through points of the specimen different (shifted) from the corresponding points in the reference position. The presence of any non-homogeneity in the specimen between these shifted positions would cause the light rays to deflect. Hence, the images recorded at each translational step were considered ‘perturbed’ or ‘deformed’ images relative to the initial recording. By correlating the speckle images from the reference and perturbed states, the optical uniformity of the specimen was assessed. The horizontal and vertical angular deflection fields (ϕ _x and ϕ _y ) for one case corresponding to a horizontal translation of 2 mm is shown in Fig. 4. (Contour levels measured for all other translation distances were similar and are not presented here for brevity.) Clearly, the resulting field shows random angular deflections variation with the largest angular deflection magnitude of less than 1 × 10⁻⁴ radians. Thus, the accuracy of angular deflection measurements based on optical homogeneity is limited to values above this threshold. Further, the displacement measurement accuracy based on the type of speckles, the recording parameters, and the correlation algorithm used in this study is 2–3 μm [23, 24]. This also translates into an angular deflection measurement accuracy of 0.5 × 10⁻⁴ to 1 × 10⁻⁴ radians when the separation distance (Δ) between the target and the specimen is in the 20–30 mm range. Thus, for the measurements to be credible, the load induced angular deflections during experiments should exceed this value.

Fig. 4

Contour plots of ϕ _x (left) and ϕ _y (right) fields corresponding to a horizontal specimen translation of 2 mm of the PMMA specimen. Contour labels are in radians

Quasi-static Line-load on an Edge of a Sheet

Experimental Details

A stress concentration problem of quasi-statically applied line-load on the edge of a large planar sheet was first studied using the DGS method. A 180 × 69.5 mm² rectangular sheet of clear PMMA specimen (elastic modulus = 3.3 GPa, Poisson’s ratio = 0.35 and C _σ = −1 × 10⁻¹⁰ m²/N) of thickness (B) 9.4 mm was used for this experiment. A photograph of the experimental setup is shown in Fig. 5. The specimen was placed on a flat rigid platform and subjected to line-loading using a cylindrical steel pin (diameter 7.7 mm). An Instron 4465 universal testing machine was used for loading the specimen in displacement control mode (cross-head speed = 0.005 mm/sec). A target plate painted with random black and white speckles was placed at a distance Δ = 30 mm away from the specimen mid-plane (Fig. 1). A few heavy black dots (see, Fig. 6) were marked on the speckle plane to relate the image dimensions to the actual specimen/target dimensions. A Nikon D100 digital SLR camera with a 28–300 mm focal length lens (aperture setting #11) and an extension tube were used to record speckles through the specimen in the load point vicinity. The camera was situated at a distance (L) of approximately 1040 mm from the specimen.

Fig. 5

Experimental setup used to measure angular deflections of light rays caused by a deformed PMMA sheet subjected to a quasi-static, compressive line-load

Fig. 6

Schematic of the quasi-static line-load problem and a representative deformed image

A reference image of the target was recorded through the transparent specimen in the region of interest at a small load of a few Newtons (<5N). As the load was increased gradually, speckle images were recorded using time-lapse photography (12 frames per minute). One of the speckle images in the load point vicinity corresponding to a 3520N load is shown in Fig. 6. It shows that due to deformation of the specimen, the speckles are noticeably smeared very close to the loading point whereas they appear relatively unaffected at far-away locations. The digitized speckle images (1504 × 1000 pixels) recorded at different load levels were correlated with the one corresponding to the reference condition using a 2D digital image correlation software ARAMIS^®. As described previously, an array of in-plane speckle displacements on the target plane (and hence the specimen plane) was evaluated and converted into local angular deflections of light rays ϕ _x and ϕ _y . A facet/sub-image size of 15 × 15 pixels (1 pixel = 36.5 μm on the target plane) without any overlap was used in the image analysis for extracting displacement components.

Comparison of Experimental and Analytical Fields

Figure 7 shows the resulting contours of ϕ _x and ϕ _y for three representative load levels in a reduced square region around the loading point. It is important to note that, accounting for rigid body motions and imposing appropriate boundary conditions of the problem to quantify the contour levels for further analysis is needed. That is, in the current problem, the boundary conditions such as asymmetric stress gradients in the y-direction relative to the x-axis, symmetric stress gradients in the x-direction about the x-axis, and vanishing stress gradients far away from the loading point could all be used.

Fig. 7

Measured ϕ _x (row 2) and ϕ _y (row 3) contours near the loading point for different load levels. Contour interval = 1 × 10⁻³ radian. (The left vertical edge of each image corresponds to the loading edge where F acts at the origin)

Knowing that the plane stress field near the line-load acting on an elastic half-space is described by the Flamant problem [33] for which,

$$ ({{\sigma }_{{xx}}} + {{\sigma }_{{yy}}}) = {{\sigma }_{{rr}}} = - \frac{{2F}}{{\pi B}}\frac{{\cos (\theta )}}{r},\,{{\sigma }_{{\theta \theta }}} = 0,\,{{\sigma }_{{r\theta }}} = 0, $$

(11)

where F is the load, B is the thickness of the half-space and (r, θ) are the polar coordinates, as shown in Fig. 6. Note that the hoop and shear stresses vanish and $\left( {{\sigma_{{xx}}} + {\sigma_{{yy}}}} \right) = \left( {{\sigma_{{rr}}}} \right)$ for plane stress. Furthermore, the radial stress σ _rr becomes singular/unbounded as the loading point (r → 0) is approached. From equations (10) and (11),

$$ {{\phi }_{x}} = {{C}_{\sigma }}B\frac{{\partial ({{\sigma }_{{rr}}})}}{{\partial x}}\quad {\text{and}}\quad {{\phi }_{y}} = {{C}_{\sigma }}B\frac{{\partial ({{\sigma }_{{rr}}})}}{{\partial y}}. $$

(12)

Using equations (11) and (12), the expressions for ϕ _x and ϕ _y fields become,

$$ {{\phi }_{x}} = {{C}_{\sigma }}B\frac{{2F}}{{\pi B}}\frac{{\cos \,(2\theta )}}{{{{r}^{2}}}},\,{{\phi }_{y}} = {{C}_{\sigma }}B\frac{{2F}}{{\pi B}}\frac{{\sin \,(2\theta )}}{{{{r}^{2}}}}. $$

(13)

For comparison, the experimental and analytical angular deflection contours for a representative load case of F = 2022N are shown in Fig. 8. The dominant stress triaxiality where plane stress assumptions are violated is expected in regions close to the loading point. In cracked bodies where a stress singularity of r ^−1/2 occurs, a region of dominant stress triaxiality is shown to exist near the crack tip ($0 \leqslant {{r} \left/ {B} \right.} \leqslant {{1} \left/ {2} \right.}$) [30]. Based on that observation, it is reasonable to expect that stress triaxiality to dominate over a region of similar size in the current case as well. Hence agreement between analytical solutions and experimental measurements is not expected at least up to r/B = 0.5. This region is shown in Fig. 8 as the one bounded by a semi-circle centered at the origin. In the region outside the zone of dominant triaxiality, a good qualitative and quantitative agreement between experimental and analytical contours is apparent.

Fig. 8

Comparison of experimental and analytical angular deflection (top: ϕ _x and bottom: ϕ _y ) contours for F = 2022N. Contour levels are in 1 × 10⁻³ radians

The ϕ _x and ϕ _y data corresponding to a particular applied load can be used to back calculate the load using equation (13). Figure 9 shows the plot of calculated load at each measurement point (sub-image) as a function of r/B along θ = 0° and θ = 45° from ϕ _x and ϕ _y fields, respectively, for the case of F = 2022N. From the graph, it can be seen that, after an initial non-conformity up to r/B ~ 0.5–0.6, the extracted load values agree with the applied load quite well.

Fig. 9

Comparison of experimentally extracted load to the known applied load; quasi-static line-load problem

Dynamic Line-load on an Edge of a Sheet

Experimental Details

A photograph of the experimental setup employed for studying the problem of dynamic line-load acting on the edge of a planar sheet using DGS is shown in Fig. 10. The loading device consisted of an Al 7075-T6 long-bar (2 m long, 25.4 mm diameter) with a cylindrical (bull-nose) head, a gas-gun and a high-speed digital image acquisition system. The long-bar was aligned with the gas-gun barrel containing a 305 mm long, 25.4 mm diameter cylindrical striker also made of aluminum. A Cordin model-550 ultra high-speed digital camera equipped with 32 CCD sensors and a five-facet rotating mirror, and two high-energy flash lamps was used for recording speckles. A computer connected to the camera was used to control parameters such as trigger delay, flash duration, framing rate and image storage. The specimen, a 129 × 67.5 × 9.4 mm³ clear PMMA plate, was placed on an adjustable platform and its long edge was registered against the cylindrical head of the long-bar as shown in Fig. 10. The loading was initiated by suddenly releasing the compressed air in the gas-gun cylinder using a solenoid valve to propel the striker placed inside the barrel. The accelerating striker impacted the long-bar and initiated a compressive stress wave that traveled along the length of the bar before imparting a transient line-load to the edge of the specimen. An electrical circuit, closed when the striker contacted the long-bar, was used to trigger a delay generator which in turn activated the camera with a user-specified delay. A strain gage (CEA-13-062UW-350 from Vishay micro-measurements) affixed to the long-bar, and connected to a LeCroy digital oscilloscope via an Ectron signal conditioner was used to measure the strain history (Fig. 11) in the long-bar during loading [34]. The measured strain history was used to calculate the particle velocity history in the specimen at the specimen/bar interface.

Fig. 10

Experimental setup used to measure angular deflections of light rays caused by a deforming transparent specimen when subjected to dynamic line-load (top). Close-up of the specimen, speckle target, and the long-bar (bottom)

Fig. 11

Measured strain history in the long-bar used to deliver a dynamic line-load on the edge of the transparent PMMA specimen. (time = 0 corresponds to the start of data acquisition and not impact loading)

The distance between the specimen and the camera lens plane (L) was ~1000 mm and the one between the specimen mid-plane and the target plane (Δ) was 30 mm. Using the high-speed camera, a set of 32 reference (undeformed) images, one for each sensor, were first captured under no-load condition at 200,000 frames per second. Next, the specimen was subjected to a dynamic line-load using the long-bar setup. During loading, a set of 32 consecutive images of the deforming specimen were captured at the same framing rate. The deformed-undeformed image pairs for each of the 32 CCD sensors were then correlated to obtain the in-plane displacement fields, δ _x and δ _y . A facet/sub-image size of 15 × 15 pixels (1 pixel = 29.2 μm on the target plane) without any overlap was used in the image analysis for extracting displacement components. The displacement fields were then used to compute the angular deflection fields (ϕ _x and ϕ _y ), and are shown in Fig. 12. Also shown in Fig. 12 are the corresponding speckle images recorded during the dynamic event. Appropriate boundary conditions were imposed as discussed previously for quantifying the contour levels.

Fig. 12

Measured ϕ _x (row 2) and ϕ _y (row 3) contours near the loading point for different time instants. Contour interval = 1 × 10⁻³ radian. (The left vertical edge corresponds to the loading edge with impact load F(t) acting at the origin along the x-axis)

Comparison of Experimental and Numerical Angular Deflection Fields

The dynamic angular deflection fields were also numerically obtained by performing an elasto-dynamic finite element (FE) analysis to compare with the measured fields. The elastic modulus and Poisson’s ratio of PMMA used in the simulation were from ultrasonic pulse echo measurement of longitudinal and shear wave speeds [35] and mass density. Using the measured incident strain history, ε _I (t), in the bar during loading, and the measured parameters listed in Table 1, the transmitted particle velocity, V _T, was calculated using [36],

$$ {V_T} = {V_I}\frac{{2{\rho_I}{C_I}{A_I}}}{{{\rho_I}{C_I}{A_I} + {\rho_T}{C_T}{A_T}}}, $$

(14)

where V _I =C _I ε _I is the particle velocity in the incident bar, and ρ, C, and A denote the mass density, bar wave speed and area, respectively, and subscripts I and T denote the incident and transmitted values. (The area values used in this work were assumed to be proportional to length over which stress wave transmission occurred.) The transmitted particle velocity history shown in Fig. 13 was used as the input for FE computations using the structural analysis software package ABAQUS. The FE model consisted of 17,004 four-node quadrilateral elements (total DOF = 33964) with the smallest element of size ~ 0.5 mm. The numerical model was solved using explicit time integration scheme and the instantaneous in-plane stress invariant (σ _xx  + σ _yy ) field near the loading point was obtained. The representative (σ _xx  + σ _yy ) contours corresponding to the time instants in Fig. 12 are as shown in Fig. 14. From this field, the data along θ = 0°, 30° and 60° were extracted and the in-built differentiation scheme embedded in ABAQUS was used to compute spatial derivatives of (σ _xx  + σ _yy ) in the x- and y-directions. For comparison with measurements, these numerically obtained stress gradient data along with the experimental ones corresponding to a time instant 30 μs after the arrival of the stress waves at the specimen/bar interface are shown in Fig. 15. From the graphs, a rather good agreement between the computational and experimental results is evident beyond the triaxial zone (r/B ~ 0.5).

Table 1 Material properties of long-bar and PMMA specimen used in the dynamic line-load experiment

Fig. 13

Particle velocity history (bottom) used in the elasto-dynamic finite element model (top)

Fig. 14

Contour plots of in-plane stress invariant at various time instants during the dynamic loading of PMMA from finite element analysis. Dotted lines correspond to paths along 0°, 30° and 60° relative to the loading direction used for computing stress gradients

Fig. 15

Comparison of analytical, finite element and experimental angular deflections (column 1: ϕ _x and column 2: ϕ _y ) in PMMA plate subjected to a dynamic line load at t = 30 μs

The (σ _xx  + σ _yy ) contours in Fig. 14 are generally circular (except very close to the loading point) and are similar to the ones expected from the Flamant solution (equation (11)). This suggests that the functional form of the instantaneous deformation fields near the transient line-load can be approximated by the Flamant’s equations.¹ Accordingly, an attempt was made to use equation (13) for a dynamic line-load problem to extract the load history. Three sets of discrete values of angular deflection fields at various (r, θ) locations, excluding the immediate vicinity of the loading point (within r/B = 0.4, 0.5 and 0.6) where triaxial deformations dominate, were collected for each time instant. These values were then used along with equation (13) to extract three values of the instantaneous load (F(t)) using an overdeterministic least-squares analysis [37] for every time instant. For each time instant, the intermediate value is plotted in Fig. 16 and the error bars show the upper and lower bounds of F(t) resulting from the usage of three different data sets. The load history was also assessed from the strain gage measurements on the long-bar as, ${F_b}(t) = { }{E_b}{A_b}{\left( {{\varepsilon_I} + {\varepsilon_R}} \right)_b}$ where E _b (=72 GPa) and A _b are the elastic modulus and cross-section area of the bar, respectively, and ε _I and ε _R denote incident and reflected strain signals. Figure 16 shows a plot of measured load histories from the strain gage along with the ones from optical data analysis. The load history extracted using ϕ _x and ϕ _y fields and equation (13) is in good agreement with the strain gage measurements until damage/failure initiation (at ~40 μs after impact) occurs at the loading point. Beyond that, the two results noticeably deviate from each other. It is evident from the graph that just after the start of local crushing/pulverization of PMMA at ~40 μs, the measured load history starts to decrease for about 20 μs before rising again. These differences are to be expected as the closed form solutions used for optical data extractions do not hold in the post-failure regime. Further, the local crushing and micro-cracking events of PMMA are sensed by the strain gage data as a drop in the signal whereas the load extracted by analyzing the optical data from undamaged regions away from the load point/s lag in revealing this information. Furthermore, the optically extracted loads based on over-deterministic analysis provide an averaged response over the region. The large error bars in the post-failure regime are due to the expanding zone of triaxiality as the failure front progresses (Fig. 17) during the dynamic event. Therefore, the optical data used for least-squares analysis had to be collected well beyond r/B = 0.5, based on the position of the instantaneous damage front. These load estimates thus correspond to optical data analyzed using measurements from 1.0 < r/B < 1.8. The corresponding errors in the post-failure regime were based on data analysis for different inner radii used during the analysis.

Fig. 16

Load histories measured using DGS (symbols) and strain gage (broken line). The agreement between the two is good up to the start of the material crushing/cracking at the impact point

Fig. 17

Failure progression (row 1) and corresponding angular deflection contours, ϕ _x (row 2) and ϕ _y (row 3) contours in PMMA plate subjected to a dynamic line load. Contour interval = 1 × 10⁻³ radian

Stress Gradients in the Post-failure Regime

The analytical and/or numerical solutions are generally valid only until the onset of failure—crushing and/or micro-cracking. In addition, they are dependent on assumptions associated with failure modes and post-failure material behavior. In such scenarios, only direct experimental measurements offer reliable data for structural analyses/design. In view of this, stress gradients even after the material has undergone cracking and crushing near the loading point is also presented. The first row in Fig. 17 shows failure progression in the specimen after the initiation of failure at the loading point. This causes the image correlation to fail in the region of intense damage. The highly saturated (or, decorrelated) gray scale around the loading point represents the damaged zone. The second and third rows in Fig. 17 show contours of ϕ _x and ϕ _y . The observed changes in contour density and their shapes relative to the ones prior to damage initiation qualitatively indicate contributions of a smeared loading front as well as the arrival of the reflected stress waves from the far edges of the specimen to the load point vicinity. Figure 18 shows photographs of the failed specimen as well as a close-up of the load point vicinity. Due to the dynamic load, PMMA is symmetrically chipped off from the plate relative to the mid-plane. A close-up of the failure surface reveals the typical mirror and hackle regions. References [38, 39] describe the mechanisms involved in the formation of conical chips in glass produced due to spherical indenters near the specimen edge. Irrespective of the indentation distance from the edge, early material failure has been shown to be characterized by a sub-surface median crack directly under the contact point. However, higher material compliance in the near-edge region and the bending moment experienced by a growing crack have been suggested as sources of chip formation when the indentation distance from the specimen edge is small (less than 0.05 mm) [38]. In the current case, the entire specimen thickness makes a line contact with the cylindrical impactor head. Given the symmetric nature of the contact, it is reasonable to expect symmetric chipping about the specimen’s mid-plane as in Fig. 18. Chai et al [39] add to the above inferences by attributing chip initiation and the radial striations in the hackle region to stress enhancement in the specimen edge and multiple stress-wave reflections at the edge respectively.

Fig. 18

Failed PMMA specimen after experiencing a dynamic line load on the edge (top). Close-up of the damaged/cracked region (bottom)

Conclusions

A full-field optical method called Digital Gradient Sensing (DGS) to measure angular deflections of light rays caused by in-plane stresses in transparent planar sheets under static and dynamic loading conditions has been developed and demonstrated. The method uses 2D digital image correlation technique to quantify deflections of light rays caused by non-uniform elasto-optical variations in planar phase objects subjected to mechanical loads. The governing equations to interpret the optical measurements are described. The analysis suggests that the angular deflection of light rays is related to the in-plane gradients of (σ _xx  + σ _yy ) under plane stress conditions. The method is demonstrated by measuring contact stress gradients due to statically and dynamically applied line loads acting on the edge of a PMMA sheet. The details of the experimental setup including those on high strain-rate loading and high-speed imaging are presented.

A test for optical homogeneity of PMMA sheet is first carried out to evaluate the reliability of measurements under imposed loads. The results indicate that the inherent optical anomalies in no-load conditions produce angular deflections that are at least an order of magnitude lower than the ones due to the applied loads. The reported angular deflections are significantly higher than the accuracy of the method (0.5 × 10⁻⁴–1 × 10⁻⁴ radians) assessed based on the smallest measurable displacement using image correlation for the chosen experimental/optical parameters.

The full-field angular deflections (ϕ _x , ϕ _y ) with respect to the two orthogonal in-plane (x, y) directions are successfully measured for specimens subjected to both quasi-static and dynamic line-loads. In regions outside the dominant zone of triaxiality, the measured angular deflections are in good agreement with the ones based on the Flamant solution for a line load on the edge of a half-space. For the impact loading case, the angular deflections are compared with numerical results obtained by performing a complementary elasto-dynamic finite element analysis of the problem using measured strain history on the long-bar as input. Based on the observed similarities in the static and dynamic stress invariant contours, the Flamant equations are used to estimate the load history from dynamic angular deflection fields through regression analysis of optical data in the impact point vicinity outside the zone of dominant triaxiality. The load history thus obtained agrees well with the one from strain gage measurements on the loading bar until the initiation of material failure. The angular deflections corresponding to post failure duration are also measured and reported.