Introduction

Chemical strengthening of glass was first studied by Kistler [1] as well as Acloque and Tochon [60] independently, who invented the currently widespread ion exchange technology in 1962. The ion exchange process is started by immersing the glass substrate into a molten salt bath, where smaller ions are replaced with larger ones in the surface layer of glass. Consequently, a residual stress profile develops in the glass [2–11]. Reviews on chemical strengthening of glass in general have been published by many authors [15, 52, 55, 61–65].

The development and use of chemically strengthened aluminosilicate glasses—e.g., Corning® Gorilla® Glass, Nippon Electric Glass Dinorex™, Schott Xensation™ Cover glass, and AGC Dragontrail™—and lithium aluminosilicate glasses [2]—e.g., SaxonGlass Ion-Armor™—has explosively increased during the last decade. Chemically strengthened aluminosilicate glass is used as protective cover glass due to its high scratch and impact resistance [3, 4]. In a recent report, chemically strengthened aluminosilicate glass was proven suitable as mirror foil for future X-ray telescopes [5] and as protective coating of space solar cells [6]. The unique mechanical properties of lithium aluminosilicate glass—ultra-high surface compression stress, deep compressive stress layer, and impact resistance—have made this glass type suitable as a layer of composite armor plate [2, 3]. Those mechanical properties are directly determined by the residual stress profile in the surface layer of chemically strengthened glass.

Build-up and relaxation of stresses in chemically strengthened glass has been investigated by many authors [7–10]. Sane and Cooper [7] concluded that the longer the ion exchange time, the greater will be the depth of the compressive stresses developed, whereas the maximum stress will be reduced. Higher salt bath temperature also causes the relaxation of stresses [8].

Non-destructive residual stress profile measurement in micron-scale has proven to be a very hard task to accomplish. Available methods can be divided into destructive (transmission photoelasticity with the use of polarization microscopy, Bradshaw’s layer removal method [11] and Sglavo’s curvature measurement method [12]) and non-destructive ones (Kishii’s differential surface refractometry method [13]). Comparative study was carried out by Pan et al. [14] to investigate chemically strengthened aluminosilicate glasses using transmission photoelasticity, Bradshaw’s method, and Kishii’s technique.

Most commonly used destructive optical method for stress profile measurement in chemically strengthened glass is based on transmission photoelasticity—a slice is cut from the sample and measured with a polarization microscope using a Berek compensator [15]. The cutting process can lead to anomalous stress profiles. Sane and Cooper [16] showed that the stress profile in a sliced sample will show a tension maximum, which was not present in the unsliced plate. Jannotti et al. [17] measured the stress profile in a chemically strengthened lithium aluminosilicate glass, but the sample had to be specifically prepared for this purpose. The two opposite surfaces of the glass sample that were perpendicular to the light propagation direction were ground and polished off to remove the layers that could influence the measurement result. It is also possible to leave those surfaces un-strengthened by coating them with a thin film of tin oxide-antimony (a method developed by Mochel [18] and used by Garfinkel and King [19]) to block ion exchange process. Applying transmission photoelasticity to measure the stress profile can only be possible if the sample is prepared as described or cut. Automatic transmission polariscope AP-07 [20] (GlasStress Ltd.) that is equipped with magnification objective can also be used [21] instead of a manually operated polarization microscope.

Cutting a sample that has high surface stresses can cause it to instantly shatter into small pieces [22]. This so-called frangibility has recently been described by Tang et al. [23] and Gulati [66]. As with thermally tempered glass, the occurrence of instant shattering is more dependent on the central tensile stresses than the surface stresses—e.g., it depends to a large extent on the thickness of glass.

Bradshaw [11] introduced a method based on etching away the surface layers and measuring the corresponding tensile stress change in the central layer of the glass using scattered light method. In order to achieve increased accuracy, Abrams et al. [24] replaced the scattered light measurement with transmission photoelasticity for central tension measurement in the Bradshaw’s method. Sglavo et al. [12] introduced curvature measurements for determining the stress profile in chemically strengthened glass. The method is based on etching away layers from one side of the chemically strengthened glass and measuring the corresponding surface curvature change.

The method of differential surface refractometry with guided waves (DSR) [13], which is the only non-destructive method available, is based on passing light into a chemically strengthened glass via a coupling prism. The angle of incidence is chosen so that the light splits into an extraordinary ray and an ordinary ray, and then bends back to the surface, and the exit points are indicators of the underlying stress profile. Multiple internal reflections and exiting light produce observable fringe pattern in infinity. Two separate fringe patterns are recorded—one for the extraordinary ray (also referred to as TM-wave) and other for the ordinary ray (TE-wave). The DSR method presented by Kishii [13] assumes that the stress profile is linear, which makes it unsuitable for measuring stress profiles with complex shape encountered in chemically strengthened lithium aluminosilicate glass or double ion-exchanged [24–27] glass. The method of surface refractometry can be considered as indirect measurement because no info is gathered from specific depth, but it relies on analysis of fringe pattern produced by resurgent light. Two different stress profiles can produce the same interference pattern.

In Kishii’s DSR method light penetrates only a few tens of microns beneath the surface, hence the depth scan is very limited with this method. Commercially available device FSM-6000 (Luceo Co., Ltd.), based on Kishii’s method, is able to measure compressive stresses in the 100-μm-thick surface layer. The latest refractometric results were presented by Thirion et al. [28], who used FSM-6000 to investigate the stress profiles of chemically strengthened glass after exposure to high electric fields. Roussev and Young [29] suggested in their recent patent that using immersion oil with refractive index 1.72 instead of 1.64 can enhance fringe contrast. According to manufacturers of FSM-6000LEIR [59], curved stress profiles can be measured using infrared light, but no scientific analysis has been published to confirm the validity of FSM-6000LEIR approach compared to other methods.

Coherence tomography is claimed to be suitable for non-destructive stress profile measurement in chemically strengthened glass in a recent patent by Sheldon et al. [30], but no direct scientific proof about the applicability of the method has yet been published. The patent info does not contain any measured stress profiles.

The influence of light ray bending on the scattered light photoelasticity has not been investigated in previous studies. Hecker and Pindera [31] studied the effect in the transmission photoelasticity, an approach called strain-gradient method. They proposed to take the overall deflection of the light ray into consideration in refining the measurement results. Aben [32, 33] investigated light ray bending in case of axi-symmetric strengthened glass. Brodland and Dolovich presented the ray tracing approach and calculated stresses in a thermally tempered glass plate [34]. Dolovich and Gladwell developed iterative methods in transmission photoelasticity [35, 36].

The possibility of scattered light method was predicted by James Clerk Maxwell [37] in 1853 and experimentally discovered by Weller [38] in 1941. Introduction of laser as a light source for the method was made by Bateson et al. [39]. The scattered light method for stress profile measurement in strengthened glass plates has been studied by many authors [40–45]. Cheng [40] introduced oblique incidence method for stress profile determination without the use of a compensator. Cheng [41] also showed the possibility of dual-observation technique. Oblique incidence method for thermally tempered glass plates was developed to the level of automation by Anton [43]. Hödemann et al. [21] introduced confocality as a detection method of scattered light. Confocal microscopy allows to scan inside the light beam and to collect Rayleigh scattered light from a microscopic volume. Confocal mapping of a line along the laser beam propagation direction, using a micro-translation stage, is equivalent to the observation of a very narrow light ray passing through the glass.

In this article, a novel non-destructive gradient scattered light method for residual stress profile measurement in chemically strengthened glass is presented. The underlying theory is explained and the experimental results are presented.

The proposed method of stress profile measurement is demonstrated for a chemically strengthened lithium aluminosilicate (LAS) glass, which is known for its ultra-high surface compression stress (~1000 MPa) and large case depth (up to 1000 μm) [2, 17].

Gradient scattered light method

Importance of laser beam incidence angle

In order to achieve a spatial resolution high enough to measure the stress profile in chemically strengthened glass, a narrow laser beam is passed through the surface layer of the glass at a considerably large incidence angle of 81.9°. This way, the increased length of laser beam path becomes observable. For example, if laser ray is passed at incidence angle of 45° through the 100-μm-thick surface layer of a glass plate, then the light travels a path length of only 141 μm and the bending of light is almost non-existent. Now if the incidence angle is changed to 81.9°, the path length observable by camera becomes 709 μm. That results in up to five times increase in resolution.

Although, at such a large incidence angle, the light ray is on the verge of bending back to the surface and the deviation from straight line propagation must be taken into account in order to obtain the correct stress profile. To address the light ray bending influence, an iterative method is developed to determine the ray trajectories in glass and incorporate these results into the calculation of the stress profile.

In a previous version of the oblique incidence scattered light method [43] for stress profile measurement in thermally tempered glass plates, light was passed through the plate at an incidence angle of 45°. Micron-scale resolution needed for determining the stress profile in chemically strengthened glass is unreachable using the 45° incidence angle. Also, no ray bending occurs at such angle and straight ray inversion to calculate stress profile from optical retardation distribution is justified. Stress profile measurement results are published in many articles [43, 45–47]. Aben et al. [46] confirmed the linear relationship between modulus of rupture (MOR) and surface stresses of thermally tempered glass plates measured with 45° oblique incidence scattered light method. Investigated glass plates had surface stresses of about 7, 60, 120, and 160 MPa. The procedure of calculating the optical retardation along the laser beam path remains unchanged for the gradient scattered light method. Gradient scattered light method is a new development in terms of changing the incidence angle from 45° to 81.9° and adding an iterative approach to remove the influence of light ray bending from the measured residual stress profile.

Principle of the method

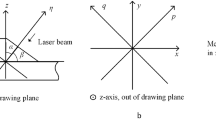
Consider a linearly polarized monochromatic light ray incident upon a flat uniformly chemically strengthened glass plate. Uniformly strengthened glass plate can be considered as a uni-axial crystal with the optic axis perpendicular to the surface. When a polarized beam of light is obliquely incident on the crystal’s optic axis, it is split into an ordinary ray (o-ray) and an extraordinary ray (e-ray). The e-ray is linearly polarized in the plane of optic axis and the o-ray perpendicular to that. The situation is depicted in Fig. 1. A global set of coordinates is defined as follows. The global x-axis lies in the incident plane and is parallel to the top surface of the glass. The global y-axis is perpendicular to the top surface of the glass and points into the glass. The global z-axis is chosen to form a left-handed triad with the x and y axes. We also define a local rectangular coordinate system \( x^{\prime} - y^{\prime} - z^{\prime} \) associated with the light ray (along the curved ray path), such that \( x^{\prime} \) is tangent to the ray, \( y^{\prime} \) is in the incident plane, and \( z^{\prime} \) is perpendicular to the incident plane. The clockwise angle between the \( x^{\prime} \) and \( y \) axes is \( \theta \).

Figure 1
figure 1

The experimental set-up for stress profile measurement. Laser beam is passed via a glass prism obliquely through the strengthened glass plate. From the observation directions of OD1 and OD2, that are at 45° to the surface of glass plate, the scattered light intensity distribution along the light path could be recorded

Full size image

Secondary principal stresses (or effective principal stresses) are defined as the stress components that are perpendicular to the propagation direction of the light ray. They induce birefringence and therefore a varying intensity distribution of scattered light is observed. Principal stress \( \sigma_{y} \) is fixed in the direction of the optic axis and is independent of the light ray propagation direction. If the light ray propagates through the glass perpendicular to the z-axis, birefringence is caused by secondary principal stresses \( \sigma_{z} \) and \( \sigma_{{y^{\prime}}} \), as seen in Fig. 1. The stress field defined in the global set of coordinates can be expressed in the local system via the stress transformation equations:

$$ \sigma_{{x^{\prime}}} = \sigma_{x} \sin^{2} \theta + \sigma_{y} \sin^{2} \theta + 2\tau_{xy} \sin \theta \cos \theta , $$
(1a)
$$ \sigma_{{y^{\prime}}} = \sigma_{x} \cos^{2} \theta + \sigma_{y} \sin^{2} \theta - 2\tau_{xy} \sin \theta \cos \theta , $$
(1b)
$$ \sigma_{{z^{\prime}}} = \sigma_{z} = \sigma \left( y \right), $$
(1c)

where \( \tau \) is shear stress. If Na+ ions, having an effective ionic radius of 98 pm, in glass substrate are replaced with larger ions such as K+ (r ionic = 133 pm), then in the middle of the glass, all tensile and compressive stresses are parallel to the surface of the glass and depend only on the depth y: \( \sigma_{x} = \sigma_{z} = \sigma \left( y \right) \). Away from the edges and in case of uniform strengthening, \( \sigma_{y} = 0 = \tau_{xy} = \tau_{yz} = \tau_{zx} \), because glass can freely swell in the direction of the y-axis. Hence in case of isotropic stresses parallel to surface, we can rewrite:

$$ \sigma_{{x^{\prime}}} = \sigma \left( y \right)\sin^{2} \theta , $$
(2a)
$$ \sigma_{{y^{\prime}}} = \sigma \left( y \right)\cos^{2} \theta , $$
(2b)
$$ \sigma_{{z^{\prime}}} = \sigma_{z} = \sigma \left( y \right). $$
(2c)

Secondary principal stresses \( \sigma_{{x^{\prime}}} \), \( \sigma_{{y^{\prime}}} \) and \( \sigma_{{z^{\prime}}} \) determine the refractive indices for light propagating in the \( x^{\prime} \)-direction by Maxwell stress-optic relations [37]

$$ n_{{y^{\prime}}} - n_{u} = C_{1} \sigma_{{y^{\prime}}} + C_{2} \left( {\sigma_{{z^{\prime}}} + \sigma_{{x^{\prime}}} } \right), $$
(3a)
$$ n_{{z^{\prime}}} - n_{u} = C_{1} \sigma_{{z^{\prime}}} + C_{2} \left( {\sigma_{{x^{\prime}}} + \sigma_{{y^{\prime}}} } \right), $$
(3b)

where \( n_{{y^{\prime}}} \) is the refractive index for the e-ray, \( n_{{z^{\prime}}} \) is the refractive index for the o-ray, and \( n_{u} \) is the refractive index of unstressed glass. Instead of being just a constant, the refractive index \( n_{u} \) can have compositionally induced depth dependence.

The parameters C 1 and C 2 are the absolute stress-optic coefficients of the material for the considered wavelength and their difference gives the photoelastic constant (stress-optic coefficient):

$$ C = C_{1} - C_{2} . $$
(4)

Explicit expressions of \( n_{{y^{\prime}}} \) and \( n_{{z^{\prime}}} \) for a given stress distribution \( \sigma \left( y \right) \) are obtained by combining Eqs. (2) and (3):

$$ n_{{y^{\prime}}} = n_{u} + \sigma \left( y \right)\left[ {C_{1} \cos^{2} \theta + C_{2} \left( {1 + \sin^{2} \theta } \right)} \right], $$
(5a)
$$ n_{{z^{\prime}}} = n_{u} + \sigma \left( y \right)\left[ {C_{1} + C_{2} } \right]. $$
(5b)

In case of a uniformly strengthened glass plate, the optic axis is perpendicular to the surfaces. Therefore, we can say that the e-ray is polarized in the plane of incidence (p-polarization), and the o-ray is polarized perpendicularly to that (s-polarization). If the optic axis is not perpendicular to the surfaces of the strengthened glass plate (for instance in case of non-uniform tempering), then the e-ray is not necessarily p-polarized.

As can be seen from Eq. (3a, 3b), the refractive index in the stressed glass depends on the polarization of light and birefringence appears. This means that if the incident laser beam is not completely s- or p-polarized, it will split into two separate beams when propagating through the glass (Fig. 1). If the incident light is completely s- or p-polarized, respectively, then only the o-ray or the e-ray is visible inside the strengthened glass plate.

If the glass is observed from direction OD3, then the curved trajectories of the rays could be experimentally measured, but only in case of flat and polished edge surface, which is usually not available. Therefore, a theoretical approach is more suitable in which the ray bending is calculated indirectly as a part of the scattered light method.

Ray tracing

According to Fermat’s principle, the path taken between two points by a light ray is the path that requires the least time. In inhomogeneous media, the path of least time is not necessarily a straight line and light rays become curved. The local curvature of a light ray in a specific spatial point depends on the refractive index gradient \( \nabla n \) in that point. The bending effect is the strongest when light propagates perpendicularly to the gradient vector. If the spatial dependence of the refractive index is fully known, then the trajectory of any light ray can be calculated by integrating the so-called ray equation [48]

$$ \frac{\text{d}}{{{\text{d}}s}}\left( {n\frac{{{\text{d}}\varvec{r}}}{{{\text{d}}s}}} \right) = \nabla n, $$
(6)

where ds is the differential length along the ray and dr is the resulting change in the position vector.

If a light ray is incident upon a flat piece of uniformly strengthened glass, then the refracted ray will be confined to the plane of incidence and therefore the ray equation can be rewritten in the global coordinates as

$$ n\frac{{{\text{d}}^{2} y}}{{{\text{d}}x^{2} }} = \left( {\frac{\partial n}{\partial y} - \frac{\partial n}{\partial x}\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)\left[ {1 + \left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)^{2} } \right]. $$
(7)

The solution \( y(x) \) of this equation describes the trajectory of the ray. The refractive index \( n = n\left( {x,y} \right) \) and its partial derivatives \( \partial n/\partial x \) and \( \partial n/\partial y \) can be directly calculated using (5a) or (5b) if the stress profile \( \sigma \left( {x,y} \right) \) is known. In our case, the stress does not depend on x, which yields \( \partial n/\partial x \) = 0 and the ray equation is further simplified to

$$ n\frac{{{\text{d}}^{2} y}}{{{\text{d}}x^{2} }} = \frac{\partial n}{\partial y}\left[ {1 + \left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)^{2} } \right]. $$
(8)

This second-order ordinary differential equation can be analytically solved for simple cases of \( \sigma \left( y \right) \) [34], but for more realistic stress profiles this becomes a tedious task and numerical methods are preferred.

Available numerical analysis packages typically contain methods for solving first-order ordinary differential equations and systems. We define new variables

$$ u_{1} = y, u_{2} = \frac{{{\text{d}}y}}{{{\text{d}}x}}, $$
(9)

to replace the second-order Eq. (8) with a system of two first-order equations.

$$ \begin{aligned} \frac{{{\text{d}}u_{1} }}{{{\text{d}}x}}& = u_{2} \hfill \\ \frac{{{\text{d}}u_{2} }}{{{\text{d}}x}}& = \frac{1}{n}\frac{\partial n}{\partial y}\left[ {1 + u_{2}^{2} } \right] \hfill \\ \end{aligned}. $$
(10)

An explicit Runge–Kutta method Dopri5 [49] was used to numerically integrate (10). The derivative

\( \partial n/\partial y \) at point \( y_{1} \) was calculated numerically:

$$ \left. {\frac{\partial n}{\partial y}} \right|_{{y_{1} }} = \frac{{n\left( {y_{1} + \frac{\delta y}{2}} \right) - n\left( {y_{1} - \frac{\delta y}{2}} \right)}}{\delta y}, $$
(11)

where \( \delta y \) is the step size.

Derivation of optical retardation along curved ray path

Model of layers

For a given stress profile, the observable scattered light intensity distribution depends on the incidence angle. As the refractive indices for e-ray and o-ray decrease from surface to the core, the light ray further bends while propagating through the strengthened glass, distorting the observable scattered light distribution. Optical retardation along the curved path is needed to take this effect into account. Optical retardation distribution can be directly calculated from scattered light intensity using a compensator (Fig. 1) and phase modulation method [42].

Wertheim law [50] in integral form combined with Eq. (3b) yields the optical retardation along a straight line segment (see Fig. 2) and can be written as

Figure 2
figure 2

Light ray passing through a flat glass plate divided into thin layers

Full size image
$$ \delta \left( {x^{\prime}} \right) = C\mathop \int \limits_{0}^{{x^{\prime}}} (\sigma_{z} - \sigma_{{y^{'} }} )\;{\text{d}}x^{\prime} = C\mathop \int \limits_{0}^{{x^{\prime}}} (\sigma_{z} - \sigma_{x} \cos^{2} \theta )\;{\text{d}}x^{\prime}. $$
(12)

The integral Wertheim law is a generalization of the classical Wertheim law for the case where stresses along the path of the light ray are not constant. Equation (12) indicates that by changing the incidence angle \( \theta \), the retardation distribution also becomes different for the same stress profile.

If a small enough segment along the curved ray path is taken under a scope, then the optical retardation (optical path length difference between the e-ray and o-ray) written for straight line can be implemented. In order to derive equations that describe optical retardation along a curved light ray path, for initially fully known residual stress profile \( \sigma \left( y \right) \), optical retardations along small straight line segments must be compiled. In case of real situation, those small straight line segments are infinitesimally small.

In order to calculate the optical retardation along each straight line segment, the incidence angle \( \theta_{i} \) must be known. Numerical solution of the ray Eq. (8) gives the trajectories of the curved e-ray and o-ray as a set of x and y coordinates.

E-ray and o-ray bend differently while propagating obliquely through chemically strengthened glass plate. Scattered light fringe pattern is observable only until the rays are spatially not yet totally separated, i.e., the separation distance is smaller than the beam diameter. Optical retardation distribution is measurable only if scattered light intensity pattern is observable. E-ray and o-ray have different ray propagation paths and both of them could be used to calculate the optical retardation along them. We calculated the optical retardation along the averaged x–y coordinates to minimize calculation errors. If \( (x_{\text{e}} ,y_{\text{e}} ) \) and \( (x_{\text{o}} ,y_{\text{o}} ) \) are trajectory coordinates for e-ray and o-ray, respectively, then the averaged \( \bar{x} = x_{\text{e}} = x_{\text{o}} \) and \( \bar{y} = (y_{\text{e}} + y_{\text{o}} )/2 \). For all these straight line segments, a separate incidence angle

$$ \theta_{i} = \arctan \left( {\frac{{\bar{x}_{i + 1} - \bar{x}_{i} }}{{\bar{y}_{i + 1} - \bar{y}_{i} }}} \right) $$
(13)

can be designated. Since \( \theta_{i} \) is inside glass it can also be called refraction angle.

Refraction on the surface

In order to calculate the paths of s- and p-polarized rays, one must also consider refraction at the interface between the prism and the glass sample. The prism has uniform refractive index \( n_{\text{prism}} \). Let \( \alpha \) be the incidence angle in the prism, which is typically a known experimental parameter. For the s-polarized ray, the refractive index in the glass sample, given by Eq. (5b), does not depend on the angle \( \theta, \) and Snell’s law can be directly applied to calculate the refraction angle:

$$ \sin\theta_{0s} = \frac{{n_{\text{prism}} }}{{n_{{z^{\prime}}} }}\sin\alpha = \frac{{n_{\text{prism}} }}{{n_{u} + \sigma_{\text{surf}} \left[ {C_{1} + C_{2} } \right]}}\sin\alpha, $$
(14)

where \( \sigma_{\text{surf}} \) is surface stress. However, the refractive index for the p-polarized ray, given by Eq. (5a), depends on \( \theta, \) and the following system of equations must be solved:

$$ \left\{ {\begin{array}{*{20}c} {\frac{\sin \alpha }{{\sin \theta_{0p} }} = \frac{{n_{{y^{\prime}}} }}{{n_{\text{prism}} }}} \\ {n_{{y^{\prime}}} = n_{u} + \sigma_{\text{surf}} \left[ {C_{1} \cos^{2} \theta_{0p} + C_{2} \left( {1 + \sin^{2} \theta_{0p} } \right)} \right]} \\ \end{array} } \right. $$
(15)

From the first equation, one obtains

$$ \sin^{2} \theta_{0p} = \frac{{n_{\text{prism}}^{2} }}{{n_{y'}^{2} }}\sin^{2}\alpha, $$
(16)
$$ \cos^{2} \theta_{0p} = 1 - \frac{{n_{\text{prism}}^{2} }}{{n_{{y^{\prime}}}^{2} }}\sin^{2}\alpha. $$
(17)

Substituting these into the second equation, regrouping and multiplying by \( n_{y'}^{2} \) yield a cubic equation for \( n_{{y^{\prime}}} \):

$$ n_{{y^{\prime}}}^{3} - \left[ {n_{u} + \sigma_{\text{surf}} \left( {C_{1} + C_{2} } \right)} \right]n_{{y^{\prime}}}^{2} - \sigma_{\text{surf}} \left( {C_{2} - C_{1} } \right)n_{\text{prism}}^{2} \sin^{2} \alpha = 0. $$
(18)

The cubic equation has a well-known analytic solution [51], which is not presented here for the sake of brevity. Finally, the refraction angle \( \theta_{0p} \) of the p-polarized ray is calculated using the obtained \( n_{{y^{\prime}}} \) in Snell’s law.

Optical retardation along curved ray path

A uniformly strengthened glass plate, with fully known stress profile \( \sigma \left( y \right) \), can be divided into a number of separate thin plates, as if a layer of glass is etched away and light ray enters new glass plate with surface stress \( \sigma \left( {y_{i} } \right) \) at an angle \( \theta_{i} \). Optical retardation distribution through each layer can be written from Eq. (12) in depth coordinates as

$$ \delta_{0} \left( y \right) = \frac{C}{{\cos \theta_{0} }}\mathop \smallint \limits_{0}^{y} \sigma \left( y \right)\sin^{2} \theta_{0} \;{\text{d}}y, $$
(19a)
$$ \begin{aligned} \delta_{1} \left( y \right) = \frac{C}{{\cos \theta_{1} }}\mathop \smallint \limits_{0}^{y} \sigma \left( {y + y_{1} } \right)\sin^{2} \theta_{1} \;{\text{d}}y \hfill \\ \quad \quad \quad \quad \quad \cdots \cdots \cdots \cdots \cdots \cdots \hfill \\ \end{aligned}, $$
(19b)
$$ \delta_{i} \left( y \right) = \frac{C}{{\cos \theta_{i} }}\mathop \smallint \limits_{0}^{y} \sigma \left( {y + y_{i} } \right)\sin^{2} \theta_{i} \;{\text{d}}y. $$
(19c)

Equation (19) does not provide a smooth optical retardation distribution because integral is starting from zero for each layer. To counter that let us introduce a new optical retardation \( \delta^{\prime}_{i} \left( y \right) \) that takes into account the optical retardation in previous layers as

$$ \delta^{\prime}_{i} \left( y \right) = \delta_{i} \left( {y - y_{i} } \right) + \delta^{\prime}_{i - 1} \left( {y_{i} } \right), $$
(20)

where \( \delta_{i} \left( {y - y_{i} } \right) \) is optical retardation in the i-th layer and \( \delta^{\prime}_{i - 1} \left( {y_{i} } \right) \) is the same equation for the previous layer. Optical retardation for all straight line segments must be compiled together in such a way that the beginnings and ends of \( \delta_{i} \left( y \right) \) are stitched together. In this way, a smooth continuous optical retardation distribution is formed. Optical retardation along the curved ray path can be written as a set of if-conditions:

$$ \delta_{c} \left( y \right) = \left\{ {\begin{array}{l} {\delta_{0} \left( y \right), y_{0} < y < y_{1} } \\{\delta_{1} \left( {y - y_{1} } \right) + \delta_{0} \left( y \right), y_{1} < y < y_{2} } \\ { \cdots \cdots\cdots\cdots\cdots\cdots } \\{\delta_{i} \left( {y - y_{i} } \right) + \delta^{\prime}_{i - 1} \left( y \right), y_{i} < y < y_{i + 1} } \\ \end{array} } \right. $$
(21)

Experimentally measured optical retardation is equivalent to \( \delta_{c} \left( y \right) \).

Straight ray inversion (SRI)

From \( \delta_{c} \left( y \right), \) two different stress profiles can be calculated using one of the following methods: (1) straight ray inversion that assumes rectilinear light ray propagation and uses only one constant incidence angle for entire path length; (2) curved ray inversion that uses different incidence angles \( \theta_{i} \) for each straight line segment. SRI yields accurate results for low incidence angles, such as 45°. By assuming that light passes through the glass plate along a straight ray path, the stress profile from \( \delta_{c} \left( y \right) \) can be calculated using Wertheim law in differential form, which can be directly derived from Eq. (12). Experimentally measured optical retardation \( \delta_{c} \left( y \right) \) is usually presented in depth coordinates, and therefore the stress profile through the thickness of the plate can be written as

$$ \sigma_{\text{sri}} \left( y \right) = \frac{\cos \alpha }{{C\sin^{2} \alpha }}\frac{\text{d}}{{{\text{d}}y}}\delta_{c} \left( y \right). $$
(22)

Curved ray inversion (CRI)

Equation (22) does not give an accurate stress profile because it neglects ray bending. To reconstruct the exact stress profile from \( \delta_{c} \left( y \right) \), a set of different incidence angles have to be applied. Curved ray inversion for stress profile calculation can be written:

$$ \sigma_{\text{cri}} \left( y \right) = \left\{ {\begin{array}{l} {\frac{{\cos \theta_{0} }}{{C\sin^{2} \theta_{0} }}\frac{\text{d}}{{{\text{d}}y}}\delta_{c} \left( y \right), y_{0} < y < y_{1} } \\ {\frac{{\cos \theta_{1} }}{{C\sin^{2} \theta_{1} }}\frac{\text{d}}{{{\text{d}}y}}\delta_{c} \left( y \right), y_{1} < y < y_{2} } \\ { \cdots \cdots \cdots \cdots \cdots \cdots } \\ {\frac{{\cos \theta_{i} }}{{C\sin^{2} \theta_{i} }}\frac{\text{d}}{{{\text{d}}y}}\delta_{c} \left( y \right), y_{i} < y < y_{i + 1} } \\ \end{array} } \right. $$
(23)

Exact refraction angles \( \theta_{i} \) along the laser ray path can only be known in case of an initially fully known stress profile. In a real situation, such information is not available. The only information we have is based on the assumption that experimentally measured optical retardation that is equivalent to \( \delta_{\text{c}} \left( y \right) \). To reconstruct the initially known stress profile from \( \delta_{\text{c}} \left( y \right) \), an iterative method can be applied.

Sequence of CRI iterative steps can be described as follows:

  1. (i)

    Straight ray inversion: stress profile is calculated from the optical retardation \( \delta_{\text{c}} \left( y \right) \) using Eq. (22). In a real situation of course, the \( \theta \) change due to ray bending, but \( \sigma_{\text{sri}} \left( y \right) \) is the best available option at the first step. SRI can alternatively also be called the zero-th iteration of CRI.

  2. (ii)

    Curved ray paths for e- and o-ray are calculated from \( \sigma_{\text{sri}} \left( y \right) \) that was found in the previous step.

  3. (iii)

    First iteration of curved ray inversion: stress is calculated from the optical retardation \( \delta_{\text{c}} \left( y \right) \) using the curved ray inversion Eq. (23) and by applying the angles obtained in the previous step.

  4. (iv)

    Curved ray paths are calculated from the stress profile found in the previous step.

  5. (v)

    Second iteration of curved ray inversion: stress profile is calculated from \( \delta_{\text{c}} \left( y \right) \) using the angles found in the previous step.

To completely remove the influence of light ray bending from the scattered light method, the iterative sequence should be repeated. The stress profile from \( \delta_{\text{c}} \left( y \right) \) can be calculated using the N-th iteration of curved ray inversion. This process does not give an exact stress profile at the first iteration, but increasingly more accurate stress profile is obtained at each new iteration. It is also needed to find out what is the optimal number of iterations to reconstruct stress profile.

Experimental procedure

Optical retardation along curved ray path is measured using a modified version of the scattered light polariscope (SCALP). A narrow laser beam with a wavelength of 630 nm is passed through the glass surface at an incidence angle of 81.9° as depicted in Fig. 1. A set of lenses was used in order to create a narrow laser beam with a diameter of 50–60 µm at focus and <150 µm at measurement area. Laser beam is with round-shaped cross-section. A glass prism with refractive index 1.515 at 630 nm was used to couple light into the surface layer of the glass. The polarization state of the laser beam was optically modulated using a compensator, and the scattered light intensity pattern along the laser path length was recorded by camera. From the intensity pattern, the optical retardation distribution was calculated using well-known methods [42, 43].

Prior to measuring, the surface of the sample was wiped clean with an optical cloth. Ultra-thin layer of Cargille immersion oil was used between the prism and the glass surface (as seen in Fig. 1) to allow unimpeded propagation of light. The experimental procedure is developed to the level of full automation and the measurement time is less than 10 s.

Chemically strengthened glass sample

Preparation of sample

Lithium aluminosilicate (LAS) glass sample, as a rectangular glass slab with dimensions 50 × 50 × 4 mm, was prepared using the roll-out process. Both sides of the glass plate were lapped and polished and as a result 50 × 50 × 3 mm, sample was obtained. The polished sample was sliced into a glass plate with dimensions 40 x 20 x 3 mm. The edge surfaces were polished after the slicing process.

The LAS glass was chemically strengthened in a molten salt mixture consisting of 80 mol% KNO3 and 20 mol% NaNO3. Varshneya et al. [2] found that the particular molar ratio of NaNO3/KNO3 produced the highest surface stresses (MOR was determined using ring-on-ring apparatus). Our sample preparation was as follows: The salt was put into a stainless steel container and then placed into an electric furnace. The glass plate was immersed into the molten salt heated up to the predetermined temperature of 480 °C. Sample was kept in these conditions for 8 h. Thereafter, the sample was taken out from the bath and naturally cooled down to room temperature. The salt purities of both KNO3 and NaNO3 were >99 %.

Experimental determination of glass composition

The composition of LAS glass was determined with energy-dispersive X-ray (EDX) microanalysis using Helios NanoLab 600 electron–ion dual beam microscope equipped with 50 mm2 X-Max SDD detector (Oxford Instruments). The energy of primary electrons was 10 keV. The spectra were analyzed using the standard procedures provided by INCA software (Oxford Instruments). To avoid charging effects, the sample was coated with a thin platinum film. Measurement was done on a sample that was already chemically strengthened. To reveal cross-sectional area, 1.7 mm of glass was lapped away from the edge. The elemental composition of LAS glass substrate was determined at a point on sample’s cross-sectional area 1.5 mm away from sample surface to avoid the influence of ion exchange. Li+ ions are not detectable by EDX microanalysis and the amount of Li2O was known from glass preparation. LAS glass composition was (in mol%) 69.9SiO2–13Al2O3–1.2MgO–9.8Li2O–0.4Na2O–0.2K2O–1.8TiO2–3.7ZrO2.

Measurement of refractive index

Refractive index of unstressed glass substrate was measured via V-block method using the refractometer KPR-2000 (Shimadzu Corp.). For this measurement, special rectangular-shaped glass sample with dimensions 20 × 20 × 10 mm was prepared and the deflection of light was measured. Refractive index of the LAS glass substrate \( n_{b} \) was calculated from Sellmeier equation and found to be 1.5208 at 630 nm. In our calculations, we neglect compositional influence of refractive index and take that \( n_{b} \approx n_{u} \). In order to get more precise results, compositional influence on refractive index should also be taken into account.

Experimental determination of stress-optic coefficient

Stress-optic coefficient was determined using the automatic birefringence measurement device ABR-10A-EX (Uniopt Co., Ltd.) as follows. Disk-shaped sample with diameter of 20 mm and thickness of 15 mm was prepared. A load was applied in the diametrical direction and the corresponding change in optical retardation was measured. The obtained stress-optical coefficient of LAS glass was \( C = 3.3 \) Br.

Determination of absolute stress-optic coefficients C 1 and C 2

Considering the difficulties in the experimental determination of the constants C 1 and C 2 , we suggest calculating them using a simplified way: it was found from literature [34, 52] that \( C_{1} \) is ~4 times smaller than \( C_{2} \). If assumed that such correlation is generally true, then we can calculate both absolute stress-optic coefficients by only knowing the experimentally measured C. By taking \( C_{1} \) = constant, \( C_{2} \) can be calculated from Eq (4) as \( C_{2} = C_{1} - C \). Some amount of error is introduced into calculation using such simplification. Absolute stress-optic coefficients were taken to be such that Eq (4) is fulfilled, hence \( C_{1} = - 7.77 \times 10^{ - 7} \) MPa−1 and \( C_{2} = - 4.077 \times 10^{ - 6} \) MPa−1. For example, BK-7 glass has reported [52] to have \( C_{1} = - 5.0 \times 10^{ - 7} \) MPa−1 and \( C_{2} = - 3.3 \times 10^{ - 6} \) MPa−1.

Numerical experiments

Simulation conditions

We performed initially a numerical simulation to test the gradient theory developed in section II by assuming a known model for the stress profile. The aim was to verify the validity of the proposed iterative approach to remove light ray bending influence from measured stress profile. We were checking whether the curved ray inversion grants the reconstruction of initially known stress profile and what would be the optimal number of iterations required.

A model stress profile through the thickness of a chemically strengthened glass can be described by

$$ \sigma \left( y \right) = \sigma_{\text{surf}} \cdot D^{ - m} \frac{m + 1}{m}\left[ {\left| {(D - y)^{m} } \right| - \frac{{D^{m} }}{m + 1}} \right], $$
(24)

where D is half-thickness and m is polynomial order. Equation (24) was formulated in such a way by Brodland and Dolovich [34] in order to produce symmetric, self-equilibrating stress distributions, like those that typically arise in a uniformly strengthened glass plate, for specimens that extend from y = 0 to y = 2D. Stress equilibrium through the thickness is granted:

$$ \mathop \smallint \limits_{0}^{2D} \sigma \left( y \right) = 0. $$
(25)

For thermally tempered glass, m = 2, which leads to the widely used parabolic formula for the stress profile. The precise shape of the stress profile in thermally tempered glass can be described by Indenbom’s [53] viscoelastic instant freezing layer theory or Narayanaswamy’s [54] theory that takes into account viscoelastic stress relaxation and also structural relaxation. It is noteworthy that both of the mentioned theories produce a stress profile that is very similar to a parabola.

The stress profile of a chemically strengthened glass can also be described by theories [55]. By increasing m in Eq. (24), the shape of the simulated stress profile becomes more characteristic to chemically strengthened glass.

Stress profile depicted in Fig. 4 was simulated using Eq. (24) with polynomial order \( m = 4 \), surface stress \( \sigma_{\text{surf}} = - 850 \)  MPa, and plate thickness of 400 µm. The absolute stress-optic coefficients were taken to be \( C_{1} = - 7.77 \times 10^{ - 7} \)  MPa−1 and \( C_{2} = - 3.35 \times 10^{ - 6} \) MPa−1 [34], refractive index of the glass prism \( n_{\text{prism}} = 1.515 \), refractive index of unstressed glass \( n_{u} = 1.515, \) and incidence angle \( \alpha = 86^\circ \). Note here that angle \( \alpha = 86^\circ \) is exaggerated (in the real experiment \( \alpha = 81.9^\circ \)) to make light ray bending more easily observable in Fig. 3.

Figure 3
figure 3

Curved ray paths of light propagating through stress field of chemically strengthened glass plate. Note, that the y-axis is magnified by a factor of approximately 16 compared to the x-axis

Full size image

Results

Figure 3 depicts curved paths of the e- and o-ray propagating through a chemically strengthened glass. According to Eq (14), the o-ray enters the glass at an angle of \( \theta_{0s} \) and from Eq (18), the e-ray at an angle of \( \theta_{0p} \).

Figure 4 (a) shows a comparison between the optical retardation \( \delta_{\text{c}} \left( y \right) \) along the curved ray path in depth coordinates (simulated using Eq. (21)) and the optical retardation \( \delta_{\text{s}} \left( y \right) \) (simulated directly from fully known \( \sigma \left( y \right) \) using Eq. (12)). Value of \( \delta_{\text{s}} \left( y \right) \) is zero at the entrance point (y = 0) and also at the exit point from glass plate (y = 2D). The increasing difference between \( \delta_{\text{c}} \left( y \right) \) and \( \delta_{\text{s}} \left( y \right) \) directly indicates the influence of light ray bending.

Figure 4
figure 4

a Initially known stress profile \( \sigma \left( y \right) \) (green line), optical retardation along curved ray \( \delta_{\text{c}} \left( y \right) \) (dashed blue line), optical retardation along rectilinear ray path \( \delta_{\text{s}} \left( y \right) \) (blue line). Negative values indicate compressive stresses and positive values tensile stresses. b Initially known stress profile \( \sigma \left( y \right) \)(dashed green line), straight ray inversion \( \sigma_{\text{sri}} \left( y \right) \) (black line), first iteration (blue line). The inset shows surface stress value as a function of CRI iteration number

Full size image

Our aim is to reconstruct \( \delta_{\text{s}} \left( y \right) \) from \( \delta_{\text{c}} \left( y \right) \). By applying SRI to \( \delta_{\text{c}} \left( y \right) \), a profile of \( \sigma_{\text{sri}} \left( y \right) \) is obtained with surface stress of −566 MPa (shown in Fig. 3b). Initially known stress profile had surface stress of \( \sigma_{\text{surf}} = - 850 \) MPa, which means that the result of SRI is wrong by 284 MPa.

Using the first iteration of CRI (step (iii) in the iterative sequence), surface stress results in −798 MPa (see Fig. 4b), which is closer to initially known surface stress, but still wrong by 52 MPa.

The 5th iteration of CRI gives a surface stress of −849.5 MPa (see inset graph in Fig. 4b), which is only 0.5 MPa wrong. Surface stresses calculated on each iteration converge rapidly to the initially known value of −850 MPa. The whole stress profile is reconstructed in the same manner.

By increasing the number of iterations, the stress profile gets only closer to initially known stress profile and does not start to add error instead of correction. In some cases, reported by Dolovich and Gladwell [35, 36], there is an optimal number of iterations which yields the most accurate reconstructed stress. In our case, by increasing the number of iterations, we gain only more accurate stresses. Hence we have shown with numerical experiment that CRI enables us to reconstruct the initially fully known stress profile.

Results of stress profile measurements in LAS glass

Figure 5 shows the experimentally measured optical retardation distribution fitted with a polynomial, from which the residual stress profile can be calculated using either SRI or CRI.

Figure 5
figure 5

Experimentally measured depth profile of optical retardation (blue circles) in chemically strengthened lithium aluminosilicate glass fitted with a polynomial (red line)

Full size image

Figure 6 depicts the residual stress profile of the LAS glass sample. Depth of the compressive layer (DOL), also named as case depth, was found to be 365 µm. Straight ray inversion gives surface stress −780 MPa. First iteration of curved ray inversion provided surface stress −1033 MPa and further iterations led to surface stress approaching to −1053 MPa (inset of Fig. 6), which can be taken as the correct result.

Figure 6
figure 6

Straight ray inversion stress profile (black line) and the first iteration of curved ray inversion (blue line). The inset shows surface stress value as a function of CRI iteration number. Negative values represent compressive stresses and positive values represent tensile stresses

Full size image

Compressive stress decreases almost linearly from a maximum value at the surface to a breaking point (at a depth of 59 µm and with a stress of 180 MPa). After the breaking point, the compressive stresses continue to decrease until reaching zero at a depth of 365 µm.

The nature of the breaking point can be explained by the fact that two types of ion exchanges took place in the LAS glass during chemical strengthening. Near the surface, Na+ ions were replaced with K+ and simultaneously Li+ ions were exchanged for Na+. After the breaking point, Li+-for-Na+ exchange process reached the depth of ~365 µm. The tensile stresses after the depth of zero-stresses are not the direct result of the ion exchange process, but just the result of stress equilibrium.

Precision and accuracy

The main source of error

The error of experimentally measured optical retardation does not accumulate along the laser beam i.e., the error at a specific point does not depend on the errors at the previous points. The main source of error originates from the fitting of experimental optical retardation with a polynomial. The precision is ±1.5 MPa for maximum stresses <20 MPa and ±3.7 % for stresses >20 MPa (Fig. 7).

Figure 7
figure 7

Precision: confidence intervals on stress profile in LAS glass

Full size image

Reference measurements

Reference transmission photoelasticity measurements were performed using a computer-controlled automatic polariscope (AP-07, GlasStress Ltd.) [20]. The glass sample was immersed into a Cargille immersion oil with matching refractive index to allow unimpeded propagation of light through the sample for edge stresses measurement. The transformation of the polarization of light in the sample was measured, and as a result, the stress profile was obtained. The polariscope consisted of a light source, a set of polaroids, and λ/4-plates that permitted precision photoelastic measurements using phase-stepping method [56]. If clear fringes were observable, then the phase-stepping method would not be necessary; however, especially in the case of lower stresses this method is needed. Polariscope used monochromatic light at 627 nm and monochrome camera.

The two stress profiles, depicted in Fig. 8, coincide in depth range from 135 to 365 µm with high accuracy. Edge stress measurement does not grant precise stress measurement results near surface (0–135 µm). Reasons for that are (1) considering the high-stress gradient near surface, light has to pass through 3 mm of glass and can bend significantly, thus distorting isochromatic fringe pattern; (2) we measure only edge stresses, which means that main surface stresses can have an impact on measurement results; (3) due to polishing, the edges of LAS sample are not perfectly rectangular, which means that effective thickeness of glass that light passes through is not constant. However, the depth of breaking point (59 µm) is identical for both stress profiles.

Figure 8
figure 8

Comparison of the stress profiles obtained using transmission photoelasticity (green circles) and the gradient scattered light method (blue line). The inset shows optical micrograph of the isochromatic fringe pattern at edge as viewed through transmission polariscope AP-07

Full size image

Transmission photoelasticity revealed significantly lower central tensile stresses (~19 MPa for edge stresses and ~65 MPa for gradient scattered light method). This can be explained by the fact that tensile stresses are only to balance the compressive stresses near surface to ensure the stress equilibrium. In case of edge stresses, tensile region is many times thicker.

Varshneya and Spinelli [2] also reported that LAS glass (NEG N-1, with very similar glass composition as our sample), that was strengthened for 8 h at temperature 475 °C in molten salt bath with same composition as ours (80 mol% KNO3 and 20 mol% NaNO3) developed surface stress of −1000 MPa.

FSM-6000 did not permit measurement of our LAS glass sample because DOL exceeds the limit of 100 µm and stress profile has non-linear shape.

Measurement limitations

Samples that have compressive stress layer with depth >25–30 µm can be measured. Let us point out that gradient scattered light method can have precise measurement result for the first 25–30 µm, just case depth has to be deeper than that.

Our method is not limited only to stress profile measurement in a flat glass, but curved glass with surface radius >300 mm can also be measured. Axi-symmetric glass samples with even smaller radius could be measured if laser beam is passed along the axis.

Very thin samples with a minimum thickness of 300 µm can be measured as well. However, in case of very thin plates, the entrance point and exit point get spatially too close. This limitation is caused by the relatively bright reflected/scattered light at the entrance point and exit point, which makes the measurement impossible. This parasitic light is more intense at the exit point due to widening of laser beam. Although the use of ultra-thin layer of immersion oil significantly reduces this artifact.

Gradient scattered light method is capable of measuring up to 3 mm deep stress profile. Usually, the sample is measured from both sides to get more accurate results and to increase the maximum measurable thickness.

Possible additional applications

New enhanced version of Bradshaw’s method

We suggest replacing the measurement of central core tensile stresses with gradient scattered light method instead of currently used transmission photoelasticity [24] or originally used scattered light method [11]. Each time when a layer with thickness of 1–2 µm is etched away using HF acid the alternation of full stress profile is induced. Reason for that is that equilibrium of stresses always remains: by removing surface layer that has compressive stress, a corresponding reduction of central tensile stresses takes place. By measuring the change of the full depth profile of the stress enhanced level of accuracy could be achieved. Bradshaw’s method is still very important in measuring stress profiles that have ultra-thin case depth <20 µm. Kishii’s differential surface refractometry method (FSM-6000) is incapable of measuring DOL under 10 µm.

Enhanced possibility to engineer LAS glass stress profiles

The presented non-destructive method opens up a possibility to engineer the LAS glass stress profile at a new level. For example, in the case of a double ion-exchanged glass the same object can be taken out of the bath, the stress profile measured and tempering conditions changed in order to achieve the desired result. The chemically strengthened LAS glass is already used as a component of bulletproof glass. Our new method makes it possibility to take the stress profile manipulation of chemical strengthening to the next level.

Micron-scale non-destructive tomography of layered polymeric GRIN materials

Optical coherence tomography (OCT) can be used to visualize and quantify characteristics (thickness and homogeneity) of layered polymeric GRIN materials [57, 58]. Gradient scattered method can potentially be used to obtain the same characteristics about layered GRIN materials. From the measured stress profile, it would be possible to distinguish separate layers.

Summary

We have presented the first direct non-destructive stress profile measurement method as applied to chemically strengthened glass. All previous methods measured the stress profile destructively or indirectly (Kishii’s DSR method). Presented theoretical and experimental results can be summarized as follows:

  1. (1)

    We have developed gradient scattered light method for micron-scale non-destructive stress profile measurement in chemically strengthened glass.

  2. (2)

    Numerical experiments showed that the iterative approach granted the complete removal of stress induced influence of ray bending from gradient scattered light method. Reconstructed surface stresses, together with the whole stress profile, approached very rapidly to initially known stresses.

  3. (3)

    The capability of the method is demonstrated by stress profile measurement in chemically strengthened LAS glass. Measured surface stress was −1053 MPa and DOL was 365 µm.

  4. (4)

    Samples that have compressive stress layer with depth >25–30 µm can be measured. It is possible to measure chemically strengthened plates with a minimum thickness of 300 µm. Maximum measurable depth is 3 mm.

  5. (5)

    Measurable glass: flat glass and curved glass with radius >300 mm.

  6. (6)

    The method is not limited to chemically strengthened glass—stress profiles in all flat transparent birefringent materials can be measured.