Introduction

The continually increasing application of polymers in engineering designs is accompanied by a corresponding need for their mechanical characterization. Nowhere is this more apparent than in connection with the dynamic responses of these materials where considerable experimental difficulties arise [1] though problems involving quasistatic deformations have not disappeared from the research domain [2]. Because the mechanical response of polymers is very sensitive to loading rate histories it is important to develop methodologies to construct their constitutive description over a wide range of strain rates even if the experimental difficulties are formidable.

The starting point in this quest is a shear compression specimen (SCS) configuration developed recently by Rittel et al. [3] for large strain testing of metals. This geometry is amenable to mechanically characterize viscoelastic materials with precision, also under small deformations. The original SCS geometry consists of a cylinder or brick in which two opposing slots are machined at 45° with respect to the longitudinal axis, thus forming a gage section of thickness smaller than the overall cross section. Compared with previous shear loading techniques, such as the torsional thin walled specimen [4], the pressure-shear plate impact geometry [5] and the double shear specimen [6], the shear compression specimen can seamlessly cover a wide range of strain rates from 10−3/s to 105/s instead of covering the narrow range of strain rates of each of the previous configurations thereby reducing errors associated with different specimen geometries, loading histories and measurement methods. It is the purpose of this paper to document the modifications for this SCS configuration to adapt it to the characterization of “softer” viscoelastic materials, including the small-deformation domain.

The first task is to examine whether the SCS specimen can be adapted for polymeric materials as was the previous version developed for metals. Particular questions to be answered are whether the dominant deformation in the SCS is still shear deformation, and whether simple stress and strain relations can be deduced reliably for typical loading histories as simply as for the original metallic specimens. Though the dominant shear stress in the gage section of the metal SCS is uniform, the stress and strain state is three-dimensional in both experiments and simulations [7, 8]. Moreover, simple constitutive relations as proposed by [9] relate the equivalent true stress and equivalent true plastic strain to the applied loads and displacements. However, this involves some constant factors for deducing the material behavior that need to be determined via experiment and simulation, which introduces uncertainty in the process. We note further, that a relatively soft polymeric material is not easily machined with high precision, and experimental precision needs to be improved to meet the characterization requirement for viscoelastic materials when small deformations dominate.

The aim of this paper is specifically to explore the applicability of a new SCS design for studying polymers and to establish the associated experimental techniques. The paper is organized into six sections. The first section introduces the subject of this work. The second section delineates the new design of the SCS for polymeric materials, specimen preparation, and relevant experimental conditions and the third presents two analytic (closed-form) models for this new design. The fourth section introduces the simulation model and its loading and boundary conditions with the fifth providing a discussion of experimental, analytic and simulation results, and their comparisons, which is then followed by a conclusion.

New Design of an SCS for Polymers

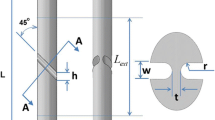
In the earlier investigation by Rittel et al. [3] the SCS specimen was machined from a single (small) block of metallic material. Such an option is not easily adapted for rubbery solids undergoing small deformations because the deformations cannot be concentrated sufficiently well in the intended gage section. More importantly, virtually insurmountable difficulties arise in the machining. As a consequence a modified form of the test configuration was developed as shown in Fig. 1, in which the thin and sheared portion of the configuration (gage section) is made of the polymer of interest while the rest of the specimen is metallic (typically, aluminum).

Fig. 1
figure 1

SCS specimen modified for compliant material (e.g., polymer) investigations: polyurea shear layer embedded between aluminum ends. Note that the compliant material is only about one fourth as wide as the metal ends

Full size image

In this paper a polyurea forms the gage section (specimen) which is initially machined into a strip 15.6 mm in length with a cross section of 2.2 mm by 2.2 mm, and then polished incrementally with sandpaper (400 grit) to a cross section of 2 mm by 2 mm with a 0.01 mm tolerance while taking great care to make the opposing surfaces parallel to each other to within 0.02 mm. The aluminum ends were cut from a brick-shaped specimen of size 11 mm × 8 mm × 15 mm severed at 45° with respect to its longitudinal axis. The two metallic ends and the polymeric gage section are joined via bonding (M-Bond 200 Adhesive, VISHAY). A special fixture is used to ensure that the two bonded surfaces remain parallel to each other and the ends remained aligned during the joining process.

The relatively small size of this specimen (c.f. Fig. 1) is mandated essentially by the intended use for dynamic tests in a split Hopkinson (Kolsky) pressure bar. With respect to quasistatic measurements it would be certainly admissible to scale the overall size of the design to dimensions that allow for larger displacements under comparable loads so as to simplify the measurement of the deformation. For the present study that option was not readily available since the concern for reproducibility limited the use of the relatively small amount of material available.

The quasistatic tests were carried out on a screw-driven testing machine (Instron) employing a ramp loading in which a constant strain rate history is followed by a constant strain as indicated in Fig. 2. Primary attention is paid to the response from the initial loading in order to access to some degree the shorter time scale relevant to dynamic situations; it is nearly impossible to generate a relaxation process under dynamic condition.

Fig. 2
figure 2

Schematic of a ramp load history employed in the quasistatic tests

Full size image

The split Hopkinson (Kolsky) pressure bar used for the dynamic measurements consists of a striker, an incident bar and transmission bar 305 or 250, 2200, and 700 mm in length, respectively, which all have a common diameter of 12.7 mm. The Young’s modulus of all aluminum 7075-T651 bars is 72 GPa, and the Poisson’s ratio is 0.33. To overcome the issue of mismatch in impedance, combined pulse shapers consisting of paper and polymer are used between incident bar and striker [1]. Since linearly viscoelastic deformation is of primary interest (small deformations), the reliability and precision of signals are essential. Two 0.254 mm thick X-cut quartz gages (12.7 mm in diameter) are mounted close to the specimen end surfaces on the incident and transmission bars to record the longitudinal force on both ends of the specimen. High resistance strain gages (1,000 Ω) with a gage factor of 3.27 are attached to the incident and transmission bars to record the strain signals during wave propagation in the bars. Two strain gages are attached on opposite sides of the transmission bar to amplify the signal and improve its signal/noise ratio. The dynamic experimental setup is shown in Fig. 3.

Fig. 3
figure 3

Split Hopkinson (Kolsky) bar arrangement

Full size image

Analytic Models for the New SCS Design

In this section two analytical models are discussed for deducing the shear behavior from the new SCS geometry. The first involves simple kinematics, which do not require explicitly tracking the relative lateral displacements of the two end pieces. The stresses are derived from overall equilibrium considerations. The second model provides for more data input through incorporating the measured lateral deformations to potentially improve the precision of the final result. Both are ultimately compared with numerically established results as outlined in “Numerical Simulation”.

Elementary Analytical Model (First Model)

Figure 4 shows the “side view” and “front view” of the specimen along with the definition of letter-terms characterizing its deformation under a “vertical”, compressive force. Because the metallic ends are much stiffer than the polymer gage section they are assumed to be rigid. The bottom surface (lower metal end) of the specimen is held fixed. The upper metallic end is allowed to move only along the η and ξ directions, but the acceleration in the ξ direction is very small and is ignored. The gage section is considered to be in a state of plane stress.

Fig. 4
figure 4

Shear compression specimen and illustration of terminology used to describe deformation in the closed form analytical solution

Full size image

We define the velocity field for any point in the elastomer layer (gage section) by

$$\upsilon = \upsilon _x i_x + \upsilon _y i_y + \upsilon _z i_z $$
(1)

which must obey the boundary conditions,

$$\upsilon _z = \upsilon _y = 0\quad \quad \operatorname{on} \quad \quad y = 0$$
(2)

and

$$\begin{array}{*{20}c} \begin{aligned} & {\mathbf{\upsilon }}^{DC} \cdot {\mathbf{i}}_\eta = - \upsilon _\eta \\ & {\mathbf{\sigma }} \cdot {\mathbf{i}}_\xi = 0 \\ \end{aligned} & {{\text{on}}} \\ \end{array} y = h\quad \quad \left( {Boundary\quad DC} \right)$$
(3)

where σ is the stress tensor and υ DC is the velocity on the boundary DC, so that we obtain

$$\begin{array}{*{20}c} {\begin{aligned} & \upsilon ^{{\operatorname{DC} }}_{z} \sin \theta + \upsilon ^{{\operatorname{DC} }}_{y} \cos \theta = - \upsilon _{\eta } \\ & \sigma _{{yz}} \cos \theta - \sigma _{{yy}} \sin \theta = 0 \\ \end{aligned} } & {{{\text{on}}}} & {{y = h\quad {\left( {\operatorname{Boundary} \,\;DC} \right)}}} \\ \end{array} .$$
(4)

In addition, the surfaces ABCD, BB′C′C, AA′D′D and A′B′C′D′ are stress free.

Assuming the velocity field in the gage section to have the simple distribution,

$$\upsilon _z = \frac{y}{h}\upsilon _z^{\operatorname{DC} } ,\quad \upsilon _y = \frac{y}{h}\upsilon _y^{\operatorname{DC} } \;,\quad \upsilon _x = xd_{xx} $$
(5)

leads to the strain rate tensor,

$${\mathbf{d}} = \left( {\begin{array}{*{20}c} {d_{xx} } & 0 & 0 \\ 0 & {d_{yy} } & {d_{yz} } \\ 0 & {d_{yz} } & {d_{zz} } \\ \end{array} } \right)$$
(6)

with

$$\left\{ {\begin{array}{*{20}c} \begin{aligned} & d_{yz} = \frac{1}{2}\frac{{\upsilon _z^{\operatorname{DC} } }}{h} \\ & \\ \end{aligned} \\ {d_{yy} = \frac{{\upsilon _y^{\operatorname{DC} } }}{h}} \\ \end{array} } \right.$$
(7)

which determines the displacement boundary condition in equation (4) as

$$2\;d_{{yz}} \sin \theta + d_{{yy}} \cos \theta = \frac{{ - \upsilon _{\eta } }}{h}.$$
(8)

For plane stress conditions one is then led to

$${\mathbf{\sigma }} = \left( {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {\sigma _{yy} } & {\sigma _{yz} } \\ 0 & {\sigma _{yz} } & {v\sigma _{yy} } \\ \end{array} } \right)$$
(9)

and for linearly elastic behavior with a Poisson’s ratio of 0.5 (incompressibility) produces,

$$\begin{array}{*{20}c} {{\tau _{{xy}} = 2G\varepsilon _{{xy}} }} \\ {{\sigma _{{yy}} = \frac{E}{{1 - \nu ^{2} }}\varepsilon _{{yy}} = 4G\;\varepsilon _{{yy}} .}} \\ \end{array} $$
(10)

For viscoelastic behavior one finds, again with Poisson’s ratio = 0.5,

$$\sigma _{yy} = 4\varepsilon _{yy} \left( 0 \right) \cdot G\left( t \right) + \int_0^t {4G\left( {t - \tau } \right)d_{yy} } d\tau $$
(11)

and

$$\sigma _{yz} = 2\varepsilon _{yz} \left( 0 \right) \cdot G\left( t \right) + \int_0^t {2G} \left( {t - \tau } \right)\frac{{d\varepsilon _{yz} }}{{d\tau }}d\tau = 2\varepsilon _{yz} \left( 0 \right) \cdot G\left( t \right) + \int_0^t {2G} \left( {t - \tau } \right)d_{yz} d\tau {\text{.}}$$
(12)

For the ramp loading shown in Fig. 2, there is no deformation before loading, so that substituting equations (11) and (12) into equation (4) renders,

$$\int_0^t {G\left( {t - \tau } \right)\left( {2d_{yz} \cos \theta - 4d_{yy} \sin \theta } \right)d\tau = 0} $$
(13)

from which it follows that,

$$2d_{yz} \cos \theta - 4d_{yy} \sin \theta = 0$$
(14)

since G(t) is always positive. Equations (8) and (14) lead to,

$$d_{yy} = \frac{{ - \upsilon _\eta }}{h}\frac{{\cos \theta }}{{4\sin ^2 \theta + \cos ^2 \theta }}$$
(15)
$$d_{xy} = \frac{{ - 2\upsilon _\eta }}{h}\frac{{\sin \theta }}{{4\sin ^2 \theta + \cos ^2 \theta }}{\text{.}}$$
(16)

With the aid of Fig. 4, one deduces that the dominant stresses are

$$\sigma _{yz} = \frac{{P\left( t \right)}}{{w\Delta }}\cos \theta \cdot \sin \theta $$
(17)
$$\sigma _{yy} = \frac{{P\left( t \right)}}{{w\Delta }}\cos ^2 \theta $$
(18)

where w is the width of the SC specimen and Δ is the thickness of the gage section, as indicated in Fig. 4. Once the loading speed υ η or the load history P(t) is prescribed, the definitions and equations (15) through (18) yield the average stress and strain histories in the gage section. Subsequently, the relaxation modulus can be deduced via equation (12) once the stress and strain histories are known.

We note that ultimately this model does not provide the best simple means of determining the viscoelastic properties, even though it has the advantage of obvious simplicity and seeming completeness of deformation representation. This finding became apparent after numerical comparisons pointed to shortcomings, though some might consider these minor.

Improved Analytical Model (Second Model)

Although the average stresses and strain rates in the gage section can be deduced with the aid of the above model from the loading history in the axial direction, the results depend on the constitutive equations of the gage material, the determination of which is ultimately the goal of the exercise. Therefore, an alternate simple geometric way to determine the strain rates is provided here without recourse to the material description model other than usual elastically compressive behavior while adhering to the same boundary conditions.

If both metallic ends are treated as rigid the velocity field for the elastomer layer can be defined, also from Fig. 4, by

$${\mathbf{\upsilon }} = \upsilon _\eta {\mathbf{i}}_\eta + \upsilon _\xi {\mathbf{i}}_\xi + \upsilon _\psi {\mathbf{i}}_\psi $$
(19)

so that the velocity on DC can be written as,

$$\matrix {\upsilon _z^{\operatorname{DC} } = \upsilon ^{\operatorname{DC} } \cdot {\mathbf{i}}_z = \left( {\sqrt {\upsilon _\eta ^2 + \upsilon _\xi ^2 } } \right)\cos \left( {\arctan \left( {\frac{{\upsilon _\eta }}{{\upsilon _\xi }} - \theta } \right)} \right)} \\ {\upsilon _y^{\operatorname{DC} } = \upsilon ^{\operatorname{DC} } \cdot {\mathbf{i}}_y = \left( {\sqrt {\upsilon _\eta ^2 + \upsilon _\xi ^2 } } \right)\sin \left( {(\arctan \left( {\frac{{\upsilon _\eta }}{{\upsilon _\xi }} - \theta } \right)} \right)} \ {\text{.}}$$
(20)

Substituting these equations into (5), equation (7) can be written as,

$$\left\{ {\begin{array}{*{20}c} {{d_{{yz}} = \frac{1}{2}\frac{{\upsilon ^{{\operatorname{DC} }}_{z} }}{w} = \frac{1}{{2w}}{\left( {{\sqrt {\upsilon _{\eta } ^{2} + \upsilon _{\xi } ^{2} } }} \right)}\cos {\left( {\arctan {\left( {\frac{{\upsilon _{\eta } }}{{\upsilon _{\xi } }} - \theta } \right)}} \right)}}} \\ {{d_{{yy}} = \frac{{\upsilon ^{{\operatorname{DC} }}_{y} }}{w} = \frac{1}{w}{\left( {{\sqrt {\upsilon _{\eta } ^{2} + \upsilon _{\xi } ^{2} } }} \right)}\sin {\left( {\arctan {\left( {\frac{{\upsilon _{\eta } }}{{\upsilon _{\xi } }} - \theta } \right)}} \right)}}} \\ \end{array} } \right..$$
(21)

The average stresses are still determined by equations (17) and (18).

From this model, it is clear that the average strain rates and ensuing stresses can be determined not only via the axial loading (vertical) histories, but by also incorporating the relative, lateral velocity history of the ends. Such an approach allows for arbitrary constitutive description as evidenced by the material but requires careful experimental measurements of boundary conditions. The relative lateral displacements can be readily recorded by means of the moiré method or laser vibrometerFootnote 1. These methods have been employed under different circumstances under dynamic loading by Lu et al. [10] and Lykotrafitis et al. [11] which could be adapted to the present study.

Numerical Simulation

With current capabilities to model deformations and stresses numerically with great accuracy, this approach is used to examine the precision with which the analytical models can represent the specimen deformations and forces for a specified constitutive model. Since quasistatic and dynamic testing is of interest, both aspects are simulated here via the commercial finite element code ANSYS.

Quasistatic Simulation

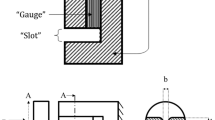
The stress and strain fields of this newly designed SCS geometry, and their relation with the loading conditions were thoroughly investigated numerically. Figure 5 shows the simplified simulation model, which has the same size as the specimen used in the measurements (Fig. 1). However, only half of the specimen is modeled because of its symmetry. Solid hexahedral elements with 20 nodes are employed, for a total element count of 47,899. The “bottom” surface is fixed with respect to the longitudinal (vertical) axis. The displacement history follows the ramp behavior shown in Fig. 2 and is applied to the “top” surface with a loading speed of 0.113 mm/s in the ramp part. The other surfaces are stress free except for the plane of symmetry. The interfaces between the gage section and aluminum ends are bonded together (no relative motion is allowed), but the glue layer is ignored in this model because of its low thickness and high strength ~20 MPa.

Fig. 5
figure 5

Mesh of the numerical model for the polymer SCS. Only one half of the specimen geometry is used due to symmetry

Full size image

The metallic ends are made of 7075-T6 aluminum alloy. The constitutive equation of the polyurea in the gage section has been chosen in the form of a Prony series for the shear relaxation modulus,

$$\sigma _{ij} = \int_0^t {G_{ijkl} \left( {t - \tau } \right)\frac{{\partial \varepsilon _{kl} }}{{\partial \tau }}} d\tau $$
(22)
$$G\left( \xi \right) = G_\infty + \sum\limits_{i = 1}^{n_G } {G_i } e^{\left( {{{ - \xi } \mathord{\left/ {\vphantom {{ - \xi } {\lambda _{_i }^G }}} \right. \kern-\nulldelimiterspace} {\lambda _{_i }^G }}} \right)} $$
(23)
$$G_i = C_i \left( {G_0 - G_\infty } \right)$$
(24)

and the bulk modulus K is considered to be a constant. For the current simulation it suffices to let n G be on the order of six, suitably chosen to represent the time scale of the anticipated deformation and stress relaxation. For this limited time scale a representation with all relaxation times would yield no different results. For completeness of discussion and for comparison with earlier work on metals, a configuration of the same size consisting totally of polyurea (no metal ends) is also included.

Dynamic Model

To investigate the linearly viscoelastic behavior of a polymer in a split Hopkinson bar, a simulation model is constructed, which consists of an incident bar, the SCS, and a transmission bar of the same diameter as those in the experiments but of shortened lengths. To simplify the problem, and improve the efficiency of calculation, the stress pulse recorded by strain gages on the incident bar is used as input to the incident bar in the model instead of also modeling the striker impact; the model lengths of the incident and transmission bars are 1,500 and 700 mm, respectively. The length of the bars used here is sufficient to investigate the response of the specimen during the initial 200 μs, which is of interest here. Pulse shapes are of the same character as were used in reference [1]. The specimen has only one plane of symmetry, so that only halves of the specimen and of the bars need to be modeled as shown in Fig. 6. During the loading process, the contact surfaces between the metal ends of the specimen and the bars allow for relative sliding in the numerical modelFootnote 2, but no relative motion is allowed at the interfaces between the gage section and the aluminum ends of the SCS. Brick elements are used for the three-dimensional simulation, and a total of 251,040 elements are used. The Young’s modulus, Poisson’s Ratio and density of the aluminum 7075-T6 alloy are 72 GPa, 0.33 and 2.785 g/cm3, respectively. The constitutive equation of polyurea has been chosen again in the form of a Prony series for the shear relaxation modulus.

$$G\left( \xi \right) = G_\infty + \sum\limits_{i = 1}^{n_G } {G_i } e^{\left( {{{ - \xi } \mathord{\left/ {\vphantom {{ - \xi } {\lambda _{_i }^G }}} \right. \kern-\nulldelimiterspace} {\lambda _{_i }^G }}} \right)} $$
(25)

with the bulk modulus K again being a constant. For this simulation it also suffices to let n G be on the order of six, as before.

Fig. 6
figure 6

Simulation model for the dynamic deformation of the new SCS geometry

Full size image

Material Parameters

The material parameters for the polyurea are listed in Tables 1 and 2 for the quasistatic and dynamic situations, respectively. They were deduced from the relaxation behavior documented by Knauss and Zhao [2], and have been employed previously and successfully in both quasistatic and dynamic simulations.

Table 1 Materials parameters of polyurea for quasistatic simulation
Full size table
Table 2 Materials parameters of polyurea for the dynamic simulation
Full size table

Results and Discussion

In the first part of this section, the results from the numerical simulations are presented. These considerations are then followed by a comparison of results from the simple analytical models with the presumably more precise numerical values. This is done to examine to what extent the simple model(s) can represent the real situation.

Stress and Strain Fields in the New SCS

Figure 7 shows the comparison of the displacement distribution in the longitudinal (vertical or over-all compression) direction for the new and the old SCS design. The displacement rate at the “top” surface of the SCS model is 0.113 mm/s along the longitudinal direction until it reaches 0.113 mm. Recall that the new design refers to the specimen with metal ends, while the term “old design” signifies that the whole specimen was made of one material (polyurea). It is clear that the new design localizes almost all the deformation into the gage section, because the aluminum ends are much stiffer than the polymer, and thus induces a more uniform shear deformation than in the old specimen.

Fig. 7
figure 7

Comparison of displacement distributions in the old specimen (polyurea only, left) and in the new SCS design (aluminum ends and polyurea interlayer, right) in quasistatic simulations

Full size image

Figure 8 shows maps of the shear strain and stress field in the midplane of the gage section. Figure 9 shows different components of stress and strain distributions in the midplane of the gage section. Both Figs. 8 and 9 employ the same local coordinates as those in Fig. 4, i.e., the x direction is along the thickness of the gage section, y is aligned along the depth of the gage section which is vertical to the bonding interfaces, and z is along the longest dimension of the gage section. From the above figures one can see that the stress and strain states in the gage section are not two but three dimensional. Though not truly uniform, the shear strain is the largest of the strains. None of the strains vary greatly through the thickness of the specimen as is apparent jointly from Figs. 8 and 9, and the stress in the x direction is very small. This behavior raises the expectation that a simplified analysis may be of great use in the data reduction process.

Fig. 8
figure 8

Shear strain and stress fields in the midplane of the gage section (half way between the polyurea-aluminum interfaces) at an overall applied shear strain of 0.04 in quasistatic simulations

Full size image
Fig. 9
figure 9

Representation of the strains and stresses along the midplane of the gage section at an overall applied 0.113 mm displacement along longitudinal axis with a loading speed of 0.113 mm/s in the quasistatic simulations

Full size image

From Fig. 10 one deduces that the relations between the average shear stress and strain at the upper interface between the gage section and metal end coincide closely with those in the middle surface which can be interpreted to mean that the distribution of the shear stress and strain in the gage section is acceptably uniform.

Fig. 10
figure 10

Average shear stress and strain relations in the top surface and middle surface of the gage section for the quasistatic case

Full size image

Comparison of the Numerical Results with the Analytical Models

Using the longitudinal loading displacement speed of 0.113 mm/s, and the load exerted on both metal ends of the SCS as input to the first analytic model, a comparison between the detailed numerical result and the analytic model is shown in Fig. 11. One observes that the predicted shear stress from the simple analytic model agrees well with that from the simulation, though there is a small difference regarding the shear strain but such that the ratio derived from this strain difference is a constant which can be estimated with the help of the improved (second) model presented above. Figure 11 also shows the shear tress and strain relation predicted from the second model, which agrees very well with that of the simulation. However, it should be noted that compared to the first analytic model this second model needs additional information, namely the lateral (relative) velocity history of the metal ends but that the result is independent of the material in the gage section. Again one must note that the analytical models employed here do not require any empirical factors as were required in the metallic specimens [9].

Fig. 11
figure 11

Stress and strain relation for the polyurea-aluminum SCS in the constant strain rate portion of load history in Fig. 2

Full size image

Comparison Between Experimental and Simulation Results

The comparison between the numerical simulation and experimental measurements is shown in Fig. 12 in the form of the shear stress history for the quasistatic loading. One observes that the experimental result yields good agreement with the simulation result when the shear strain is below 0.047. In reality, the deformation deviates slightly from a constant rate history because of the response of the testing machine, which may explain why the numerical and experimental results are not completely coincident for shear strains below 0.047. When the shear strain exceeds 0.047, a discrepancy between the experimental and simulation results is observed, which is attributed to the nonlinear viscoelastic behavior of the polyurea. Since only linearly viscoelastic behavior is employed in the simulations with strain levels not exceeding 4%, this figure assures that in the measurement range theory and experiment should be close.

Fig. 12
figure 12

Comparison of the numerical and experimental results under the same quasistatic loading

Full size image

Figure 13 shows the response of the polyurea SCS under split Hopkinson bar loading. The experimental result yields good agreement with the simulation and demonstrate that the current SCS specimen functions as well as the specimen of the original design.

Fig. 13
figure 13

Comparison of the numerical and experimental results for the load histories (incident bar-Q1 and transmission bar-Q2) under dynamic loading

Full size image

Figure 14 shows the response of the polyurea SCS with different strain rates, in which the response of a polyurea is deformed to moderately large strains beyond the linear regime. We include this data as a demonstration of the fact that deformation rate changes evidence significant and readily observed changes in the response characteristics, while also showing a “softening” effect in the stress response. We cannot, however, argue at this time that these traces represent only nonlinear behavior. The reason is that the strain history leading to these responses is not close to a constant strain rate prescription. For more information on this point we refer the reader to reference [1]. Apart from this clarification in the present work we observe that the new SCS can also be used for investigating the large deformation and high-strain-rate behavior of elastomers.

Fig. 14
figure 14

Measured response of the polyurea SCS at different strain rates when deformed to moderately large strains

Full size image

Conclusions

The development and evaluation of a new design of a shear compression specimen intended for use with “soft” polymers for the determination of their viscoelstic shear behavior has been presented. It has been configured such that it is useful in both quasistatic and in wave-dynamic loading environments. One can draw the following conclusions based on the present investigation.

  1. 1.

    The deformation in the gage section of the newly developed SCS is more uniform than that for one machined from a homogenous material block, and its shear stress and strain distributions are acceptably uniform.

  2. 2.

    Both analytic models developed here serve well in predicting the shear stress and shear strain in the gage section, but the improved analytic model provides higher precision and is independent of the constitutive behavior of the material under investigation.

  3. 3.

    The new SCS specimen and its models are demonstrated to provide reliable results both in experiment and in simulation.