A Shear-Tension Specimen for Large Strain Testing

Abstract

A new shear-tension specimen (STS) is designed, evaluated and tested quasi-statically and dynamically. The specimen consists of a long cylinder having an inclined gauge section created by two diametrically opposed semi-circular slots which are machined at 45° with respect to the longitudinal axis. The geometry imposes stress condition within the gauge section which correspond to a Lode parameter of ~ −0.5, between pure shear (0) and uniaxial tension (−1). It thus provides a wider span of loading conditions for a material. A thorough numerical study reveals that the stresses and strains within the gauge are rather uniform, and the average Mises stress and plastic strain on the mid-section of the gauge represent the material true stress–strain characteristics. The data reduction technique to determine the stresses and strains is presented. Quasi-static and dynamic tests at strain rate of 10⁴ 1/s were carried out on specimens made of 1020 cold-rolled steel. No necking or softening was observed with this specimen, and the fracture location was always well within the gauge. The obtained stress–strain curves and ductility were validated numerically. The STS is a new specimen to study the combined influence of tension and shear on the mechanical characteristics of a material.

Introduction

Numerical simulations are widely used in both industry and research communities in the field of materials mechanics. The accuracy of a simulation depends on the material properties used, with emphasis on the true stress–strain curves and ductility. These properties are usually strain-rate and temperature dependent, and the researcher often needs to generate its own data which is not available in the literature. Recent experiments on metals [1–4] have shown that the hydrostatic stress and the Lode parameter (the third invariant of the stress deviator) influence these properties. While the hydrostatic pressure has a significant effect on the ductility, and an insignificant effect on the stress-plastic strain relationship, the Lode parameter has an opposite role. Therefore, for an accurate simulation, the stress–strain curves and ductility should be known over a wide range of strains, strain rates, temperatures, hydrostatic pressures and Lode parameters.

Tensile tests are usually used for elasto-plastic characterization of metals. These tests provide information about the mechanical properties of materials, including the modulus of elasticity, yield strength, tensile strength, elongation, and the true stress–strain relationship until necking takes place. In other words, the equivalent von Mises stress as a function of the equivalent plastic strain for a given material [5]. In order to extend the range of stress–strain curves, knowledge of the stress and strain distributions on the necked cross-section of the tensile specimens is needed [6]. A correction for round cross-section tensile specimens was suggested by Bridgman [7]. This correction might lead to material curves fraught by an error of more than 10 %, while requiring a significant amount of experimental work in order to measure the evolving curvature radius of the necking profile at different stages of each tensile test [5]. For non circular cross sections, there is no established method to determine the complete true stress–strain relationship and an hybrid experimental – numerical approach is needed [8–14]. The location of the neck is not always predictable especially in dynamic testing even if notches exit [15].

In this study a new shear-tension specimen (STS) is designed, evaluated and tested quasi-statically and dynamically. The specimen is similar to the known shear compression specimen (SCS) which was introduced in [16] and was validated numerically for static and dynamic loading and parabolic hardening materials in [17–19]. The SCS was used in several investigations [20–27] and was recently modified to have a circular gauge [28]. The STS consists of a long cylinder having an inclined gage section created by two diametrically opposed semi-circular slots which are machined at 45° with respect to the longitudinal axis. While uniaxial tension test correspond to Lode parameter of −1, the shear-tension test corresponds to an approximately constant Lode parameter ~ −0.5 which is imposed by the geometry. No necking or softening is observed with this specimen, and the fracture location is known ahead of time, yielding reliable data on the stress–strain curves and ductility.

Second section of this manuscript presents a thorough numerical evaluation of the new specimen. Third section is divided into two parts: quasi-static and dynamic. In the first part the quasi static experimental results are detailed, followed by numerical validation. In the second part the dynamic experimental results are detailed followed by numerical validation. Discussion and summary are given in the fourth section followed by concluding remarks.

Numerical Evaluation of an STS

The numerical analyses were performed with the commercial finite element software Abaqus standard and Abaqus explicit 6.14 [29]. The purpose of the numerical simulations is to demonstrate that:

• 1) The field variables such as Mises stress (σ _M ), hydrostatic pressure (p) and equivalent plastic strain (ε _p ) are evenly distributed on the mid-section of the gauge during the entire loading history.

• 2) The evolution of the average Mises stress $\left({\overset{\frown }{\sigma}}_M\right)$ and the averaged equivalent plastic strain $\left({\overset{\frown }{\varepsilon}}_p\right)$ on the mid-section of the gauge replicate the material property σ ^t − ε ^t _p (which is input into the simulation).

• 3) Develop a data reduction technique in which the measured P-d (load–displacement) curve of the specimen is reduced into the averaged $\left({\overset{\frown }{\sigma}}_M\right)$ and $\left({\overset{\frown }{\varepsilon}}_p\right)$ on the mid-section of the gauge, which accurately represent the material property σ ^t − ε ^t _p .

Geometry

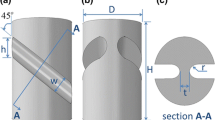
The geometry of the STS specimen is shown in Fig. 1. The front view of the STS is shown in Fig. 1(a), and a side view in Fig. 1(b); A cut view perpendicular to the gauge is shown in Fig. 1(c). The dimensions of the specimen are: L = 120 mm, D = 10 mm, t = 1.6 mm. The circular gauge has a radius of r = 1.5 mm. The gauge width is W = 2r = 3 mm. The vertical height of the gauges is $h=2\sqrt{2\;}\;r=4.24\kern0.24em mm$. L _ext represents the distance between the locations of the reflecting tape stripes used for optical laser extensometry.

Fig. 1

A STS specimen with a circular gauge. (a). Front view (b). Side view. (c). A cut view (A-A) perpendicular to the gauge inclination

Numerical Model, Mesh, Boundary Conditions and Material Properties

The meshed specimen is shown in Fig. 2. Due to its symmetry, only half of the physical model is included in the numerical model. The front and back views of the zoomed region adjacent to the gauge are shown in Fig. 2(b), (d) respectively, while a side view is shown in Fig. 2(c).

Fig. 2

The meshed numerical model. (a). Front view of the whole specimen. (b). Front view on the zoomed area. (c). Side view of the specimen. (d). Back view of the zoomed area

The typical mesh shown in Fig. 2 comprises 215652 nodes and 201670 linear hexahedral elements of type C3D8R. The seed size within the gauge is 0.25 mm while within the whole specimen 0.5 mm. A tensional vertical displacement of 1 mm was applied on the upper face of the specimen (Fig. 2(a)). Symmetry conditions were applied along the cut (Fig. 2(c)) and on the bottom face (Fig.2(a)). The center point of the bottom face was fixed. When an explicit solution scheme was used for static calculations, the displacement load was applied “slowly” – during 0.002 s.

In the following numerical verifications, we modeled a representative elasto-plastic material model with Mises plasticity. The density is: 7870 $\frac{Kg}{m^3}$; Young’s modulus: 210 GPa, and Poisson’s ratio: 0.3. The flow stress versus equivalent plastic strain is shown in Fig. 3.

Fig. 3

The characteristic σ ^t − ε ^t _p of a model material used for numerical simulations

Numerical Results

Real specimens vary slightly in their dimensions, hence the applied experimental load–displacement curves can be different for each specimen. In order to overcome this problem the applied displacement and load curves are presented in the sequel in a normalized form. Due to the normalization, the obtained load–displacement curve depends mainly on the specimen’s material properties. The applied displacement is normalized by the vertical height of the gauge ${\varepsilon}_{ap}=\frac{d}{h}$ and the applied load by the vertical projection area of the gauge: ${\sigma}_{ap}=\frac{P}{D\cdot t}$.

The deformed specimen is shown in Figs. 4 and 5. The deformation and distributions shown in Figs. 4 and 5 are typical for large plastic deformations, and correspond to an applied vertical displacement of d = 1.0 mm, which in turn corresponds to normalized applied displacement of ε _ap  = 0.24.

Fig. 4

Distribution of ε _p and σ _M at applied vertical displacement of d = 1.0 [mm]. (a). Front view of a deformed specimen with color maps of ε _p . (b). A cut view of a deformed specimen with color maps of ε _p . (c). Front view of a deformed specimen with color maps of σ _M . (d). A cut view of a deformed specimen with color maps of σ _M

Fig. 5

Stress and strain distribution along the mid-section of the circular gauge specimen at vertical applied displacement of 1.0 mm. (a). Mises stress distribution. (b). Hydrostatic pressure distribution. (c). Equivalent plastic strain distribution

The distributions of the equivalent plastic strain and Mises stress are shown in Fig. 4(a), (b), and (c) (d), respectively.

The results show that the Mises stress and the equivalent plastic strain are distributed quite evenly over a wide part of the mid-section. The equivalent plastic strain is slightly less uniform - end effects (shown in Fig. 4(a), (b)) are noticeable on the two edges of the gauge, in which the value of the equivalent plastic strain is lower.

The Mises equivalent stress distribution is shown in Fig. 5(a), the hydrostatic pressure distribution in Fig. 5(b), and the equivalent plastic strain distribution in Fig. 5(c). It can be observed that the Mises stress and the pressure are distributed evenly, while the equivalent plastic strain is less even. It has its maximum value of ~1 (red) on the mid outer face while at the region of the end effects (green) it reaches lower values than 0.6. The average value on the mid section is 0.74.

A ductile failure criterion was added to the analyses of the specimen. According to this failure criterion, an element failed and was deleted when the equivalent plastic strain reached an arbitrarily set value of ε ^f _p  = 0.5. A vertical displacement of 1 mm was applied again on the top face of the specimens. The evolution of the fracture in the gauge is shown in Fig. 6. Only the gauge area (Fig. 2(a)) is shown.

Fig. 6

Failure patterns of the specimen in gauge area (Fig. 2a). Color map of the equivalent plastic strain. (a). The specimen just before failure. (b). Two separate cracks appear at the center of the gauge at two different heights. (c). Partial fracture: the cracks coalescence at the center and propagate toward the ends of the gauge. (d). Complete fracture: the crack propagate and cuts the ends of the gauge

The failure patterns of the STS specimens is different from that of an SCS specimen [28, 30]. In the STS, a crack initiates at the center of the gauge and propagates toward its ends, while in SCS specimen the opposite happens, namely the crack starts at the ends and propagates towards the center. It can be observed in Figs. 5(c) and 6(a) that the equivalent plastic strain is higher at the center of the gauge, causing fracture initiation in this area.

The average values $\left({\overset{\frown }{\varepsilon}}_p,\;{\overset{\frown }{\sigma}}_M,\overset{\frown }{p}\right)$ on the mid-section were estimated at each time interval by taking the average values of all elements along the two paths shown in Fig. 5(a), namely mid-section and edge of the gauge. Figure 7 shows the average Mises stress $\left({\overset{\frown }{\sigma}}_M\right)$ against the averaged equivalent plastic strain $\left({\overset{\frown }{\varepsilon}}_p\right)$. These values are compared to Abaqus input (Fig. 3) for the assumed material stress–strain curves. It can be observed that the average values on the mid section replicate very well the inputted material behavior (σ ^t, ε ^t _p ) used in the analyses.

Fig. 7

Comparison of the averaged values $\left({\overset{\frown }{\sigma}}_M,{\overset{\frown }{\varepsilon}}_p\right)$ along the mid-cut section obtained by both types of specimens to the input material property (σ ^t, ε ^t _p )

Figure 8 shows the applied load–displacement curves (Δd, p) for the specimens. Δd (like d) is normalized by the vertical height of the gauge h. As shown in Fig. 8, the load has a maximum value at Δd/h ≃ 0.05, and for Δd/h > 0.05 the load decreases.

Fig. 8

The applied normalized load–displacement curves for the specimen

One should note that this load evolution is different from that typically observed with an SCS specimen, for which the load increases monotonically with the applied displacements [17, 19, 28] until fracture. It will be shown later that while the macroscopic load decreases, the average Mises stress on the mid-section keeps increasing, thus indicating a lack of material softening effect.

The triaxiality (t _r ) and the Lode parameter (μ) are defined by equations (1)–(2), respectively: ([31]):

$$ {t}_r=\frac{p}{\sigma_M} $$

(1)

$$ \mu =\frac{2{\sigma}_2-{\sigma}_1-{\sigma}_3}{\sigma_1-{\sigma}_3} $$

(2)

Where the hydrostatic pressure (p) and the equivalent Mises stress (σ _M ) are given in equations (3)–(5):

$$ p=-{\sigma}_m=-\frac{1}{3}{\sigma}_{ii}=-\frac{1}{3}\left({\sigma}_1+{\sigma}_2+{\sigma}_3\right) $$

(3)

$$ {\sigma}_M=\sqrt{\frac{3}{2}{s}_{ij}{s}_{ij}}=\sqrt{\frac{1}{2}\left[{\left({\sigma}_1-{\sigma}_2\right)}^2+{\left({\sigma}_2-{\sigma}_3\right)}^2+{\left({\sigma}_3-{\sigma}_1\right)}^2\right]} $$

(4)

$$ {s}_{ij}={\sigma}_{ij}-\frac{1}{3}{\sigma}_{ii} $$

(5)

The stresses σ ₁, σ ₂ and σ ₃ are the principal stresses with σ ₁ > σ ₂ > σ ₃.

Three special values of the Lode parameter are: −1,0 and 1, which are for generalized tension, generalized shear and generalized compression, respectively.

These two parameters are important since they are known to influence the flow behavior and ductility (equivalent plastic strain to failure) of materials [1–4]. Figure 9 shows the variation of the averaged triaxiality and Lode parameters $\left({\overset{\frown }{t}}_r,\overset{\frown }{\mu}\right)$ on the mid-section of the gauge during the plastic deformation. The results indicate that the averaged (over the gauge section) triaxiality $\left({\overset{\frown }{t}}_r\right)$ on the mid-section during plastic deformation is rather constant, in the range $-0.39<{\overset{\frown }{t}}_r<-0.32$ for the range of plastic deformation $0<{\overset{\frown }{\varepsilon}}_p<0.38$. The average of ${\overset{\frown }{t}}_r$ during the plastic deformation is −0.36 and is shown as a horizontal line in Fig. 9. The behavior of the averaged Lode parameter $\left(\overset{\frown }{\mu}\right)$ is also quite constant $-0.48<\overset{\frown }{\mu }<-0.65$. The average of $\overset{\frown }{\mu }$ during the plastic deformation is −0.52 and is shown as an horizontal line in Fig. 9.

Fig. 9

Variation of the averaged triaxiality and Lode parameter along the mid-cut section during plastic deformation

Data Reduction Technique

During an experiment with the STS, the applied load (P) and vertical displacement (Δd) are measured, as shown in Fig. 8 from numerical simulations. The goal of the data reduction technique is to reduce the measured P − Δd curve into the characteristic equivalent σ ^t − ε ^t _p of the material. It was shown (Fig. 7) that the averaged ${\overset{\frown }{\sigma}}_M-{\overset{\frown }{\varepsilon}}_p$ on the mid-section represents well the true material properties σ ^t − ε ^t _p . The mapping procedure of the displacement into equivalent plastic strain is similar to what is detailed in [16, 17, 19, 28]. First we map the applied displacement Δd into the averaged equivalent plastic strain ${\overset{\frown }{\varepsilon}}_p$. We do it for Δd > Δd _Y where Δd _Y is the applied displacement in which the mid-section of the gauge yields.

$$ {\overset{\frown }{\varepsilon}}_p={\displaystyle \sum_{i=1}^N{k}_{i+1}{\left(\frac{\varDelta d-\varDelta {d}_Y}{h}\right)}^i}\kern3em for\kern0.36em \varDelta d>\varDelta {d}_Y $$

(6)

The yield point on the normalized applied load–displacement curve (σ _ap  − ε _ap ) is shown in Fig. 8.

Figure 10 shows the variation of the averaged plastic strain $\left({\overset{\frown }{\varepsilon}}_p\right)$ on the mid-section of the gauge, with the applied normalized displacement ${\varepsilon}_{ap}=\frac{\varDelta d}{h}$. It can be observed that the dependence is almost linear, so that a first degree polynomial approximation (equation (6)) of the type: ${\overset{\frown }{\varepsilon}}_p={k}_2\frac{\varDelta d-\varDelta {d}_y}{h}$ where k ₂ = 3.7625 is sufficient for accurate mapping, as in [16, 19, 21]).

Fig. 10

Variation of the averaged plastic strain $\left({\overset{\frown }{\varepsilon}}_p\right)$ in the mid-cut section of the gauge with the applied normalized displacement $\left(\frac{\varDelta d}{h}\right)$. The arrow indicates the beginning of plasticity $\left(\frac{\varDelta {d}_Y}{h}\right)$

Next, we map the applied load P for P > P _Y into the averaged Mises stress by:

$$ {\overset{\frown }{\sigma}}_M={k}_1\left({\overset{\frown }{\varepsilon}}_p\right)\frac{P\left({\overset{\frown }{\varepsilon}}_p\right)}{D\cdot t}\kern5.04em for\kern0.24em P>{P}_Y $$

(7)

For the SCS ${k}_1\left({\overset{\frown }{\varepsilon}}_p\right)={K}_1\left(1-{K}_2{\overset{\frown }{\varepsilon}}_p\right)$ where K ₁ and K ₂ are constants. This function is not suitable for the STS since the applied load does not increase monotonically.

In order to determine ${k}_1\left({\overset{\frown }{\varepsilon}}_p\right)$ for the STS, the normalized applied load $\frac{P}{D\cdot t}$ is plotted against the averaged plastic strain ${\overset{\frown }{\varepsilon}}_p$ on the mid section. This can also be done by application of equation (6) to the experimental results of Fig. 8. The averaged Mises stress on the mid section ${\overset{\frown }{\sigma}}_M$ is plotted as well against the plastic averaged plastic strain ${\overset{\frown }{\varepsilon}}_p$. These two curves are shown in Fig. 11(a). It can be observed visually in Fig. 11(a) that for ε _p  > 0.2 the normalized applied load decreases while the ${\overset{\frown }{\sigma}}_M={\sigma}^t$ continues to increase. This indicates that the decreasing applied load does not mean softening. According to equation (7) the ratio between these two curves is ${k}_1\left({\overset{\frown }{\varepsilon}}_p\right)$. This ratio is shown in Fig. 11(b). The ratio is for the range $0<{\overset{\frown }{\varepsilon}}_p<{{\overset{\frown }{\varepsilon}}^f}_p$ where ${{\overset{\frown }{\varepsilon}}^f}_p$ is the averaged fracture strain on the mid-section. The ratio ${k}_1\left({\overset{\frown }{\varepsilon}}_p\right)$ can be approximated by: ${k}_1\left({\overset{\frown }{\varepsilon}}_p\right)={a}^{\ast }{e}^{b^{\ast}\;{\overset{\frown }{\varepsilon}}_p}+{c}^{\ast }{e}^{d^{\ast}\;{\overset{\frown }{\varepsilon}}_p}$ where: a ^∗ = 0.0515, b ^∗ = − 156.5, c ^∗ = 0.9094 and d ^∗ = 0.2616 . The variation is quite even with $0.92<{k}_1\left({\overset{\frown }{\varepsilon}}_p\right)<1.01$.

Fig. 11

(a). The normalized applied load P/(Dt) versus ${\overset{\frown }{\varepsilon}}_p$ in comparison to the characteristic curve. (b). The ratio ${k}_1\left({\overset{\frown }{\varepsilon}}_p\right)$ between the characteristic stress (σ ^t) normalized applied load (σ _ap )

The total strain is: $\overset{\frown }{\varepsilon }={\overset{\frown }{\varepsilon}}_p+{\overset{\frown }{\varepsilon}}_e={\overset{\frown }{\varepsilon}}_p+\frac{\overset{\frown }{\sigma }}{E}$. For most metals the elastic strain is negligible in comparison with the plastic strain $\left({\overset{\frown }{\varepsilon}}_e<<{\overset{\frown }{\varepsilon}}_p\right)$, hence using $\overset{\frown }{\varepsilon}\simeq {\overset{\frown }{\varepsilon}}_p$ is justified.

Experimental Results

The quasi-static tests and the dynamic tests are detailed in the next two subsections.

Quasi-Static Tests

The quasi static tests include a comparison of the STS results to test results obtained by using cylindrical specimens in compression and dog-bone specimen in tension.

Results and Data Reduction

All specimens were manufactured from 12 mm diameter cold drawn round steel bars C22E (DIN) or 1020 (AISI/SAE), in the as-received condition. Dog-bone, cylindrical and STS specimens were machined.

The cylinders were sandwiched between loading rods and compression was applied, while the dog-bone and the STS specimens were tested in tension. All specimens were tested quasi-statically on a servo-hydraulic with a crosshead speed of 1 [mm/min]. The vertical displacements were measured with an optical laser extensometer, while the applied force by the load cell of the machine. The tests stopped when the specimens deformed drastically (in compression) or fractured. The dimensions of the dog-bone type and cylinder type specimen are shown in Fig. 12, and the dimensions of the circular gauge STS are shown in Fig. 1 and detailed in “Geometry” section.

Fig. 12

Geometry and dimensions of the cylindrical and dog-bone specimens. All dimensions in mm

The normalized experimental results for 5 specimens are shown in Fig. 13. The applied load on each specimen (i) is normalized by its gauge’s vertical area projection (D ⋅ t _i ). The applied displacement is normalized by the vertical height of the gauge h. Each curve has a distinct apparent yield and fracture strain. The averaged experimental curve is shown as well. The average curve was obtained by first plotting the experimental results of each specimen for the plastic region, using translation: ${\varepsilon}^{(i)}=\frac{\varDelta d-\varDelta {d}_Y^{(i)}}{h},\kern0.6em i=1\ldots 5$. Then the plastic strain region was divided into N points and for each point j = 1...N the average of the applied stress was calculated by ${\sigma}_{(j)}=\frac{1}{5}{\displaystyle \sum_{i=1}^5{\sigma}^{(i)}}$ where ${\sigma}^{(i)}=\frac{P^{(i)}}{D\cdot {t}^{(i)}}$. Figure 14 shows the translated average stress–strain curve from yield (Δd _Y ) up to the fracture strain (Δd _f ), as a function of $\frac{\varDelta d-\varDelta {d}_Y}{h}$. It can clearly be observed that the experimental applied force has a maximum point at ~0.025 and for larger displacements the load is decreasing. This phenomenon was predicted by the numerical simulations shown in Figs. 8 and 12(a), and as mentioned does not mean that strain-softening occurs, as is shown in Fig. 11(a) .

Fig. 13

The five experimental results showing the normalized applied load σ = P/(Dt) versus the normalized applied displacement Δd/h. Note the average experimental curve

Fig. 14

The averaged normalized experimental results in the range of displacements: Δd _Y  < ε < Δd _f

The data reduction technique (equations (6)–(7)) is applied to the data of Fig. 14 to yield the characteristic $\overset{\frown }{\sigma }-{\overset{\frown }{\varepsilon}}_p$ curve of the material (Fig. 15), together with the results of compression cylinders and tension of dog-bone specimens [28]. The hardening of the STS curve is similar, but lower to that of the cylindrical specimens for the small plastic strain range. The flow stress is ~50 MPa lower. This difference is probably due to the effect of the third invariant of the deviator stress, i.e., Lode parameter [2]. Let us remind that in our compression tests, μ = 1, and in tension μ = − 1, as opposed to the in shear-tension test where μ = − 0.52. Indeed, it can be found in the literature [3] that the effect of the Lode parameter on the fracture strain is negligible while its effect on the plastic flow is notable.

Fig. 15

The characteristic σ ^t − ε ^t _p curve of steel 1020 obtained by STS in comparison to those obtained by cylinders and dog-bone specimens [28]

Using the STS, the 1020 steel could be characterized up to ε _p  = 0.23 where fracture occurred, while dog-bone specimens would allow to reach only up to ε _p  = 0.025, one order of magnitude less than the STS.

It should be noticed that the average plastic strain on the mid-section at fracture is not the ductility (fracture strain) of the material. This is understood by considering the fact that in “Numerical evaluation of an STS” section we fixed the failure strain ε ^f _p  = 0.5 but the calculations showed that the averaged failure strain is smaller (see Fig. 7): ${\overset{\frown }{\varepsilon}}_p^f=0.38$. It means that the real fracture strain is higher by ~32 % from the observed averaged fracture strain so that ${\varepsilon}_p^f=1.32\;{\overset{\frown }{\varepsilon}}_p^f$. This is the result of the strain distribution on the mid-section, and its averaging, as compared to its maximum value on the mid-section where fracture starts. Such a result suggests that the averaged true failure strain will always be underestimated to some extent, although, as discussed in the next section, this point can be remedied.

Numerical Validation

In the first iteration, the STS characteristic curve of Fig. 15 was extrapolated to higher values of plastic strain as shown in Fig. 16(a), and was then input into Abaqus (see Numerical model, mesh, boundary conditions and material properties). The red markers on the curves of Fig. 16(a) indicate extrapolation while the characterized region is indicated by green markers. The numerically obtained $\frac{P}{D\cdot t}-\frac{\varDelta d}{h}$ curves of Fig. 16(a) are compared to the averaged experimental curve in Fig. 16(b). Even though there is a good agreement, it can be observed that the numerical curve is slightly lower than the experimental one for $\frac{\varDelta d}{h}<0.04$ and is slightly higher for $\frac{\varDelta d}{h}>0.05$. Hence the obtained characteristic curve was slightly modified (2nd iteration) as shown in Fig. 16(a). The modified curve of the 2nd iteration was once again input for another numerical analysis. A very good agreement can be observed in Fig. 16(b) between the experimental and numerical $\frac{P}{D\cdot t}-\frac{\varDelta d}{h}$ curves for the modified characteristic curve. A ductile failure criterion with damage evolution [32] was then added to the analysis. The $\frac{P}{D\cdot t}-\frac{\varDelta d}{h}$ curves for 3 values of the failure strain (0.35, 0.40 and 0.45) are shown in Fig. 16(b). The results clearly show that the failure strain of steel 1020 is ~0.42 in quasi-static tension for Lode parameter of −0.52 and triaxiality of −0.36.

Fig. 16

(a). The obtained (1st iteration) and modified (2nd iteration) characteristic $\overset{\frown }{\sigma }-{\overset{\frown }{\varepsilon}}_p$ curve of steel 1020 obtained by STS. (b). Comparison of the experimental average $\frac{P}{D\cdot t}-\frac{\varDelta d}{h}$ curve to the numerical ones obtained by using the characteristic curves of Fig. 17a. Note that the three normalized load–displacement curves for the modified $\overset{\frown }{\sigma }-{\overset{\frown }{\varepsilon}}_p$ in 17b coincide until fracture

Summary of Data Reduction and Validation Steps for Quasi-Static Loading

The data reduction and validation steps for taking advantage of the STS under quasi-static loading can be summarized as follows:

• 1. Perform a numerical analysis of the specimen using the best known stress–strain curve for the material (Numerical evaluation of an STS).

• 2. Obtain the numerical results for:

  $$ time(i),\kern0.24em \varDelta d\left[ time(i)\right],\kern0.24em P\left[ time(i)\right],\kern0.24em {\overset{\frown }{\sigma}}_M\left[ time(i)\right],\kern0.24em {\overset{\frown }{\varepsilon}}_P\left[ time(i)\right] $$

  where time is the solution time 0 ≤ time(i) ≤ 1 and i is the number of the time step during the numerical solution.

• 3. Plot ${\overset{\frown }{\varepsilon}}_p\kern0.36em vs\kern0.72em \frac{\varDelta d}{h}$ and obtain by curve fitting the coefficients for equation (6) (k ₂).

• 4. Plot $\frac{P}{D\cdot t}\kern0.24em vs\kern0.24em {\overset{\frown }{\varepsilon}}_p$ and ${\overset{\frown }{\sigma}}_M\;vs\kern0.24em {\overset{\frown }{\varepsilon}}_p$ on another figure and get the ratio ${k}_1\left({\overset{\frown }{\varepsilon}}_p\right)$ for equation (7).

• 5. Perform an experiment and obtain the curve: P ^exp − Δd ^exp.

• 6. Identify\estimate on the obtained experimental curve of step 5 the yield point (P ^exp _Y  , Δd ^exp _Y ) and replot the translated normalized experimental curve: $\frac{P^{\exp }}{D\cdot t}\kern0.48em vs.\kern0.36em \frac{\varDelta {d}^{\exp }-\varDelta {d}_Y^{\exp }}{h}$ for Δd ^exp > Δd ^exp _Y .

• 7. Get a first estimation of σ ^t − ε ^t _p by applying the data reduction equations (6)–(7) with the results of steps 3–4 on the experimental curve of step 6.

• 8. Validate σ ^t − ε ^t _p by substituting it into the analysis of step 1. Make small adjustments to σ ^t − ε ^t _p until a satisfactory agreement between the experimental $\frac{P^{\exp }}{D\cdot t}\kern0.48em vs.\kern0.36em \frac{\varDelta {d}^{\exp }-\varDelta {d}_Y^{\exp }}{h}$ and the numerical ones is obtained.

• 9. Add a ductile failure criterion (fracture strain) to the analysis of step 8 and find the ductility by a trial and error process while comparing the experimental $\frac{P^{\exp }}{D\cdot t}\kern0.48em vs.\kern0.36em \frac{\varDelta {d}^{\exp }-\varDelta {d}_Y^{\exp }}{h}$ to the numerical one. (A rough estimation can be obtained by multiplication the observed failure strain of step 7 by 1.32).

Dynamic Tests

Experimental Results

Five specimen were tested using hardened C300 maraging steel split Hopkinson tension bars (SHTB). The geometry of the specimens is the same as for the quasi-static tests (Fig. 1) with L = 80 mm and D = 8 mm. The only difference is an outer thread ~11 mm long, as shown in Fig. 17(a), which allows for specimen mounting into the bars.

Fig. 17

(a). The dynamic STS specimen. (b). During impact testing before fracture. (c). During impact testing before fracture 25 μs after 18b (d). Fracture occur. (e). The fractured STS specimen

A fast camera (Kirana, Specialized Imaging) recorded the impact at 1,000,000 fps. Four characteristic frames are shown in Fig. 17(b)-(e). The pictures were taken at 150, 175, 190 and 225 μs from trigger. Cracks can be observed at the ends of the gauge and its center in Fig. 17(d), while Fig. 17(e) shows the fully fractured gauge. The fracture pattern resembles the letter Z and the fracture face is stepped. The 5 fractured specimens are shown in Fig. 18.

Fig. 18

The five dynamically fractured STS specimens

The recorded pulses during the 5 tests are shown in Fig. 19. All tests were performed with the same pressure within the air tank: 3 bar and it can be observed that there is a good repetability of the results (the “spike” is probably the result of a shorted gauge wire).

Fig. 19

The experimental recorded pulses

Numerical Model, Mesh, Materials and Boundary Conditions

The numerical model included 3 parts: 1) Half of the incident bar. 2) The SCS specimen. 3) The transmitted bar. The assembly of these parts is shown in Fig. 20(a). A magnified region of the STS specimen is shown in Fig. 20(b). The front view on top of Fig. 20(b) and the back view on the bottom of 20b. It was assumed in the analysis that the STS specimen is perfectly bonded to the incident and transmitted bars. The bonded area can be seen in the back view. Because of symmetry only half of the three merged parts were modeled, as shown in the cut section of Fig. 20(c).

Fig. 20

The model assembly which was used for the numerical validation. (a). The assembly. (b). Magnification of the specimen area showing the connection to the bars. (c). A cut section through the model showing the face on which symmetry condition were applied

The model uses a total number of 386812 linear hexahedral elements of type C3D8R. The mesh size in the SCS gauge region is ~0.2 mm and on the bars ~1 mm.

Symmetry conditions were applied all along the assembly on the face shown in Fig. 20(c). The load was applied at the right end of the half incident bar. At that location in the experimental setup, a strain gauge is used to measure the incident and reflected pulses. The average of the measured incident strain pulses multiplied by the Young’s modulus of the bars was applied as a negative pressure. The incident pulses are shown in Fig. 19.

An elastic material model was used for the SHPB bars (Table 1). An elastic–plastic material model was used for the 1020 steel (Table 1). The stress-plastic strain curve was input into Abaqus for the STS is shown in Fig. 16(a). A ductile failure criterion with a displacement type damage evolution [32] of 5 μm was used.. The purpose of the analyses is to obtain and validate the stress–strain results in the dynamic regime.

Table 1 Material properties

Numerical Results

The dynamic flow behavior and ductility of the STS is obtained by hybrid numerical-experimental technique using “trial and error” procedure. As a first guess, we use the quasi-static σ ^t − ε ^t _p curve. The experimentally measured strain pulse is applied as pressure (multiplied by Young’s modulus of the bar) on the incident bar, and the reflected pulse is determined at the location (Fig. 20(a)) of the strain gauge and compared to experimentally measured transmitted pulse. The σ ^t − ε ^t _p which are input to numerical analyses is iteratively modified until a good agreement is reached.

Likewise, the ductility is also found by trial and error procedure. Different values are tested until a good agreement is reached between the experimental and numerical transmitted pulses.

We show in Fig. 21(a) three σ ^t − ε ^t _p curves. The lower curve (a) is the quasi-static curve of Fig. 16(a). The middle curve (b) is 50 MPa higher than curve (a). The upper curve (c) is 100 MPa higher than (a).

Fig. 21

(a). Characteristic ε _p  − σ curves which correspond to the quasi-static curve (a) and an elevated stress by 50 and 100 MPa (b) and (c). (b). The corresponding numerically obtained transmitted pulses due to the characteristic curves in comparison to the experimental transmitted pulse

The results of 4 numerical analyses are shown in Fig. 21(b). The first 3 correspond to using the σ ^t − ε ^t _p curves (a)-(b)-(c) with fracture strain of ε ^f _p  = 0.5 and the 4th to the curve (b) without any failure criterion. These four numerically obtained transmitted pulses are compared to the average of the 5 experimentally obtained transmitted pulses.

The experimental results do have a “ringing effect” due to inertia [33]. This ringing effect is attenuated as the plastic strain within the gauge increases. Hence, the numerical results do not replicate the first experimental (inertial) peak value, but it does replicate the next three ones. Curve (a) coincides with the minimum of the 2nd extreme value. Curve (c) coincides with the maximum of the 3rd extreme value. Curve (b) seem to flatten the ringing effect, and to be more similar to the experimental pulse. It means that due to the strain-rate effect the material hardens by ~ 50 MPa. The strain rate is ~ 10000 1/s and is obtained by derivation of the numerical results for ${\overset{\frown }{\varepsilon}}_p$ . The 4th numerical pulse shows how would the transmitted pulse behave if there was no fracture. The value of ε ^f _p  = 0.5 seems adequate for simulating the fracture.

Summary of Data Reduction and Validation Steps for Dynamic Loading

The data reduction and validation steps for taking advantage of the STS under dynamic loading can be summarized as follows:

• 1. Perform an experiment on a SHTB and obtain the incident, reflected and transmitted strain pulses.

• 2. Apply a numerical analysis of the experimental setup (similar to Numerical results section) in which the static σ ^t − ε ^t _p serves as a first guess for the true dynamic σ ^t − ε ^t _p and the experimentally measured incident pulse serve as the applied load.

• 3. Monitor the numerically obtained transmitted strain pulse and compare it to the experimental one. Apply changes to the static σ ^t − ε ^t _p until satisfactory agreement between the numerical and experimental transmitted strain pulses.

• 4. Add a ductile failure criterion (fracture strain) to the analysis of step 2 and find the ductility by a trial and error procedure by comparing the experimental transmitted strain pulse to the numerical one (see Fig. 21(b)).

Summary and Conclusion

This paper introduces a new specimen that is capable of applying shear and tension simultaneously, namely the Shear Tension Specimen (STS). This specimen is inspired by the Shear Compression Specimen (SCS) with a modification (rounding) of the gauge geometry that avoids unwanted stress concentrations in the fillets. The application is due to its simple geometry and does not require special equipment as in (for example) the investigation [31] who studied various ratios between the shear and tension by application of torque and tension simultaneously and keeping a constant ratio between them during loading.

The paper has presented a thorough evaluation of the new specimen in both the static and the dynamic regimes, in which numerical simulations and experiments were combined.

The main characteristics of this specimen are:

• The uniformity of the plastic strains and stresses in the gauge section

• The good uniformity and constancy of the stress triaxiality and Lode parameters.

• The feasibility of the specimen for quasi-static and dynamic tests alike.

With that, a detailed procedure for the reduction of the applied loads and displacements into equivalent stress and strain, respectively, was presented. This procedure involves basic numerical simulation work. Keeping in mind that there is no accepted specimen to investigate shear under tension (Lode parameter: − 1 ≤ μ ≤ 0), whose availability might help to discover interesting properties of materials. it is believed that the data reduction procedure is reasonably straightforward and justifies the use of the STS.