Fitting Nonlinear Ordinary Differential Equation Models with Random Effects and Unknown Initial Conditions Using the Stochastic Approximation Expectation–Maximization (SAEM) Algorithm

Abstract

The past decade has evidenced the increased prevalence of irregularly spaced longitudinal data in social sciences. Clearly lacking, however, are modeling tools that allow researchers to fit dynamic models to irregularly spaced data, particularly data that show nonlinearity and heterogeneity in dynamical structures. We consider the issue of fitting multivariate nonlinear differential equation models with random effects and unknown initial conditions to irregularly spaced data. A stochastic approximation expectation–maximization algorithm is proposed and its performance is evaluated using a benchmark nonlinear dynamical systems model, namely, the Van der Pol oscillator equations. The empirical utility of the proposed technique is illustrated using a set of 24-h ambulatory cardiovascular data from 168 men and women. Pertinent methodological challenges and unresolved issues are discussed.

From difference scores (see e.g., Bereiter, 1963; Cronbach & Furby, 1970; Harris, 1963) to confirmatory models grounded on differential/difference equations, the study of change remains a central question of interest to researchers in the social and behavioral sciences. In the realm of nonlinear dynamic systems analysis, the last decade has evidenced a gradual shift from heavy reliance on geometrically based exploratory nonlinear analytic techniques (see e.g., Kaplan & Glass, 1995; Longstaff & Heath, 1999) to confirmatory approaches of studying nonlinear dynamic processes via model fitting (Molenaar & Newell, 2003; Ramsay, Hooker, Campbell, & Cao, 2007).

Differential equation models provide a direct representation of change processes while allowing the data to be irregularly spaced. Such data have become increasingly prevalent in studies aimed at collecting experience sampling or ecological momentary assessment data (Stone & Shiffman, 1994). Most experience sampling studies require respondents to provide assessments on relevant constructs over a specified period at specific times of the day (interval-contingent), at random times when prompted by an experimenter-invoked signal (signal-contingent), or as triggered by an event in everyday life (event-contingent; Bolger, Davis, & Rafaeli, 2003). Signal- and event-contingent data are typically irregularly spaced by nature of the study designs.

Currently, there has been a scarcity of tools for fitting models to irregularly spaced data in the psychometric literature. Standard growth curve and the related mixed effects models (Browne & du Toit, 1991; Mcardle & Hamagami, 2003; Meredith & Tisak, 1990) provide a straightforward way of handling irregularly spaced intensive repeated measures data when time appears explicitly in the fitted functions. When that is not the case, this approach cannot be used without further modifications. Differential equation models, in contrast, can be used to extend conventional growth curve models in a number of ways. First, most growth curve (e.g., linear, Gompertz and exponential, among many others) models can be viewed as the integral solutions of various differential equations. Thus, growth curve models can be conceived as special cases of differential equation models. Second, differential equation models, when compared to standard growth curve expressions, focus explicitly on representing the mechanisms of change: that is, changes in the constructs of interest appear explicitly on the left-hand-side of the equations. In this way, differential equations have greater flexibility in capturing the interdependencies among multiple change processes, especially when the fitted functions do not depend explicitly on time.

Despite the proliferation of work on ODE modeling in the econometric, engineering, and statistical literature (Ait-Sahalia, 2008; Jones, 1984; Mbalawata, Särkkä, & Haario, 2013; Beskos, Papaspiliopoulos, Roberts, & Fearnhead, 2006; Beskos, Papaspiliopoulos, & Roberts, 2009; Ramsay et al., 2007; Särkkä, 2013), much of the progress in ODE modeling in the field of psychometrics has been limited to linear ODE modeling. Notable advances include efforts to extend earlier approaches of fitting the nonlinear integral solutions of linear ordinary differential equations (ODEs) as linear structural equation models without the necessary constraints (Arminger, 1986) to alternative state-space approaches (Jones, 1984, 1993), SEM implementation of state-space approaches (Singer, 1992, 2010, 2012; Oud & Jansen, 2000; Oud & Singer, 2010), two-stage derivative estimation approaches (Boker & Graham, 1998; Boker & Nesselroade, 2002), as well as comparisons between the two-stage and other single-stage approaches (Oud, 2007). Still, these approaches were designed primarily to fit longitudinal linear ODEs and stochastic differential equations (SDEs). Generalizing standard SEM procedures (e.g., product indicator techniques or related approaches involving nonlinear constraints; Kenny & Judd, 1984; Klein & Muthén, 2007; Marsh, Wen, & Hau, 2004) to nonlinear dynamic models (e.g., nonlinear ODEs) is far from simple. Implementing such constraints in the simpler linear growth curve models has proven to be difficult (Duncan, Duncan, Strycker, Li, & Alpert, 1999; Li, Duncan, & Acock, 2000; Wen, Marsh, & Hau, 2002), not to mention other less widely tested nonlinear dynamic models.

Despite the difficulties involved, nonlinear differential equation models have distinct merits compared to linear models that make the associated efforts worth pursuing. For instance, nonlinear differential equation models are capable of predicting ongoing oscillations between different locally stable behaviors (Hale & Koçak, 1991). In this vein, Boker and Graham (1998) used a cubic oscillator model to represent adolescent substance abuse behavior as having two attractor states: substance use and non-use. Perhaps of particular interest to social and behavioral scientists is nonlinear differential equation models’ flexibility in representing the dependencies of a change process on—or in other words, how the process is moderated by—other key variables in the system. Examples of applications along this line include the use of a modified Van der Pol oscillator equation to represent human circadian rhythms (Brown & Luithardt, 1999; Brown, Luithardt, & Czeisler, 2000), and variations of the predator–prey model to represent dyadic interaction (Chow, Ferrer, & Nesselroade, 2007), human cerebral development (Thatcher, 1998), and cognitive aging (Chow & Nesselroade, 2004). Thus, differential equation models share the merits of their discrete-time counterparts (such as state-space models and the SEM-based latent difference approach; Durbin & Koopman, 2001; McArdle & Hamagami, 2001) in providing a platform to represent change mechanisms in concrete terms, while offering more flexibility in accommodating irregular time intervals.

In the present article, we present a frequentist approach to fitting nonlinear ODE models with random effects and unknown initial conditions by means of a stochastic approximation expectation–maximization (SAEM) algorithm. The proposed approach extends previous work on fitting ODEs in the statistical, biostatistical, and psychometric literature in several ways. First, contrary to other existing linear approaches (Boker & Nesselroade, 2002; Oud & Jansen, 2000; Jones, 1984), we consider the problem of fitting nonlinear ODEs to irregularly spaced data. The proposed approach can also be used with linear ODEs. Second, unlike other applications using a fully Bayesian approach (e.g., Carlin, Gelfand, & Smith, 1992; Chow, Tang, Yuan, Song, & Zhu, 2011; Durbin & Koopman, 2001; Geweke & Tanizaki, 2001; Mbalawata et al., 2013; Särkkä, 2013), we combine a Markov chain Monte Carlo (MCMC) procedure with the expectation–maximization (EM) algorithm to yield maximum likelihood (ML) point and standard error estimates of the time-invariant modeling parameters (as in Kuhn & Laviellem, 2005; Donnet & Samson, 2007). Considerable modeling flexibility is gained due to the ease with which MCMC procedures handle more complex models. Yet, we can still adopt familiar Frequentist-based statistics and approaches (e.g., confidence intervals) for inferential purposes. Third, we represent the structural parameters (i.e., parameters that govern the dynamics of a system) as composed of a series of fixed and random effects—a modeling feature not considered in other studies, including studies that utilize other Frequentist and/or simulation-based approximation approaches to fit ODEs or SDEs (e.g., Beskos et al., 2009, 2006; Chow et al., 2007; Ramsay et al., 2007; Gordon, Salmond, & Smith, 1993; Hürzeler & Künsch, 1998; Kitagawa, 1998; Mbalawata et al., 2013; Singer, 1995, 2002, 2007; Tanizaki, 1996). Finally, while the performance of the SAEM algorithm in handling mixed effects ODEs featuring manifest variables only has been evaluated elsewhere (Donnet & Samson, 2007; Kuhn & Laviellem, 2005), these researchers’ prior work did not explicitly consider the performance of the SAEM in situations where the initial conditions are unknown and differ between subjects. Thus, as distinct from the work of Kuhn and Laviellem (2005) and Donnet and Samson (2007), the proposed modeling framework contributes uniquely to the literature on ODE modeling by (1) including a factor analytic model as a measurement model to enable modeling at the latent variable level, and (2) allowing the means and interindividual differences in the initial conditions of latent variables to be estimated as modeling parameters. Additionally, a simulation study is conducted to evaluate the performance of the estimation procedures under different initial condition specifications, including scenarios where the initial conditions are misspecified and interindividual differences in initial conditions are ignored.

1 Nonlinear Ordinary Differential Equation (ODE) Models with Random Effects and Possibly Unknown Initial Conditions

We consider the problem of fitting linear and nonlinear ODEs with random effects in the structural parameters under situations in which the initial conditions of the ODEs may be unknown. Letting $D\varvec{x}_i(t)$ denote the differential operator applied on $\varvec{x}_i(t)$, i.e., $D\varvec{x}_i(t) = \mathrm{d}\varvec{x}_i(t)/\mathrm{d}t$, the nonlinear ODEs of interest take on the general form of

$$\begin{aligned} D \varvec{x}_i(t)&= \varvec{f}[\varvec{x}_i(t),\varvec{\theta }_{f,i}, t] ,\quad i=1,\ldots n \nonumber \\ \varvec{\theta }_{f,i}&= \varvec{\mathrm {H}}_i \varvec{\beta } + \varvec{\mathrm {Z}}_i \varvec{b}_i, \end{aligned}$$

(1)

where $i$ indexes person and $t$ indexes time, $\varvec{f}(.)$ is a vector of (possibly nonlinear) drift functions; $\varvec{x}_i(t)$ is an $n_x \times$ 1 vector of latent variables of interest at time $t$; and $D\varvec{x}_i(t)$ denotes the corresponding $n_x \times$ 1 vector of first derivatives. Note that $\varvec{x}_i(t)$ may include latent derivative variables needed to define higher-order ODEs. $\varvec{\theta }_{f,i}$ represents a $q \times$ 1 vector of person-specific structural parameters of interest that affect the dynamic functions in Eq. (1), expressed as a function of $\varvec{\beta }$, a $p_{\beta } \times$ 1 vector of fixed effects parameters, and $\varvec{b}_i$, a $d \times$ 1 vector of random effect; $\varvec{\mathrm {H}}_i$ and $\varvec{\mathrm {Z}}_i$ are $q \times p_{\beta }$ and $q \times d$ design matrices typically seen in the linear mixed effects framework. We further assume that $\varvec{b}_i$ follows a multivariate normal distribution as $\varvec{b}_i \sim N(\varvec{0}, \varvec{\mathrm {\Sigma }}_b)$, where $\varvec{\theta }_b$ contains all the unknown parameters in $\varvec{\mathrm {\Sigma }}_b$.

The initial conditions for the ODEs are denoted as $\varvec{x}_i(t_{i,1})$, and are specified to be functions of $\varvec{\theta }_{f,i}$. In this way, fixed effects parameters governing the initial conditions are estimated as part of $\varvec{\beta }$, while individual-specific deviations in initial conditions are captured by the random effects in $\varvec{b}_i$. Our illustrative application provides a concrete example of one possible way of representing unknown initial conditions across multiple subjects using this formulation.

The latent variables in $\varvec{x}_i(t_{i,j})$ at discrete time point $t_{i,j}$ are indicated by an $n_y \times$ 1 vector of manifest observations assumed to be measured at individual-specific and possibly irregularly spaced time intervals, at $t = t_{i,j}, j = 1, \ldots , T$, with $\Delta _{i,j}=t_{i, j+1}-t_{i, j}$. The vector of manifest observations is denoted as $\varvec{y}_i(t_{i,j})$, with

$$\begin{aligned} \varvec{y}_i(t_{i,j})&= \varvec{\mu } + \varvec{\mathrm {\Lambda }} \varvec{x}_i(t_{i,j}) + \varvec{\epsilon }_i(t_{i,j}), \end{aligned}$$

(2)

where $\varvec{\mu }$ is an $n_y \times 1$ vector of intercepts, $\varvec{\Lambda }$ is an $n_y \times n_x$ factor loading matrix, and $\varvec{\epsilon }_i(t_{i,j})$ denotes multivariate normally distributed measurement error processes such that $E[\varvec{\epsilon }_i(t_{i,j})] = \varvec{0}, E[\varvec{\epsilon }_i(t_{i,j}) \varvec{\epsilon }_i(t_{i,j})^\mathrm{T}]=\varvec{\mathrm {\varvec{\mathrm {\Sigma }}}}_\epsilon , \varvec{\epsilon }_i(t_{i,j})$ and $\varvec{x}_i(t_{i,j})$ are independent, and $\varvec{\epsilon }_i(t_{i,j})$ and $\varvec{\epsilon }_i(t_{i,k})$ are independent for $t_{i,j}\not =t_{i,k}$, with a diagonal structure for $\mathop {\mathrm {Cov}}(\varvec{\epsilon }_i(t_{i,j})) = \varvec{\mathrm {\Sigma }}_{\epsilon }$. We also assume generally that when multiple indicators are used to identify a latent factor, at least one factor loading is fixed for identification purposes.

In continuous time, given the initial conditions of the system at any arbitrary time $t_{0}$, one may define a t-advance mapping or evolution function $g(t, \varvec{x}_i(t_{0}))$ that moves an initial state to a later state at time $t$. The evolution function, $g(t, \varvec{x}_i(t_{0}))$, can be used to map out the trajectories of all the latent variables in $\varvec{x}_i(t)$. Once these values are known, the solution to the hypothesized ODE is also known. Thus, one can obtain the solution of the ODE through repeated application of the evolution function, e.g., first from time $t_0$ to $s$, and subsequently to $t$, as $g(t+s,\varvec{x}_i(t_{0}))=g(t,g(s,\varvec{x}_i(t_{0})))$. Thus, if the vector of true latent differences, defined as $\Delta \varvec{x}_i(t_{i,j}) = \varvec{x}_i(t_{i, j})- \varvec{x}_i(t_{i, j-1})$, are known at at a series of discrete time points, $t_{i,j}, j = 1, \ldots , T$, one can obtain a discrete t-advance mapping as

$$\begin{aligned} \varvec{x}_i(t_{i,j})&= \varvec{x}_i(t_{i, j-1})+\Delta \varvec{x}_i(t_{i,j}) ,\nonumber \\&= \varvec{x}_i(t_{i,1})+\sum ^{j}_{k=2}\Delta \varvec{x}_i(t_{i,k}). \end{aligned}$$

(3)

With few exceptions, most nonlinear ODEs do not have analytic solutions. One common approach is to use numerical methods such as Euler’s or Runge–Kutta methods to obtain approximate t-advance mapping at discrete intervals. In other words, we approximate the vector of true latent differences, $\Delta \varvec{x}_i(t_{i,j+1}) = \varvec{x}_i(t_{i, j+1})- \varvec{x}_i(t_{i, j})$ using $\varvec{x}^{*}_i(t_{i, j})$, namely, numerical interpolations of the latent changes at the next time point based on the hypothesized ODE to yield numerical solution, $\tilde{\varvec{x}}_i(t_{i,j})$, as

$$\begin{aligned} \tilde{\varvec{x}}_i(t_{i,j})&= \tilde{\varvec{x}}_i(t_{i, j-1})+\sum ^{1/\Delta ^*}_{k=1} \varvec{x}^{*}_i(t_{i, j-1+k\Delta ^{*}}),\nonumber \\&= \varvec{x}_i(t_{i,1})+\sum ^{(j-1)/\Delta ^*}_{k=1}\varvec{x}^{*}_i(t_{i, 1+k\Delta ^{*}}), \end{aligned}$$

(4)

where the numerical latent differences, $\varvec{x}^{*}_i(t_{i, j})$, are typically obtained at an equally spaced interval, $\Delta ^*$, whose magnitude is considerably smaller than the observed measurement intervals, $\Delta _{i,j}$, to improve the accuracy of the solutions.

We define $t_{i,j*} = t_{i,j-1+k\Delta ^{*}}$ as a time point at which observed measurements might not be available but we are interested in “imputing” the values of the latent changes at this point, $\varvec{x}^{*}_i(t_{i, j^*})$, to improve estimation accuracy. A variety of numerical solvers can be used to obtain $\varvec{x}^{*}_i(t_{i, j^*})$. One such example is the second-order Heun’s method, which is implemented as

$$\begin{aligned} \varvec{x}^{*}_i(t_{i, j^{*}})&= \frac{\Delta ^*}{2} \left\{ \varvec{k}_1 (t_{i, j^* - \Delta ^{*}})+\varvec{k}_2 (t_{i, j^{*}}) \right\} ,\nonumber \\ \varvec{k}_1( t_{i, j^*-\Delta ^*})&= f\left( \tilde{\varvec{x}}_i(t_{i, j^* - \Delta ^{*}}), \varvec{\theta }_{f,i},t_{i, j^*-\Delta ^*}\right) ,\nonumber \\ \varvec{k}_2(t_{i, j^{*}})&= f\left( \tilde{\varvec{x}}_i(t_{i, j^* - \Delta ^{*}})+\Delta ^*\varvec{k}_1( t_{i, j^* - \Delta ^{*}}), \varvec{\theta }_{f,i},t_{i, j^*}\right) . \end{aligned}$$

(5)

Conditional on $\varvec{b}_i$, if the initial condition variables in $\varvec{x}_i(t_{i,1})$ are known or can be estimated, then $\tilde{\varvec{x}}_i(t_{i,j})$ is also known. This reflects the deterministic nature of ODEs. The fitted model thus becomes

$$\begin{aligned} \varvec{y}_i(t_{i, j})| \tilde{\varvec{x}}_i(t_{i,j}) \mathop {\sim }\limits ^\mathrm{{approx}}N(\varvec{\mu } + \varvec{\mathrm {\Lambda }} \tilde{\varvec{x}}_i(t_{i,j}), \varvec{\mathrm {\Sigma }}_{\epsilon }), \end{aligned}$$

(6)

where the notation $\mathop {\sim }\limits ^\mathrm{{approx}}$ denotes approximately distributed as, used to highlight the fact that the numerical solutions given by $\tilde{\varvec{x}}_i(t_{i,j})$ contain truncation errors, namely, errors stemming from using the ODE solver to numerically approximate the true solutions of the ODE.¹ It is important to emphasize that the true latent variables, $\varvec{x}_i(t_{i, j})$, as well as the associated approximation terms, $\varvec{x}^{*}_i(t_{i, j})$ and $\tilde{\varvec{x}}_i(t_{i,j})$, are all functions of $\varvec{\theta }_{f,i}$. Here, we suppress the notational dependency to ease presentation.

Our interest is in estimating the parameters in $\varvec{\theta } = (\varvec{\beta }^\mathrm{T}, \varvec{\theta }_{\varvec{\mu }}^\mathrm{T}, \varvec{\theta }^\mathrm{T}_{\varvec{\mathrm {\Lambda }}}$,$\varvec{\theta }^\mathrm{T}_{\varvec{\epsilon }}, \varvec{\theta }^\mathrm{T}_{\varvec{b}}$) via the SAEM algorithm (Zhu & Gu, 2007). Here, $\varvec{\theta }_{\varvec{\mu }}$ is a $p_{\mu } \times$ 1 (where $p_{\mu } \le n_y$) vector of freed parameters in $\varvec{\mu }, \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}$ is a $p_{\Lambda } \times$ 1 vector containing all unknown factor loadings in $\varvec{\mathrm {\Lambda }}, \varvec{\theta }_{\varvec{\epsilon }}$ is a $p_{\epsilon } \times$ 1 vector containing all the unknown parameters in $\varvec{\mathrm {\Sigma }}_{\varvec{\epsilon }}$, and $\varvec{\theta }_{\varvec{b}}$ is a $p_{b} \times$ 1 vector containing all the unknown parameters in $\varvec{\mathrm {\Sigma _{\varvec{b}}}}$.

1.1 Stochastic Approximation Expectation–Maximization (SAEM) Algorithm

Prior to describing the SAEM algorithm, we first introduce some key notations. Let $\varvec{\mathrm {Y}}_{i} (t_{i,j}) = \{\varvec{y}_i(t_{i, 1}), \ldots , \varvec{y}_i(t_{i, j}))\}, \varvec{\mathrm {Y}}_i = \{\varvec{y}_i(t_{i,1}), \ldots , \varvec{y}_i(t_{i,T})\}$, and $\varvec{\mathrm {Y}} = \{\varvec{\mathrm {Y}}_1, \ldots , \varvec{\mathrm {Y}}_n\}$ is the observed data array for all $n$ participants; let $\tilde{\varvec{\mathrm {X}}}_{i} (t_{i,j}) = \{\tilde{\varvec{x}}_i(t_{i, 1}), \ldots , \tilde{\varvec{x}}_i(t_{i, j})\}, \tilde{\varvec{\mathrm {X}}}_i = \{\tilde{\varvec{x}}_i(t_{i,1}), \ldots , \tilde{\varvec{x}}_i(t_{i,T})\}$, and $\tilde{\varvec{\mathrm {X}}} = \{\tilde{\varvec{\mathrm {X}}}_1, \ldots , \tilde{\varvec{\mathrm {X}}}_n\}$ is the array of numerical solutions of the latent variables for all $n$ participants. Further, we denote the augmented complete data array as $\varvec{\mathrm {Z}}=\{\varvec{\mathrm {Y}},\varvec{b}\}$. In standard Expectation–Maximization (EM) procedures (Dempster, Laird, & Rubin, 1977), maximum likelihood estimates (MLEs) are obtained by cycling iteratively through an expectation (E)-step and a maximization (M)-step. The E-step typically involves analytically computing terms that appear in a pseudo-loglikelihood function given by the conditional expectation of the complete-data loglikelihood function with respect to the distribution $p(\varvec{b}|\varvec{\mathrm {Y}};\varvec{\theta })$. The M-step involves updating the parameter estimates using analytic formulas that serve to maximize the pseudo-loglikelihood function. SAEM differs from conventional E–M algorithms in the use of a stochastic approximation procedure in the E-step, coupled with a gradient-type updating procedure (e.g., the Newton–Raphson and Gauss–Newton algorithms; Ortega, 1990) in the M-step. That is, while the required expectations are analytically intractable, the E-step is made possible by replacing analytic expectations with summary statistics computed using samples drawn from the conditional distribution, $p(\varvec{b}|\varvec{\mathrm {Y}};\varvec{\theta })$, by means of Markov chain Monte Carlo (MCMC) procedures. A Newton–Raphson algorithm is then used to obtain MLEs of $\varvec{\theta }$ in the maximization (M)-step during which a sequence of gain constants, $\gamma$, is used to control the degree to which updates of parameter estimates are weighted in subsequent iterations.

In the present context, the complete-data probability density function is given by

$$\begin{aligned} p(\varvec{\mathrm {Y}}, \varvec{b}; \varvec{\theta }) = \int p(\varvec{\mathrm {Y}}|\tilde{\varvec{\mathrm {X}}},\varvec{b}; \varvec{\theta })p(\tilde{\varvec{\mathrm {X}}}|\varvec{b}; \varvec{\theta }) p(\varvec{b}; \varvec{\theta }) \mathrm{d}\tilde{\varvec{\mathrm {X}}}. \end{aligned}$$

However, due to the deterministic nature of the ODE, $p(\tilde{\varvec{\mathrm {X}}}|\varvec{b}; \varvec{\theta })$ is known conditional on $\varvec{b}$.² Thus, the integration over $\tilde{\varvec{\mathrm {X}}}$ vanishes, and the complete-data loglikelihood function reduces to

$$\begin{aligned} \log [p(\varvec{\mathrm {Y}}, \varvec{b}; \varvec{\theta }) ] \mathop {=}\limits ^\mathrm{{\Delta }}L(\varvec{\mathrm {Z}};\varvec{\theta })&= \sum _{i=1}^{n} \left[ L_{i}(\varvec{b};\varvec{\theta }) + \sum _{j=1}^\mathrm{T} L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b};\varvec{\theta })\right] ,\;\text {with}\nonumber \\ L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b};\varvec{\theta })&= -\frac{1}{2} \left\{ ( n_y) \log (2\pi ) + \log |\varvec{\mathrm {\Sigma }}_{\varvec{\epsilon }}| +[\varvec{y}_i(t_{i, j})-\varvec{\mu }-\varvec{\mathrm {\Lambda }}\tilde{\varvec{x}}_i(t_{i, j})]^\mathrm{T}\varvec{\mathrm {\Sigma }}_{\varvec{\epsilon }}^{-1}\right. \nonumber \\&\quad \left. [\varvec{y}_i(t_{i,j})-\varvec{\mu } - \varvec{\mathrm {\Lambda }} \tilde{\varvec{x}}_i(t_{i, j})] \right\} \text {, and}\nonumber \\ L_{i}(\varvec{b};\varvec{\theta })&= -\frac{1}{2} \left\{ d\log (2\pi ) + \log |\varvec{\mathrm {\Sigma }}_{\varvec{b}}| +\varvec{b}_i^\mathrm{T}\varvec{\mathrm {\Sigma }}_{\varvec{b}}^{-1}\varvec{b}_i\right\} , \end{aligned}$$

(7)

where the associated score vector and information matrix are denoted as $\varvec{s}_{\varvec{\mathrm {Z}}}(\varvec{\theta }; \varvec{\mathrm {Z}})$ and $\varvec{\mathrm {I}}_{\varvec{\mathrm {Z}}}(\varvec{\theta }; \varvec{\mathrm {Z}})$. Detailed analytical forms of $\varvec{s}_{\varvec{\mathrm {Z}}}(\varvec{\theta }; \varvec{\mathrm {Z}})$ and $\varvec{\mathrm {I}}_{\varvec{\mathrm {Z}}}(\varvec{\theta }; \varvec{\mathrm {Z}})$ are included in Appendix .

To use any gradient-type algorithm such as the Newton–Raphson (Ortega, 1990) requires the score vector and the information (or negative Hessian) matrix of the loglikelihood function, denoted as $s_{\varvec{Y}}(\varvec{\theta };\varvec{\mathrm {Y}})$ and $I_{\varvec{Y}}(\varvec{\theta };\varvec{\mathrm {Y}})$, respectively. They can be obtained as (Dempster et al., 1977; Louis, 1982)

$$\begin{aligned} \varvec{s}_{\varvec{Y}}(\varvec{\theta };\varvec{\mathrm {Y}})&= \frac{\partial L(\varvec{\mathrm {Y}};\varvec{\theta })}{\partial \varvec{\theta }} = E(\varvec{s}_{\varvec{\mathrm {Z}}}(\varvec{\theta }; \varvec{\mathrm {Z}})| \varvec{\mathrm {Y}};\varvec{\theta }),\text { and} \\ \varvec{\mathrm {I}}_{\varvec{\mathrm {Y}}}(\varvec{\theta };\varvec{\mathrm {Y}})&= -\frac{\partial ^2 L(\varvec{\mathrm {Y}};\varvec{\theta })}{\partial \varvec{\theta } \partial \varvec{\theta }^\mathrm{T}} \nonumber \\&= E \left[ \varvec{\mathrm {I}}_{\varvec{\mathrm {Z}}}(\varvec{\theta };\varvec{\mathrm {Z}})-\varvec{s}_{\varvec{\mathrm {Z}}}(\varvec{\theta }; \varvec{\mathrm {Z}}) \varvec{s}_{\varvec{\mathrm {Z}}}(\varvec{\theta };\varvec{\mathrm {Z}})^\mathrm{T} \Big | \varvec{\mathrm {Y}};\varvec{\theta } \right] + \varvec{s}_{\varvec{Y}}(\varvec{\theta };\varvec{\mathrm {Y}}) \varvec{s}_{\varvec{\mathrm {Y}}}(\varvec{\theta };\varvec{\mathrm {Y}})^\mathrm{T},\nonumber \end{aligned}$$

(8)

where $E(.|\varvec{\mathrm {Y}},\varvec{\theta })$ denotes expectation taken with respect to the conditional distribution of $p(\varvec{b}|\varvec{\mathrm {Y}};\varvec{\theta })$. Once the score function and information matrix, $s_{\varvec{Y}}(\varvec{\theta };\varvec{\mathrm {Y}})$ and $I_{\varvec{Y}}(\varvec{\theta };\varvec{\mathrm {Y}})$, are available, one can then obtain updated estimates of the parameter vector, $\varvec{\theta }$, at iteration $m$ using any gradient-type algorithm, such as the Newton–Raphson as (Gu & Zhu, 2001; Zhu & Gu, 2007; Ortega, 1990)

$$\begin{aligned} \varvec{\theta }^{(m)}&= \varvec{\theta }^{(m-1)} + [\varvec{\mathrm {I}}_{\varvec{\mathrm {Y}}}(\varvec{\theta }^{(m-1)};\varvec{\mathrm {Y}})]^{-1} \varvec{s}_{\varvec{Y}}(\varvec{\theta }^{(m-1)};\varvec{\mathrm {Y}}). \end{aligned}$$

(9)

While the classical EM algorithm and the Newton–Raphson procedure shown in (9) both serve to provide iterative updates of the parameter estimates to yield ML estimates for which $s_{\varvec{Y}}(\varvec{\theta };\varvec{\mathrm {Y}}) = \varvec{0}$, the Newton–Raphson algorithm and other related gradient-type algorithms typically outperform the classical EM in terms of convergence speed (Dembo & Zeitouni, 1986; Ortega, 1990; Singer, 1995).

Based on Eq. (7) and its constituent elements shown in Appendix , taking the expectations of $\varvec{s}_{\varvec{\mathrm {Z}}}(\varvec{\theta }; \varvec{\mathrm {Z}})$ and $\varvec{\mathrm {I}}_{\varvec{\mathrm {Z}}}(\varvec{\theta };\varvec{\mathrm {Z}})$ with respect to the distribution $p(\varvec{b}|\varvec{\mathrm {Y}}; \varvec{\theta })$ requires the computation of terms such as $E[\tilde{\varvec{x}}(t_{i,j})|\varvec{\mathrm {Y}}; \varvec{\theta }^{(m-1)}], E\big (\frac{\partial \tilde{\varvec{x}}_i(t_{i,j})}{\partial \varvec{\theta }_{f,i}}|\varvec{\mathrm {Y}}; \varvec{\theta }^{(m-1)} \big ), E[\tilde{\varvec{x}}(t_{i,j})\tilde{\varvec{x}_i}(t_{i,j})^\mathrm{T}|\varvec{\mathrm {Y}}; \varvec{\theta }^{(m-1)}]$, and $E(\frac{\partial \tilde{\varvec{x}_i}(t_{i,j})^\mathrm{T}}{\partial \varvec{\theta }_{f,i}}\varvec{\mathrm {W}}^{*} \tilde{\varvec{x}}(t_{i,j})|\varvec{\mathrm {Y}}; \varvec{\theta }^{(m-1)} )$, where $\varvec{\mathrm {W}}^{*}$ is a function involving vectors/matrices of modeling parameters such as $\varvec{\mathrm {\Lambda }}$ and $\varvec{\mathrm {\Sigma }}_{\epsilon }$. These terms, in turn, require integration over $p(\varvec{b}|\varvec{\mathrm {Y}};\varvec{\theta })$. Because $\varvec{b}_i$ is involved in the nonlinear $f(.)$ in the computation of $\tilde{\varvec{x}}(t_{i,j})$, such integration is analytically formidable. In the present article, we chose to perform a variation of the EM algorithm—the SAEM algorithm—for parameter estimation purposes.

E-step with stochastic approximation In the E-step, a MCMC technique of choice is used to simulate a sequence of random draws from the conditional distribution, p($\varvec{b}|\varvec{\mathrm {Y}};\varvec{\theta })$. For reasons detailed in Appendix , $p(\varvec{b}|\varvec{\mathrm {Y}};\varvec{\theta })$ is non-standard, and sampling from this distribution cannot be performed directly by means of Gibbs sampling. We thus adopt the Metropolis–Hasting sampling procedure described in Appendix  to simulate samples of $\varvec{b}_i$ probabilistically from an alternative proposal distribution that does have a standard form to obtain $\varvec{\mathrm {Z}}_{k}^{(m)} = (\varvec{\mathrm {Y}}, \varvec{b}_{k}^{(m)}$), which is then used in the E-step to compute the summary statistics

$$\begin{aligned} \overline{\varvec{s}}_{\varvec{\mathrm {Z}}}^{(m)}&= \frac{1}{N_m}\sum _{k=1}^{N_m}\varvec{s}_{\varvec{\mathrm {Z}}}\Big (\varvec{\theta }^{(m-1)};\varvec{\mathrm {Z}}_{k}^{(m)} \Big )\text {, } \overline{\varvec{S}}_{\varvec{\mathrm {Z}}}^{(m)} =\frac{1}{N_m}\sum _{k=1}^{N_m}\varvec{s}_{\varvec{\mathrm {Z}}}\Big (\varvec{\theta }^{(m-1)};\varvec{\mathrm {Z}}_{k}^{(m)} \Big )\varvec{s}_{\varvec{\mathrm {Z}}}\Big (\varvec{\theta }^{(m-1)};\varvec{\mathrm {Z}}_{k}^{(m)}\Big )^\mathrm{T} \text { and} \nonumber \\ \overline{\varvec{\mathrm {I}}}_{\varvec{\mathrm {Z}}}^{(m)}&= \frac{1}{N_m}\sum _{k=1}^{N_m}\varvec{\mathrm {I}}_{\varvec{\mathrm {Z}}}\Big (\varvec{\theta }^{(m-1)};\varvec{\mathrm {Z}}_{k}^{(m)}\Big ), \end{aligned}$$

(10)

where $\varvec{s}_{\varvec{\mathrm {Z}}}(\varvec{\theta }; \varvec{\mathrm {Z}})$ and $\varvec{\mathrm {I}}_{\varvec{\mathrm {Z}}}(\varvec{\theta }\varvec{\mathrm {Z}})$ are defined, respectively, in Eqs. (17) and (18) of Appendix . These summary statistics are then used in the M-step to update the parameter estimates in $\varvec{\theta }$.

M-step In the M-step, the goal is to obtain updated parameter estimates, $\varvec{\theta }^{(m)}$, for the $m$th iteration using a modified Newton–Raphson procedure involving $\overline{\varvec{s}}_{\varvec{\mathrm {Z}}}^{(m)}$ and current estimates of the information matrix, $\varvec{\mathrm {I}}_{\varvec{\mathrm {Y}}}^{(m)}(\varvec{\theta }; \varvec{\mathrm {Y}})$, abbreviated below as $\varvec{\mathrm {I}}_{\varvec{\mathrm {Y}}}^{(m)}$. Doing so in turn requires (see Eq. 9) current estimates of the score function, $\varvec{s}_{\varvec{Y}}(\varvec{\theta };\varvec{\mathrm {Y}})^{(m)}$, abbreviated below as $\varvec{s}_{\varvec{\mathrm {Y}}}^{(m)}$, current estimates of $E[\varvec{\mathrm {I}}_{\varvec{\mathrm {Z}}}(\varvec{\theta };\varvec{\mathrm {Z}})|\varvec{\mathrm {Y}},\varvec{\theta }]$, denoted as $E_{\varvec{\mathrm {I}}}^{(m)}$, and estimates of $E[\varvec{s}_{\varvec{\mathrm {Z}}}(\varvec{\theta };\varvec{\mathrm {Z}}) \varvec{s}_{\varvec{\mathrm {Z}}}(\varvec{\theta };\varvec{\mathrm {Z}})^\mathrm{T}| \varvec{\mathrm {Y}},\varvec{\theta }]$, denoted as $E_{\varvec{S}}^{(m)}$. These elements are computed as

$$\begin{aligned} \varvec{s}_{\varvec{\mathrm {Y}}}^{(m)}&= \varvec{s}_{\varvec{\mathrm {Y}}}^{(m-1)}+ \gamma ^{(m)} [\overline{\varvec{s}}_{\varvec{\mathrm {Z}}}^{(m)} - \varvec{s}_{\varvec{\mathrm {Y}}}^{(m-1)}],\nonumber \\ \varvec{\mathrm {I}}^{(m)}_{\varvec{\mathrm {Y}}}&= E_{\varvec{\mathrm {I}}}^{(m)} - E_{\varvec{S}}^{(m)} +(\varvec{s}^{(m)}_{\varvec{\mathrm {Y}}})(\varvec{s}^{(m)}_{\varvec{\mathrm {Y}}})^\mathrm{T}, \nonumber \\ E_{\varvec{S}}^{(m)}&= E_{\varvec{S}}^{(m-1)} + \gamma ^{(m)}[\overline{\varvec{S}}_{\varvec{\mathrm {Z}}}^{(m)} -E_{\varvec{S}}^{(m-1)}],\nonumber \\ E_{\varvec{\mathrm {I}}}^{(m)}&= E_{\varvec{\mathrm {I}}}^{(m-1)} + \gamma ^{(m)}[\overline{\varvec{\mathrm {I}}}_{\varvec{\mathrm {Z}}}^{(m)} -E_{\varvec{\mathrm {I}}}^{(m-1)}],\nonumber \\ \varvec{\theta }^{(m)}&= \varvec{\theta }^{(m-1)} + \gamma ^{(m)}[\varvec{\mathrm {I}}_{\varvec{\mathrm {Y}}}^{(m)}]^{-1}\overline{\varvec{s}}_{\varvec{\mathrm {Z}}}^{(m)}, \end{aligned}$$

(11)

where $\gamma ^{(m)}$ is a gain constant that controls the degree to which new estimates are weighted at iteration $m$ in comparison with the estimates from iteration $m-1$. The gain constant is a control parameter that is modified in two stages to (1) prevent the estimation algorithm from settling too quickly into local minima in earlier iterations (stage 1; for iteration $m = 1, \ldots , K_1$); and (2) help speed convergence toward a final set of parameter estimates during the later iterations (stage 2; for iteration $m = K_1+1, \ldots , K_2$). The use of a gain function is the key feature that distinguishes the SAEM from the stochastic and Monte Carlo EM procedures (Diebolt & Celeux, 1993; Lee & Song, 2003).³

The SAEM algorithm alternates between the E-step and the M-step until some predefined convergence criteria have been met (Zhu & Gu, 2007).⁴ An offline averaging procedure is implemented concurrently as the scoring algorithm in stage 2 of the SAEM. At the conclusion of stage 1 (i.e., at the $K_1$th iteration), the averaging procedure is initiated with $\tilde{\varvec{s}}^{(1)}_{\varvec{\mathrm {Y}}} = \varvec{s}^{(K_1)}_{\varvec{\mathrm {Y}}}, \tilde{E}_{\varvec{S}}^{(1)} = E_{\varvec{S}}^{(K_1)}, \tilde{E}_{\varvec{\mathrm {I}}}^{(1)} = E_{\varvec{\mathrm {I}}}^{(K_1)}, \tilde{\varvec{\mathrm {I}}}^{(1)}_{\varvec{\mathrm {Y}}} = \varvec{\mathrm {I}}^{(K_1)}_{\varvec{\mathrm {Y}}}$, and $\tilde{\varvec{\theta }}^{(1)} = \varvec{\theta }^{(K_1)}$. These offline estimates are subsequently updated as

$$\begin{aligned} \tilde{\varvec{s}}^{(m)}_{\varvec{\mathrm {Y}}}&= \tilde{\varvec{s}}^{(m-1)}_{\varvec{\mathrm {Y}}} + (\varvec{s}^{(m)}_{\varvec{\mathrm {Y}}} - \tilde{\varvec{s}}^{(m-1)}_{\varvec{\mathrm {Y}}} )/m,~~ ~ \tilde{E}_{\varvec{S}}^{(m)}= \tilde{E}_{\varvec{S}}^{(m-1)} + (E_{\varvec{S}}^{(m)}- \tilde{E}_{\varvec{S}}^{(m-1)})/m, \nonumber \\ \tilde{E}_{\varvec{\mathrm {I}}}^{(m)}&= \tilde{E}_{\varvec{\mathrm {I}}}^{(m-1)} + (E_{\varvec{\mathrm {I}}}^{(m)}-\tilde{E}_{\varvec{\mathrm {I}}}^{(m-1)})/m, ~~ ~ \tilde{\varvec{\mathrm {I}}}^{(m)}_{\varvec{\mathrm {Y}}}= \tilde{\varvec{\mathrm {I}}}^{(m-1)}_{\varvec{\mathrm {Y}}} + (\varvec{\mathrm {I}}^{(m)}_{\varvec{\mathrm {Y}}}-\tilde{\varvec{\mathrm {I}}}^{(m-1)}_{\varvec{\mathrm {Y}}})/m, \nonumber \\ \tilde{\varvec{\theta }}^{(m)}&= \tilde{\varvec{\theta }}^{(m-1)} + (\varvec{\theta }^{(m)} - \tilde{\varvec{\theta }}^{(m-1)} )/m. \end{aligned}$$

(12)

Theoretically, this averaging procedure automatically leads to an optimal convergence without estimating the information matrix (Polyak, 1990; Polyak and Juditski, 1992). Under some conditions, the offline average $( \tilde{\varvec{\theta }}^{(m)} , \tilde{\varvec{s}}^{(m)}_{\varvec{\mathrm {Y}}})$ converges to $(\hat{\varvec{\theta }}_{MLE}, \hat{\varvec{s}}_{MLE}(\varvec{\theta };\varvec{\mathrm {Y}}) )$ almost surely, as $K_1+K_2$ approaches infinity (Zhu & Gu, 2007). Finally, at convergence, we use the offline average, $( \tilde{\varvec{\theta }}^{(K_2)}, \tilde{\varvec{\mathrm {I}}}^{(K_2)}_{\varvec{\mathrm {Y}}})$, as our final estimate of $(\hat{\varvec{\theta }}, \hat{\varvec{\mathrm {I}}}_{\varvec{\mathrm {Y}}}(\varvec{\theta };\varvec{\mathrm {Y}}))$, where square roots of the diagonal elements of $\hat{\varvec{\mathrm {I}}}_{\varvec{\mathrm {Y}}}(\varvec{\theta };\varvec{\mathrm {Y}})$ are used as the standard error (SE) estimates of the parameters.

2 Illustrative Application

To illustrate the empirical utility of the proposed approach, we reanalyzed a set of previously published data (Carels, Blumenthal, & Sherwood, 2000; Sherwood, Steffen, Blumenthal, Kuhn, & Hinderliter, 2002) involving 172 employed men and women, aged 25–45 years, who participated in the Duke Biobehavioral Investigation of Hypertension study. The sample comprised 96 participants with normal blood pressure (BP), 41 with high normal BP, and 35 with stage 1 hypertension. Clinic systolic blood pressure that was greater than 180 mmHg or diastolic blood pressure that was greater than 100 mmHg, use of cardiovascular medications, and use of tobacco products were specified as exclusion criteria.

The AccuTracker II ABP Monitor (Suntech AccuTracker II, Raleigh, NC) was worn for approximately 24 h to measure BP and heart rate noninvasively. It was programmed to take four measurements hourly at random intervals ranging from 12 to 28 minutes apart. Participants were instructed to follow their normal schedule and to complete a diary entry indicating posture, activity, location, positive affect, and negative affect at each reading. The same procedure was implemented in the evening waking hours. Sleep was defined by diary activity ratings, which included an indication of “going to sleep.” The monitor was programmed to take only two readings hourly during sleeping hours, customized to the participants’ sleep habits.

The dynamics of individuals’ ambulatory BP and other related cardiovascular measures during a typical workday were the focus of our modeling example. In the study of 24-h ambulatory BP, BP dipping, an important prognostic indicator of cardiovascular morbidity and mortality, is derived by subtracting the mean nighttime sleep BP from the mean daytime waking BP (Sherwood et al., 2001, 2002). Consequently, the intensive BP readings collected throughout the study period (which typically exceed 50 measurements per participant) are aggregated and reduced to only mean-level information (Pickering, Shimbo, & Haas, 2006). Even in the few studies where within-subject linkages between ambulatory BP and related risk factors were explored without further data aggregation (e.g., Carels, 2000), emphasis was placed almost exclusively on examining concurrent linkages between multiple processes as opposed to lagged interdependencies among change processes. In this way, within-subject correlations between successive repeated measurements may be allowed (e.g., via Generalized Estimating Equations as in Carels, 2000) but the precise mechanisms of change (e.g., interdependencies among change processes) as well as related interindividual differences therein are not modeled explicitly. In the present analysis, we used the modified Van der Pol oscillator model to evaluate individual differences in the dynamics of diurnal cardiovascular fluctuations. In particular, we examined whether negative and positive emotion ratings throughout the day would help predict individual differences in the amplification of diurnal cardiovascular fluctuations.

Brown and colleagues (Brown & Luithardt, 1999; Brown et al., 2000) adapted the well-known Van der Pol oscillator equations to model human circadian data. In the present context, constrained by the lack of sufficient time points to capture slower circadian cycles and deviations therein, we considered a modified Van der Pol oscillator model as

$$\begin{aligned} D\begin{bmatrix} x_{i1}(t) \\ x_{i2}(t) \end{bmatrix}&= \begin{bmatrix} x_{i2}(t)\\ - \Big ( \frac{2 \pi }{\gamma } \Big )^2 x_{i1}(t)+ \zeta _i [1- x_{i1}^2(t)] x_{i2}(t), \end{bmatrix}, \quad \varvec{x}_i(t_{i,1}) = \begin{bmatrix} {x}_{i1}(t_{i,1})\\{x}_{i2}(t_{i,1}) \end{bmatrix},\nonumber \\ \varvec{\theta }_{f,i}&= \begin{bmatrix} \zeta _i\\{x}_{i1}(t_{i,1})\\{x}_{i2}(t_{i,1}) \end{bmatrix} = \begin{bmatrix} 1&\quad u_{1i}&\quad u_{2i}&\quad 0&\quad 0\\ 0&\quad 0&\quad 0&\quad 1&\quad 0\\ 0&\quad 0&\quad 0&\quad 0&\quad 1 \end{bmatrix} \begin{bmatrix} \zeta _0 \\ \zeta _1 \\ \zeta _2\\ \mu _{x1}\\ \mu _{x2} \end{bmatrix} + \begin{bmatrix} 1&\quad 0&\quad 0\\ 0&\quad 1&\quad 0\\ 0&\quad 0&\quad 1 \end{bmatrix} \begin{bmatrix} b_{\zeta ,i}\\ b_{x1,i}\\ b_{x2,i} \end{bmatrix}\nonumber \\ \begin{bmatrix} y_{i1}(t_{i, j})\\ y_{i2}(t_{i, j})\\ y_{i3}(t_{i, j}) \end{bmatrix}&= \begin{bmatrix} \mu _1\\ \mu _2\\ \mu _3 \end{bmatrix} + \begin{bmatrix} 1&\quad 0\\ \lambda _{21}&\quad 0\\ \lambda _{31}&\quad 0\\ \end{bmatrix} \begin{bmatrix} x_{i1}(t_{i,j})\\ x_{i2}(t_{i,j}) \end{bmatrix} + \begin{bmatrix} \epsilon _{i1}(t_{i, j})\\ \epsilon _{i2}(t_{i, j})\\ \epsilon _{i3}(t_{i, j}) \end{bmatrix}, \end{aligned}$$

(14)

where $x_{i1}(t)$ represents the level of a dependent variable of interest (in our case, cardiovascular reactivity) and $x_{i2}(t)$ is its corresponding first derivative. In the present application, $x_{i1}(t)$ was indicted by three manifest variables, namely, systolic blood pressure, diastolic blood pressure, and heart rate, with $\mu _1$–$\mu _3$ as their respective intercepts. $\zeta _i$ is a general damping or amplification parameter that governs the oscillation amplitude of person $i$, and $(2\pi /\gamma )^2$ is the squared frequency of cardiovascular reactivity in radians in the absence of damping or amplification, with $\gamma$ representing the period of human circadian rhythm, fixed at 2 (i.e., corresponding to a period of 24 h) in the current context.⁵ The amount of damping (or amplification) is further moderated by a quadratic term in $x_{i1}(t)$. Formulated this way, the amplification (if $\zeta _{i} >$ 0) at small values of $x_{i1}(t)$ is expected to turn into massive damping at extreme values of $x_{i1}(t)$ due to the quadratic term, $x_{i1}^2(t)$. This yields a system that is slow to rise to its peak, followed by damping (manifested as a pronounced drop in amplitude) when it hits extreme values. In contrast, if $\zeta _i$ is negative, this yields a system with damping dynamics at small values of $x_{i1}(t)$, and pronounced amplification at extreme values of $x_{i1}(t)$. If the initial level and rate of change of the system are extreme (i.e., far away from zero), the quadratic term, $x_{i1}^2(t)$, would dominate the system’s dynamics by moderating and magnifying the system’s amplification, resulting in an explosive system—a scenario that is rare in CV dynamics. Since we expected $\zeta _i$ to be positive, we refer to this parameter as the amplification parameter throughout. In this illustrative example, $\zeta _{i}$ is further expressed as a function of a group intercept, $\zeta _0$, two person-specific covariates, $u_{1i}$ and $u_{2i}$ (with fixed effects parameters, $\zeta _{1}$ and $\zeta _{2}$, respectively), and $b_{\zeta ,i}$, person $i$’s deviation in $\zeta _i$ that is not accounted for by other fixed effects terms. As an example of some of the between-person heterogeneities in dynamics one may obtain from the hypothesized model, simulated trajectories of $x_{i1}(t_{i,j})$ using different values of $\zeta$ and initial conditions are shown in Figure 1a. The two trait-level covariates used in the present context to predict individual differences in the amplification parameter were (overtime) aggregate ratings of negative emotion (NE), obtained by averaging the participants’ responses over three items: stress, anger, and tense; and positive emotion (PE), obtained by averaging participants’ responses over the items happy and in control.

Fig. 1

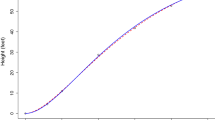
a Simulated trajectories of $x_{i1}(t_{i,j})$ using different values of $\zeta$ and initial conditions. The values shown in $x(1)$ are $x_{i1}(t_{i,1})$ and $x_{i2}(t_{i,1})$, respectively. b Observed composite cardiovascular data and estimates of the latent cardiovascular reactivity obtained using the Van der Pol oscillator model. Time corresponds to time since each participant’s first measurement, as opposed to clock time. c Histogram of the random effect estimates of all participants. Observed data = composite cardiovascular measure of each participant on each occasion; Predicted trajectory $= \tilde{\varvec{x}}_i(t_{i,j})$ generated using the final $\hat{\varvec{\theta }}$ from the SAEM; Pred: high PE & NE $= \tilde{\varvec{x}}_i(t_{i,j})$ for a hypothetical individual with PE and NE that were 2 standard deviations higher than the sample average and no person-specific deviations in the amplification parameter and initial conditions; Pred: low PE & NE $= \tilde{\varvec{x}}_i(t_{i,j})$ for a hypothetical individual with PE and NE that were 2 standard deviations lower than the sample average and no person-specific deviations in the amplification parameter and initial conditions.

The present application also serves to demonstrate how the proposed modeling framework can be used to represent the unknown initial conditions at time 1, ${x}_{i1}(t_{i,1})$ and ${x}_{i2}(t_{i,1})$, as part of $\varvec{\theta }_{f,i}$. The formulation adopted in (14) dictates that individual $i$’s initial conditions at time 1, namely, ${x}_{i1}(t_{i,1})$ and ${x}_{i2}(t_{i,1})$, follow a multivariate normal distribution with mean vector $[\mu _{x1} \mu _{x2}]^\mathrm{T}$, and a covariance matrix composed of the lower 2 $\times$ 2 submatrix of $\varvec{\mathrm {\Sigma _b}}$. We assume that the random effects covariance matrix conforms to the structure

$$\begin{aligned} \varvec{\mathrm {\Sigma }}_b = \begin{bmatrix} \sigma ^2_{b_{\zeta }}\\ 0&\quad \sigma ^2_{b_{x1}} \\ 0&\quad \sigma _{b_{x1,x2}}&\quad \sigma ^2_{b_{x2}} \end{bmatrix}, \end{aligned}$$

(15)

where the person-specific deviation in $\zeta _i, b_{\zeta ,i}$, is assumed to be uncorrelated with other person-specific deviations in initial conditions, while $b_{x1,i}$ and $b_{x2,i}$ are allowed to covary because interindividual differences in initial level and first derivative are often expected to show non-negligible associations. This particular way of structuring the initial conditions of a dynamic model as unknown parameters to be estimated has rarely been explicitly utilized in ODE modeling, but is commonly adopted in discrete-time state-space and time series models (e.g., Harvey & Souza, 1987; Chow, Ho, Hamaker, & Dolan, 2010; Du Toit & Browne, 2001), as well as growth curve-type models (Meredith & Tisak, 1990; McArdle & Hamagami, 2001). In addition, the presence of statistically significant interindividual differences in the amplification parameter and the two initial latent variables was deduced in the present context from the statistical significance of the variance parameters in $\varvec{\mathrm {\Sigma }}_b$, namely, by means of a Wald test. A possible alternative to the Wald test will be highlighted in the Discussion section.

After removing data from individuals who contributed less than 50 readings, 168 participants were retained for model fitting purposes. Among these participants, the available measurement occasions ranged from 58 to 98 time points within each individual. Time was rescaled such that one unit of time corresponded to 12 h, with $\Delta _{i,j}$ ranging from 0.001 to 0.48. We fitted the multiple-indicator Van der Pol oscillator model to the ambulatory cardiovascular data. Several preliminary data treatment steps were performed prior to model fitting. First, we observed that substantial interindividual differences were present in the means of these indicator variables (which had to be modeled by allowing for random effects in the intercepts $\mu _1$–$\mu _3$). Because such interindividual differences were not the focus of our illustrative model, we removed these differences by subtracting each individual’s mean on each variable from the corresponding time series and used the residual scores for subsequent model fitting. Thus, the intercept parameters, while freed to be estimated as parameters in the present context, were expected to take on values that were close to zero. Second, to remove arbitrary scale differences across the three indicator variables while preserving potential interindividual differences in the amplification parameter, $\zeta _i$, we standardized each individual’s time series using the group standard deviation of each indicator variable.

Third, there were substantial individual differences in when the participants took their first measurements of the day, with the first time point ranging in clock time from 7:07 am to 4.82 pm. To eliminate confounds due to individual differences in lifestyle, the participants’ dynamics were modeled in terms of time since each participant’s first measurement, as opposed to clock time. Finally, the sparse measurements at night, coupled with the dense daytime measurements, gave rise to highly irregularly spaced time intervals (with $\Delta _{i,j}$ ranging from 0.001 to 0.48). If these time intervals were used as they were, some of the larger time intervals would lead to very large approximation errors regardless of the choice of the ODE solvers, thereby jeopardizing the solvers’ numerical stability; the smallest time intervals were so much smaller by comparison that using them directly in the ODE solver would greatly increase computational costs. We adopted some strategies to strike a balance between numerical stability/modeling accuracy and computational time. That is, to improve the numerical stability of the ODE solver, missing data were inserted at the interval of $\Delta _{i,j} = 0.01$ to avoid the need to interpolate over large time intervals. Additionally, we aggregated data that were too densely measured to yield a minimum $\Delta _{i,j}$ of 0.01. This essentially yielded a set of equally spaced data for model fitting purposes. We note that the proposed estimation framework can, in principle, handle irregularly spaced and person-specific $\Delta _{i,j}$. While the first step is needed to improve the numerical stability of the estimation procedures, the latter step is not needed and was implemented simply to reduce computational costs. In practice, the interpolation intervals used in deriving numerical ODE solutions are almost always smaller than the crudest empirically observed measurement intervals. If computational time is not a constraint, then a smaller interpolation interval can help improve numerical accuracy under most circumstances. However, depending on the dynamics of the system, it may not be computationally efficient to always set the interpolation interval to the smallest possible time step. Here, our simulation study showed that interpolating with $\Delta _{i,j} =0.01$ as the smallest time step in the presence of irregularly spaced time intervals yielded reasonable estimates for the model considered in the present article.

A plot of the composite scores obtained by averaging the participants’ rescaled residual scores on the three indicator variables is shown in Figure 1b. Relatively clear diurnal trends can be seen from the observed scores, with the participants’ cardiovascular data rising to their peaks and staying at relatively high levels throughout the 12 h (i.e., from time = 0 to about 1) after their first measurements. Declines in cardiovascular levels became evident after $t = 1.2$, with the lowest “dipping” occurring at approximately $t = 1.5$ (corresponding to approximately 18 h after the first measurements).

Parameter estimates obtained from model fitting are shown in Table 1, and the predicted trajectories, $\tilde{\varvec{x}}_i(t_{i,j})$, generated using the final estimates $\hat{\varvec{\theta }}$ from the SAEM, are plotted in Figure 1b. All parameters, except for the interindividual variance in initial condition for the first derivative, $\sigma ^2_{b_{x2}}$, were significantly different from zero. This indicates that substantive interindividual differences were only present in the initial cardiovascular level at the first time point, but not in its first derivative. The fixed effects associated with PE and NE were both positive and statistically different from 0. The sign of these fixed effects indicated that overall, heightened PE, as well as NE, was found to increase the amplification magnitude of an individual’s diurnal cardiovascular oscillations. Such oscillations, characterized by a slow buildup followed by a sudden discharge to relax the stress accumulated during the buildup (Strogatz, 1994, p. 212), appeared to be amplified by emotions of high intensity, regardless of valence. Thus, an individual who experienced heightened PE as well as NE over the course of the study period would show greater build up as well as discharge compared to individuals who did not show high PE and/or NE during the same period. For illustrative purposes, we plotted the trajectories of a hypothetical individual with high PE and NE (defined as 2 standard deviations above the sample average) and low PE and NE (defined as 2 standard deviations below the sample average) in Figure 1b. The fixed effect coefficient for NE was slightly smaller in standardized value compared to that for PE, which is in contrast to commonly held beliefs regarding the close linkages between NE and cardiovascular health. This may be related, however, to differences in the roles of the two emotions in affecting the buildup vs. the discharge phases of cardiovascular dynamics. For instance, while heightened NE may lead to greater buildup of cardivascular activities in the daytime, it may also be associated with attenuated BP nighttime dipping. Such reversal in damping effects is not captured by the fitted version of the Van der Pol oscillator. A possible modification is to incorporate regime-switching (Chow, Grimm, Guillaume, Dolan, & McArdle, 2013; Chow & Zhang, 2013) or multiphase (Cudeck & Klebe, 2002) extensions wherein the amplification parameter is allowed to show phase-dependent relationships on the covariates.

Table 1 Parameter estimates from fitting the modified Van der Pol Oscillator Model to empirical data.

Several other observations can be noted from the modeling results. First, substantial interindividual differences in cardiovascular amplification remained after the effects of the two covariates had been accounted for. Such differences gave rise to further deviations in the amplitude of diurnal fluctuations (see trajectories of the participants’ $\tilde{\varvec{x}}_i(t_{i,j})$ in Figure 1b, generated using the participants’ own random effect estimates as shown in Figure 1c). Second, despite the use of residual scores for model fitting purposes, the three intercept parameters were estimated to be negative and significantly different from zero. Third, the factor loadings for the second and third indicators, namely, diastolic BP and heart rate, were low compared to the loading for systolic BP, which was fixed at 1.0 for identification purposes. These latter findings suggest some possible inadequacies of the multivariate Van der Pol oscillator model in capturing the dynamics of the observed data, particularly differences in the diurnal dynamics of the three indicators.

Given the short time series lengths, the relatively small sample size, and other data-related constraints, the results reported here have to be interpreted with caution. For instance, the data collected barely spanned one complete cycle. Thus, there were insufficient time points (and importantly, number of replications in cycle) to clearly distinguish the nature of the oscillations and amplification/damping evidenced by the system over time. In particular, relatively few time points were available during sleeping hours—the time during which the heavy damping as predicted by the Van der Pol oscillator model was supposed to unfold. Nevertheless, our illustration demonstrated the potential promises of the proposed modeling approach and the ways in which future studies of diurnal cardiovascular patterns may be adapted to effectively utilize this approach.

3 Simulation Study

The performance of the SAEM algorithm in handling dynamic models featuring manifest variables only has been evaluated elsewhere (Donnet & Samson, 2007). The novel contributions of this article lie in presenting an alternative formulation that explicitly captures the dynamics of a system and interindividual differences in initial conditions at the latent level. We conducted a simulation study to specifically assess the performance of the SAEM with respect to these novel features. Unlike previous studies that assessed the performance of ODE modeling techniques using small and equally spaced time intervals (e.g., with $\Delta _{i,j} = 0.001$ for all $i$ and $j$), we used person-specific, irregularly spaced time intervals that mirror those observed in empirical studies.

We used a fourth-order Runge Kutta solver to generate the true latent differences at the population level, while the second-order Heun’s method summarized in Eq. (5) was used for model fitting purposes. Three manifest indicators were used to identify $x_{i1}(t)$, with $\varvec{\mathrm {\varvec{\mathrm {\Sigma }}}}_\epsilon = 0.5\varvec{\mathrm {I}}_{3}$. The first factor loading was set to unity for identification purposes. We set the period of oscillation, $\gamma$, to 0.8 (fixed and not estimated), $\zeta _0 = 3, \zeta _1 = 0.5, \zeta _2 = 0.5, \lambda _{21} = 0.7, \lambda _{31} = 1.2$, and $\mu _1 = \mu _2 = \mu _3 = 0$. The covariates $u_{1i}$ and $u_{2i}$ were both simulated from a uniform distribution over the interval [0, 5].

Two sample size configurations were considered: (1) $n = 200$ and $T = 300$, with $\Delta _{i,j}$ ranging between 0.005 and 0.07, and (2) $n = 200$ and $T = 150$, with $\Delta _{i,j}$ ranging between 0.006 and 0.161. We also considered two variations of true initial conditions. In the first condition, the initial conditions at time $t_{i,1}$ were set to the constant values, $\mu _{x1} = \mu _{x2} = 1.0$ for all individuals, with the true $\varvec{\mathrm {\Sigma }}_b$ specified to be

$$\begin{aligned} \varvec{\mathrm {\Sigma }}_b = \begin{bmatrix} 0.5\\ 0&\quad 0\\ 0&\quad 0&\quad 0 \end{bmatrix}. \end{aligned}$$

This condition is denoted as the condition with fixed initial conditions.

For the second condition (denoted as the condition with random initial conditions), we considered initial conditions that conformed to a multivariate normal distribution as follows. We assumed that the process conformed to the hypothesized ODE model both prior to, and after, the first available measurements. To implement this scenario, we began simulating data using the hypothesized ODE fifty time points prior to the first retained measurement occasion, starting at $t_{i,1}$ with $\mu _{x1} = \mu _{x2} = 1.0$ and

$$\begin{aligned} \varvec{\mathrm {\Sigma }}_b = \begin{bmatrix} 0.5\\ 0&\quad 1.0 \\ 0&\quad 0.3&\quad 1.0 \end{bmatrix}. \end{aligned}$$

(16)

Then, at $j = 51$, we centered each individual’s latent variable scores at the 51st time point using the across-individual means (thus resetting $\mu _{x1}$ and $\mu _{x2}$ to zero) and retained data from the 51st time point and beyond for model fitting purposes. Given the deterministic nature of the Van der Pol model, the variances and covariances among the true $\varvec{b}_i$ estimates in the retained data should still mirror the values shown in (16) at the population level. An alternative way of generating data with multivariate normally distributed initial conditions is to simply draw values of $x_{i1}(t_{i,1})$ and $x_{i2}(t_{i,1})$ from a multivariate normal distribution with mean vector $[\mu _{x1} \mu _{x2}]'$ and an arbitrary choice of $\varvec{\mathrm {\Sigma }}_b$. However, doing so dictates that the dynamics of the ODE system at time $t_{i,1}$ need not follow the dynamics of the system at other remaining time points. We adopted our specification to enforce the assumption of (overtime) homogeneity in dynamics.

Data generated using the two true initial conditions (fixed vs. random) were matched with two fitted initial condition specifications, namely, one where $\mu _{x1}$ and $\mu _{x2}$ were fixed at the constant value of 1.0 (i.e., with fixed initial conditions), and another one where $\mu _{x1}, \mu _{x2}, \sigma ^2_{b_{x1}}, \sigma _{b_{x1,x2}}$, and $\sigma ^2_{b_{x2}}$ were all estimated as modeling parameters (i.e., with random initial conditions). This yielded a total of four true–fitted initial condition specifications, with fixed–fixed, fixed–random, random–fixed, and random–random initial conditions. Among the conditions with fixed true initial condition specification, the fixed–fixed configuration was expected to yield slightly better performance (e.g., with fewer numerical problems) than the fixed–random condition, which is also able to capture the fixed initial conditions as a special case of our proposed modeling framework.

Among the conditions with random true initial condition specification, the random–random configuration was expected to yield substantially better performance than the random–fixed configuration in which $\mu _{x1}$ and $\mu _{x2}$ (which had a true value of 0) were fixed at the incorrect constant value of 1.0, with no interindividual differences therein. Note that this configuration is worth considering because this is a strategy often adopted by uninformed users of ODE solvers who, in the absence of knowledge concerning the true initial conditions, resort to fixing the initial conditions at arbitrary constant values. Results across the different true/fitted initial condition specifications also help provide insights into the sensitivity of modeling results to misspecification in the true initial conditions.

Simulated data from 50 randomly selected subjects are plotted in Figures 2a, b. In this particular parameter range, the Van der Pol oscillator model is expected to yield limit cycle behavior (Strogatz, 1994), or in other words, ongoing, isolated oscillations that either attract or repel neighboring trajectories (i.e., trajectories started out with similar values would either spiral toward or away from the cycle). Unlike cyclic oscillations that arise in linear dynamic systems where the amplitudes of oscillations are determined solely by initial conditions, the amplitudes of the oscillations in a Van der Pol system (or other similar systems) depend on latent variables in the system (see Strogatz, 1994, pp. 196–227, chap. 7). In this way, systems such as the Van der Pol model are appropriate for representing natural systems that exhibit self-sustained oscillations.

Fig. 2

a Plot of the true $x_{i1}(t_{i,j})$ and noisy observations, $y_{i1}(t_{i,j})$, of 50 randomly selected subjects from the Van der Pol model over time; b plot of two of the latent variables, $x_{i1}(t_{i,j})$ and its first derivatives, $x_{i2}(t_{i,j})$, over all time points.

To summarize, we considered 2 (sample size configurations) $\times$ 2 (true initial conditions) $\times$ 2 (fitted initial conditions) = 8 conditions in our simulation study. Statistical properties of the point and standard error (SE) estimates over 200 Monte Carlo replications, and the corresponding average correlations between the true and estimated $b_{\zeta ,i}$ across the 8 conditions, are shown in Tables 2 and 9. The root mean squared errors (RMSEs) and relative biases were used to quantify the performance of the point estimates. The empirical SE of a parameter (i.e., the standard deviation of the parameter estimates across all Monte Carlo runs) was used as the “true” standard error. As a measure of the relative performance of the SE estimates, we used the average relative deviance of a SE estimate of an estimator (denoted as RDSE, namely, the difference between the average SE estimate and the true SE over the true SE). Ninety-five percent confidence intervals were constructed for each of the 200 simulation samples by adding and subtracting $1.96*\widehat{\mathrm{SE}}$ in each replication to the parameter estimate from the replication. We then computed power estimates⁶ by tallying the proportion of Monte Carlo trials in which the 95 % CIs did not include zero. For parameters that had a true value of zero (i.e., $\mu _1$–$\mu _3$, and $\sigma ^2_{b_{x1}}, \sigma ^2_{b_{x2}}$ and $\sigma _{b_{x1,x2}}$ in the fixed–random condition), this proportion can be taken as a type I error estimate, namely, the proportion of Monte Carlo trials in which the true parameter values of zero were incorrectly concluded as statistically significantly different from zero. To minimize the effects of outliers, we screened for cases manually, as well as winsorized 5 % of the most extreme estimates (i.e., replacing cases that were lower or higher than the 5th and 95th percentiles by values of the 5th and 95th percentiles, respectively) before comparing the results across conditions. The percentages of retained cases used for comparison purposes are summarized in the footnotes of Tables 2 and 3.

We first focus on elaborating results from the fixed–fixed conditions (i.e., with fixed true and fitted initial conditions), as this is the specification typically assumed in comparing ODE modeling methods. Results indicated that biases of the point estimates (as indicated by relative biases and RMSEs) and discrepancies in SE estimates in comparison with the MC SDs (as indicated by RDSEs) were relatively small. Biases in the point and SE estimates were both observed to decrease with increasing time points (see Tables 2, 3). Slightly large RMSEs, relative biases, and RDSEs were observed in the point and SE estimates of the fixed effects dynamic parameters, $\zeta _{0}$–$\zeta _{3}$, and the random effect variance, $\sigma ^2_{b_\zeta }$. This is to be expected, because a second-order ODE solver was used to approximate the trajectories generated using a fourth-order ODE solver. In other words, some approximation errors were inherently present in estimates of the latent variables, namely, $\tilde{\varvec{x}}_i(t_{i,j})$, especially with large time intervals. These biases, in turn, would likely affect estimates of the dynamic parameters in $\varvec{\theta }_{f,i}$. The biases in point estimates were still within reasonable ranges given the time intervals considered in this simulation study; a larger number of time points and/or participants are likely needed to further improve properties of the point and SE estimates for all of the dynamic and random effect-related parameters.

The discrepancies in SE estimates reduced considerably from $T = 150$ to $T = 300$, with the exception of the fixed effects parameters for the two covariates, $\zeta _1$ and $\zeta _{2}$, which did not show clear gain in accuracy and precision from $T = 150$ to 300. Thus, consistent with findings concerning power issues in growth curve modeling (Raudenbush & Liu, 2001), it may be necessary to increase the number of participants to improve the estimation properties of $\zeta _1$ and $\zeta _{2}$ and the initial condition parameters. In addition, power estimates were generally close to 1.00 for the sample sizes considered in this simulation study, although the type I error rates associated with the three intercept parameters, $\mu _1$–$\mu _3$, whose true values were equal to zero, also appeared slightly elevated.

The performance measures just noted for the fixed–fixed conditions can be contrasted directly with the measures obtained from the fixed–random (i.e., fixed true initial conditions and random fitted initial conditions) because the same 200 sets of MC data were used to compare the performances of the two fitted initial condition specifications. Results indicated that specifying the initial conditions as conforming to a multivariate distribution with unknown mean vector and covariance matrix still led to satisfactory estimation results (see Tables 4, 5). In particular, all the measurement parameters remained unbiased and showed comparable levels of precision (in terms of MC SDs) compared to conditions with the fixed–fixed specification at equivalent sample sizes. Slight increases in biases were observed for the three fixed effects dynamic parameters, $\zeta _0$–$\zeta _3$; however, higher precision (i.e., reduced MC SDs) and smaller RDSEs were obtained for almost all of the parameters. When the initial conditions were fixed at known and correctly specified values, the algorithm was able to yield close to unbiased point estimates for $\zeta _0$–$\zeta _3$, but at the expense of lower precision, possibly due to the approximation errors. In contrast, when the initial conditions were freely estimated, even though greater biases were present in $\zeta _0$–$\zeta _3$ and the average correlation between the true and estimated $b_{\zeta ,i}$ did decrease slightly (see footnotes of Tables 2, 3, 4, 5), the uncertainties in the initial conditions appeared to help compensate for some of these approximation errors and gave rise to higher precision and relatedly, smaller RSDEs.

The average initial condition parameters, $\mu _{x1}$ and $\mu _{x2}$, were correctly estimated in the fixed–random condition, and the associated variance–covariance parameters (including $\sigma ^2_{b_{x1}}, \sigma ^2_{b_{x2}}$, and $\sigma _{b_{x1,x2}}$) were estimated to be close to the correct value of zero. The SE for $\sigma ^2_{b_{x2}}$ was clearly overestimated, however, and the type I error rates for all of the initial condition variance–covariance parameters, including $\sigma ^2_{b_{x1}}, \sigma ^2_{b_{x2}}$ and $\sigma _{b_{x1,x2}}$, also deviated quite substantially from the nominal value of 0.05. These findings did not arose in the random–random condition, and they may stem from the fact that in the fixed–random condition, we were performing estimation near the boundary values of the initial condition variance–covariance parameters, whose true values were equal to zero.⁷ A related consequence was that a higher percentage of cases with numerical problems arose in the fixed–random condition than in the fixed–fixed condition, although the percentages of replications that had converged to theoretically plausible values remained generally satisfactory (close to or above 90 %). As in the fixed–fixed condition, the fixed effects parameters for the two covariates, $\zeta _1$ and $\zeta _{2}$, also did not show improvement in accuracy from $T = 150$ to 300, verifying again the need to increase the number of subjects in future studies to improve the estimation properties of these parameters.

Our next set of findings concerns properties of the SAEM algorithm when the initial conditions were random, but paired with fitted initial conditions that were either correctly or incorrectly specified. Statistical properties of the point and SE estimates are summarized in Tables 6, 7, 8, and 9. To aid interpretation, we grouped the parameters into four major types and aggregated the performance measures by parameter type. Graphical summary of the RMSEs and RDSEs by initial condition specification and parameter type is shown in Figure 3a–d. The four parameter types considered were (1) fixed effects dynamic parameters, including $\zeta _0, \zeta _1, \zeta _2, \mu _{x1}$, and $\mu _{x2}$; (2) measurement parameters, including the intercept parameters $\mu _1$–$\mu _3$ and factor loadings $\lambda _{21}$ and $\lambda _{31}$; (3) the random effect variance for the amplification parameter, $\sigma ^2_{b_{\zeta }}$, and (4) random effect variance and covariances for the initial conditions, including $\sigma ^2_{b_{x1}}, \sigma ^2_{b_{x2}}$, and $\sigma _{b_{x1,x2}}$.

Fig. 3

a–d Plots of the RMSEs and RDSEs across the four true–fitted initial condition specifications and two sample size configurations. F–F Fixed–fixed, F–R fixed–random, R–F random–fixed, R–R random–random. The numbers in the plots indicate parameter type: 1 fixed effects dynamic parameters, including $\zeta _0, \zeta _1, \zeta _2, \mu _{x1}$, and $\mu _{x2}$, 2 measurement parameters, including the intercept parameters $\mu _1$–$\mu _3$ and factor loadings $\lambda _{21}$ and $\lambda _{31}$, 3 the random effect variance for the amplification parameter, $\sigma ^2_{b_{\zeta }}$, and 4 random effect variance and covariances for the initial conditions, including $\sigma ^2_{b_{x1}}, \sigma ^2_{b_{x2}}$ and $\sigma _{b_{x1,x2}}$. To avoid skewing the graphical presentation of results from the remaining conditions, the high RMSEs and RDSEs for $\sigma ^2_{b_{\zeta }}$ (i.e., parameter type 3) in the R–F condition were omitted from the plots.

Several key results can be noted from the tables with full results for the conditions with random true initial condition specification. First, specifying the mean and variance–covariance parameters of the initial condition distribution as part of the parameters in $\varvec{\beta }$ and $\Sigma _b$ led to reasonable point and SE estimates, as well estimates of $\varvec{b}_i$. In contrast, misspecifying the random initial conditions as fixed, and with $\mu _{x1}$ and $\mu _{x2}$ fixed at incorrect values, led to high biases in the point estimates of $\zeta _0$–$\zeta _3$, the factor loadings, and all the variance parameters. Particularly high biases were observed in the point and SE estimates for the random effect variance parameter, $\sigma ^2_{b_{\zeta }}$. In fact, the RMSEs and RDSEs for the point and SE estimates of $\sigma ^2_{b_{\zeta }}$ were so high for both sample size conditions that these two values were omitted from the plots in Figure 3 to avoid skewing the graphical presentation of the other conditions. Under this particular misspecification in initial conditions, the estimates of $b_{\zeta , i}$ were completely biased and showed near-zero correlations with the true $b_{\zeta ,i}$ values, regardless of sample size. These results suggested that the type of misspecification in initial condition specification considered in the present simulation study can greatly compromise the quality of the estimation results—an effect that is not necessarily circumvented by increases in sample size (i.e., the number of time points).

Second, for the random–random condition, doubling the number of time points from 150 to 300 led to increases in the accuracy (in terms of relative biases and RMSEs) and precision (in terms of RMSEs and MC SDs) of most parameters, as well as an increase in the average correlation between the true and estimated values of $b_{\zeta ,i}$ from 0.65 to 0.78. Third, power estimates for all of the parameters in the R–R condition were generally high, with the exception of the covariance parameter between the interindividul differences in initial level and first derivative, $\sigma _{b_{x1,x2}}$. “Type I error” rates for the five parameters whose true values were equal to zero ($\mu _1$–$\mu _3, \mu _{x1}$, and $\mu _{x2}$) remained slightly elevated as in the conditions with fixed true initial conditions. Finally, slight decrements in performance were observed from the F-R conditions to the R–R conditions across both sample size configurations in terms of the quality of the point and SE estimates. Particularly notable was the increased variability (i.e., MC SDs) of all the point estimates, and the higher RDSEs for the fixed effects dynamic and measurement parameters (i.e., parameter types 1 and 2 in Figure 3). Despite these decrements in performance, the estimates from the R–R condition were still far better than those from the R–F conditions, whose estimation was based on the same 200 sets of MC data as the former. Even though the RDSEs for the dynamic and measurement parameters (parameter types 1 and 2) appeared reasonable for the R–F conditions, the corresponding point and $b_{\zeta ,i}$ estimates were too biased to be practically useful.

4 Discussion

In the present article, we presented an SAEM algorithm for fitting linear or nonlinear dynamic models with random effects in the dynamic parameters and unknown initial conditions. Although the illustrative and simulation examples are all nonlinear in nature, the proposed algorithm is applicable to linear ODEs as special cases. Using a modified Van der Pol oscillator model as an illustrative model, we evaluated the estimation properties of the proposed technique using an empirical example and a simulation study.

Our simulation results indicated that the proposed technique yielded satisfactory point and SE estimates for most of the parameters. Further developments are needed, however, to improve the accuracy of the SE estimates of the dynamic parameters. The problem is especially pronounced in cases involving random, as opposed to fixed initial conditions. We also demonstrated the feasibility of the proposed approach in handling situations with unknown initial conditions, either with or without interindividual differences in initial conditions. In our previous work in which different initial condition specifications were compared using linear discrete-time state-space models, the proposed approach of estimating means and variance–covariance parameters of the unknown initial condition distribution as modeling parameters was found to yield reasonable estimates for a broad array of initial condition scenarios (Losardo, 2012). Here, we extended our earlier results to the case of nonlinear continuous-time models with specific parametric assumptions on the distribution of the random effect. Possible extensions may include adding covariates as predictors of the interindividual differences in initial conditions. Other alternative approaches that may be adopted in future studies include using other parametric (e.g., exponential and Laplace) and nonparametric (e.g., Chow et al., 2011) distributions for the random effects distribution, and relaxing the linear functional form of $\varvec{\theta }_{f,i}$ in Eq. 1.

Slight decrements in the performance of the SAEM approach were observed when the number of random effects in the model was increased from one to three. Difficulties involved in estimating multiple random effects in dynamic models are related directly to whether the structural parameters are orthogonal to each other and whether the model is empirically identifiable with multiple random effects. In our empirical example, we fixed the oscillation frequency based on the expectation of a 24-h diurnal cycle to circumvent the issue of having insufficient complete cycles of data to identify other cycles of slower frequencies. In addition, we fixed one of the factor loadings at unity to set the metrics of the latent variables. The issue of parameter and model identifiability is, however, a much more complex problem than what we have alluded to thus far. In many dynamic models, similar differences in dynamics can be attained by incorporating random effects in more than one way. Obviously, estimation issues and difficulties arise if high correlations are present among the structural parameters. To this end, techniques aimed at evaluating model identifiability and dependencies among parameters are important to consider (Miao, Xin, Perelson, & Wu, 2011).

We adopted a Frequentist approach to parameter estimation because it offers a well-understood framework for performing hypothesis testing, and explicit criteria for assessing model convergence. However, there are still some subtle differences between the proposed SAEM approach and other standard Frequentist procedures in that the random effects in $\varvec{b}_i$ are estimated using MCMC procedures. In this way, the proposed procedure may be regarded as a compromise between the practical advantages of the MCMC framework in handling models of high complexity and (possibly) intractable integration, and the advantages offered by the Frequentist framework in assessing the convergence of modeling parameters and performing significance tests (e.g., test of the statistical significance of the random effects variances). In our empirical example, we highlighted the possibility of using a Wald test to determine the number of random effects to be included in a model and their corresponding covariance structure. Another possibility is to perform a score test using by-products from the SAEM under a null hypothesis model that assumes no random effect in the model (Zhu & Zhang, 2006).

Compared to approaches for fitting discrete-time dynamic models, continuous-time nonlinear ODE models pose additional challenges in deriving the ODE solutions needed to obtain latent variable estimates. In the present study, we opted to use a numerical integration method of two orders lower in the estimation process than that used in the data generation process. The estimates appeared reasonable, but improved performance may be attained with the use of a higher-order numerical solver, particularly adaptive solvers that can handle stiff systems. Other approaches using splines (Cao, Huang, & Wu, 2012; Liang, Miao, & Wu, 2010; Ramsay et al., 2007) or Langevin sampling techniques (Stuart, Voss, & Wilberg, 2004; Hairer, Stuart, Voss, & Wiberg, 2005) to replace the use of numerical solvers are also viable alternatives.

One of the primary reasons we opted to use a Monte Carlo-based EM techniques is to circumvent the difficulties involved in integrating over the random effects in $b_i$. One alternative to the estimation procedure proposed here is to augment the latent variable vector, $\varvec{x}(t_{i,j})$, with $\varvec{b}_i$ to yield $\varvec{x}_a(t_{i,j}) = [\tilde{\varvec{x}_i}(t_{i,j})^\mathrm{T}\varvec{b}^\mathrm{T}_i]^\mathrm{T}$ and subsequently utilize some of the newer hybrid nonlinear filtering approaches (Kulikov & Kulikova, 2014) to obtain a direct way of computing elements such as $E(\varvec{x}_a(t_{i,j})|\varvec{\mathrm {Y}}; \theta )$ required in the E-step. In this way, because the random effects are now part of the latent variable vector, no integration over $p(\varvec{b}_i|\varvec{\mathrm {Y}}; \varvec{\theta })$ is needed, and the E-step is thus greatly simplified. An optimization technique of choice can then be used in the M-step to update the parameter estimates. Thus, unlike our proposed approach in which the computation of the latent variable estimates is separated from the sampling of $b_i$, sampling of the latent variable and $b_i$ estimates is obtained jointly in this alternative approach. The performance of these two approaches should be compared in future studies under conditions with different modeling complexities (e.g., with linear and nonlinear ODEs and SDEs), as well as different numbers of random effects.

Whereas nonlinear dynamic models open up myriad new possibilities for evaluating more complex models, many methodological issues remain unresolved and have to be handled with caution. Parallel to the increase in model complexity are, of course, new challenges in deriving appropriate model fit indices and diagnostic measures. Sensitivity of the modeling results to parameter starting values, initial condition specification, choices of ODE solvers, integration time steps, and the number of random effects parameters are all important issues that warrant further attention. In addition, we made the assumption that all individuals were characterized by the same set of ODE functions, with the only source of between-individual differences residing in the individual-specific dynamic parameters in $\varvec{\theta }_{f,i}$. This assumption may not be tenable in all applications and across all variables (Molenaar, 2004). Alternative formulations that combine exploratory procedures for identifying individual differences with a confirmatory framework that assumes some levels of homogeneity in the change functions may be a promising alternative (e.g., Gates & Molenaar, 2012).

Our empirical dataset was not designed with the goal to evaluate complex nonlinear dynamics and is therefore characterized by several limitations often encountered in psychological datasets. While the sample size configurations considered in our simulation study ($n = 200, T = 150$ or 300) may seem high to many social and behavioral scientists, particularly psychologists, multiple-subject data of such time lengths are no longer an insurmountable goal. With the advent of ecological momentary assessment designs and new technological developments for collecting data in near real-time, intensive repeated measures data have become increasingly prevalent in psychology and other related disciplines. Furthermore, the random effects framework presented in this article constitutes one possible way of pooling together information from multiple subjects, all of which may have time series data of finite lengths.

We outline some other design-related issues here in hopes of offering some suggestions to researchers interested in collecting intensive repeated measures studies for dynamic modeling purposes. First, if researchers wish to capture sustained oscillations (e.g., circadian rhythms) in a construct of interest, it is generally recommended to collect data that span at least two (or preferably more) complete cycles. This is, of course, in addition to the requirements of having sufficient time points and participants to attain reasonable estimation properties, and sampling at least twice as fast as the frequency of interest. Second, smaller time intervals (and hence integration time steps) typically help improve the numerical stability of the estimation algorithm. In practice, the time scale used in model fitting can be rescaled (e.g., from milliseconds to hours) to yield smaller time intervals. However, if the time steps are too irregularly spaced, simple rescaling per se does not alleviate the problem. For instance, in our empirical data, the participants’ integration time steps ranged from 0.001 to 0.48. A simple rescaling may yield unnecessarily high computational costs at the smaller time steps while numerical instability may still arise at the larger time steps. Thus, researchers may want to consider the timing of change of the process of interest in selecting appropriate measurement intervals for a study. Finally, researchers should consider design-related enhancements to ensure that they sample individuals sufficiently around the times when complex, nonlinear changes are expected to unfold rapidly. Otherwise, some of the critical dynamics of a system may still be bypassed even with a very large number of time points. Other design-related issues implicated in the study of dynamic processes have also been discussed by Wu (2005).

All the models presented in this article were fitted using our own scripts written in MATLAB. Other statistical programs that can handle matrix operations, such as R (2009) and SAS/IML (2008), may also be used. Because the estimation algorithm was written in MATLAB and not using a primary programming language such as Fortran or C++, the computational time is relatively high. For instance, each replication in our simulation study may take 5–9 h—depending on the sample size and the number of random effects in the model—using a single core of an Intel Xeon Processor X5560 with less than 2 GB of memory. Ultimately, the high computational time is related directly to the number of time points available from each participant, because the numerical solution for each participant at each time point has to be derived sequentially based on the numerical solution for the participant at the previous time point. However, we still note that if the algorithm is reprogrammed in a more efficient primary programming language, the amount of computational time should be shorter compared to the typical computational time needed to estimate a model of comparable complexity using a fully Bayesian approach. This is because in the latter, there is no explicit criterion to guide convergence decisions; a large number of burn-in iterations has to be included before any inferences can be made utilizing the posterior distributions. In contrast, because the SAEM does not use a fully Bayesian approach, our experience has suggested that the number of burn-in iterations required to complete the two computational stages of the SAEM is substantially less than that required to complete the computations in a fully Bayesian approach.

As a discipline, psychology has generally seemed reluctant to embrace the promises and relatedly, some of the data collection/analytic challenges brought on by dynamic systems modeling techniques. Methodological difficulties and lack of understanding concerning the strengths and limitations of nonlinear systems have fostered a deeply rooted bias against nonlinear models—an unfortunate limit imposed by methodology on theory. Undoubtedly, several methodological issues remain in evaluating nonlinear dynamic models with random effects and related variations. Nonetheless, developing and evaluating estimation techniques that allow a direct mapping between more complex mathematical models of change and empirical measurements are among the first steps toward revoking the belief that nonlinear dynamic models are but a theoretical metaphor in social and behavioral research (see e.g., Kincanon & Powel, 1995). Our hope is that the work presented here can help inspire more research into alternative methods that are suited for studying change—including both linear and nonlinear dynamic models.

Appendices

Appendix 1: Score Vector and Information Matrix of the Complete-Data Loglikelihood Function

The elements in $\varvec{s}_{\varvec{\mathrm {Z}}}(\varvec{\theta }; \varvec{\mathrm {Z}})$ and $\varvec{\mathrm {I}}_{\varvec{\mathrm {Z}}}(\varvec{\theta }\varvec{\mathrm {Z}})$, namely, the score vector and information matrix of the complete-data loglikelihood function, are computed as

$$\begin{aligned} \varvec{s}_{\varvec{\mathrm {Z}}}(\varvec{\theta }; \varvec{\mathrm {Z}})&= \frac{\partial L(\varvec{\mathrm {Z}};\varvec{\theta })}{\partial \varvec{\theta }} = \displaystyle {\sum _{i=1}^{n}} \begin{bmatrix} \Big (\sum _{j=1}^\mathrm{T}\frac{\partial L_{i,j}(\varvec{\mathrm {Y}}| \varvec{b}; \varvec{\theta }) }{\partial \varvec{\beta }}\Big )\\ \Big (\sum _{j=1}^\mathrm{T}\frac{\partial L_{i,j}(\varvec{\mathrm {Y}}| \varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{\mu }}}\Big )\\ \Big (\sum _{j=1}^\mathrm{T}\frac{\partial L_{i,j}(\varvec{\mathrm {Y}}| \varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}} \Big )\\ \Big (\sum _{j=1}^\mathrm{T}\frac{\partial L_{i,j}(\varvec{\mathrm {Y}}| \varvec{b}; \varvec{\theta })}{\partial \varvec{\theta }_{\varvec{\epsilon }}}\Big )\\ \Big (\frac{\partial L_{i}(\varvec{b}; \varvec{\theta })}{\partial \varvec{\theta }_{\varvec{b}}}\Big ) \end{bmatrix}, \end{aligned}$$

(17)

$$\begin{aligned} \varvec{\mathrm {I}}_{\varvec{\mathrm {Z}}}(\varvec{\theta };\varvec{\mathrm {Z}})&= -\frac{\partial ^2 L(\varvec{\mathrm {Z}};\varvec{\theta })}{\partial \varvec{\theta } \partial \varvec{\theta }^\mathrm{T}}=- \displaystyle {\sum _{i=1}^{n}} \mathop {\mathrm {Diag}}\begin{bmatrix} \sum _{j=1}^\mathrm{T}\frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}| \varvec{b};\varvec{\theta }) }{\partial \varvec{\beta } \partial \varvec{\beta }^\mathrm{T}}\\ \sum _{j=1}^\mathrm{T}\frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}| \varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{\mu }} \partial \varvec{\theta }^\mathrm{T}_{\varvec{\mu }}} \\ \sum _{j=1}^\mathrm{T}\frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}| \varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{\mathrm {\Lambda }}} \partial \varvec{\theta }^\mathrm{T}_{\varvec{\mathrm {\Lambda }}}}\\ \sum _{j=1}^\mathrm{T}\frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}| \varvec{b}; \varvec{\theta })}{\partial \varvec{\theta }_{\varvec{\epsilon }} \partial \varvec{\theta }^\mathrm{T}_{\varvec{\epsilon }}}\\ \frac{\partial ^2 L_{i}(\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{b}} \partial \varvec{\theta }^\mathrm{T}_{\varvec{b}}} \end{bmatrix}, \end{aligned}$$

(18)

where $\mathop {\mathrm {Diag}}(.)$ denotes a block diagonal matrix formed by stacking the appropriate second partial derivative matrices in its diagonal section and zero matrices in its off-diagonal sections.

Using Heun’s method, with $\tilde{\varvec{x}}_i(t_{i,j})$ as defined in Eq. (4) and $\varvec{z}_i(t_{i,j}) = [\varvec{y}_i(t_{i, j})-\varvec{\mu }-\varvec{\mathrm {\Lambda }}\tilde{\varvec{x}}_i(t_{i, j})]$, first-order partial derivative elements of the complete-data loglikelihood are given by

$$\begin{aligned} \frac{\partial L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\beta }}&= -\,\frac{1}{2} \Bigg \{ \frac{\partial \varvec{\theta }_{f,i}}{\partial \varvec{\beta }} \frac{\partial \tilde{\varvec{x}}_i(t_{i,j})}{\partial \varvec{\theta }_{f,i}} \frac{\partial \varvec{z}_i(t_{i,j})}{\partial \tilde{\varvec{x}}_i(t_{i,j})} \frac{\partial \varvec{z}_i(t_{i,j})^\mathrm{T}\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} \varvec{z}_i(t_{i,j})}{\partial \varvec{z}_i(t_{i,j})} \Bigg \} \nonumber \\&= \varvec{\mathrm {H}}^\mathrm{T}_i \frac{\partial \tilde{\varvec{x}_i}(t_{i,j})^\mathrm{T}}{\partial \varvec{\theta }_{f,i}}\varvec{\mathrm {\Lambda }}^\mathrm{T} \varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} \varvec{z}_i(t_{i,j}), \nonumber \\ \frac{\partial L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{\mu }}}&= -\,\frac{1}{2} \Bigg \{\frac{\partial \varvec{\mu }}{\partial \varvec{\theta }_{\varvec{\mu }}} \frac{\partial \varvec{z}_i(t_{i,j})}{\partial \varvec{\mu }}\frac{\partial \varvec{z}_i(t_{i,j})^\mathrm{T}\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} \varvec{z}_i(t_{i,j})}{\varvec{z}_i(t_{i,j})} \Bigg \} \nonumber \\&= \frac{\partial \varvec{\mu }}{\partial \varvec{\theta }_{\varvec{\mu }}} \varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1}\varvec{z}_i(t_{i,j}),\nonumber \\ \frac{\partial L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}}&= -\,\frac{1}{2} \Bigg \{\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Lambda }})}{\partial \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}} \frac{\partial \varvec{z}_i(t_{i,j})}{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Lambda }})}\frac{\partial \varvec{z}_i(t_{i,j})^\mathrm{T}\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} \varvec{z}_i(t_{i,j})}{\partial \varvec{z}_i(t_{i,j})} \Bigg \} \nonumber \\&= \frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Lambda }})}{\partial \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}} \mathop {\mathrm {vec}}\Big [ \varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1}\varvec{z}_i(t_{i,j})\tilde{\varvec{x}_i}(t_{i,j})^\mathrm{T}\Big ],\nonumber \\ \frac{\partial L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{\epsilon }}}&= -\,\frac{1}{2} \frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}})}{\partial \varvec{\theta }_{\varvec{\epsilon }}} \Bigg \{\frac{\partial \varvec{z}_i(t_{i,j})^\mathrm{T}\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} \varvec{z}_i(t_{i,j})}{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma }}_{\varvec{\epsilon }})} + \frac{\partial \log |\varvec{\mathrm {\Sigma }}_{\varvec{\epsilon }}|}{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma }}_{\varvec{\epsilon }})} \Bigg \} \nonumber \\&= \frac{1}{2} \frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}})}{\partial \varvec{\theta }_{\varvec{\epsilon }}}\Bigg \{ [\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} \otimes \varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1}] \mathop {\mathrm {vec}}[\varvec{z}_i(t_{i,j}) \varvec{z}_i(t_{i,j})^\mathrm{T}-\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}] \Bigg \}, \nonumber \\ \frac{\partial L_{i}(\varvec{b}; \varvec{\theta })}{\partial \varvec{\theta }_{\varvec{b}}}&= -\frac{1}{2} \frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{b}}}})}{\partial \varvec{\theta }_{\varvec{b}}} \Bigg \{ \frac{\partial \varvec{b}^\mathrm{T}_i \varvec{\mathrm {\Sigma _{\varvec{b}}}}^{-1} \partial \varvec{b}_i}{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma }}_{\varvec{b}})} + \frac{\partial \log |\varvec{\mathrm {\Sigma }}_{\varvec{b}}|}{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma }}_{\varvec{b}})} \Bigg \} \nonumber \\&= \frac{1}{2} \frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{b}}}})}{\partial \varvec{\theta }_{\varvec{b}}} \Bigg \{ [\varvec{\mathrm {\Sigma _{\varvec{b}}}}^{-1} \otimes \varvec{\mathrm {\Sigma _{\varvec{b}}}}^{-1}] \mathop {\mathrm {vec}}(\varvec{b}_i \varvec{b}_i^\mathrm{T}-\varvec{\mathrm {\Sigma _{\varvec{b}}}}) \Bigg \}, \end{aligned}$$

(19)

where the $\mathop {\mathrm {vec}}(\varvec{\mathrm {W}})$ operator stacks the columns of the $m \times n$ matrix $\varvec{\mathrm {W}}$ into an $mn$-dimensional column vector and $\frac{\partial \tilde{\varvec{x}}_i(t_{i, j})^\mathrm{T}}{\partial \varvec{\theta }_{f,i}}$ is dictated by the dynamic model under consideration. Terms such as $\frac{\partial \varvec{\mu } }{\partial \varvec{\theta }_{\varvec{\mu }}}, \frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Lambda }})}{\partial \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}}, \frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}})}{\partial \varvec{\theta }_{\varvec{\epsilon }}}, \frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{\eta }}}})}{\partial \varvec{\theta }_{\varvec{\eta }}}$, and $\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{b}}}})}{\partial \varvec{\theta }_{\varvec{b}}}$ also depend on the model specification adopted in a particular application. Cases where some elements of $\varvec{\mathrm {\Lambda }}, \varvec{\mathrm {\Sigma }}_{\varvec{\epsilon }}, \varvec{\mathrm {\Sigma }}_{\varvec{\eta }}$, and $\varvec{\mathrm {\Sigma }}_{\varvec{b}}$ are fixed at known values can be readily accommodated through appropriate specification of these matrices of partial derivatives.

Second-order partial derivative elements of the complete-data loglikelihood function are computed as

$$\begin{aligned} \frac{\partial ^2 L_{i,j}({\varvec{\mathrm {Y}}}|\varvec{b}; \varvec{\theta })}{\partial \varvec{\beta } \partial {\varvec{\beta }}^\mathrm{T}}&= \Big (\varvec{z}_i(t_{i,j})^\mathrm{T}\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1}\varvec{\mathrm {\Lambda }}^\mathrm{T}\otimes \varvec{\mathrm {I}}_{p_{\beta }} \Big ) \frac{\partial \mathop {\mathrm {vec}}}{\partial {\varvec{\beta }}^\mathrm{T}}\Bigg \{\varvec{\mathrm {H}}^\mathrm{T}_i\frac{\partial \tilde{\varvec{x}_i}(t_{i,j})^\mathrm{T}}{\partial \varvec{\theta }_{f,i}} \Bigg \}\\&\quad +\; \Bigg (\varvec{\mathrm {H}}^\mathrm{T}_i \frac{\partial {\tilde{\varvec{x}_i}(t_{i,j})^\mathrm{T}}}{\partial \varvec{\theta }_{f,i}}\Bigg ) \frac{\partial \varvec{\mathrm {\Lambda }}^\mathrm{T}\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} \varvec{z}_i(t_{i,j})}{\partial \varvec{z}_i(t_{i, j})^\mathrm{T}}\frac{\partial \varvec{z}_i(t_{i,j})}{\partial \tilde{\varvec{x}}_i(t_{i,j})^\mathrm{T}} \frac{\partial \tilde{\varvec{x}}_i(t_{i, j})}{\partial {\varvec{\theta }}^\mathrm{T}_{f,i}} \frac{\partial \varvec{\theta }_{f,i}}{\partial {\varvec{\beta }}^\mathrm{T}} \\&= \Big (\varvec{z}_i(t_{i,j})^\mathrm{T}\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1}\varvec{\mathrm {\Lambda }}\otimes \varvec{\mathrm {I}}_{p_{\beta }} \Big ) (\varvec{\mathrm {I}}_{n_x} \otimes \varvec{\mathrm {H}}^\mathrm{T}_i)\frac{\partial \mathop {\mathrm {vec}}}{\partial \varvec{\theta _{f,i}}^\mathrm{T}}\Bigg \{\frac{\partial \tilde{\varvec{x}_i}(t_{i,j})^\mathrm{T}}{\partial {\varvec{\theta }}_{f,i}} \Bigg \}\varvec{\mathrm {H}}_i\\&\quad -\; \varvec{\mathrm {H}}^\mathrm{T}_i \frac{\partial \tilde{\varvec{x}_i}(t_{i,j})^\mathrm{T}}{\partial \varvec{\theta }_{f,i}}\varvec{\mathrm {\Lambda }}^\mathrm{T}\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1}\varvec{\mathrm {\Lambda }}\frac{\partial \tilde{\varvec{x}}_i(t_{i,j})}{\partial \varvec{\theta }^\mathrm{T}_{f,i}}\varvec{\mathrm {H}}_i,\\ \frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{\mu }} \partial \varvec{\theta }^\mathrm{T}_{\varvec{\mu }}}&=\Big (\varvec{z}_i(t_{i,j})^\mathrm{T}\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} \otimes \varvec{\mathrm {I}}_{p_{\mu }}\Big )\frac{\partial \mathop {\mathrm {vec}}}{\partial \varvec{\theta }^\mathrm{T}_{\varvec{\mu }}}\Bigg \{\frac{\partial \varvec{\mu }}{\partial \varvec{\theta }_{\varvec{\mu }}}\Bigg \} - \frac{\partial \varvec{\mu }}{\partial \varvec{\theta }_{\varvec{\mu }}} \varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} \frac{\partial \varvec{\mu }}{\partial \varvec{\theta }_{\varvec{\mu }}^\mathrm{T}}, \\ \frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{\mathrm {\Lambda }}} \partial \varvec{\theta }^\mathrm{T}_{\varvec{\mathrm {\Lambda }}}}&= \Bigg \{\mathop {\mathrm {vec}}[\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1}\varvec{z}_i(t_{i,j})\tilde{\varvec{x}_i}(t_{i,j})^\mathrm{T}]^\mathrm{T}\otimes \varvec{\mathrm {I}}_{p_{\Lambda }}\Bigg \}\frac{\partial \mathop {\mathrm {vec}}}{\partial \varvec{\theta }^\mathrm{T}_{\varvec{\mathrm {\Lambda }}}}\Bigg \{\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Lambda }})}{\partial \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}} \Bigg \} \\&\quad -\,\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Lambda }})}{\partial \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}} [\tilde{\varvec{x}}_i(t_{i,j})\tilde{\varvec{x}_i}(t_{i,j})^\mathrm{T}\otimes \varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1}] \frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Lambda }})}{\partial \varvec{\theta }^\mathrm{T}_{\varvec{\mathrm {\Lambda }}}}, \end{aligned}$$

$$\begin{aligned} \frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{\epsilon }} \partial \varvec{\theta }^\mathrm{T}_{\varvec{\epsilon }}}&= \frac{1}{2}\Big [\mathop {\mathrm {vec}}\Big (\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1}\varvec{z}_i(t_{i,j})\varvec{z}_i(t_{i,j})^\mathrm{T}\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} \Big )^\mathrm{T} \otimes \varvec{\mathrm {I}}_{p_{\epsilon }} \Big ] \frac{\partial \mathop {\mathrm {vec}}}{\partial \varvec{\theta }^\mathrm{T}_{\varvec{\mathrm {\epsilon }}}} \Bigg \{\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}})}{ \partial \varvec{\theta }_{\varvec{\mathrm {\epsilon }}} } \Bigg \} \\&\quad -\;\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}})}{ \partial \varvec{\theta }_{\varvec{\mathrm {\epsilon }}} } [\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} \otimes \varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1}\varvec{z}_i(t_{i,j})\varvec{z}_i(t_{i,j})^\mathrm{T}\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} ]\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}})}{ \partial \varvec{\theta }^\mathrm{T}_{\varvec{\mathrm {\epsilon }}} }\\&\quad -\;\frac{1}{2}[\mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma ^{-1}_{\varvec{\epsilon }}}})^\mathrm{T} \otimes \varvec{\mathrm {I}}_{p_{\epsilon }}]\frac{\partial \mathop {\mathrm {vec}}}{\partial \varvec{\theta }^\mathrm{T}_{\varvec{\mathrm {\epsilon }}}}\Bigg \{\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}})}{ \partial \varvec{\theta }_{\varvec{\mathrm {\epsilon }}} } \Bigg \}\\&\quad +\;\frac{1}{2}\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}})}{ \partial \varvec{\theta }_{\varvec{\mathrm {\epsilon }}} } (\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} \otimes \varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1})\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}})}{ \partial \varvec{\theta }^\mathrm{T}_{\varvec{\mathrm {\epsilon }}} },\\ \end{aligned}$$

$$\begin{aligned} \frac{\partial ^2 L_{i}(\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{b}} \partial \varvec{\theta }^\mathrm{T}_{\varvec{b}}}&=\frac{1}{2}\Big [\mathop {\mathrm {vec}}\Big (\varvec{\mathrm {\Sigma _{\varvec{b}}}}^{-1}\varvec{b}_i\varvec{b}^\mathrm{T}_i \varvec{\mathrm {\Sigma _{\varvec{b}}}}^{-1} \Big )^\mathrm{T} \otimes \varvec{\mathrm {I}}_{p_{b}} \Big ] \frac{\partial \mathop {\mathrm {vec}}}{\partial \varvec{\theta }^\mathrm{T}_{\varvec{b}}} \Bigg \{\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{b}}}})}{ \partial \varvec{\theta }_{\varvec{b}} } \Bigg \} \nonumber \\&\quad -\; \frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{b}}}})}{ \partial \varvec{\theta }_{\varvec{b}} } \left[ \varvec{\mathrm {\Sigma _{\varvec{b}}}}^{-1} \otimes \varvec{\mathrm {\Sigma _{\varvec{b}}}}^{-1}\varvec{b}_i\varvec{b}^\mathrm{T}_i \varvec{\mathrm {\Sigma _{\varvec{b}}}}^{-1} \right] \frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{b}}}})}{ \partial \varvec{\theta }^\mathrm{T}_{\varvec{b}}}\nonumber \\&\quad -\;\frac{1}{2} [\mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma ^{-1}_{\varvec{b}}}})^\mathrm{T} \otimes \varvec{\mathrm {I}}_{p_{b}}]\frac{\partial \mathop {\mathrm {vec}}}{\partial \varvec{\theta }^\mathrm{T}_{\varvec{b}}}\Bigg \{\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{b}}}})}{ \partial \varvec{\theta }_{\varvec{b}} } \Bigg \}\nonumber \\&\quad +\; \frac{1}{2}\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{b}}}})}{ \partial \varvec{\theta }_{\varvec{b}} } (\varvec{\mathrm {\Sigma _{\varvec{b}}}}^{-1} \otimes \varvec{\mathrm {\Sigma _{\varvec{b}}}}^{-1})\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Sigma _{\varvec{b}}}})}{ \partial \varvec{\theta }^\mathrm{T}_{\varvec{b}}}, \nonumber \\ \frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta _{\varvec{\mu }}} \partial \varvec{\theta _{\varvec{\mathrm {\Lambda }}}}^\mathrm{T}}&= -\, \frac{\partial \varvec{\mu }}{\partial \varvec{\theta }_{\varvec{\mu }}} \varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1} [\tilde{\varvec{x}}_i(t_{i,j})^\mathrm{T} \otimes \varvec{\mathrm {I}}_{n_y} ] \frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Lambda }})}{\partial \varvec{\theta }^\mathrm{T}_{\varvec{\mathrm {\Lambda }}}},\nonumber \\ \frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{\mu }}\partial \varvec{\beta }^\mathrm{T}}&= -\,\frac{\partial \varvec{\mu }}{\partial \varvec{\theta }_{\varvec{\mu }}} \varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1}\frac{\partial \varvec{z}_i(t_{i,j})}{\partial \tilde{\varvec{x}}_i(t_{i,j})^\mathrm{T}} \frac{\partial \tilde{\varvec{x}}_i(t_{i, j})}{\partial \varvec{\theta }^\mathrm{T}_{f,i}} \frac{\partial \varvec{\theta }_{f,i}}{\partial \varvec{\beta }^\mathrm{T}},\nonumber \\&=-\,\frac{\partial \varvec{\mu }}{\partial \varvec{\theta }_{\varvec{\mu }}} \varvec{\mathrm {\Sigma _{\varvec{\epsilon }}}}^{-1}\varvec{\mathrm {\Lambda }}\frac{\partial \tilde{\varvec{x}}_i(t_{i,j})}{\partial \varvec{\theta }^\mathrm{T}_{f,i}}\varvec{\mathrm {H}}_i,\nonumber \\ \frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}\partial \varvec{\mathrm {\beta }}^\mathrm{T}}&=\frac{\partial \mathop {\mathrm {vec}}(\varvec{\mathrm {\Lambda }})}{\partial \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}} \Bigg \{ (\varvec{\mathrm {I}}_{n_x}\otimes \varvec{\mathrm {\Sigma }}_{\epsilon }^{-1}) \Big [ -(\tilde{\varvec{x}}_i(t_{i,j})^\mathrm{T} \otimes \varvec{\mathrm {I}}_{n_y})\varvec{\mathrm {\Lambda }}\frac{\partial \tilde{\varvec{x}}_i(t_{i,j})}{\partial \varvec{\theta }^\mathrm{T}_{f,i}}\varvec{\mathrm {H}}_i \nonumber \\&\quad +\; (\varvec{\mathrm {I}}_{n_x} \otimes \varvec{z}_i(t_{i,j})) \frac{\partial \tilde{\varvec{x}}_i(t_{i,j})}{\partial \varvec{\theta }^\mathrm{T}_{f,i}} \varvec{\mathrm {H}}_i\Big ]\Bigg \}. \end{aligned}$$

(20)

Other second-order derivative elements are equal to null matrices, including $\frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta })}{\partial \varvec{\beta }\partial \varvec{\theta }^\mathrm{T}_{\varvec{\theta }_{\varvec{\mu }}}},$ $\frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta })}{\partial \varvec{\beta }\partial \varvec{\theta }^\mathrm{T}_{\varvec{\theta }_{\varvec{\mathrm {\Lambda }}}}}, \frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta })}{\partial \varvec{\beta }\partial \varvec{\theta }^\mathrm{T}_{\varvec{\theta }_{\varvec{\epsilon }}}}, \frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta })}{\partial \varvec{\beta }\partial \varvec{\theta }^\mathrm{T}_{\varvec{b}}}, \frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta })}{\partial \varvec{\theta _{\varvec{\mu }}} \partial \varvec{\theta }^\mathrm{T}_{\varvec{b}}}, \frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta })}{\partial \varvec{\theta _{\varvec{\mathrm {\Lambda }}}} \partial \varvec{\theta }^\mathrm{T}_{\varvec{b}}}$ and $\frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b};\varvec{\theta })}{\partial \varvec{\theta _{\varvec{\mathrm {\epsilon }}}}\partial \varvec{\theta }^\mathrm{T}_{\varvec{b}}}$. Under the assumption that the model is correctly specified, the elements in $\frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta _{\varvec{\mathrm {\Lambda }}}} \partial \varvec{\theta }^\mathrm{T}_{\varvec{\epsilon }}}, \frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta _{\varvec{\mu }}} \partial \varvec{\theta _{\varvec{\epsilon }}}^\mathrm{T}}$ and $\frac{\partial ^2 L_{i,j}(\varvec{\mathrm {Y}}|\varvec{b}; \varvec{\theta }) }{\partial \varvec{\theta _{\varvec{\beta }}} \partial \varvec{\theta _{\varvec{\epsilon }}}^\mathrm{T}}$ are close to zeros at the MLEs of the modeling parameters. These elements are thus set to null matrices in the proposed estimation algorithm to stabilize the algorithm when initial parameter estimates are far from the MLEs and are not shown here. In addition, the off-diagonal elements shown in the last three equations in (20) are non-zero even near the MLEs. However, setting all the off-diagonal blocks of the information matrix of the complete-data loglikelihood function to null matrices helps stabilize the algorithm in case this information matrix is not positive definite in the optimization process. In our preliminary simulations, we verified that setting these three matrices to null matrices, as opposed to the forms as shown in Eq. (20), actually helped reduce numerical problems in the optimization process while having negligible effects on the final point and SE estimates because we are not using this matrix directly as the Fisher information matrix to derive the final SE estimates. We thus proceeded to setting all the off-diagonal elements, including the last three matrices shown in Eq. (20), to null matrices.

Appendix 2: Sampling From $p(\varvec{b}| \varvec{\mathrm {Y}};\varvec{\theta }^{(m-1)})$

The superscript $(m-1)$ of $\varvec{\theta }$ is temporarily suppressed for notational simplicity. It can be shown that $p(\varvec{b}| \varvec{\mathrm {Y}};\varvec{\theta })=\prod _{i=1}^{n} p(\varvec{b}_i| \varvec{\mathrm {Y}};\varvec{\theta })$, where $p(\varvec{b}_i| \varvec{\mathrm {Y}};\varvec{\theta })$ is non-standard and cannot be sampled directly. Specifically, $p(\varvec{b}_i| \varvec{\mathrm {Y}};\varvec{\theta }) \propto p(\varvec{b}_i;\varvec{\theta }_{\varvec{b}})p(\varvec{\mathrm {Y}}_i | \varvec{b}_i;\varvec{\theta }_{\varvec{\mu }}, \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}, \varvec{\theta }_{\varvec{\epsilon }},\varvec{\beta })$, in which $p(\varvec{\mathrm {Y}}_i | \varvec{b}_i;\varvec{\theta }_{\varvec{\mu }}, \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}, \varvec{\theta }_{\varvec{\epsilon }},\varvec{\beta })$ is given by

$$\begin{aligned} p(\varvec{\mathrm {Y}}_i | \varvec{b}_i;\varvec{\theta }_{\varvec{\mu }}, \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}, \varvec{\theta }_{\varvec{\epsilon }},\varvec{\beta }) = \prod _{j=1}^\mathrm{T} p(\varvec{y}_i(t_{i, j}) | \varvec{b}_i;\varvec{\theta }_{\varvec{\mu }}, \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}, \varvec{\theta }_{\varvec{\epsilon }},\varvec{\beta }), \end{aligned}$$

(21)

where $p(\varvec{y}_i(t_{i, j}) | \varvec{b}_i;\varvec{\theta }_{\varvec{\mu }}, \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}, \varvec{\theta }_{\varvec{\epsilon }},\varvec{\beta })$ is a multivariate normal density function with mean $\varvec{\mu }+\varvec{\mathrm {\Lambda }}\tilde{\varvec{x}}_i(t_{i, j})$ and covariance matrix $\varvec{\mathrm {\Sigma }}_{\epsilon }$. As $\varvec{b}_i$ is involved in the nonlinear $f(.)$ in $p(\varvec{y}_i(t_{i, j}) | \varvec{b}_i;\varvec{\theta }_{\varvec{\mu }}, \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}, \varvec{\theta }_{\varvec{\epsilon }},\varvec{\beta }), p(\varvec{b}_i| \varvec{\mathrm {Y}};\varvec{\theta })$ is usually non-standard. To sample from $p(\varvec{b}_i| \varvec{\mathrm {Y}};\varvec{\theta })$, we adopt a Metropolis-Hastings (MH) algorithm as follows. At the $m$th iteration with current values in $\varvec{b}_i^{(m)}$, a new candidate $\varvec{b}_i$ is generated from a proposal distribution, chosen to be the normal distribution $\text{ N }(\varvec{b}_i^{(m)},\sigma _{b}^{2} \varvec{\mathrm {\Omega }}_{bi})$, where $\sigma _{b}^{2}$ is a scaling constant, $\varvec{\mathrm {\Omega }}_{bi} = (\varvec{\mathrm {\Sigma }}_{\varvec{b}}^{-1}+\sum _{j=1}^\mathrm{T}\varvec{\mathrm {D}}_{bit}^\mathrm{T}\varvec{\mathrm {\Sigma }}_{\epsilon }^{-1} \varvec{\mathrm {D}}_{bit})^{-1}, \varvec{\mathrm {D}}_{bit}=\partial \tilde{\varvec{x}}_i(t_{i, j})/\partial \varvec{b}_{i}^\mathrm{T} |_{\varvec{b}_i=\varvec{b}_i^{*}}$, and $\varvec{b}_i^{*}$ is a fixed value with high $p(\varvec{b}_i^{*}| \varvec{\mathrm {Y}};\varvec{\theta })$. One possibility is to use the mean of $p(\varvec{b}_i;\varvec{\theta }_{\varvec{b}})$ as $\varvec{b}_i^{*}$, which we have found to lead to good performance. The new $\varvec{b}_i$ is accepted with probability

$$\begin{aligned} \text{ min }\left\{ 1,\frac{p(\varvec{b}_i;\varvec{\theta }_{\varvec{b}}) \prod _{j=1}^\mathrm{T} p(\varvec{y}_i(t_{i, j}) | \varvec{b}_i;\varvec{\theta }_{\varvec{\mu }}, \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}, \varvec{\theta }_{\varvec{\epsilon }},\varvec{\beta })}{p(\varvec{b}^{(m)}_i;\varvec{\theta }_{\varvec{b}}) \prod _{j=1}^\mathrm{T} p(\varvec{y}_i(t_{i, j}) | \varvec{b}_i^{(m)}; \varvec{\theta }_{\varvec{\mu }}, \varvec{\theta }_{\varvec{\mathrm {\Lambda }}}, \varvec{\theta }_{\varvec{\epsilon }},\varvec{\beta })} \right\} , \end{aligned}$$

(22)

The scaling constant, $\sigma _{b}^2$, can be chosen such that the average acceptance rate is approximately 0.4.