Bayesian Estimation of Multinomial Processing Tree Models with Heterogeneity in Participants and Items

Abstract

Multinomial processing tree (MPT) models are theoretically motivated stochastic models for the analysis of categorical data. Here we focus on a crossed-random effects extension of the Bayesian latent-trait pair-clustering MPT model. Our approach assumes that participant and item effects combine additively on the probit scale and postulates (multivariate) normal distributions for the random effects. We provide a WinBUGS implementation of the crossed-random effects pair-clustering model and an application to novel experimental data. The present approach may be adapted to handle other MPT models.

Multinomial processing tree (MPT) models are theoretically motivated stochastic models for the analysis of categorical data. MPT models can be used to measure the contribution of the different cognitive processes that determine performance in various experimental paradigms. Due to their simplicity, MPT models have become increasingly popular over the last decades and have been applied to a variety of areas in cognitive psychology (for reviews, see Batchelder & Riefer 1999; Erdfelder, Auer, Hilbig, Aßfalg, Moshagen, & Nadarevic, 2009).

MPT models assume that the observed category responses follow a multinomial distribution. MPT models reparametrize the category probabilities of the multinomial distribution in terms of a number of model parameters that are assumed to represent underlying cognitive processes. The category probabilities are generally expressed as nonlinear functions of the underlying model parameters. Specifically, MPT models assume that the observed response categories result from one or more hypothesized sequences of cognitive events, a structure that can be represented by a rooted tree architecture such as the one depicted in Figure 1. The formal properties of MPT models are described by Hu and Batchelder (1994), Purdy and Batchelder (2009), and Riefer and Batchelder (1988). For computer software for fitting and testing MPT models, see for instance Hu and Phillips (1999), Moshagen (2010), and Wickelmaier (2011).

Figure 1.

Multinomial processing tree for the pair-clustering paradigm.

Traditionally, statistical inference for MPT models is carried out on data that are aggregated across participants and items using the classical maximum-likelihood approach (e.g., Hu & Batchelder 1994). This approach relies on the assumption of homogeneity in participants and items, that is, the assumption that participants and items do not differ substantively in terms of the cognitive processes or characteristics represented by the model parameters. However, heterogeneity in participants and items is more likely to be the rule rather than the exception. For example, participant variables such as age and IQ are likely to influence performance on many cognitive tests, and the same holds for item variables such as word frequency and word length. The cognitive processes represented by the model parameters may not only be variable, but may also be highly correlated. For example, two cognitive abilities that both reflect, say, some aspect of memory retrieval are likely to be related, resulting in correlations between the model parameters representing these abilities. Most importantly, in the presence of parameter heterogeneity, the analysis of aggregated data may bias parameter estimation and statistical inference (e.g., Ashby, Maddox, & Lee, 1994; Clark 1973; Curran & Hintzman 1995; Estes 1956; Hintzman 1980, 1993; Klauer 2006; Rouder & Lu 2005; Smith & Batchelder 2008).

In recent years, researcher have become increasingly interested in developing approaches to MPT modeling that incorporate parameter heterogeneity (e.g., Klauer 2006, 2010; Rouder, Lu, Morey, Sun, & Speckman, 2008; Smith & Batchelder 2010). These attempts typically involve Bayesian hierarchical or multilevel modeling that allows the model parameters to vary either over participants or over items in a statistically specified way (e.g., Farrell & Ludwig 2008; Gelman, Carlin, Stern, & Rubin, 2003; Gelman & Hill 2007; Gill 2002; Lee 2011; Lee & Newell 2011; Lee & Wagenmakers in press; Nilsson, Rieskamp, & Wagenmakers, 2011; Rouder & Lu 2005; Shiffrin, Lee, Kim, & Wagenmakers, 2008).

A prominent approach to deal with parameter heterogeneity in MPT models is the recently developed latent-trait method (Klauer 2010). The latent-trait approach relies on Bayesian hierarchical modeling and postulates a multivariate normal distribution for the probit transformed parameters. The latent-trait approach deals with parameter heterogeneity as a result of differences either between participants or between items, but not both. In many situations, however, it is reasonable to assume that the model parameters differ both between the participants and between the particular items used in an experiment. In this case, both sources of variability—participant and item—should be modeled as random effects.

The goal of the present paper is therefore threefold. First, we extend Klauer’s (2010) latent-trait approach to accommodate heterogeneity in participants as well as items. Second, we illustrate the use of the resulting crossed-random effects approach with novel experimental data. Lastly, to facilitate the use of Bayesian hierarchical methods in MPT modeling, we provide software implementations of the latent-trait and the crossed-random effects approach using WinBUGS (Bayesian inference Using Gibbs Sampling for Windows; Lunn, Jackson, Best, Thomas, & Spiegelhalter, 2012; Lunn, Thomas, Best, & Spiegelhalter, 2000; Lunn, Spiegelhalter, Thomas, & Best, 2009). WinBUGS is a general purpose statistical software for Bayesian analysis that implements the Markov chain Monte Carlo (MCMC; Gamerman & Lopes 2006; Gilks, Richardson, & Spiegelhalter, 1996) algorithm necessary for Bayesian parameter estimation (for an introduction for psychologists, see Kruschke 2010; Lee & Wagenmakers in press; Sheu & O’Curry 1998). We will use the pair-clustering model—one of the most extensively studied MPT models—as an example. However, the crossed-random effects approach presented here may in principle be adapted to handle many other MPT models as well.

The paper is organized as follows. The first section introduces various methods to accommodate parameter heterogeneity in MPT models. The second section introduces the pair-clustering MPT model in more detail. The third section presents the WinBUGS implementation of the latent-trait pair-clustering model. The fourth section presents the crossed-random effects pair-clustering model with the corresponding WinBUGS implementation and describes the results of applying the model to novel experimental data. The fifth section concludes the paper.

1 Parameter Heterogeneity in MPT Models

The data for an MPT model consist of category responses from several participants to each of a set of items. MPT model parameters, θ _p , p=1,…,P, represent probabilities of latent cognitive capacities, such as attending to an item, storing an item in memory, retrieving an item from memory, detecting the source of an item, making an inference, or guessing a response. Such parameters are functionally independent and each has parameter space [0,1].

Parameter estimation and statistical inference for MPT models is traditionally carried out on response category frequencies aggregated over participants and items using maximum likelihood methods (e.g., Hu & Batchelder 1994). This approach is based on the assumption of parameter homogeneity. If this assumption is violated, the analysis of aggregated data may lead to erroneous conclusions. The consequences of variability are especially troubling for nonlinear models, such as MPT models. In particular, reliance on aggregated data in the presence of parameter heterogeneity may lead to biased parameter estimates, the underestimation of confidence intervals, and the inflation of Type I error rates (e.g., Batchelder 1975; Batchelder & Riefer 1999; Heathcote, Brown, & Mewhort, 2000; Klauer 2006; Riefer & Batchelder 1991; Rouder & Lu 2005). Moreover, the specific pattern of the parameter correlations can greatly influence the magnitude of the deleterious effects of unmodeled parameter heterogeneity (Klauer 2006).

In recent years, a growing number of researchers has started to use cognitive models that accommodate heterogeneity in participants and/or items (e.g., DeCarlo 2002; Karabatsos & Batchelder 2003; Lee 2011; Lee & Webb 2005; Navarro, Griffiths, Steyvers, & Lee, 2006; Rouder & Lu 2005; Rouder, Sun, Speckman, Lu, & Zhou, 2003; Rouder, Lu, Sun, Speckman, Morey, & Naveh-Benjamin, 2007). In the context of MPT models, Klauer (2006) and Smith and Batchelder (2008) proposed statistical tests for detecting parameter heterogeneity. Moreover, a number of approaches that deal with parameter heterogeneity are now available for MPT models.

These approaches rely on hierarchical modeling and postulate population-level (hyper) distributions for the model parameters. The population-level distributions describe the variability in parameters either across participants or across items (e.g., Gelman et al. 2003; Gelman & Hill 2007; Gill 2002). For instance, Klauer (2006; see also Stahl & Klauer 2007) proposed the use of latent-class MPT models with discrete population-level distributions to model the between-participant variability and the correlations between the model parameters. In contrast, Smith and Batchelder (2010) proposed to capture the between-participant variability of the model parameters using independent beta distributions (see also Batchelder & Riefer 2007; Karabatsos & Batchelder 2003; Riefer & Batchelder 1991).

Here we will focus on yet another alternative—the latent-trait approach—which assumes a multivariate normal distribution for the participant differences in the probit transformed parameters and accounts for the correlations between the model parameters (Klauer 2010). The latent-trait approach relies on Bayesian parameter estimation, but the MCMC algorithm for estimating the model parameters is currently not implemented in any off-the-shelf software package.

All the above described alternatives deal with parameter heterogeneity as a result of differences either between participants or between items, but not both, and rely on data that are aggregated either over items or over participants. It is, however, often reasonable to assume that the model parameters vary between participants as well as between items. In such situations, participant and item differences should be modeled as crossed-random effects (Clark 1973) and inference should be based on participant-by-item data.

In psychometrics, there is a long tradition of simultaneously modeling variability in participants and items (e.g., De Boeck 2008; Lord & Novick 1986). In cognitive psychology, in contrast, such modeling constitutes a relatively recent trend (e.g., Baayen 2008). For instance, Rouder et al. (2007) and Rouder and Lu (2005) have recently developed hierarchical signal detection models that incorporate random participant and item effects. In MPT modeling, attempts to simultaneously model heterogeneity in participants and items are scarce.

Augmenting MPT models with participant and item variability requires a separate parameter for each participant-item combination, θ _ijp , where i=1,…,I indexes the participants, j=1,…,J indexes the items, and p=1,…,P indexes the model parameters in θ=(θ _ijp ). This requirement leads to I×J×P parameters for only I×J data points, resulting in problems with model identification. We can reduce the number of parameters by using, for example, a reparametrization of the two-parameter Rasch model (e.g., Fischer & Molenaar 1995). We can then model each participant-item combination using

$$ \theta_{ijp} = \frac{\alpha_{ip}\beta_{jp}}{\alpha_{ip}\beta _{jp}+(1-\alpha_{ip})(1-\beta_{jp})}, $$

(1)

for α _ip ,β _jp ∈(0,1) (Batchelder 1998, 2009). Here α _ip and β _jp denote the ith participant effect and the jth item effect relating to parameter p, respectively. Karabatsos and Batchelder (2003) developed this Rasch model approach for the General Condorcet MPT Model. Batchelder and Browther (1997) also used a Rasch model decomposition and modeled the logit transformed participant-item parameters as additive functions of the participant and item effects. See De Boeck and Partchev (2012) for an alternative approach to model heterogeneity in participants and items in MPT models using item response theory.

In the present paper we will explore an alternative that extends Klauer’s (2010) latent-trait approach to simultaneously deal with heterogeneity in participants and items. Specifically, we will model the probit transformed θ _ijp parameters as additive combinations of participant and item effects. The participant and item effects are then assumed to come from (multivariate) normal distributions. Rouder et al. (2008) used a similar approach for a simple hierarchical process dissociation model, where they assumed the additivity of the probit transformed participant and item effects and modeled these using multivariate normal priors (see also Rouder & Lu 2005; Rouder et al. 2007).

To summarize, a number of hierarchical approaches are now available for MPT models to deal with heterogeneity introduced either by the participants or by the items. The latest among these methods, Klauer’s (2010) latent-trait approach, assumes a multivariate normal distribution for the probit transformed parameters and incorporates the possibility of parameter correlations. The latent-trait approach deals with parameter heterogeneity as a result of differences either between participants or between items, but not for both sources. The latent-trait approach may readily be augmented to accommodate crossed-random effects by assuming additivity of participant and item effects on the probit scale.

2 The Pair-Clustering MPT Model

The pair-clustering model—one of the most extensively studied MPT models—was developed for the measurement of the storage and retrieval processes that underlie performance in the pair-clustering paradigm (e.g., Batchelder & Riefer 1980, 1986). The pair-clustering paradigm involves a free recall memory experiment, where participants study a list of words that consists of two types of items: semantically related word pairs (e.g., dog–cat, father–son) and singletons (i.e., unpaired words, such as paper and train). Participants are presented with the study list in a word-by-word fashion, such as dog–paper–father–train–cat–son–etc. After the presentation of the study list, participants are required to recall, in any order, as many words as they can. The general finding is that semantically related word pairs are recalled consecutively, as a ‘pair-cluster’.

Since its development, the pair-clustering model has facilitated the interpretation of numerous free recall phenomena, such as retroactive inhibition and the effects of presentation rate and stimulus spacing (see Batchelder & Riefer 1999). Moreover, the pair-clustering model has been used successfully to investigate memory deficits in various age groups and clinical populations (e.g., Bröder, Herwig, Teipel, & Fast, 2008; Golz & Erdfelder 2004; Riefer & Batchelder 1991; Riefer, Knapp, Batchelder, Bamber, & Manifold, 2002; see Batchelder & Riefer 2007 for a review).

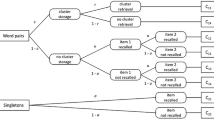
The architecture of the pair-clustering model can be represented by a rooted tree structure shown in Figure 1. The responses of each participant fall into two independent category systems, namely responses to word pairs and responses to singletons. Each category system k=1,2 is modeled by a separate subtree of the multinomial model, where each subtree consists of a finite number of branches terminating in one of the response categories C _kl , l=1,…,L _k . The recall of word pairs is scored into four response categories (L ₁=4): C ₁₁, both members of a word pair are recalled consecutively; C ₁₂, both members of a word pair are recalled but not consecutively; C ₁₃, only one member of a word pair is recalled; and C ₁₄, neither member of a word pair is recalled. The recall of singletons is scored in two response categories (L ₂=2): C ₂₁, singleton is recalled; and C ₂₂, singleton is not recalled.

The pair-clustering model explains the observed data by reparametrizing the category probabilities, Pr(C _kl ), of the multinomial distribution in terms of p=1,…,4 functionally independent model parameters θ=(c,r,u,a), with θ _p ∈(0,1). Parameter c represents the probability that a word pair is clustered and stored in memory. Parameter r is the conditional probability that a word pair is retrieved from memory, given that it was clustered. Parameter u is the conditional probability that a member of a word pair is stored and retrieved from memory, given that the word pair was not stored as a cluster. As the u parameter taps both the storage and retrieval of unclustered words, it is typically regarded as a nuisance parameter. Parameter a is the probability that a singleton is stored and retrieved from memory. As illustrated later, it is frequently assumed that a=u, i.e., the probability that a singleton is stored and retrieved (a) equals the probability that a member of a word pair is stored and retrieved, given that it was not clustered (u). The pair-clustering model has four free response categories and it features at most four model parameters. The identification of the pair-clustering model has been established elsewhere (e.g., Batchelder & Riefer 1986).

According to the model, if a word pair is successfully clustered and retrieved with joint probability cr, the two members of the word pair are retrieved consecutively, resulting in recall category C ₁₁. If a word pair is successfully clustered (c) but is not retrieved (1-r), neither member of the word pair is retrieved, resulting in recall category C ₁₄. The model thus assumes that clustered pairs are either retrieved as a pair or are not retrieved at all. In contrast, if word pairs are not clustered (1-c), either member of the word pair can be stored and retrieved independently with probability u, resulting in recall category C ₁₂ or C ₁₃. Retrieved items from unclustered word pairs are thus not recalled consecutively.

The probabilities of the six response categories are expressed in terms of the model parameters as follows:

$$ \begin{aligned} \mathrm{Pr}(C_{11}|\boldsymbol{\theta})& = cr\\ \mathrm{Pr}(C_{12}|\boldsymbol{\theta})& = (1-c)u^2\\ \mathrm{Pr}(C_{13}|\boldsymbol{\theta})& = (1-c)2u(1-u)\\ \mathrm{Pr}(C_{14}|\boldsymbol{\theta})& = c(1-r)+(1-c)(1-u)^2\\ \mathrm{Pr}(C_{21}|\boldsymbol{\theta})& = a\\ \mathrm{Pr}(C_{22}|\boldsymbol{\theta})&= 1 - a. \end{aligned} $$

(2)

The raw data in category system k consist of the response of a given participant i=1,…,I to a particular item j=1,…,J _k , represented by a vector of length L _k . For a given participant-word pair combination, the raw data n _ij,1 thus consist of a vector of length L ₁=4, where the entry n _ijl equals 1 if the response of participant i to word pair j falls into response category l, and zero otherwise. For example, if participant i recalls both members of word pair j consecutively (i.e., response category C ₁₁), the raw data are given by the vector (1,0,0,0). Similarly, for a given participant-singleton combination, the raw data n _ij,2 consist of a vector of length L ₂=2, where n _ijl equals 1 if the response of participant i to singleton j falls into response category l, and zero otherwise. For example, if participant i does not recall singleton j (i.e., response category C ₂₂), the raw data are given by the vector (0,1). Traditional analysis of pair-clustering data assumes that observations over participant and items are independent and identically distributed. Parameter estimation is generally carried out on category responses summed over participants and items (e.g., Batchelder & Riefer 1986).

3 The Latent-Trait Pair-Clustering Model

The main goal of the present paper is to augment Klauer’s (2010) Bayesian latent-trait approach to handle heterogeneity in both participants and items. To facilitate this, we first introduce the latent-trait approach in more detail and provide a WinBUGS implementation of the latent-trait pair-clustering model. We then report the results of a parameter recovery study. In what follows we assume that the items are homogeneous and use the latent-trait approach to model individual differences between participants. Note, however, that the latent-trait approach may just as well be used to capture the variability between items instead of participants. In this case, we would assume that participants are homogeneous and model the differences between the items.

3.1 Introduction to the Latent-Trait Approach

The symbols and notation used in the text, figures, and the WinBUGS scripts are summarized in Table 1. As we focus on parameter heterogeneity as a result of individual differences between participants, the raw data are aggregated over the J ₁ word pairs and the J ₂ singletons but not over the i=1,…,I participants. The data of participant i consist thus of the frequency of responses, n _ikl , falling into recall category C _kl , k=1,2, l=1,…,L _k .

Table 1. Notation.

For each participant i in each category system k, the observed category frequencies are assumed to follow a multinomial distribution with category probabilities Pr(C _kl |θ _i ). Formally, let B _klm be the mth branch terminating in C _kl , m=1,…,M _kl . The probability that participant i follows branch B _klm is given by

$$ \mathrm{Pr}(B_{klm}|\boldsymbol{\theta}_i) = \prod^P_{p=1}\theta^{v_{klmp}}_{ip} (1-\theta)^{w_{klmp}}_{ip}, $$

(3)

where v _klmp ≥0 and w _klmp ≥0 are the number of nodes on branch B _klm that is associated with parameter θ _p , p=1,…,P, and 1−θ _p , respectively. The probability of each response category is given by adding the probabilities of all the branches that lead to that category:

$$ \mathrm{Pr}(C_{kl}|\boldsymbol{\theta}_i) = \sum^{M_{kl}}_{m=1} \prod ^P_{p=1}\theta^{v_{klmp}}_{ip} (1- \theta_{ip})^{w_{klmp}}. $$

(4)

The data of participant i across the two category systems, n _i =(n _i1,n _i2), are assumed to follow a multinomial distribution:

$$ \mathrm{Pr}(\mathbf{N}_i = \mathbf{n}_i| \boldsymbol{\theta}_i) = \prod^K_{k=1} \Biggl\{ {\frac{J_k!}{n_{ik1}! \times n_{ik2}! \times\cdots\times n_{ikL_k}!}}\prod^{L_k}_{l=1} \bigl[\mathrm{Pr}(C_{kl}|\boldsymbol{\theta}_i) \bigr]^{n_{ikl}} \Biggr\} . $$

(5)

The latent-trait approach relies on Bayesian hierarchical modeling that allows the individual model parameters θ _ip to vary over participants in a statistically specified way. The method postulates a multivariate normal distribution to capture the between-participant variability and the correlations between the model parameters. The latent-trait approach relies on MCMC sampling to approximate the posterior distributions of the model parameters. In what follows, we present an easy-to-use WinBUGS implementation of the latent-trait approach that enables researchers to obtain samples from the posterior distribution of the model parameters.

3.2 WinBUGS Implementation of the Latent-Trait Pair-Clustering Model

The graphical model for the WinBUGS implementation of the latent-trait pair-clustering model is shown in Figure 2. Observed variables are represented by shaded nodes and unobserved variables are represented by unshaded nodes. Continuous variables are represented by circles and discrete variables are represented by squares. The graph structure indicates dependencies between the nodes and the plates represent independent replications (e.g., Lee 2008). The graphical model depicts the basic pair-clustering model for I participants responding to J ₁ word pairs and J ₂ singletons, with the constraint that a=u. The corresponding WinBUGS script is available as supplemental material at http://dora.erbe-matzke.com/publications.html and https://www.dropbox.com/sh/stgt80dkegskdfk/3KvGGJ6Th7/MPT_OnlineAppendix.zip.

Figure 2.

Graphical model for the latent-trait pair-clustering model. θ _i1=c _i , θ _i2=r _i , and θ _i3=u _i . Note. To maintain consistency with the WinBUGS syntax, the multivariate normal and independent normal distributions are parametrized in terms of the precision (i.e., inverse variance).

Data

For each participant, the data for word pairs, n _i1, follow a multinomial distribution, with category probabilities Pr(C ₁₁|θ _i ), Pr(C ₁₂|θ _i ), Pr(C ₁₃|θ _i ), Pr(C ₁₄|θ _i ), and J ₁. For each participant, the data for singletons, n _i2, follow a multinomial distribution with Pr(C ₂₁|θ _i ), Pr(C ₂₂|θ _i ), and J ₂.

Prior Distributions

The basic model depicted in Figure 2 assumes three parameters per participant (P=3): θ _i =(c _i ,r _i ,u _i ). Thus, we assume that a _i =u _i . The individual model parameters θ _ip are transformed from the probability scale to the real line using a probit link so that the transformed parameters $\theta_{ip}^{\mathrm{prt}}$ are given by Φ ⁻¹(θ _ip ), where Φ is the standard normal cumulative distribution function. The use of probit transformed probabilities has a long history in psychometrics, and is also common practice in Bayesian cognitive modeling (e.g., Rouder & Lu 2005; Rouder et al. 2007, 2008). To model participant heterogeneity and parameter correlations, we assume that the probit transformed parameters $\boldsymbol{\theta}^{\mathrm{prt}}_{i}$ follow a multivariate normal distribution with mean μ and variance–covariance matrix S _part. The $\theta ^{\mathrm{prt}}_{ip}$ parameters are reparametrized as follows:

$$ \theta^{\mathrm{prt}}_{ip} = \mu_p + \delta_{\mathrm{part}_{ip}}, $$

(6)

where μ _p is the group mean for parameter p and $\delta _{\mathrm{part}_{ip}}$ is the ith participant’s deviation from it. The $\boldsymbol{\delta}_{\mathrm{part}_{i}}$ parameters are then drawn from a zero-centered multivariate distribution with variance–covariance matrix S _part.

Hyper-Prior Distributions

The population-level μ and S _part parameters are estimated from the data and therefore require prior distributions. The priors for the μ _p parameters are independent normal distributions with $\mu_{\mu_{p}} = 0$ and $\sigma^{2}_{\mu_{p}} = 1$. Note that the original formulation of the latent-trait approach (Klauer 2010) assumes independent normal distributions with $\mu_{\mu_{p}} = 0$ and $\sigma^{2}_{\mu_{p}} = 100$. However, we prefer to use $\sigma ^{2}_{\mu_{p}} = 1$ because it corresponds to a uniform distribution on the probability scale (Rouder & Lu 2005).

The prior for the variance–covariance matrix S _part is a scaled Inverse-Wishart distribution. The Inverse-Wishart is a frequently used prior for variance–covariance matrices (Gelman & Hill 2007). The Inverse-Wishart prior has two parameters: the degrees of freedom that is set to one plus the number of free participant parameters (1+P) and the scale matrix that is set to the P×P identity matrix (W). The advantage of the Inverse-Wishart is that it results in an uninformative uniform prior distribution between −1 and 1 for the ρ _pp′ correlation parameters. The disadvantage is that the Inverse-Wishart with 1+P degrees of freedom imposes a very restrictive prior on the standard deviations. To be able to estimate the standard deviations more freely, we augment the Inverse-Wishart with a set of scale parameters, $\boldsymbol{\xi}_{\mathrm{part}} = [\xi_{\mathrm{part}_{1}},\ldots,\xi_{\mathrm{part}_{P}}]$ (Gelman & Hill 2007). The resulting scaled Inverse-Wishart distribution still implies a uniform prior distribution for the correlation parameters, but it allows the standard deviations to be estimated more freely than does the Inverse-Wishart. The variance–covariance matrix S _part is then modeled as

$$ \mathbf{S}_{\mathrm{part}} = \mathrm{Diag}(\boldsymbol{ \xi}_{\mathrm{part}}) \mathbf{T}_{\mathrm{part}} \mathrm{Diag}(\boldsymbol{ \xi}_{\mathrm{part}}), $$

(7)

where Diag(ξ) is a diagonal matrix containing the scale parameters. T _part follows an Inverse-Wishart distribution with 1+3 degrees of freedom, with a scale matrix that is set to the 3×3 identity matrix. The standard deviations can be obtained by

$$ \sigma_{\mathrm{part}_p} = |\xi_{\mathrm{part}_p}| \times\sqrt{T_{\mathrm{part}_{pp}}}. $$

(8)

The correlation parameters are given by

$$ \rho_{\mathrm{part}_{pp'}} = \frac{\xi_{\mathrm{part}_p} \xi _{\mathrm{part}_{p'}}T_{\mathrm{part}_{pp'}}}{|\xi_{\mathrm{part}_p}| \sqrt{T_{\mathrm{part}_{pp}}}\times |\xi_{\mathrm{part}_{p'}}| \sqrt{T_{\mathrm{part}_{p'p'}}}}. $$

(9)

The $\xi_{\mathrm{part}_{p}}$ parameters are given uniform distributions ranging from 0 to 100 (e.g., Gelman & Hill 2007). Klauer (2010) used normal distributions with a mean of one and a variance of 100 as prior for the scaling parameters. In our WinBUGS implementation, these priors occasionally resulted in convergence problems for the variance and the correlation parameters. Note that the use of redundant multiplicative parameters, such as $\xi_{\mathrm{part}_{p}}$, has been reported to increase the rate of convergence in hierarchical models (Gelman & Hill 2007). As a result of the new parametrization, Equation (6) can be reformulated as follows:

$$ \theta^{\mathrm{prt}}_{ip} = \mu_p + \xi_{\mathrm{part}_p} \times\delta^{\mathrm{raw}}_{\mathrm{part}_{ip}}, $$

(10)

where μ _p is the group mean for parameter p, $\xi_{\mathrm{part}_{p}}$ is the scaling factor of the scaled Inverse-Wishart distribution, and $\delta^{\mathrm{raw}}_{\mathrm{part}_{ip}}$ is the ith participant’s unscaled deviation from the group mean.

3.3 Parameter Recovery Study

We conducted a series of parameter recovery studies to assess whether the WinBUGS implementation of the latent-trait pair-clustering model adequately recovers true parameter values. Here we report the results of a study where we generated free recall data for synthetic participants responding to a set of word pairs and singletons in two sessions of the pair-clustering task. The resulting data sets were fit with the latent-trait pair-clustering model using WinBUGS.

Methods

Each synthetic participant performed the pair-clustering task two consecutive times. For each participant, the data from the two sessions were scored into four category systems: word pairs and singletons for the first session and word pairs and singletons for the second session. We ran three sets of simulations, each comprising 100 data sets. First, each data set contained observations from 63 (I=63) synthetic participants, responding to 10 word pairs (J ₁=10) and 5 singletons (J ₂=5) in each of the two sessions. Second, each data set contained observations from 63 participants, responding to 20 word pairs and 10 singletons in each of the two sessions. Third, each data set contained observations from 126 participants, responding to 10 word pairs and 5 singletons in each of the two sessions.

Similar to Klauer’s (2010) recovery study, we used five parameters (P=5) per participant across the two sessions: $\boldsymbol{\theta}_{i} = (c_{1_{i}}, r_{i}, u_{1_{i}}, c_{2_{i}},u_{2_{i}})$. The following parameter constraints were imposed: $r_{1_{i}} = r_{2_{i}}$, $a_{1_{i}} = u_{1_{i}}$, and $a_{2_{i}} = u_{2_{i}}$. The generating population-level parameter values are shown in Figure 3. We conducted several recovery studies using alternative true parameter values. The results were essentially the same as the ones reported here. Note that the details of the recovery study, including the true parameter values and the number of participants and items, are identical to those used in Klauer’s paper.

Figure 3.

Posterior medians from the parameter recovery study for the latent-trait pair-clustering model using WinBUGS. Each set of simulations consisted of 100 data sets. The black bullets indicate the mean of the posterior median of the parameters across the 100 replications. The black vertical lines are based on the mean of the posterior standard deviation across the 100 replications. The gray vertical lines indicate the standard error of the posterior median across the 100 replications.

For each analysis reported in this article, we ran three MCMC chains and used randomly generated overdispersed starting values to confirm that the chains have converged to the stationary distribution. Convergence is confirmed if the individual chains are indistinguishable from each other. Convergence was formally assessed with the $\hat{R}$ statistic (Brooks & Gelman 1998; Gelman & Rubin 1992), a quantitative measure of convergence that compares the within-chain variance to the between-chain variance. The results reported in this article are based on analyses where $\hat{R}$ for all parameters of interest (i.e., group means, random effects, and the standard deviation and the correlation of the random effects) is lower than 1.05. In light of the possibility of high autocorrelations between successive MCMC samples, we ran relatively long MCMC chains and thinned each chain by retaining samples from only every third iteration.

The latent-trait pair-clustering model was fit to the synthetic data sets using WinBUGS. For each data set, we discarded the first 2,000 samples of each chain as burn-in and based inference on a total of 54,000 recorded samples.

Results

The results of the recovery study for the group-level parameters are shown in Figure 3. We follow Klauer’s (2010) practice and use the median and the standard deviation to summarize the posterior distribution of the parameters. Also, the posterior median is often preferable over the posterior mode or the posterior mean for non-symmetric or heavy tailed posterior distributions. Note that the group c ₁, r, u ₁, c ₂, and u ₂ parameters are reported on the probability scale, while their standard deviations and correlations are reported on the probit scale. The group parameters and their standard deviations are recovered relatively well using the posterior median even for the first set of simulations with relatively few participants and very few items. Naturally, as the number of items or the number of participants increases, the bias, the posterior standard deviation, and the standard error of the recovered parameters decrease. The storage-retrieval u ₁ and u ₂ parameters and their standard deviations are estimated most precisely, as indicated by the small posterior standard deviation of the estimates. The cluster-retrieval r parameter and its standard deviation are estimated the least precisely as evidenced by the greater posterior uncertainty of the estimates, especially for the first set of simulations.

With respect to the correlation parameters, the results are less clear-cut. Similar to Klauer’s (2010) findings, the posterior median underestimates the parameter correlations especially in data sets with few participants and items. The posterior standard deviations are rather large, indicating large uncertainty in the estimates. Nevertheless, as the number of participants or the number of items increases, the bias, the posterior standard deviations and the standard error of the recovered correlations decrease. As for the standard deviations, correlations involving the cluster-retrieval r parameter are the least well estimated, especially for the first set of simulations.

To sum up, the results of the simulation study indicated that the WinBUGS version of the latent-trait pair-clustering model adequately recovered the true parameter values. In the next section, we extend the latent-trait pair-clustering model and the corresponding WinBUGS script to handle heterogeneity in both participants and items.

4 The Crossed-Random Effects Pair-Clustering Model

In many applications of MPT models, it is reasonable to assume that the model parameters do not only differ between participants but also between the items used in a particular experiment. We should then treat both participant and items effects as random, define parameters for each participant-item combination and base statistical inference on the unaggregated data. This section introduces a crossed-random effects pair-clustering model that is based on an extension of Klauer’s (2010) latent-trait approach. Our crossed-random effects model assumes that the participant and item effects combine additively on the probit scale. The participant and item effects are modeled with multivariate normal and independent normal distributions, respectively, with means and (co)variances estimated from the data.

4.1 Introduction to the Crossed-Random Effects Approach

In the crossed-random effects pair-clustering model, statistical inference is based on unaggregated participant-by-item data. In a given category system k, k=1,2, the raw category responses of each participant-item combination, i=1,…,I, j=1,…,J _k , are assumed to follow a multinomial distribution with category probabilities $\mathrm{Pr}(C_{kl}|\boldsymbol{\theta}_{ij_{k}})$, l=1,…,L _k , where $\boldsymbol{\theta}_{ij_{k}}$ contains the p=1,…,P _k model parameters of participant-item combination ij in category system k.

The requirement of a separate parameter for each participant-item combination leads to a very large number of parameters, resulting in problems of model identification. To reduce the number of parameters, we assume that the probit transformed parameters are given by the additive combination of participant and item effects (e.g., Rouder & Lu 2005; Rouder et al. 2007, 2008). More formally, the crossed-random effects pair-clustering model assumes that the probit transformed participant-item parameters in category system k are given by

$$ \theta_{ijp_k}^{\mathrm{prt}} = \mu_{p_k} + \delta_{{\mathrm{part}}_{ip_k}} + \delta_{{\mathrm{item}}_{jp_k}}, $$

(11)

where $\mu_{p_{k}}$ is the group mean for parameter p in category system k, and $\delta_{{\mathrm{part}}_{ip_{k}}}$ and $\delta_{{\mathrm{item}}_{jp_{k}}}$ are the ith participant effect and the jth item effect, respectively. We postulate a multivariate normal distribution to describe variability between participants and independent normal distributions to capture the variability between items. The participant effects are thus allowed to be correlated a priori, whereas the item effect are not. Naturally, we may model the correlations between the item effects—similar to the participant effects—using a multivariate normal distribution. The possibility to incorporate correlated participant and correlated item effects will be demonstrated shortly using experimental data. The next section presents an easy-to-use WinBUGS implementation of the crossed-random effects pair-clustering model.

4.2 WinBUGS Implementation of the Crossed-Random Effects Pair-Clustering Model

The graphical model for the WinBUGS implementation of the crossed-random effect pair-clustering model is shown in Figure 4. The graphical model depicts the basic pair-clustering model for I participants responding to J ₁ word pairs and J ₂ singletons. The corresponding WinBUGS script is available as supplemental material.

Figure 4.

Graphical model for the crossed-random effects pair-clustering model. θ _ij1=c _ij , θ _ij2=r _ij , θ _ij3=u _ij . Note. To maintain consistency with the WinBUGS syntax, the multivariate normal and independent normal distributions are parametrized in terms of the precision (i.e., inverse variance).

4.2.1 Data

The raw data of each participant-word pair combination, n _ij,1, follow a multinomial distribution, with category probabilities $\mathrm{Pr}(C_{11}|\boldsymbol{\theta}_{ij_{1}})$, $\mathrm{Pr}(C_{12}|\boldsymbol{\theta}_{ij_{1}})$, $\mathrm{Pr}(C_{13}|\boldsymbol{\theta}_{ij_{1}})$, $\mathrm{Pr}(C_{14}|\boldsymbol{\theta}_{ij_{1}})$. Similarly, the raw data for each participant-singleton combination, n _ij,2, follow a multinomial distribution, with category probabilities $\mathrm{Pr}(C_{21}|\boldsymbol{\theta}_{ij_{2}})$, $\mathrm{Pr}(C_{22}|\boldsymbol{\theta}_{ij_{2}})$.

4.2.2 Prior Distributions

The crossed-random effects pair-clustering model posits a separate parameter for each participant-item combination in each category system k. These $\theta_{ijp_{k}}$ parameters are transformed from the probability scale to the real line using the probit link. As given in Equation (11), the probit transformed parameters $\theta_{ijp_{k}}^{\mathrm{prt}}$ are given by the additive combination of participant and item effects.

In the category system for word pairs, the model assumes three participant effects for each participant (i.e., $\delta_{{\mathrm{part}}_{ic}}$, $\delta_{{\mathrm{part}}_{ir}}$, and $\delta_{{\mathrm{part}}_{iu}}$) and three item effects for each word pair (i.e., $\delta_{{\mathrm{item}}_{jc}}$, $\delta _{{\mathrm{item}}_{jr}}$, and $\delta_{{\mathrm{item}}_{ju}}$). The model postulates thus three parameters for each participant-word pair combination (P ₁=3): $\boldsymbol{\theta}_{{ij}_{1}} = (c_{ij}, r_{ij}, u_{ij})$. For singletons, the model assumes one participant effect per participant ($\delta_{{\mathrm{part}}_{ia}}$) and one item effect per singleton ($\delta _{{\mathrm{item}}_{ja}}$). The model postulates thus one parameter for each participant-singleton combination $(P_{2} = 1): \theta_{{ij}_{2}} = a_{ij}$.

In the basic pair-clustering model depicted in Figure 4, the constraint that a=u may be implemented as follows. First, the group mean of the singleton storage-retrieval a parameter is constrained to be equal to the group mean of the storage-retrieval u parameter: μ _a =μ _u . Second, note that the basic model assumes that each participant is presented with J ₁ word pairs and J ₂ singletons. We are thus able to place across-category system constraints on the participant effects, because responses from a given participant are available in both category systems: $\delta_{\mathrm{part}_{ia}} = \delta_{\mathrm{part}_{iu}}$. Third, we are unable to place across-category system constraints on the items effects because a given item appears in only one of the category systems: responses to each of the J ₁ word pairs are only available in the first category system, whereas responses to each of the J ₂ singletons are only available in the second category system. Nevertheless, we may assume that the standard deviation of the item effects relating to a and u are equal: $\sigma_{{\mathrm{item}}_{a}} = \sigma _{{\mathrm{item}}_{u}}$. A possibility for across-category system constraints on the item effects will be illustrated shortly using experimental data.

The $\boldsymbol{\delta}_{{\mathrm{part}}_{i}}$ parameters are assumed to come from a zero-centered multivariate normal distribution, with variance–covariance matrix S _part estimated from the data. The $\delta_{{\mathrm{item}}_{jp_{k}}}$ parameters are drawn from zero-centered independent normal distributions, with the standards deviations $\sigma_{{\mathrm{item}_{p}}_{k}}$ estimated from the data.

4.2.3 Hyper-Prior Distributions

The priors for the grand mean $\mu_{p_{k}}$ parameters are weakly informative independent normal distributions with $\mu_{\mu_{p_{k}}} = 0$ and $\sigma^{2}_{\mu_{p_{k}}} = 1$. The prior for S _part is a scaled Inverse-Wishart distribution. The degrees of freedom of the scaled Inverse-Wishart equals one plus the number of free participant effects. In the model shown in Figure 4, we postulate three participant effects across the two category systems, resulting in four degrees of freedom. The scale matrix is set to the 3×3 identity matrix (W). The scaling factor ξ _part parameters of the Inverse-Wishart are given uniform distributions ranging from 0 to 100. The standard deviations and the correlations of the participant effects can be obtained using Equation (8) and (9), respectively.

The priors for the $\sigma^{2}_{{\mathrm{item}}_{p_{k}}}$ variance parameters are independent scaled inverse gamma distributions with α=1 and β=1. The inverse gamma distribution with α and β set to low values, such as 1, 0.01, or 0.001 is a frequently used prior for variance parameters (e.g., Spiegelhalter, Thomas, Best, Gilks, & Lunn, 2003). In order to increase the rate of convergence, we augment each variance parameter with a redundant multiplicative scaling parameter ξ _item, a technique called parameter expansion (Gelman & Hill 2007). In the expanded model, the item standard deviations are given by

$$ \sigma_{{\mathrm{item}}_{p_k}} = |\xi_{{\mathrm{item}}_{p_k}}| \times\lambda_{{\mathrm{item}}_{p_k}}, $$

(12)

where $\xi_{{\mathrm{item}}_{p_{k}}}$ is the scaling factor and $\lambda _{{\mathrm{item}}_{p_{k}}}$ is the unscaled item standard deviation for parameter p in category system k. The ξ _item parameters are given uniform distributions ranging from 0 to 100. As a result of expanding the model with the ξ _part and ξ _item parameters, Equation (11), can be reformulated as follows:

$$ \theta^{\mathrm{prt}}_{ijp_k} = \mu_{p_k} + \xi_{{\mathrm{part}}_{p_k}} \times\delta ^{\mathrm{raw}}_{{\mathrm{part}}_{ip_k}} + \xi_{{\mathrm{item}}_{p_k}}\times\delta ^{\mathrm{raw}}_{{\mathrm{item}}_{jp_k}} , $$

(13)

where $\delta^{\mathrm{raw}}_{{\mathrm{part}}_{{ip}_{k}}}$ and $\delta ^{\mathrm{raw}}_{{\mathrm{item}}_{{jp}_{k}}}$ are the unscaled effects for participant i and item j relating to parameter p in category system k, respectively.

4.3 Parameter Recovery Study

We conducted a series of parameter recovery studies to examine whether the crossed-random effects pair-clustering model adequately recovers true parameter values. Here we report the results of a study where we generated free recall data for synthetic participants responding to the same set of word pairs and the same set of singletons in two sessions of the pair-clustering task. We analyzed the resulting data sets with the crossed-random effects pair-clustering model using WinBUGS.

Methods

Each synthetic participant performed the pair-clustering task two consecutive times using the same set of word pairs and the same set of singletons. For each participant-word pair combination, the data from the two sessions were scored into two separate category systems. Similarly, for each participant-singleton combination, the data from the two sessions were scored into two separate category systems. We conducted three sets of simulations, each comprising 100 synthetic data sets. First, each data set contained observations from 63 (I=63) synthetic participants, responding to the same set of 10 word pairs (J ₁=10) and the same set of 5 singletons (J ₂=5) in each of the two sessions. Second, each data set contained observations from 63 participants, responding to 20 word pairs and 10 singletons in each of the two sessions. Third, each data set contained observations from 126 participants, responding to 10 word pairs and 5 singletons in each of the two sessions. We used five (P ₁=5) parameters for each participant-word pair combination: $\boldsymbol{\theta}_{{ij}_{1}} = (c_{1,ij}, r_{ij}, u_{1,ij}, c_{2,ij}, u_{2,ij})$. The cluster-retrieval r parameter was thus constrained to be equal across the two sessions, r _1,ij =r _2,ij =r _ij . We used two (P ₂=2) parameters for each participant-singleton combination: $\boldsymbol{\theta}_{{ij}_{2}} = (a_{1,ij}, a_{2,ij})$.

As the same set of word pairs and singletons were used across the two sessions, the J ₁ items effects relating to c, r, and u, and the J ₂ item effects relating to a were assumed to be equal across the two sessions. We followed the approach described earlier to implement the constraint that a=u. The generating parameter values for the population-level parameters are shown in Figure 5.

Figure 5.

Posterior medians from the parameter recovery study for the crossed-random effects pair-clustering model using WinBUGS. Each set of simulations consisted of 100 data sets. The black bullets indicate the mean of the posterior median of the parameters across the 100 replications. The black vertical lines are based on the mean of the posterior standard deviation across the 100 replications. The gray vertical lines indicate standard error of the posterior median across the 100 replications.

The crossed-random effects pair-clustering model was fit to the synthetic data sets using WinBUGS. As before, we monitored samples from every third iteration, we discarded the first 2,000 samples of each chain as burn-in, and based inference on a total of 54,000 recorded samples.

Results

The results of the recovery study for the group-level model parameters are shown in Figure 5. As before, the group c ₁, r, u ₁, c ₂, and u ₂ parameters are reported on the probability scale, while the standard deviations and the correlations are reported on the probit scale. The group parameters and the participant and item effect standard deviations are approximated well using the posterior median even for the first set of simulations with relatively few participants and very few items. Again, the storage-retrieval u ₁ and u ₂ parameters and the corresponding standard deviations are estimated most precisely and the cluster-retrieval r parameter and the corresponding standard deviations are estimated least precisely. As the number of items or the number of participants increases, the bias, the posterior standard deviation, and the standard error of the recovered parameters decrease.

With respect to the participant effect correlations, the results are again less straightforward. The posterior median underestimates the parameter correlations, especially in the first set of simulations with relatively few participants and very few items. The posterior standard deviations are quite large, suggesting large uncertainty in the estimates. Naturally, increasing the number of participants or the number of items decreases the bias, the posterior standard deviation, and the standard error of the recovered correlations. Again, correlations involving the cluster-retrieval r parameter are the least well estimated.

To sum up, the results of the simulation study indicated that the WinBUGS implementation of the crossed-random effects pair-clustering model adequately recovered the true parameter values. In the next section, we apply the model to novel experimental data and illustrate the possibility to incorporate correlated participant as well as correlated item effects.

4.4 Fitting Real Data: A Pair-Clustering Experiment on Word Frequency

In order to illustrate the use of the crossed-random effects pair-clustering model and the possibility to incorporate correlated participant as well as correlated item effects, we applied the model to novel experimental data that featured orthographically related word pairs and the manipulation of word frequency. A common finding in memory research is that free recall performance is better for pure lists of high frequency (HF) words than for pure lists of low frequency (LF) words (e.g., Deese 1960; Hall 1954; Postman 1970; Sumby 1963). For mixed lists of both HF and LF words, however, the HF advantage is often eliminated (e.g., DeLosh & McDaniel 1996; Duncan 1974; Gregg 1976). Models of free recall performance typically explain this pure list–mixed list word frequency paradox in terms of differences in the relative contribution of order/relational processing and item specific processing (e.g., DeLosh & McDaniel 1996; Merritt, DeLosh, & McDaniel, 2006). The word frequency effect has never been investigated using the pair-clustering paradigm. The goal of the present experiment was therefore to demonstrate the word frequency effect in pair-clustering and to use the crossed-random effects approach to explore the changes in cognitive processes that underlie the pure list–mixed list paradox. Moreover, contrary to previous applications of the pair-clustering paradigm, we employed orthographically related word pairs in order to examine orthographic clustering effects in free recall.

Methods

All 70 participants were undergraduate psychology students from the University of Amsterdam. Five participants did not comply with the instructions and the requirements of the experiment (e.g., making notes of the presented words, not being native speaker of Dutch, answering a mobile phone during the experimental session) and were excluded from all subsequent analyses. The remaining 65 participants (44 females) were native Dutch speakers, with a mean age of 22 years. Participation was rewarded either with course credits or with 7 euro.

The experimental stimulus pool consisted of 45 HF and 45 LF word pairs. The stimuli are available as supplemental material. The HF words had a mean occurrence of 185.03 per million and the LF words had a mean occurrence of 2.51 per million. Word length varied between 3 and 7 letters, with a mean length of 4.27 and 4.36 for HF and LF words, respectively. The word pairs were orthographically related Dutch nouns, where the two members of each word pair differed only in terms of one consonant (e.g., book–cook and house–mouse). Each word was orthographically similar only to its pair and orthographically dissimilar to all other words in the stimulus pool.

Each participant was presented with six experimental lists: two lists consisting of 10 HF word pairs and 5 HF singletons (i.e., pure HF lists), two lists consisting of 10 LF word pairs and 5 LF singletons (i.e., pure LF lists), one list consisting of 5 HF and 5 LF word pairs and 3 HF and 2 LF singletons, and one list consisting of 5 HF and 5 LF word pairs and 2 HF and 3 LF singletons (i.e., mixed lists). The study words were randomized across participants. For each participant, 30 HF and 30 LF word pairs were randomly assigned to the different experimental lists. The remaining 15 HF and 15 LF pairs were used to create singletons by randomly selecting one of the two members of each word pair. The 15 HF and 15 LF singletons were then randomly assigned to the different experimental lists. Word pairs and singletons were randomly intermixed within each list, with the constraint that the lag between the presentation of the two members of a given word pair was at least two and at most five words. The order of list presentation was randomized across participants.

Apart from the experimental stimulus items, each list contained 6 primacy buffer items at the beginning and 6 recency buffer items at the end of the list. The buffer items were orthographically dissimilar to each other and to the experimental stimuli. The pure HF lists contained only HF buffers, the pure LF lists contained only LF buffers, and the mixed lists contained six HF and six LF buffers that were randomly assigned to the 12 buffer positions. In total, each experimental list consisted of 37 words: 12 buffer items, 10 word pairs and 5 singletons.

The presentation of the six experimental lists was preceded by a practice test session. The mixed frequency practice list consisted of 10 orthographically related word pairs, 5 singletons, and 12 buffer items. Words in the practice list were orthographically dissimilar to words in the experimental lists.

Testing took place in small groups of maximum eight participants using personal computers. At the beginning of the testing session, participants read the instructions and signed the informed consent. The instructions emphasized the orthographic similarity of the words to encourage participants to cluster related word pairs. After the practice session, participants were presented with the six experimental lists. Words were presented one at a time on the computer screen at a rate of 4 sec/word. After the presentation of each list, participants were instructed to recall and type in the words without paying attention the their presentation order. After each 3 minute recall period, participants were given a 1 minute break during which they played the popular computer game Tetris.

Behavioral Results

Buffer items were excluded from all subsequent analyses. Data were collapsed per list type (pure vs. mixed) and word frequency (HF vs. LF), resulting in the following four conditions: (1) one pure HF condition consisting of 20 HF word pairs and 10 HF singletons originally presented in the two pure HF lists, (2) one pure LF condition consisting of 20 LF word pairs and 10 LF singletons originally presented in the two pure LF lists, (3) one mixed HF condition consisting of 10 HF word pairs and 5 HF singletons originally presented in the two mixed lists, and (4) one mixed LF condition consisting of 10 LF word pairs and 5 LF singletons originally presented in the two mixed lists. The data are available as supplemental material.

As shown in the upper left panel of Figure 6, the free recall data demonstrated the typical pure list–mixed list word frequency paradox. Recall performance was better for the pure HF condition than for the pure LF condition; however, in the mixed condition the HF advantage was largely eliminated. We formally assessed the word frequency × list type interaction using Bayesian null-hypothesis testing (Masson 2011; Raftery 1995; Wagenmakers 2007). Specifically, we used the Bayesian information criterion (BIC) approximation to the Bayes factor (e.g., Raftery 1999) to compute the posterior probabilities of the null (H ₀) and the alternative hypotheses (H _A ). We assumed that the H ₀ and the H _A are equally likely a priori, i.e., P(H ₀)/P(H _A )=1. The resulting posterior probability of 0.89 for the alternative hypothesis, P _BIC(H _A |Data), provides positive evidence for the presence of the word frequency × list type interaction (e.g., Raftery 1995).

Figure 6.

Mean proportion of correct recall across participants and posterior medians for the group-level c, r, and u parameters for each condition of the word frequency experiment. CR=crossed-random effects. For the recall proportions, the vertical lines show the standard errors. For the model parameters, the black circles and triangles show the posterior median of the group-level parameters from the crossed-random effects analysis of the pure and the mixed list, respectively. The black vertical lines indicate the size of the posterior standard deviation of the group-level parameters. The gray circles and triangles show parameter estimates from the aggregate analysis of the pure and the mixed list, respectively.

4.4.1 Model Fitting

Each participant i=1,…,65 was presented with each HF stimulus pair j=1,…,J _HF=45 either in the HF pure or in the HF mixed condition. A given participant therefore observed a specific HF stimulus pair either as a word pair or as a singleton, and either in the pure or in the mixed condition. Similarly, each participant was presented with each LF stimulus pair j=1,…,J _LF=45 either in the LF pure or the LF mixed condition. A given participant therefore observed a specific LF stimulus pair either as a word pair or as a singleton, and either in the pure or in the mixed condition. However, the additive structure of the model parameters enables us to estimate parameters for each participant-stimulus pair combination c _ij , r _ij , u _ij , a _ij for each of the four conditions.

The key group-level c, r and u parameters were free to vary across the four conditions. We imposed the following parameter constraints. Note that the constraints were chosen purely on the basis of inspection of the unconstrained parameter estimates. Formal model selection for MPT models using Bayes factors (e.g., Kass & Raftery 1995) is beyond the scope of this article. The present analysis merely serves as an illustration of parameter estimation in the crossed-random effects pair-clustering model. First, as information on each participant and each stimulus pair was available in both category systems, we were able to place across–category system constraints on the participant as well as the item effects, resulting in a _ij =u _ij for each participant-stimulus pair combination in each condition. Second, we constrained the participant effects relating to the cluster-retrieval r parameter $\delta_{\mathrm{part}_{i_{r}}}$ to be equal across the four conditions. Lastly, we assumed that the item effects $\delta_{\mathrm{item}_{j}}$ for c, r, and u are the same regardless whether the stimulus pair is shown in the pure condition or in the mixed condition. To illustrate the possibility to incorporate correlated participant as well as correlated item effects, we modeled both types of random effects—$\boldsymbol{\delta}_{{\mathrm{part}}_{i}}$, and $\boldsymbol{\delta}_{{\mathrm{itemHF}}_{j}}$ and $\boldsymbol{\delta}_{{\mathrm{itemLF}}_{j}}$—using multivariate normal distributions, with variance–covariance matrices estimated from the data.

The crossed-random effects model was fit to the data set using WinBUGS. We monitored samples from every third iteration, we discarded the first 8,000 samples of each chain as burn-in, and based inference on a total of 72,000 recorded samples. Examples of thinned and un-thinned MCMC chains are available as supplemental material.

The posterior medians and the posterior standard deviations of the estimated group parameters c, r, and u for each condition are shown in Figure 6. Both the cluster-storage c and the cluster-retrieval r parameters indicate that participants indeed stored and retrieved orthographically similar words in clusters. The value of the cluster-retrieval r parameter is within the range of values typically encountered in the pair-clustering paradigm. The cluster-storage c parameter is somewhat lower than in typical applications using semantically related word pairs (e.g., Riefer et al. 2002). Nevertheless, these results indicate that, in the present experiment, orthographic relatedness fostered clustered storage and clustered retrieval.

Figure 6 also shows that the group parameters are estimated relatively well as indicated by the reasonable posterior standard deviations. Because the pure conditions featured twice as many items as each of the two mixed conditions, the group parameters are estimated slightly better in the HF and LF pure conditions than in the HF and LF mixed conditions. Note also that the cluster-retrieval r parameter is estimated less precisely than the cluster-storage c and storage-retrieval u parameters. This result is not surprising because the response categories involving the cluster-retrieval r parameter (i.e., C ₁₁) are reached infrequently due to the relatively low value of the cluster-storage c parameter. The cluster-retrieval r parameter is therefore less well constrained by the data than the other group parameters.

To explore the effects of the experimental manipulations on the model parameters, we computed Bayesian p values for the c, r, and u parameters in the HF pure vs. LF pure and the HF mixed vs. LF mixed comparisons. Specifically, for each parameter, we computed the proportion of posterior samples where μ _HF is smaller (or larger) than μ _LF (see also Klauer 2010). The storage-retrieval u parameter mirrors the behavioral results and demonstrates the typical word frequency paradox (p<0.01 for $\mu_{u_{\mathrm{HFP}}} < \mu _{u_{\mathrm{LFP}}}$ and p=0.04 for $\mu_{u_{\mathrm{HFM}}} < \mu_{u_{\mathrm{LFM}}}$). This result is to be expected because the u parameter quantifies the joint probability of the storage and retrieval of unclustered words. In contrast, the posterior medians of the c and r parameters show an entirely different pattern for the word frequency × list type interaction. With respect to the cluster-storage parameter, c is lower in the pure HF condition than in the pure LF conditions and does not differ between the mixed HF and mixed LF conditions (p=0.04 for $\mu_{c_{\mathrm{LFP}}} < \mu_{c_{\mathrm{HFP}}}$ and p=0.39 for $\mu_{c_{\mathrm{LFM}}} < \mu_{c_{\mathrm{HFM}}}$). Lastly, with respect to the cluster-retrieval parameter, r does not seem to differ between the pure LF and pure HF conditions, but it appears to be lower in the mixed HF condition than in the mixed LF condition (p=0.68 for $\mu _{r_{\mathrm{LFP}}} < \mu_{r_{\mathrm{HFP}}}$ and p=0.36 for $\mu_{r_{\mathrm{LFM}}} < \mu _{r_{\mathrm{HFM}}}$). Note, however, that the Bayesian p value for the LF mixed vs. HF mixed comparison is not convincing; the posterior distribution of the $\mu_{r_{\mathrm{LFM}}}$ and $\mu_{r_{\mathrm{HFM}}}$ parameters overlap considerably as a result of the larger posterior uncertainty in estimating the r parameter (see bottom left panel in Figure 6).

We also assessed the effects of the experimental manipulations on the model parameters without taking into account the uncertainty of the parameter estimates. For each parameter, we computed the P _BIC(H _A |Data) for the word frequency × list type interactions shown in Figure 6 using the posterior median of the participant parameters (i.e., $\mu+ \delta_{{\mathrm{part}}_{i}}$). For all three parameters c, r, and u, we obtained P _BIC(H _A |Data)>0.99, a result that provides very strong evidence for the presence of the word frequency × list type interaction.

The model-based analysis uncovered a number of interesting phenomena that were not apparent in the behavioral results. First, in the pure condition, participants are slightly more likely to cluster LF than HF word pairs, suggesting that orthographic similarity is more readily apparent for LF words than for HF words. Alternatively, participants may strategically compensate for the difficulty of encoding LF words in the pure condition by paying more attention to their orthographic similarity. Second, in the mixed condition, participants are more likely to recall clustered LF word pairs than clustered HF word pairs. This result suggests that once intra–word associations are created, LF word pairs in the mixed condition are easier to recall, possibly as a result of their distinctiveness in a mixed list environment.

For comparison, we aggregated the word frequency data across participants and items and computed maximum likelihood parameter estimates using the closed form expressions presented in Batchelder and Riefer (1986). The aggregate results are presented in Figure 6 using the solid and dashed gray lines. Similar to the crossed-random effects analysis, the u parameter from the aggregate analysis mirrored the word frequency paradox apparent in the behavioral data. In contrast, the c and r parameters from the aggregate analysis did not reproduce the pattern of the word frequency × list type interaction from the crossed-random effects analysis.

The posterior distributions of the participant and item standard deviations are shown in Figure 7. The standard deviations are estimated most precisely for the participant and item effects involving the storage-retrieval u parameter. Standard deviations involving the cluster-retrieval r parameters are estimated with the largest posterior uncertainty due to the relatively low value of the cluster-storage c parameter across all conditions. Evidence for heterogeneity in participants is convincing for all participant standard deviations, with the exception of $\sigma _{{{\mathrm{part}}_{c}}_{\mathrm{LFmixed}}}$, a parameter for which the lower bound of the 95 % Bayesian credible interval approaches zero (i.e., 0.02). Heterogeneity in items is evident for all item standard deviations, with the exception of $\sigma_{{{\mathrm{item}}_{c}}_{\mathrm{HF}}}$ and $\sigma _{{{\mathrm{item}}_{r}}_{\mathrm{HF}}}$, with a lower bound of 0.04 and 0.01, respectively.

Figure 7.

Posterior distributions for the participant and item effect standard deviations for the word frequency experiment. The black triangles show the median of the posterior distributions. The horizontal lines indicate the size of the 95 % Bayesian credible intervals.

The posterior medians and standard deviations for the participant and item effect correlations are shown in Table 2. Correlations between the participant effects relating to the storage-retrieval u parameter (i.e., $u_{{\mathrm{part}}_{\mathrm{HFP}}}$, $u_{{\mathrm{part}}_{\mathrm{HFM}}}$, $u_{{\mathrm{part}}_{\mathrm{LFP}}}$, $u_{{\mathrm{part}}_{\mathrm{LFM}}}$) are estimated most precisely as indicated by the small posterior standard deviations. In contrast, correlations involving the participant effect $c_{{\mathrm{part}}_{\mathrm{LFM}}}$ are generally the least well constrained by the data. Participant effects relating to the cluster-storage c parameter are relatively strongly correlated across the different conditions, suggesting that participants who tend to cluster orthographically related word pairs in one condition are likely to cluster also in the other conditions. Similarly, participant effects relating to the storage-retrieval u parameter are highly correlated across the different conditions, indicating that participants who are good at recalling unclustered words in one condition are also expected to perform well in the other conditions. The participant effects $c_{{\mathrm{part}}_{\mathrm{HFP}}}$, $c_{{\mathrm{part}}_{\mathrm{HFM}}}$ and $c_{{\mathrm{part}}_{\mathrm{LFP}}}$ show relatively strong negative correlations with the storage-retrieval u parameter across all conditions. The $c_{{\mathrm{part}}_{\mathrm{LFM}}}$ effect, however, seems to be uncorrelated with u. Participant effects relating to the cluster-storage c parameter are uncorrelated with participant effects for cluster-retrieval r. In contrast, participant effects relating to the storage-retrieval u parameter seem to correlate positively with r.

Table 2. Posterior medians of the correlation parameters in the word frequency experiment.

For HF items, the $c_{{\mathrm{item}}_{\mathrm{HF}}}$ effect is negatively correlated with the cluster-retrieval r parameter and is positively correlated with the storage-retrieval u parameter. The item effects $r_{{\mathrm{item}}_{\mathrm{HF}}}$ and $u_{{\mathrm{item}}_{\mathrm{HF}}}$ seem to be uncorrelated. For LF items, the items effects relating to the three parameters (i.e., $c_{{\mathrm{item}}_{\mathrm{LF}}}$, $r_{{\mathrm{item}}_{\mathrm{LF}}}$, and $u_{{\mathrm{item}}_{\mathrm{LF}}}$) are positively correlated. Note, however, that the correlations between the item effects–especially for HF items– are estimated rather imprecisely, as evidenced by the large posterior standard deviation of the estimates.

Assessing Model Fit

We used posterior predictive model checks (e.g., Gelman & Hill 2007; Gelman, Meng, & Stern, 1996) to examine whether the WinBUGS implementation of the crossed-random effects pair-clustering model with the chosen parameter constraints adequately describes the observed data. In posterior predictive model checks, we assess the adequacy of the model by generating new data (i.e., predictions) using samples from the joint posterior distribution of the estimated parameters. If our implementation of the crossed-random effects pair-clustering model adequately describes the modeled data, the predictions based on the model parameters should closely approximate the observed data.

We formalized the model checks with posterior predictive p values (e.g., Gelman & Hill 2007; Gelman et al. 1996; Klauer 2010). We first defined a test statistic T and for each of d=1,…,1200 draws from the posterior distribution of the parameters, we computed its value for the observed data using the participant-item parameters, $T(\mathrm{data},\boldsymbol{\theta}_{ij}^{d})$. We then generated new pair-clustering data for each draw d from the joint posterior and computed the value of T for each predicted data set, $T(\mathrm{data}^{*,d},\boldsymbol{\theta}_{ij}^{d})$. The posterior predictive p value is given by the fraction of times that $T(\mathrm{data}^{*,d}, \boldsymbol{\theta}_{ij}^{d})$ is larger than $T(\mathrm{data},\boldsymbol{\theta}_{ij}^{d})$. Extreme p values close to 0 (e.g., lower than 0.05) indicate that the model does not describe the observed data adequately.

For each condition of the experiment, we conducted three sets of posterior predictive checks using Klauer’s (2010) test statistics T ₁(data,θ) and T ₂(data,θ), which Klauer proposed to assess the recovery of the mean and the covariance of the observed category frequencies, respectively. First, we examined the recovery of the observed data that are summed over items and averaged over participants using T ₁. Second, we examined the recovery of the covariance structure of the observed data that (1) are summed only across the items and (2) are summed only across the participants using T ₂. Lastly, we examined the recovery of the participant-wise and item-wise frequency counts using T ₁.

Table 3 shows the posterior predictive p values for the recovery of the aggregated category frequencies and the participant and item covariances. Table 4 shows the percentage of participants and items with posterior predictive p values lower than 0.05 for the participant and item-wise analysis. The results indicate that the crossed-random effects pair-clustering model adequately describes the aggregated data and the covariance structure of the observed category frequencies. Although the model fares somewhat better in predicting the observed participant-wise category frequencies, it also provides adequate predictions for the majority of the items.

Table 3. Results of the posterior predictive model checks: Aggregate and covariance structure analysis.

Table 4. Results of the posterior predictive model checks: Participant and item-wise analysis.

Figure 8 shows examples of model fit for the participant and item-wise posterior predictive model checks. Each panel depicts a discrete violin plot (e.g., Hintze & Nelson 1998) for each response category in each category system. Discrete violin plots conveniently combine information available from histograms with information about summary statistics in the form of box plots. The top panels of Figure 8 show examples of satisfactory model fit; the observed category frequencies (i.e., gray triangles) all fall well within the 2.5th and 97.5th percentiles of the posterior predictions. The bottom panels show examples of poor model fit; for most response categories, the observed category frequencies are severely over or underestimated by the posterior predictions.

Figure 8.

Examples of satisfactory (panel a and b) and poor (panel c and d) model fit in the word frequency orthographic clustering experiment The gray triangles indicate the observed data that are summed over the items (panel a and d) or over the participants (panel b and c). The circles indicate the median of the predicted category frequencies over the 1,200 posterior simulations. The black area in each violin plot is a box plot, with the box ranging from the 25th to the 75th percentile of the posterior predictive samples.

In summary, our crossed-random effects pair-clustering model provided reasonable population-level parameter estimates in the word frequency experiment. Posterior predictive model checks indicated that the model resulted in participant-stimulus pair parameter estimates that adequately described the observed data. The storage-retrieval u parameter mimicked the pattern of the behavioral results and demonstrated the typical pure list–mixed list word frequency paradox. The cluster-storage c parameter showed a small clustering advantage for LF word pairs over HF word pairs in the pure condition, possibly as a result of strategy use or the enhanced accessibility of orthographic information for LF words. The cluster-retrieval r parameter showed a recall advantage for clustered LF word pairs over clustered HF word pairs in the mixed condition, possibly as a result of the distinctiveness of LF words in a mixed list environment.

5 Discussion

MPT models are theoretically motivated stochastic models for the analysis of categorical data. Traditionally, statistical analysis for MPT models is carried out on aggregated data, assuming homogeneity in participants and items. If this assumption is violated, the analysis of aggregated data may lead to erroneous conclusions. Fortunately, various methods are now available to incorporate heterogeneity either in participants or in items within MPT models.

Here we focused on Klauer’s (2010) latent-trait approach that postulates a multivariate normal distribution to model individual differences between the probit transformed model parameters. We provided a WinBUGS implementation of the latent-trait pair-clustering model and demonstrated that it provides well calibrated parameter estimates in synthetic data. We then expanded the latent-trait pair-clustering model to incorporate item variability. The resulting crossed-random effects approach assumes that participant and item effects combine additively on the probit scale. The random effects are modeled using (multivariate) normal distributions. First, we used simulations to show that the WinBUGS implementation of the crossed-random effects approach adequately recovers the true parameter values. The group parameters and their standard deviations were recovered with little bias even in data sets with very few items per participant. Precise estimation of the corresponding correlation parameters required a larger sample size and/or a greater number of items. Second, we applied the crossed-random effects model to novel experimental data and examined the changes in cognitive processes that underlie the pure list–mixed list word frequency paradox.

Approaches that are based on the additivity of probit transformed participant and item effects have been recently proposed in other research contexts as well (e.g., Pratte & Rouder 2011; Rouder & Lu 2005; Rouder et al. 2007, 2008). Here we demonstrated that this type of crossed-random effects modeling can be extended to the pair-clustering MPT model. We chose the pair-clustering model as our running example because is it one of the most extensively studied MPT models and it has been widely used to investigate memory deficits in various age groups and clinical populations (e.g., Batchelder & Riefer 2007). It is well-known that using items with varying difficulties aids the estimation of individual differences. The crossed-random effects extension therefore makes the pair-clustering paradigm better equipped for assessing individuals with memory deficits.

Although we focused exclusively on pair-clustering, the crossed-random effects approach may be extended to many other MPT models. The issue of model identification must, however, be carefully considered. Specifically, problems may arise in models, such as the source monitoring model (Batchelder & Riefer 1990; Schmittmann, Dolan, Raijmakers, & Batchelder, 2010), where one or more subtrees are unidentified so that a given subtree has more parameters than free response categories. In such situations, parameter constraints are required between the category systems to reduce the number of parameters and identify the model. In many applications, however, each item features in only one of the category systems of the model. As a result, we cannot use across-subtree constraints for the item effects, resulting in parameters that are not identified at the level of the individual items. In these models, we can obtain information on each item in each category system by—as in the present experiment—randomizing the items across the participants and the experimental conditions or trial types. In this way, we can place across-subtree constraints on the item effects and, due to the additive structure of the model, we can estimate parameters for each participant-item combination. Note, however, that the present approach deals only with models that are identified for each participant after collapsing across items and for each item after collapsing across the participants. In paradigms where items are restricted to certain category systems, model identification remains an issue that requires further development.

A related issue concerns the storage-retrieval u parameter. We indexed the u parameter by word pairs rather than by individual items, assuming that the two members of a word pair are homogeneous. To the best of our knowledge, all previous applications of the pair-clustering model have used this homogeneity assumption. Nevertheless, in certain situations—as with asymmetric stimuli, such as category-exemplar word pairs—the homogeneity assumption will most likely be violated. In such situations, we may want to index the u parameter by individual items rather than by word pairs. To be able to estimate a separate u parameter for each item and, at the same time, maintain model identifiability, we may split up C ₁₃ in two response categories and record whether the first or the second member of the word pair has been recalled. In our experience, however, the extra degree of freedom resulting from recording the order of the recall of word pairs does not offer enough benefits to offset the sparseness resulting from splitting the response categories.

Throughout the article, we used WinBUGS to sample from the posterior distribution of the model parameters. WinBUGS is a user–friendly standard MCMC software that does not require substantial knowledge of the underlying sampling algorithm. The basic WinBUGS scripts can be easily extended to multiple testing conditions with various parameter constraints or can be adopted to accommodate other MPT models. Due to its generality, however, WinBUGS is not tailored to the particular model at hand. For models with zero–centered random effects, WinBUGS might be slow to converge as a result of the high autocorrelation between successive MCMC draws. WinBUGS then requires more samples from the posterior distribution of the parameters than a tailor–made Gibbs sampler that uses block-wise sampling for groups of correlated parameters (e.g., Klauer 2010; Rouder et al. 2007). Nevertheless, WinBUGS is a helpful tool for fitting Bayesian hierarchical MPT models in general and the pair-clustering model in particular, as long as the convergence of the MCMC chains is carefully monitored. Of course, several alternatives to WinBUGS are now available. The OpenBUGS (Lunn et al. 2009) and JAGS (Plummer 2003) projects, for instance, provide more options for block-wise sampling than does WinBUGS, but to the best of our knowledge, the development of blocked updating is still work in progress. For yet another—recently developed—alternative, see the Stan project (Stan Development Team 2012).

5.1 Prior Distributions

The latent-trait approach and its crossed-random effects extension rely on Bayesian parameter estimation and as such require the specification of prior distributions. As uninformative priors might lead to unrealistic and poorly calibrated estimates, we followed Klauer’s (2010) work and used weakly informative hyper-priors. Our priors for the group means are more informative and the priors for the standard deviations are more diffuse than the priors used in Klauer’s original formulation of the latent-trait approach. Bayesian parameter estimation is, however, not sensitive to the choice of the prior distributions as long as sufficiently informative data are available. Consider, for example, uniform prior distributions with different ranges (i.e., 0–5, 0–10, and 0–100) for the scaling factor ξ parameters of the participant and item standard deviations. Although the priors for ξ influence the shape of the priors for σ _part and σ _item, the results of additional simulations suggest that the recovered parameter estimates are not sensitive to these choices.

In our crossed-random effects approach, we modeled the synthetic data using uncorrelated item effects, whereas we modeled the experimental data using correlated item effects. The two approaches thus differed in terms of prior assumptions; the first model assumed that the item effects are independent a priori, whereas the latter model allowed them to be correlated. With sufficiently informative data, however, the data quickly overwhelm the prior. The correlations between the a priori independent random effects may therefore also be examined using the posterior of the individual item parameters. Nevertheless, in small data sets, the assumption of a priori uncorrelated item effects may induce bias in the estimated correlations between the item parameters (e.g., Rouder et al. 2007).

If the item effects are likely to be correlated, one may capture these—similar to the participant effects—using a multivariate normal distribution. Modeling the item correlations, however, increases the amount of data that is necessary to obtain stable parameter estimates. For our experimental data, we were unable to derive sufficiently precise estimates for the item correlations despite the relatively large item pool. Similarly, additional simulations indicated that precise estimates of item correlations in the pair-clustering paradigm require a rather large number of items, a requirement that is often difficult to satisfy in clinical applications. Nevertheless, explicitly modeling the item correlations, even if they cannot be estimated precisely, has the potential to correct for bias that might result from fitting a simpler, but unrealistic model.

5.2 Conclusion

Here we introduced WinBUGS implementations of the latent-trait pair-clustering model and its crossed-random effects extension. The models allow researchers to analyze pair-clustering data without relying on aggregation and the underlying unrealistic assumption of parameter homogeneity. The WinBUGS implementation can in principle be adopted to accommodate other multinomial models and therefore provides a useful contribution to the growing arsenal of analysis techniques that address the issue of parameter heterogeneity in MPT models.