Introduction

When a species colonizes a new area, it spreads across that area in the form of an invasion wave. The speed of this wave is determined by the vital rates of the population (birth, death, etc.) and by individual dispersal ability. Since the pioneering work of Skellam (1951), the spatial propagation of invasions has been extensively studied using diffusion equations combined with population growth. Mathematical analyses of these models suggest that the range front of an invading species advances at a constant velocity (Fisher 1937; Skellam 1951; Okubo 1980; Okubo and Levin 2001). This result was subsequently found to apply to many invading organisms (Hengeveld 1989; Andow et al. 1990, 1993; Williamson 1996; Shigesada and Kawasaki 1997). Recently, integral-kernel-based models that incorporate dispersal distance distribution and/or age structure have been presented by Mollison (1977), Van den Bosch et al. (1992), Kot et al. (1996), Clark (1998), Neubert and Caswell (2000), and many others. Most of these models have been formulated using deterministic equations for the dynamics of the expected population density or population range. In these models, as long as the dispersal kernels have shorter tails than an exponentially bounded distribution, the range expands at a constant speed, forming a traveling wave. More recently, increasing attention has been focused on stochastic versions of deterministic models, where the effects of stochasticity in dispersal and/or reproduction on the rate of spread are investigated, mostly in the framework of one-dimensional models (Lewis and Pacala 2000; Lewis 2000; Snyder 2003; Kot et al. 2004).

On the other hand, cellular automaton (CA) models (also known as lattice models or interacting particle models) have become a popular tool for modeling population dynamics in two-dimensional space. The CA models divide the space into a discrete lattice, and describe the state at each location (“cell” or “patch”) on the lattice using a discrete variable. The states of the cells are updated (in either discrete or continuous time) as a function of their state and the states of the cells in the local neighborhood.

These CA models have been used to describe cell colony growth (Eden 1961; Richardson 1973), plant populations with multiple modes of reproduction (Harada and Iwasa 1994; Harada et al. 1995), forest gap expansion (Kubo et al. 1996; Satake et al. 2004), competition (Caswell and Cohen 1991; Caswell and Etter 1992, 1999; Etter and Caswell 1994; Tilman et al. 1997; Durrett and Levin 1998; Buttel et al. 2002; Cannas et al. 2003), predation (Hassell et al. 1991), epidemics (Mollison and Kuulasmaa 1985; Tainaka 1988; Sato et al. 1994; Filipe and Maule 2004), and game-theoretical interactions (Nowak et al. 1995; Nakamaru et al. 1996; Nakamaru and Levin 2004). A series of works by Levin and Durrett have provided comprehensive guides to ecological applications of stochastic CA models (Levin 1992; Durrett and Levin 1994a, 1994b; Levin and Durrett 1997; Chave et al. 2002).

While the CA model is advantageous in easily incorporating stochasticity, it generally makes mathematical analysis more difficult than the diffusion and integral-kernel-based models. As well as this, most previous CA models have not addressed the speed of invasion, apart from the spatial pattern of the species involved and the conditions required for their coexistence or extinction. As an exception, Ellner et al. (1998) presented a pair-edge approximation method to deal with the speed and the conditions required for successful invasion in a lattice population model.

In this paper, we investigate invasion waves that are generated by stochastic short- and/or long-distance colonization in a time-continuous CA model for a single species on a two-dimensional homogenous landscape. We first demonstrate, using computer simulations, that stochasticity can dramatically increase the speed of the invasion waves compared to the deterministic version of the model or the corresponding one-dimensional model. For invasion involving only short-distance colonization, we develop a mathematical model to describe spatio-temporal changes in the distribution of frontal positions, and present several approximation methods for solving the model. Our analyses show that the increased wave speed in the stochastic model is due to irregularity in the shape of the wavefront, which is present in the stochastic model for two-dimensional space, but not in the corresponding deterministic model or in the corresponding stochastic model for one-dimensional space.

Further extension of this model to include long-distance colonization demonstrates that stochasticity influences speeds to even greater extents. Based on these results, we discuss how important stochasticity and spatial dimensionality are in the enhancement of invasion speed.

A time-continuous stochastic CA model and its computer simulation

Consider a square lattice in which each cell is either in state 1 (occupied) or in state 0 (vacant). A cell in state 0 changes to state 1 at the rate αn, where n is the number of the eight adjacent cells that are in state 1 and α is the colonization rate from an occupied adjacent cell. Thus, the transition probability p 10 from state 0 to state 1 during dt is given by

$$ {\text{Case }}(1):{\text{ }}p_{{10}} = \alpha ndt{\text{.}} $$
(1)

More exactly, the probability that state 0 remains unchanged during dt is exp(−αn dt). We refer to this case as Case (1). This model is analogous to the basic contact model (Durrett 1988; Ellner et al. 1998) except that the death process is eliminated. In the following, we focus on the case where the cells at the left boundary are initially in state 1 and all other cells are in state 0.

Before tackling this problem, we also consider a special case (referred to as Case (1s)), in which a cell in state 0 cannot change to state 1 unless its left neighbor is occupied. Thus Eq. 1 is rewritten as:

$$ {\text{Case }}(1{\text{s}}):{\text{ }}p_{{10}} = \sigma \alpha ndt{\text{.}} $$
(2)

where σ=1 if the left neighboring cell is in state 1, and σ=0 if it is in state 0. This case may not be biologically realistic, but it is analytically tractable and provides a good reference point for further analyses.

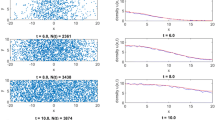
We first simulate the model for a 100×200 grid with periodic boundary conditions on the upper and lower edges. The lower and left boundaries of the CA are set on the x- and the y-axes, respectively. As shown in Fig. 1, computer simulations demonstrate that the range of occupied cells expands to the right and the front exhibits wavy patterns for both Cases (1s) and (1). The waviness (irregularity) is more accentuated in Case (1) than in Case (1s).

Fig. 1
figure 1

The progression of invasion wavefronts in the continuous-time stochastic CA model. a Case (1s) for α=1; b Case (1) for α=1. dt=0.001

Full size image

To define the front of the invasion wave, we focus on the configuration of states in each row. The cells in each row are numbered sequentially from left to right. The right-most occupied site in each row is defined as the front (i.e., the furthest-forward location). We introduce the front distribution function f(i, t), which gives the probability that the front of a randomly chosen row is located at site i at time t. Figure 2a, b shows f(i, t) obtained from simulations for Cases (1s) and (1), respectively. The average location of the front is given by

$$ {\left\langle i \right\rangle } = {\sum\limits_{i = 1}^{200} i }f{\left( {i,t} \right)}. $$
(3)

As seen in Fig. 3, the average front location advances at a constant rate for each case: 3.38α in Case (1s), and 6.55α in Case (1).

Fig. 2
figure 2

The probability distribution f(i, t) of the front position at time t in the CA model. a Case (1s) for α=1; b Case (1) for α=1. dt=0.001

Full size image
Fig. 3
figure 3

The progress of the mean front position with time in Case (1s) for α=1 and Case (1) for α=1. dt=0.001

Full size image

In contrast, if we consider a corresponding deterministic model, each front advances by one cell at every time interval of 1/3α. Accordingly, the range front forms a straight line, and its advancing speed is 3α. Therefore the speeds in the stochastic model for Case (1s) and Case (1) are 1.12 and 2.18 times higher than that in the deterministic model, respectively. We are interested in why such discrepancies in speed occur between the stochastic and deterministic rules.

Dynamical equations for the front distribution

To understand the increase in front speed in the stochastic simulations compared with the corresponding deterministic model, we construct a dynamical model for the distribution of front positions and develop some approximation methods to solve the model.

Case (1s)

We begin with Case (1s), in which colonization of a cell can occur only if the neighboring cell on the left is occupied. In this case, each row in the CA consists of state 1 cells that are consecutively aligned from the left boundary to a certain position, and state 0 cells for the remaining sites.

The dynamical equation for f(i, t) is given by

$$ \frac{{df{\left( {i,t} \right)}}} {{dt}} = r{\left( {i,t} \right)}f{\left( {i - 1,t} \right)} - r{\left( {i + 1,t} \right)}f{\left( {i,t} \right)}{\text{ for }}i \geqslant 1, $$
(4)

where f(0, t)=0, and r(i+1, t) is the average rate at which the front at site i advances to site i+1 in unit time. From Eq. 4, we obtain the speed of the average front as:

$$ \frac{{d{\left\langle i \right\rangle }}} {{dt}} = \frac{d} {{dt}}{\left( {{\sum\limits_{i = 1}^\infty {if{\left( {i,t} \right)}} }} \right)} = {\sum\limits_{i = 1}^\infty {r{\left( {i + 1,t} \right)}} }f{\left( {i,t} \right)}. $$
(5)

The rate of change in the variance of the front location is given by

$$ \frac{d} {{dt}}{\left( {{\sum\limits_{i = 1}^\infty {{\left( {i - {\left\langle i \right\rangle }} \right)}^{2} f{\left( {i,t} \right)}} }} \right)} = 2{\sum\limits_{i = 1}^\infty {ir{\left( {i + 1,t} \right)}} }f{\left( {i,t} \right)} + {\left( {1 - 2{\left\langle i \right\rangle }} \right)}\frac{{d{\left\langle i \right\rangle }}} {{dt}}. $$
(6)

To solve Eq. 4, we need the functional form of r(i+1, t). If we assume that the front distributions of the adjacent upper and lower rows are given by the common probability density f(i, t), and that they are statistically independent of each other and of the row under consideration, r(i+1, t) is given by

$$ r{\left( {i + 1,t} \right)} = \alpha + 2\alpha f{\left( {i,t} \right)} + 4\alpha f{\left( {i + 1,t} \right)} + 6\alpha {\sum\limits_{k = 2}^\infty {f{\left( {i + k,t} \right)}} } $$
(7)
$$ \equiv \alpha + \rho {\left( {i + 1,t} \right)}. $$
(8)

The first term α on the right-hand side of Eq. 7 represents the rate at which cell i at the front causes the adjacent right cell i+1 to change from state 0 to state 1. The second term is the rate at which cell i+1 is colonized from the upper and lower rows when the fronts in the upper and lower rows are located at site i. The third term represents the contribution from the upper and lower rows when their fronts are located at site i+1, and the fourth term is the contribution from the upper and lower rows when their fronts are located further ahead of site i+1. Thus function ρ(i+1, t) defined in Eq. 8 represents the average rate at which cell i+1 is occupied by the colonization from cells in the upper and lower adjacent rows.

We first numerically solve Eq. 4 with 7, and obtain the front distribution f(i, t), which is illustrated in Fig. 4. Substituting this solution for f(i, t) in the right-hand side of Eq. 5 yields an average speed of 3.32α, which is close to the speed obtained from simulation, 3.38α. It should be noted that the front distribution, f(i, t), shows a nearly triangular shape with a base length of about 6. In contrast, the front distribution obtained from the simulation (see Fig. 2a) exhibits an irregular localized pattern, consisting of multiple steep peaks. We infer that the front distribution obtained from simulations may be given by superposing multiple triangular distributions as derived above.

Fig. 4
figure 4

The front distribution for Case (1s) obtained from dynamical model 4 with 7

Full size image

Based on the results from numerical computations, here we develop an analytical model for the front distribution f(i, t). Let us assume that f(i, t) has an isosceles triangular shape with base length 2b, and moves at a constant speed c without changing its form. Thus we put:

$$ f{\left( {i,t} \right)} = \left\{ {\begin{array}{*{20}c} {0} & {{i < ct - b}} \\ {{{{\left( {i - ct + b} \right)}} \mathord{\left/ {\vphantom {{{\left( {i - ct + b} \right)}} {b^{2} }}} \right. \kern-\nulldelimiterspace} {b^{2} }}} & {{ct - b \leqslant i < ct}} \\ {{{{\left( { - i + ct + b} \right)}} \mathord{\left/ {\vphantom {{{\left( { - i + ct + b} \right)}} {b^{2} }}} \right. \kern-\nulldelimiterspace} {b^{2} }}} & {{ct \leqslant i < ct + b}} \\ {0} & {{ct + b \leqslant i}} \\ \end{array} } \right. $$
(9)

Note here that, whereas the area of the isosceles triangle is one, the summation of f(i, t) with respect to integer i gives an approximate value, which is not necessarily one. By substituting Eqs. 9 and 7 into 5 and 6, we obtain the rate of change in the mean front location and its variance, as

$$ \frac{d} {{dt}}{\left\langle i \right\rangle } = \alpha {\left( {4 - \frac{2} {b} + \frac{1} {{b^{3} }}} \right)}, $$
(10)
$$ \frac{d} {{dt}}{\left( {{\left\langle {i^{2} } \right\rangle } - {\left\langle i \right\rangle }^{2} } \right)} = \alpha {\left( {4 - \frac{7} {5}b + \frac{1} {{3b}} + \frac{1} {{15b^{3} }}} \right)}. $$
(11)

Since we assumed that the spatial pattern of f(i, t) moves at speed c without changing its form, we set the right-hand side of Eq. 10 equal to c, and the right-hand side of Eq. 11 equal to zero. Then we obtain b=2.94 and c=3.36α. Again the speed is fairly close to that obtained from simulations of the CA model (3.38α). Furthermore, the base length 2b=5.88 agrees well with that numerically obtained, ~6, as noted above.

Case (1)

Here we relax the restriction that colonization can occur only if the left adjacent neighbor is occupied. The calculations become more complex, because more routes to colonization must be considered, but we can use basically the same procedure as in the previous cases.

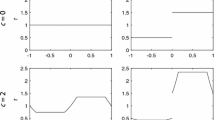
State 1 cells do not necessarily occur consecutively from the left boundary. State 0 cells may intervene locally in the sequence of state 1 cells. We classify the sequence of cell states in each row into one of two types, f 1- and f 2-type (Fig. 5). In an f 1-type row, state 1 cells are consecutively aligned from the left boundary. In an f 2-type row, the cell directly to the left of the front is in state 0 and the remaining cells to the left of that 0 state cell are all in state 1. Although the computer simulations permit state 0 cells to occur at sites more than one cell to the left of the front, the above classification assumes that any such cells change immediately to state 1. We introduce f 1(i, t) to denote the probability that a randomly chosen row is of f 1-type and its front is located at site i, and f 2(i, t) to denote the probability that an randomly chosen row is of f 2-type and its front is located at site i. Thus we have the following set of equations:

$$ \frac{{df_{1} {\left( {i,t} \right)}}} {{dt}} = -{\left\{ {\alpha + {\sum\limits_{k = 1}^\infty {\sigma {\left( {i + k,t} \right)}} }} \right\}}f_{1} {\left( {i,t} \right)} + {\left\{ {2\alpha + \sigma {\left( {i - 1,t} \right)}} \right\}}f_{2} {\left( {i,t} \right)} + {\left\{ {\alpha + \sigma {\left( {i,t} \right)}} \right\}}{\left\{ {f_{1} {\left( {i - 1,t} \right)} + f_{2} {\left( {i - 1,t} \right)}} \right\}}, $$
(12)
$$ \frac{{df_{2} {\left( {i,t} \right)}}} {{dt}} = -{\left\{ {3\alpha + \sigma {\left( {i - 1,t} \right)} + {\sum\limits_{k = 1}^\infty {\sigma {\left( {i + k,t} \right)}} }} \right\}}f_{2} {\left( {i,t} \right)} + {\sum\limits_{k = 2}^\infty {\sigma {\left( {i,t} \right)}} }{\left\{ {f_{1} {\left( {i - k,t} \right)} + f_{2} {\left( {i - k,t} \right)}} \right\}}, $$
(13)

where σ(j, t) is the average rate at which a cell at site j is colonized by the cells in the adjacent upper and lower rows at time t. The meanings of the terms in the right-hand side of Eq. 12 are as follows. The first term, \( {\left\{ {\alpha + {\sum\limits_{k = 1}^\infty {\sigma {\left( {i + k,t} \right)}} }} \right\}}f_{1} {\left( {i,t} \right)} \), represents the loss rate of an f 1-type row with front at site i: α is the rate at which the cell to the right of site i is colonized by the front cell, and the summation term is the rate at which any cell to the right of site i is colonized by the cells in the upper and lower rows (see Fig. 6a). The second term \( {\left\{ {2\alpha + \sigma {\left( {i - 1,t} \right)}} \right\}}f_{2} {\left( {i,t} \right)} \) in Eq. 12 represents the creation of an f 1-type row from an f 2-type row by colonization of the empty cell to the left of its front (Fig. 6b). The third term, \( {\left\{ {\alpha + \sigma {\left( {i,t} \right)}} \right\}}{\left\{ {f_{1} {\left( {i - 1,t} \right)} + f_{2} {\left( {i - 1,t} \right)}} \right\}} \), represents the rate at which an f 1-type (f 2-type) row with front at site (i−1) advances its front by one cell (this case corresponds to Fig. 6a, in which k=1 and i is replaced by i−1). Equation 13 is constructed in a similar fashion.

Fig. 5
figure 5

Frontal patterns of f 1- and f 2-type rows

Full size image
Fig. 6
figure 6

The transition rates between f 1- and f 2-type rows (see Eqs. 12 and 13, and their explanations in the text). The cell with 1/0 is either in state 1 or in state 0. f 1/2 represents f 1 when the cell with 1/0 is in state 1, and f 2 when the cell with 1/0 is in state 0. δ k1 is the Kronecker delta (δ k1=1 if k=1 and δ k1=0 if otherwise). Cells located more than one cell to the left of the front are assumed to change immediately to state 1

Full size image

To determine σ(j, t), we need the front distributions for the adjacent upper and lower rows. Let us first assume that the front distributions of f 1- and f 2-type in the adjacent upper and lower rows are the same as f 1(i, t) and f 2(i, t), respectively. Then, via a similar procedure used to derive ρ(j, t) in Eq. 7, we obtain the following equation:

$$ \begin{aligned} \sigma \left( {j,t} \right) = & 2\alpha \left\{ {f_1 \left( {j - 1,t} \right) + 2f_1 \left( {j,t} \right) + 3\sum\limits_{k = 1}^\infty {f_1 \left( {j + k,t} \right) + f_2 \left( {j - 1,t} \right) + f_2 \left( {j,t} \right) + 2f_2 \left( {j + 1,t} \right)} } \right. \\ & \left. { + 2f_2 \left( {j + 2,t} \right) + 3\sum\limits_{k = 3}^\infty {f_2 \left( {j + k,t} \right)} } \right\} \\ \end{aligned} $$
(14)

Here we again adopt a triangle approximation similar to that employed in Case (1s). Let us assume that the front distributions of f 1- and f 2-type are given by isosceles triangles with bases 2b 1 and 2b 2, respectively, both of which move at constant speed c without changing their forms. Thus we put:

$$ f_{1} {\left( {i,t} \right)} = \left\{ {\begin{array}{*{20}c} {0} & {{i < ct - b_{1} }} \\ {{{\theta _{1} {\left( {i - ct + b_{1} } \right)}} \mathord{\left/ {\vphantom {{\theta _{1} {\left( {i - ct + b_{1} } \right)}} {b^{2}_{1} }}} \right. \kern-\nulldelimiterspace} {b^{2}_{1} }}} & {{ct - b_{1} \leqslant i < ct}} \\ {{{\theta _{1} {\left( { - i + ct + b_{1} } \right)}} \mathord{\left/ {\vphantom {{\theta _{1} {\left( { - i + ct + b_{1} } \right)}} {b^{2}_{1} }}} \right. \kern-\nulldelimiterspace} {b^{2}_{1} }}} & {{ct \leqslant i < ct + b_{1} }} \\ {0} & {{ct + b_{1} \leqslant i}} \\ \end{array} } \right., $$
(15)
$$ f_{2} {\left( {i,t} \right)} = \left\{ {\begin{array}{*{20}c} {0} & {{i < ct + d - b_{2} }} \\ {{{\theta _{2} {\left( {i - ct + d + b_{2} } \right)}} \mathord{\left/ {\vphantom {{\theta _{2} {\left( {i - ct + d + b_{2} } \right)}} {b^{2}_{2} }}} \right. \kern-\nulldelimiterspace} {b^{2}_{2} }}} & {{ct + d - b_{2} \leqslant i < ct + d}} \\ {{{\theta _{2} {\left( { - i + ct + d + b_{2} } \right)}} \mathord{\left/ {\vphantom {{\theta _{2} {\left( { - i + ct + d + b_{2} } \right)}} {b^{2}_{2} }}} \right. \kern-\nulldelimiterspace} {b^{2}_{2} }}} & {{ct + d \leqslant i < ct + d + b_{2} }} \\ {0} & {{ct + d + b_{2} \leqslant i}} \\ \end{array} } \right., $$
(16)

where θ 1 and θ 2 are the fractions of f 1- and f 2-type, respectively, and d is the relative distance between the two triangles. If Eqs. 15 and 16 are good enough to describe the front distributions, the following set of equations should hold:

$$ \frac{d} {{dt}}{\sum\limits_{i = 1}^\infty {f_{1} {\left( {i,t} \right)}} } = 0, $$
(17)
$$ \frac{d} {{dt}}{\sum\limits_{i = 1}^\infty {{if_{1} {\left( {i,t} \right)}} \mathord{\left/ {\vphantom {{if_{1} {\left( {i,t} \right)}} {\theta _{1} }}} \right. \kern-\nulldelimiterspace} {\theta _{1} }} } = \frac{d} {{dt}}{\left\langle i \right\rangle }_{{f_{1} }} = c,{\text{ }}\frac{d} {{dt}}{\sum\limits_{i = 1}^\infty {{if_{2} {\left( {i,t} \right)}} \mathord{\left/ {\vphantom {{if_{2} {\left( {i,t} \right)}} {\theta _{2} }}} \right. \kern-\nulldelimiterspace} {\theta _{2} }} } = \frac{d} {{dt}}{\left\langle i \right\rangle }_{{f_{2} }} = c, $$
(18)
$$ \frac{d} {{dt}}{\sum\limits_{i = 1}^\infty {{\left( {i - {\left\langle i \right\rangle }_{{f_{1} }} } \right)}^{2} {f_{1} {\left( {i,t} \right)}} \mathord{\left/ {\vphantom {{f_{1} {\left( {i,t} \right)}} {\theta _{1} }}} \right. \kern-\nulldelimiterspace} {\theta _{1} }} } = 0,{\text{ }}\frac{d} {{dt}}{\sum\limits_{i = 1}^\infty {{\left( {i - {\left\langle i \right\rangle }_{{f_{2} }} } \right)}^{2} {f_{2} {\left( {i,t} \right)}} \mathord{\left/ {\vphantom {{f_{2} {\left( {i,t} \right)}} {\theta _{2} }}} \right. \kern-\nulldelimiterspace} {\theta _{2} }} } = 0. $$
(19)

Equations 17 and 19, respectively, mean that the fractions and variances of the front distributions of f 1- and f 2-type are maintained constant with time, and Eq. 18 means that the average front positions advance at constant speed c for both f 1- and f 2-type. Thus df 1/dt and df 2/dt in Eqs. 17, 18, and 19 are substituted by the right-hand sides of Eqs. 12 and 13 in which f 1(i, t) and f 2(i, t) are replaced with Eqs. 15 and 16, respectively. Then the resulting set of equations are numerically solved to give all parameter values included in Eqs. 15 and 16 as follows:

$$ c = 8.15\alpha ,{\text{ }}b_{1} = 2.94,{\text{ }}b_{2} = 2.79,{\text{ }}d = 0.96,{\text{ }}\theta _{1} = 0.780{\text{ and }}\theta _{2} = 0.223. $$

The speed, 8.15α, is fairly close to, though higher than, the speed 6.55α from simulating the CA. One of the reasons for the discrepancy between the two speeds may come from the assumption that state 0 cells occurring at sites more than one cell to the left of the front change immediately to state 1.

Figure 7 illustrates f 1(i, t) and f 2(i, t) given by Eqs. 15 and 16 for the parameter values obtained above. The front distribution, f 1(i, t)+f 2(i, t), ranges within about six cells. This means that the front positions of adjacent two rows could differ by at most six cells, and thus colonization from the leading front to the adjacent row could result in the retarding front of the latter jumping forward by up to six cells. Accumulated effects of such events could explain accelerated speeds in wavy fronts. Note, however, that such a jump is not allowed in Case (1s) by definition. This is why the speed in Case (1s) remains close to that in the deterministic model.

Fig. 7
figure 7

Frontal distributions of f 1- and f 2-type in Case (1) derived from the assumption that they are approximated by isosceles triangles that move at a constant speed without changing their forms and their relative distance. Open and shaded bars represent f 1(j, t) and f 2(j, t), respectively

Full size image

Cases with narrower landscapes

If the above reasoning is valid, we may expect that reducing the landscape size (i.e., the number of rows along the y-axis) will decrease the front speed, because a wavy pattern is less likely to develop when the landscape size is small. To examine this, we carry out computer simulations for Case (1) with grids of size (L×200) from L=1 to 128. The result is illustrated in Fig. 8. The front speed increases with L, tending to an asymptote at 6.55α. When L=1, the speed is 3α. This is because the CA is subject to a periodic boundary condition where upper and lower cells are at the same state as the focal cell so that the front proceeds at speed 3α on average. When L=2, the speed increases to 4.29α. Specifically for this case, we develop a different analytical model to evaluate the speed.

Fig. 8
figure 8

The average speed of the frontal wave in Case (1) as a function of landscape size L

Full size image

Let us focus on the (2×2) array of cells at the front, in which at least one of the right-most cells of the front is occupied. The possible configurations of the four cells are classified into four types, (1)–(4), as illustrated in the left-most column of Fig. 9. Each type includes a pair of configurations in which the upper and lower rows are commuted. These four types interconvert among them by colonization, as shown to the right of arrows. Here we assume that all of the cells on the left of the four focal cells are in state 1. Then the transition rates, which are calculated under the periodic boundary condition where the upper and lower cells are connected, are given by the values indicated below the resultant individual configurations. Using these transition rates, the average distance gained by each type of front per unit time is given in the rightmost column of Fig. 9.

Fig. 9
figure 9

Possible colonization processes and their transition rates for Case (1) with L=2. The (2×2) array of cells at the front are classified into four types (1)–(4), which are illustrated in the leftmost column. Each type includes a pair of configurations, in which the upper and lower rows are commuted. All of the cells on the left of the four focal cells are assumed to be at state 1. The transition rates between the four possible types are indicated below the respective resultant states. State 1 enclosed by a dotted square represents a newly colonized cell. State 1 enclosed by a solid circle represents a cell automatically colonized upon shifting the four focal cells rightwards, according to the above assumption. The average distance gained by each type of front per unit time is given in the rightmost column

Full size image

Let us now denote the frequency of type (i) at time t by p i (t). Then the stochastic equations for p i (t) are given by the transition matrix as follows:

$$ \frac{d} {{dt}}{\left( {\begin{array}{*{20}c} {{p_{1} }} \\ {{p_{2} }} \\ {{p_{3} }} \\ {{p_{4} }} \\ \end{array} } \right)} = {\left( {\begin{array}{*{20}c} {{ - 6\alpha }} & {{5\alpha }} & {{4\alpha }} & {{3\alpha }} \\ {{6\alpha }} & {{ - 8\alpha }} & {{7\alpha }} & {{6\alpha }} \\ {0} & {\alpha } & {{ - 13\alpha }} & {\alpha } \\ {0} & {{2\alpha }} & {{2\alpha }} & {{ - 10\alpha }} \\ \end{array} } \right)}{\left( {\begin{array}{*{20}c} {{p_{1} }} \\ {{p_{2} }} \\ {{p_{3} }} \\ {{p_{4} }} \\ \end{array} } \right)}. $$
(20)

The stationary distribution, p*, is given by the eigenvector corresponding to the eigenvalue 0 of the matrix in Eq. 20, which is

$$ p^{ * } = {\left( {\begin{array}{*{20}c} {{0.4337}} \\ {{0.4315}} \\ {{0.0404}} \\ {{0.0944}} \\ \end{array} } \right)}. $$
(21)

By averaging the speed of advance with these stationary frequencies, we get the mean speed,

$$ c{\text{ = 3}}\alpha \times {\text{0}}{\text{.4337 + 5}}\alpha \times {\text{0}}{\text{.4315 + 11}}{\text{.5}}\alpha \times {\text{0}}{\text{.0404 + 4}}\alpha \times {\text{0}}{\text{.0944 = 4}}{\text{.301}}\alpha {\text{,}} $$
(22)

which closely agrees with the speed derived from simulation, 4.29α. This means that the above assumption of assigning state 1 to all of the cells on the left of the four focal cells is reasonable, and that the possible differential in front positions between the two rows could be at most 2.

Effects of long-distance dispersal

The dispersal often involves two modes, short-distance dispersal and long-distance dispersal. When offspring depart from their parents, most of them undergo short-distance dispersal to settle near the parent’s range, while a minor fraction is infrequently observed at distant locations (Hengeveld 1989; Shigesada and Kawasaki 1997; Higgins et al. 2003). To accommodate both short- and long-distance dispersal, Shigesada et al. (1995) previously formulated the stratified diffusion model, in which the invading species extends its range concentrically at a constant speed c by short-range dispersal, while at the same time producing long-distance migrants to create nuclei of new colonies at positions well-separated from the parent. In that model, the number of nuclei produced per unit time by long-distance migrants from a parent colony per unit area is a random variable chosen from a Poisson distribution with average λ, and their dispersal distances are probabilistically determined by a dispersal kernel k(|x|), where |x| indicates the distance from the source (see also Shigesada and Kawasaki 1997, 2002).

In this section, we construct a stochastic CA model that corresponds to the stratified diffusion model. In the CA model, the transition probability of a cell from state 0 to state 1 due to short-distance colonization is given by rule 1 (i.e., corresponding to Case (1)), while the transition probability of a cell from state 0 to state 1 due to long-distance colonization is given by the product of λ dt and \( {\sum\limits_j {k{\left( {{\left| {\varvec{x}_{i} - \varvec{x}_{j} } \right|}} \right)}} } \) where λ represents the rate of generation of long-distance dispersers from a cell in state 1, i indicates the cell in question and the summation means all contributions from any cell j in state 1. For the functional form of the dispersal kernel, we adopt a modified Bessel function of order zero kind, \( {K_{0} {\left( {r \mathord{\left/ {\vphantom {r {d_{{\text{L}}} }}} \right. \kern-\nulldelimiterspace} {d_{{\text{L}}} }} \right)}} \mathord{\left/ {\vphantom {{K_{0} {\left( {r \mathord{\left/ {\vphantom {r {d_{{\text{L}}} }}} \right. \kern-\nulldelimiterspace} {d_{{\text{L}}} }} \right)}} {{\left( {2\pi d^{{\text{2}}}_{{\text{L}}} } \right)}}}} \right. \kern-\nulldelimiterspace} {{\left( {2\pi d^{{\text{2}}}_{{\text{L}}} } \right)}} \), where r=|x i −x j | and d L represents the mean dispersal distance due to long-range dispersal. This functional form of the dispersal kernel is obtained if we assume that organisms become sedentary at a constant rate while undergoing random diffusion (Broadbent and Kendall 1953; Shigesada 1980; Metz et al. 2000). Thus the model contains three independent parameters: the colonization rate due to short-distance dispersal, α, the rate of generation of new colonies due to long-distance dispersers from an occupied cell, λ, and the average distance of long-range dispersal, d L. We carry out numerical computations for this model on a 100×400 grid for a variety of values of d L, λ and α with the same periodic boundary conditions as used before. Figure 10 shows snapshots of a simulation with fixed α=1, λ=0.01, and d L=20 at t=5, 10, and 15, in which cells in state 1 sporadically arise at distant locations forming patchy distributions ahead of the contiguous distributed range.

Fig. 10
figure 10

Invasion wave progression due to both short- and long-distance colonization at three time points t=5, 10, and 15. The parameters used were α=1, λ=0.01, d L=20, and L=100

Full size image

From Fig. 10, we calculate the mean front position (the mean of the furthest-forward locations) as defined by Eq. 3 and plotted it as a function of time as shown in Fig. 11. For each d L, results of individual simulations are indicated by thin lines and the average of 20 such runs is given by a thick line. Although the individual thin lines show irregular fluctuations with time, each thick line exhibits a smoothly rising curve, which asymptotically approaches a linear slope. This tendency generally applies to cases with other parameter values too. The slope of the linear curve at the later phase gives the final average speed attained. Figure 12a illustrates the average speed (closed circles) as a function of d L for each value of λ. The speed starts at 6.55 (the speed due to short-distance colonization alone), and gradually increases with increases in d L up to ~6 due to increasing contributions from long-range dispersal. Above this range, long-range dispersal makes a major contribution and thus the speed increases almost linearly with d L. On the other hand, Fig. 12b shows that the speed as a function of the generation rate of long-distance dispersers, λ, rises sharply from 6.55 at first, and then the rate of increase in speed gradually slows down as λ increases from zero. In Fig. 12c, the speed is plotted as a function of α for various λ values, which shows a similar trend as observed in Fig. 12b, though its initial rise is less sharp.

Fig. 11
figure 11

The mean front positions of invasion waves due to both short- and long-distance colonization as a function of time for various fixed values of d L. The other parameters used were α=1, λ=0.01, and L=100. The three thin curves given for each d L represent results from arbitrary runs. The thick curves are the averages over 20 runs

Full size image
Fig. 12
figure 12

Dependence of speed on parameter values. a Speed as a function of d L for various values of λ with α=1. b Speed as a function of λ for various values of d L with α=1. c Speed as a function of α for various values of λ with d L=20. Closed circles and bars, respectively, indicate the mean speed and one standard deviation of 20 simulation results for the two-dimensional CA model. The solid lines indicate speeds given by the semi-empirical formula 23 for the two-dimensional CA model. Open circles and bars, respectively, indicate the mean speed and one standard deviation of 20 simulation results for the one-dimensional CA model. The dashed lines indicate speeds given by the semi-empirical formula 24 for the one-dimensional CA model

Full size image

Using dimensional analysis, we deduced the following semi-empirical formula for the speed:

$$ V \approx 1.93c^{{2/3}} {\left( \lambda \right)}^{{1/3}} d_{{\text{L}}} , $$
(23)

Here c=6.55α, the speed due to short-range colonization. (By retrospectively applying the same analysis, we realized that the corresponding formula in the stratified diffusion model (Eq. 17.7 in Shigesada and Kawasaki 2002) should be corrected to \( V \approx 1.9c^{{2/3}} {\left( \lambda \right)}^{{1/3}} d_{{\text{L}}} \)). We plot this function in Fig. 12 (solid lines), and this agrees fairly well with all of the simulation results. Briefly, the idea used to obtain this equation is as follows. Let us assume that the speed is given by \( V = Ac^{x} \lambda ^{y} d^{z}_{{\text{L}}}, \) where A, x, y, and z are constant. Since the dimensions of V, c, λ, and d L are L/T, L/T, 1/L 2 T, and L, respectively, x+y=1 and x−2y+z=1 should hold. Based on the simulation results in Fig. 12a, we further assume that the speed increases linearly with d L, so that z is put equal to one. Then we have x=2/3 and y=1/3. The coefficient 1.93 is obtained by regression. It is remarkable to note that Eq. 23 automatically fits to all of the data sets upon fixing only a single parameter A, except in the case of small d L, where the assumption of linear dependency of d L does not hold. Incidentally, the value A=1.93 is derived specifically for the modified Bessel function used here. However, we may suppose that Eq. 23 still holds upon adjusting A, even if we employ a different functional form for the dispersal kernel, as long as it has an exponentially bounded tail.

We further examine how the speed is influenced when the landscape of the CA is reduced from L=100 to 1, as in the “Cases for narrower landscapes” section. We find that the speed slows down monotonically with decreasing L even more drastically than in the case without long-range colonization. In Fig. 12, the results are indicated for L=1 (open circles), which is several times lower than the case for a sufficiently large L. It should be noted here that the case for L=1 corresponds to a one-dimensional CA in which the rate of short-range colonization is 3α and the dispersal kernel for long-range colonization is \( k{\left( x \right)} = {\exp {\left( {{ - {\left| x \right|}} \mathord{\left/ {\vphantom {{ - {\left| x \right|}} {d_{{\text{L}}} }}} \right. \kern-\nulldelimiterspace} {d_{{\text{L}}} }} \right)}} \mathord{\left/ {\vphantom {{\exp {\left( {{ - {\left| x \right|}} \mathord{\left/ {\vphantom {{ - {\left| x \right|}} {d_{{\text{L}}} }}} \right. \kern-\nulldelimiterspace} {d_{{\text{L}}} }} \right)}} {2d_{{\text{L}}} }}} \right. \kern-\nulldelimiterspace} {2d_{{\text{L}}} } \). The great enhancement in speed in the two-dimensional CA may be explained by a mechanism analogous to that previously suggested for the CA model involving only short-range colonization: a colonization from leading patches to an unoccupied cell on another row could result in a big leap of the furthest-forward front of that row with a high probability.

Using a similar dimensional analysis, we derive a semi-empirical formula for the speed in one dimension as

$$ V \approx 1.5{\left( {c\lambda } \right)}^{{1/2}} d_{{\text{L}}} , $$
(24)

where c=3α. Equation 24 is illustrated by dashed lines in Fig. 12, which again fits all simulated results well when the single parameter A is adjusted to be 1.5.

Discussion

In this work, we presented a stochastic CA model for invasion waves generated by colonization due to short- and/or long-distance dispersal. When colonization only occurs from the eight adjacent cells, the frontal wave shows a wavy pattern, through which the frontal speed is accelerated by up to twofold compared with the speed in the corresponding deterministic model. To better understand the mechanism of this accelerated speed, we developed dynamical equations for the distribution of the front position in each row. Analyzing the equations demonstrated that the distribution of frontal positions along a row falls within about six cells. Thus, the possible difference in front positions between two adjacent rows could be six at the most, so there would be a chance of long-range colonization jumping about six cells ahead of the front of a row. This jump in colonization is inevitably accompanied by greater irregularities (or waviness) in the shape of the frontal wave in the two-dimensional space. Despite the marked irregularity of the global frontal shape as seen in Fig. 1, its average speed is virtually constant with time (see Fig. 2). As we reduce the width of the landscape, the frontal irregularities gradually diminish, leading to monotonic decreases in speed. Since the irregular boundary of the frontal wave cannot occur in one-dimensional space, we may conclude that the presence of both stochasticity and two-dimensional space is essential for an enhancement in speed. As a matter of fact, if we consider a stochastic one-dimensional CA, the average speed is exactly the same as the speed in the corresponding deterministic CA.

Recently, Ellner et al. (1998) dealt with a similar lattice population model using an alternative mathematical method, the pair-edge approximation. Their model included death processes and was restricted to the case of colonization from the eight neighboring cells. The pair approximation method takes the correlations between nearest neighbor sites in account and provides a good approximation of the speed of the frontal wave and the conditions needed for successful invasion. On the other hand, our approach focuses on the distribution of the front position in each row. It thus provides detailed insights into how leaping colonizations can take place, even though each event is engaged by nearest neighborhood colonizations.

When we take into account both short- and long-distance dispersals, mathematical analyses become formidable. Thus we carry out computer simulations for the case corresponding to the stratified diffusion model (Shigesada and Kawasaki 2002), although the mathematical frameworks of these models are essentially different. Space is taken as continuous in the stratified diffusion model, but discrete in the CA model. On the other hand, stochasticity is incorporated into long-distance dispersal in both models, while stochasticity in short-distance dispersal is only included in the CA. Nevertheless, essentially similar features are derived for the speed in either model: the speed increases almost linearly with average long-range dispersal distance, d L, while it increases more slowly as the generation rate of long-distance dispersers, λ and the colonization rate, α increase. We deduced a semi-empirical formula for the speed, which fits the simulation results remarkably well for wide ranges of d L, λ and α. The patchy patterns characteristic of the stratified diffusion model and its CA version are caused by the combined effect of short- and long-distance colonization, but never occur when there is only long-range colonization with an exponentially bounded dispersal kernel. However, Shaw (1994) demonstrated that in an epidemic CA model with time delay, fat-tailed dispersal kernels like a Cauchy distribution can generate patch-like patterns, although the fronts of the wave cannot be defined very well. From a different approach based on diffusion–reaction equations, Petrovskii et al. (2005) also showed that patchy invasion of a predator or infectious disease occurs in two-dimensional space, whereas the species become extinct in the corresponding one-dimensional system.

Apart from the CA model, the effects of stochasticity on range expansion have been extensively studied by integro-differential or integro-difference equations (integral-kernel-based models) in one-dimensional space by Mollison (1977), Lewis and Pacala (2000), Lewis (2000), Clark et al. (2001) and Snyder (2003). More recently, Kot et al. (2004) analyzed an integro-difference model using branching random walks and proved that speeds of invasion are never affected by stochasticity in either reproduction or dispersal or both in the absence of density-dependent effects. On the other hand, in density-dependent models, stochasticity generally decreases the speed (Mollison 1977; Lewis and Pacala 2000; Clark et al. 2001; Snyder 2003). The CA model dealt with here inevitably contains density dependence in the sense that recolonization of a preoccupied cell is ignored. Nonetheless, the stochasticity accelerates speeds in the two-dimensional CA, whereas it has no effect on the average speed in the one-dimensional CA. The apparent discrepancy between the present CA model and the integral-kernel-based models may be attributed to the fact that most mathematical analyses of the latter models appear to deal with one-dimensional space.

In nature, dispersal is stochastic and real invasion wavefronts are almost certainly irregular. Therefore, stochastic CA models may be useful for capturing some basic aspects of invasion that are difficult to explain using their deterministic or one-dimensional analogs.