1 Introduction

Nearly two third of people in the world will get internet access by 2023 and there will be 5.3 billion internet users (66 percent of world population) up from 3.9 billion (51 percent of world population) in 2018 [1]. There are some challenges like demand for high data rates, even 4G can’t fulfill. High data rates directly demand more spectrum for increasing mobile services. This leads to spectrum scarcity [2,3,4]. Fixed frequency policies proposed by government agencies cannot solve the problems of spectral shortages and underutilization. To solve the spectral efficiency problem, the FCC proposed the concept of a dynamic spectral access (DSA) policy. This policy allows CUs to access the underutilized licensed spectra [5, 6].

In [7], J. Mitola coined cognitive radio (CR) as an unlicensed device, it can operate on both licensed channels (LC) and unlicensed channels (UC) via dynamic spectrum access policy. This increases the spectral capacitance in a heterogeneous spectral environment (HetSE). Cognitive radio requires important features for significant access to LCs and UCs. That is, spectrum acquisition, spectrum management, spectrum sharing, and spectrum mobility [8, 9]. This article focuses primarily on the spectral mobility performance of various spectral strategies (opportunistic and negotiated) under HetSE from two licensed spectral pools for a single cognitive user.

In a cognitive radio network, the arrival rate of PUs has directly a negative impact on the performance of the CU. When the PU arrives at its own channel, the current CU must leave the channel and switch to another free channel, either LC or UC, to ensure quality of service (QoS) on both networks [10]. In HetSE, LC can be shared by both PU and CU, but UC follows the IEEE 802.11 standard and only shares interrupted CU and classic users (CU *) without cognitive ownership.

1.1 Related Literature to SHO Performance

In the literature, most researchers have evaluated the performance of cognitive users when operating between LCs and UCs in CR networks (CRNs). In [11], Tang et al. designed the call blocking probability and dropping probability and analyzing the performance of a secondary system where users perceive using an overlay approach that shares licensed spectrum resources with the primary system. In [12], the authors designed a Markovian model to analyze the performance of spectral transmission with buffering for new and interrupted cognitive users. In [13], Lai et al. dynamic placement and two channel reservation schemes have been proposed to minimize the probability of CU killing. In [14], the author extensively investigated the connection retention probabilities of various frequency handover schemes in cognitive radio networks. In [15], a SHO scheme based on adaptive power control was proposed to improve effective data rate of a cognitive user.

In [16], the author developed a queuing model for analyzing channel usage behavior to derive blocking and connection failure probabilities to monitor traffic on PU and CU. In [17], the author derived the probability of spectral handover and studied the effect of the time distribution remaining in the spectral gap. In [18], a joint strategy of resource allocation for SHO is proposed to analyze CU performance in CRN. In [19], the author developed a hybrid HO model on the PU activity for opportunistic CRNs. The probability of SHO and the expected number of SHOs of a CU were obtained in [20, 21] for different distributions of residual time, not taking into account the presence of UC and CU in the system.

In [22], the author tested the existence of UC and CU in HetSE to evaluate the performance of CU in CR ad hoc network. In [23], the author proposed a dynamic spectrum sharing model that considers both licensed channels (LCs) and non-licensed channels (UCs) to improve the performance of CR ad hoc network research. In [24], an analytical Markov model is developed to investigate the blocking, dropping probabilities and throughput of CUs in ad-hoc CRNs. However, the spectral access policies proposed in the literature can cause unwanted underutilization of spectrum in most cases. In [11,12,13,14,15,16,17,18,19,20,21,22, 24, 25], CUs performance is analyzed only on distributed or ad hoc cognitive radio network architectures. Various DSA schemes have been proposed in [26] to evaluate the performance of distributed and centralized CRNs, as well as various DSA schemes based on preferred CU traffic. In [26, 27] the author proposed spectral management guidelines for assessing CU performance in centralized and distributed cognitive radio networks without counting the presence of UC and CU.

In [28], the author developed both opportunistic and negotiated spectrum management schemes between HetSE CRNs with backup channels to assess CU performance. In [29], the author developed a 3D Markov chain to evaluate the blocking probability and throughput of CU considering two licensed frequency pools under HetSE in both in ad hoc and centralized situations, to assess CU performance. He also introduced the concepts of in-pool and inter-pool handoffs and evaluated their various performance metrics. In [30], the author also incorporated the concept of inter-pool and inter-pool handover of a stationary CU to study the probability of link maintenance and failure considering of two LSPs under HetSE. In [31], author analyzed the cell based SHO performance of a non-stationary CU under a HetSE in a CRN. However, a detailed analysis of pool-based SHO performance in terms of link maintenance & failure probabilities, probability mass function of SHO of a non-stationary CU is not reported in existing literature.

1.2 Contributions to the Article

The following pool-based SHO performance parameters: link retention probability, link failure probability, and probability mass function of SHO of a non-stationary CU have not been fully investigated in the existing literature. Analysis and analysis models for these parameters in HetSE for ad hoc and centralized CRNs are not available. These parameters are very important for building an effective and optimized CRN and need to be analytically modeled. Our main goal is to develop an analytical model to demonstrate the performance of CU under HetSE in ad hoc and centralized networks.

  • We propose a spectrum management scheme by considering Inter-Pool and Intra-Pool spectrum handoff strategies and derive CU performance parameters: link maintenance probability and link failure probability under HetSE for both opportunistic situation (OS) and negotiated situation (NS).

  • We use Monte-Carlo simulation mechanism to simulate the performance of CU by considering random values for the arrival rates and distributions under HetSE for both ad-hoc and centralized CRNs. The theoretical results are compared with the simulation results to validate the proposed model.

  • Thereafter, the expression of probability mass function (PMF) is derived to analyze the behavior of CU for both complete and incomplete service periods under HetSE in order to characterize the long term behavior of the network.

In Sect. 2, the proposed model of pool based spectrum is presented along with the theoretical analysis of the spectrum handoff performance parameters. The algorithm for the simulation step of the model also included in this section. Section 3 presents and discusses the both theoretical and simulation results of various performance parameters. Section 4 concludes the paper.

2 System Model and Analysis

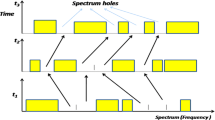
In this section, we present the system model of the CRN and investigate the performance of CU in both theoretical and simulation under HetSE for complete and incomplete CU services. We assume that HetSE have two licensed spectrum pools which consists of C1 and C2 channels respectively. These can be shared between PUs, interrupted CU and classical CU (CU*). PUs are considered with higher priority in their channels than the CU, when a PU arrives into its respective channel, CU will have to vacate that channel and need to reconnect to any other vacant channels. If there are no vacant channels, CU needs to wait for a period of Dth. If any channel vacant in Dth period CU will connect to that channel, otherwise it terminates its services. From Fig. 1 we can observe the process of Inter-Pool handoff and Intra-Pool handoff. When a CU interrupted by PU and CU finds a vacant channel in the same licensed spectrum pool in order to continue its service within Dth period, it is referred as Intra-Pool spectrum handoff. If CU finds a vacant channel in other LSP to complete the ongoing service within a Dth period, it can be referred as Inter-Pool spectrum handoff.

Fig. 1
figure 1

Pool-based spectrum handoff model under HetSE of LSP1 and LSP2

Full size image

Two LSPs are referred as LSP1 and LSP2 with C1 and C2 number of channels respectively. We assume that PUs following poison random process with mean arrival rates λpu1 and λpu2 in both LSPs respectively. Let the service periods of PUs in both LSPs are represented by the random variables (RV) \(t_{pu}\) and \(t_{{pu^{^{\prime}} }}\) \(t_{{pu^{^{\prime}} }}\) \(t_{{pu^{^{\prime}} }}\) \({\mathrm{t}}_{{\mathrm{pu}}^{\mathrm{^{\prime}}}}{\mathrm{t}}_{{\mathrm{pu}}^{\mathrm{^{\prime}}}}\), with service rates μpu1 and μpu2, residual service times \(t_{pu}^{r}\) and \(t_{{pu^{^{\prime}} }}^{r}\), probability density functions (PDFs).\(f_{{t_{pu} }} \left( t \right)\) and \(f_{{t_{{pu^{^{\prime}} }} }} \left( t \right)\), cumulative distribution functions (CDFs) \(F_{{t_{pu} }} \left( t \right)\) and \(F_{{t_{{pu^{^{\prime}} }} }} \left( t \right)\) respectively. Let a Random Variable (RV) \(t_{cu}\) represents the service period of a CU with a service rate \(\mu_{cu}\), residual period \(t_{cu}^{r}\), PDF \(f_{{t_{cu} }} \left( t \right)\) and CDF \(F_{{t_{cu} }} \left( t \right)\). The switching delays for intra-pool and inter-pool spectrum handoff are \(t_{sw}\) and \(t_{{sw^{^{\prime}} }}\) respectively. If all the channels are used by PUs in LSP1, a CU will not get service and will be blocked in LSP1. The steady state probability (pi) and blocking probability (pb1) of the CU can be obtained by Erlang-B formulae as [32]

$${\text{P}}_{{\text{i}}} = \frac{{\rho_{1}^{{\text{i}}} }}{{{\text{i}}!}}\left[ {\mathop \sum \limits_{{{\text{i}} = 0}}^{{{\text{c}}_{1} }} \frac{{\rho_{1}^{{\text{i}}} }}{{{\text{i}}!}}} \right]\;{\text{for}}\; \, 0 \le i \le \, C_{1}$$
(1)

Here i represents the channel state.

The blocking probability of CU when all LSP1 channels are blocked is defined as

$$Pb_{1} = \frac{{\rho_{1}^{{c_{1} }} }}{{c_{1} !}}\left[ {\mathop \sum \limits_{i = 0}^{{{\text{c}}_{1} }} \frac{{\rho_{1}^{i} }}{i!}} \right]^{ - 1}$$
(2)

where, \(\rho_{1} = \frac{{\lambda_{{PU_{1} }} }}{{\mu_{{PU_{1} }} }}\).

If all the channels are busy in LSP1, the CU will transfer the service to any available channel of LSP2. When all LSP2 channels are occupied by other users, the service of CU will be blocked in LSP2 and the blocking probability of CU can be obtained as

$$Pb_{2} = \frac{{\rho_{2}^{{c_{2} }} }}{{c_{2} !}}\left[ {\mathop \sum \limits_{i = 0}^{{{\text{c}}_{2} }} \frac{{\rho_{2}^{i} }}{i!}} \right]^{ - 1}$$
(3)

where, \(\rho_{2} = \frac{{\lambda_{{PU_{2} }} }}{{\mu_{{PU_{2} }} }}\).

The CU can start its service in LSP1 if there is at least one channel free in that spectrum pool. However, if any PU arrives in the same channel, the CU requires to vacate that channel immediately. The vacating probability of the CU due to the arrival of PU in opportunistic situation is obtained as

$$P_{v} = \frac{{\mathop \sum \nolimits_{i = 0}^{{c_{1} - 1}} \frac{1}{{\left( {c_{1} - 1} \right)}}P_{i} }}{{1 - P_{b1} }}$$
(4)

In case of negotiated situation,

$$P_{v\_neg} = \frac{{\mathop \sum \nolimits_{i = 0}^{{c_{1} - 1}} \left( {1 - \frac{1}{{\left( {c_{1} - 1} \right)}}} \right)P_{i} }}{{1 - P_{b1} }}$$
(5)

2.1 Link Maintenance and Link Failure Probabilities

When a PU arrives during the service period of CU, then multiple scenarios may arise. They are:

Case 1: At least one vacant channel in LSP1.

The service of CU will be maintained if the switching delay to that vacant channel is less than Dth. Switching delay is defined as

$$T_{1} = \min \left( {t_{sw,1} ,t_{sw,2} , \ldots ,t_{sw,i} ) 1 \le i \le } \right.C_{1} - 1$$
(6)

Case 2: All channels are busy in LSP1, but at least one channel is vacant in LSP2 Though all channels busy in LSP1, service of CU is maintained if switching delay to that vacant channel in LSP2 is less than Dth. Switching delay to LSP2 is defined as

$$T_{2} = \min \left( {t_{{sw^{^{\prime}} ,1}} ,t_{{sw^{^{\prime}} ,2}} , \ldots ,t_{{sw^{^{\prime}} ,i}} ) 1 \le i \le } \right.C_{2}$$
(7)

Case 3: When All channels are busy in both LSP1 and LSP2.

Service of CU is maintained if any channel is vacant within Dth period in both LSPs.

$${\text{T}}_{3} = \min \left( {{\text{t}}_{{{\text{pu}},1}}^{{\text{r}}} + {\text{t}}_{{{\text{sw}},1}} ,{\text{t}}_{{{\text{pu}},2}}^{{\text{r}}} + {\text{ t}}_{{{\text{sw}},2}} , \ldots ,{\text{t}}_{{{\text{pu}},{\text{C}}_{1} - 1}}^{{\text{r}}} + {\text{t}}_{{{\text{sw}},{\text{C}}_{1} - 1}} ,{\text{t}}_{{{\text{pu}},{\text{C}}_{1} }} } \right)$$
(8)
$${\text{T}}_{4} = \min \left( {{\text{t}}_{{{\text{pu}}^{^{\prime}} ,1}}^{{\text{r}}} + {\text{t}}_{{{\text{sw}}^{^{\prime}} ,1}} ,} \right.{\text{t}}_{{{\text{pu}}^{^{\prime}} ,2}}^{{\text{r}}} + {\text{t}}_{{{\text{sw}}^{^{\prime}} ,2}} , \ldots \ldots {\text{t}}_{{{\text{pu}}^{^{\prime}} ,{\text{C}}_{2} }}^{{\text{r}}} + { }\left. {{\text{t}}_{{{\text{sw}}^{^{\prime}} ,{\text{C}}_{2} }} } \right)$$
(9)
$${\text{T}}_{{{\text{sw}}}} = \min \left( {{\text{T}}_{3} ,{\text{T}}_{4} } \right)$$
(10)

2.1.1 Opportunistic (Ad-Hoc) Situation

In ad-hoc, there is no centralized controller. Let assume qS_OPP as total Link Maintenance Probability of cognitive user when it changes from one LSP to another or within same LSP

$$\begin{gathered} {\text{q}}_{{{\text{S}}\_{\text{OPP}}}} = {\text{P}}_{{\text{v}}} \left[ {\left( {1 - {\text{Pb}}_{1} } \right){\text{P}}_{{\text{r}}} \left( {{\text{T}}_{1} \le {\text{D}}_{{{\text{th}}}} } \right)} \right. + {\text{P}}_{{{\text{b}}1}} \left[ {\left( {1 - {\text{Pb}}_{2} } \right){\text{P}}_{{\text{r}}} \left( {{\text{T}}_{2} \le {\text{D}}_{{{\text{th}}}} } \right) + {\text{Pb}}_{1} {\text{Pb}}_{2} {\text{P}}_{{\text{r}}} \left( {{\text{T}}_{{{\text{sw}}}} \le {\text{D}}_{{{\text{th}}}} } \right)} \right] \hfill \\ \quad \quad \quad = {\text{P}}_{{\text{v}}} \left[ {\left( {1 - {\text{Pb}}_{1} } \right)(1 - \alpha^{{{\text{C}}_{1} }} } \right) + {\text{P}}_{{{\text{b}}1}} \left[ {\left( {1 - {\text{Pb}}_{2} } \right)\left( {1 - \beta^{{{\text{C}}_{2} }} } \right) + {\text{Pb}}_{1} {\text{Pb}}_{2} \left( {1 - \beta_{1}^{{{\text{C}}_{1} - 1}} \gamma \xi^{{{\text{C}}_{2} }} } \right)} \right] \hfill \\ \end{gathered}$$
(11)

where,

$$\alpha = \Pr \left( {t_{sw} > D_{th} } \right) = 1 - F_{{t_{sw} }} \left( {D_{th} } \right)$$
$$\beta = \Pr \left( {t_{{sw^{^{\prime}} }} > D_{th} } \right) = 1 - F_{{t_{{sw^{^{\prime}} }} }} \left( {D_{th} } \right)$$
$$\beta_{1} = \Pr \left( {\left( {t_{pu}^{r} + t_{sw} } \right) > D_{th} } \right) = 1 - F_{{t_{pu}^{r} + t_{sw} }} \left( {D_{th} } \right)$$
$$\gamma = \Pr \left( {t_{pu} > D_{th} } \right) = 1 - F_{{t_{pu} }} \left( {D_{th} } \right)$$
$$\xi = \Pr \left( {\left( {t_{pu}^{r} + t_{{sw^{^{\prime}} }} } \right) > D_{th} } \right) = 1 - F_{{t_{pu}^{r} + t_{{sw^{^{\prime}} }} }} \left( {D_{th} } \right)$$

If all channels in both LSPs are busy and no channel going to be vacant in Dth period, then link failure occurs, it is referred as qf_OPP.

$$\begin{gathered} {\text{q}}_{{{\text{f}}\_{\text{OPP}}}} = {\text{P}}_{{\text{v}}} {\text{Pb}}_{1} {\text{Pb}}_{2} {\text{P}}_{{\text{r}}} ({\text{T}}_{{{\text{sw}}}} > {\text{D}}_{{{\text{th}}}} ) \hfill \\ \quad \quad \quad = {\text{P}}_{{\text{v}}} {\text{Pb}}_{1} {\text{Pb}}_{2} {\text{P}}_{{\text{r}}} \beta_{1}^{{C_{1} - 1}} \gamma \xi^{C2} \hfill \\ \end{gathered}$$
(12)

In Intra-Pool spectrum handoff, link maintenance and link failure probabilities are:

$${\text{q}}_{{{\text{s}}1\_{\text{OPP}}}} = {\text{P}}_{{\text{v}}} \left[ {\left( {1 - {\text{Pb}}_{1} } \right){\text{P}}_{{\text{r}}} ({\text{T}}_{1} \le {\text{D}}_{{{\text{th}}}} } \right) + {\text{ Pb}}_{1} {\text{Pb}}_{2} {\text{P}}_{{\text{r}}} \left( {{\text{T}}_{3} \le {\text{D}}_{{{\text{th}}}} } \right)]$$
(13)
$$\begin{gathered} {\text{q}}_{{{\text{f}}1\_{\text{OPP}}}} = {\text{P}}_{{\text{v}}} {\text{Pb}}_{1} {\text{Pb}}_{2} {\text{P}}_{{\text{r}}} ({\text{T}}_{3} > {\text{D}}_{{{\text{th}}}} )] \hfill \\ \quad \quad \quad = {\text{P}}_{{\text{v}}} {\text{Pb}}_{1} {\text{Pb}}_{2} \left( {\beta_{1}^{{C_{1} - 1}} } \right)] \hfill \\ \end{gathered}$$
(14)

In case of Inter-Pool handoff, link maintenance and link failure probabilities are derived as

$${\text{q}}_{{{\text{s}}2\_{\text{OPP}}}} = {\text{P}}_{{\text{v}}} {\text{Pb}}_{1} \left[ {\left( {1 - {\text{Pb}}_{2} } \right){\text{P}}_{{\text{r}}} ({\text{T}}_{2} \le {\text{D}}_{{{\text{th}}}} } \right) + {\text{P}}_{{\text{r}}} \left( {{\text{T}}_{4} \le {\text{D}}_{{{\text{th}}}} } \right)]$$
(15)
$$\begin{gathered} {\text{P}}_{{\text{v}}} {\text{Pb}}_{1} \left[ {\left( {1 - {\text{Pb}}_{2} } \right)\left( {1 - \beta^{{C_{2} }} } \right) + {\text{ Pb}}_{2} (1 - \xi^{{C_{2} }} } \right)] \hfill \\ {\text{q}}_{{{\text{f}}2\_{\text{OPP}}}} = {\text{P}}_{{\text{v}}} {\text{Pb}}_{1} {\text{Pb}}_{2} {\text{P}}_{{\text{r}}} ({\text{T}}_{4} > {\text{D}}_{{{\text{th}}}} ) = {\text{P}}_{{\text{v}}} {\text{Pb}}_{1} {\text{Pb}}_{2} \xi^{{C_{2} }} \hfill \\ \end{gathered}$$
(16)

2.1.2 Negotiated (Centralized) Situation

In negotiated situation, there is a centralized controller which assigns a channel to CU. Let assume qs_neg and qf_neg as LMF and LFP respectively.

$$\begin{gathered} {\text{q}}_{s\_neg} = {\text{P}}_{v\_neg} \left[ {\left( {1 - {\text{Pb}}_{2} } \right){\text{P}}_{{\text{r}}} \left( {{\text{T}}_{2} \le {\text{D}}_{{{\text{th}}}} } \right) + {\text{ Pb}}_{2} {\text{P}}_{{\text{r}}} \left( {{\text{T}}_{{{\text{sw}}}} \le {\text{D}}_{{{\text{th}}}} } \right)} \right] \hfill \\ \quad \quad \quad = {\text{P}}_{v\_neg} \left[ {\left( {1 - {\text{Pb}}_{2} } \right)\left( {1 - \beta^{{C_{2} }} } \right) + {\text{Pb}}_{2} \left( {1 - \beta_{1}^{{C_{1} - 1}} \gamma \xi^{{C_{2} }} } \right)} \right] \hfill \\ \end{gathered}$$
(17)
$$\begin{gathered} {\text{q}}_{{{\text{f}}\_{\text{neg}}}} = {\text{P}}_{{{\text{v}}\_{\text{neg}}}} {\text{Pb}}_{2} {\text{P}}_{{\text{r}}} ({\text{T}}_{{{\text{sw}}}} > {\text{D}}_{{{\text{th}}}} ) \hfill \\ \quad \quad \quad = {\text{P}}_{{{\text{v}}\_{\text{neg}}}} {\text{Pb}}_{2} \beta_{1}^{{C_{1} - 1}} \gamma \xi^{{C_{2} }} \hfill \\ \end{gathered}$$
(18)

Let’s dive into more detail, in case of Intra-Pool spectrum handoff, link maintenance and link failure probabilities are derived as

$$\begin{gathered} {\text{q}}_{s1\_neg} = {\text{P}}_{{{\text{v}}\_{\text{neg}}}} [{\text{Pb}}_{2} {\text{P}}_{{\text{r}}} \left( {{\text{T}}_{3} \le {\text{D}}_{{{\text{th}}}} } \right)] \hfill \\ \quad \quad \quad = {\text{P}}_{{{\text{v}}\_{\text{neg}}}} \left[ {{\text{Pb}}_{2} \left( {1 - \beta_{1}^{{C_{1} - 1}} } \right)} \right] \hfill \\ \end{gathered}$$
(19)
$$\begin{gathered} {\text{ q}}_{{{\text{f}}1\_{\text{neg}}}} = {\text{P}}_{{{\text{v}}\_{\text{neg}}}} {\text{P}}_{{\text{r}}} \left( {{\text{T}}_{3} \le {\text{D}}_{{{\text{th}}}} } \right) \hfill \\ \quad \quad \quad = {\text{P}}_{{{\text{v}}\_{\text{neg}}}} \left( {1 - \beta_{1}^{{C_{1} - 1}} } \right) \hfill \\ \end{gathered}$$
(20)

In case of Inter-Pool spectrum handoff, link maintenance and link failure probabilities are derived as

$$\begin{gathered} {\text{q}}_{{{\text{s}}2_{{{\text{neg}}}} }} = {\text{P}}_{{{\text{v}}_{{{\text{neg}}}} }} \left[ {\left( {1 - {\text{Pb}}_{2} } \right){\text{P}}_{{\text{r}}} \left( {{\text{T}}_{2} \le {\text{D}}_{{{\text{th}}}} } \right) + {\text{Pb}}_{2} {\text{P}}_{{\text{r}}} \left( {{\text{T}}_{4} \le {\text{D}}_{{{\text{th}}}} } \right)} \right. \hfill \\ \quad \quad = {\text{P}}_{{{\text{v}}\_{\text{neg}}}} \left[ {\left( {1 - {\text{Pb}}_{2} } \right)\left( {1 - \beta^{{C_{2} }} } \right) + {\text{ Pb}}_{2} \left( {1 - \xi^{{C_{2} }} } \right)} \right] \hfill \\ \end{gathered}$$
(21)
$${\text{q}}_{{{\text{f}}2\_{\text{neg}}}} = {\text{P}}_{{{\text{v}}\_{\text{neg}}}} {\text{Pb}}_{2} {\text{P}}_{r} ({\text{T}}_{4} > {\text{D}}_{{{\text{th}}}} ) = P_{v\_neg} Pb_{2} \xi^{{C_{2} }}$$
(22)

These equations are later used to model the PMF and the conditions are used in Monte-Carlo simulation to verify the performance of spectrum handoff of CU in terms of both theorical and simulation.

2.2 PMF of Spectrum Handoff

This section derives Probability Mass Function of SHO for both complete and incomplete services of the CU in OSs. Performs multiple spectral handovers during the CU's service period before it completes successfully. Suppose you need to perform "n" spectral handovers to complete the service. Performing all "n" handovers is said to be the full service of the CU. If you only perform the "n1" handover and end with the "nth" handover, this is called an incomplete service on the CU. The probability mass function (PMF) focuses primarily on the discrete probabilities of RVs. This gives you the probability of "n" spectral.

For the Poisson arrival process, the PU arrival time Sn during the CU working hours follows the Erlang distribution [33], the pdf of Sn can be defined as

$$f_{{S_{n} }} \left( t \right) = \frac{{{\uplambda }_{{{\text{pu}}}}^{n} t^{n - 1} e^{{ - {\uplambda }_{{{\text{pu}}}} t}} }}{{\left( {n - 1} \right)!}} , n \ge 1$$
(23)

where,

$$S_{n} = t_{pu,1} + t_{pu,2} + \ldots + t_{pu,n} = \mathop \sum \limits_{n = 1}^{m} t_{pu,n}$$
(24)

where Tpu, n represents the time between arrivals between the (n-1) th and nth PU arrivals. If the CU's service period is shorter than the time between arrivals of the same PU, the CU may experience a zero-spectral handover. The channel or PU arrives at another channel in the LSP. This allows the PMF of the zero-spectrum handover from the CU in the OS to be described as:

$$\Pr \left( {H = 0} \right)$$
$$\begin{gathered} = \left( {T_{cu} < t_{pu,1} } \right) + \mathop \sum \limits_{m = 1}^{\infty } \Pr \left( {S_{m} < T_{cu} < S_{m + 1} } \right)\left( {1 - P_{v} } \right)^{m} \hfill \\ = f_{{T_{cu} }}^{*} \left( {{\uplambda }_{{{\text{pu}}}} } \right) + \mathop \sum \limits_{m = 1}^{\infty } \frac{{\left( {{\uplambda }_{{{\text{pu}}}} {\text{P}}_{{\text{v}}} - {\uplambda }_{{{\text{pu}}}} } \right)^{m} }}{m!}f_{{T_{cu} }}^{*\left( m \right)} \left( {{\uplambda }_{{{\text{pu}}}} } \right) \hfill \\ \end{gathered}$$
(25)

where \(f_{{T_{cu} }}^{*} \left( {. } \right)\) represents the Laplace transform of \(f_{{T_{cu} }} \left( { .} \right)\) and \(f_{{T_{cu} }}^{*\left( m \right)} \left( { .} \right)\) represents mth order derivative of \(f_{{T_{cu} }}^{*} \left( \right)\).

Apply the Taylor’s theorem (infinite series) in 2nd term of (25), we get the simplified form of Pr(H = 0) as

$$\begin{gathered} \Pr \left( {H = 0} \right) = f_{{T_{cu} }}^{*} \left( {{\uplambda }_{{{\text{pu}}}} } \right) + \left[ {f_{{T_{cu} }}^{*} \left( {{\uplambda }_{{{\text{pu}}}} {\text{P}}_{{\text{v}}} } \right) - f_{{T_{cu} }}^{*} \left( {{\uplambda }_{{{\text{pu}}}} } \right)} \right] \hfill \\ = f_{{T_{cu} }}^{*} \left( {{\uplambda }_{{{\text{pu}}}} {\text{P}}_{{\text{v}}} } \right) \hfill \\ \end{gathered}$$
(26)

Let say (m + n) PUs are arriving in the LSP and consider ‘m’ PUs are not hitting the same channel of CU and ‘n’ are coming to same channel where CU is servicing. CU service is completed if it performs all ‘n’ handoffs successfully otherwise, it is an incomplete service. The PMF by considering these two situations is expressed as

$${\text{P}}\left( {{\text{H}} = {\text{n}}} \right) = {\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{{\text{succ}}}} + {\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{\text{term }}}$$
(27)

where \({\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{{\text{succ}}}}\) refers to complete service and \({\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{\text{term }}}\) incomplete service probabilities of CU.

During complete service of CU two cases may arise, they are:

CASE 1: All ‘n’ handoffs occur in same LSP. It is defined in [28] as

$${\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{{\text{succ}}1}} { } = \frac{{\left( { - {\uplambda }_{{{\text{pu}}1}} {\text{q}}_{{{\text{s}}1}} } \right)^{{\text{n}}} }}{{{\text{n}}!}}{\text{f}}_{{{\text{T}}_{{{\text{cu}}}} }}^{{\text{*n}}} \left( {{\uplambda }_{{{\text{pu}}1,}} {\text{P}}_{{\text{v}}} } \right)$$
(28)

CASE 2: (n—r) spectrum handoffs occur in one LSP and ‘r’ handoffs occur in another LSP. It can be defined as

$$\begin{gathered} {\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{{\text{succ}}2}} = \mathop \sum \limits_{{{\text{r}} = 1}}^{{\text{n}}} \frac{{\left( { - {\uplambda }_{{{\text{pu}}1}} {\text{q}}_{{{\text{s}}1}} } \right)^{{{\text{n}} - {\text{r}}}} \left( { - {\uplambda }_{{{\text{pu}}2}} {\text{q}}_{{{\text{s}}2}} } \right)^{{\text{r}}} }}{{\left( {{\text{n}} - {\text{r}}} \right)!{\text{r}}!}} \hfill \\ \quad \quad \quad \quad\quad \times {\overline{\text{F}}}_{{{\text{T}}_{{{\text{cu}}}} }}^{{{*}\left( {{\text{n}} - {\text{r}}} \right)}} \left( {{\uplambda }_{{{\text{pu}}1}} {\text{P}}_{{\text{v}}} } \right){\overline{\text{F}}}_{{{\text{T}}_{{{\text{cu}}}} }}^{{\text{*r}}} \left( {{\uplambda }_{{{\text{pu}}2}} {\text{P}}_{{\text{v}}} } \right) \hfill \\ \end{gathered}$$
(29)

where ‘r’ represents a variable ranging from 1 to ‘n’ inclusively.

From (28) and (29) we can write \({\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{{\text{succ}}}}\) as

$${\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{{\text{succ}}}} = {\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{{\text{succ}}1}} + {\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{{\text{succ}}2}}$$
(30)

Next, the probability of handoff failure or service termination is derived due to the failure of nth handoff during its total service time. Here we assume, during the service of CU, (n—r) spectrum handoffs are successfully performed in LSP1 and (r—1) spectrum handoffs are successfully performed in LSP2. Therefore, the CU successfully completes total (n—1) spectrum handoff and nth handoff is terminated due to unavailable vacant channels in Dth time. The probability of handoff failure of the CU for this case can be modeled as

$$\begin{gathered} {\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{{\text{term}}}} = \mathop \sum \limits_{{{\text{r}} = 1}}^{{\text{n}}} \frac{{\left( { - {\uplambda }_{{{\text{pu}}1}} {\text{q}}_{{{\text{s}}1}} } \right)^{{{\text{n}} - {\text{r}}}} \left( { - {\uplambda }_{{{\text{pu}}2}} {\text{q}}_{{{\text{s}}2}} } \right)^{{{\text{r}} - 1}} }}{{\left( {{\text{n}} - {\text{r}}} \right)!{\text{r}}!}} \hfill \\ \quad \quad \quad \quad \quad \times \, {\overline{\text{F}}}_{{{\text{T}}_{{{\text{cu}}}} }}^{{{*}\left( {{\text{n}} - {\text{r}}} \right)}} \left( {{\uplambda }_{{{\text{pu}}1}} {\text{P}}_{{\text{v}}} } \right){\overline{\text{F}}}_{{{\text{T}}_{{{\text{cu}}}} }}^{{{*}\left( {{\text{r}} - 1} \right)}} \left( {{\uplambda }_{{{\text{pu}}2}} {\text{P}}_{{\text{v}}} } \right){\text{q}}_{{\text{f}}} \hfill \\ \end{gathered}$$
(31)

By Substituting \({\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{{\text{succ}}}}\) and \({\text{P}}_{{\text{r}}} \left( {\text{H}} \right)_{{\text{term }}}\) from (30) and (31) in (27), the term P(H = n) can be calculated as

$$\begin{gathered} {\text{P}}\left( {{\text{H}} = {\text{n}}} \right) = \frac{{\left( { - {\uplambda }_{{{\text{pu}}1}} {\text{q}}_{{{\text{s}}1}} } \right)^{{\text{n}}} }}{{{\text{n}}!}}{\text{f}}_{{{\text{T}}_{{{\text{cu}}}} }}^{{\text{*n}}} \left( {{\uplambda }_{{{\text{pu}}1,}} {\text{P}}_{{\text{v}}} } \right) + \mathop \sum \limits_{{{\text{r}} = 0}}^{{\text{n}}} \frac{{\left( { - {\uplambda }_{{{\text{pu}}1}} {\text{q}}_{{{\text{s}}1}} } \right)^{{{\text{n}} - {\text{r}}}} \left( { - {\uplambda }_{{{\text{pu}}2}} {\text{q}}_{{{\text{s}}2}} } \right)^{{\text{r}}} }}{{\left( {{\text{n}} - {\text{r}}} \right)!{\text{r}}!}}{\overline{\text{F}}}_{{{\text{T}}_{{{\text{cu}}}} }}^{{{*}\left( {{\text{n}} - {\text{r}}} \right)}} \left( {{\uplambda }_{{{\text{pu}}1}} {\text{P}}_{{\text{v}}} } \right) \hfill \\ \quad \quad \times \, {\overline{\text{F}}}_{{{\text{T}}_{{{\text{cu}}}} }}^{{\text{*r}}} \left( {{\uplambda }_{{{\text{pu}}2}} {\text{P}}_{{\text{v}}} } \right) + \mathop \sum \limits_{{{\text{r}} = 1}}^{{\text{n}}} \frac{{\left( { - {\uplambda }_{{{\text{pu}}1}} {\text{q}}_{{{\text{s}}1}} } \right)^{{{\text{n}} - {\text{r}}}} \left( { - {\uplambda }_{{{\text{pu}}2}} {\text{q}}_{{{\text{s}}2}} } \right)^{{{\text{r}} - 1}} }}{{\left( {{\text{n}} - {\text{r}}} \right)!{\text{r}}!}} \hfill \\ \quad \quad \times \, {\overline{\text{F}}}_{{{\text{T}}_{{{\text{cu}}}} }}^{{{*}\left( {{\text{n}} - {\text{r}}} \right)}} \left( {{\uplambda }_{{{\text{pu}}1}} {\text{P}}_{{\text{v}}} } \right){\overline{\text{F}}}_{{{\text{T}}_{{{\text{cu}}}} }}^{{{*}\left( {{\text{r}} - 1} \right)}} \left( {{\uplambda }_{{{\text{pu}}2}} {\text{P}}_{{\text{v}}} } \right){\text{q}}_{{\text{f}}} \hfill \\ \end{gathered}$$
(32)

2.3 Simulation Algorithm for the Model

In this section, we develop a simulation algorithm for the above defined system model to evaluate the performance measuring metrics of SHO such as link maintenance and link failure probabilities under HetSE in both ad-hoc (opportunistic) and centralized (negotiated) situations. In Fig. 2 represents the algorithm for the Monte–Carlo simulation of the various SHO performance metrics which is performed by using multi-paradigm programming language in Python software. Here, the term ‘n’ represents the number of iterations in Monte Carlo simulations and we have taken it as 1,00,000 to obtain spectrum handoff performance accurately. Other parameters: tsw, tcp, \(t_{pu}\), \({\text{t}}_{{{\text{pu}}}}^{{\text{r}}}\) and \({\text{t}}_{{{\text{pu}}^{^{\prime}} }}^{{\text{r}}}\) are randomly generated according to their distribution function. While simulating, parameters like \(\alpha , \beta , \beta_{1} \gamma {\text{and}} \xi\) are calculated and at last their average values are taken to calculate link maintenance and link failure probabilities under HetSE for both ad-hoc and centralized CRNs.

Fig. 2
figure 2

Monte-Carlo simulation algorithm

Full size image

In Fig. 2, Dth = Threshold time period.tsw1 = Intra-pool Spectrum Handoff delay.tsw2 = Inter-pool Spectrum Handoff delay.tcp = Service Period of Pus.tcpr1 = Residual Service Period of PUs in LSP-1.tcpr2 = Residual Service Period of PUs in LSP-2. RVs = Random Variables.

3 Results and Discussion

This section investigates the SHO parameters such as link maintenance and link failure probabilities along with simulations in both ad-hoc and centralized CRNs. Also presents probability mass function of CU under HetSE. We assume the values without any specifications for following parameters: \(\mu_{{pu^{^{\prime}} }} = 1/180s\), \(\lambda_{pu2} = 0.05 pu^{^{\prime}} /s\), \(\lambda_{cu} = 0.05 cu/s\), \(1/\mu_{cu} = 180s\), \(D_{th} = 18\), \(C_{1} = 12\). The IEEE 802.11a and 802.11 h standards support up to 12 and 11 unique channels, respectively. Therefore, it is considered as C2 = 10 in the analysis. These parameters values are replaced in the above equations to calculate LMP, LFP and PMF of CU under different situations.

Figure 3a and b depict the LMP and LFP, respectively with varying \({\uplambda }_{{{\text{pu}}1}}\) under both opportunistic (ad-hoc) and negotiated (centralized) situations. From Results, we can clearly say that the ad-hoc situation has a high LMP (maximum 0.94) than centralized situation (maximum 0.27) of the CRN. While increasing arrival rate of PUs, both LMP and LFP are increasing in OS. But in negotiated situation, both probabilities are increasing to certain point and then decreasing because of higher vacating probability of CU in ad-hoc scenario when compared to centralized network scenario.

Fig. 3
figure 3

a LMP and b LFP with varying \({\lambda }_{pu1}\) in opportunistic and negotiated situations

Full size image

From Fig. 4a and b, we can observe that while increasing \({\uplambda }_{{{\text{pu}}1}}\), the LMP during inter-pool SHO (qs1) is increasing, whereas the LMP during intra-pool SHO (qf1) is decreasing. But the LFP during intra-pool SHO (qs2) is gradually increasing with increasing \({\uplambda }_{{{\text{pu}}1}}\) whereas LFP during inter-pool SHO (qf2) is almost constant. From Fig. 5a and b, we can notice that the intra-pool LFP is dominating LMP, but both are decreasing with increasing \({\uplambda }_{{{\text{pu}}1}}\). Both inter-pool LMP and LFP are decreasing gradually after certain peak.

Fig. 4
figure 4

LMP and LFP of a Intra-Pool and b Inter-Pool SHOs in OS with varying \({\lambda }_{pu1}\)

Full size image
Fig. 5
figure 5

LMP and LFP of a Intra-Pool and b Inter-Pool SHOs in negotiated situation with varying \({\lambda }_{pu1}\)

Full size image

Figure 6a shows the LMPs during intra-pool and inter-pool SHO in OS of the CRN. Here, we can observe that by increasing arrival rate of PUs, inter-pool LMP is increasing but intra-pool LMP is decreasing in OS, which is because of more PUs are arriving in LSP1. Therefore, the CU is required to vacate the channel more due to the more number of interruption during its service. Upon all the channels are occupied by PUs in LSP1, the CU will move to vacant channel of LSP2 which is the root cause for the increase of LMP during inter-pool SHO process. Figure 6b presents the intra-pool and inter-pool LFP of CU in OS. From Fig. 6b, we can observe that the intra-pool LFP is gradually increasing than inter-pool LFP because of the more arrival of PUs in LSP1 than LSP2.

Fig. 6
figure 6

Intra-Pool and Inter-Pool a LMPs and b LFPs in OS with varying \({\lambda }_{pu1}\)

Full size image

The LMP and LFP during both intra-pool & inter-pool SHO schemes under negotiated situation are depicted in Fig. 7a and b, respectively. By observing Fig. 7a and b, we can conclude that the performance of the metrics are totally different for both opportunistic and negotiated situations. The Inter-Pool LMP is dominating from the beginning as a controller is assigning more PUs to LSP2 than LSP1 due to more vacant channels are present in LSP2 at early stage of arrival of PUs.

Fig. 7
figure 7

Intra-Pool and Inter-Pool a LMPs and b LFPs in negotiated situation with varying \({\uplambda }_{{{\text{pu}}1}}\)

Full size image

Figure 8a, b and c present the PMFs of zero, 1st and 2nd SHO respectively, of a non-stationary CU in both the opportunistic and negotiated scenarios of the CRN. By investigating Fig. 8a, we can conclude that by increasing arrival rate of PUs the chance of occurring zero spectrum handoff is decreasing in both opportunistic and negotiated situations. However, in Fig. 8b, the chances of occurring one spectrum handoff is increasing with increasing arrival rate of PUs in OS. In negotiated situation, first we saw a peek of increasing probability for 1st handoff, later it is slowly decreasing. This is because of no controller is there in OS to manage incoming PUs and CUs, so the chances of occurring handoff is increasing with more arriving PUs. Similarly, in Fig. 8c, both situations are following same trend for PMF of 2nd SHO as 1st SHO in Fig. 8b with a small change of characteristics in OS. From result, we can conclude that the higher SHOs also follow the same trend which found in Fig. 8b and c, respectively. From the Results, it is clearly seen that both the opportunistic and negotiated situations offers significant differences in the analysis of various spectrum handoff performance measuring metrics.

Fig. 8
figure 8

PMF of a zero, b 1st and c 2nd SHO respectively in both situations

Full size image

4 Conclusions

This article thoroughly explores the performance and characteristics of pool-based spectrum handoffs of a CU in HetSE under ad-hoc (opportunistic) and centralized (negotiated) situations. We model the various performance metrics such as LMP, LFP, & probability mass function (PMF) of n SHOs of a non-stationary CU in CRN. We also perform the Monte-Carlo simulation algorithm for the metrics in Python software platform to investigate the performance of the CRN under HetSE in both opportunistic and negotiated situations. We have seen a clear-cut difference between the performance metrics: LMP, LFP and the probability mass function of zero, 1st and 2nd SHOs under both opportunistic and negotiation situations. We have also seen that under the influence of arrival rate of PUs, the LMP and LFP in intra-pool and inter-pool SHO seen a significance difference in both situations. The maximum value of LMPs are observed as 0.944 and 0.27 in opportunistic situation and negotiated situation, respectively. As the channel vacating probability is lower in negotiated situation, the LMP also lower in negotiated situation as compared to opportunistic situation. The comparison between theoretical and simulation results ensures our correctness of the proposed model and designed schemes. Both the techniques and results are important for analyzing and designing the CRNs along with the coexistence of PUs and CUs.