1 Introduction

Spectrum is the most important resource of wireless technology. The spectrum allocated to wireless application is so far static. However, recent research shows that a large portion of the assigned spectrum is used sporadically leading to underutilization and wastage of valuable frequency resources [1]. Even in a highly crowded area the occupancy is <35 % of the radio spectrum below 3 GHz [2]. To address spectrum underutilization, cognitive radio (CR) [3–5] is envisaged as a potential technology for dynamic allotment of unused frequency bands, called white spaces or spectrum hole. To explore the potentiality of CR, Federal Communications Commission (FCC) has approved the use of unlicensed devices in licensed bands [3].

Cognitive radio is an intelligent wireless communication system that is responsive towards surrounding; quickly learns and adapts the internal states according to the statistical fluctuations of the incoming radio frequency (RF) signal through required changes in selected operating parameters in real time scenario [5–8]. There are two aspects of CR (a) highly reliable and seamless communications everywhere and (b) efficient utilization of the radio spectrum resource.

Spectrum mobility is a major component for successful implementation of CR. The main purpose of spectrum mobility in cognitive radio networks (CRNs) is to perform seamless channel switchover to maintain the ongoing secondary user (SU) communication and, thereon confirming quality of service (QoS) and throughput [9]. Spectrum mobility is divided into two processes: spectrum handoff and connection management. Spectrum handoff is defined as the process of transferring ongoing communication from the current channel to another free channel without disrupting the connection and ensuring quality of service. Therefore, additional latency is associated with the SU communication which sooner or later affects SU performance. It is the connection management process which administers the protocol stack parameters depending on present scenario.

Call holding time and channel holding time plays a major role in determining the performance metric of tele-traffic analysis of a system. The call holding time is defined as the period from the instant the accepted call starts to the instant the call completes. The channel holding time is defined as the period from the instant an active call occupies the channel to the instant the active call releases the channel.

Most of the existing literature assumed the channel holding time as exponentially distributed [10–14] for tele-traffic analysis. Channel holding time controls the other key network design parameters such as call blocking probability, the probability of handoff etc. [12]. Bolotin [15] found that channel throughput falls considerably under an exponential call holding time distribution model compared to the actual measured call holding time distribution. This observation is expected to be true for personal communication system (PCS) networks. In [16], Liu et al. presented the probability and time relationship model of spectrum handoff considering both the distribution of CR user’s call holding time and residual time of spectrum holes as Poisson’s random process. The residual time (h) of spectrum hole indicates the remaining time at the current spectrum hole after the commencement of the service call. However, Barcelò and Jordan [17, 18], based on some experiments on the cellular telephone system have concluded that the negative exponential distribution is not a good approximation of the channel holding time.

The traditional exponential distribution used for call holding time and channel holding time may not be appropriate for hostile mobile environment [19]. It is mentioned that for the holding time, Erlang function and Log–normal distribution functions are found to be better approximation than the exponential.

A comprehensive study and an analytical model for spectrum handoff under CR environment are very significant for implementation of efficient spectrum management. However, a detailed study on the effect of various distribution models on probability of handoff in CR is not reported so far to the best of our knowledge.

In this paper, we have introduced the probability and time relationship model of spectrum handoff for diverse distribution of residual time of spectrum holes. We establish a standard generalized analytical model for probability of handoff under diverse distribution model for residual time of spectrum holes considering departure rate of cognitive user to be as Poisson random process. We have considered the following distribution functions for residual time of spectrum holes in our analysis: (1) exponential, (2) Erlang-2, (3) Erlang-3, (4) Erlang-3, 23 and (5) Lognormal. In [16], the authors have provided spectrum handoff analysis without switching delay. However, switching delay is an important factor which is directly related to link failure and hence the Quality of Service (QoS) [20]. In our model we have introduced a finite switching delay (t r ) which is assumed to be the combination of sensing time and transition delay between spectrum holes. Any delay greater than switching delay will lead to degradation of quality of service and link failure.

The rest of the paper is organized as follows: In Sect. 2, the basics of spectrum mobility and spectrum handoff is investigated. The motivation behind the work is also explained in this section. In Sect. 3, we have introduced probability and time relationship model of spectrum handoff for different distribution models and established a generalized standard analytic form for the same. The algorithm for computer simulation of the analytical models is presented in Sect. 4. We present the simulation along with analytical results in Sect. 5. Also the results of spectrum handoff probability with and without switching delay are included. An exhaustive comparison of these results for all considered distribution models are explored in this Sect. 6 concludes the paper including future work directions.

2 Spectrum Mobility and Spectrum Handoff

Cognitive radio has four major tasks: spectrum sensing, spectrum management, spectrum sharing and spectrum mobility. A comprehensive research has been conducted on spectrum sensing over the last decade. Spectrum mobility necessitates much more attention for an effective implementation of the secondary network. It is important to maintain uninterrupted communication of secondary user (SU) during the transition from one channel to another free channel resulting in key issue of spectrum handoff.

When an unused frequency band, as decided through spectrum sensing, is utilized by cognitive user (or SU) and a licensed user arrives, then CR user shall perform one of the following actions: (a) it continues the access if the primary user (PU) request band is non-overlapping and (b) release the licensed channel immediately sensing incoming PU activity in the same band. There may be two PU related procedures which can activate spectrum handoff for the above cited issues [9].

Firstly, licensed user (PU) arrival in the licensed channel essentially compels CR user to carry out spectrum handoff. Secondly, because of spatial movement of CR users, there is a chance of spectrum overlap with an active band; hence spectrum handoff can occur because of CR user mobility over the spatial domain.

While the impetus of CR technology is straight forward, the design and implementation put greater challenges. Spectrum handoff is the most important intricacy and an intrinsic capability parameter to support reliable service.

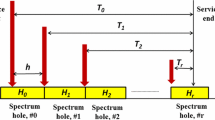
Figure 1 describes the mobility of spectrum holes. The yellow boxes symbolize spectrum which are being used by licensed users at any particular time instant, while the empty slots indicate spectrum holes which can be used by unlicensed or cognitive users. The arrow indicates the probable movement of spectrum holes to ensure seamless communication of secondary users without any link failure. Changing of its own operating frequency band at different time instants is the key of spectrum handoff. In the next section we derive the analytical expression for the probability of spectrum handoff for different distribution models.

Fig. 1
figure 1

Spectrum mobility at different time in different bands

Full size image

3 Derivation of Probability of Spectrum Handoff

Spectrum handoff is directly associated with the QoS and hence the system performances. A spectrum handoff strategy in advance offers a better management of system performance. In this section, we derive a state of the art standard form of spectrum handoff probability considering one call service time of secondary cognitive user without switching delay. While deriving the expressions following are the basic assumptions required to be satisfied.

  • For CR User or Secondary User

The service call arrival and departure of cognitive user are both Poisson random process [13]. The cognitive user is stationary i.e. the user does not change its geographical position during one call duration. Also it is assumed that there are spectrum holes available during this period.

Let us consider 1/µ is the mean time of each call’s duration. Then, the probability density function (pdf) of cognitive user’s call duration, approximating exponential distribution model, is given as:

$$ \Phi (x) = \left\{{\begin{array}{ll} {\mu e^{ - \mu x} } \hfill & {{\text{for}}\;\; x \ge 0} \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(1)

where µ is the departure rate of cognitive user.

  • For Spectrum Holes

The holding time H i of each spectrum hole is a continuous random variable and H i (where i = 0, 1, 2….) has the identical and independent distribution (i.i.d) corresponding to the spectrum hole nomenclature as #0, #1, #2…. The cognitive user, in one service call duration, uses these available spectrum holes in sequence. The probability density function is indicated by Ψ(x) and the mean value is presented by 1/λ. The expectation of the i.i.d random variable should be equal to the mean value and variance must have a finite value. Mathematically,

$$ \begin{aligned} E[X_{i} ] = \frac{1}{\lambda } & < \infty \quad \forall i\;\; [i = 0,1,2 \ldots ] \\ Var[X_{i} ] & < \infty \quad \forall i\;\; [i = 0,1,2 \ldots ] \\ \end{aligned} $$

where E[.] is the statistical estimation parameter and Var[.] is the variance of the random parameter and λ is the average departure rate of spectrum hole.

  • Numbering of Spectrum Holes (#0, #1, #2,…)

It is assumed that the CR controller organizes the list of available spectrum holes through proper spectrum sensing and decision rule. In a service call the cognitive user starts accessing the spectrum holes with tag #0 and subsequent holes will be accessed in sequence.

  • For Spectrum Switching Delay (t r )

We assume that the distribution of switching delay is characterized by call arrival process of PU in the cognitive environment.

3.1 Spectrum Handoff Probability

During one service call holding time, the time relation between spectrum hole, holding time and residual time is shown in Fig. 2a. As shown in Fig. 2a, h is residual time of accessed spectrum hole when a service begins. Here a single service call duration time of cognitive user is denoted by T 0. In Fig. 2a, H i denotes the holding time of spectrum hole #i occupied by cognitive user corresponding to the service call duration time T i of cognitive user.

Fig. 2
figure 2

Time relationship model of spectrum handoff; (a) without switching latency and (b) with switching latency

Full size image

It is observed from Fig. 2a that if call service time T 0 is less than the residual time h then there is no handoff. The probability of no spectrum handoff or the probability of zero occurrence of spectrum handoff is denoted by P 0 which is obtained as:

$$ {\mathbf{P}}_{0} = {\mathbf{Pr}}\{{\mathbf{T}}_{0} \le {\text{h}}\} = \mathop{\iint}\limits_{a < b} {\Phi (a)\Psi (b)dadb} $$
(2)

where ϕ(x) is the probability density function (pdf) of cognitive user’s call duration and ψ(x) is probability distribution function of residual time of spectrum holes. From the property of density function we obtain that the area under the probability density function is unity, i.e. \( \int_{0}^{\infty } {\varPsi \left( x \right)dx = 1} \). If T 0 is one service call duration time then from Fig. 2a it can be seen that there will be multiple (say r times) spectrum handoffs within that time.

The probability of r time spectrum handoff (Pr) can be obtained as:

$$ \begin{aligned} \text{P}_{r} & = \Pr \{h < {\rm T}_{0},\,{\rm H}_{1} < {\rm T}_{1} , \ldots,\,{\rm H}_{r - 1} < {\rm T}_{r - 1},\,{\rm H}_{r} > {\rm T}_{r}\} \\ & = \Pr \{h < {\rm T}_{0}\} \cdot \Pr \{{\rm H}_{1} < {\rm T}_{1}\} \cdot \Pr \{{\rm H}_{r - 1} < {\rm T}_{r - 1}\} \cdot \Pr \{{\rm H}_{r} > {\rm T}_{r}\} \\ & = \Pr \{h < {\rm T}_{0}\} \cdot (\Pr \{ {\rm H}_{1} < {\rm T}_{1}\} )^{r - 1} \cdot \Pr \{ {\rm H}_{r} > {\rm T}_{r}\} \\ & = (1 - \Pr \{ {\rm T}_{0} \le h\} ) \cdot (\Pr \{ {\rm H}_{1} < \,{\rm T}_{1}\} )^{r - 1} \cdot (1 - \Pr \{ {\rm H}_{r} \le {\rm T}_{r}\} ) \,\\ & = (1 - \text{P}_{0} ) \cdot (\Pr \{ {\rm H}_{1} < {\rm T}_{1}\} )^{r - 1} \cdot (1 - \Pr \{ {\rm H}_{r} \le {\rm T}_{r}\} ) \\ & = (1 - \text{P}_{0} ) \cdot (\Pr \{ {\rm H}_{1} < {\rm T}_{1}\} )^{r - 1} \cdot (1 - \Pr \{ {\rm H}_{r} \le {\rm T}_{r}\} ) \,\\ \end{aligned} $$
(3)

3.2 Analytical Model of Probability of Handoff for Different Residual Time Distribution

In this section we derive analytical models of probability of spectrum handoff under diverse distribution model of residual time of spectrum holes without switching delay. We consider the following five distribution model for our analysis: (1) exponential, (2) Erlang-2, (3) Erlang-3, (4) Erlang-3, 23 and (5) lognormal. Poisson’s process is one of the most celebrated model in tele-traffic analysis. However, Erlang family of distribution is considered as a convincing model for tele-traffic analysis and is widely used as a backbone model for designing telecommunication switching systems. A correlated model of exponential distribution is normal or log–normal function which is also found to be fit for practical tele traffic analysis. The closeness of these mathematical distribution function to the practical tele-traffic analysis motivates us to analyze their effect on spectrum handoff and establish a closed form expression for standardisation of the same.

3.2.1 Poisson’s Random Distribution Process

Due to the memoryless property of exponential distribution, it is commonly used for modeling the inter arrival time process. So we use this distribution as a reference in our work. The probability distribution function (pdf) of residual time of spectrum holes with exponential distribution is given as:

$$ \Psi (x) = \left\{ {\begin{array}{*{20}l} {\beta e^{ - \beta x} } \hfill & {{\text{for}}\;\; x \ge 0} \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. \,$$
(4)

where (1/β) is the scale parameter.

Therefore, from Eq. (2), the probability of ‘0’ times handoff (P0) and ‘r’ times handoff (Pr) may be derived as:

$$ \begin{aligned} {\text{P}}_{0} & = {\text{Pr}}\{{\rm T}_{0} \le h\} = \mathop{\iint}\limits_{a < b} {\Phi (a)\Psi (b)dadb} = \int_{0}^{\infty } {\Psi (b)\int\limits_{0}^{b} {\Phi (a)dadb \,} } \\ & = \int_{0}^{\infty } {\Psi (b)\int\limits_{0}^{b} {\mu e^{ - \mu a} dadb} } = \int_{0}^{\infty } {\Psi (b)} (1 - e^{ - \mu b} )db \,\\ & = \int_{0}^{\infty } {\Psi (b)} db - \int\limits_{0}^{\infty } {\Psi (b)} e^{ - \mu b} db = 1- \int\limits_{0}^{\infty } {\beta e^{ - \beta b} } e^{ - \mu b} db \\ & { = 1} - \int\limits_{0}^{\infty } {\beta e^{ - (\beta + \mu )b} } db = 1 - \frac{\beta }{\beta + \mu } \,\\ \end{aligned} $$
(5)

Now,

$$ \begin{aligned} {\text{Pr}}\{{\rm H}_{1} < {\rm T}_{1}\} & = 1- {\text{Pr}}\{h \,\ge {\text{ T}}_{1} \} = 1 - \mathop{\iint}\limits_{p < q} {\Phi (p)\Psi (q)dpdq} \\ & = 1- \int_{0}^{\infty } {\Psi (q)\int\limits_{0}^{q} {\mu e^{ - \mu p} dpdq} } =1 - \int_{0}^{\infty } {\Psi (q)} dq - \int\limits_{0}^{\infty } {\Psi (q)} \,e^{ - \mu q} dq \,\\ & = 1- \left( { 1- \frac{\beta }{\beta + \mu }} \right)=\frac{\beta }{\beta + \mu } \,\\ \end{aligned} $$
(6)

Similarly,

$$ {\text{Pr}}\{{\rm H}_{r} \le {\rm T}_{r}\} = \frac{\beta }{\beta + \mu } \,$$
(7)

Now from Eq. (3),

$$ {\text{P}}_{r} = \left( {1 - 1 + \frac{\beta }{\beta + \mu }} \right)\left( {\frac{\beta }{\beta + \mu } \,} \right)^{r - 1} \left( {1 - \frac{\beta }{\beta + \mu }} \right)=\frac{{\mu \beta^{r} }}{{(\beta + \mu )^{r + 1} }}\,\,\, $$
(8)

3.2.2 Erlang-m Distribution Process

Erlang distribution is a continuous probability distribution with wide applicability mostly due to its relation to the exponential and Gamma distributions. The Erlang distribution was developed by Erlang to examine the number of telephone calls [21] within any period of observation with call arrival and termination rate as basic parameters. Erlang-m distribution is the distribution of the sum of m independent and identically distributed random variables each having an exponential distribution. It is the result of a succession of memory-less exponential stages. When m = l, the distributions of residual time has an exponential distribution. The coefficient of variation (CV) for Erlang-m is always lower than one [22]. Here the probability distribution function is given as:

$$ \Psi (x) = \left\{ {\begin{array}{*{20}l} {\beta^{m} \cdot \frac{{x^{m - 1} }}{(m - 1)!} \cdot e^{ - \beta x} } \hfill & {{\text{for}}\;\; {\text{x}} \ge 0} \hfill \\ 0\hfill & { {\text{otherwise}}} \hfill \\ \end{array} } \right. \,$$
(9)

where (1/β) is the scale parameter and m is a shape parameter.

The most appropriate function among the Erlangen family is the Erlang-3 compared to Erlang-2 [19]. We consider both Erlang-3 and Erlang-2 for our analysis. The probability of zero spectrum handoff (P0) for Erlang-3 is obtained as,

$$ \begin{aligned} {\text{P}}_{0} = {\text{Pr}}\{{\rm T}_{0} \le h\} & = \mathop{\iint}\limits_{a < b} {\Phi (a)\Psi (b)dadb} = 1- \int\limits_{o}^{\infty } {\beta^{3} \cdot \frac{{b^{2} }}{2!} \cdot e^{ - b\beta } } e^{ - \mu b} db \\ & = 1 - \int\limits_{o}^{\infty } {\beta^{3} \cdot \frac{{b^{2} }}{2!} \cdot e^{ - (\beta + \mu )b} } db = 1- \left( {\frac{\beta }{\beta + \mu }} \right)^{3} \,\\ \end{aligned} $$
(10)

Now,

$$ \begin{aligned} {\text{Pr}}\{ {\rm H}_{1} < {\text{T}}_{1}\} & = 1- {\text{Pr}}\{h \,\ge {\text{ T}}_{1}\} = 1- \mathop{\iint}\limits_{p < q} {\Phi (p)\Psi (q) \,dpdq} \\ & { = 1} - \,\int\limits_{0}^{\infty } {\Psi (q)\int\limits_{0}^{q} {\mu e^{ - \mu p} dpdq} } = 1 - \int\limits_{0}^{\infty } {\Psi (q)dq} - \int\limits_{0}^{\infty } {\Psi (q)} e^{ - \mu q} dq \,\\ & { = 1} - \left( { 1- \left( {\frac{\beta }{\beta + \mu }} \right)^{3} } \right)=\left( {\frac{\beta }{\beta + \mu } \,} \right)^{3} \\ \end{aligned} $$
(11)

Similarly,

$$ {\text{Pr}}\{{\rm H}_{r} \le {\rm T}_{r}\} = \left( {\frac{\beta }{\beta + \mu }} \right)^{3} $$
(12)

Substituting the values of Eqs. (10)–(12) in Eq. (3), P r can be calculated as,

$$ \begin{aligned} {\text{P}}_{r} & = \left( {1 - 1 + \left( {\frac{\beta }{\beta + \mu }} \right)^{3} } \right)\left( {\frac{\beta }{\beta + \mu }} \right)^{3(r - 1)} \left( {1 - \left( {\frac{\beta }{\beta + \mu }} \right)^{3} } \right) \,\\ & = \left( {\frac{\beta }{\beta + \mu }} \right)^{3r} \left( {1 - \left( {\frac{\beta }{\beta + \mu }} \right)^{3} } \right) = \left( {\frac{\beta }{\beta + \mu }} \right)^{3r} - \left( {\frac{\beta }{\beta + \mu }} \right)^{3r + 3} \\ \end{aligned} $$
(13)

For Erlang-2 the probability of zero handoff is obtained as

$$ {\text{P}}_{0} = {\text{Pr}}\{{\rm T}_{0} \le h\} = \mathop{\iint}\limits_{a < b} {\Phi (a)\Psi (b)dadb} = 1- \left( {\frac{\beta }{\beta + \mu }} \right)^{2} $$
(14)

Now

$$ {\text{Pr}}\{{\rm H}_{1} < {\rm T}_{1}\} = 1- {\text{Pr}}\{h \ge {\text{T}}_{1} \} = 1 - \mathop{\iint}\limits_{p < q} {\Phi (p)\Psi (q)dpdq}=\left( {\frac{\beta }{\beta + \mu }} \right)^{2} $$
(15)

Similarly, we can express

$$ {\text{Pr}}\{{\rm H}_{r} \le {\rm T}_{r}\} = \left( {\frac{\beta }{\beta + \mu }} \right)^{2} $$
(16)

Therefore the generalized expression for probability of r handoff (r = 0, 1, 2….) P r may be given as,

$$ \begin{aligned} {\text{P}}_{r} & = \left( {1 - 1 + \left( {\frac{\beta }{\beta + \mu }} \right)^{2} } \right)\left( {\frac{\beta }{\beta + \mu }} \right)^{2(r - 1)} \left( {1 - \left( {\frac{\beta }{\beta + \mu }} \right)^{2} } \right) \\ & = \left( {\frac{\beta }{\beta + \mu }} \right)^{2r} - \left( {\frac{\beta }{\beta + \mu }} \right)^{2r + 2} \,\\ \end{aligned} $$
(17)

3.2.3 Erlang-m, n Distribution Process

Erlang-m, n distribution is basically a combination of Erlang-m and Erlang-n distributions with same scale parameter. Erlang-m, n distribution displays a greater adaptability, fitting random variables or coefficient of variation lower or greater than one [23]. The corresponding pdf is,

$$ \Psi (x) = \left\{ {\begin{array}{*{20}l} {p\beta^{m} \cdot \frac{{x^{m - 1} }}{(m - 1)!} \cdot e^{ - \beta x} { + }\left( {1 - p} \right)\beta^{n} \cdot \frac{{x^{n - 1} }}{(n - 1)!} \cdot e^{ - \beta x} } \hfill & {{\text{for}}\;\;{\text{x}} \ge 0} \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. $$
(18)

where m and n are shape parameters, and (1/β) is the scale parameter of the distribution function, p and (1 − p) are the probability of traffic shared by Erlang-m and Erlang-n, respectively.

Therefore, the probability of zero handoff, P 0, may be obtained as

$$ \begin{aligned} {\text{P}}_{0} \,& = {\text{Pr}}\{{\rm T}_{0} \le h\} = \mathop{\iint}\limits_{a < b} {\Phi (a)\Psi (b)dadb} = \int_{0}^{\infty } {\Psi (b)\int\limits_{0}^{b} {\mu e^{ - \mu a} dadb} } \\ & = \int_{0}^{\infty } {\Psi (b)} db - \int\limits_{0}^{\infty } {\Psi (b)} e^{ - \mu b} db \,\\ & = 1- \int\limits_{0}^{\infty } {\left( {p\beta^{m} \cdot \frac{{b^{3 - 1} }}{(3 - 1)!} \cdot e^{ - \beta b} { + }\left( {1 - p} \right)\beta^{n} \cdot \frac{{b^{23 - 1} }}{(23 - 1)!} \cdot e^{ - \beta b} } \right)db} \\ & = 1 - \left( {p\left( {\frac{\beta }{\beta + \mu }} \right)^{3} + \left( {1 - p} \right)\left( {\frac{\beta }{\beta + \mu }} \right)^{23} } \right) = 1- {\text{S}} \\ \end{aligned} $$
(19)

where,

$$ {\text{S}} = p\left( {\frac{\beta }{\beta + \mu }} \right)^{3} + \left( {1 - p} \right)\left( {\frac{\beta }{\beta + \mu }} \right)^{23} $$
(20)

Now,

$$ \begin{aligned} {\text{Pr}}\{{\rm H}_{1} < {\rm T}_{1}\} & = 1- {\text{Pr}}\{h \,\ge {\text{ T}}_{1} \} = 1 - \mathop{\iint}\limits_{p < q} {\Phi (p)\Psi (q)dpdq} \,\\ & =p\left( {\frac{\beta }{\beta + \mu }} \right)^{3} +\,(1 - p)\left( {\frac{\beta }{\beta + \mu }} \right)^{23} = {\text{S}} \\ \end{aligned} $$
(21)

Similarly,

$$ {\text{Pr}}\{{\rm H}_{r} \le {\rm T}_{r}\} = p\left( {\frac{\beta }{\beta + \mu }} \right)^{3} + \left( {1 - p} \right)\left( {\frac{\beta }{\beta + \mu }} \right)^{23} = {\text{S}} $$
(22)

Using Eq. (3), the probability of r time spectrum handoff is obtained as

$$ \begin{aligned} {\text{P}}_{r} & = \left( {1 - 1 + \left( {p\left( {\frac{\beta }{\beta + \mu }} \right)^{3} + \left( {1 - p} \right)\left( {\frac{\beta }{\beta + \mu }} \right)^{23} } \right)} \right).\left( {p\left( {\frac{\beta }{\beta + \mu }} \right)^{3} + \left( {1 - p} \right)\left( {\frac{\beta }{\beta + \mu }} \right)^{23} } \right)^{r - 1} \\ & \quad \times \,\left( {1 - \left( {p\left( {\frac{\beta }{\beta + \mu }} \right)^{3} + \left( {1 - p} \right)\left( {\frac{\beta }{\beta + \mu }} \right)^{23} } \right)} \right){\text{ = S}} \cdot {\text{S}}^{r - 1} \cdot \left( {1 - {\text{S}}} \right) = {\text{S}}^{r} \left( { 1- {\text{S}}} \right) \\ \end{aligned} $$
(23)

3.2.4 Lognormal Distribution Process

The lognormal distribution provides a useful mathematical tool for modeling real traffic in a mobile environment. The lognormal function has been proved to give one of the best modeling for channel holding time [24, 25]. In the current analysis the residual time of spectrum hole is assumed to be varying as per lognormal distribution.

The probability distribution function for lognormal distribution is given as:

$$ \Psi (x) = \left\{ {\begin{array}{*{20}l} {\frac{1}{{x\sqrt {2\pi \sigma^{2} } }}. \,e^{{{\raise0.7ex\hbox{${ - (\log x - \beta )^{2} }$} \!\mathord{\left/ {\vphantom {{ - (\log x - \beta )^{2} } {2\sigma^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2\sigma^{2} }$}}}} } \hfill & { {\text{for}}\;\;{\text{x}} \ge 0} \hfill \\ 0 \hfill & {{\text{otherwise}}} \hfill \\ \end{array} } \right. $$
(24)

where β is the scale parameter and σ is the shape parameter.

Therefore, the probability of ‘r’ time’s spectrum handoff is obtained as

$$ {\text{P}}_{r} = L^{\,r} \cdot (1 - L) $$
(25)

where

$$ L = \left( {\frac{{\exp \left( { - \frac{{W^{2} \left( {\mu \sigma^{2} \exp \left( \beta \right)} \right){ + 2}W\left( {\mu \sigma^{2} \exp \left( \beta \right)} \right)}}{{2\sigma^{2} }}} \right)}}{{\sqrt {1 + W\left( {\mu \sigma^{2} \exp \left( \beta \right)} \right)} }}} \right) $$
(26)

Here W(μσ 2 exp (β)) is the Lambert-W function. The derivation of Eq. (25) is shown in “Appendix”.

4 Algorithm for Simulation of Proposed Models

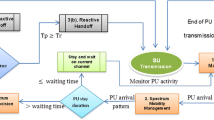
The algorithm for implementation of the proposed model is explained through the flow diagram as shown in Fig. 3. The average departure rate of cognitive user (µ), average departure rate of spectrum hole (λ) and threshold of switching time before link failure (t rmax ) are initialised. The exponential distribution function for call service time (T 0) is generated. For the range of departure rate of spectrum holes and cognitive users the distribution of residual time H i r ; (i = 1, 2, 3, 4, 5) [i = 1: exponential; 2: Erlang-2; 3: Erlang-3; 4: Erlang-3, 23; 5: lognormal] is generated as per various distribution functions. The condition for zero handoff is checked and probability of zero handoff is obtained. The process continues for first, second and third handoff and the respective probabilities are acquired. The results are compared with the theoretical results for all the distribution models. Individual probabilities of zero, first, second and third handoffs are also obtained with respect to average departure rate of cognitive user (µ), average departure rate of spectrum hole (λ).

Fig. 3
figure 3

Flow diagram of algorithm for probability of spectrum handoff without switching delay

Full size image

The algorithm for simulating the probability of spectrum handoff with switching delay (Fig. 2b) is also shown. After initializing the basic parameters as like the previous algorithm, the switching delay distribution t r (i) is generated for all the distribution models used and presented in this paper. The conditions for probability of handoff are checked and probability of zero spectrum handoff is calculated. The results of probability of first, second and third handoffs for all the distribution models are obtained and are compared with respect to average departure rate of cognitive user (µ) and average departure rate of spectrum hole (λ).

figure e

Table 1 shows the statistical characteristic of various distribution functions presented in this paper. The corresponding relationships between the scale and shape parameters for all the distribution functions are stated in the table. The expectation or mean of the distribution functions are obtained and summarized in the table. The expectation parameter is important in analyzing the simulation model for probability of spectrum handoff.

Table 1 Statistical tools and relation between their parameters
Full size table

5 Simulation Results and Discussion

The simulation results of the time relationship model of probability of spectrum handoff as discussed in Sect. 3 is projected under this section. The Monte–Carlo simulation of all the models is carried out in MATLAB®. In our simulation the distribution of one service call duration of cognitive user is taken as Poisson’s random process and residual time of spectrum holes are taken as mentioned in Sect. 3.2. We restrict our analysis up to third spectrum handoff (zero to third) in this paper. The generalised expression derived is capable of analysing and examining any number of spectrum handoff required. The range of departure rate of cognitive user, µ, is ranging from 1 to 720 calls/h and departure rate of spectrum holes, λ, ranges between 40 and 320 spectrum holes/h. The typical range of values is assumed for a comprehensive analysis of the measuring parameter.

5.1 Comparison of Results for Exponential and Erlang-3 Distribution

The simulated and established theoretical results for exponential distribution and Erlang-3 distribution are shown in Figs. 4 and 5 considering µ = 120 calls/h and average departure rate of spectrum hole (λ) varying from 40 to 320 spectrum holes/h.

Fig. 4
figure 4

Impact of departure rate of spectrum holes (λ) on the spectrum handoff for exponential distribution

Full size image
Fig. 5
figure 5

Impact of departure rate of spectrum holes (λ) on the spectrum handoff for Erlang-3 distribution

Full size image

From Figs. 4 and 5 it is observed that, in both the cases simulated results closely match with theoretical results for the probability of zero spectrum handoff (P 0), probability of first spectrum handoff (P 1) and second spectrum handoff (P 2) under impact of parameter λ.

Similarly the simulated and theoretical results of probability of spectrum handoff for exponential and Erlang-3 distribution under the impact of departure rate of cognitive user (µ) are shown in Figs. 6 and 7. The range of departure rate of cognitive user (µ) is varying from 1 to 720 calls/h and departure rate of spectrum holes (λ) remains constant at 180 spectrum holes/h.

Fig. 6
figure 6

Impact of departure rate of cognitive user (µ) on the spectrum handoff for exponential distribution

Full size image
Fig. 7
figure 7

Impact of departure rate of cognitive user (µ) on the spectrum handoff for Erlang-3 distribution

Full size image

In both the cases the simulated results show close match with the theoretical results for probability of zero to second handoff (P 0 − P 2). In Fig. 7, the simulated result of probability of zero to second handoff (P 0 − P 2) for Erlang-3 distribution is also found to be closely matching with the theoretical results. However, for Erlang-3 distribution, the simulated results are slightly deviating from the theoretical results due to the system resource constrains.

5.2 Results for Different Distribution Functions Under Zero Switching Delay with Varying Departure Rate of Spectrum Holes (λ)

We have compared spectrum handoff probability varying from zero to third (P 0, P 1, P 2 and P 3) under different realistic distribution model of residual time of spectrum holes which is shown in Figs. 8, 9, 10 and 11. In this analysis we have kept average departure rate of cognitive user (µ) constant at 120 calls/h and vary average departure rate of spectrum hole (λ) from 40 to 320 spectrum holes/h.

Fig. 8
figure 8

Impact of departure rate of spectrum holes (λ) on zero spectrum handoff (P 0)

Full size image
Fig. 9
figure 9

Impact of departure rate of spectrum holes (λ) on probability of first handoff (P 1)

Full size image
Fig. 10
figure 10

Impact of departure rate of spectrum holes (λ) on probability of second handoff (P 2)

Full size image
Fig. 11
figure 11

Impact of departure rate of spectrum holes (λ) on probability of third handoff (P 3)

Full size image

As observed in Fig. 8, with the increased departure rate of spectrum holes (λ), the mean departure time of spectrum holes (1/λ) decreases and hence the probability of spectrum handoff increases. As a result, the probability of zero spectrum handoff (P 0) decreases as shown in Fig. 5. Erlang-3, 23 offers 14.09 % higher probability of no handoff with respect to exponential distribution. The same for Erlang-2, Erlang-3 and Lognormal is 8.71, 11.89 and 3.37 % respectively as compared to exponential distribution.

From Fig. 9 it is observed that the probability of first spectrum handoff (P 1) increases up to a certain level of departure rate of spectrum holes (λ). This is because of large value of λ indicating fast moving rate of spectrum holes; resulting in increase of P 1. For the exponential and lognormal distribution, P 1 increases till λ ≈ 120 spectrum holes/h and for Erlang-2; Earlang-3 and Erlang-3, 23 distribution P 1 increases till λ ≈ 140 spectrum holes/h after which P 1 tends to settle down to minimal variation.

We observe from Figs. 8 and 9 that Erlang-3, 23 offers minimum probability of first handoff (P 1) under the presented scenario. Likewise, the impact of departure rate of spectrum holes (λ) on P 2 and P 3 are shown in Figs. 10 and 11. In both the cases it is observed that the probabilities of spectrum handoff are less in Erlang-2 distribution as compared to exponential distribution but the values are minimum in Erlang-3, 23 distribution as compared to all other distribution mentioned here.

Table 2 shows a comparison of average percentage improvement in probability of handoff (one to third) of Erlang-2; Eralng-3; Erlang-3, 23 and lognormal distribution with respect to exponential distribution. The result shows Erlang-3, 23 offers superior improvement as compared to other distribution models used in this paper.

Table 2 Percentage improvement of spectrum handoff probability (zero to third) for different distribution models compared to exponential distribution under the impact of departure rate of spectrum holes (λ)
Full size table

5.3 Results for Different Distribution Functions Under Zero Switching Delay with Varying Departure Rate of Cognitive Users (µ)

The impact of departure rate of cognitive user (µ) on spectrum handoff is important to asses. In this section we have fixed the departure rate of spectrum holes λ = 180 spectrum holes/h and varied the departure rate of cognitive users from 1 to 720 calls/h. The results are shown in Figs. 12, 13, 14 and 15, which compares probability of zero to third handoff (P 0 ~ P 3) under different distribution strategies.

Fig. 12
figure 12

Impact of departure rate of cognitive user (µ) on probability of zero handoff (P 0)

Full size image
Fig. 13
figure 13

Impact of departure rate of cognitive user (µ) on probability of first handoff (P 1)

Full size image
Fig. 14
figure 14

Impact of departure rate of cognitive user (µ) on probability of second handoff (P 2)

Full size image
Fig. 15
figure 15

Impact of departure rate of cognitive user (µ) on probability of third handoff (P 3)

Full size image

The result of probability of zero handoff (P 0) in Fig. 12 shows an increase rate of spectrum handoff with respect to average departure rate of cognitive user (µ). This is because as the value of µ increases, the mean departure time of cognitive user (1/µ) decreases resulting in reduction of probability of spectrum handoff.

As a result, the probability of no spectrum handoff (P 0) increases. The result in Fig. 12 shows that Erlang-3, 23 model tenders 15.71 % higher probability of no handoff compared to exponential distribution whereas the same for Erlang-2, Erlang-3 and Lognormal is 9.77, 12.66 and 2.22 %, respectively. Under the presented scenario the result obtained for Erlang-3, 23 is better in comparison with other distribution functions applied in the work.

Figure 13 shows that probability of first handoff (P 1) increases up to certain value of departure rate of cognitive user (µ) after which it decrease for all the distribution approaches. The peak values of probability of first handoff for the applied distribution, namely, exponential, Erlang-2; Erlang-3; Erlang-3, 23 and lognormal, are measured to be at µ = 221, 201, 201, 201 and 241 calls/h, respectively. Though the maximum value of probability of first handoff is observed in case of Erlang-3, 23 but considering the entire set of results it is inferred that Erlang-3, 23 offers best output in terms of utilization of band with minimum handoff.

Likewise, the characteristic curves for probability of second (P 2) and third handoff (P 3) are shown in Figs. 14 and 15 respectively. The patterns of the results show much similarity with that of P 1 in Fig. 13 but with different instantaneous values. In both the cases, Erlang-3, 23 distribution provides better result as compared to others in terms of probability of handoff.

The average percentage improvement in spectrum handoff probability (one to third) of various distribution models with respect to exponential distribution is summarized in Table 3. The result shows Erlang-3, 23 offers better result in terms of probability of handoff (one to third) compared to other distribution functions used in this paper.

Table 3 Percentage improvement of spectrum handoff probability (zero to third) for different distribution models compared to exponential distribution under the impact of departure rate of cognitive user (µ)
Full size table

5.4 Results for Different Distribution Functions with Nonzero Switching Delay with Varying Departure Rate of Spectrum Holes (λ)

In this section we investigate the variation of probability of spectrum handoff with respect to departure rate of spectrum holes (λ) for various distribution functions with non-zero switching delay (t r ).

In this case, we keep µ constant at 120 calls/h and typical switching delay t r  = 5 ms (switching delay varies considerably across different implementation strategies). We vary departure rate of spectrum holes (λ) from 40 to 320 spectrum holes/h for simulation.

From Figs. 16, 17, 18 and 19, results of probability of zero handoff to third handoff (P 1 − P 3) are compared for exponential, Erlang-2; Erlang-3; Erlang-3, 23 and lognormal distribution of residual time considering switching delay t r in between the spectrum holes.

Fig. 16
figure 16

Impact of departure rate of spectrum holes (λ) on probability of zero spectrum handoff (P 0) with switching delay

Full size image
Fig. 17
figure 17

Impact of departure rate of spectrum holes (λ) on probability of first handoff (P 1) with switching delay

Full size image
Fig. 18
figure 18

Impact of departure rate of spectrum holes (λ) on probability of second handoff (P 2) with switching delay

Full size image
Fig. 19
figure 19

Impact of departure rate of spectrum holes (λ) on probability of third handoff (P 3) with switching delay

Full size image

The average value of probability of zero handoff (P 0) with respect to departure rate of spectrum holes (λ) with non-zero switching delay is greater than the value obtained without the switching delay, as shown in Figs. 8 and 16 because switching delay enhances the residual time distribution. The result explains, the value of probability of zero handoff (P 0) is maximum for Erlang-3, 23 distribution compared to all other distribution functions used. For probability of zero handoff (P 0), Erlang-3, 23 offers 9.34 % improvement with respect to exponential distribution whereas Erlang-2, Erlang-3 and lognormal offers an improvement of 5.94, 7.73 and 0.96 % as compared to exponential distribution respectively.

Due to the similar reasons the average values of probability of first, second and third (P 1, P 2 and P 3) comes out to be less in comparison to the results obtained without t r as shown in Figs. 17, 18 and 19. Erlang-3, 23 offers minimum value of probability of handoff (P 1, P 2 and P 3) as compared to other distribution functions used in this paper.

The results in Table 4 highlight the average percentage of improvement in probability of spectrum handoff (one to third) for Erlang-2; Erlang-3; Erlang-3, 23 and lognormal distribution functions in comparison with exponential distribution. Presented result in Table 4 specifies the superior performance improvement of Erlang-3, 23 in terms of number of spectrum handoff (one to third) in comparison to other distribution models used in this work.

Table 4 Percentage improvement of spectrum handoff probability (zero to third) with non-zero switching delay for different distribution models compared to exponential distribution under the impact of departure rate of spectrum holes (λ)
Full size table

5.5 Results for Different Distribution Functions Under Nonzero Switching Delay with Varying Departure Rate of Cognitive User (µ)

In this section we investigate the variation of probability of spectrum handoffs keeping departure rate of spectrum holes (λ) fixed at 180 spectrum holes/h and switching time tr = 5 ms and varied the departure rate of cognitive users from µ = 1–720 calls/h. For different distributions of residual time (exponential, Erlang-2; Erlang-3; Erlang-3, 23 and lognormal) the comparison of probability of spectrum handoff, zero to third, (P 0 − P 3) are obtained considering switching delay t r and are presented in Figs. 20, 21, 22 and 23, respectively.

Fig. 20
figure 20

Impact of departure rate of cognitive user (µ) probability of zero handoff (P 0) with switching delay

Full size image
Fig. 21
figure 21

Impact of departure rate of cognitive user (µ) on probability of first handoff (P 1) with switching delay

Full size image
Fig. 22
figure 22

Impact of departure rate of cognitive user (µ) on probability of second handoff (P 2) with switching delay

Full size image
Fig. 23
figure 23

Impact of departure rate of cognitive user (µ) on probability of third handoff (P 3) with switching delay

Full size image

Table 5 shows the probability of zero spectrum handoff for various distribution functions with zero and non-zero switching delay. The results show Erlang-3, 23 offers maximum probability of zero spectrum handoff under both switching delay conditions as compared to other distribution functions used and presented in this paper.

Table 5 Comparison of values of zero spectrum handoff probability at an arbitrarily chosen value of µ = 301 calls/h under zero and t r  = 5 ms switching delay
Full size table

The result exhibits that Erlang-3, 23 is best performing distribution which offers maximum value of probability of no handoff (P 0). Erlang-3, 23 shows 22.74 % higher probability of no handoff with respect to exponential distribution, whereas, Erlang-2, Erlang-3 and lognormal offers 13.95, 18.42 and 4.65 % improvement over exponential distribution respectively.

As shown in Figs. 21, 22 and 23, the values of probability of first, second and third (P 1, P 2 and P 3) are increasing initially up to a certain value of µ in the range between 0 and 80 users/h and decreasing thereafter. The result shows that Erlang-3, 23 distributions offers minimum values of probability of first spectrum handoff compared to other distribution functions considered in this paper.

Percentage improvements in probability of handoff (one to third) for various distribution functions in comparison with exponential distribution are summarized in Table 6. The results in Table 6 reflect that Erlang-3, 23 offers better result in terms of spectrum handoff (one to third) compared to all other distribution models used in our work.

Table 6 Percentage improvement of spectrum handoff probability (zero to third) with non-zero switching delay for different distribution models compared to exponential distribution under the impact of departure rate of cognitive radio (µ)
Full size table

5.6 Probability of Spectrum Handoff Versus Number of Handoff

We also investigate the variation of probability of spectrum handoff with respect to the number of handoffs (restricted to 10) for all the distribution models. The result is shown in Fig. 24. The variation of the same for different departure rate of spectrum holes and cognitive user for exponential and Erlang-3, 23 are also acquired for a more realistic implication of the models. The aim is to understand the effect of number of handoffs on probability of spectrum handoff.

Fig. 24
figure 24

Probability of spectrum handoff (P r ) versus number of handoffs (r) for various distribution model

Full size image

In Fig. 24 the probability of spectrum handoff in exponential, Erlang-2; Erlang-3 and Erlang-3, 23 distributed environment is compared to the number of handoff as parameters with λ = 320 spectrum holes/h and µ = 120 calls/h.

The probability of spectrum handoff at r = 0 (i.e. probability of zero spectrum handoff) is the highest in case of Erlang-3, 23. However, its value reduces considerably and acquires the least value from first handoff onwards which establishes the efficiency of Erlang-3, 23 model over the other distribution models used in our analysis. It may also be observed that the total number of handoff is reduced considerably if Erlang-3, 23 distribution is applied in the spectrum handoff model as compared to other distribution models presented in this research work.

Figures 25 and 26 show the result of P r for different values of departure rate of spectrum holes (λ) and cognitive users (µ) which also establishes the superior performance of Erlang-3, 23 distribution function in spectrum handoff estimation.

Fig. 25
figure 25

Probability of spectrum handoff (P r ) versus Number of handoffs (r) with different departure rate of spectrum holes (λ) for exponential and Erlang-3, 23

Full size image
Fig. 26
figure 26

Probability of spectrum handoff (P r ) versus number of handoffs (r) for different departure rate of cognitive user (µ) for exponential and Erlang-3, 23

Full size image

6 Conclusion

The probability of spectrum handoff is one of the fundamental components to critically analyze the performance of the spectrum mobility and spectrum management in a cognitive radio network (CRN). In this paper, we have investigated important distribution functions for tele-traffic analysis and their impact on a spectrum handoff in CR. We have established a state of the art generalized structure to estimate the spectrum handoff for diverse distribution models which has practical significance for implementation of system design. We presented a detailed comparison of percentage improvement of probability of handoff (zero to third) for various distribution models with respect to exponential distribution. In all our results Erlang-3, 23 distribution function confirms better performance as compared to exponential, lognormal and other Erlangian family such as Erlang-2 or 3. We also have analyzed the effect of switching delay in the measurement of spectrum handoff. However, in many practical scenarios lognormal-3 and Hyper-Erlang are found to be promising distribution model which will be included in our future work for analysis of spectrum mobility. Spectrum handoff with multiple users and inter cell spectrum handoff under random user-mobility scenario are two important research challenges to be addressed in the domain of spectrum mobility in CR.