1 Introduction

Information security has gained great attention of researchers in the last few decades. Different types of data security techniques are proposed by cryptographers. These techniques can be divided into two basic categories. One is called cryptography and the other is called steganography [8]. The working principle of cryptographic techniques is to convert secret data into an unreadable form by using key(s). In steganography, the confidential data is embedded into another data in such a way that the unauthorized party cannot notice its presence. According to Shannon, a cryptosystem is secure if it can produce confusion and diffusion in the data up to a certain level [9]. In many cryptographic techniques, substitution box is the only non-linear component which creates confusion and diffusion. Generally, an S-box is said to be good if it can provide high resistance against linear, differential and algebraic cryptanalysis [10,11,12,13,14,15].The resistance of S-box against common attacks is measured by non-linearity (NL), linear approximation probability (LAP), strict avalanche criterion (SAC), bit independence criterion (BIC), differential approximation probability (DAP) and algebraic complexity (AC).

Rijndael block cipher [16] is adopted by National Institute of Standard and Technology (NIST) as Advanced Encryption Standard (AES). Nowadays, AES is one of the most commonly used cryptosystem. Due to the importance of AES many researchers studied cryptographic properties of its S-box. In [17], a simple algebraic representation of AES S-box is presented. Another, representation of AES S-box is presented in [18]. The study in [18] reveals that AES can be expressed by spare over-determined system of multivariate quadratic equation. The non-linear part of AES is further analyzed in [19] by studying its polynomial representation. They found that AES S-box has only few non-zero terms in its permutation polynomial and has low algebraic complexity. The findings in [18, 19] indicate that the security of AES is suspected against algebraic attacks [13,14,15].

Because of crucial role of S-box in AES, many cryptographers proposed improved S-box transformations based on different mathematical structures such as algebraic and differential equations. In [20], an upgraded version of AES S-box is presented by exchanging the orders of mapping of AES S-box. Affine function is used in improving the complexity of AES S-box against algebraic attacks in [21]. The resultant S-box has 253 non-zero terms. In [22], Gray codes are used before the implementation of AES S-box. This generates an S-box with 255 non-zero terms. A generalization of Gray S-box based on group action is presented in [23]. In [24], affine mapping and orbit of power function are used for generation of multiple strong S-boxes. Mobius functions are used in [7] for the construction of S-boxes. In [3], logistic map and Baker map are used to develop new S-boxes. Based on Baker and Chebyshev maps, a method of generation of good S-boxes is presented in [4]. In [6], S-boxes are constructed by the combination of neural network and chaotic map. Similarly, many other S-box generation techniques are presented e.g., see [25,26,27,28,29,30,31].

Elliptic curves (EC) are also used in developing strong cryptosystems. The concept of elliptic curve was first time introduced in cryptography in [32]. Furthermore, a cryptosystem is presented in [32] which is 20 percent faster than Diffie–Hellman protocol. In [33], a cryptosystem based on EC over finite field is discussed. In [34], a relationship between the points of hyperelliptic curves and non-linearity of S-box is presented. The concept of discrete logarithmic problem is used in [35] to develop a highly secure and fast security system. In [36], elliptic curve cryptography (ECC) is compared with RSA. It is noticed that ECC with smaller key size has better security than that of RSA with larger key size. The applications and advantages of ECC are discussed in [37]. Similarly, different ECC techniques are discussed in [38]. In literature [39,40,41,42], elliptic curves are used for generation of pseudo random numbers which are very important for many cryptosystems.

The aim of this paper is to present a simple and efficient algorithm for construction of cryptographically strong S-boxes based on elliptic curves over prime field. The proposed technique uses the \(x\)-coordinate of ordered pairs of EC followed by modulo operation 256. Rest of the paper is organized as follow: Sect. 2 contains some preliminaries. The algorithm is presented in Sect. 3. The experimental results and their comparison are given in Sect. 4.

2 Preliminaries

2.1 Modulo Operation

The modulo operation outputs the remainder when one number a is divided by another number b, where \(b \le a\). The result of modulo operation on numbers a and b is often denoted by a mod b. For example, “258 mod 256” is equal to 2 because after dividing 258 by 256, the remainder is 2.

2.2 Elliptic Curve Over a Finite Prime Field

Consider a prime field \(F_{p}\) having \(p\) elements, where \(p\) is a prime number. For each prime \(p\) number there exists exactly one prime field \(F_{p}\). For any two integers of \(F_{p}\) say \(a\) and \(b\), the elliptic curve on field \(F_{p}\) is defined as:

$$E\left( {F_{p} } \right) = \left\{ {\left( {x,y} \right) \, \in \, F_{p}^{2} | \, (y^{2} = \, x^{3} + ax + b) \, \left( {mod \, p} \right) \, \text{ and } a,b,x,y \, \in \, F_{p} } \right\} \cup \left\{ { \, O} \right\},$$

provided \((4a^{3} +\)\(27b^{2}\) \(\ne 0)\left( {\bmod \, p} \right),\) where O denotes the infinite point. The number of elements \(\# \left( {E(F_{p} )} \right)\) in elliptic curve \(E(F_{p} )\) is equal to the number of points lying on elliptic curve over \(F_{p}\). Hasse Theorem [43] gives the bounds of total number of points on elliptic curve:

$$p + 1 - 2\sqrt p \le \, \# E\left( {F_{p} } \right) \, \le p + 1 + 2\sqrt p .$$

The expression \(4a^{3} + 27b^{2}\) is called the discriminant of the elliptic curve.

3 S-Box Construction Technique

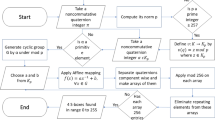
A simple technique for generation of cryptographically strong S-boxes is discussed in this section. The construction technique is based on elliptic curve over a prime field \(F_{p}\). The proposed algorithm consists of four main steps which are given below:

  • Step 1. Choose two distinct elements \(a \, \,{\text{and }}\,b\) from prime field \(F_{p}\), where \(p\) is large prime. The large value of \(p\) is selected so that the corresponding elliptic curve EC has at least 256 ordered pairs. The lower bound of \(p\) for proposed algorithm is calculated by using Hasse’s Theorem which is \(p\, > 289\).

  • Step 2. Generate the elliptic curve \(E_{p} (a,b){\text{ by using the equation:}}\)

    $$(y^{2} \, = \,x^{3} + \,ax\, + \,b)\,\,(\bmod \,p).$$

  • Step 3. Let \(E_{p,{x}} (a,b)\) denotes the set of \(x\)-coordinate of all ordered pairs of \(E_{p} (a,b)\). Now, apply modulo 256 on \(E_{p,x} (a,b)\) to get \(E_{p,x}^{256} (a,b)\). This operation is used to restrict the values of \(E_{p,x} (a,b)\) in the range 0–255.

  • Step 4. Finally, an S-box \(S_{a}^{b}\) is generated by selecting first 256 distinct integers of \(E_{p,x}^{256} (a,b)\).

A flowchart of the proposed technique is presented in Fig. 1. The proposed algorithm is implemented on several ECs for generation of S-boxes. For example, the S-box \(S_{1878}^{785}\) generated by \(E_{2861} (1878\,,785)\) is presented in Table 1. The points of \(E_{2861} (1878\,,785)\) are shown in Fig. 2.

Fig. 1
figure 1

Flowchart of proposed technique

Full size image
Table 1 S-box \(S_{1878}^{785}\) generated by proposed algorithm over the EC \(E_{2861} (1878,785)\)
Full size table
Fig. 2
figure 2

Points of \(E_{2861,x} (1878,785)\)

Full size image

4 Analysis and Comparison

Different security performance tests including non-linearity test, linear approximation probability, strict avalanche criterion, bit independence criterion, differential approximation probability and algebraic complexity test are applied on the S-box \(S_{1878}^{785}\) generated by the proposed algorithm. These tests are implemented to investigate the efficiency of the proposed technique. A brief introduction to these tests and their experimental results are presented in this section. A comparison of results of \(S_{1878}^{785}\) with some of the prevailing S-boxes generated by other construction techniques is also presented in this section.

4.1 Bijective

The step 4 of the proposed algorithm ensures that all newly developed S-boxes are bijective.

4.2 Non-linearity (NL)

The concept of non-linearity is introduced in [10] to quantify the confusion creation ability of an S-box. For a given S-box \(S:GF(2^{8} ) \to GF(2^{8} )\), NL is measured by calculating the distance \(\delta (S)\) of \(S\) to affine functions over \(GF(2^{8} )\):

$$\delta (S) = \mathop {\hbox{min} }\limits_{\alpha ,w,\beta } \# \left\{ {x \in GF(2^{8} )|\alpha \cdot S(x) \ne \beta \cdot x \oplus w} \right\},$$

where \(\alpha \in GF(2^{8} ),w \in GF(2),\beta \in GF(2^{8} )\backslash \{ 0\}\) and “·” denotes the dot product over GF(2).

The optimal value of non-linearity of a bijective S-box over \(GF(2^{8} )\) is 120. It is also noticed in [10], that an S-box with maximum non-linearity may not satisfies other cryptographic criterion. Furthermore, the study in [10] suggests that an S-box with nearly optimal NL and satisfying other security test is of special interest. We calculated the non-linearity of the S-box \(S_{1878}^{785}\) generated by the proposed algorithm. The result of this test is 100.

4.3 Linear Approximation Probability (LAP)

In [11], linear approximation probability of an S-box is introduced. This calculates the probability of obtaining a linear approximation of a given S-box. LAP of an S-box depends upon the coincidence of input bits with output bits. The mathematical expression of LAP is given below:

$$\begin{aligned} N(a,\beta ) = \# \left\{ {x \in GF(2^{8} )|\alpha \cdot x = \beta \cdot S(x)} \right\} - 2^{n - 1} , \hfill \\ LAP(S) = \frac{1}{{2^{n} }}\left\{ {\mathop {\hbox{max} |N(a,\beta )|}\limits_{\alpha ,\beta } } \right\}, \hfill \\ \end{aligned}$$

\({\text{where}}\;\alpha \in GF(2^{8} ),\beta \in GF(2^{8} )\backslash \left\{ 0 \right\}\) and “·” denotes the dot product over GF(2).

The LAP of newly generated S-box \(S_{1878}^{785}\) is 0.0547.

4.4 Strict Avalanche Criterion (SAC)

This criterion is developed in [44] by combining the concepts of avalanche effect and completeness. The probability of change in output bits when a single input bit is inverted is calculated in this test. SAC of an S-box is calculated with an \(8 \times 8\) dependence matrix whose entries are calculated by:

$$\left\{ {\frac{1}{{2^{n} }}\left[ {w\,\left( {S_{i} (x + \alpha_{j} ) + S_{i} (x)} \right)} \right]\,\,\left| {\alpha_{j} \in \,GF(2^{8} ),\,w(\alpha_{j} ) = \,1\,\,{\text{and }}1 \le i,\,j \le 8} \right.} \right\},$$

where \(w(\alpha_{j} )\,\) is the number of non-zero bits in \(\alpha_{j}\). SAC is satisfied if all entries of dependence matrix are closer to 0.5. The SAC result for \(S_{1878}^{785}\) is presented in Table 2. The minimum value of SAC is 0.4219 while its maximum value is 0.5938.

Table 2 Strict avalanche results of \(S_{1878}^{785}\)
Full size table

4.5 Bit Independence Criterion (BIC)

BIC is also proposed in [44] to analyze the independence between pair of output bits when an input bit is complemented. BIC of pair of output bit A and B is calculated by finding correlation coefficient of A and B. The minimum and maximum value of BIC of \(S_{1878}^{785}\) are 0.4688 and 0.5293 respectively. The BIC result is given in Table 3.

Table 3 BIC of \(S_{1878}^{785}\)
Full size table

4.6 Differential Approximation Probability (DAP)

Differential approximation probability is presented in [12] to find the probability effect of a specific difference in the input bit on the difference of the resultant output bits. The mathematical expression for DAP of an S-box \(S\) is given below:

$$DAP(S) = \,\mathop {\hbox{max} }\limits_{\Delta x,\,\Delta y} \left\{ {\# \left\{ {x \in GF(2^{8} )\,\left| {\,S(x\, + \,\Delta x)\, - \,S(x) = \,\Delta y} \right.} \right\}} \right\},$$

where \(\Delta x\), \(\Delta y \in \,GF(2^{8} ).\) We applied DAP test on the proposed S-box and the result is given in Table 4. The DAP of \(S_{1878}^{785}\) is 0.0391.

Table 4 DAP of \(S_{1878}^{785}\)
Full size table

4.7 Algebraic Complexity (AC)

Linear polynomial for an S-box is defined in [45]. The algebraic complexity of an S-box is measured by the number of non-zero terms in its linear polynomial expression. In Table 5, coefficients of polynomial corresponding to \(S_{1878}^{785}\) are presented. The AC of S-box \(S_{1878}^{785}\) generated by the proposed algorithm is 255.

Table 5 AC of \(S_{1878}^{785}\)
Full size table

4.8 Performance Comparison

The former tests are also applied on some of the well-known S-boxes presented in [1,2,3,4,5,6,7] to compare the efficiency of proposed algorithm with other S-box generation algorithms. The results are presented and compared in Table 6.

Table 6 Comparison of newly generated S-boxes with some of the existing S-boxes
Full size table

Table 6 shows that the NL of S-boxes in [2, 7] is less than or equal to the NL of the S-box constructed by the proposed algorithm. The LAP of \(S_{1878}^{785}\) is less than that of the S-boxes presented in [1, 4, 5, 7]. This fact reveals that the \(S_{1878}^{785}\) creates high confusion in the data and hence higher resistance against linear attack [11] as compared to [1, 4, 5, 7]. The SAC and BIC results of \(S_{1878}^{785}\) and other S-boxes used in Table 6 are almost the same. Thus, the S-box generated by the proposed technique and S-boxes presented in Table 6 create diffusion in the data of equal magnitude. The DAP of \(S_{1878}^{785}\) is less than or equal to the DAP of S-boxes [1,2,3,4,5,6,7]. Thus, the proposed encryption technique generates S-box with high resistance against differential cryptanalysis [12] as compared to the others. The AC of \(S_{1878}^{785}\) is maximum which shows that it is secure against algebraic attacks [13,14,15]. Similarly, the analysis results of another newly generated S-box \(S_{1710}^{2429}\) over EC \(E_{2609} (1710\,,2429)\) are listed in Table 6. It is evident from Table 6 that the performance of \(S_{1710}^{2429}\) is also comparable with the other S-boxes.

5 Conclusion

A novel S-box construction technique is presented in this article. The proposed algorithm uses the \(x\)-coordinate of ordered pairs of an elliptic curve over prime field \(E_{p} \left( {a,b} \right)\) for the generation of cryptographically strong S-box \(S_{b}^{a}\), where \(p\) is a prime greater than 289 and \(a\) and \(b\) belong to finite field \(F_{p}\). Several tests are applied on newly developed S-boxes \(S_{b}^{a}\) to analyze their cryptographic strength. Furthermore, cryptographic properties of \(S_{b}^{a}\) are compared with some of the existing prevailing S-boxes. Experimental results showed that the proposed algorithm is capable of generating S-boxes with high resistance against linear, differential and algebraic attacks.

The S-boxes generated by the proposed technique depend upon the selection of \(p\), \(a\) and \(b\). In other words, by changing either \(p\), \(a\) or \(b\), another S-box will be generated. Thus, the proposed algorithm can also be extended to an image encryption technique that uses dynamic S-boxes generated by varying the values of parameters \(p\), \(a\) and \(b\). In such encryption technique \(p\), \(a\) and \(b\) will behave as keys. Furthermore, the proposed algorithm can be extended for generation of more secure S-boxes based on classification of Rossby wave triads by elliptic curves, see [46].