A Binary PSO Approach for Improving the Performance of Wireless Sensor Networks

Abstract

Wireless sensor networks are used for low-cost unsupervised observation in a wide-range of environments and their application is largely constrained by the limited power sources of their constituent sensor nodes. Techniques such as routing and clustering are promising and can extend network lifetime significantly, however finding an optimal routing and clustering configuration is a NP-hard problem. In this paper, we present an energy efficient binary particle swarm optimization based routing and clustering algorithm using an intuitive matrix-like particle representation. We propose a novel particle update strategy and an efficient linear transfer function which outperform previously employed particle update strategies and some traditional transfer functions. Detailed experiments confirmed that our routing and clustering algorithm yields significantly higher network lifetime in comparison to existing algorithms. Furthermore, our results suggest that Binary PSO is better equipped to solve discrete problems of routing and clustering than its continuous counterpart, PSO.

1 Introduction

A WSN consists of spatially dispersed tiny sensor devices, networked together over a wireless medium, and one or more conveniently located powerful sinks collecting information from these sensor nodes (SNs). Characterized by their scalability, mobility, fault tolerance and simplicity of use, WSNs have emerged as effective low-cost alternatives for unsupervised observation of a wide range of environments, and have been used in diverse areas of application such as agriculture, military, inventory, environment monitoring etc. However, WSNs and their widespread application is primarily constrained by the limited energy sources of SNs. Many novel areas of research such as low-powered energy communication hardware [5], energy-aware medium access control [32] etc. have emerged to tackle these issues. Energy efficient routing and clustering protocols present a promising solution to various energy limitation issues faced by WSNs.

Liu [22] presented an extensive survey on clustering and routing protocols and expounded various advantages of clustering such as localization of route setup within a cluster and increased scalability of response to events in the environment. Routing in WSNs can be classified as flat and hierarchical [22]. While in a flat routing framework all nodes have the same functionality, in hierarchical routing different nodes perform different tasks. Hierarchical routing WSNs are organized into many clusters, and each cluster comprises of a leader referred as the cluster head (CH), and multiple SNs. CHs might transmit data to the sink either directly, or indirectly via other CHs through a multi-hop routing path. The latter scenario is referred to as a two-tier WSN.

In hierarchical networks, CHs bear the transmission load of multiple SNs and also expend energy for aggregating and eliminating redundant data from SNs. This can result in their overloading and early death [14]. In this regard, multiple researchers [3, 20, 21] suggested using special nodes with extra energy, called gateways. In the remainder of the paper, we use the term gateways and CHs interchangeably. Moreover like SNs, CHs are also battery-powered and therefore have a limited power supply. In WSNs with static sinks, CHs close to the sink can die prematurely since they lie at the intersection of several multi-hop routes and consequently expend a significant amount of power to transmit huge quantities of information from other nodes to the sink [16]. The death of a CH can potentially destabilize the network, disrupt its topology and lead to packet loss. Therefore, it is important to balance loads on CHs and SNs in order to prolong the lifetime of a network (Fig. 1).

Fig. 1

A two-tier WSN

Both routing and clustering are NP-hard problems. Furthermore, the computational complexity of finding an optimal routing and clustering configuration rises as the size of the WSN increases. For a WSN having $|{\mathcal {G}}|$ gateways and $|{\mathcal {S}}|$ SNs, if each gateway and SN on an average has $\overline{{\mathcal {G}}}$ and $\overline{{\mathcal {S}}}$ gateways within communication range, there are $|{\mathcal {G}}|^{\overline{{\mathcal {G}}}}$ and $|{\mathcal {S}}|^{\overline{{\mathcal {G}}}}$ possible routing and clustering configurations, respectively. Therefore, brute force approaches are extremely inefficient in solving these problems. In order to obtain good routing and clustering configurations efficiently and quickly, meta-heuristic approaches such as BPSO, Genetic Algorithms (GA), Ant Colony Optimization (ACO) etc. are highly suitable. In the past, meta-heuristic algorithms have shown promising results in finding optimal routing and clustering configurations [20, 21, 27].

In this paper, we develop routing and clustering algorithms based on Binary Particle Swarm Optimization (BPSO). We chose BPSO partly since its continuous counterpart, Particle Swarm Optimization had performed extremely well in solving the routing and clustering problem [20], and more so because we expect BPSO to be better suited for the optimization problems at hand by virtue of its discrete nature. Experimental results comparing both the algorithms confirm the superior optimization performance of BPSO over continuous PSO (Sect. 7.6). However, using BPSO is not straightforward owing to the multi-dimensional nature of routing and clustering. In particular, routing and clustering require a unique two-dimensional particle representation different from the uni-dimensional representation that traditional applications of BPSO use (Sect. 6.1.2). The new particle representation also necessitates new velocity and position update strategies that take into account the two-dimensional nature of the particles (Sect. 6.1.4). In this paper, we propose a novel stochastic position update strategy and note significant improvements in the optimization process over its alternative, the max update strategy proposed by Izakian et al. [15] (Sect. 7.4). Still, the velocity matrices lie in a continuous space, while the routing and clustering configurations are discrete in nature, and therefore BPSO uses a transfer function to map a continuous search space into a discrete binary space (Sect. 6.1.8). To this end we propose a novel linear transfer function $\xi _L$ which is not only computationally simple but also outperforms traditional alternatives such as sigmoid$\xi _S$ and hyperbolic tan$\xi _T$ transfer functions in terms of network lifetime (Sect. 7.3).

In order to evaluate routing and clustering configuration, prior work Kuila and Jana [20] usually deploy CHs and SNs uniformly randomly across the deployment region. However, rigorous experiments on the uniform deployment revealed that the CHs closer to the base station expend a huge amount of energy to forward incoming packets from other CHs, and thus die quickly. To this end, we also examined a random Gaussian deployment of gateways to increase their number around the base station, and found the that it increases the network lifetime significantly.

Thus, our major contributions can be summarized as follows:

• BPSO based routing and clustering algorithms along with carefully designed fitness functions and a novel particle representation. In particular, we model the lifetime of a WSN in terms of its constituent CHs, and devise fitness functions which can effectively prolong network lifetime.

• A novel stochastic particle position update strategy to drive the optimization process in a efficient manner.

• A novel computationally-simple linear transfer function $\xi _L$ that outperforms traditional non-linear transfer functions (sigmoid $\xi _S$ and hyperbolic tan $\xi _T$) in terms of metrics such as network lifetime.

• A detailed performance comparison of discrete BPSO and its widely-used continuous counterpart PSO, highlighting the former’s superior performance in solving the considered optimization problems.

• An analysis of a gaussian strategy for randomly deploying CHs in the sensing area. The gaussian strategy effectively balances the load of CHs near the base station.

The paper is organized as follows. Relation to prior work is presented in Sect. 2. Section 3 provides a brief overview of binary particle swarm optimization. Section 4 discusses the energy model and terminologies, while Sect. 5 formulates the problem statement. Section 6 discusses the proposed algorithms. The experimental setup and detailed experimental results are given in Sect. 7 and we conclude the paper with avenues of future work in Sect. 8.

2 Literature Review

A lot of research has been done in last few decades to achieve an energy efficient WSN. Heinzelman et al. [14] proposed a low energy adaptive clustering hierarchy (LEACH). A drawback of LEACH is that the CHs are selected without considering the crucial parameters like residual energy which makes the algorithm inefficient in some cases [23]. Heinzelman et al. [14] presented LEACH-C where the base station takes the responsibility of cluster formation. In Younis and Fahmy [33] another extension to LEACH protocol, hybrid energy efficient distributed clustering (HEED) is proposed. HEED mainly focus on the residual energy of each SN. Souissi and Meddeb [26] proposed a weight based clustering algorithm which minimizes intra cluster distance. Later, Tang et al. [28] proposed the concept of a high energy relay node to be placed between CHs for long distance communication. Cardinality of CHs was proposed by Gupta and Younis [10] where cardinality was defined in terms of number of SNs associated with a CH. Many approaches have been used in which nature inspired algorithms are used to improve the WSN lifetime. Kuila et al. [21] proposed a genetic algorithm based load balancing, clustering algorithm. Heinzelman et al. [13] presented a single hop routing model in which direct transmission of energy takes place during the routing process. A minimum hop model was proposed by Gupta and Younis [11]. They emphasized on finding a multi hop route which minimizes the number of hops required to send data from a SN to the sink. Heinzelman et al. [14] presented a random routing model where a SN i randomly selects the next hop j, given that j is in transmission range of i and is located close to the sink. Bari et al. [3] used GA for WSN routing. Later, Gupta et al. [12] proposed another routing algorithm that uses GA for minimizing network energy dissipation. Kuila and Jana [20] try to find a tradeoff between number of hops and transmission distance in such a way to find equilibrium between delay and transmission distance. Srinivasa Rao and Banka [27] proposed an energy efficient clustering approach using a chemical reaction optimization approach. The gravitational search algorithm was used by Ebrahimi Mood and Javidi [8] to achieve an energy efficient network. Later, Kaur and Mahajan [17] presented a tree based data aggregation protocol to achieve energy efficient WSN.

3 Binary Particle Swarm Optimization: An Overview

Particle swarm optimization (PSO) is a popular optimization technique for non-linear continuous functions, originally introduced by Kennedy and Eberhart [18, 25]. PSO is inspired by flocks of birds and their search for food and shelter, and has been successfully used to solve a number of problems [6, 9, 18, 29]. The PSO algorithm comprises of a swarm (flock) of dynamic and interactive particles (birds) that intelligently search through a high-dimensional search space using collaborative trial and error. Each particle represents a potential solution to the problem having a randomly-initialized position and velocity. Each particle’s velocity governs the next position that it flies to. PSO iteratively improves each potential solution based on a measure of quality (called the fitness function), guided by the direction of its fittest position (pbest), and the fittest position of any particle in the swarm (gbest). The fittest position that a particle has visited thus far (pbest), and the fittest position that the swarm has achieved (gbest) represent the cognitive and social components that guide the swarm’s search for the solution (food).

A few years later, Kennedy and Eberhart [19] presented the binary version of their algorithm for discrete optimization problems. While BPSO inherits all the basic ideas of its continuous counterpart, it defines a particle’s position and velocity in terms of changes in probabilities that a bit will be in one state or another. In the binary setting, each particle can be viewed as a vertex of a D-dimensional hypercube. Furthermore, the velocity of a particle in each dimension denotes the probability that the corresponding position bit will be ON (1) or OFF (0). Unlike other optimization paradigms, the position of a particle in BPSO is transitory i.e. a particle may have different positions in different instances given the same velocity. For example, consider Eq. 6 which maps the velocity $v_{i,d}^{t}$ of a particle to its position at the next time step $\rho _{i,d}^{t + 1}$. Notice that the final position of a particle does not depend solely on its velocity, but also on the random number $r_{i,d}$.

Formally, we denote a particle $\rho _i$ in a D-dimensional space as:

$$\begin{aligned} \rho _i = [x_{i,1}, x_{i,2}, \ldots , x_{i,D}] \end{aligned}$$

(1)

where each $x_{i,d} \ \in \ \{0,1\}, \ d \ \in \ \{1,2, \ldots \ ,D\}$. Each particle $\rho _i$ possesses velocity represented as:

$$\begin{aligned} V_i = [v_{i,1}, \ v_{i,2}, \ \ldots \ ,v_{i,d}]^T \end{aligned}$$

(2)

where each $v_{i,d} \ \in \ [v_{min}, v_{max}] , \ v_{min} \ \text {and} \ v_{max}$ denote the maximum and minimum velocity. Let us denote the personal best position of a particle, and the global best position of swarm as:

$$\begin{aligned} pbest_i&= {} [\rho x_{i,1}, \ \rho x_{i,2}, \ldots , \ \rho x_{i,D}]^T \end{aligned}$$

(3)

$$\begin{aligned} gbest_i& = {} [gx_{i,1}, \ gx_{i,2}, \ \ldots , \ gx_{i,D}]^T \end{aligned}$$

(4)

Then, Eqs. 5 and 6 can be used to update the position and velocity of the ith particle’s dth dimension at the tth iteration:

$$\begin{aligned} V_{i,d}^{t+1}& = {} V_{i,d}^{t} + c_1r_1 ( pbest_{i,d}^{t} - \rho _{i,d}^{t} ) + c_2r_2 ( gbest_{i,d}^{t} - \rho _{i,d}^{t} ) \end{aligned}$$

(5)

$$\begin{aligned} \rho _{i,d}^{t + 1}& = {} {\left\{ \begin{array}{ll} 1 &{} {\text {if}} \ \xi _S(v_{i,d}^{t}) > r_{i,d} \\ 0 &{} {\text {otherwise}} \end{array}\right. } \end{aligned}$$

(6)

where $\xi _S(v_{i,d}^{t}) = \frac{1}{1 + e^{- v_{i,d}^{t}} }$. $\xi$ denotes a transfer function (Sect. 6.1.8). Traditionally, BPSO uses the sigmoid $\xi _S$ transfer function.

$c_1$ and $c_2$ are positive acceleration constants that govern the influence of the cognitive and social components on the search process. Also, $r_1$, $r_2$ and $r_{i,d}$ are uniform random numbers in the range [0, 1]. Algorithm 3 presents the BPSO optimization algorithm for minimization problems.

4 Energy Model and Terminologies

4.1 Energy Model

We used the simplified first-order radio model Heinzelman et al. [14] to dissipate energy of SNs and CHs. In this model, the transmitter expends energy to run the power amplifier and transmitter electronics, while the receiver expends energy to run the receiver electronics. The energy expended to transmit a l-bit message over the distance d, using free-space and multi-path fading channels is given by Eq. 7:

$$\begin{aligned} E_{T}(l,d) = {\left\{ \begin{array}{ll} lE_{elec} + lE_{fs}d^2 , \quad \text {when }d < d_o \\ lE_{elec} + lE_{mp}d^4 , \quad \text {when }d \ge d_o \end{array}\right. } \end{aligned}$$

(7)

where $E_{Elec}$, $E_{fs}$ and $E_{mp}$ is the energy required by the electronics circuit, and the amplifier in the free-space and multipath models respectively and $d_o = \sqrt{\frac{E_{fs}}{E_{mp}}}$. To receive a l-bit message, the receiver expends energy as given by Eq. 8:

$$\begin{aligned} E_{R}(l) = lE_{elec} \end{aligned}$$

(8)

The electronics energy $E_{elec}$ depends on a number of factors such as digital coding, modulation, filtering and spreading of the signal. On the other hand, the amplifier energy $E_{fs}$ and $E_{mp}$ depend on the distance to the receiver and the acceptable bit error-rate.

4.2 Network Model

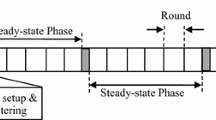
Our WSN model comprises of a number of immobile SNs and gateways which are deployed uniform randomly at the start of the simulation.¹ Each SN communicates with a single gateway in its communication range, and is said to be assigned to that gateway. These assignments result in clusters of SNs, which allow data from nodes within a cluster to be processed locally (in their assigned gateway) and reduce the data that needs to be transmitted to the base station. Similar to LEACH [14], the operation of our model is divided into rounds. In each round, SNs collect data and send it to their corresponding CH. A CH is a gateway to which all SNs of a cluster are assigned. In the remaining sections of the paper, we refer to CHs and gateways interchangeably. A CH aggregates data to eliminate redundant information and transmits it to the remote base station via the next hop CH. In order to save energy, all nodes turn off their radios between adjacent rounds. In the presented model, MAC transmissions are accomplished using Time-Division Multiple Access (TDMA) protocol [4].

Table 1 A summary of notation

5 Problem Formulation

Table 1 summarizes the notations used in our algorithms. The lifetime of a WSN is an important measure for evaluating different application-specific network configurations. Several metrics have been proposed in the literature to measure the lifetime of a sensor network [7] based on the number of alive nodes, sensor coverage, connectivity and quality of service requirements. Among these, the n-of-n lifetime $(L_n^n)$ is one the most widely used definitions of network lifetime:

$$\begin{aligned} L_n^n = \underset{i \ \in \ N}{min} \ L_i \end{aligned}$$

In this definition, the lifetime of a network is the time until the first node dies. This is a convenient definition since it is easy to compute, and does not have to consider changes in topology after the death of the first node. $L_n^n$ is used when all the nodes are of equal importance and favours algorithms that uniformly deplete the energy of each node in the network [7]. Since it may be either inconvenient or impossible to recharge and replace node batteries [14], in this paper, our main objective is to maximize n-of-n network lifetime of a sensor network.

The n-of-n network lifetime can be expressed in terms of residual energy of cluster heads at the start of network operation and the highest energy expended per round by any CH as shown in Eq. 9:

$$\begin{aligned} L_n^n = \underset{i \ \in \ N}{min} \ L_i \ = \ \underset{c_i \ \in \ {\mathbb {C}}}{min} \ \left\lfloor {\frac{E_{res}(c_i)}{E(c_i)}}\right\rfloor \end{aligned}$$

(9)

where $E_{res}(c_i)$ is the residual energy of the CH $c_i$, and $E(c_i)$ is the energy it expends per round. It must be noted that in the real life $E(c_i)$ may vary for every round of operation due to extraneous factors, however for the sake of simplicity we assume that $E(c_i)$ is constant throughout the operation of a CH. If the residual energy ($E_{res}$) for all CHs is equal at the start of operation, then the lifetime of a network has an inverse relationship with the highest energy expended per round by any CH, as shown in Eq. 10:

$$\begin{aligned} L_n^n = \underset{i \ \in \ N}{min} \ L_i \ = \underset{c_i \ \in \ {\mathbb {C}}}{min} \left\lfloor {\frac{E_{res}(c_i)}{E(c_i)}}\right\rfloor \approx \underset{c_i \ \in \ {\mathbb {C}}}{min} \left( \frac{\epsilon }{E(c_i)}\right) \end{aligned}$$

(10)

where $\ \forall c_i \in {\mathbb {C}}, \ E_{res}(c_i) = \epsilon$. Alternatively, $\epsilon$ is called the initial energy of CHs.

Each CH expends energy for receiving data sensed by its member SNs, aggregating the data, and eventually sending it to the base station. Furthermore, every CH $c_i$ also consumes energy to forward data received from any CH $c_j$ whose routing path to the base station passes through $c_i$. Therefore, the energy expended by each CH has two components: an intra-cluster component due to receiving, aggregating and transmitting data sensed by its member SNs, and a forwarding component due to relaying data sensed in other parts of the network. The intra-cluster component shown in Eq. 11 is formulated using Eqs. 7 and 8 as follows:

$$\begin{aligned} E_{{\mathcal {C}}}(c_i) = \eta \, E_R(l) + \eta \, E_D(l) + E_T(m, d(c_i, NH_{c_i})) \end{aligned}$$

(11)

where $\eta$ is the number of member SNs of $c_i$, $\eta E_R(l)$ is the total energy expended by $c_i$ to receive l-bit messages from each of its $\eta$ member SNs, and $\eta E_D(l)$ is the total amount of energy consumed in aggregating a total of $\eta \times l$ bits of messages from member SNs (each member SN sends a l-bit message to the CH) into a fixed m-bit packet which is transmitted from the CH $c_i$ to the base station. This aggregation mechanism, where SNs transmit l-bit messages to their assigned CH, which thereby aggregates all the messages into a single m-bit message, follows from prior work [8, 20, 27]. The energy spent on transmitting the aggregated m-bits of packet is given by $E_T(m, \ d(c_i, NH_{c_i}))$.

Similarly, the forwarding component is formulated in Eq. 12:

$$\begin{aligned} E_{{\mathcal {F}}}(c_i) = {\mathcal {N}}(c_i) E_R(m) + {\mathcal {N}}(c_i) E_T(m, d(c_i, NH_{c_i})) \end{aligned}$$

(12)

where ${\mathcal {N}}(c_i)$ is the number of inbound data packets from all CHs $c_j$ whose next hop relay is $c_i$. We can recursively compute ${\mathcal {N}}(c_i)$ as shown in Eq. 13:

$$\begin{aligned} {\mathcal {N}}(c_i) = {\left\{ \begin{array}{ll} 0, &{} \text {if} \ NH_{c_j} \ne c_i \forall \ c_j \ \in \ {{\mathbb {C}}}\\ \sum _{}^{} ({\mathcal {N}}(c_j) + 1) &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(13)

The total energy expended by a CH $c_i$ is given in Eq. 14:

$$\begin{aligned} E(c_i)& = {} E_{{\mathcal {C}}(c_i)} + E_{{\mathcal {F}}(c_i)} \\& = {} \eta \, E_R(l) + \eta \, E_D(l) + {\mathcal {N}}(c_i) E_R(m) + ({\mathcal {N}}(c_i) + 1) E_T(m, d(c_i, NH_{c_i})) \end{aligned}$$

(14)

Therefore, the energy consumed by a CH depends on the number of SNs assigned to it ($\eta$), the number of inbound data packets ($N(c_i)$) and the distance between the CH and its next hop ($d(c_i,NH_{c_i})$). While $N(c_i )$ and ($d(c_i,NH_{c_i})$) depends on the routing setup, $\eta$ depends on the clustering configuration of the network. By carefully formulating fitness functions for routing and clustering, we can effectively minimize the energy consumption for each CH and prolong their lifetime. Mathematically,

$$\begin{aligned} max(L_n^n) \propto max\left( \underset{c_i \ \in \ {\mathbb {C}}}{min} \left( \frac{1}{E(c_i)}\right) \right) \end{aligned}$$

(15)

Essentially, maximizing network lifetime is equivalent to maximizing the lifetime of the CH which has minimum lifetime.

6 BPSO-Based Routing and Clustering

The network is setup in three different phases: bootstrapping, routing, and clustering. First each entity (CH and SN) in the network is assigned a unique ID. Next, each entity broadcasts it’s ID using the Carrier Sense Multiple Access with Collision Avoidance (CSMA/CA) MAC layer protocol, which allows all the gateways and SNs to collect IDs of entities which are within their communication range. This information is then sent to the base station which executes the proposed routing and clustering algorithm. The base station utilizes the best route returned by the routing algorithm to find the best clustering configuration. Later, each gateway is informed of its next hop relay, while each SN is informed about the ID of the gateway that it is assigned to.

6.1 Routing Algorithm

6.1.1 Formulating the Routing Problem

Our main objective for routing is to minimize the forwarding energy $E_F(c_i)$ of CHs in order to effectively minimize their total energy consumption $E(c_i)$ and thereby increase their lifetime. We must remember that the routing setup influences the essential components of $E_F(c_i)$, namely the number of inbound packets (${\mathcal {N}}(c_i)$) and the distance between a CH and its next hop ($d(c_i,NH_{c_i})$).

6.1.2 Particle Representation in BPSO

Representing particles is fundamental to designing effective BPSO algorithms since it maps a BPSO particle to the solution of a problem. Our particle representations, namely the indirect and direct representation, are inspired from Izakian et al. [15]. In the direct representation or alternatively the position vector of a particle, a solution is encoded as a $1 \times m$ vector where each dimension contains an integer in the closed interval [1, n]. Figure 2 illustrates the direct representation of a particle representing a routing solution. We note the following characteristics of the direct representation:

• 1. The length of the vector m is equal to the number of CHs in the network $|{\mathbb {C}}|$.

• 2. The ith dimension of the vector is j, if the CH $c_i$ routs to $c_j$ i.e. $NH_{c_i} = c_j$.

• 3. Since a CH can route to another CH or the base station, each dimension must contain an integer in the closed interval $[1 , m + 1]$. The ith dimension of the vector is $m+1$ if the CH $c_i$ routs directly to the base station ${\mathbb{b}}$ i.e. $NH_{C_i} = {\mathbb{b}}$. Alternatively, we can justify the choice of interval $[1 , m + 1]$ by arguing that n must be equal to the number of potential next hop relays for any CH, and since a CH can route to any entity in ${\mathbb {C}} \cup {\mathbb{b}}$, we have: $n= |{\mathbb {C}} \cup {\mathbb{b}}| = |{\mathbb {C}}|+1 = m+1$.

• 4. In Fig. 2, $m=5$ and the CH $c_1$ routs to $c_2$; $c_2$, $c_3$ and $c_4$ route to $c_5$ and $c_5$ routs to the ${\mathbb{b}}$.

Fig. 2

A direct representation of a routing particle (position vector)

Fig. 3

An indirect representation of a routing particle (position matrix)

In the indirect representation or alternatively the position matrix of a particle, a solution is encoded as a $n \times m$ matrix, where each cell contains either 0 or 1 representing the absence or presence of a communication link. As an example, consider Fig. 3 which illustrates the indirect representation of the same routing configuration as Fig. 2. The indirect representation of a routing particle has the following properties:

• 1. All elements of the matrix have either the value 0 or 1.

• 2. m is equal to the number of CHs in the network $|{\mathbb {C}}|$ and $n=m+1$.

• 3. $M[c_i,c_j] = 1$ if $c_j$ routs to $c_i$ and 0 otherwise.

• 4. In each column of the matrix M only one element is 1 and all other elements are 0. This is because a CH $c_j$ only routs to a single CH $c_i$.

As apparent from Figs. 2 and 3 , the direct and indirect representations of a particle are easily convertible to each other. While the indirect representation results in sparse matrices consisting of binary numbers, the direct representation is concise and requires less memory. While we use the direct representation to encode our particles for both routing and clustering, the indirect representation is useful in interpreting velocity matrices.

6.1.3 Particle Velocity, pbest and gbest

Each particle’s velocity can be represented as a $n \times m$ matrix where each element lies between $v_{min}$ and $v_{max}$. If $V_k$ represents the velocity of the kth particle, then its velocity matrix is given by:

$$\begin{aligned} V_k(i, j) = v \in [v_{min}, v_{max}] \ \forall i, j, \ i \in \{1, 2, \ldots n\}, j \in \{1, 2, \ldots m\} \end{aligned}$$

(16)

The velocity matrix has the same shape as the position matrix, since the velocity $V_k(i, j)$ essentially indicates the probability that $c_j$ routs to $c_i$.²

Since a particle’s pbest and the swarm’s gbest also represent routing configurations, they can be also be represented by direct and indirect representations discussed in the previous section.

6.1.4 Updating a Particle’s Velocity and Position

Most researchers [1, 24, 30], using BPSO in the past have used uni-dimensional position and velocity matrices to represent solutions. However, in this paper we use two-dimensional position³ and velocity matrices to intuitively represent routing and clustering configurations. Figures 3 and 4 concretely illustrate the difference between two-dimensional and uni-dimensional position matrices, respectively.

Fig. 4

An example of a uni-dimensional position matrix. This position matrix may represent a solution to the 0/1 knapsack problem by considering $a_i$ to be the ith object, where 1 indicating that the ith object is included in the knapsack

Two-dimensional position matrices require different position and velocity update strategies than their uni-dimensional counterparts, which give rise to the need of new velocity and position update strategies.

6.1.5 A Two-Dimensional Velocity Update Strategy

The velocity of particles having two-dimensional position matrices can be updated by augmenting the velocity update equation used in traditional BPSO (refer Eq. 5) with two positional indices to refer any element present in the ith row and jth column of its velocity matrix. Accordingly, the two-dimensional velocity update strategy is given by Eq. 17:

$$\begin{aligned} V_k^{t+1}(i, j)& = {} V_k^{t}(i, j) + c_1r_1 (pbest_{k}^{t}(i, j) - X_{k}^{t}(i, j)) \\&+ c_2r_2 (gbest_{k}^{t}(i, j) - X_{k}^{t}(i, j)) \end{aligned}$$

(17)

where $X_k^{t+1}(i,j)$ represents the element of the ith row and the jth column of the kth particle’s position matrix at the ${t+1}$th time step while $V_k^{t+1}(i,j)$ represents the ith row and the jth column of the kth particle’s velocity matrix. $c_1$ and $c_2$ are positive acceleration constants that govern the influence of the cognitive and social components on the search process. Also, $r_1$, $r_2$ are uniform random numbers in the range [0, 1].

6.1.6 Max and Stochastic Position Update Strategies

In addition to velocity update, the position update strategy is principal to the optimization process since it facilitates a particle’s exploration and exploitation of the search space. A correct position update strategy for the routing problem must ensure that the updated position of a particle represents a valid routing configuration. Therefore, it must ensure that in the updated routing configuration:

• 1. Each column in a particle’s routing position matrix M must contain a single 1 only.

• 2. Each gateway must only route to another gateway in its communication range.

Condition 2 can be easily handled by initializing the velocities in each dimension i of a column j to negative infinity if $c_i$ is not in the communication range of $c_j$, as shown in Eq. 18.

$$\begin{aligned} V_k^{t+1}(i,j) = - \infty \ \forall i, j \ s.t. \ d(c_i, c_j) > {\mathcal {D}} \end{aligned}$$

(18)

Initializing the velocity to negative infinity ensures that any updates to the velocity $V_k^{t+1}(i,j)$ always results in negative infinity. Furthermore, we constrain our normalizing function $\xi$, such that it always returns 0 on an input of $-\infty$ i.e. $\xi (-\infty ) = 0$. This ensures that the probability that $c_j$ routs to $c_i$ always remains 0 i.e. $P_k^{t+1}(i,j) = 0$ and therefore, ${\mathbb {N}}_{c_j}$ can never take the value i.

A naive position update strategy can be formulated by making the same additions to Eq. 6 as the two-dimensional velocity update strategy:

$$\begin{aligned} M_{k}(i,j)^{t+1} = {\left\{ \begin{array}{ll} 1 &{} \text {if} \ \xi ( \ V_k^{t+1}(i, j) \ ) > r \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(19)

where $\xi : [v_{min}, v_{max}] \cup \{-\infty \} \rightarrow [0, 1]$ is a normalizing function (detailed explanation in Sect. 6.1.8). However, it can be clearly seen that the naive strategy may lead to an invalid routing configuration since it has no way of guaranteeing that conditions 1 and 2 hold for the updated position of a particle.

To this end, Izakian et al. [15] had proposed what we call the Max position update strategy. The Max update strategy however limits the exploration, and therefore results in premature convergence to local optima. To overcome its limitations, we propose the Stochastic update strategy which encourages more exploration owing to its probabilistic nature (Sect. 7.4). We now explain the max and stochastic update strategies in detail.

For each gateway $c_j$, let the random variable ${\mathbb {N}}_{c_j}$ map its next hop $NH_{c_j}$ to integers in the closed interval $[ 1 , m + 1 ]$, such that if $NH_{c_j} = c_i$ then ${\mathbb {N}}_{c_j}$, $i \in [1 , m + 1 ]$. Therefore, each column of the position matrix and each element of the position vector can be summarized using random variables ${\mathbb {N}}$ as [ ${\mathbb {N}}_{c_1}$${\mathbb {N}}_{c_2}$ ... ${\mathbb {N}}_{c_{|{\mathbb {C}}|}}$ ].

Let us consider that we carry out the following transformations in each particle’s velocity matrix:

• 1. Normalization Pass each velocity element $V_k^{t}(i, j)$ through a normalizing function $\xi$ such that it lies in the range [0, 1].

• 2. Re-scaling Re-scale each column such that the sum of the velocity elements in a column is 1.

These transformations result in the Probability Matrix P in which each element P[i, j] represents the probability that $c_j$ routs to $c_i$ i.e. $P(NH_{c_j} = c_i) = P[i,j]$. The second transformation ensures that sum of the probabilities of all mutually exclusive events such as $NH_{c_j} = c_i$ and $NH_{c_j} = c_k$ is 1. Both the transformations can be summarized in Eq. 20:

$$\begin{aligned} P_k^{t}(i, j) = \frac{\xi (V_k^{t}(i, j))}{\sum _{i=1}^{m}{\xi (V_k^{t}(i, j))}}, \ \forall i \in \ [1, n], j, \ \in \ [1, m] \end{aligned}$$

(20)

Each column in the probability matrix P can be seen as representing a discrete probability distribution, which provides the probabilities that a particular gateway routs to another gateway in the network or base station. Alternatively, for each gateway $c_j$, the random variable ${\mathbb {N}}_{c_j}$ has a probability distribution given by the jth column of the probability matrix P.

Given the Probability Matrix P of a particle, the Max [15] and Stochastic strategies update the positions of particles as follows:

• Max Position Update strategy Izakian et al. [15] proposed the following equation for updating a particle’s position:

  $$\begin{aligned} X_k^{t+1}(i, j) = {\left\{ \begin{array}{ll} 1 &{}\text {if} \ P_k^{t}(i, j) = max \{\xi (V_k^{t}(i, j))\} \ \forall i \in \{1, 2, \ldots n\} \\ 0 &{}\text {otherwise} \end{array}\right. } \end{aligned}$$

  (21)

  where $X_k^{t+1}(i, j)$ represents the element of the ith row and the jth column of the kth particle’s position matrix at the ${t+1}$th time step while $P_k^{t}(i, j)$ represents the ith row and the jth column of the kth particle’s probability matrix at the same time.

  Therefore, Eq. 21 assigns $c_i$ as next hop to $c_j$ ($X_k^{t+1}(i, j) = 1$) when the probability $P(NH_{c_j} = c_i) = P[i,j]$ is the highest. If $P[i,j] = P[k,j]$i.e. the probability that $c_j$ routs to either $c_i$ or $c_k$ is equal,⁴ then the next hop CH is chosen at random between them. We must note that Eq. 21 ensures that condition 1 always holds.

• Stochastic position update strategy Our proposed update strategy is consistent with the stochastic nature of the position update equation of classical BPSO. In this strategy, for each gateway $c_j$ we sample the probability distribution corresponding to ${\mathbb {N}}_{c_j}$ once, using inverse transform sampling. The sampled value $\phi \ \in \ [1, m + 1]$ indicates the updated next hop relay $c_{\phi }$ of $c_j$.

Algorithms 1 and 2 can be used to carry out max and stochastic position updates, respectively. Both the algorithms take the Probability matrix P as input, and return the routing solution $S_r$. Both the algorithms can be easily modified to support clustering.

Algorithm 1 assumes that CHs are enumerated from 1 to $|{\mathbb {C}}|$, and $|{\mathbb {C}}| + 1$ represents the base station such that a CH $c_j$ is denoted by j. For each j it then finds the row i corresponding to the maximum probability value (P[i][j]) in the column j of the probability matrix P. Subsequently, it assigns i (corresponding to $c_i$) as the next hop relay of j (corresponding to $c_j$).

Time and Space Complexity Analysis The time complexity of Algorithm 1 is ${\mathcal {O}}(|{\mathbb {C}}|^{2})$ in the worst case owing to the two nested for loops in lines 3 and 6 which are executed for every combination of a gateway and its probable next hops. The algorithm however, has constant space complexity (${\mathcal {O}}(1)$).⁵

Like Algorithm 1, Algorithm 2 also assumes that CHs are enumerated from 1 to $|{\mathbb {C}}|$, and $|{\mathbb {C}}|+1$ represents the base station. Then, for each CH j, the algorithm iteratively builds a array CDF which represents its discrete Cumulative Distribution Function. This array (${CDF_j}$) is subsequently utilised to perform inverse transform sampling to find the next hop relay i (corresponding to CH $c_i$) for the cluster head j.

The worst case time complexity of Algorithm 2 is also ${\mathcal {O}}(|{\mathbb {C}}|^{2})$ due to the nested for loops on lines 3 and 6 which are executed for every combination of a gateway and its probable next hops. Unlike Algorithm 1, this algorithm has a linear (${\mathcal {O}}|{\mathbb {C}}|$) space complexity owing to the generation of the CDF array.

While both the update strategies have comparable time complexities, the stochastic strategy has slightly higher (linear) space complexity in comparison to the max strategy (constant). While space complexity is undoubtedly an important factor in practical applications, we must also consider the significantly superior optimization performance (Sect. 7.4) of the stochastic strategy as against the max strategy.

6.1.7 Stochastic Update Strategy Parallels the Particle Update Equation in Classical BPSO

The position update equation of classical BPSO is given by Eq. 22:

$$\begin{aligned} \rho _{i,d}^{t} = {\left\{ \begin{array}{ll} 1 &{} \text {if} \ \xi _S( \ v_{i,d}^{t+1} \ ) > r_{i,d} \\ 0 &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(22)

where $\xi _S(v_{i,d}^{t+1}) = \frac{1}{1 + e^{- v_{i,d}^{t+1}}}$ and $r_{i, d}$ is a uniformly distributed random number in the range [0, 1]. It can be seen that the velocity $v_{i,d}^{t+1}$ serves as a probability threshold that partitions the interval $[\xi _S \, (v_{min}), \ \xi _S \, (v_{max})]$ into two sub-intervals $I_1 = [\xi _S \, (v_{min}), \ \xi _S \, (v_{i,d}^{t+1})]$ and $I_2 = [\xi _S \, (v_{i,d}^{t+1}), \ \xi _S \, (v_{max})]$. If the uniformly distributed random number $r_{i,d} \in [0, 1]$ lies in interval $I_1$ then the corresponding bit is set to 1, whereas if it lies in $I_2$ then the bit is set to 0. Therefore, if the optimal solution contains 1 at some position, then BPSO learns to gradually increase the corresponding velocity in order to increase the length of interval $I_1$ and accordingly increase the chance that the random number $r_{i,d}$ lies inside it.

In order to understand the essence of the BPSO optimization process in case of the stochastic update strategy, let us assume that gateway $c_j$ routs to gateway $c_i$ in the optimal solution. BPSO gradually increases the velocity $V_k^{t+1}(i,j)$ thereby increasing the probability mass on the outcome i of the random variable ${\mathbb {N}}_{c_j}$. Increasing the probability mass on the outcome i increases the chance of i being sampled from the probability distribution of ${\mathbb {N}}_{c_j}$ such that $NH_{c_j} = c_i$. Like the position update equation in classical BPSO, the stochastic update strategy ensures that the position of a particle is ephemeral, i.e. the same velocity matrix can be interpreted as an altogether different position matrix and routing configuration. On the other hand, the max update strategy would always return the same position matrix for the same velocity matrix (Sect. 6.1.11).

6.1.8 The Choice of the Transfer Function $\xi$

A transfer function $\xi : [v_{min}, v_{max}] \cup \{-\infty \} \rightarrow [0,1]$ is a mapping that takes an input in the closed interval $[v_{min}, v_{max}]$ or ${-\infty }$ and outputs a number in the closed interval [0, 1]. The transfer function is also called the normalizing function, and helps in the process of mapping a continuous search space to a discrete binary space. While routing and clustering configurations are discrete in nature, the velocity matrices lie in a continuous space. BPSO essentially searches for a velocity matrix in a continuous search space which maps to the optimal routing or clustering configuration in the discrete space.

Transfer functions must be effective as well as computationally simple since they are evaluated in numerous occasions, for every dimension of each particle every time its position is updated. To get an idea as to how many times a transfer function is called while executing BPSO for routing, let us consider a WSN with 60 gateways. Let us also assume that we run BPSO for 300 iterations with a swarm size of 50. Therefore, the transfer function is applied $60 \times 61 \times 50 \times 300$ or 54,900,000 times in total.

In this paper, we propose a linear transfer function$\xi _L$ which not only reduces the computational complexity of BPSO, but also outperforms traditional alternatives such as sigmoid $\xi _S$ and hyperbolic tan $\xi _T$ transfer functions in terms of network lifetime and average increase in network lifetime (Sect. 7.3).

$$\begin{aligned} \xi _L(V_k^{t+1}(i,j)) = \frac{V_k^{t+1}(i,j) - v_{min}}{v_{max} - v_{min}} = \frac{V_k^{t+1}(i,j)}{v_{max} - v_{min}} + \frac{- v_{min}}{v_{max} - v_{min}} \end{aligned}$$

(23)

Traditional transfer functions, $\xi _S$ and $\xi _T$ are given by Eqs. 24 and 25, respectively:

$$\begin{aligned} \xi _S(V_k^{t+1}(i,j)) = \frac{1}{1 + e^{(V_k^{t+1}(i,j))}} \end{aligned}$$

(24)

$$\begin{aligned} \xi _T(V_k^{t+1}(i,j)) = \frac{tanh(V_k^{t+1}(i,j)) + 1}{2} \end{aligned}$$

(25)

It must be noted that the slope of the linear transfer function $\xi _L$ depends on the difference between $v_{min}$ and $v_{max}$, in contrast to $\xi _S$ and $\xi _T$ which have fixed slopes.

6.1.9 Fitness Function

Now we design a fitness function in order to evaluate each particle of the population. The fitness function is a measure of goodness of a routing solution offered by a particle. Since our main objective for routing is to minimize the forwarding energy $E_{{\mathcal {F}}_{c_i}}$ of CHs, the fitness function for routing is given by:

$$\begin{aligned} fitness = \underset{i \ \in \ {\mathbb {C}}}{{{{\mathop {{\text {arg max}}}}\,}}} \ E_{{\mathcal {F}}}(c_i) \end{aligned}$$

(26)

The lower is the fitness value, the better is the particle position and corresponding routing configuration.

6.1.10 A Summary of BPSO-Based Routing

Algorithm 3 presents the proposed BPSO based routing algorithm which minimizes the routing fitness given by Eq. 26. It takes the coordinates of all the CHs (${\mathbb {S}}$) and the number of particles in the swarm ($N_p$) as input. The algorithm begins by randomly initializing each particle’s velocity matrix in the range $[v_{min}, v_{max}]$ (Sect. 6.1.3). In order to ensure that Condition 2 (Sect. 6.1.6) holds, every cell V(i, j) for which $c_j$ is not in the communication range of $c_i$, is initialized to $-\infty$. Next, the global best (gbest) position and personal best (pbest) positions of all particles in the swarm are updated by comparing their fitness values in lines [3-5]. In order to compute the fitness of a particle its position, which corresponds to a routing configuration, must be found. To this end, its velocity matrix (V) is transformed into a probability matrix (P) using Eq. 20, and then a routing configuration (position) is generated either using the Max (Algorithm 1) or Stochastic (Algorithm 2) position update strategy. Subsequently, a particle’s fitness is calculated using Eq. 26. The algorithm then proceeds to optimize the routing configuration in an iterative fashion (lines [7–17]) by first updating each particle’s velocity matrix using Eq. 17, finding their new fitness values and updating the global and their personal best positions in the same way as discussed above. Thus, the velocity updates for each particle is encapsulated in the $Update (P_i)$ procedure.

6.1.11 Illustration

Let us consider a WSN with 5 gateways ${\mathbb {C}} = \{ c_1 , c_2 , c_3 , c_4 , c_5 \}$ and 15 SNs ${\mathbb {S}} = \{ s_1 , s_2 , \ldots , s_{15} \}$. Therefore, the dimensions of the routing position vector and matrix are $1 \times 5$ and $6 \times 5$ respectively. The velocity matrix has the same shape as the position matrix. The directed acyclic graph G(V, E) shown in Fig. 5 illustrates the WSN. The vertices (V) of the graph G represents the set of gateways $({\mathbb {C}})$ and the base station (${\mathbb{b}}$). The set of edges (E) consists of dotted red lines which denote probable next hops and black lines which denote the chosen routing path. Table 2 comprises of the probable next hops for each gateway $c_j \in {\mathbb {C}}$. Algorithm 3 can be used to perform BPSO-based routing.

Fig. 5

A possible routing path

Fig. 6

Probability distributions of random variables ${\mathbb {N}}_{c_1}$, ${\mathbb {N}}_{c_2}$ etc

Table 2 Probable next hops for each gateway

We initialize the velocity matrix $V_k$ of a particle k by setting each of its elements $V_k(i,j)$ to a random number between $v_{max} = 10$ and $v_{min} = -10$ if $c_i$ is a probable next hop of $c_j$ i.e. $c_i \in pNH_{c_j}$, and $- \infty$ otherwise.

$$\begin{aligned} V_k = {\begin{pmatrix} - \infty &{} - \infty &{} - \infty &{} - \infty &{} - \infty \\ 6.49 &{} - \infty &{} - \infty &{} - \infty &{} - \infty \\ 6.19 &{} 3.00 &{} - \infty &{} - \infty &{} - \infty \\ -4.22 &{} 1.46 &{} - \infty &{} - \infty &{} - \infty \\ - \infty &{} 4.21 &{} 7.71 &{} -4.54 &{} - \infty \\ - \infty &{} - \infty &{} -8.33 &{} -8.90 &{} -9.39 \\ \end{pmatrix}} \quad P_k = {\begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0.4368 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0.4366 &{} 0.3544 &{} 0 &{} 0 &{} 0 \\ 0.1264 &{} 0.2929 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0.3577 &{} 0.9997 &{} 0.9906 &{} 0\\ 0 &{} 0 &{} 0.0002 &{} 0.0093 &{} 1 \end{pmatrix}} \end{aligned}$$

(27)

After using the sigmoid transfer function to normalize the elements of $V_k$ and re-scaling the probability values using Eq. 20, the probability matrix $P_k$ is given by $P_k$. Each column j of the probability matrix $P_k$ represents a probability distribution of the random variable ${\mathbb {N}}_{c_j}$. The probability distributions of all the random variables ${\mathbb {N}}_{c_1}$, ${\mathbb {N}}_{c_2}$, ${\mathbb {N}}_{c_3}$, ${\mathbb {N}}_{c_4}$ and ${\mathbb {N}}_{c_5}$ are illustrated in Fig. 6. Using the probability matrix P and the max update strategy, the indirect and direct encoding of the particle is given by: $X_k = {\begin{pmatrix} 2&5&5&5&6 \end{pmatrix}}$. On the other hand, the stochastic update strategy could also yield the following particles⁶: $X_k = {\begin{pmatrix} 2&5&5&5&6 \end{pmatrix} \ \text {or} \ \ \begin{pmatrix} 3&3&5&5&6 \end{pmatrix}}$

6.2 Clustering Algorithm

6.2.1 Formulating the Clustering Problem

Our main objective for clustering is to maximize the lifetime of the network and minimize the energy dissipation of SNs. As discussed in Sect. 5, maximizing the lifetime of a network is equivalent to maximizing the lifetime of the gateway with the minimum lifetime. After the routing configuration is finalised, clustering adjusts the number of SNs assigned ($\eta$) to each gateway, such that gateways having high forwarding energy are assigned fewer SNs and dissipate less intra-cluster energy.

At the same time, it is important to maximise the lifetime of SNs since they perform the basic function of sensing and collecting data. SNs also dissipate a significant amount of energy in transmitting data to their assigned CHs. In order to transmit a l-bit message to a CH at a distance d, the SN dissipates energy as follows: $E_T(s_i) = E_T(l, d)$. While maximising the lifetime of CHs by reducing the number of SNs that are assigned to each CH, some SNs may be assigned to CHs far away from them. These SNs may die quickly due to long distance communication with their respective CHs. Therefore, SNs must be assigned to their nearest CH whenever possible.

6.2.2 Particle Representation and Velocity Matrices

Clustering particles and their pbest and gbest can also be represented using direct and indirect representation. The direct representation or the position vector of a clustering particle exhibits the following characteristics:

• 1. The length of the vector m is equal to the number of SN in the network $| {\mathbb {S}} |$.

• 2. The ith dimension of the vector is j if the SN $s_j$ is assigned to the CH $c_i$.

• 3. SNs can only be assigned to a single CH in the network, and therefore each dimension of the position vector must contain an integer in the closed interval $[1 ,| {\mathbb {C}} |]$.

Similarly, some characteristics of the indirect representation of a clustering particle are as follows:

• 1. All elements of the matrix M have either the value 0 or 1. Same as the direct representation, m is equal to the number of SNs in the network $| {\mathbb {S}} |$ and $n = | {\mathbb {C}} |$.

• 2. $M [c_i,s_j] = 1$ if $s_j$ is assigned to $c_i$ and 0 otherwise.

• 3. In each column of the matrix M only one element is 1 and all other elements are 0 since each SN can be assigned to a single CH only.

Figures 7 and 8 illustrate direct and indirect representations of a clustering particle, respectively.

The velocity vector of each clustering particle has the same shape as its position matrix i.e. $| {\mathbb {C}} | \times | {\mathbb {S}} |$. Equation 17 and either the stochastic or the max update strategy can be used to update the velocity and position of the particles, respectively.

Time and Space Complexity Analysis. of Max & Stochastic strategies Following an analysis similar to Sect. 6.1.6, both the Max and Stochastic update strategies have a time complexity of ${\mathcal {O}}(|{\mathbb {S}}| \times |{\mathbb {C}}|)$ owing to the nested for loops which must now iterate over every combination of a CH and every SN. Moreover, the Max update strategy has constant space complexity (${\mathcal {O}}(1)$) while the Stochastic strategy has a space complexity of ${\mathcal {O}}(|{\mathbb {S}}|)$ owing to the generation of a CDF array with as many dimensions as the number of SNs in the WSN.

Fig. 7

A direct representation of a clustering particle (position vector)

Fig. 8

An indirect representation of a clustering particle (position matrix)

6.2.3 Fitness Function

The fitness function is derived in keeping with the main objective of clustering i.e. to prolong the lifetime of gateways and SNs. Therefore, our first objective is to maximize the lifetime of the WSN, or alternatively maximise the lifetime of the gateway with the minimum lifetime. We must note that maximizing the lifetime of a gateway takes into account the residual energy $E_{res}(c_i)$ of gateways at the start of WSN operation. Consequently, the clustering algorithm can assign fewer member SNs to gateways having less residual energy. In addition, the lifetime of SNs can be prolonged if they are assigned to the CHs nearest to them. Therefore, we must also minimize the average distance between SNs and their corresponding CHs in order to minimise their energy consumption. We can therefore construct the following fitness function:

$$\begin{aligned} fitness = \kappa \times \frac{L_n^n}{\frac{1}{| {\mathbb {S}} |} \sum _{i=1}^{| {{\mathbb {S}}} |} d(s_i, CH_{s_i})} \end{aligned}$$

(28)

The higher is the fitness of a solution, the better is the position of a particle.

6.2.4 A Summary of BPSO-Based Clustering

Algorithm 3 (Sect. 6.1.10) can be slightly modified to serve as the BPSO-based clustering algorithm, with the only difference being that:

• it would take the coordinates of all SNs (${{\mathbb {S}}}$) as input instead of the set of CHs (${\mathbb {C}}$), and return a clustering solution $S_c$ as output,

• the fitness of each particle is evaluated using Eq. 28,

• and the clustering fitness given by Eq. 28 is maximised unlike the routing fitness which is minimised. In particular, after initialization, positions corresponding to the maximum fitness are assigned as the pbest and gbest, respectively (line 5). Again in lines 10 and 13, positions corresponding to greater fitness is assigned as the pbest and gbest positions, respectively (Table 3).

7 Experimental Evaluation

7.1 Experimental Setup

In this section, we evaluate the effectiveness of our proposed algorithm and compare them against state-of-the-art models. We carried out several experiments with different numbers of SNs ranging from 200 to 500 in two different gateway configurations, with 60 and 90 gateways, respectively. For a true comparison with previous literature, our simulation parameters were the same as Kuila and Jana [20]. Each SN had 2J of initial energy while each gateway had 10 J ($\epsilon = 10$). We assume that the communication energy dissipation is based on the first-order radio model (Sect. 4.1). Furthermore, we use the same energy and distance constants as Heinzelman et al. [14] in our simulations (Table 4). We implemented and simulated our algorithms using Python, and all experiments were carried out in a computer system with an Intel i7-8550U chipset, 2GHz CPU and 16 GB RAM running Microsoft Windows 10.

Table 3 Energy and distance parameters

Table 4 Parameters of the BPSO optimizer

Our proposed algorithms are simulated for WSNs which have a sensing field of $500 \times 500 \ m^2$ area and for each of the networks, the base station is situated at the centre of the region i.e. (250, 250). In order to optimize the performance of our algorithms, we fine tuned various parameters of BPSO and selected the parameters for which our algorithms performed the best. We tested the following ranges of parameter values: $c_1$ and $c_2$ in [1, 3], ${{\mathbb {N}}}_p = [ 10 , 100 ]$ and $v_{max} = [ 1 , 100]$. Based on experimental results, our algorithms performed the best for parameter values shown in Table 4.

7.2 Gaussian Gateway Deployment is Better than Uniform Deployment

In our experiments, SNs and gateways are deployed uniformly randomly across the sensing area for a true comparison with previous literature. Our experiments revealed that CHs closer to the base station expend a huge amount of forwarding energy to route in-bound data packets towards the base station, and therefore die quickly. To this end, we examine a random-gaussian deployment of gateways, which can effectively reduce their forwarding energy by randomly placing more gateways nearer to the base station. Increasing the number of gateways around the base station distributes the routing load among multiple gateways, reduces their forwarding energy and effectively increases their lifetime (refer Table 5). The gaussian-random coordinates of gateways can be generated as shown in Eq. 29:

$$\begin{aligned} (x_i, y_i) = (r_{i,1} \sim {\mathcal {N}}({\mathbb {c}}, {\mathbb {s}}), r_{i,2} \sim {\mathcal {N}}({\mathbb {c}}, {\mathbb {s}})) \end{aligned}$$

(29)

Here, $(x_i, y_i)$ denotes the x and y-coordinate pair of the ith gateway, and $r_{i,1}$ and $r_{i,2}$ are sampled from a gaussian distribution having ${\mathbb {c}}$ mean and ${\mathbb {s}}$ standard deviation. The parameter ${\mathbb {c}}$ corresponds to the coordinates of the base station which is situated at (250, 250), and therefore we set ${\mathbb {c}} = 250$. On the other hand, the parameter ${\mathbb {s}}$ corresponds to the spread of gateways from the base station and determines the concentration of gateways around the base station and the extent of gateway coverage in the WSN. For our experiments, we found that ${\mathbb {s}} = 100$ provided sufficient coverage and good network performance.

Table 5 Comparison of Gaussian and uniform deployment: the Gaussian deployment results in lower maximum forwarding energy of gateways and higher network lifetime

For our experiments, we consider a WSN with the same parameters as shown in Table 4 and having 60 gateways and 200 SNs. Table 5 summarizes experimental results derived by running the proposed algorithms on 40 independent distributions of SNs and CHs for both the deployment strategies. It must be noted that SNs are uniform randomly distributed across the sensing field in both the deployment strategies. Both the routing and clustering algorithms used the stochastic position update strategy and the proposed linear transfer function with $v_{max} / v_{min} = +2.5 / -2.5$. The gaussian deployment of gateways results in a 42.5% reduction in the maximum forwarding energy⁷ on an average, and a significantly longer network lifetime. Furthermore, we observe that while the forwarding energy reduces sharply in case of the gaussian deployment, the inter-cluster component is comparable in both the deployment strategies. Figs. 9 and 10 illustrate 60 gateways deployed using the uniform-random and gaussian distributions, respectively. The base station is represented by a black dot and is situated at (250, 250). From the figures, it can be seen that a large number of gateways are concentrated around the base station for the gaussian deployment.

Fig. 9

Gateways deployed using Uniform random deployment are spread uniformly across the WSN

Fig. 10

Gateways deployed using Gaussian deployment are concentrated around the base station

Despite the impressive performance of the gaussian deployment, gateways are distributed uniform-randomly in all the following experiments to present a true comparison with previous work.

7.3 The Linear Transfer Function $\xi _L$ Outperforms Traditional $\xi _S$ and $\xi _T$

For comparing the performance of our proposed linear transfer function against sigmoid and $hyperbolic \ tan$, we consider the same network parameters as given in Table 4. We chose to compare against sigmoid and hyperbolic tan transfer functions only, since they have been widely used in the past for a number of applications [1, 24, 30, 31]. We tuned the maximum and minimum velocity parameters for each of the transfer functions in the range [1, 100], and chose the values of $v_{max}$ and $v_{min}$ (refer Table 4) for which they performed the best. We found that the linear transfer function performed well for $v_{max} = 2.5$ and $v_{min} = - 2.5$ for which it linearly approximates the sigmoid function over a large range. Table 6 summarizes the experimental results on 40 randomly and independently generated sets of coordinates of gateways and SNs for each network configuration having 200, 300, 400 or 500 SNs. We chose to test the three transfer functions on the same sets of coordinates to do away with any variation due to input coordinates. We found that the linear transfer function performed well for $v_{max} = 2.5$ and $v_{min} = - 2.5$ for which it linearly approximates the sigmoid function over a large range (refer Fig. 11).

Table 6 Comparison between transfer functions: the linear transfer function outperforms other traditional transfer functions

Fig. 11

Various transfer functions

Firstly, we evaluated the transfer functions based on the average network lifetime achieved by our routing and clustering algorithms using each transfer function. Our results revealed that the linear transfer function resulted in a longer network lifetime on an average for each network configuration (refer Fig. 12). Next, we evaluated the average increase in lifetime for 40 runs of our algorithm using each transfer function. The average increase in lifetime (First Gateway Died) can be computed as follows:

$$\begin{aligned} Average \ increase \ in \ lifetime = \frac{gbest_k.lifetime - gbest_1.lifetime}{Number \ of \ runs} \end{aligned}$$

(30)

where k is the number of iterations and $gbest_i.lifetime$ is the lifetime of the gbest particle at the ith iteration. We found that the linear transfer function increased the network lifetime more on an average in comparison to sigmoid and $hyperbolic \ tan$ transfer functions for all the network configurations (Fig. 13).

Fig. 12

First gateway died: the linear transfer function achieves a high network lifetime consistently

Fig. 13

Average increase in first gateway died: the linear transfer function mostly results in a higher average increase in lifetime

The increasing trend in the average increase in lifetime can be attributed to the fact that network configurations with greater numbers of SNs have a larger clustering search space, and therefore at the start of the optimization process, randomly-generated yet good clustering solutions occur with a smaller probability. From Figs. 14 and 15 we can see that the linear transfer function updates the global best solution more often than tanh and sigmoid transfer functions. This is due to the fact that our linear function does not have a vanishing gradient, and therefore is equally sensitive to a change in a particle’s position at all velocities i.e. the proportion of rise in the probability that a bit is ON to an equal rise in velocity remains constant across the interval $[ v_{min}, v_{max} ]$.

Fig. 14

Average updates in routing: the linear transfer function has greater updates than other transfer functions

Fig. 15

Average updates in clustering: the linear transfer function has greater updates other transfer functions

For the WSN configuration with 200 SNs, we also evaluated the running time (refer Table 6) of our algorithms using the three transfer functions. Our results revealed that using the linear transfer function as against sigmoid and tanh, led to a 7–12% reduction in average routing time and 11.5–17% reduction in average clustering time. This reduction can be attributed to the computational simplicity of the linear transfer function.

7.4 The Stochastic Update Strategy Outperforms Max Update Strategy

In order to evaluate the performance of the stochastic and max position update strategies, we compared the average lifetime and average increase in lifetime produced by our routing and clustering algorithms for both the position update strategies. We evaluated both the strategies on 40 sets of randomly and independently generated coordinates for each network configuration. Our results (refer Figs. 16, 17) confirmed that the stochastic update strategy outperforms the max update strategy, by achieving considerably longer network lifetimes and a significant increase in the lifetime on an average for all the network configurations.

Fig. 16

Lifetime versus number of SNs: stochastic update strategy outperforms the max update strategy in increasing the lifetime of the network

Fig. 17

Average increase in lifetime (first gateway died) versus number of SNs: the stochastic update strategy increases network lifetime more than the max update strategy

Figures 18 and 19 illustrate the average number of updates for the global best solution during routing and clustering. Clearly, the stochastic update strategy updates the global best solution more often than the max update strategy. This is due to the fact that the stochastic update strategy encourages more exploration owing to its probabilistic nature.

Fig. 18

Average updates in routing: the stochastic update strategy achieves a higher number of updates than the max update strategy

Fig. 19

Average updates in clustering: the stochastic update strategy achieves a significantly higher number of updates than the max update strategy

7.5 Lifetime Comparison with State-of-the-Art Algorithms

Fig. 20

Network lifetime (60 gateways): BPSO achieves significantly high network lifetime

Fig. 21

Network lifetime (90 gateways): BPSO outperforms other state-of-the-art algorithms in terms of lifetime (first gateway died)

In order to compare the performance of our routing and clustering algorithms with other state-of-the-art algorithms, we executed the PSO-based routing and clustering algorithm proposed by Kuila and Jana [20] and three other clustering algorithms: GA-based clustering [21], Greedy Load-Balanced Clustering Algorithm (GLBCA)[23] and Least Distance Clustering (LDC) [2]. All these clustering algorithms assumed that the base station is within the direct communication range of all the gateways and therefore did not consider multi-hop routing. For a true comparison with our proposed algorithms, we executed the popular GA-based multi-hop routing algorithm proposed by Bari et al. [3] for each of the three-clustering algorithm (GA-based clustering, GLBCA and LDC). We ran our experiments for 40 sets of independently and uniform-randomly generated coordinates of gateways and SNs for each unique network configuration. Moreover, we compared the lifetime of the network for several network configurations by varying the number of SNs between 200 and 500, and for 60 and 90 gateways. Figures 20 and 21 illustrate the results we obtained. It can be seen that our proposed algorithm leads to a better network lifetime than other state-of-the-art algorithms. This is due to the fact that our proposed routing algorithm recognizes that gateways dissipate a significant amount of forwarding energy (refer Table 5), and minimizes it to effectively prolong network lifetime (Figs. 22, 23).

Fig. 22

Energy consumption: our algorithm consumes appreciably lower energy than state-of-the-art of algorithms

Fig. 23

Packets received by base station (BS): our algorithm delivers significantly higher packets to BS than state-of-the-art of algorithms

From Fig. 23, it can be observed that the total packets received by the base station in our approach is appreciably higher than other algorithms. This is a direct consequence of the fact that our approach has a better network lifetime than other state-of-the-art algorithms. Figure 22, compares the energy consumption of our algorithm with other state-of-the-art algorithms for 60 gateways and 600 SNs. Our WSN has significantly lower energy consumption as compared to other algorithms. This demonstrates the efficacy of our proposed fitness functions which are directly aimed at minimizing forwarding and intra-cluster energy consumption of CHs, thereby minimizing the total energy consumption of the network.

7.6 BPSO Outperforms PSO at Routing and Clustering

In this sub-section, we compare the performance of continuous PSO and its discrete counterpart BPSO. For this comparison, we ran PSO and BPSO-based routing and clustering on a WSN having the same network parameters as Table 4 having 200 SNs and 60 gateways. Both the algorithms were run on 40 sets of input coordinates using our fitness functions. We represented particles in PSO in the same manner as Kuila and Jana [20]⁸ and used their indexing function to map particle positions in a continuous space to a discrete space. As discussed previously, BPSO searches for a velocity matrix in a continuous search space which maps to a good particle position in a discrete space. In contrast, PSO searches for a velocity vector which maps to good particle position, both of which are in a continuous search space. In PSO, the indexing function is used to map the continuous position of a particle to a discrete routing or clustering configuration.

Fig. 24

BPSO versus PSO routing fitness: BPSO is less prone to local minima as compared to its counterpart

Fig. 25

BPSO versus PSO clustering fitness: BPSO is less prone to local maxima as compared to its counterpart

Table 7 Comparison of PSO and BPSO: BPSO is better equipped to find an efficient routing & clustering solution than PSO

Our results summarized in Table 7 suggest that BPSO achieves a significantly longer average network lifetime than PSO. Furthermore, BPSO is better able to minimize the routing fitness and average distance of SNs from their clusters. Figures 24 and 25 illustrate the routing and clustering fitness per iteration for both BPSO and PSO for the same set of input coordinates. It can be clearly seen that BPSO quickly minimizes the routing fitness and reaches a fitter routing solution in comparison to PSO. During clustering, BPSO starts at a higher fitness than PSO owing to its better routing solution, and improves the fitness over iterations. Furthermore, in order to evaluate the overall increase in lifetime due to optimization over random routing and clustering configurations, we ran BPSO and PSO based routing and clustering for a single iteration over the same sets of 40 input coordinates. The routing and clustering solutions after a single iteration are as good as random. The results summarized in Table 7 show that BPSO increases the lifetime of a WSN by 1294 rounds over a random routing and clustering configuration on an average, as against PSO which is only able to increase the lifetime by 768 rounds. During both routing and clustering, BPSO was able to effectively optimize the fitness functions, while PSO repeatedly got trapped in local maxima. This is due to the fact that BPSO is better suited to handle discrete problems such as finding optimal routing and clustering solutions.

8 Conclusion and Future Work

In this paper, we proposed an energy efficient BPSO based routing and clustering algorithm, which uses an intuitive two-dimensional particle representation along with a novel particle update strategy and transfer function. Results from detailed experimental evaluation show that our transfer function and particle update strategy outperform traditional transfer functions and particle update strategies proposed in the past. Our experiments also reveal that our algorithm effectively maximizes network lifetime, and achieves a significantly higher lifetime in comparison to state-of-the-art algorithms. Furthermore, our results confirm that BPSO is better equipped to solve discrete optimization problems like efficient routing and clustering than continuous PSO. Future work may include experimenting with fitness functions which take into account the reliability of wireless links.