1 Introduction

Wireless sensor network (WSN) is an undeniably essential innovation that attracts considerable research interest [1]. A typical WSN comprises large number of nodes with implicit sensors which are engaged in sensing the events that occur in the surrounding environment [2]. Localization is crucial challenge in WSNs, as location information of an event is also required along with the sensing information in several types of applications, such as wild life surveillance, fire surveillance, water quality monitoring, intrusion detection, health monitoring and precision agriculture etc. In these applications, the estimation/event information is not much use unless the location where the event has taken place is available [3]. Localization algorithms determine the position of nodes by exploiting knowledge of absolute positions of few nodes called beacons. GPS can be used as solution for localization, but it is not a feasible solution because of its size, energy consumption and high cost.

The localization algorithms are of two kinds: range-based or range-free [4]. Range-based algorithm [5,6,7,8,9] gives high precision due to use of special equipment which increases its cost, although its estimates are affected by noise and multi-path fading. On the other hand, range-free algorithms [10,11,12,13,14] require connectivity information and no specialized hardware, thus they are cost effective. Most of the researchers have paid higher attention towards range-free rather than range-based technique due to its low cost. In previous studies, localization algorithms mainly focus on 2D space, but generally, nodes are deployed in 3D space for many applications. Thus, localization technique should be developed for 3D space to make it more realistic. Among range-free algorithms, DV-Hop algorithm is extremely popular because of its simplicity, cost-effectiveness, and robustness, but still it has low accuracy. Therefore researchers are still working on improving this algorithm.

In this paper, we put forward the application of Grey-Wolf-based optimization technique with DV-Hop algorithm in both 2D and 3D WSN. We have proposed two algorithms that use Grey-Wolf-based optimization technique. Simulation results prove that Grey-Wolf-based optimization technique if merged with DV-Hop, results in high localization accuracy.

The paper is structured as: Sect. 2 discusses the localization problem. Section 3 gives the introduction of DV-Hop algorithm and its error analysis. Section 4 discusses the overview of Grey-Wolf optimization. Section 5 is followed by implementation of proposed algorithms. The simulation is presented in Sect. 6. Then, Sect. 7 discusses concluding remarks and future work.

2 Problem Statement

Localization is the process of obtaining absolute coordinates of nodes in a WSN [15]. In this problem, we take a WSN having N total nodes. There are three varieties of nodes.

  1. (a)

    Beacon nodes—Those that know their position.

  2. (b)

    Settled nodes—Those that initially are unaware of their location, but then are able to get this information by applying localization technique.

  3. (c)

    Unsettled nodes—Those that are unaware of their location.

Assuming there are m beacon nodes and n unsettled nodes (m is at least 10% of N), the localization problem is to convert these n unsettled nodes to settled ones.

3 Related Work

Here, we present a brief overview of DV-Hop and its various improved versions proposed in the literature.

3.1 Traditional DV-Hop Localization Scheme

DV-Hop was first put forwarded by Niculescu et al. [11] in 2003. It is a distributed hop counting technique. The symbol table used for DV-Hop Algorithm applied for 3D space is given in Table 1.

Table 1 Symbol table for DV-Hop algorithm
Full size table

This algorithm works in three phases for 3D space that are described as follows:

Phase 1: All beacon nodes pass packets containing their coordinate information (x i ,y i ,z i ) along with their id i, hop count(hop i , initially set to 0) to all other nodes within their communication range. All the nodes maintain their own hop count table containing ids, position information and hop counts of all beacons in the network with the help of these packets. The receiving node first increments the hop count value and then updates it in its table for given beacon i if it is the first packet received from beacon, otherwise it verifies the hop count value from its table and if the received incremented value is smaller than the value stored in the table, then the node replaces the stored value by received value. This phase allows every node to know minimum hop counts from every beacon in the network.

Phase 2: After the first phase, all the beacons reckon average distance in one hop (AvgHopSize i ) by utilizing Eq. (1).

$$AvgHopSize_{i } = \frac{{\mathop \sum \nolimits_{j = 1 i \ne j}^{m} \sqrt {\left( {x_{j } - x_{i} } \right)^{2} + + \left( {y_{j } - y_{i} } \right)^{2} + \left( {z_{j } - z_{i} } \right)^{2} } }}{{\mathop \sum \nolimits_{i = 1 i \ne j}^{m} hop_{j} }}$$
(1)

where i is the id of beacon i, (x i ,y i ,z i ), (x j ,y j ,z j ) are coordinates of beacons i and j, j lies between 1 to m(j ≠ i), hop j is the hop count of beacon j from beacon i.

Then, they send one more packet containing calculated AvgHopSize i to all other nodes. A receiving one (assuming having id u) computes approximate distances (d j ) from each beacon node j by multiplying AvgHopSize i of its nearest beacon i by hop count (hop j ) obtained from its hop count table [Eq. (2)].

$$d_{j} = AvgHopSize_{i } \times hop_{j}$$
(2)

Phase 3: This is the last phase applied by unsettled nodes to move to settled status. They apply trilateration/multilateration method to get their absolute coordinates. The whole process is explained below:

Let the coordinates of unsettled node u and beacon B j be (x u ,y u ,z u ) and (xj,yj,zj) \(\{ j \in \left( {1,m} \right)\}\). The following system of equations can be formed:

$$\left. {\begin{array}{*{20}c} {\left( {x_{u} - x_{1} } \right)^{2} + \left( {y_{u} - y_{1} } \right)^{2} + \left( {z_{u} - z_{1} } \right)^{2} = d_{1}^{2} } \\ {\left( {x_{u} - x_{2} } \right)^{2} + \left( {y_{u} - y_{2} } \right)^{2} + \left( {z_{u} - z_{2} } \right)^{2} = d_{2}^{2} } \\ \cdots \\ \vdots \\ {\left( {x_{u} - x_{m} } \right)^{2} + \left( {y_{u} - y_{m} } \right)^{2} + \left( {z_{u} - z_{m} } \right)^{2} = d_{m}^{2} } \\ \end{array} } \right\}$$
(3)

Equation (4) can be derived from Eq. (3).

$$\left. {\begin{array}{*{20}c} { - x_{m}^{2} + y_{1}^{2} - y_{m}^{2} + z_{1}^{2} - z_{m}^{2} - d_{1}^{2} - d_{m}^{2} = 2 \times x_{u } \times \left( {x_{1 } - x_{m } } \right) + 2 \times y_{u} \times \left( {y_{u } } \right) + 2 \times z_{u} \times \left( {z_{1 } - z_{u } } \right)} \\ {x_{2}^{2} - x_{m}^{2} + y_{2}^{2} - y_{m}^{2} + z_{2}^{2} - z_{m}^{2} - d_{2}^{2} - d_{m}^{2} = 2 \times x_{u } \times \left( {x_{2 } - x_{m } } \right) + 2 \times y_{u } \times \left( {y_{2 } - y_{u } } \right) + 2 \times z_{u } \times \left( {z_{2 } - z_{u } } \right)} \\ \vdots \\ {x_{m - 1}^{2} - x_{m}^{2} + y_{m - 1}^{2} - y_{m}^{2} + z_{m - 1}^{2} - z_{m}^{2} - d_{{\left( {m - 1} \right)}}^{2} - d_{m}^{2} = 2 \times x_{u } \times \left( {x_{m - 1 } - x_{m } } \right) + 2 \times y_{u } \times \left( {y_{m - 1 } - y_{u } } \right) + 2 \times z_{u } \times \left( {z_{m - 1 } - z_{u } } \right)} \\ \end{array} } \right\}$$
(4)

The matrix form of Eq. (4) is Eq. (5) as given below:

$$AX_{u} = B$$
(5)

where \(A = 2 \times \left[ {\begin{array}{*{20}c} {x_{1} - x_{m} } & {y_{1} - y_{m} } & {z_{1} - z_{m} } \\ {x_{2} - x_{m} } & {y_{2} - y_{m} } & {z_{2} - z_{m} } \\ \vdots & \vdots & \vdots \\ {x_{m - 1} - x_{m} } & {y_{m - 1} - y_{m} } & {z_{m - 1} - z_{m} } \\ \end{array} } \right],\quad X_{u} = \left[ {\begin{array}{*{20}c} {x_{u} } \\ {y_{u} } \\ {z_{u} } \\ \end{array} } \right],\) and \(B = \left[ {\begin{array}{*{20}c} {x_{1}^{2} - x_{m}^{2} + y_{1}^{2} - y_{m}^{2} + z_{1}^{2} - z_{m}^{2} - d_{1}^{2} - d_{u}^{2} } \\ {x_{2}^{2} - x_{m}^{2} + y_{2}^{2} - y_{m}^{2} + z_{2}^{2} - z_{m}^{2} - d_{2}^{2} - d_{m}^{2} } \\ \vdots \\ {x_{m - 1}^{2} - x_{m}^{2} + y_{m - 1}^{2} - y_{m}^{2} + z_{m - 1}^{2} - z_{m}^{2} - d_{m - 1}^{2} - d_{m}^{2} } \\ \end{array} } \right]\)

Equation (5) can be transformed to Eq. (6) as follows:

$$X_{u} = \left( {A^{T } A} \right)^{ - 1} A^{T } B$$
(6)

Equation (6) is solved to obtain the coordinates of the node by using Least Square (LS) method.

The algorithm is exceptionally prominent algorithm as it is very simple, feasible, scalable and applicable for nodes having less than 3 neighbour nodes. The nodes that are having less than 3 neighbours can also be localized using this algorithm due to its distributed nature. But its accuracy is affected by several factors.

The algorithm has served as motivation for many range free localization algorithms. Extensive research has been done in enhancing its accuracy. In [16], Tomic proposed three distinct kinds of algorithms (iDV-Hop1, iDV-Hop2, and Quad DV-Hop). The first two algorithms add one more step which includes geometry techniques which consider the impact of nearest beacon to increase the accuracy. The third algorithm replaces the third phase by applying non-linear method called quadratic programming solver to increase the accuracy. Two more improved methods were proposed in [17] by Song et al. that has utilized weighted method in place of lateration method in third phase. In second algorithm, he used a non-linear method called hyperbolic algorithm in the third phase. The first algorithm reduces the complexity of DV Hop with a small improvement in accuracy, whereas, second approach improves the accuracy to a large extent. In [18], Zhang introduced two algorithms which apply weighted approach in the final phase. Both algorithms choose the weight that is inversely proportional to number of hops. The concept in these algorithms was that the beacon which is closer to the node should have higher role than the beacon that is far from it. Both these algorithms achieve higher accuracy. In [19], Fang added a compensation coefficient to correct distance between beacons and regular nodes. An improvement was made in [20] by optimizing location of node in third phase of DV-Hop algorithm by applying genetic algorithm which results in higher accuracy. In [21], Gui et al. introduced a small low computational step as fourth phase to improve the accuracy of algorithm. Gui et al. also proposed another algorithm in [21] which replaces third phase with very complex method selecting 3 best beacons for each particular node to determine its location. In [22], Shahzad et al. computed the optimal value of max_hop that is used by node to determine its location. If the beacons are within this max-hop value, then only that beacon is selected by the node to get its location, otherwise it is discarded.

In [23], Wang et al. introduced a weighted algorithm which also uses Genetic algorithm and simplex method in its third phase to solve the problem of high localization error of weighted DV-Hop. Experiments prove that localization accuracy is improved significantly by applying hybrid algorithm of genetic algorithm and simplex method in third phase of DV-Hop algorithm. Kumar et al. [24] also proposed an improved algorithm which uses an improvement term to refine the hop-size of anchor nodes in second phase of DV-Hop and uses unconstrained optimization technique in place of least square method in third phase to attain better localization accuracy.

These entire algorithms have tried to improve localization accuracy to some extent, but still there is scope to improve the accuracy further. Based on this fact, we are proposing an improved variant of DV-Hop by refining the value of average hop distances computed by all beacons which is the root cause of localization error.

4 Error Analysis of DV-Hop Localization Scheme

The main factor which contributes most to localization error is the error in computing average hop distance by each beacon. The beacon i compute its exact distance from any beacon j (d j ) by applying following Eq. (7).

$$d_{j} = \sqrt {\left( {x_{i} - x_{j } } \right)^{2 } + \left( {y_{i} - y_{j } } \right)^{2 } + \left( {z_{i} - z_{j } } \right)^{2 } }$$
(7)

If AvgHopSize i is average distance per hop for beacon i, then its approximate distance (d1 j ) from beacon j is product of hop j and AvgHopSize i [Refer Eq. (3)]. The error e i is the difference in these two values (e i = d j  − d1 j ). The optimized AvgHopSize i should reduce the value of e i as small as possible. To reduce this error in computing average hop size, grey wolf optimization algorithm is applied.

The objective function used in grey wolf optimization is described as follows:

$$\begin{aligned} \hbox{min} \quad e_{i} & = \mathop \sum \limits_{j = 1,j \ne i}^{m} (d_{j} - d1_{j } ) \\ 0 & <\;AvgHopSize_{i}\; \le \mathop {\hbox{max} }\limits_{{}} d_{j} \\ \end{aligned}$$
(8)

where \(d1_{j} = AvgHopSize_{i } \times hop_{j}\). The problem is to find optimum value of average hop size of beacon i by minimizing the above function.

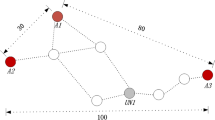
Consider a WSN network as shown in Fig. 1 in which there are three beacons B1, B2 and B3 and unsettled node (UN) that wants to locate itself. All these beacons know their distances from each other after phase 1 of DV-Hop. Let the distances be 10, 20 and 30 respectively. B1 is 2 hops apart from UN, B2 is 3 hops apart from UN and B3 is 1 hop apart from UN. Let the length of each hop be 5 m and B3 is 10 m apart from UN. In the phase 2, all Beacon nodes compute their AvgHopSizes by applying Eq. (1).

Fig. 1
figure 1

Example of DV-Hop algorithm

Full size image
$$AvgHopSize_{1} = \frac{10 + 20}{3 + 5} = 3.75$$
$$AvgHopSize_{2} = \frac{20 + 30}{5 + 4} = 5.56$$
$$AvgHopSize_{3} = \frac{10 + 30}{3 + 4} = 5.71$$

The beacon nodes pass average hop distances to all other nodes. The unsettled node picks the first received average hop size and discards other. The UN node chooses average hop size of B3 node as it is just 1 hop apart from it. Thus according to DV Hop phase 2, B3 is 5.71 m apart from UN, although actual distance is 10 m. Thus, localization error is 10 − 5.71 = 4.29 m, that is almost 40% of actual distance. Due to this high error, the UN node localizes itself incorrectly. From above analysis, we infer that the localization error of the DV-Hop is influenced by approximate calculation of average hop sizes by beacons. Thus, to reduce localization error, the average hop sizes need to have better approximation.

5 Overview of the Grey-Wolf Optimization (GWO) Algorithm

Grey-Wolf optimization algorithm was proposed by Mirjalili et al. [25]. It is a new meta-heuristic optimization technique inspired by hunting mechanism of grey wolves. The reason to select this algorithm is that it is very simple, flexible and it tries to search entire search space rather than selecting only local optima solution. In [25], the given algorithm has been compared with other well known optimization algorithms for 28 benchmark functions and it has been proved that grey-wolf is superior to other meta-heuristic optimization algorithms. GWO algorithm depends on the classification of grey wolfs. The grey wolves are of 4 kinds. The first category called alphas that are leaders to help in taking choices about chasing, rest place, time to wake and many more. The next category is of betas that are subordinates of alpha. The lowest in this hierarchy are omegas and deltas.

For GWO, we consider that the best solution is alpha (α). The next two best solutions are beta (β) and delta (\(\delta\)). The rest solutions are omega \((\omega )\). During hunting, the wolves encircle the prey which can be depicted using following mathematical model:

$$D = C \cdot X_{p } \left( i \right) - X\left( i \right)$$
(9)
$$X\left( {i + 1} \right) = X_{p } \left( i \right) - A \cdot D$$
(10)

where i is the iteration, A and C are coefficient vectors, Xp is the position of prey and X is the position vector of grey wolf. The vectors A and C are computed as follows:

$$A = 2a \cdot r_{1} - a$$
(11)
$$C = 2 \cdot r_{2}$$
(12)

where a is a vector which decreases linearly from 2 to 0 and r1, r2 are random vectors in range from 0 to 1.

In GWO, it is assumed that the alpha, beta and delta knows better about prey. Thus, following formulas are proposed to get the location of prey.

$$D_{ \propto } = C_{1} \cdot X_{ \propto } - X,\quad D_{\beta } = C_{2} \cdot X_{\beta } - X,\quad D_{\delta } = C_{3} \cdot X_{\delta } {-} X$$
(13)
$$X_{1} = X_{ \propto } - A_{1} \cdot D_{ \propto } ,\quad X_{2} = X_{ \beta } - A_{1} \cdot D_{\beta } , \quad X_{3} = X_{\delta } - A_{1} \cdot D_{\delta }$$
(14)
$$X\left( {i + 1} \right) = \frac{{X_{1 + } X_{2} + X_{3} }}{3}$$
(15)

The pseudo code of GWO is depicted in Fig. 2.

Fig. 2
figure 2

Steps used in the Grey wolf optimization algorithm

Full size image

6 Proposed Algorithms

In this section, we present two algorithms, called Grey wolf optimization based DV-Hop (GWO-DV-Hop), and weighted grey wolf optimization based DV-Hop (Weighted GWO-DV-Hop). They work for both 2D and 3D space, although we describe below for 3D space only.

6.1 GWO-DV-Hop Algorithm

The proposed GWO-DV-Hop localization algorithm works in three phases. The assumptions are: circular radio range, symmetric radio connectivity, no additional hardware, no obstructions, lack of line-of-sight, no multipath and fading.

Phase 1: Calculating minimum hop counts from each beacon: Each node gets position and minimum number of hop counts from each beacon by applying broadcasting mechanism. The phase is similar to the phase 1 of the traditional DV-Hop.

Phase 2: Refinement of Average Hop Distance by the beacon: In this phase, the beacons calculate their average hop sizes by applying Eq. (1) and then compute their distances from each beacon by applying Eq. (7). After this, the beacons use grey wolf algorithm to refine average hop distances. The fitness function used to achieve optimized average hop distance is mentioned by Eq. (8). This phase helps all the beacons to get their refined average hop sizes. All these average hop sizes are broadcasted to all other nodes in the network who then derive their distances from every beacon by taking the product of refined average hop size of nearest beacon to the given node and minimum hop counts. This distance information is used in the next phase. The steps of using grey wolf algorithm for obtaining the optimum average hop size by every beacon are given in Fig. 3.

Fig. 3
figure 3

Phase 2 of proposed algorithm

Full size image

Phase 3: Converting the unsettled node to settled node: The unsettled nodes locate themselves by applying lateration method [11] such as least square method as described in Phase 3 of Sect. 3.1.

6.2 Weighted GWO-DV Hop Algorithm

Phase 1: Calculating minimum hop counts from each beacon: Same as in 6.1.

Phase 2: Refinement of Average Hop Distance by the beacon: Same as Phase 2 in GWO-DV-Hop.

Phase 3: Converting the unsettled node to settled node: The unsettled nodes compute their own average hop distance by considering impact of average hop distances of all the beacons. The beacon that is closer to the node has higher weight than the beacon that is far away from the node. The average hop distance computed by the node u is described using Eq. (16).

$$AvgHopSize_{u} = \frac{{\mathop \sum \nolimits_{i = 1}^{m} w_{i} \times AvgHopSize_{i} }}{{\mathop \sum \nolimits_{i = 1}^{m} w}}$$
(16)

where \(w_{i} = \frac{1}{{hop_{i} }}\) is the weight of each beacon i.

Then, the node u obtain its distances from every beacon (say with id i) by applying Eq. (17).

$$d_{i} = AvgHopSize_{u} \times hop_{i}$$
(17)

After obtaining all these distances from every beacon, the unsettled node settles itself by applying lateration method [11] which uses least square method.

7 Results and Analysis

This section presents a detail performance comparison of the proposed algorithm with the state-of-art DV-Hop algorithm and discusses its performance by varying different network parameters. Nest, complexity analysis of the proposed algorithm with the DV-Hop are listed and discussed.

7.1 Performance Evaluation and Discussions

To evaluate the performance of the proposed algorithms, we implemented all the algorithms and compared their performance on the basis of Localization Error (in %). The algorithms are implemented in both 2D and 3D environment. The parameters used for the simulation are described in Table 2 for 2D space and in Table 3 for 3D space. The minimum communication radius for 2D is set to 15 m and for 3D is 20 m. It is observed that the value of communication radius depends upon the node density. Smaller the node density, larger is the value of communication radius so that all the nodes are able to communicate with each other. This is the reason that the minimum value of communication radius for 3D is greater than that used in 2D space. The percentage of beacons used should be 10% of total nodes.

Table 2 Simulation parameters for 2D space
Full size table
Table 3 Simulation parameters for 3D space
Full size table

The localization accuracy [26,27,28,29,30,31,32,33] is formulated as follows:

$$localization \;error = \frac{1}{n \times r}\mathop \sum \limits_{i = 1}^{n} \sqrt {\left( {x_{a} - x_{u} } \right)^{2} + + (y_{a} - y_{u} )^{2} + (z_{a} - z_{u} )^{2} }$$
(18)

where n is the total number of unknown nodes, (x a ,y a ,z a ) are the actual coordinates and (x u ,y u ,z u ) are the estimated coordinates of unknown node and r is the communication radius of sensors.

The localization accuracy enhances as the localization error reduces.

It can be seen from Figs. 4, 5, 6, 7, 8, 9, 10, and 11 that grey-wolf based perform better in terms of localization accuracy. Figures 4, 5, 6, and 7, represent results for 2D space, and Figs. 8, 9, 10, and 11 represent results for 3D space.

Fig. 4
figure 4

Comparison by varying number of beacons (total nodes = 200, border length = 100, r = 15 m)

Full size image
Fig. 5
figure 5

Comparison by varying total number of nodes (beacon nodes = 10% of total nodes, border length = 100, r = 15 m)

Full size image
Fig. 6
figure 6

Comparison by varying communication radius (total nodes = 200, border length = 100, beacon nodes = 20)

Full size image
Fig. 7
figure 7

Comparison by varying border area (total nodes = 300, beacon nodes = 30, communication radius = 15 m)

Full size image
Fig. 8
figure 8

Comparison by varying total number of beacons (total nodes = 200, border length = 100, communication radius = 20 m)

Full size image
Fig. 9
figure 9

Comparison by varying total number of nodes (beacon nodes = 10% of total nodes, border length = 100, communication radius = 20 m)

Full size image
Fig. 10
figure 10

Comparison by varying communication radius (total nodes = 200, border length = 100, beacon nodes = 20)

Full size image
Fig. 11
figure 11

Comparison by varying border area (total nodes = 300, beacon nodes = 30, communication radius = 20 m)

Full size image

Figure 4 illustrates that the proposed algorithms reduces the localization error when the percentage of beacon nodes is increased from 10 to 40% for WSN area 100 × 100 and total nodes = 200. It is observed that the average localization error decreases as the percentage of beacon nodes increases in all the algorithms. This is due to the reasons that when there are more beacon nodes in the network, percentages of nodes which have at least four neighbouring beacons becomes greater and localization is done easily and accurately. It is observed that if there is more than 60% of the beacon node, then the nodes localize themselves very accurately. They are very near to the actual coordinates. It is seen from Fig. 4. The localization error for GWO-DV Hop and Weighted GWO-DV Hop reduces from 50 to 35% with the increase in beacon nodes from 20 to 80, whereas Original DV Hop is reduced from 60 to 45%. Thus there is improvement of 10% in accuracy.

Figures 5 and 6 show the impact of total number of nodes and communication radius on average localization error, respectively. If the network size considered is 100 × 100 m2, then for Fig. 5 where the total nodes are increased from 200 to 450 with beacon percentage as 10% of total nodes, the localization error is reduced with both proposed algorithms from 42 to 35%. It can be noticed that both the proposed algorithms behave similarly, but better than DV-Hop algorithm. It is also observed that localization accuracy depends upon beacon percentage. There is slight effect on localization accuracy even if total nodes are varied, but the percentage of beacons remains constant. In Fig. 6, communication radius is changed from 15 to 35 in \(100 \times 100\) m2 WSN area with 200 total nodes and 10% beacons. The localization error is reduced by 5% with our proposed algorithms.

Figure 7 shows the average localization errors of above said algorithms with different border area in the 2D network. The border area is increased from \(100 \times 100\) to \(300 \times 300\) m2. It can be seen that with the increase in the border area with the same number of nodes, the node density decreases, thus the localization error increases.

Figures 8 and 9 show the impact on localization error by changing the beacon nodes and total number of nodes, respectively. The beacon nodes are tuned from 20 to 80 for 3D network in Fig. 8 and total nodes are tuned from 200 to 350 for 3D network in Fig. 9 with 10% of beacon nodes. In the both cases, the proposed algorithms outperform the original algorithm.

Figures 10 and 11 show the comparison by varying communication radius and border area. Overall, it is obvious that the GWO-DV Hop performs best with least localization error. The weighted GWO-DV Hop is better than DV-Hop and has slight higher error than GWO-DV Hop algorithm.

7.2 Complexity Analysis of Proposed Algorithms

The complexity is considered in terms of communication cost and computation cost [34, 35]. The Communication cost is total number of packets transmitted in the network. There is no change in communication cost for the proposed algorithms.

The Computation cost that is sum of mathematical operations required to run the algorithms is shown in Table 4.

Table 4 Computation cost
Full size table

From Table 4, it is observed that the algorithms give higher accuracy with slight increase in computation cost.

8 Conclusions

In order to reduce localization error of DV-Hop localization algorithm due to approximate computation of average hop sizes by each beacon, Grey wolf optimization algorithm is used to improve the estimate of the average hop size. Based on Grey wolf algorithm, two algorithms are proposed. The first algorithm refines the second phase of DV-Hop by obtaining refined average hop size. The second algorithm first applies grey wolf algorithm and then weighted approach is applied to get better approximation of average hop sizes and to consider the impact of every beacon. The simulation results prove that two algorithms perform better than previous DV-Hop. The localization error is reduced by almost 10% by applying grey wolf algorithm in second phase of DV-Hop.