Energy-Efficient Resource Allocation for Adaptive Modulated MIMO–OFDM Heterogeneous Cloud Radio Access Networks

Abstract

In this paper, an optimal resource allocation method in multiple-input multiple-output-orthogonal frequency division multiplexing heterogeneous cloud radio access network is proposed for downlink transmission. Our problem formulation takes into account inter-tier interference and quality of service requirement for RRH/HPN association policy. We formulate two non-convex optimization problems for resource block (RB) assignment and power allocation, and then solve both problems using their equivalent convex feasibility problems. By considering Lagrange dual decomposition technique, a closed form expression for joint power and RB allocation in order to improve energy efficiency (EE) is derived. In addition, the adaptive modulation is investigated to realize practical scenario. Finally, the efficiency of the proposed algorithms in enhancing EE is confirmed through Monte Carlo simulations.

1 Introduction

Wireless communication traffic is dramatically growing due to the rise in popularity of smartphones and tablets [1]. Demand to the revolutionary development of information and communication technology (ICT) to achieve high quality services for this huge amount of users, arises some new challenges. One of the most significant obstacle is energy consumption of ICT industry, which causes up to 2% of the global energy consumption [2]. Since both transmission rate and power consumption need to be considered, thus designing energy efficient wireless networks instead of pursuing optimal capacity and spectral efficiency is pressing [3].

Energy-efficient architecture designation is the first step in improving network performance. Since traditional network architectures fail to achieve ever-increasing data rates, a new network deployment strategy, HetNet, has emerged to enhance both network capacity and coverage [4]. In HetNet various types of cells are deployed and due to improvement of spatial frequency reuse, the system capacity increases. However, deploying more BSs causes two major challenges: (1) inter-tier interference mitigation and handover process result in more processing and signaling load. (2) Even though capacity of system increases, due to more power consumption as a direct result of more deployed BSs, EE performance degrades.

To overcome the above-mentioned problems, a promising architecture, cloud radio access network (CRAN), is introduced in [5–7]. This architecture is composed of a baseband unit (BBU) that is in charge of baseband processing and remote radio head (RRH) that acts as soft relay [5]. Despite tremendous advantages offered by CRAN, drawbacks such as long delay, non-ideal fronthaul with limited capacity and need to decouple control plane to attain high transmission data rates impairs C-RAN performances.

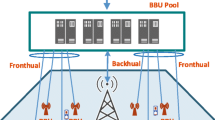
The emergence of a new architecture, heterogeneous cloud radio access network (HCRAN), which meets the challenges of both HetNets and C-RAN and takes full advantage of both structures is a turning point in designing energy-efficient network architecture. The proposed architecture is shown in Fig. 1. In HCRAN, RRHs are cooperated in the cloud which leads to obtain a high cooperation gain and low power consumption at the same time. The high power nodes (HPNs) are interfaced with the cloud by S1 and X2 interfaces. S1 and X2 are in charge of coordinating the inter-tier interference and transferring data and control plane, respectively. Furthermore, shifting the control functionality of the RRHs to the HPNs is beneficial in easing the fronthaul constraint in C-RAN.

Fig. 1

MIMO-based HCRAN architecture

As another step, we consider multiple-input multiple-output (MIMO) and orthogonal frequency-division multiplexing (OFDM) technologies. MIMO improves both spectral efficiency (SE) and system performance in fading channels. However, due to inter-symbol interference (ISI) and frequency selective nature of wireless channels, high data rate transmission is restricted and the efficiency of MIMO technology for 5G is questionable. OFDM, with its ability in reducing ISI, converts a frequency selective MIMO channel into a parallel series of frequency flat-fading subchannels and enables MIMO technique to increase data rate significantly [8, 9]. Due to simplicity and high SE, orthogonal frequency division multiple access (OFDMA), which is multiuser/multiple access version of OFDM, will be the dominant multiple access scheme for next generation wireless networks (5G).

In addition, by assuming perfect CSI, adaptive modulation (AM) utilization improves the performance of MIMO–OFDM systems [10, 11]. By using adaptive modulation, each subcarrier is adapted to its appropriate constellation size. The combination of these three technologies (AM–MIMO–OFDM), would consist a collection of advantages and play an indispensable role in the future of high data rate wireless communication systems.

Significant advantages of HCRAN, as a promising network architecture candidate for 5G, especially its impact on EE and SE improvement has attracted a lot of attention. An energy efficient resource allocation and power management algorithm is investigated for HCRAN in [12], in which by considering different QoS-requirement and inter-tier interference in an OFDMA based network, a nonconvex problem is solved and optimal power and channel matrices are obtained. In [13] the maximization of the averaged weighted EE in HCRAN by taking fronthaul capacity, inter-tier interference and queue length is considered for MIMO HCRAN.

In [14], a power and subchannel allocation problem for OFDM HetNet is investigated in which by considering all user’s rate requirements and inter-cell interference, a nonconvex problem is formulated for power saving purposes. An EE-oriented power and beamforming vector allocation problem of OFDMA HetNet is proposed in [15], where by decomposing main problem to multiple single constraint problems, a nonconvex problem is solved. In paper [16], authors propose a joint power and admission control (JPAC) for OFDMA HetNet aimed at maximizing EE/SE under power and interference constraints.

Due to ability of MIMO in achieving both multiplexing gain and diversity gain, a MIMO-based network may increase throughput and decrease energy consumption, which leads to better EE performance. To improve EE in MIMO–OFDM network several criteria is investigated and the closed form expression for the EE–SE tradeoff is derived in [17]. In [18] the optimal power allocation is researched for MIMO–OFDM in order to maximize EE by QoS consideration in multimedia communication systems where by exploiting SVD, a multichannel joint optimization problem turns into a multi-target single-channel optimization problem.

Eigenvalue-based AM Scheme for MIMO–OFDM Systems are proposed in [10, 19–22]. In [10] an adaptive modulation scheme taking both BER and total bit rate constraints into account, is presented. By considering both perfect and imperfect CSI, continuous and discrete modulation constellation is adaptively allocated with the aim of average SE maximization in [22], in which transmit rate and power constraints in each subchannel have been taken under consideration.

In this paper, optimal resource allocation algorithms are proposed to enhance the EE performance in MIMO–OFDM HCRAN. To maximize EE, inter-tier interference and different QoS requirement are taken under consideration. Then, a joint power and RB allocation optimization problem is investigated. Finally, by adapting appropriate constellation sizes to different MIMO–OFDM subchannels, a practical energy efficient network architecture is achieved.

The rest of this paper is organized as follows. In Sect. 2, we describe the system model and formulate the optimization problem. In Sect. 3, optimization problem is transformed to a convex optimization problem using Lagrange dual decomposition method and solved using an iterative algorithm. Section 4 represents simulation results which verifies the effectiveness of the proposed architecture and resource allocation algorithms. Finally, the paper is concluded in Sect. 5.

2 System Model

2.1 Cellular Network Model

We assume downlink of a two-tier heterogeneous network including one HPN and a set of coexisting RRHs. OFDMA is used in both type of base stations in order to serve multiple users. Due to severe inter-tier interference between HPN and RRHs, association of users with neighbor RRH/HPN based on the strongest receiving SINR is not efficient all the time. Hence, closed-access policy is assumed so none of unregistered mobile stations (MSs) can access to RRHs even if they are at their coverage area. As two key factors in improving both EE and SE, inter-tier and intra-tier interference mitigation attracted a lot of attention. Some advanced algorithms, such as cell association, fractional frequency reuse (FFR) and coordinated multipoint (CoMP) have been proposed for this purpose. Several researches indicate that CoMP method, utilizing advanced beamforming algorithm attain significant success in mitigating interference [23–25]. In our scenario exploiting CoMP method to mitigate intra-tier interference among different RRHs, looks to be efficient. the reason is that, all RRHs are connected to BBU pool and their baseband processes are done in cloud. Consequently, RRHs can use same frequency spectrum without performance degradation. However, inter-tier interference mitigation among HPN and RRHs need to be coordinated in BBU, which enforces a heavy burden of computational complexity on the BBU pool. By employing different spectrum deployment scheme instead, extra burden of BBU pool will be dwindled. Co-channel and orthogonal channel deployment are two major choices, which due to their disadvantages in balancing performance and attaining desired SE at the same time, the combination of them was introduced in [12]. The proposed enhanced-FFR (e-FFR) shows better SE performance, so proved to be a better choice to be used in this paper. In the mentioned scheme, frequency spectrum is bisected and each portion is assigned to different types of subscribers. It is proved that the division of spectrum by two brings a good trade-off between performance gain and implementation complexity. Users accessing RRHs (denoted by RUEs) are divided into two groups, high-QoS and low-QoS required users. High-QoS required users occupy unshared resource blocks (RBs), while low-QoS required users share their spectrum by users accessing HPNs (denoted by HUEs) and suffer from inter-tier interference. Since these users do not need high-QoS required services, by adjusting their power and assigning the most appropriate channel, can achieve their desired QoS. Figure 2 illustrates the spectrum scheme utilized in this paper.

Fig. 2

Enhanced S-FFR scheme

2.2 Channel Model

We consider a point-to-point MIMO–OFDM system with $\mathop{n}\nolimits _{T}$ transmit antennas and $\mathop{n}\nolimits _{R}$ receive antennas. Two different implementation of MIMO are known: (1) MU–MIMO systems, which can provide high data rates by transmitting to multiple MSs simultaneously over the same spectrum. (2) SU–MIMO, which allocate different subchannels to each MS. Although MU–MIMO offers higher data rate than SU–MIMO do, but severe interference is caused due to the use of shared spectrum. Therefore, SU–MIMO deployment is assumed throughout this paper. Channel matrix $H\sim {\mathbb{C}}{\mathbb{N}}(0,1)$, whose entries $\mathop{H}\nolimits _{i}=\left[ \mathop{h}\nolimits _{i,\mathop{n}\nolimits _{T},\mathop{n}\nolimits _{R}} \right]$ representing independent channel coefficients for sub-carrier i, is assumed to be flat faded. This assumption is known to be accurate due to utilizing OFDM technique. Additive white Gaussian noise (AWGN), $N\sim {\mathbb{C}}{\mathbb{N}}(0,{{\sigma }^{2}})$, is considered which includes $\mathop{n}\nolimits _{R}\times 1$ column vector. As shown in Fig. 3, by assuming perfect CSI and applying SVD to H, we can reduce each original MIMO–OFDM system into $S=m\triangleq \min (\mathop{n}\nolimits _{T},\mathop{n}\nolimits _{R})$ independent scalar subchannels [22].

Fig. 3

Equivalent scalar subchannels for MIMO system

2.3 Performance Metrics

We assume N high-QoS required RUEs with QoS requirement denoted as $\mathop{\eta }\nolimits _{1}$ and M low QoS-required RUEs with QoS requirement, $\mathop{\eta }\nolimits _{2}$. As shown in Fig. 2, total K RBs (denoted as $\mathop{\Omega }\nolimits _{T}$) are divided into $\mathop{\Omega }\nolimits _{1}$ and $\mathop{\Omega }\nolimits _{2}$, where $\mathop{\Omega }\nolimits _{1}$ is occupied by high QoS-required RUEs and $\mathop{\Omega }\nolimits _{2}$ is shared between low-QoS required RUEs and users of HPN. As a result of using shared spectrum, an interference term must be considered for low QoS-required RUEs. Hence, channel to interference plus noise ratio (CINR) for n-th RUE occupying the k-th RB at s-th subchannel, is defined as,

$$\begin{aligned} {{\sigma }_{n,k,s}}= {\left\{ \begin{array}{ll} {\mathop{d}\nolimits _{n}^{R}\mathop{h}\nolimits _{n,k,s}^{R}}/{\mathop{B}\nolimits _{0}\mathop{N}\nolimits _{0}}\;&{}k\in \mathop{\Omega }\nolimits _{1} \\ {\mathop{d}\nolimits _{n}^{R}\mathop{h}\nolimits _{n,k,s}^{R}}/{\left( {{P}^{H}}d_{n}^{H2R}h_{n,k,s}^{H2R}+\mathop{B}\nolimits _{0}\mathop{N}\nolimits _{0} \right) }\;&{}k\in \mathop{\Omega }\nolimits _{2} \end{array}\right. } \end{aligned}$$

(1)

where $\mathop{d}\nolimits _{n}^{R}$ and $\mathop{d}\nolimits _{n}^{H2R}$ are pathloss from considered RRH and HPN to RUE n, respectively. $\mathop{h}\nolimits _{n,k,s}^{R}$ and $\mathop{h}\nolimits _{n,k,s}^{H2R}$ represent the channel gain from the RRH and HPN to RUE n on the k-th RB at s-th subchannel, respectively. Since main purpose of deploying HPN is to extend coverage area and to supply low-QoS required services, the allowed transmit power allocated to each RB in HPN is equal and obtained as $\mathop{p}\nolimits ^{H}={\frac{\mathop{P}\nolimits _{\max }^{H}}{H}}$, in which $\mathop{P}\nolimits _{\max }^{H}$ denotes the maximum allowable transmit power of HPN and H indicates the number of total shared subchannels. The estimated power spectrum density of both sum of noise and weak inter-RRH interference is shown by N₀ (in dBm/Hz).

The sum data rate of each RRH is calculated as

$$C({\mathbf{a}},{\mathbf{p}})=\sum \limits _{n=1}^{N+M}{\sum \limits _{k=1}^{K}{{a}_{n,k}}{B}_{0}}\sum \limits _{s=1}^{S}{{{\log }_{2}}(1+{\sigma }_{n,k,s}{p}_{n,k,s})}$$

(2)

where matrices ${\mathbf{a}} ={{\left[ \mathop{a}\nolimits _{n,k}\right] }_{(N+M)\times K}}$ And ${\mathbf{p}} ={{\left[ \mathop{p}\nolimits _{n,k,s}\right] }_{(N+M)\times K\times S}}$ indicate the feasible RB and power allocation policies, in which $\mathop{a}\nolimits _{n,k}$ can only be 1 and 0 showing whether k is allocated to user n. The significant effect of the different energy consumption models on EE metric, highlights the importance of defining model more meticulously. So based on [26] the total power consumption of RRH is expressed as

$${P}_{T}={\frac{1}{\eta }}\sum \limits _{n=1}^{N+M}{\sum \limits _{k=1}^{K}{{a}_{n,k}{\sum \limits _{s=1}^{S}{{p}_{n,k,s}}}_{{}}}}+{n}_{T}{P}_{dyn}+{P}_{sta}$$

(3)

in which $\eta$, $\mathop{P}\nolimits _{sta}$ and $\mathop{P}\nolimits _{dyn}$ are power amplifier efficiency, static and dynamic circuit power, respectively. Moreover, $\mathop{n}\nolimits _{T}$ stands for number of transmit antennas.

Since just low-QoS required users is considered for HPN, the SINR of HUE is expressed as

$${{\rho }_{t,k,s}}={{{P}^{H}}d_{t}^{H}h_{t,k,s}^{H}}/{(L\times \delta +{{B}_{0}}{{N}_{0}})}, \quad k\in {{\Omega }_{2}}$$

(4)

where $\mathop{d}\nolimits _{t}^{H}$ and $\mathop{h}\nolimits _{t,k,s}^{H}$ are representing path loss and channel gain of t-th user and $\delta$ is used to show the interference caused by each RRH, which is multiplied by the number of RRH, since we have dense RRH deployed network.

Similarly, the sum data rate and total power consumption of HPN are computed as

$$\begin{aligned} {{C}^{H}}({\mathbf{a}}^{H},{\mathbf{p}}^{H})=&\sum \limits _{t=1}^{T}{\sum \limits _{k={K}_{1}+1}^{{K}_{2}}{a_{t,k}^{H}{{B}_{0}}\sum \limits _{s=1}^{S}{{{\log }_{2}}(1+{{\rho }_{t,k,s}})}}} \\ P_{T}^{H}=&{\frac{P_{\max }^{H}}{\eta}}+{{n}_{T}}{{P}_{dyn}}+{{P}_{sta}} \end{aligned}$$

(5)

in which $t\in \left\{ 1,\ldots ,T \right\}$ denotes the HUE allocated to the shared RB and ${\mathbf{a}}^{H}$and ${\mathbf{p}}^{H}$ stand for RB and power allocation, respectively. $\eta$, $\mathop{P}\nolimits _{sta}$ and $\mathop{P}\nolimits _{dyn}$ indicate power amplifier efficiency and static and dynamic circuit power.

As the Main parameter discussed in this paper, EE, can be defined as

$$\varepsilon ={\frac{L\times C({\mathbf{a}},{\mathbf{p}})+{{C}^{H}}({\mathbf{a}^{H}},{\mathbf{p}^{H}})}{L\times {{P}_{T}}({\mathbf{a}},{\mathbf{p}})+\mathop{P}\nolimits _{T}^{H}({\mathbf{a}^{H}},{\mathbf{p}^{H}})}}$$

(6)

where L is the number of RRHs that in dense metropolitan area is a large number. If the value of L increases, such that the total amount of sum data rate and power consumption of all RRHs surpass the ${{C}^{H}}({\mathbf{a}^{H}},{\mathbf{p}^{H}})$ and $\mathop{P}\nolimits _{T}^{H}({\mathbf{a}^{H}},{\mathbf{p}^{H}})$, then these parameters can be neglected and the overall EE can be shrunk to

$$\varepsilon \approx {\frac{L\times C({\mathbf{a}},{\mathbf{p}})}{L\times {{P}_{T}}({\mathbf{a}},{\mathbf{p}})}}={\frac{C({\mathbf{a}},{\mathbf{p}})}{{{P}_{T}}({\mathbf{a}},{\mathbf{p}})}}$$

(7)

so (7) is a simple form that should be solved only for one RRH.

Problem 1

The EE maximization of downlink HCRAN is formulated as:

$$\underset{\left\{ \textbf{a},\textbf{p} \right\}}{\mathop{\max }}\,\frac{C(\textbf{a},\textbf{p})}{{{P}_{T}}(\textbf{a},\textbf{p})}=\frac{\sum\limits_{n=1}^{N+M}{\sum\limits_{k=1}^{K}{\mathop{a}_{n,k}\mathop{B}_{0}\mathop{\sum\limits_{s=1}^{S}{\mathop{\log }_{2}}}_{{}}\left( 1+\mathop{\sigma }_{n,k,s}\mathop{p}_{n,k,s} \right)}}}{\frac{1}{\eta }\sum\limits_{n=1}^{N+M}{\sum\limits_{k=1}^{K}{\mathop{a}_{n,k}\mathop{\sum\limits_{s=1}^{S}{\mathop{p}_{n,k,s}}}_{{}}+\mathop{n}_{T}\mathop{P}_{dyn}+\mathop{P}_{sta}}}}$$

(8)

$$s.t. \ {C}_{1}:\sum \limits _{n=1}^{N+M}{{a}_{n,k}}=1,\quad {a}_{n,k}\in \left\{ 0,1 \right\} ,\quad \forall k$$

(9)

$${C}_{2}:\sum \limits _{n=N+1}^{N+M}{{a}_{n,k}{\sum \limits _{s=1}^{S}{{{p}_{n,k,s}d}_{n}^{R2H}{h}_{n,k,s}^{R2H}}}_{{}}\le {\delta }, \quad k\in {\Omega }_{2}}$$

(10)

$${C}_{3}:\sum \limits _{n=1}^{N+M}{\sum \limits _{k=1}^{K}{{a}_{n,k}{\sum \limits _{s=1}^{S}{{p}_{n,k,s}}}_{{}}\le {P}_{\max }^{R},\quad {p}_{n,k,s}\ge 0, \; \forall k,\;\forall n}}$$

(11)

$${C}_{4}:\sum \limits _{k=1}^{K}{{c}_{n,k}\ge {\eta }_{1}},\quad 1\le n\le N$$

(12)

$${C}_{5}:\sum \limits _{k=1}^{K}{{c}_{n,k}\ge {\eta }_{2}},\quad N+1\le n\le N+M$$

(13)

where constraint $\mathop{C}\nolimits _{1}$ specifies that each RB can be occupied only by one user at the same time, and also none of RBs should be left empty behind. Even though, our maximization problem was dwindled to consider only RRHs, we need a constraint which assure us about the QoS achieved by HUEs. For this purpose, constraint $\mathop{C}\nolimits _{2}$ enforces allocated powers to RUEs, to be below the threshold, $\delta$. Constraint $\mathop{C}\nolimits _{3}$ puts the limitation of the total value of power which can be allocated by each RRHs. Finally, constraint $\mathop{C}\nolimits _{4}$ and $\mathop{C}\nolimits _{5}$ are responsible for making sure each type of users attain at least their minimum required data rates.

Problem 2

In Problem 1 our objective function is based on capacity, which is a theoretical upper-bound for data rate. Since we intend to introduce a more practical scenario, we reformulate above problem by constituting data rate as objective function,

$$\begin{aligned}&\underset{\left\{ \textbf{a},\textbf{p} \right\} }{\mathop{\max }}\,{\frac{R({\mathbf{a}} ,{\mathbf{p}} )}{{P}_{T}({\mathbf{a}} ,{\mathbf{p}} )}}={\frac{\sum \nolimits _{n=1}^{N+M}{\sum \nolimits _{k=1}^{K}{{{a}_{n,k}}{{B}_{0}}\sum \nolimits _{s=1}^{S}{k({{\gamma }_{s}})}}}}{\frac{1}{\eta }\sum \nolimits _{n=1}^{N+M}{\sum \nolimits _{k=1}^{K}{{{a}_{n,k}}\sum \nolimits _{s=1}^{S}{{{p}_{n,k,s}}}+{{n}_{T}}{{P}_{dyn}}+{{P}_{sta}}}}}} \\&{\text{s.t.}}\, \mathop{C}\nolimits _{1},\mathop{C}\nolimits _{2},\mathop{C}\nolimits _{3},\mathop{C}\nolimits _{4},\mathop{C}\nolimits _{5} \end{aligned}$$

(14)

in which

$$\begin{aligned}&k={\log }_{2}(1+{k({{\gamma }_{s}})}) \\&K\triangleq {\frac{1.5}{\ln (0.2/{\textit{BER}})}} \end{aligned}$$

(15)

where ${\gamma }_{s}$ stands for received SINR [27].

3 Solution of the Optimization Problem

The objective functions in (8) and (14) are classified as nonlinear fractional programming which results in a non-convex problem. Since there is no standard solution for solving non-convex problem, our first attempt would be transforming objective function to a more simple form using nonlinear fractional programming. Since both proposed optimization problems can be solved similarly, we solve the first problem and the second one can be solved the same way.

3.1 Transformation of the Objective Function

For the sake of notation simplicity, we define ${\mathbb{F}}$ as the set of feasible solution of optimization problem in (8) and $\left\{ a,p \right\} \in {\mathbb{F}}$. Without loss of generality, we define the optimal value of nonnegative variable $\varepsilon$ as

$${\varepsilon }^{*}={\frac{C\left( \mathbf{a }^{*},\mathbf{p }^{*} \right) }{{P}_{T}\left( \mathbf{a }^{*},\mathbf{p }^{*} \right)}}=\underset{\left\{ a,p \right\} }{\mathop{\max }}\,{\frac{C\left( \mathbf{a }^{{}},\mathbf{p }^{{}} \right) }{{P}_{T}\left( \mathbf{a }^{{}},\mathbf{p }^{{}} \right)}}$$

(16)

The maximum EE, $\mathop{\varepsilon }\nolimits ^{*}$, is achieved if and only if

$$\underset{\left\{ {\mathbf{a}} ,{\mathbf{p}} \right\} }{{\max }}\,C\left( \mathbf{a }^{{}},\mathbf{p }^{{}} \right) -{\varepsilon }^{*}{P}_{T}\left( \mathbf{a }^{{}},\mathbf{p }^{{}} \right) =C\left( \mathbf{a }^{*},\mathbf{p }^{*} \right) -{\varepsilon }^{*}{P}_{T}\left( \mathbf{a }^{*},\mathbf{p }^{*} \right) =0$$

(17)

in which $\left\{ a,p \right\}$ is any feasible solution of proposed problem to satisfy constraints $\mathop{C}\nolimits _{1}-\mathop{C}\nolimits _{5}$ [28].

To prove, we must consider sufficient and necessary conditions. By defining $\mathbf{a }^{*}$ and $\mathbf{p }^{*}$ as the optimal RB and power allocation policies, ${\varepsilon }^{*}$ holds,

$${{\varepsilon }^{*}}={\frac{C({\mathbf{a }^{*}},{\mathbf{p }^{*}})}{{P}_{T}({\mathbf{a }^{*}},{\mathbf{p }^{*}})}}\ge {\frac{C({\mathbf{a}} ,{\mathbf{p}} )}{{P}_{T}({\mathbf{a}} ,{\mathbf{p}} )}}$$

(18)

so we can derive the following formulas:

$$\begin{aligned} {\left\{ \begin{array}{l} C({\mathbf{a}} ,{\mathbf{p}} )-{{\varepsilon }^{*}}{P}_{T}({\mathbf{a}} ,{\mathbf{p}} )\le 0 \\ C({\mathbf{a}^{*}},{\mathbf{p}^{*}})-{{\varepsilon}^{*}}{P}_{T}({\mathbf{a}^{*}},{\mathbf{p}^{*}})=0 \end{array}\right. } \end{aligned}$$

(19)

we can conclude that $\underset{\left\{ {\mathbf{a}} ,{\mathbf{p}} \right\} }{{\max }}\,C\left( \mathbf{a},\mathbf{p} \right) -{\varepsilon }^{*}{P}_{T}\left( \mathbf{a},\mathbf{p} \right) =0$ which is attainable for optimal resource allocation policies.

To prove necessary condition, $\mathbf{a ^{\prime *}}$ and $\mathbf{p ^{\prime *}}$ are assumed as optimal policies for transformed objective function so we have $C\left( \mathbf{a ^{\prime *}}, \mathbf{p ^{\prime *}} \right) -{\varepsilon }^{*}{P}_{T}\left( \mathbf{a ^{\prime *}}, \mathbf{p ^{\prime *}} \right) =0$. For any feasible a and p,

$$C({\mathbf{a}} ,{\mathbf{p}} )-{{\varepsilon }^{*}}{P}_{T}({\mathbf{a}} ,{\mathbf{p}} )\le C(\mathbf{a ^{\prime *}}, \mathbf{p ^{\prime *}})-{{\varepsilon }^{*}}{P}_{T}(\mathbf{a ^{\prime *}},\mathbf{p ^{\prime *}})=0$$

(20)

The above inequality can be derived as

$${\frac{C({\mathbf{a}} ,{\mathbf{p}} )}{{P}_{T}({\mathbf{a}} ,{\mathbf{p}} )}}\le {{\varepsilon }^{*}},\quad {\frac{C(\mathbf{a ^{\prime *}},\mathbf{p ^{\prime *}})}{{P}_{T}(\mathbf{a ^{\prime *}},\mathbf{p ^{\prime *}})}}={{\varepsilon }^{*}}$$

(21)

Therefore, the optimal resource allocation policies $\mathbf{a ^{\prime *}}$ and $\mathbf{p ^{\prime *}}$ for the transformed objective function are also the optimal resource allocation policies for the original objective function.

As a result, based on aforementioned proof for any optimization problem with an objective function in fractional form, there is an equivalent optimization problem with an objective function in subtractive form, which leads to the same solution. Hence, we can concentrate on the equivalent problem in the rest of the paper.

3.2 Iterative Algorithm For EE

By considering theorem which has been proved in previous subsection, the equivalent problem can be reformulated as

$$\begin{aligned}&\underset{\left\{ {\mathbf{a}} ,{\mathbf{p}} \right\} }{{\max }}\,C\left( \mathbf{a }^{{}},\mathbf{p }^{{}} \right) -{\varepsilon }^{*}{P}_{T}\left( \mathbf{a }^{{}},\mathbf{p }^{{}} \right) \\&\hbox {s.t.}\, \mathop{C}\nolimits _{1},\mathop{C}\nolimits _{2},\mathop{C}\nolimits _{3},\mathop{C}\nolimits _{4},\mathop{C}\nolimits _{5} \end{aligned}$$

(22)

hence we should find optimal value of $\varepsilon$. Since $\mathop{\varepsilon }\nolimits ^{*}$ cannot be obtained directly, an iterative algorithm (known as the Dinkelbach method [29]) is proposed, in which, the obtained solution ensures the condition stated above. The proposed iterative method is summarized in Algorithm 1 and the convergence to the optimal solution is guaranteed if we are able to solve the inner problem in (22).

As shown in Algorithm 1 in each iteration of the outer loop we solve the optimization problem for a given $\varepsilon$. Since $\varepsilon$ increases in each loop, the optimal solution can be obtained. To achieve this, two constraints should be taken under consideration. First, by defining $F\left( \varepsilon \right) ={\underset{\left\{ {\mathbf{a}} ,{\mathbf{p}} \right\} }{{\max }}}\,C\left( \mathbf{a},\mathbf{p} \right) -{\varepsilon }^{{}}P\left( \mathbf{a},\mathbf{p} \right)$ one should prove that for all feasible a, p and $\varepsilon$, $F(\varepsilon )$ is a strictly monotonic decreasing function in $\varepsilon$ and $F(\varepsilon )\ge 0$. Moreover, convergence of Algorithm 1 to the global optimal solution has to be proved. Both constraints have been addressed in [12].

Due to integer nature of a, $F(\varepsilon )$ becomes a continuous but nondifferentiable function of $\varepsilon$. By updating $\mathop{\varepsilon }\nolimits ^{(i+1)}$ in each iteration, using $C(\mathbf{a }^{\left( i \right) },\mathbf{p }^{\left( i \right) })$ and $P(\mathbf{a }^{\left( i \right) },\mathbf{p }^{\left( i \right) })$ obtained in the last iteration, the optimal value is attainable.

3.3 Resource Allocation Optimization in the Inner Loop

$$\begin{aligned}&\underset{\left\{ {\mathbf{a}} ,{\mathbf{p}} \right\} }{{\max }}\,C\left( \mathbf{a }^{{}},\mathbf{p }^{{}} \right) -{\varepsilon }^{\left( i \right) }{P}_{T}\left( \mathbf{a }^{{}},\mathbf{p }^{{}} \right) \\&\hbox {s.t.}\, \mathop{C}\nolimits _{1},\mathop{C}\nolimits _{2},\mathop{C}\nolimits _{3},\mathop{C}\nolimits _{4},\mathop{C}\nolimits _{5} \end{aligned}$$

(23)

Since the problem is non-convex, we cannot use the convex optimization methods to solve that. By defining the dual of mentioned problem and determining whether the duality gap between main problem and its dual is negligible, we may be able to solve our optimization problem utilizing its convex dual. We show that for sufficiently large number of RBs, the duality gap between (23) and its dual problem is nearly zero.

For the given RB allocation scheme, (23) can be expressed as

$$\begin{aligned}&{{\Gamma }^{*}}=\max \sum \limits _{k=1}^{K}{{{d}_{k}}({{p}_{n,k,s}})} \\&\hbox {s.t.} \sum \limits _{k=1}^{K}{{{q}_{k}}({{p}_{n,k,s}})} \end{aligned}$$

(24)

where

$${{d}_{k}}({{p}_{n,k,s}})=\sum \limits _{n=1}^{N+M}{{{a}_{n,k}}{{B}_{0}}}\sum \limits _{s=1}^{S}{{{\log }_{2}}}(1+{{\sigma }_{n,k,s}}{{p}_{n,k,s}})-\sum \limits _{n=1}^{N+M}{{{\varepsilon }^{(i)}}{\frac{1}{\eta }}}{{a}_{n,k}}\sum \limits _{s=1}^{S}{{{p}_{n,k,s}}}-{\frac{{{\varepsilon }^{*}}}{K}}({{n}_{T}}{{P}_{dyn}}+{{P}_{sta}})$$

(25)

in which ${{p}_{n,k,s}}\in {{\mathbb{C}}^{N}}$, ${{d}_{k}}(.):{{\mathbb{C}}^{N}}\rightarrow {\mathbb{R}}$ and $\sum \nolimits _{k=1}^{K}{{{q}_{k}}({{p}_{n,k,s}})}$ expresses constraints as the function of ${{p}_{n,k}}$. ${{q}_{k}}(.):{{\mathbb{C}}^{N}}\rightarrow {{\mathbb{R}}^{L}}$ and L represents number of constraints. To prove the duality gap between (23) and the optimal value of its dual ${{{\mathrm O}}^{*}}$ is zero, a perturbian function is defined as

$$\begin{aligned}&{v({\mathbf{Q}})}=\max \sum \limits _{k=1}^{K}{{{d}_{k}}({{p}_{n,k,s}})} \\&\hbox {s.t.}\, \sum \limits _{k=1}^{K}{{{q}_{k}}({{p}_{n,k,s}})}\le {\mathbf{Q}} \end{aligned}$$

(26)

where ${\mathbf{Q}} \in {{\mathbb{R}}^{L}}$ is the perturbation vector.

If $V({\mathbf{Q}} )$ is a concave function of Q, the duality gap between ${{\Gamma }^{*}}$ and ${{{\mathrm O}}^{*}}$ is zero [30]. So in order to prove concavity of $V({\mathbf{Q}} )$ a time-sharing condition should be demonstrated.

3.3.1 Time-Sharing Condition

If $p_{n,k,s}^{1*}$ and $p_{n,k,s}^{2*}$ be the optimal solution of (26) to $V({\mathbf{Q }_{1}})$ and $V({\mathbf{Q }_{2}})$ respectively, (24) satisfies the time-sharing condition if for any $V({\mathbf{Q }_{1}})$ and $V({\mathbf{Q }_{2}})$, there always exists $p_{n,k,s}^{3*}$ for which

$$\sum \limits _{k=1}^{K}{{q}_{k}(p_{n,k,s}^{3})}\le \alpha {\mathbf{Q}}_{1}+(1-\alpha ){\mathbf{Q}}_{2}$$

(27)

$$\sum \limits _{k=1}^{K}{{{d}_{k}}}\left( p_{n,k,s}^{3}\right)\ge \alpha {{d}_{k}}\left( p_{n,k,s}^{1*}\right) +(1-\alpha ){{d}_{k}}\left( p_{n,k,s}^{2*}\right)$$

(28)

where $0\le \alpha \le 1$.

It has been proved in [31] that the time-sharing condition is always satisfied for the multicarrier system when the number of carriers goes to infinity, such as the OFDMA-based HCRAN in this paper. Hence $V({\mathbf{Q}} )$ is a concave function of Q and the duality gap between ${{\Gamma }^{*}}$ and ${{{\mathrm O}}^{*}}$ is zero.

3.3.2 Lagrange Dual Decomposition Method

In this subsection we solve the resource allocation optimization problem by defining its dual for a given value of $\varepsilon$. For this purpose we need the Lagrangian function of the primal problem which is given by

$$\begin{aligned}&\underset{{}}{\mathop{D\left( \alpha ,\beta ,\mu \right) =\underset{\left\{ \textbf{a},\textbf{p} \right\} }{\mathop{\max }}\,}}\,L\left( \textbf{a},\textbf{p},\alpha ,\beta ,\mu \right) = \\&\quad \underset{\{a,p\}}{\mathop{\max }}\,\left\{ \sum \limits _{n=1}^{N+M}{\sum \limits _{k=1}^{K}{{a}_{n,k}{B}_{0}{\sum \limits _{s=1}^{S}{{\log }_{2}\left( 1+{\sigma }_{n,k}{p}_{n,k,s}\right) }}_{{}}}} -{\varepsilon }^{(i)}\left( {\frac{1}{\eta }}\sum \limits _{n=1}^{N+M}{\sum \limits _{k=1}^{K}{{a}_{n,k}{\sum \limits _{s=1}^{S}{{p}_{n,k,s}}}_{{}}+{n}_{T}{P}_{dyn}+{P}_{sta}}}\right) \right. \\&\quad \left. +\sum \limits _{n=1}^{N}{{\alpha }_{n}\left( \sum \limits _{k=1}^{K}{{c}_{n,k}-{\eta }_{1}}\right) }+\sum \limits _{n=N+1}^{N+M}{{\alpha }_{n}}\left( \sum \limits _{k=1}^{K}{{c}_{n,k}-{\eta }_{2}}\right) +\sum \limits _{k=1}^{K}\left( \beta _{k}\left( {\delta }-\sum \limits _{n=N+1}^{N+M}{{a}_{n,k}{\sum \limits _{s=1}^ {S}{{p}_{n,k,s}{d}_{k}^{R2H}{h}_{n,k,s}^{R2H}}}_{{}}}\right) \right. \right. \\&\quad \left. \left. +\mu \left( {P}_{\max }^{R}-\sum \limits _{n=1}^{N+M}{\sum \limits _{k=1}^{K}{{a}_{n,k}\sum \limits _{s=1}^{S}{{p}_{n,k,s}}}}\right) \right) \right\} \end{aligned}$$

(29)

and the dual problem may be written as

$$\begin{aligned}&\underset{\left\{ \alpha ,\beta ,\mu \right\} }{{\min }}\,D\left( \alpha ,\beta ,\mu \right) \\&\hbox {s.t.} \, \alpha \ge 0,\beta \ge 0,\mu \ge 0 \end{aligned}$$

(30)

which is solved using the dual decomposition approach. In order to use the dual decomposition method to solve the dual problem, we decompose the problem into K independent problems as

$$g(\alpha ,\beta ,\mu )=\sum \limits _{k=1}^{K}{{g}_{k}(\alpha ,\beta ,\mu )-{\varepsilon }^{(i)}\left( {n}_{T}{P}_{dyn}+{P}_{sta} \right) } -\sum \limits _{n=1}^{N}{{\alpha }_{n}{\eta }_{1}-\sum \limits _{n=N+1}^{N+M}{{\alpha }_{n}{\eta }_{2}+\sum \limits _{k=1}^{K}{\underset{{}}{{\beta }_{n}}\,}}}{\delta }_{{}}+\mu {P}_{\max }^{R}$$

(31)

where

$$\begin{aligned}{g}_{k}\left( \alpha ,\beta ,\mu \right) &= \underset{\left\{ \textbf{a},\textbf{p} \right\} }{{\max }}\,\left\{ \sum \limits _{n=1}^{N+M}\sum \limits _{s=1}^{S}\left[ \left( 1+{\alpha }_{n} \right) {a}_{n,k}{B}_{0}{\log }_{2}\left( 1+{\sigma }_{n,k}{p}_{n,k,s} \right) \right. \right. \\&\quad \left. \left. -{\varepsilon }^{\left( i \right) }{\frac{1}{\eta }}{a}_{n,k}{p}_{n,k,s}-{\beta }_{k}{a}_{n,k}{p}_{n,k,s}{d}_{k}^{R2H}{h}_{n,k,s}^{R2H}-\mu {a}_{n,k}{p}_{n,k,s}\right] \right\} \end{aligned}$$

(32)

Since the problem is now in a standard concave form, the KKT conditions which are first order necessary and sufficient condition for optimality, may be used in order to find the optimal solution. The optimal power may be readily obtained as

$${p}_{n,k,s}^{*}={\left[ {w}_{n,k,s}^{*}-{\frac{1}{{\sigma }_{n,k,s}}} \right] }^{+}$$

(33)

where $\mathop{\left[ \cdot \right] }\nolimits ^{+}$ denotes $\max \left( 0,\cdot \right)$ and the optimal waterfilling level is expressed as

$${w}_{n,k,s}^{*}={\frac{\mathop{B}\nolimits _{0}\left( 1+\mathop{\alpha }\nolimits _{n} \right) }{\ln 2\left( \mathop{\varepsilon }\nolimits ^{(i)}\mathop{\frac{1}{\eta }}_{{}}+\mathop{\beta }\nolimits _{k}\mathop{d}\nolimits _{k}^{R2H}\mathop{h}\nolimits _{n,k,s}^{R2H}+\mu \right)} }$$

(34)

Having calculated the optimal power, the optimal subcarrier allocation may be derived using the first order derivation as follows

$$\begin{aligned} {a}_{n,k}^{*}=\left\{ \begin{array}{ll} 1,& n= \underset{1\le n\le N+M}{{\arg\max }}\,{\sum \limits _{s=1}^{S}{{H}_{n,k,s}}}/{}_{S} \\ 0,& otherwise \\ \end{array} \right. \end{aligned}$$

(35)

where

$${H}_{n,k,s}={\left[ \left( 1+{\alpha }_{n} \right) {\log }_{2}\left( {w}_{n,k,s}^{*}{\sigma }_{n,k,s} \right) \right] }^{+} -{\frac{\left( 1+{\alpha }_{n} \right) }{\ln 2}}{\left[ 1-{\frac{1}{{w}_{n,k,s}^{*}{\sigma }_{n,k,s}}} \right] }^{+}$$

(36)

Thus constraints $\mathop{C}\nolimits _{1} - \mathop{C}\nolimits _{5}$ are satisfied and the optimal primal variables are obtained for given $\alpha$, $\beta$ and $\mu$.

Sub-gradient method can be used for updating the dual variables $\alpha ,\beta$ and $\mu$, in the subgradient direction. The subgradient update equations are given by

$$\begin{aligned} {\alpha }_{n}^{(m+1)}= & {} {\left[ {\alpha }_{n}^{\left( m \right) }-{\xi }_{1}^{\left( m+1 \right) }\times \left( \sum \limits _{k=1}^{K}{{{C}_{n,k}^{\left( m \right) }}_{{}}-{\eta }_{1}} \right) \right] }^{+}, \quad 1\le n\le N \\ {\alpha }_{n}^{(m+1)}= & {} {\left[ {\alpha }_{n}^{\left( m \right) }-{\xi }_{1}^{\left( m+1 \right) }\times \left( \sum \limits _{k=1}^{K}{{{C}_{n,k}^{\left( m \right) }}_{{}}-{\eta }_{2}} \right) \right] }^{+}, \quad N+1\le n\le N+M \end{aligned}$$

(37)

$$\begin{aligned} {\beta }_{n}^{(m+1)}= & {} {\left[ {\beta }_{n}^{\left( m \right) }-{\xi }_{2}^{\left( m+1 \right) }\times \left( {\delta }_{0}-\sum \limits _{n=1+N}^{N+M}{{a}_{n,k}^{\left( m \right) }\sum \limits _{s=1}^{S}{{p}_{n,k,s}^{\left( m \right) }}} \right. \right. {{\left. \left. {d}_{k}^{R2H}{h}_{n,k,s}^{R2H} \right) \right] }}^{+}}\quad \forall k\in {\Omega }_{2} \\ {\beta }_{n}^{(m+1)}= & {} 0\quad \forall k\in {\Omega }_{1}\end{aligned}$$

(38)

$${\mu }_{{}}^{(m+1)}= {\left[ {\mu }_{{}}^{\left( m \right) }-{\xi }_{3}^{\left( m+1 \right) }\times \left( {P}_{\max }^{R}-\sum \limits _{n=1}^{N+M}{\sum \limits _{k=1}^{K}{{a}_{n,k}^{\left( m \right) }{\sum \limits _{s=1}^{S}{{p}_{n,k,s}^{\left( m \right) }}}_{{}}}} \right) \right] }^{+}$$

(39)

where i is the iteration number and $\mathop{\xi }\nolimits _{1}^{\left( m+1 \right) }$, $\mathop{\xi }\nolimits _{2}^{\left( m+1 \right) }$ and $\mathop{\xi }\nolimits _{3}^{\left( m+1 \right) }$ are positive step sizes. $\mathop{a}\nolimits _{n,k}^{\left( m \right) }$ and $\mathop{p}\nolimits _{n,k,s}^{\left( m \right) }$ are the RB and power allocation policies derived in m-th iteration, respectively. It is proved that the subgradient method is guaranteed to converge to the optimal Lagrange multipliers, as long as step sizes are chosen sufficiently small.

According to prior explanation, this algorithm is designed for dense areas in which large number of RRHs are deployed. Due to recent researches, some methods are proposed to put light loaded RRHs into sleep mode to enhance EE. In (7) we have neglected the effect of HPN, but if we put some RRHs to sleep mode, the capacity and power consumption of HPN should be taken under consideration. Here we propose two simple but efficient resource allocation algorithms for HPN in which the total EE would be optimal.

3.3.3 Algorithm GRA (General Resource Allocation)

The SINR of user t in s-th subchannel of k-th RB is expressed as

$${\rho }_{t,k,s}={{P}^{H}d}_{t}^{H}{h}_{t,k,s}^{H}/{\left( {L\times {\delta }_{{}}{+B}_{0}{N}_{0}}_{{}} \right) },\quad k\in {\Omega }_{2}$$

(40)

in which, $\delta$, has been introduced as threshold in order to manage interference caused by RRHs so received information can be decoded accurately.

The power is assumed to be fixed for each user and RB is assigned to user with the highest $\sum\limits_{s=1}^{S}{{}^{{{\rho }_{t,k,s}}}/{}_{S}}$.

3.3.4 Algorithm CRA (Cloud-Based Resource Allocation)

Since there is an interface between cloud and HPN, we have access to CSI of all RRHs, so can achieve favorable information of RRHs and define more accurate $\rho$ for HPN. The enhanced definition is described as

$${\rho }_{t,k,s}= {\frac{\mathop{\mathop{P}\nolimits ^{H}d}\nolimits _{t}^{H}\mathop{h}\nolimits _{t,k,s}^{H}}{\mathop{\mathop{\sum \nolimits _{n=N+1}^{N+M}{\mathop{\mathop{a}\nolimits _{n,k}\sum \nolimits _{s=1}^{S}{\mathop{p}\nolimits _{n,k,s}}\mathop{d}\nolimits _{n}^{R2H}\mathop{h}\nolimits _{n,k,s}^{R2H}}_{{}}}}_{{}}\mathop{+\,B}\nolimits _{0}\mathop{N}\nolimits _{0}}_{{}}}}, \quad k\in {\Omega }_{2}$$

(41)

where $\mathop{I=\sum \nolimits _{n=N+1}^{N+M}{\mathop{\mathop{a}\nolimits _{n,k}\sum \nolimits _{s=1}^{S}{\mathop{p}\nolimits _{n,k,s}}\mathop{d}\nolimits _{n}^{R2H}\mathop{h}\nolimits _{n,k,s}^{R2H}}_{{}}}}_{{}}$ is the precise interference caused by RRHs, and channels are allocated as described for algorithm GRA. By utilizing proposed algorithm, EE increases noticeably in compare with algorithm GRA which will be shown through simulation results.

4 Simulation and Numerical Results

In this section the EE performance of the proposed algorithms are evaluated by simulation. The two-tier heterogeneous network is simulated by assuming 1 HPN and L RRHs in which N high-QoS required RUEs and M low-QoS required RUEs are served. The maximum total number of RUEs is 25, however the ratio between high-QoS required RUEs and total number of RUEs is kept constant and is equal to ${\frac{1}{3}}$. The high and low-rate constrained QoS requirement are expressed as $\mathop{\eta }\nolimits _{1}=128$ kbit/s and $\mathop{\eta }\nolimits _{2}=64$ kbit/s, respectively. The path-loss model for RRH-to-RUE is represented as $31.5+40.0\times \mathop{\log }\nolimits _{10}(d)$, where d is the distance in meters and is given as $\mathop{d}\nolimits _{n}^{R}=50$ m for $1\le n\le N$ and $\mathop{d}\nolimits _{n}^{R}=75$ m in the case of $N+1\le n\le N+M$. Path-loss for the HPN-to-RUE, RRH-to-HUE and HPN-to-HUE is modeled as $31.5+35.0\times \mathop{\log }\nolimits _{10}(d)$, in which $\mathop{d}\nolimits _{n}^{H2R}=450$ m for $1\le n\le N$, $\mathop{d}\nolimits _{n}^{H2R}=375$ m in the case of $N+1\le n\le N+M$ and $\mathop{d}\nolimits _{n}^{R2H}=125$ m and $\mathop{d}\nolimits _{t}^{H}=325$ m.

The system bandwidth is $B=5$ MHz which is shared among $K=25$ RBs. Since our scenario is based on MIMO and downlink transmission is considered, the number of users antennas cannot be more than 2 due to 5G standards, hence we assume $2\times 2$ and $4\times 2$ MIMO structures.

Number of simulation snapshots is set at 1000. In each snapshot, the small scale fading coefficients are generated as i.i.d Rayleigh random variables with unit variance. We assume the static and dynamic power consumption of HPN and the PA efficiency to be $\mathop{P}\nolimits _{sta}=10$ W, $\mathop{P}\nolimits _{dyn}=18$ W and ${\eta }=4$, respectively. For RRHs these parameters are assumed to be $\mathop{P}\nolimits _{sta}=0.1$ W, $\mathop{P}\nolimits _{dyn}=0.2$ W and ${\eta }=2$, respectively.

4.1 Performance Comparision

To evaluate the EE performance of the proposed algorithms, a scenario including 16 RRH is considered for N = 3 and M = 6, where two algorithms are presented as baselines. The first baseline algorithm, called fixed power allocation, sets same and fixed transmit power to different RBs and the second baseline algorithm is denoted as sequential RB allocation, in which the RB is allocated to RUEs sequentially. The EE is depicted under varied number of iteration and is shown in (bits/J) scale. According to Fig. 4, even though computing complexity is increased in our proposed algorithm, convergence speed is acceptable compared with other two algorithms. Furthermore, as expected, EE has increased significantly for both capacity and rate based proposed algorithms and our proposed algorithms surpass two baseline algorithms. To evaluate EE performance further, another scenario including 1 HPN and 8 RRHs is considered. The EE, in (bps/Hz/W) scale, is depicted according to varied number of high QoS-required RUEs, in which the ratio between high and low QoS-required users, keeps constant to ${\frac{1}{2}}$. An algorithm proposed in [12], is assumed as baseline, in which a jointly power and RB allocation algorithm is investigated for single antenna scenario.

Fig. 4

Performance comparisons among proposed algorithms and two baseline algorithms

In Fig. 5, performances are compared among proposed algorithms and algorithm in [12]. For simplicity, combination of algorighm 1 and GRA is called CGRA and combination of algorighm 1 and CRA is called CCRA. As expected, since CGRA and CCRA are computing capacity of system, are upper-band of RGRA (combination of algorighm 2 and GRA) and RCRA (combination of algorighm 2 and CRA). Nonetheless, algorithm RCRA and RGRA offer valuable information for practical deployment. Comparison between algorithm CGRA and CCRA, shows that due to utilizing features offered by cloud, algorithm CCRA has better EE performance in compare with CGRA. In addition, since algorithm CGRA is using MIMO structure it outperforms algorithm proposed in [12] in EE enhancement and shows the benefit offered by MIMO structure.

Fig. 5

Performance comparisons among proposed algorithms and algorithm in [12]

4.2 Convergence of the Proposed Iterative Algorithm

A cell with 16 RRHs is assumed, in which N = 2 and M = 4 are stand for high and low QoS-required RUEs. Figure 6 illustrates EE performance per user of proposed algorithms under different number of iteration. As it is obvious, both algorithms converges within 3 iteration number. The parameter which is taken under consideration in Fig. 6 is maximum allowed inter-tier interference, $\delta$, which is calculated based on SINR threshold of HPN through (4). Two different values are considered for ${{\eta }_{HPN}}$ to make sure messages received by HUE can be decoded correctly and even can forbid RRHs to allocate specific RBs to its user. As expected, by increasing ${{\eta }_{HPN}}$ (from 0 to 20 dB), we enforce $\delta$ to decline. As a result, less power can be allocated to each RUEs that leads to reduction in EE.

Fig. 6

Convergence of iterative algorithm based on Dinkelbach’s method

4.3 EE Performance of the Proposed Solution

In order to evaluate the EE performance of the proposed algorithms, some key parameters need to be taken under consideration. Since our scenario is based on MIMO, the number of antennas influence EE. Moreover, by considering constraint ${{C}_{1}}-{{C}_{5}}$ in optimization problem, $\delta$ and ratio of allocated RBs to each type of users, are another key factors which their impact need to be evaluated, that the impact of $\delta$ is investigated in Fig. 6. Impact of deploying adaptive modulation for practical deployment, can be supposed as another key parameter which need to be investigated.

The main purpose of Fig. 7 is to compare performance of AM with the case in which only BPSK is used. BPSK, 4QAM, 16QAM and 64QAM are assumed as possible constellation sizes which are assigned to each channel for desirable BER. By considering $BER={{10}^{-3}}$ and for different number of high-QoS required RUEs, EE performance of all algorithms are depicted in Fig. 7. Even though algorithm CCRA shows better EE performance in Fig. 5, with deploying AM and by increasing the number of RUEs, algorithm RCRA outperforms other algorithms. To justify, since SE is determined as the objective function in algorithm RCRA, power is allocated more efficiently, so less power is wasted and better EE performances is achieved.

Fig. 7

EE performance comparisons between adaptive modulated and non-adaptive form of proposed algorithms

In Fig. 8 the number of transmit antenna is chosen as the effective parameter. The number of RRHs is set to 8 and ${{\eta }_{HUE}}$ is assumed to be 0 dB. We consider two sets of antennas as $2\times 2$ and $4\times 2$. Due to simulation result, which is plotted for AM modulated form of algorithms, by increasing the number of antennas to $2\times 2$, EE increases but by further increase EE shrinks. To clarify, we can claim that by taking more antennas under deployment, SE increases but regarding to definition of total energy, energy consumption increases significantly. Since EE depends both on data rate and power consumption, calculating the optimal number of antenna and taking advantage of antenna selection methods can improve energy efficiency, that numerous investigations have been done in this area [32].

Fig. 8

Impact of number of transmitting antenna on EE performance of system

EE performance for different ratio of allocated RBs to each type of users is illustrated in Fig. 9. As aforementioned, low-QoS required RUEs share their RB with HUEs, so due to inter-tier interference their SINR is less than high QoS required RUEs. RUEs which have their own share of RBs, may adopt higher constellation sizes which result in higher data rates. Hence by allocating more RBs to high QoS-required RUEs, data rate increases significantly which leads to increase in EE. However, by considering fairness and seamless coverage goal, we cannot just focus on EE enhancement and other parameters should be taken into account. Determining the optimal ratio is an open issue for future work.

Fig. 9

Evaluation of EE performance for different ratio of $\Omega _{1}$ to $\Omega _{T}$

5 Conclusion

In this paper, a MIMO–OFDM HCRAN scenario is investigated from EE point of view. By considering interference mitigation and QoS constraints, nonconvex optimization problems with the aim of jointly allocating power and assigning channel are proposed and solved by Lagrange dual decomposition method. Four algorithms are proposed and their performance from EE aspect are analyzed, in which the adaptive modulated form of RCRA outperforms other 3 algorithms. According to simulation results, combination of HCRAN structure, MIMO and AM improve EE significantly and due to its practicality, is a cardinal candidate to be used in 5G deployment. To maximize EE further, massive MIMO deployment and optimal antenna selection algorithm should be taken under consideration for future works.